Mechanical constraints imposed by 3D cellular geometry and arrangement modulate growth patterns in the Arabidopsis embryo

Significance

During plant growth and development, the gene expression that promotes growth does not always spatially correlate with observed growth. This suggests that additional factors guide morphogenesis. Here we propose that mechanical cues play an instructive role and test our hypothesis by using a full 3D cellular-level finite-element simulation model of the mature Arabidopsis embryo. We demonstrate that the size, shape, and arrangement of plant cells all influence their ability to grow in response to growth-promoting gene expression. These principles were sufficient to explain the displacement of growth from the center of growth-promoting gene expression. These findings represent a previously undescribed mechanism governing 3D growth patterns in multicellular plant organs.

Abstract

Morphogenesis occurs in 3D space over time and is guided by coordinated gene expression programs. Here we use postembryonic development in Arabidopsis plants to investigate the genetic control of growth. We demonstrate that gene expression driving the production of the growth-stimulating hormone gibberellic acid and downstream growth factors is first induced within the radicle tip of the embryo. The center of cell expansion is, however, spatially displaced from the center of gene expression. Because the rapidly growing cells have very different geometry from that of those at the tip, we hypothesized that mechanical factors may contribute to this growth displacement. To this end we developed 3D finite-element method models of growing custom-designed digital embryos at cellular resolution. We used this framework to conceptualize how cell size, shape, and topology influence tissue growth and to explore the interplay of geometrical and genetic inputs into growth distribution. Our simulations showed that mechanical constraints are sufficient to explain the disconnect between the experimentally observed spatiotemporal patterns of gene expression and early postembryonic growth. The center of cell expansion is the position where genetic and mechanical facilitators of growth converge. We have thus uncovered a mechanism whereby 3D cellular geometry helps direct where genetically specified growth takes place.

Central to developmental biology is the question of how gene expression leads to morphogenesis and the creation of form (1, 2). However, there are few studies that link genes directly with shape change in a mechanistic way (3–5). In plants, where cells do not move, nearly all shape change and morphogenesis occur through the tightly regulated control over the mechanical properties of the cell wall. Mathematical models of plant cell growth are based on the turgor-driven Lockhart model and its derivatives (6, 7) that link the rate of cell wall expansion to the stress experienced by the wall. This model fits well with the biochemistry of the cell wall, which is composed of a strong cellulose microfibril network embedded in a pectin matrix with cross-links of hemicellulose, structural proteins, and other polysaccharides (8). Stress on the cell wall from turgor pressure causes elastic expansion, which becomes plastic as remodeling enzymes rearrange the network and incorporate new material (8). Thus, the physical manifestation of growth, cell expansion, results from a balance between genetically controlled enzymatic activity and the mechanical forces experienced by the cell wall.

A common simplifying assumption is that gene expression associated with cell wall modification directly specifies the rate of growth of cells. This assumption is, however, limited as growth-promoting gene expression rarely correlates well with gradients of active cell expansion (9, 10). This suggests that gene expression patterns alone are not sufficient to predict the influence of genes on shape generation. Evidence is accumulating that additional unidentified nongenetic mechanisms influence multicellular morphogenesis, such as the feedback of mechanical stresses on growth (11).

In plants, several spatially distinct cellular organizing centers that coordinate and organize organ development programs have been identified (3, 12, 13), as have genes that promote cell expansion through the loosening of cell walls (8). However, efforts to uncover growth regulatory mechanisms in plants are complicated by asynchronous cell division, in addition to variable gradients of spatial differentiation across complex and dynamically growing organs such as roots, meristems, and leaves (3, 14, 15). The induction of growth of the Arabidopsis embryo (Fig. 1A) during seed germination avoids many of these confounding factors. This developmental transition from seed to seedling is driven exclusively by cell shape change in the absence of cell division (16, 17). Following a largely environmentally determined switch that terminates dormancy, a discrete induction of cell expansion is invoked by the hormone gibberellic acid (GA) (18, 19). This binary growth switch represents an ideal system for examining the relationship between the induction of growth-promoting gene expression and the morphogenesis within a multicellular organ.

Fig. 1.

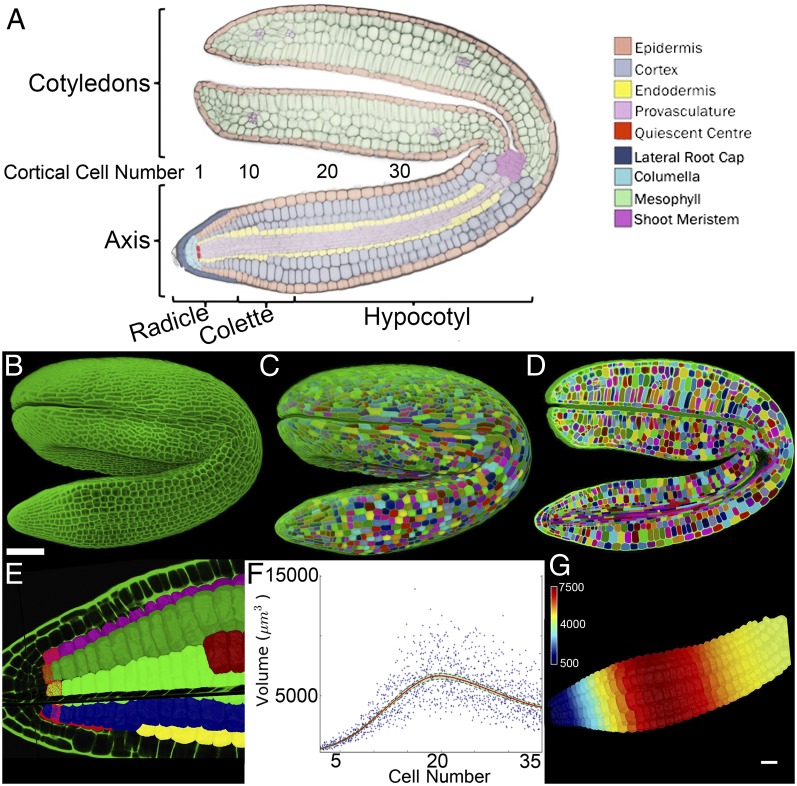
Quantification of volumetric increases at specific cell positions. (A) Cellular anatomy of the mature dormant Arabidopsis embryo. (B) Maximum-intensity projection of a confocal z stack of a complete Arabidopsis embryo. (C) Three-dimensional segmentation of the embryo in B. Different colors are used to illustrate unique labels. (D) Cross section through the segmented embryo in C. (E) Virtual isolation of outer cortical cells each labeled along their linear cell files. Cortical cells at a defined position are selected (red cells) and the origin of cutting planes is positioned upon the quiescent center. (F) Plot of cortical cell volume by cell number along the embryo axis, using aggregated data from four individual samples. Cell 1 corresponds to the first cortical cell within the embryo radicle as indicated in A. The 95% confidence interval is indicated in green. (G) False-colored heat map upon the cortical cells of an embryo axis illustrating the output within the graph in F. (Scale bars: G, in μm³; B, 100 μm.)

Mechanical models of growth controlled by genetics provide insight into morphogenesis in a way that is not possible within other frameworks. Because shape is an emergent property of the models, it is possible to understand the often unintuitive relationships between gene expression patterns and the resulting organ shapes (1, 20–23). Using computational models, we demonstrate that the 3D shape of cells and their arrangement within multicellular plant organs can profoundly affect their growth response to gradients of expansion-promoting gene expression. This represents an additional mechanism through which the shape and geometry of cells influence the response of plant organs to growth-promoting gene expression.

Results and Discussion

Spatiotemporal Cellular Growth Dynamics in the Arabidopsis Embryo.

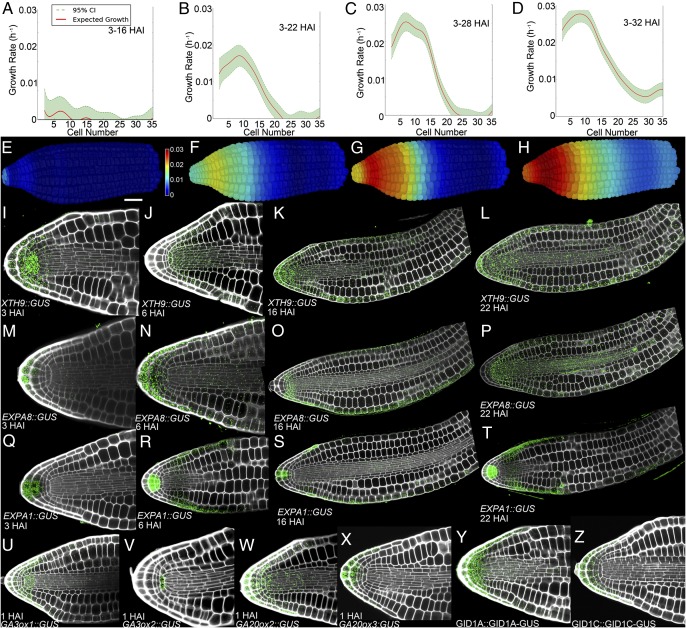
To uncover the spatial and temporal pattern of cellular growth during the initial expansion of Arabidopsis embryos, samples were collected over a time course after seed imbibition (Fig. S1A). Z stacks were taken from fixed samples, using confocal microscopy (Fig. 1B), and cells within the embryos were segmented in 3D, using MorphoGraphX (24) (Fig. 1 C and D; Fig. S2; SI Text, SI Materials and Methods; and Movie S1, www.MorphoGraphX.org). Using tools we developed in MorphoGraphX, the cortical cell layer was isolated from the rest of the embryo and labeled into cell files (Fig. 1E, Fig. S2, and Movie S1). An origin was positioned at the quiescent center of the embryo axis (Fig. 1E), allowing the calculation of average cell volume as function of cell number, by counting along cell files from the quiescent center. We found that the cortical cells had very consistent volume between different individual embryos at similar stages (Fig. 1 F and G and Fig. S3) and a gradient of cell volume along the axis. The absence of cell division and the calculation of average cell volume as a function of cell number allowed us to determine growth rates on data from fixed samples pooled at different stages and determine volumetric expansion rates relative to their initial cell size at 3 h after imbibition (3 HAI) (Fig. 2 A–D). Absolute differences in volumetric expansion suggested that initial cell-expansion events occur within the lower hypocotyl of the embryo between 16 HAI and 22 HAI (Fig. S4 A–D), a time concurrent with the onset of visible testa rupture (Fig. S1A). Whereas these cells make the largest absolute contribution to total growth, absolute measurements fail to capture cellular differences in growth (for example, to growth signals) due to their inherent bias toward cells that have a greater initial size. An examination of relative growth rate of cells revealed that expansion in fact occurred within the radicle and was greatest around cell number 8, within the transition region, or collet, of the embryo axis (Figs. 1A and 2 B and F and Figs. S3 and S4 F and J). During subsequent stages of germination (from 22 HAI to 28 HAI; Fig. 2 C and G), the domain of expansion extended along the axis, with the greatest relative growth extending to include the transition region and radicle. The final phase of cell expansion (28–32 HAI) was responsible for driving the completion of germination by endosperm rupture, and the region of expansion extended to include cells of the upper hypocotyl (Fig. 2 D and H). Growth of the embryo during this timescale did not include a significant increase in cotyledon volume (Fig. S1B).

Fig. 2.

Spatiotemporal pattern of gene expression and cell expansion during Arabidopsis seed germination. Graphs show relative cell expansion at (A) 3–16 HAI, (B) 3–22 HAI, (C) 3–28 HAI, and (D) 3–32 HAI. False-colored axes illustrate progressive relative cell expansion at (E) 3–16 HAI, (F) 3–22 HAI, (G) 3–28 HAI, and (H) 3–32 HAI. Cell expansion rates were determined using four embryos at each time point. (I–L) XTH9 promoter activity at (I) 3 HAI, (J) 6 HAI, (K) 16 HAI, and (L) 22 HAI. (M–P) EXPA8 promoter activity at (M) 3 HAI, (N) 6 HAI, (O) 16 HAI, and (P) 22 HAI. (Q–T) EXPA1 promoter activity at (Q) 3 HAI, (R) 6 HAI, (S) 16 HAI, and (T) 22 HAI. (U–X) Promoter activities of GA synthesis enzymes 1 h after imbibition in nondormant seeds of (U) GA3ox1::GUS, (V) GA3ox2::GUS, (W) GA20ox2::GUS, and (X) GA20ox3::GUS. (Y and Z) Protein localization of the GA receptors (Y) GID1A::GID1A-GUS and (Z) GID1C::GID1C-GUS in dormant embryos. The colored scale bar in E indicates growth rate. (White scale bar in E, 50 μm.)

Spatiotemporal Patterns of Growth-Driving Gene Expression.

To identify genes driving cell expansion in the growing embryo, we examined the germination subnetwork of the condition-dependent gene-correlation network SeedNet (25) (Fig. S1C). This region of the network contains coexpressed genes that are up-regulated by the germination-stimulating hormone GA and includes an abundance of growth-promoting cell wall remodeling genes (19, 25). The spatiotemporal induction of multiple cell expansion-promoting genes from SeedNet was examined, including the xyloglucan endotransglucosylases/hydrolase (XTH) genes XTH9 and XTH19 (26) and the expansins EXPA1, EXPA8, and EXPA15. We observed that the promoter activities of each gene were first induced at 3 HAI principally within the radicle tip (Fig. 2 I, M, and Q and Fig. S5 A–E) and the domain of expression progressively extended along the length of the embryo axis at 6 HAI, 16 HAI, and 22 HAI (Fig. 2 J–L, N–P, and R–T and Fig. S5 A–E). Other GA-induced transcripts including FACKEL and adenosine-5′-phosphosulfate kinase 2 (APK2) show a similar spatiotemporal induction pattern (Figs. S1C and S5 F and G). This wave of expansion-promoting gene expression precedes the observed wave of cell expansion along the embryo axis (Fig. 2 A–D).

The de novo synthesis of the hormone GA is necessary to induce postembryonic cell expansion (18). To determine the initial source of GA production, we examined the earliest spatial activation of promoters regulating key GA synthesis genes GA-20-oxidase2 and -3 (27) and GA-3-oxidase1 and -2 (28). Promoter activities were preferentially induced within the tip of the embryonic radicle at 1 HAI in nondormant seeds (Fig. 2 U–X and Fig. S6 A–E). This suggests that the cells of the radicle are the primary source of GA during the seminal induction of early embryo growth. Next we looked at signaling components that mediate the GA response to induce postembryonic growth and cell expansion. The GA-receptor proteins GID1A and GID1C (Fig. 2 Y and Z and Fig. S6 F–H) were all enriched within the cells of the root cap, columella, and quiescent center of the radicle and observed at much lower levels in epidermal and vascular cells throughout the embryo. Collectively, these data support the notion that the tip of the radicle functions to initiate postembryonic plant growth.

The progressive increase in the domain of cell expansion (Fig. 2 A–D) and progressive induction of XTH9, XTH19, EXPA1, EXPA8, and EXPA15 promoter activities along the length of the Arabidopsis embryo axis suggest the presence of a mobile inductive growth factor. Because GA is a key promoter of embryonic cell expansion, we examined the effect of exogenous GA application to investigate whether GA or a GA-derived signal might represent this factor. We found that global application of GA to the nongerminating GA biosynthetic mutant ga1-3 mutant (29) resulted in a broad domain of cell expansion along the entire length of the embryonic axis by 22 HAI with a peak of expansion close around cell 9 as observed in the wild type (Figs. S7–S9). This is in contrast to the radicle and collet-specific expansion in the wild type at the same time stage (Fig. 2 B and F). Microapplication of GA to a central position of the hypocotyl region of the embryo axis was sufficient to induce a discrete domain of localized cell expansion in ga1-3 embryos at 22 HAI (Fig. S9 C–K).

The 3D Geometry of Cells Influences Their Capacity to Expand.

We identified the radicle as the region where promoter activity driving cell wall-remodeling gene expression is first observed (Fig. 2 I, M, and Q), and this domain spreads along the length of the axis by 22 HAI when the first cell expansion events are detected. This is in conflict with the observation that the greatest cell growth rates are observed at around cell 8 in the axis (Fig. 2B). We hypothesized that nongenetic factors may account for the spatial disconnect between gene expression and relative cell expansion and explored the possibility that mechanical constraints on cell expansion could result from the considerably different size of the cells within the radicle and hypocotyl regions (Fig. 1 A, F, and G).

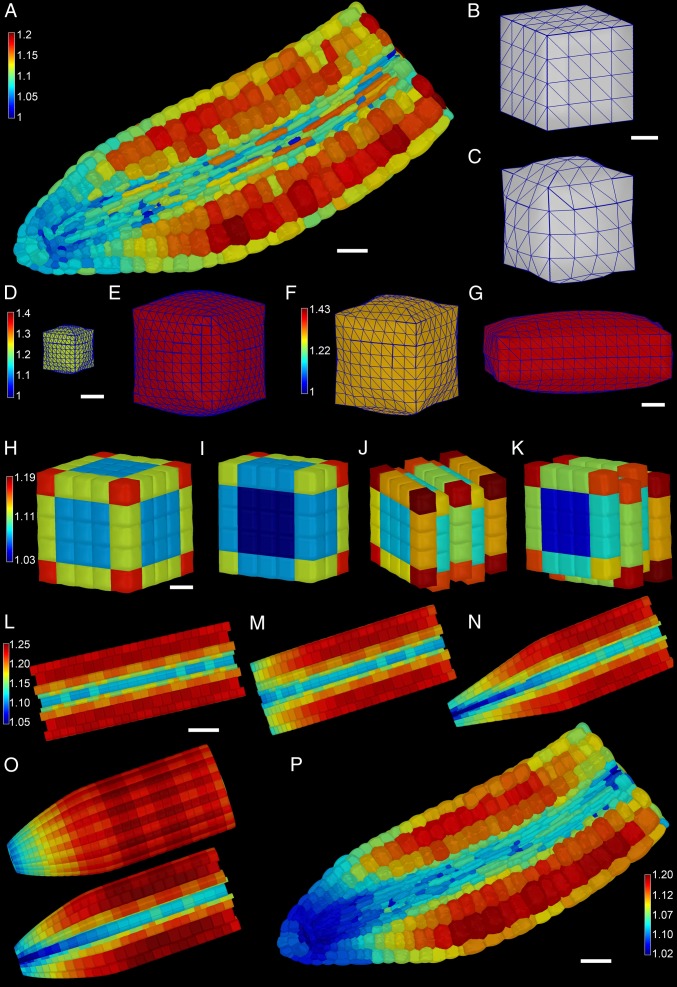
To test this hypothesis, we built a 3D mechanical model of the Arabidopsis embryo to explore the effects of cellular geometry and arrangement on cell expansion within a multicellular organ. The geometry of the model was extracted from a high-resolution confocal stack of a mature embryo segmented in 3D (Fig. 1B). The mechanical model was developed with the finite-element method (FEM), using linearly hyperelastic triangular membrane elements (SI Text, SI Materials and Methods). In the model, the Young’s modulus of the cell wall was set to 120 MPa, and the thickness of the exterior walls was set to 1 μm and that of interior walls to 400 nm, based on empirically derived measurements (30). Starting from an initial rest state with no turgor, the structure was pressurized to 0.5 MPa, and relative volumetric expansion of the cells was calculated (Fig. 3A). Although the same pressure and material properties were applied throughout the model, a gradient in the capacity of individual cells to expand is observed emanating away from the radicle tip. This demonstrates that 3D cellular geometry impacts the ability of cells to expand within the native geometry of the mature Arabidopsis embryo.

Fig. 3.

Geometric constraints on cellular expansion, using 3D mechanical models. (A) Three-dimensional mechanical growth simulations using the real cellular geometry derived from an Arabidopsis embryo. (White scale bar, 30 μm.) Colored scale bar shows relative cell expansion. (B and C) An artificially designed square cuboid cell before pressurization (B) and following pressurization (C). (White scale bar in B, 5 mm.) (D and E) An 8,000-μm³ (D) and a 125,000-μm³ (E) cell each pressurized to 5 Bar and colored using the same scale shown in E. (White scale bar in D, 10 mm.) (F and G) A square cuboid (F) and rectangular cuboid (G) cell pressurized to 5 Bar and colored using the scale in F. (White scale bar in G, 5 μm.) (H) Surface view of the expansion of a 5 × 5 x 5 block of cells. (I) Inside view of H. (J) Same as H with the cells staggered one-half between adjacent cell layers. (K) Inside view of J. H–K are colored using scale in H. (White scale bar in H, 20 μm.) (L) An artificially designed embryo shaped as a cylinder. (White scale bar, 50 μm.) (M) The same as L but with shorter cells toward the tip. (N) The same as L but with narrower cells toward the tip. (O) An artificially designed embryo where the cells get progressively shorter and narrower toward the tip, using the same parameters as in M and N, inclusive. The colored scale bar in L indicates relative growth rate, and L–O have the same scale. (P) Actual embryo template geometry heat map colored showing changes in surface area. (White scale bar, 30 μm.)

To better understand how cell size, shape, and arrangement may affect the ability of cells to expand in response to pressure, we simulated the pressurization of simple shapes that represent idealized plant cells (Fig. 3 B–G). The simplest demonstration of the effect of cellular geometry can be seen in the response of two different-sized cubes. When a small cube (8,000 μm³, Fig. 3D) and a large cube (125,000 μm³, Fig. 3E) were pressurized to 0.5 MPa, the larger cell expanded more than the smaller one with the same wall thickness and material properties. This is because the cross-sectional area of the wall holding the stress grows as a linear factor of length, whereas the stress on the wall from the pressure inside grows quadratically. Next we investigated the effect of cell shape on cell expansion by looking at two cells of equal volume, a cube (Fig. 3F) and a brick-shaped cell (Fig. 3G). Following the application of 0.5 MPa pressure to these cells, the brick-shaped cell expanded more despite having the same volume as the cube. This demonstrates that cell shape also influences the capacity of cells to expand. In an effort to understand how cell arrangement affects expansion, such as in the context within multicellular tissues, we constructed different arrangements of cubic cells. In the first instance we constructed a 5 × 5 × 5 regular grid of cells aligned evenly with respect to each other (Fig. 3 H and I). The pressurization of this block of cells showed an overall trend of greater expansion of the cells on the outside of the structure, with outer cells showing differential expansion based on their exposed surface area. Interior cells expanded uniformly and much less than outer cells. Cells within the Arabidopsis embryonic axis are not aligned evenly with respect to one another as in the model in Fig. 3 H and I, but rather are staggered between adjacent cell files. To mimic this arrangement we created a model using the same cubic cells, but staggered their position by one-half cell length with respect to one another (Fig. 3 J and K). The entire structure expanded more, 10.5% compared with 8.6% for the nonstaggered model. Again the outer cells showed differential expansion based on the number of exposed faces, with inner cells expanding less. Next we designed cellular template models representing idealized variations of mature Arabidopsis embryos. These template models had both radial symmetry and relative cell sizes that were roughly proportional to those of biological samples (Fig. 3 L–O, Fig. S10, and SI Text, SI Materials and Methods). A cylindrical embryo axis with identical cell geometries along its length was generated first. Expansion of the cells of this cylinder was uniform across the length of the axis (Fig. 3L), save for a small periodic effect due to the alignment of cell staggering with adjacent layers. As in the cube models, cells in the interior expanded less, as did smaller cells. Next we made the cells progressively shorter toward one end of the axis, which reduced their capacity to expand in response to pressure (Fig. 3M). Cells where the radial width was progressively shortened also were restrained in their capacity to expand (Fig. 3N). When both the length and the radial width of cells were simultaneously reduced, an additive effect in the decrease in cell expansion was observed (Fig. 3O). This final template geometry most closely resembled the wild-type Arabidopsis embryo and suggests that both cell length and radial width may act to limit cell expansion within the mature embryo.

Geometry Influences the Cellular Interpretation of Gradients of Growth-Promoting Gene Expression.

To test the effects of geometry on growth, we built a growing FEM model of the embryo (SI Text, SI Materials and Methods). Although volumetric expansion is the most common metric for growth, mathematical models tie extension of the cell wall to stress/strain in the wall itself (6, 7). The mathematical theory assumes that growth depends on two factors, the abundance of growth-promoting cell wall-remodeling agents and the amount of stretch in the cell wall. To quantify the second parameter, cell wall stretch, we looked at the surface area expansion of cells pressurized using the real sample geometry in our elastic model. The result is visualized in Fig. 3P. At the cellular level, the increase in surface area is qualitatively similar to that of volumetric expansion (Fig. 3A), with less local variation between cells.

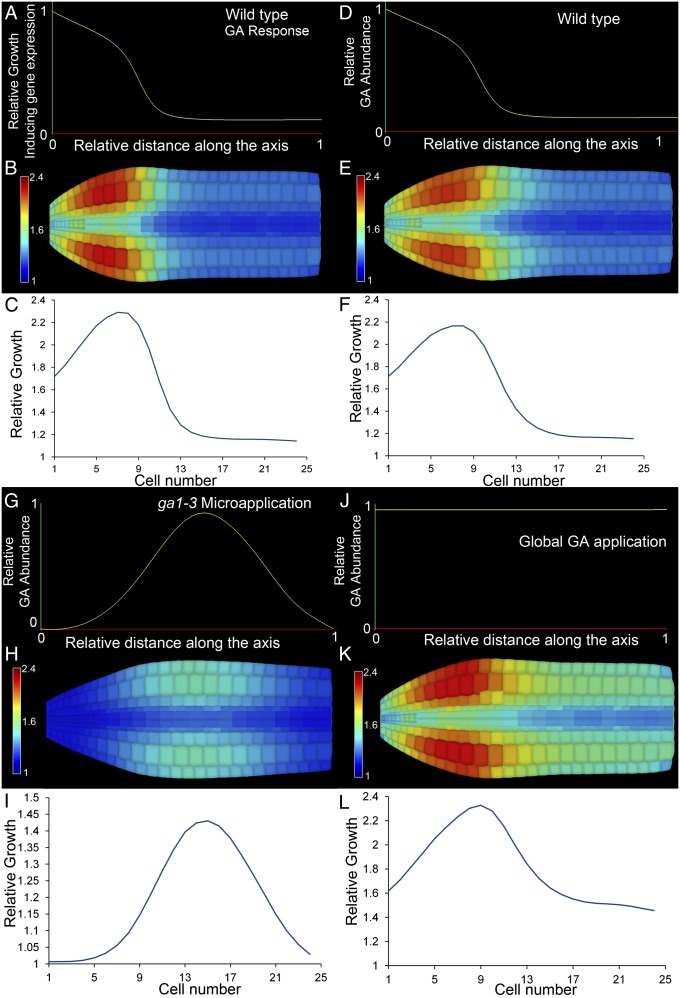
We then added a Lockhart-type growth model to our FEM simulation, with growth calculated as the integration of the output of GA response and the amount of stretch in the cell wall due to turgor pressure. The gradient of growth-promoting factors represented the collective influence of GA-induced cell wall remodeling genes and was defined as a function of the distance from the tip (Fig. 4A). To calculate the growth of each element, the growth factor was combined with the strain on the cell wall, resulting from turgor pressure (Figs. 4 A–C and Movie S2). The resulting output of relative growth in the model matched that observed in our growth analysis (Fig. 2 A–D). A slight radial swelling at the tip suggests a contribution for cell anisotropy in the generation of the final shape.

Fig. 4.

Growing 3D FEM simulation of embryo cell expansion in response to the observed growth gene expression gradient. (A) Function used to define the GA signaling output. (B) False-colored axis showing relative cell expansion along the wild-type embryo axis. (C) Graph of relative cortical cell expansion in the embryo in B. GA receptor abundance in D–L used the same function as in A. (D) GA abundance in the wild-type embryo. (E) False-colored axis showing relative cell expansion along the embryo axis in D. (F) Graph of relative cortical cell expansion in the embryo in E. (G) GA abundance in ga1-3 embryos with GA microapplied. (H) False-colored axis of relative cell expansion from G. (I) Graph of relative cortical cell expansion in the embryo in H. (J) GA abundance in ga1-3 embryos with GA applied globally. (K) False-colored axis showing relative cell expansion from J. (L) Graph of relative cortical cell expansion in the embryo in K.

The output of GA signaling is dependent upon both the presence of GA and the ability to respond to it. We then examined the relationship between these two variables within the 3D geometry of the template model Arabidopsis embryo by defining separate functions for the GA receptor and GA abundance (Fig. 4 D–L). The abundance of the GA receptor is highest in the radicle and present to a lesser degree along the length of the axis (Fig. S6 F–H). We used the function in Fig. 4A in subsequent simulations to ascribe the distribution of the GA receptor along the length of the axis. In the wild-type context, GA is initially produced in the radicle tip and progressively moves along the embryo axis. The combination of these two distributions in the simulation recapitulates the observed cell expansion pattern (Figs. 2D and 4 D–F). We simulated the microapplication of GA to a central position on the axis by changing the GA distribution (Fig. 4G) leading to localized cell expansion in this region (Fig. 4 H and I, Fig. S9 C and D, and Movie S3). The simulation of the global application of GA to the embryo (Fig. 4 J–L and Movie S4) revealed a similar pattern of relative cell expansion to that observed in the ga1-3 mutant where GA is globally applied (Fig. S9 A and B). The models therefore provide a plausible explanation why gene expression does not match the growth rates observed in the Arabidopsis embryo while being capable of recapitulating experimentally observed perturbations in the system.

Conclusion

Morphogenesis is driven by genetic and signaling networks that control the division and expansion of cells within organs. In multicellular plant tissue, cells are not free to expand independently, but are restricted by mechanical constraints of neighboring cells. This can create differences between growth-promoting gene expression patterns and the observed growth rates of the cells. Kennaway et al. (1) make a distinction between specified growth, as instructed by gene expression, and resultant growth, which includes the effects from the mechanical constraints of neighboring tissue. They showed that the difference between these is often not trivial, and even with very simple shapes it is not intuitive how to go from genes to final form. In their simulations (1, 3–5), plant tissue is modeled as a continuous 2D sheet of material, with any effects from the underlying cellular structure homogenized into the material parameters. Here we have extended this paradigm by considering the effect of the full 3D cellular geometry and topology on cell expansion, both in cellular plant tissues obtained from confocal images and in computer-generated templates. This approach revealed that cell size and 3D shape substantially affect the stress on the cell wall and the ability of cells to expand elastically in response to turgor pressure (Figs. 3 and 4). This expansion is further influenced by the arrangement of the cells’ connections to neighbor cells, as well as the location of the cells within the 3D tissue.

In current theories of plant cell growth, elastic expansion in the cell wall in response to turgor becomes plastic, i.e., irreversible, by cell wall remodeling enzymes (8). It is thus a combination of the amount of stretch in the cell wall and the amount of cell wall remodeling activity that determines the growth rate. This can be seen in the Lockhart equation for growth (7) where one parameter controls the stretch (or turgor pressure in one dimension) and the other controls the growth factor (cell wall remodeling). Because our model includes both turgor pressure and gene expression, we were able to directly apply the Lockhart -type mathematical models and explore the effect of different 3D cellular shape and arrangement on the overall growth of plant tissues.

Our data indicate that the radicle tip of the Arabidopsis embryo is the primary location of growth-promoting gene expression during early postembryonic growth, but that the center for cell expansion was more than eight cells away. Given the dramatic differences in the shape and size of the cells in these two domains and the effect this can have on their elastic expansion, we propose that the location of the center of cell expansion results from a combination of genetic, signaling, and mechanical factors. Cells within the small tightly packed area within the tip of the embryo radicle, although high in GA receptor abundance and growth-promoting gene expression, are inhibited from expanding relative to the larger cells in the transition zone of the collet. Our cellular-level 3D finite-element simulations of growing embryos confirm this hypothesis, and our results show that a gradient of gene expression emanating from the radicle tip together with geometrical inputs are sufficient to explain the positioning of the cell expansion center in the transition region. Thus, it is not necessary to invoke additional factors (e.g., tissue competence or further gene expression) as contributing to distribution of growth in this tissue context. Although it has not been considered in this study, the mechanical restraint to growth imposed by the surrounding seed coat and endosperm cannot be discarded.

These results have implications for further studies of genetic control of morphogenesis. In cases where there are large differences in cell size or shape, cell expansion is not predicted to be a direct readout of growth-promoting gene expression. One such mismatch has been previously described in a study correlating expansin gene expression with cell elongation in tomato (31). Our results also suggest a link between cell size and arrangement with the organ tissue material properties. Areas of high cell proliferation might be expected to grow more slowly than areas with more expanded cells, given the same gene expression and cell wall thickness. Thus, a focus on the direct correlation of genes with cell expansion rates may prove inadequate, if the 3D cellular structure of the tissue is not considered. This effect of cell size on a cell’s ability to expand may also explain why mutants that should have stiffer cell walls, such as the micro-RNA knockdown of multiple expansin genes in the Arabidopsis leaf (32), produce smaller plants but with bigger cells. Larger cells would be expected to counteract the increase in stiffness in the cell wall due to the loss of expansin activity.

In the mature Arabidopsis embryo, our model suggests that the location of the center for axis expansion is developmentally encoded in the geometry of the embryo itself. Despite the source of the expansion-promoting hormone and downstream gene expression being principally present within the radicle tip, the displacement of the primary site of expansion is predetermined by the developmentally defined cellular geometries of the mature embryo. Although the shapes of individual cells can encode information mediating local subcellular signaling (33), the morphogenetic future of the organ may be imprinted through the collective cell shapes and arrangements defined during its development.

Materials and Methods

Plant Growth Conditions and Germination.

Arabidopsis plants of ecotype Colombia were grown to maturity in environmentally controlled cabinets, using 16 h light (light intensity 150–175 μmol⋅m⁻²⋅s⁻¹) at 23 °C and 8 h dark at 18 °C. When plants had ceased flowering and siliques began to brown, seeds were harvested, cleaned through a 500-μm mesh, and stored at 24 °C in glassine bags in the dark for 1 mo to remove primary dormancy. To induce primary dormancy in seeds, mother plants were grown at 18 °C and 8 h dark, producing seeds that were completely dormant up to 1 mo following dry storage. Primary dormant seeds were assayed for GUS activity within 1 wk after harvest.

Confocal Imaging and GUS Staining.

Arabidopsis embryos were dissected from germinating seeds with a scalpel and foreceps, using a binocular microscope. Samples were prepared for confocal microscopy as described previously (34) and imaged using a Zeiss LSM 710.

GUS staining was performed using 2 mM 5-bromo-4-chloro-3-indolyl-β-d-glucuronic (Sigma) acid as a substrate within a pH 7.0 phosphate buffer and 1 mM potassium ferro- and ferricyanate. Embryos were stained until a blue substrate was first visible or for extended periods of time (>24 h). Reporter lines used in this study were XTH9::GUS (At4g03210), XTH19::GUS (At4g30290) (26), GID1A::GID1A-GUS (At3g05120) (35), GID1C::GID1C-GUS (At5g27320) (35), GA3ox1::GUS (At1g1555) (36), GA3ox2::GUS (At1g80340) (36), GA20ox1::GUS (At4g25420) (27), GA20ox2::GUS (At5g51810) (27), GA20ox3::GUS (At5g07200) (27), FK::GUS (At3g52940) (37), and APK2::GUS (At4g39940) (38). EXPA1::GUS (At1g69530), EXPA8::GUS (At2g40610), and EXPA15::GUS (At2g03090) reporters were generated for this study, using 1.2 kb of sequence upstream of the start codon, and placed into the pKANGWF7 reporter vector.

Microapplication Experiments.

GA-deficient ga1-3 seeds were imbibed for 3 h and embryos were dissected using a scalpel under a binocular microscope. Embryos were placed with their cotyledons facing down upon 1.4% (wt/vol) agarose plates such that the embryonic axis was not in contact with the media. GA was prepared as previously described (39) and microapplied to the middle of the embryo axis.

Cell Growth Analysis.

Confocal stacks of embryos at the different stages were processed with the MorphoGraphX 3D image analysis software (24). Samples were segmented in 3D and the cortical cells isolated. To obtain growth rates from non–time-lapse data, a coordinate system for the embryo was positioned at the quiescent center. The cells were then indexed by cell number, counting from the quiescent center. This allowed the pooling of volume data from multiple samples at each stage. The pooled data from the different time points were then used to calculate cell growth as a function of cell number. Four embryo samples were used at each time point. For more details refer to SI Text, SI Materials and Methods.

Three-Dimensional Finite-Element Models.

All finite-element models were custom coded in C++, using the Virtual Laboratory modeling environment (40).