Commonness and rarity in the marine biosphere

Significance

Tests of biodiversity theory have been controversial partly because alternative formulations of the same theory seemingly yield different conclusions. This has been a particular challenge for neutral theory, which has dominated tests of biodiversity theory over the last decade. Neutral theory attributes differences in species abundances to chance variation in individuals’ fates, rather than differences in species traits. By identifying common features of different neutral models, we conduct a uniquely robust test of neutral theory across a global dataset of marine assemblages. Consistently, abundances vary more among species than neutral theory predicts, challenging the hypothesis that community dynamics are approximately neutral, and implicating species differences as a key driver of community structure in nature.

Abstract

Explaining patterns of commonness and rarity is fundamental for understanding and managing biodiversity. Consequently, a key test of biodiversity theory has been how well ecological models reproduce empirical distributions of species abundances. However, ecological models with very different assumptions can predict similar species abundance distributions, whereas models with similar assumptions may generate very different predictions. This complicates inferring processes driving community structure from model fits to data. Here, we use an approximation that captures common features of “neutral” biodiversity models—which assume ecological equivalence of species—to test whether neutrality is consistent with patterns of commonness and rarity in the marine biosphere. We do this by analyzing 1,185 species abundance distributions from 14 marine ecosystems ranging from intertidal habitats to abyssal depths, and from the tropics to polar regions. Neutrality performs substantially worse than a classical nonneutral alternative: empirical data consistently show greater heterogeneity of species abundances than expected under neutrality. Poor performance of neutral theory is driven by its consistent inability to capture the dominance of the communities’ most-abundant species. Previous tests showing poor performance of a neutral model for a particular system often have been followed by controversy about whether an alternative formulation of neutral theory could explain the data after all. However, our approach focuses on common features of neutral models, revealing discrepancies with a broad range of empirical abundance distributions. These findings highlight the need for biodiversity theory in which ecological differences among species, such as niche differences and demographic trade-offs, play a central role.

Determining how biodiversity is maintained in ecological communities is a long-standing ecological problem. In species-poor communities, niche and demographic differences between species can often be estimated directly and used to infer the importance of alternative mechanisms of species coexistence (1–3). However, the “curse of dimensionality” prevents the application of such species-by-species approaches to high-diversity assemblages: the number of parameters in community dynamics models increases more rapidly than the amount of data, as species richness increases. Moreover, most species in high-diversity assemblages are very rare, further complicating the estimation of strengths of ecological interactions among species, or covariation in different species’ responses to environmental fluctuations. Consequently, ecologists have focused instead on making assumptions about the overall distribution of demographic rates, niche sizes, or other characteristics of an assemblage, and then deriving the aggregate assemblage properties implied by those assumptions (4–8). One of the most commonly investigated of these assemblage-level properties is the species abundance distribution (SAD)—the pattern of commonness and rarity among species (9–11). Ecologists have long sought to identify mechanisms that can explain common features of, and systematic differences among, the shapes of such distributions, and have used the ability to reproduce empirical SADs as a key test of biodiversity theory in species-rich systems (4, 6, 11–14).

Over the last decade, one of the most prevalent and influential approaches to explaining the structure of high-diversity assemblages has been neutral theory of biodiversity (12, 15, 16). Neutral models assume that individuals are demographically and ecologically equivalent, regardless of species. Thus, variation in relative abundance among species arises purely from demographic stochasticity: chance variation in the fates of individuals (i.e., birth, death, immigration, and speciation events). Most studies investigating neutral theory aim to determine whether community structure in nature is consistent with the theory’s core species equivalence assumption. This is typically done by assessing the fit of a neutral model to empirical data, sometimes relative to a putatively nonneutral alternative (17–20). However, although all neutral models share the species equivalence assumption, they differ with respect to auxiliary assumptions, such as the mode of speciation assumed, leading to different predictions for SADs and other ecological patterns. Indeed, attempts to draw conclusions from tests of neutral theory are almost invariably disputed, largely due to arguments about the extent to which alternative auxiliary assumptions can materially alter neutral theory’s ability to explain the data (11, 12, 18, 21).

An alternative, potentially more robust approach to evaluating neutral theory was proposed by Pueyo (22), based on approximating neutral and nonneutral dynamics as successively higher-order perturbations of a model for the idealized case of pure random drift in abundances. This approach predicts that a gamma distribution should approximate the distribution of species abundances for small departures for random drift, whereas assemblages exhibiting greater departures from neutrality should be better approximated by a lognormal distribution. This raises the possibility that a comparison of gamma and lognormal SADs could offer a robust test for the signature of nonneutrality in species abundance data, provided that the gamma distribution provides a sufficiently close approximation to SADs produced by neutral models.

Here, we evaluate Pueyo’s framework and apply it to patterns of commonness and rarity in 1,185 SADs from 14 marine ecosystems ranging from shallow reef platforms to abyssal depths, and from the tropics to polar regions (Fig. 1 and Tables S1 and S2). First, we test the gamma neutral approximation against several models of community dynamics that share the core neutrality assumption of species equivalence, but make different assumptions about the speciation process, spatial structure of the metacommunity, and the nature of competition between individuals. Then, we analyze the marine species abundance data, to evaluate whether they are consistent with the hypothesis that marine assemblages are neutrally structured. Finally, we ask whether patterns of commonness and rarity deviate from neutral expectation in idiosyncratic ways, or whether there are particular features of real SADs that cannot be captured by neutral models.

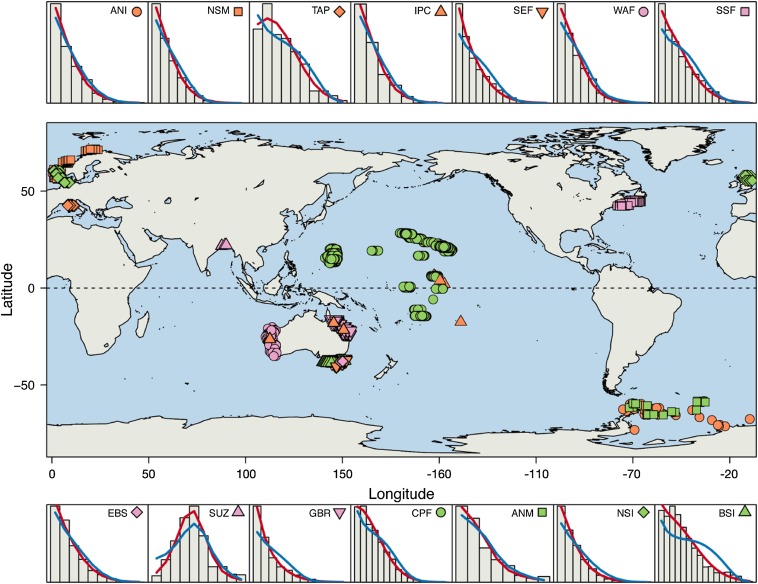
Fig. 1.

Sampling locations of SADs. Color and symbol combinations correspond to particular ecosystems. These symbols are reproduced in the surrounding panels, which show observed and fitted SADs for the site-level data (averaged across sites) of the corresponding ecosystem. The bars represent the mean proportion of species at each site in different octave classes of abundance, across all sites in the corresponding dataset [the first bar represents species with abundance 1, then abundances 2–3, abundances 4–7, etc. (10)]. The blue and red lines show the mean of fitted values from site-by-site fits of the Poisson-gamma and Poisson-lognormal distributions to the data, respectively.

Results

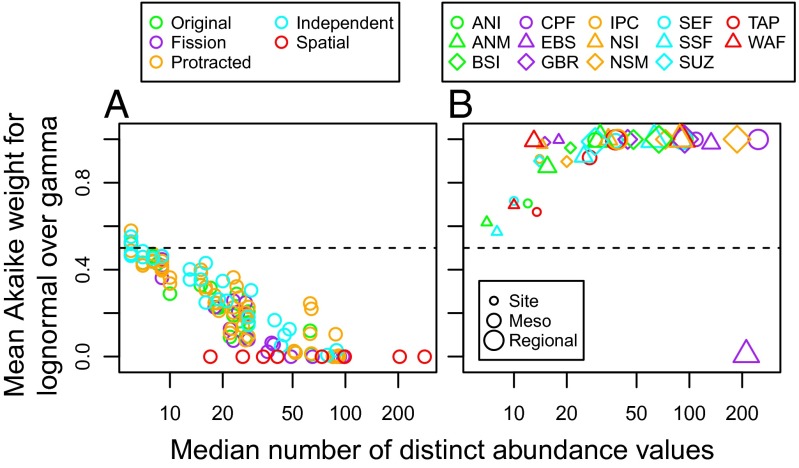
A gamma distribution of species abundances closely approximates several alternative neutral models across a broad range of neutral model parameter values (Fig. S1; see SI Results for further discussion). Moreover, the gamma consistently outperforms the lognormal when fitted to data simulated from neutral models. Specifically, as the number of distinct species abundance values in the simulated data increases, the relative support for the gamma distribution becomes consistently stronger for all of the neutral models we considered (Fig. 2A). This reflects the fact that datasets with only a small number of abundance values (e.g., a site containing 11 species, 10 of which are only represented by one individual) provide very little information about the shape of the SAD, whereas those with more abundance values provide more information (e.g., a site with 100 species whose abundances are spread over 10–20 different values).

Fig. 2.

Species abundances are better approximated by (A) a gamma distribution for simulated neutral communities, but (B) a lognormal distribution for the empirical data. Percentage support for the lognormal versus the gamma is plotted as a function of the number of observed distinct species abundances. In A, different neutral models are plotted with different colors, and each point represents a particular neutral model parameter combination from Fig. S1. In B, each combination of symbol and color represents a different marine ecosystem, whereas increasing symbol size indicates the increasing scale at which abundances were pooled (site, mesoscale, and regional).

In contrast to their relative fit to simulated neutral SADs, the lognormal consistently outperforms the gamma distribution when fitted to real marine species abundance data. When considered in terms of average support per SAD, relative support for the lognormal becomes consistently stronger as the number of observed species abundance values increases, in direct contrast with the simulated neutral data (Fig. 2B). Moreover, when the strength of evidence is considered cumulatively across all sites for each dataset, the lognormal has well over 99% support as the better model in each case (Table 1). This substantially better fit of the lognormal is retained in every case when data are pooled to the mesoscale, and, in all cases save one, when data are pooled at the regional scale (Table 1, Fig. 2B, and Figs. S2 and S3). The lognormal also remained strongly favored when we tested the robustness of our results by classifying species into taxonomic and ecological guilds, and restricting our analysis to the most species-rich guild within each dataset (see SI Results and Table S3).

Table 1.

Model selection for analysis at whole-dataset level

	Site		Mesoscale		Regional
Dataset	LN	Gamma	LN	Gamma	LN	Gamma
Antarctic Isopods (ANI)	>0.9999	<0.0001	>0.9999	<0.0001	>0.9999	<0.0001
Antarctic Molluscs (ANM)	0.9981	0.0019	0.9995	0.0005	0.9992	0.0008
Tuscany Archipelago Fish (TAP)	>0.9999	<0.0001	0.9999	0.0001	0.9983	0.0017
Indo-Pacific Coral Crustaceans (IPC)	>0.9999	<0.0001	NA	NA	>0.9999	<0.0001
SE Australia: Shelf Fish (SEF)	>0.9999	<0.0001	>0.9999	<0.0001	>0.9999	<0.0001
W Australia: Deep Fish (WAF)	>0.9999	<0.0001	>0.9999	<0.0001	>0.9999	<0.0001
Scotian Shelf Fish (SSF)	>0.9999	<0.0001	>0.9999	<0.0001	0.9984	0.0016
Eastern Bass Strait Invertebrates (EBS)	>0.9999	<0.0001	>0.9999	<0.0001	0.0087	0.9913
Sunderban Zooplankton (SUZ)	>0.9999	<0.0001	NA	NA	0.9892	0.0108
Great Barrier Reef Fish (GBR)	>0.9999	<0.0001	>0.9999	<0.0001	>0.9999	<0.0001
Central Pacific Reef Fish (CPF)	>0.9999	<0.0001	>0.9999	<0.0001	>0.9999	<0.0001
Norwegian Shelf Macrobenthos (NSM)	>0.9999	<0.0001	>0.9999	<0.0001	>0.9999	<0.0001
North Sea Invertebrates (NSI)	>0.9999	<0.0001	>0.9999	<0.0001	>0.9999	<0.0001
Bass Strait Intertidal (BSI)	>0.9999	<0.0001	>0.9999	<0.0001	0.9998	0.0002
Overall	>0.9999	<0.0001	>0.9999	<0.0001	>0.9999	<0.0001

Values indicate percentage support for the gamma and lognormal (LN) models fitted to the species abundance data at three scales: site level, mesoscale, and regional. Each row represents a different dataset. For IPC and SUZ, there were too few SADs to create mesoscale groupings. The last row is an overall test, based on summing the log-likelihoods across all datasets. Where one of the models has at least 95% support, the model’s weight is shown in bold.

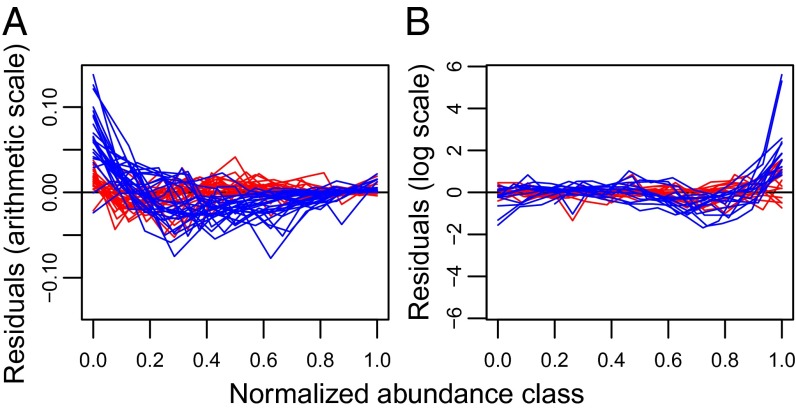
Inspection of the lack of fit of the gamma neutral approximation indicates that it deviates from the data in highly consistent ways: real SADs exhibit substantially more heterogeneity than the gamma distribution can generate (Fig. 3). Specifically, the gamma is unable to simultaneously capture the large number of rare species and the very high abundances of the most common species. For abundance distributions lacking an internal mode (i.e., where the leftmost bar in the SAD is the largest one), this is manifested as an excess of rare species and paucity of species with intermediate abundance, relative to the best-fit neutral approximation (Fig. 3A, blue lines). Conversely, when an internal mode is present in the data, the abundances of the most highly abundant species are consistently higher than the gamma distribution can produce (Fig. 3B, blue lines). In contrast, discrepancies between the data and the lognormal are much smaller in magnitude, and more symmetrically distributed around zero, compared with the gamma (Fig. 3, red lines).

Fig. 3.

Residuals (observed minus predicted number of species) of gamma (blue lines) versus lognormal (red lines) fits, illustrating why the gamma performs worse than the lognormal. Each line represents one ecosystem at one spatial scale, with log₂ abundance class normalized so that each dataset’s uppermost octave is 1.0. (A) Residuals for abundance distributions lacking an internal mode, plotted on an arithmetic scale to highlight the lack of fit for the smaller (leftmost) abundance classes. (B) Residuals for abundance distributions with an internal mode, plotted on a logarithmic scale to illustrate the lack of fit for the larger (rightmost) abundance classes.

Detailed analysis of variation in the strength of evidence against neutrality, within and among datasets, indicates that the relative performance of the lognormal over the gamma is substantially driven by the fact that the most abundant species is, on average, too dominant to be captured by the gamma neutral approximation. After controlling for the effects of the number of abundance values in the sample on statistical power, the relative abundance of the most-abundant species explained over one-half of the variation in the strength of support for the lognormal over the gamma, for site-level, mesoscale, and regional-scale abundance distributions (Table S4, Fig. S4, and SI Results). Conversely, the prevalence of rarity was a poor predictor of the strength of evidence against the gamma neutral approximation (Table S4, Fig. S5, and SI Results).

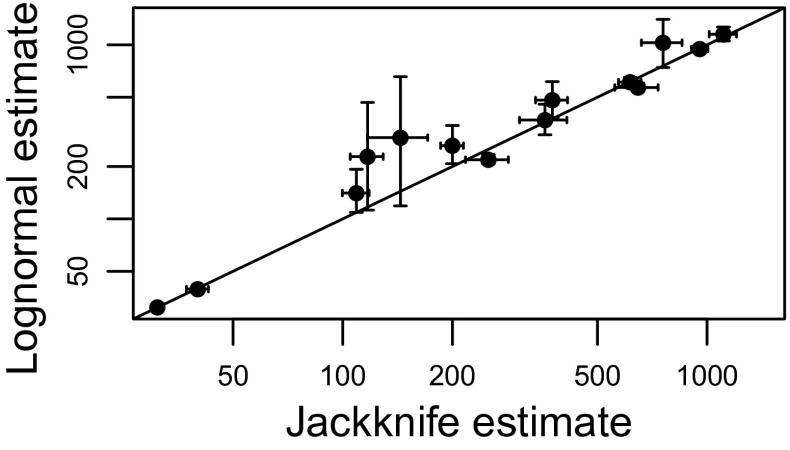
In addition to outperforming the gamma neutral approximation, tests of the absolute goodness of fit of the lognormal suggest that it approximates the observed species abundance data well. Statistically significant lack of fit (at α = 0.05) to the lognormal was detected in 4.8% of sites, approximately equal to what would be expected by chance, under the null hypothesis that the SADs are in fact lognormal. Moreover, lognormal-based estimates of the number of unobserved species in the regional species pool are realistic, and very similar to those produced by an alternative, nonparametric jackknife method that relies on presence–absence rather than abundance data (Fig. 4).

Fig. 4.

Agreement between lognormal-based and nonparametric estimates of the total number of species in the community. Points on the horizontal axis are richness estimates produced by the nonparametric jackknife, based on presence–absence data across sites. The points on the vertical axis are estimates produced by the lognormal model, fitted to the pooled regional abundance distributions. Error bars are 95% confidence intervals. The solid line is the unity line, where the lognormal and the nonparametric jackknife produce the same estimate of the number of unobserved species.

Discussion

Recently, the use of SADs to test biodiversity theory has been criticized because different species abundance models often generate very similar predictions, which can be difficult to distinguish when fitted to species abundance data (9). Consequently, some researchers have focused on other properties of assemblages, such as community similarity (12), species–area and species–time relationships (23, 24), and relationships between species traits or phylogeny and species abundance (25, 26). Such approaches are powerful when evaluating the performance of particular species abundance models. However, because models combine multiple assumptions, attributing a model’s failure to one assumption in particular, such as species equivalence, is problematic. Indeed, in the debate over neutral theory of biodiversity, studies that show failure of a neutral model (12, 25, 27) are almost invariably followed by responses showing that packaging neutrality with a different set of alternative assumptions can explain the data after all (11, 28, 29). Although the identification of alternative auxiliary assumptions that preserve a theory’s core prevents premature abandonment of a promising theory, it also can hinder progress by inhibiting the reallocation of scientific effort to more promising research programs (30). Given the proliferation of alternative theories of biodiversity (8, 14, 31, 32), identifying and testing predictions that are robust to auxiliary assumptions, and therefore better target a theory’s core assumptions, should be a high priority.

Here, we showed that, as previously hypothesized (22), a gamma distribution successfully captures features common to several models that share the core neutrality assumptions of species equivalence, but make very different auxiliary assumptions. We then found that this approximation cannot simultaneously account for the large number of very rare species, and the very high abundances of the most abundant species, in marine species abundance data. These discrepancies are highly consistent across diverse taxa, habitat types, and geographical locations, suggesting that this shortcoming of neutral theory is likely to be widespread in nature.

In contrast to the simulated neutral assemblages, analysis of the real data reveals that the lognormal distribution captures much better the observed heterogeneity in species abundances, and produces realistic estimates of the number of unobserved species at the regional scale. Lognormal SADs are generated by models that make a variety of different assumptions about how variation in abundances is determined, but all those proposed to date explicitly or implicitly incorporate niche or demographic differences among species. For instance, Engen and Lande (33) derived the lognormal from stochastic community dynamics models that allow for differences in species’ intrinsic growth rates and carrying capacities, and for arbitrary patterns of covariation in species’ responses to environmental fluctuations (4). More generally, Pueyo (22) derived the lognormal as a generic approximation for deviations from neutral community dynamics. Alternatively, niche apportionment models explain variation in species abundances based on variation in niche size, rather than stochastic population fluctuations (8). The lognormal can arise from the hierarchical apportionment of niche space due to a central limit theorem-like phenomenon (34). It can also be expected to arise more generally when there are multiple niche dimensions, and niche overlap may occur. As niche dimensions increase, the niche hypervolume becomes the product of idiosyncratically varying niche widths along an increasingly large number of niche axes. Provided abundance is proportional to the niche hypervolume (potentially along with other factors, such as body size and the proportion of resources within the niche that have not been preempted by other species), abundance will tend toward a lognormal distribution, again by the central limit theorem (13, 18).

The fairly general conditions under which lognormal distributions can arise suggests that a broad range of nonneutral characteristics, such as high-dimensional niche differences, low-dimensional life history trade-offs, or differential responses to environmental fluctuations, may give rise to approximately lognormal abundance distributions, such as those found in this study (13, 18, 22). Thus, although the comparatively poor performance of the gamma relative to the lognormal provides strong evidence against neutral dynamics as the principal driver of variation in abundances among species, the seemingly excellent fit of the lognormal distributions cannot, by itself, unambiguously identify which nonneutral processes are most responsible for the heterogeneity in species abundances in a given assemblage. Consequently, methods for apportioning the heterogeneity in species abundances among its potential causes, and which can yield inferences about species-rich assemblages, warrant further development. Some such methods, such as those based on relationships between abundance and species’ functional traits (34), or on spatiotemporal trends in relative abundances (35), explicitly predict lognormal SADs, and therefore are likely to be particularly promising.

Conclusions

Neutral theory explains variation in the abundances and distribution of species entirely as a consequence of demographic stochasticity—chance variation in the fates of individuals (15, 36). Although proponents of neutral theory have always acknowledged the existence of ecological differences between species, neutral theory assumes that those differences are overwhelmed by the phenomena that are explicitly included in neutral models (14, 36). The formulation and testing of neutral theory has drawn attention to the potential importance of demographic stochasticity as a process that contributes to differences in species abundances that are unrelated to species’ ecological traits, such as niche size or competitive ability. Such effects should be particularly important among rare species (4). Indeed, our finding that there are common features of different neutral models suggests that it can play a role as a robust null expectation, at least for some aspects of community structure (16). However, the most abundant few species often numerically dominate communities and play a disproportionately large role in community and ecosystem processes (37). We have shown that neutral theory consistently underestimates among-species heterogeneity in abundances across a broad range of marine systems. The fact that its performance is closely linked to abundances of the most common species indicates that it is the ecological dominance of these very highly abundant species that cannot be explained by neutral processes alone. Commonness itself is poorly understood, but the identities of the most common species in ecosystems tend to remain quite consistent over ecological timescales (38). Thus, the key to understanding the distribution of abundances in communities, even species-rich ones, may lie as much in understanding how the characteristics of common species allow them to remain so abundant, as in understanding the dynamics and persistence of rare species.

Materials and Methods

Approximating Neutrality.

Pueyo’s framework starts with a stochastic differential equation for random drift in population size (i.e., birth rate equals death rate, no density dependence, immigration, emigration, or speciation) and considers approximating departures from this model in terms of successively higher-order perturbations to it. Here, we take as our candidate neutral approximation the gamma distribution and, as our alternative model, the lognormal distribution. More specifically, because species abundance data are discrete, whereas the gamma and lognormal are continuous distributions, we use the Poisson-gamma (i.e., negative binomial) and Poisson-lognormal mixture distributions, as these distributions are commonly used to approximate discrete, random samples from underlying gamma or lognormal community abundance distributions (see SI Materials and Methods for further details).

To assess whether the Poisson-gamma distribution provides a good approximation to the SADs produced under neutrality, we tested it against five different neutral models: Hubbell’s original neutral model (39), a protracted speciation neutral model (21), a fission speciation model (40), an independent species model (11, 41), and a spatially explicit neutral model (42). We chose these five models because they encompass models that relax key assumptions of neutral theory as originally formulated; moreover, each of them meets a strict definition of neutrality: every individual has the same demographic rates, and the same per-capita effects on other individuals, regardless of species. We tested the approximation in two ways. First, we assess how closely (in absolute terms) the Poisson-gamma can approximate neutral abundance distributions. Second, we assess whether the Poisson-gamma outperforms the Poisson-lognormal when fitted to data generated according to neutral model assumptions (see SI Materials and Methods for details).

Empirical Data.

Data were contributed to the Census of Marine Life (CoML) project and represent a diverse range of taxa, ocean realms, depths, and geographic locations (Table S1). To be included in our analysis, contributed data needed to meet several criteria (see SI Materials and Methods for details). Where datasets included samples over multiple years from the same sites, only the most recent year of data was used. Finally, we only fitted SADs if they contained more than five distinct species abundance values, to minimize convergence problems associated with fitting species abundance models to very sparse data. However, the data from such sites were still used in the analyses that pooled abundance distributions at larger scales.

Fitting Models to Species Abundance Data.

For both the simulated neutral data, and the real species abundance data, we fitted our models using maximum-likelihood methods (see SI Materials and Methods for details). For the empirical data, in addition to fitting our species abundance models at the site level, we also fitted pooled species abundances at a mesoscale level, and at the regional (whole-dataset) level. For datasets that were spatially hierarchically organized, we used this hierarchy to determine how to pool sites at the mesoscale [e.g., for the Central Pacific Reef Fish (CPF) data, sites were nested within islands, so pooling was done to the island level]. For data that were not explicitly hierarchically organized [Antarctic Isopods (ANI), Antarctic Molluscs (ANM), Scotian Shelf Fish (SSF), Bass Strait Intertidal (BSI)], cluster analysis was used to identify mesoscale-level groupings. In two cases [Sunderban Zooplankton (SUZ), Indo-Pacific Coral Crustaceans (IPC)], there were only a few sites sampled, and no natural hierarchical structure, so these data were omitted from the mesoscale analysis.

For both the analysis of the marine species abundance data, and the analysis of the simulated neutral communities, model selection was based on Akaike weights, which are calculated from Akaike’s information criterion values and estimate the probability (expressed on a scale of 0–1) that a model is actually the best approximating model in the set being considered. Because the Poisson-gamma and the Poisson-lognormal have the same number of estimated parameters, this is equivalent to calculating model weights based on the Bayesian information criterion. For the empirical data, model selection was done at the whole-dataset level by summing the log-likelihoods for all individual sites (for the site-level analysis) or mesoscale (for the mesoscale analysis) abundance distributions for a dataset, and calculating Akaike weights based on these values (Table 1). However, this approach does not make sense for the analysis of the simulated neutral SADs, because an arbitrary degree of confidence can be obtained by simulating a large number of sites. Therefore, we instead calculated an expected level of model support on a per-SAD basis, for each neutral model and parameter combination, by calculating the mean difference in log-likelihoods across the 100 simulated datasets, and converting this mean into an Akaike weight. We examined these Akaike weights as functions of the number of distinct observed species abundance values, because we would expect our ability to distinguish between alternative models to increase as the number of distinct observed species abundance values increases. For comparison, we also calculated per-SAD Akaike weights for the marine species abundance data. This approach is less powerful than the aggregate whole-dataset comparisons shown in Table 1, but it facilitates visualization of the differences between the simulated neutral SADs (Fig. 2A) and the real marine SADs (Fig. 2B).

Analysis of Variation in Performance of Neutral Approximation.

The discrepancies between the data and the gamma neutral approximation suggest that real data exhibit too much heterogeneity in species’ abundances to be captured by the neutral approximation. To better understand this, we examined whether the relative model support varied systematically within or among datasets as a function of the prevalence of rare species, and the abundances of the most abundant species. As a measure of relative model support, we used a per-observation difference in log-likelihoods (see SI Materials and Methods for details). We first confirmed that this standardization controlled for the effect of sample size on statistical power (i.e., the trend illustrated in Fig. 2B). Then, we asked whether the variation in standardized model support was better explained by the numerical dominance of the most common species, or by the prevalence of very rare species, using mixed-effects linear models.

Testing the Absolute Fit of the Lognormal Distribution.

Goodness of fit of the lognormal distribution to the empirical data was assessed with parametric bootstrapping (see SI Materials and Methods for details). Also, for each dataset’s regional-scale SAD, we compared lognormal-based estimates of total number of species in the species pool with estimates using the nonparametric jackknife (10). See SI Materials and Methods for further details.