Abstract
Many clustering algorithms are unable to solve the clustering problem of protein-protein interaction (PPI) networks effectively. A novel clustering model which combines the optimization mechanism of artificial bee colony (ABC) with the fuzzy membership matrix is proposed in this paper. The proposed ABC-IFC clustering model contains two parts: searching for the optimum cluster centers using ABC mechanism and forming clusters using intuitionistic fuzzy clustering (IFC) method. Firstly, the cluster centers are set randomly and the initial clustering results are obtained by using fuzzy membership matrix. Then the cluster centers are updated through different functions of bees in ABC algorithm; then the clustering result is obtained through IFC method based on the new optimized cluster center. To illustrate its performance, the ABC-IFC method is compared with the traditional fuzzy C-means clustering and IFC method. The experimental results on MIPS dataset show that the proposed ABC-IFC method not only gets improved in terms of several commonly used evaluation criteria such as precision, recall, and P value, but also obtains a better clustering result.
1. Introduction
With the completion of human genome project, researches on protein-protein interaction (PPI) networks [1] have been a hot topic in the life science area, which can not only provide clues to explore biological functions to deeply understand the essence of life activities, but also give important information to understand mechanism of diseases. Currently, a number of methods have been proposed in order to detect protein functional modules and predict protein functions from PPI networks, such as Markov random field method and spectral clustering method [2]. However, PPI networks are complex because of enormous data volume. Furthermore, PPI networks usually consist of a large number of high-density protein nodes and some sparse connection nodes, which causes the networks to show the small-world and scale-free features. Hence, clustering is the primary tool for data mining in PPI networks.
Clustering methods are typical tools in data mining. Recently many clustering methods emerged [3], such as traditional partitioning methods [4], which can only find the globular cluster and, meanwhile, the cluster number should be known in advance, hierarchical methods [5–8] which are computationally expensive and are difficult in determining the merging threshold, density-based methods [9–13] which cannot categorize the network that has a large number of sparse nodes, MCL-based methods [14] which are suitable to hard clustering, spectral clustering methods [15] in which it is difficult to determine the neighborhood matrix, fuzzy clustering methods [16] which are sensitive to initial value and are easy to fall into local minimum, and so on. Functional flow clustering algorithm [17, 18] is a new clustering method for PPI networks, which regards each node as a “reservoir” and passes on the flow to the next node by the connecting edge. The algorithm is easy to be implemented and suitable for PPI networks. But the precision and recall values are not good enough. Thus it can be seen that these methods have different degrees of drawbacks in mining PPI networks due to the unique characteristics of PPI networks. We have done some researches on PPI networks clustering issues based on swarm intelligent optimization methods [19–21], but the performance of the algorithms still needs to be improved.
Some classical clustering algorithms split samples into some disjoint clusters; that is, one sample belongs to only one cluster absolutely. Results of these methods are not ideal for PPI networks in that there are some overlapping functional modules in PPI networks. In fact, proteins in PPI networks do not belong to a single cluster. According to the definition of fuzzy partition, Dunn [22] has extended hard clustering to fuzzy clustering, which allows one protein to belong to multiple clusters. This expresses the fuzzy concept of “it belongs to both this cluster and that cluster.” Therefore, fuzzy clustering algorithm is more suitable for clustering proteins in PPI networks. Fuzzy c-means (FCM) clustering method [23], optimal fuzzy clustering algorithm [24], and intuitionistic fuzzy clustering (IFC) [25] algorithm are commonly used. Traditional fuzzy clustering algorithms adopt distance as the measure of sample similarity criteria. As most nodes in PPI networks are unreachable, it is difficult to apply them to PPI networks effectively.
In this paper a new clustering model is proposed by combining artificial bee colony (ABC) optimization and intuitionistic fuzzy membership. Specifically, the proposed methods employ fuzzy membership matrix for partitioning initial clusters first. Then, a new clustering objective function is presented by taking characteristics of PPI networks, the similarity among clusters, and the density and the weights of interaction nodes within clusters into consideration. The new method also takes advantage of ABC algorithm to optimize the values of the objective function to gain the cluster results. In addition, the new algorithm makes use of ABC algorithm to optimize cluster centers automatically to overcome defects of sensitivity to cluster centers through fuzzy c-means clustering and intuitionistic fuzzy clustering algorithm. Computational experiments show that the new model and algorithm perform better than existing algorithms.
The rest of this paper is organized as follows. In Section 2, basic concepts and principles are introduced firstly; secondly the proposed ABC fuzzy clustering model is discussed, and then the flow chart and the computational step are listed, along with the time complexity analysis of the algorithm. Performance and evaluation of the ABC-IFC algorithm is shown by comparing with FCM and IFC in Section 3. Section 4 concludes this study.
2. Materials and Methods
2.1. Two Properties of PPI Networks
Watts and Strogatz [26] presented small-world property of complex networks, stating that most nodes are not neighbors of one another, while they can be reached from any of other nodes by a small number of hops or steps. A small-world network has smaller average distance than random networks and larger clustering coefficient than regular networks. There are some subnetworks in which almost any two nodes are connected because of the effect of the large clustering coefficient. On the other hand, any two nodes are connected mostly through one short path.
Regarding each network as an undirected graph, the e degree of node v is called k if node v has k adjacent node. P(k) represents the frequency of nodes with the degree of k; if P(k) follows the power-law distribution such as P(k) ∝ k −γ, with γ ∈ [2,3], the graph is considered scale-free. With scale-free property [27], only the degree of a small number of nodes is large while that of most nodes is small. Statistical physicists used to call the phenomenon following power-law distribution as scale-free phenomenon.
2.2. Fuzzy C-Means Clustering
Fuzzy C-means clustering (FCM) algorithm is described by Ruspini [28]. It is defined as follows: X = {x 1, x 2,…, x n} is cluster sample, n is the number of samples, c is the number of clusters, 1 < c < n, d ij = ||x i − v j|| is Euclidean distance between the sample x i and the cluster center v j, V = [v 1, v 2,…, v c] is cluster center matrix, U = [u ij] is n∗c membership matrix, and u ij is the degree of membership of x i that belongs to the cluster j. Update the degree of membership u ij and the cluster center v j by
| (1) |
where m = 2. The objective function is defined as
| (2) |
J will obtain the extremum when the matrix U is normalized.
2.3. Intuitionistic Fuzzy Clustering (IFC)
2.3.1. Intuitionistic Fuzzy Set Theory
Let X be a given domain; an intuitionistic fuzzy set R on X is given by
| (3) |
where μ R(x) : X → [0, 1] and ν R(x) : X → [0,1] denote degree of membership and nonmembership of R, respectively. For x ∈ X in R, it is true that 0 ≤ μ R(x) + ν R(x) ≤ 1. The general intuitionistic fuzzy set is denoted by R = 〈x, μ R(x), ν R(x)〉. The general intuitionistic fuzzy set is also marked as R = {〈x, μ R(x), 1 − μ R(x)〉 | x ∈ X}. π R(x) = 1 − u R(x) − ν R(x) denotes intuitionistic index of x in R, which is a measurement of uncertain degree.
2.3.2. Intuitionistic Fuzzy Clustering Algorithm
Let X = {x 1, x 2,…, x n} be a set of samples to be clustered; P = {p 1, p 2,…, p c} is a set of c clustering prototypes, where c is the number of clusters. The intuitionistic fuzzy set is given by R = {〈(x i, p j), μ, ν〉 | x i ∈ X, p j ∈ P}; (x i, p j) is the degree of membership of the sample i in the cluster j. V = [v 1, v 2,…, v c] is a group of cluster centers. Clustering prototype model (p ij), degree of hesitation (π ij), degree of membership (u ij), and degree of nonmembership (v ij) can be computed as follows:
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
where α = 0.4. e λk in (5) is solved according to the fast secant method. In intuitionistic fuzzy clustering algorithm, the degree of hesitation is always set in advance. In this paper, the degree of hesitation π is determined according to the PPI network nodes interaction weight w e.
Clustering analysis can be converted to optimization problem which aims at minimizing the objective function (clustering criterion function) J:
| (9) |
d(x i, p j) = (x i − p j)(x i − p j)T is the square of Euclidean distance between the sample i and clustering prototypej and must satisfy equation u ij + v ij + π ij = 1.
2.4. The ABC Algorithm
Artificial bee colony algorithm is an intelligent optimization algorithm proposed by Karaboga et al. [29–31] to solve the multivariate function optimization problems based on the intelligent behavior of honey bee swarm. Srinivasa Rao et al. [32] used it to solve network reconfiguration problem in distributed systems. Other researchers proposed chaotic artificial bee colony [33] and discrete artificial bee colony [34] algorithms. The artificial bee colony has become a research hotspot due to its simple idea, fast convergence rate, and superior performance. Our team had adopted it to optimize the threshold of clustering problem and achieved good results [35].
The ABC algorithm is a new metaheuristic bionic algorithm, where each bee can be viewed as an agent, and swarm intelligence is achieved through the cooperation between the individuals. The ABC algorithm includes two different mechanisms consisting of foraging behavior and propagating behavior. The ABC algorithm based on propagating mechanism was inspired by marriage behavior of bee colony [36]; the queen maintains good genes to make colony more adaptive to the environment. While the ABC algorithm based on foraging mechanism finds optimal solution through collaboration between the various types of bees and role conversion mechanism, the ABC algorithm provides a new idea for the heuristic algorithm research and becomes one of the important research directions of solving complex optimization problems.
The ABC algorithm based on foraging behavior typically contains four groups: nectar source, employed bees, onlooker bees, and scouts bees. A nectar source corresponds to an employed bee; the position of a nectar source represents a possible solution of optimization problem and its value depends on many factors, such as the degree of proximity between the nectar source and honeycomb or the degree of nectar source concentration and so on. The fitness is usually used to describe the nectar source features. The employed bees associate with certain nectar source, carrying a lot of nectar source information that is related to income level. The onlooker bees search and update new nectar source near honeycomb; if there are no nectar source for update, the scouts bees will search new nectar source in the global scope. Nectar source search follows two steps: firstly, the employed bees find nectar source and record the nectar source location and nectar quantity. Then the onlooker bees use the information the employed bees provided to decide which nectar source to go to, or scouts bees go on global searching to explore the new nectar source.
Based on foraging behavior, the ABC algorithm finds the global optimal value by each individual bees' local search, which has a faster convergence speed, higher precision, and few parameters. Therefore the ABC algorithm is used in this paper to optimize the IFC algorithm. The nectar sources stand for a set of clustering center of IFC algorithm; the cluster centers are optimized and updated by employed bees, onlookers bees, and scouts bees. It overcomes the sensitivity to clustering center of the IFC algorithm, while improving the effect of clustering.
2.5. ABC Fuzzy Clustering Model
2.5.1. The Solution Space
The small-world and scale-free properties of PPI networks make few nodes have a large degree; these nodes may have an important impact on protein functions. Most of the other nodes own a relatively small degree, and even the degree of some nodes is zero which are named isolated nodes. In PPI networks, a protein may possess diverse functions; as a result, it is inadvisable to hold the idea that all the protein nodes in a cluster are regarded as having an identical function. Therefore, a lot of clustering methods without considering the characteristics perform unsatisfactory toward PPI networks. IFC clustering algorithm fits well with PPI networks of a protein belonging to several functional modules. As mentioned above, ABC algorithm performs admirably; we establish a corresponding relationship between clustering and the optimization mechanism of bee colony (Table 1). Accordingly, a model based on the combination of ABC optimization mechanism and intuitionistic fuzzy method is put forward in this paper. We name the model ABC intuitionistic fuzzy clustering mode (ABC-IFC, for short). The method takes advantage of ABC algorithm to determine the optimal cluster centers and overcomes the weakness of sensitivity to cluster centers by fuzzy c-means clustering and intuitionistic fuzzy clustering algorithm. Utilizing intuitionistic fuzzy algorithm to cluster PPI networks is expected to improve the clustering effect because the idea is in line with the characteristics of PPI networks.
Table 1.
Corresponding relationship between clustering and mechanism of bee colony optimization.
| Foraging behavior of honey bees | Clustering |
|---|---|
| Position of nectar sources | Cluster centers |
| Amount of nectar sources | Value of objective function |
| Responsibilities of onlooker bees and scout bees | Searching for optimizing cluster centers |
| Highest nectar amount of nectar sources | Best cluster centers |
2.5.2. Principle of ABC Fuzzy Clustering Model
In the IFC clustering algorithm, a group of cluster centers are given randomly at the very beginning; afterwards the membership degree matrix is calculated and partitions are made according to it. Meanwhile the value of criteria is calculated until the algorithm satisfies the stopping condition and obtains the final clustering results. A set of initial cluster centers is generated randomly in IFC clustering algorithm, in which there are no rules to follow. Moreover the clustering criteria function is based on distance, which is unreasonable to deal with PPI networks. Hence, it is inefficient to cluster PPI networks by IFC clustering algorithm.
Since some nodes in PPI networks are unreachable, distance is not the suitable measure for clustering. As we know, there are interactions among nodes in PPI networks. We can compute the similarities among protein modules, density within modules, and average interactions using the interactions among the nodes. Accordingly, we redesign the criteria of IFC and evaluate the results in light of intermodule similarity, innermodule density, and similarity.
The new model ABC-IFC is proposed to seek the optimal cluster centers in this paper by combining IFC clustering algorithm and ABC algorithm. The ABC algorithm consists of three kinds of bees: employed bees, onlooker bees, and scout bees. In the ABC-IFC model, a nectar source stands for a group of cluster centers; the number of nectar sources is the number of clusters. Onlooker bees are responsible for exploiting new sources adjacent to employed bees and then updating the cluster centers. If onlooker bees fail to find the nectar source, scout bees will update cluster centers and search the whole area to revise the cluster centers. Finally, ABC algorithm will obtain the optimal cluster centers. IFC clustering algorithm will compute the fuzzy membership degree matrix based on the optimal cluster centers and, meanwhile, clusters are divided according to the membership degree matrix to obtain the clustering results in the end.
2.5.3. Objective Function
Traditional clustering algorithms usually adopt distance to define the objective function; moreover in weighted networks, the reciprocal of the weights is regarded as the measure of distance between two nodes. The shortest path distance between two nodes is usually regarded as the distance when the two nodes are not connected. However, some nodes in PPI networks are unreachable, and the reciprocal of weights becomes infinite when there is no interaction between two protein nodes, so it is unreasonable to use the shortest path distance as the distance between two nodes. Thus, a new objective function is designed to evaluate the cluster results. Our objective function includes two parts: the first part is the similarity between interclusters; the second part is the reciprocal of the average of summation of inner cluster's density and the weights between nodes within a cluster. The less the first part and the second part, the better the performance will be. Thus the objective function is defined as
| (10) |
where sim(I i, J j) = (∑x∈Ii,y∈Jj c(x, y))/max(|I i|, |J j|) stands for the similarity between two clusters,
| (11) |
n i represents the number of protein nodes in cluster i, e represents the number of interactions among the cluster and others in PPI networks, and w e represents the weights between nodes within a cluster.
The first part of (10) is similarity between two clusters, which is used to evaluate the similarity of two clusters; the smaller the similarity, the better the cluster effects will be, and vice versa. The second part is the reciprocal of the average of summation of inner cluster's density and the weights between nodes within a cluster, which reflects the strength of the interaction within a cluster. If there is no interaction between two nodes, the value of denominator of the second part may equal zero; that is, the second part tends to be infinitely small, and thus the first part becomes the criteria for cluster results. Otherwise, when the value of the second part is not zero, then the combination of similarity between two clusters, the density and weights within a cluster, can evaluate the cluster effect more comprehensively.
2.6. ABC-Based Fuzzy Clustering Algorithm
2.6.1. Algorithm Description
Step 1 —
Initialize the iterations iter = 1, maximum iteration maxiter, and clustering number c and randomly select clustering center V, limit = 0, and max_limit. Set gbestV = inf initially; gbestV represents a group of optimal cluster centers; gbest_cluster is the clustering result of the optimal cluster centers which is set randomly at the beginning.
Step 2 —
Calculate the degree of membership matrix U using (5)–(7), cluster is formed according to the membership degree matrix, and evaluate the fitness value fval(cluster) based on (10).
Step 3 —
If fval (cluster) < fval (gbest_cluster), gbestV = V and gbest_cluster = cluster.
Step 4 —
Onlookers bees search new nectar source near employed bees; if the search is successful, go to Step 6.
Step 5 —
If the search is a failure and limit > max limit, scouts bees start global searching; set limit = 0.
Step 6 —
Update the clustering center V.
Step 7 —
Set iter = iter + 1.
Step 8 —
If iter < = max iter, go to Step 2, otherwise out put the cluster result gbest_cluster.
2.6.2. Time Complexity of Algorithm
In time complexity analysis, asymptotic method is usually used to express the order of magnitude of program execution steps to estimate the performance of the algorithm. In ABC algorithm, if c represents cluster numbers, n is protein node, maximum iterations is maxiter, the population size is N which is twice the value of c, the node number of a class is num, and the time complexity of algorithm is as follows:
the time complexity of initializing the clustering center is O(n);
the time complexity of calculating the degree of membership matrix is O(n∗c);
the time complexity of updating the clustering center is O(max iter∗N∗num);
the time complexity of updating global optimal value is O(N);
the time complexity of cluster division is O(n∗c);
the time complexity of judging stopping condition is O(max iter).
From the above analysis we could find that the time complexity of (2) is dominating, the algorithm spends much time on the clustering center updating, which increases the time complexity.
3. Results and Discussions
3.1. Dataset and Criteria
In the experiments, the dataset of PPI networks comes from MIPS database [37], which consists of two sets of data: one is the experimental data which contains 1376 protein nodes and the 6880 interactive protein-pairs, which is considered the training database; the other describes the result that the proteins belong to identical functional module, which is regarded as the standard dataset [38], containing 89 clusters.
Precision, recall, P value, and their harmonic mean come to be the metric for evaluating the clustering in this paper. Precision [39] is the ratio of the maximal number of common nodes between experimental results and standard dataset to the number of nodes in experimental results. Recall [39] is the ratio of the maximal number of common nodes between experimental results and standard dataset to the number of nodes in the standard dataset. The equations are as follows:
| (12) |
where C stands for the obtained cluster results and F represents the standard dataset of MIPS. |C| is the number of nodes in the set C, |F| stands for the number of nodes in the standard dataset. MMS(C, F) denotes the number of the maximum matching nodes between experimental result and standard dataset.
A protein may possess various kinds of functions in PPI networks, so it is not advisable to consider that all the protein nodes in a cluster are regarded as having identical function. Thus, the definition of P value [40] comes to evaluate the reasonableness of this assignment. Suppose that the number of a cluster in the experiment is m, the number of protein nodes which possess identical function is d, the number of proteins in the standard database isM, and Dis the number of proteins which have the same function as each other. The P value is expressed as follows:
| (13) |
According to (13), the lower the P value is, the more confident the protein nodes comes from one cluster module and possess identical function, which provides instructive information for researchers to analyze the function of unknown proteins.
In general, large modules own high recall value because a large module C contains a lot of nodes in the set of F, and extremely, all nodes are gathered in the same cluster; in this case the recall value tends to the highest. On the contrary, small modules possess high precision because small modules have the same properties. Extremely each node can be a module and these modules have the highest precision. Hence, f-measure comes to be the metric for clustering in this paper which is shown in (14). Consider
| (14) |
3.2. Algorithm Parameter Analysis
In ABC algorithm, there are two important parameters, one is the prob, which is the probability that the onlooker bees select the nectar source, the other is the limit, which is the threshold indicating whether the scout bees will go on global searching.
Onlooker bees search the nectar source according to prob. A random number rand, arranged from 0 to 1, is generated firstly; if rand > prob, the onlooker bee chooses the node with the largest amount of information among the adjacent nodes of the employed bee to be the new cluster centers; otherwise, the node which has the second largest information is chosen to be the new cluster centers. Also limit is another important parameter in ABC algorithm. While there is no improvement of the cluster centers after limit times of loops, the cluster centers will be abandoned and the scout bees will search for a new solution of cluster centers.
Figure 1 shows the influence of parameter prob on the clustering results, prob is the parameter that onlooker bees select the nectar source according to the roulette wheel selection strategy. If the parameter is set too small, the possibility of onlooker bees searching local optimal clustering center is big and, meanwhile, the algorithm is easy to fall into local optimal. On the other hand, if it is too large, it could ensure the algorithm's diversity but onlooker bees could just find local suboptimal solution. From Figure 1, we find that the cluster effect is best when prob = 0.4.
Figure 1.
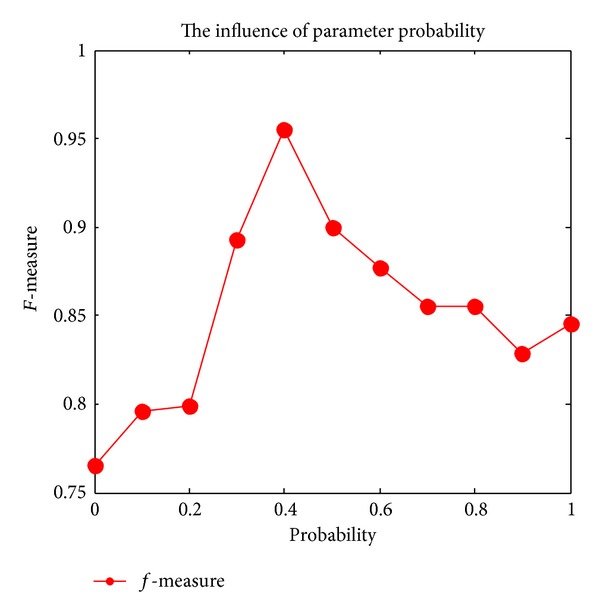
The influence of parameter prob.
Figure 2 shows the influence of parameter limit on the clustering results; limit is an important parameter in ABC algorithm which is used to determine whether the scout bees search the global area and update clustering center. From Figure 2, we can see that if limit is too small, the scout bees will constantly search new cluster centers to replace the current cluster centers, the algorithm will discard the optimal cluster centers. If limit is too large, the frequency of the scout bees searching the new solution will decrease and cause the algorithm to fall into local optimal and this will seriously affect the cluster results. Figure 2 show that when limit = 5, the algorithm reaches the best cluster results, and then when limit gradually increases, the cluster effect will gradually become poor.
Figure 2.
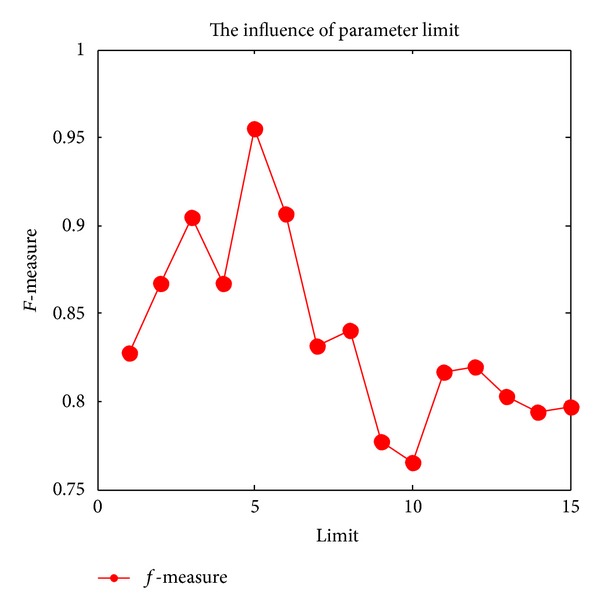
The influence of parameter limit.
3.3. Comparison of Performance among FCM, IFC, and ABC-IFC Algorithms
FCM clustering algorithm is very sensitive to the cluster centers; the performance of cluster results is poor. IFC algorithm is proposed based on fuzzy clustering, which performs better than FCM clustering, but the cluster effect is still not well enough. ABC-IFC algorithm overcomes the above drawbacks. Comparisons of precision, recall, P value, and f-measure of FCM algorithm, ICM algorithm and ABC-IFC algorithm are shown in Figures 3 to 6, respectively.
Figure 3.
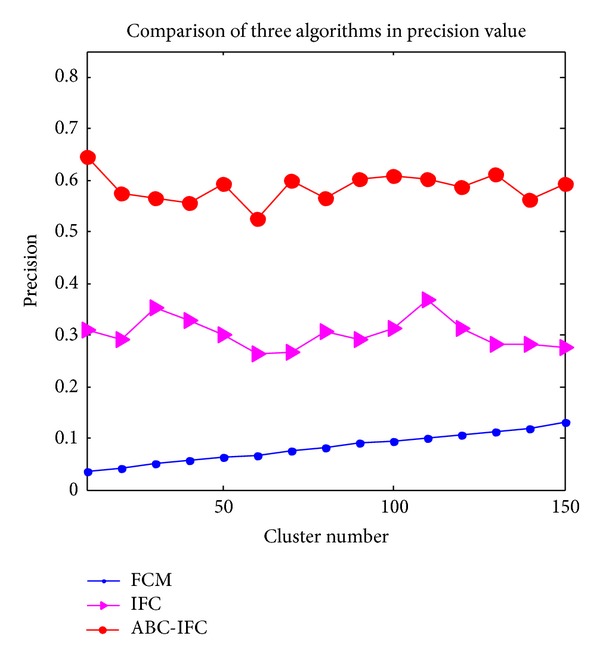
Comparison of three algorithms in precision value.
Figure 6.
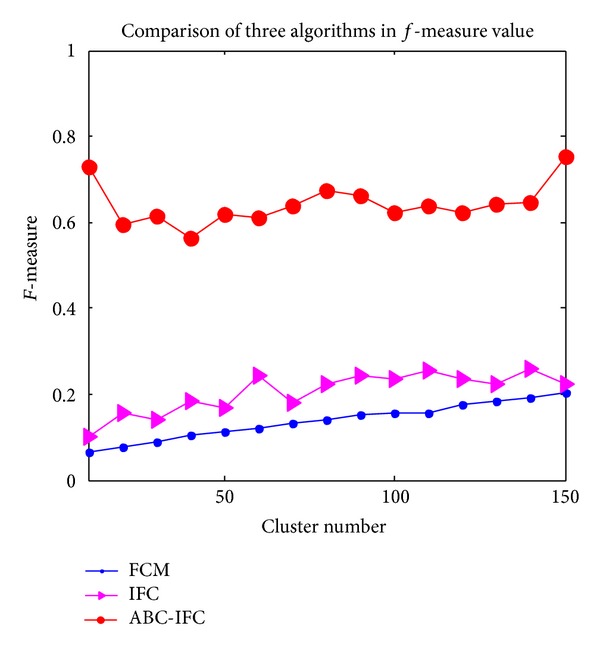
Comparison of three algorithms in f-measure value.
Figure 3 shows the comparison of precision of three algorithms. In Figure 3, it can be seen that ABC-IFC obtains the highest precision among three algorithms. The values of precision fluctuate largely when the number of clusters arranges from 20 to 70 and become steady and reach the best when the number of clusters is between 80 and 120. The precision values of IFC algorithm are between FCM and ABC-IFC algorithms; the highest precision is achieved when the cluster number is 110. Although precision tends to increase with the augment of cluster numbers in FCM algorithm, the precision of FCM is the lowest among three algorithms.
Figure 4 represents the comparison of recall value in three algorithms. Even if the values of ABC-IFC algorithm fluctuate strongly, they are the highest compared with the other algorithms. The values of FCM algorithm are higher than IFC but lower than ABC-IFC. From Figure 4, when the number of clusters is 110, the value tends to be the lowest. Recall of IFC is the worst among three algorithms.
Figure 4.
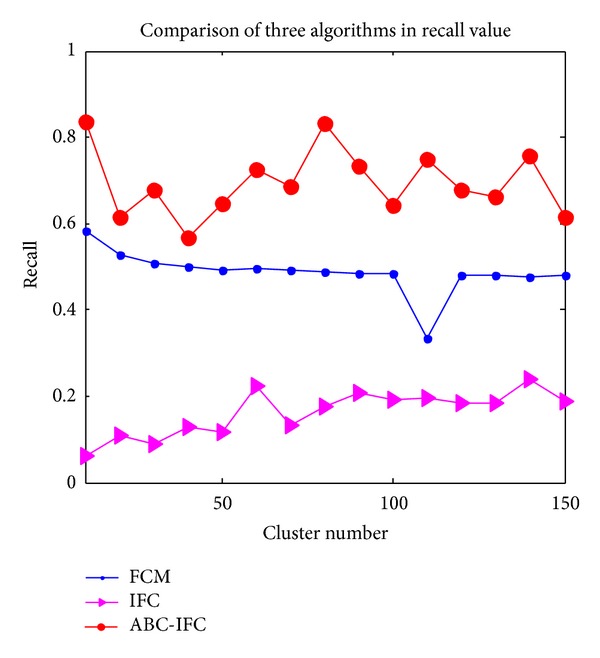
Comparison of three algorithms in recall value.
Figure 5 describes the comparison of P value among three algorithms. P value of ABC-IFC decreases with the cluster number increasing at the beginning. P value increases gradually after the cluster number increases to 80. What is more, P value becomes lower and holds steady when the number of clusters arranges from 80 to 120. P value of IFC is between ABC-IFC and FCM. The highest value and strongest fluctuation of P value appears in FCM.
Figure 5.
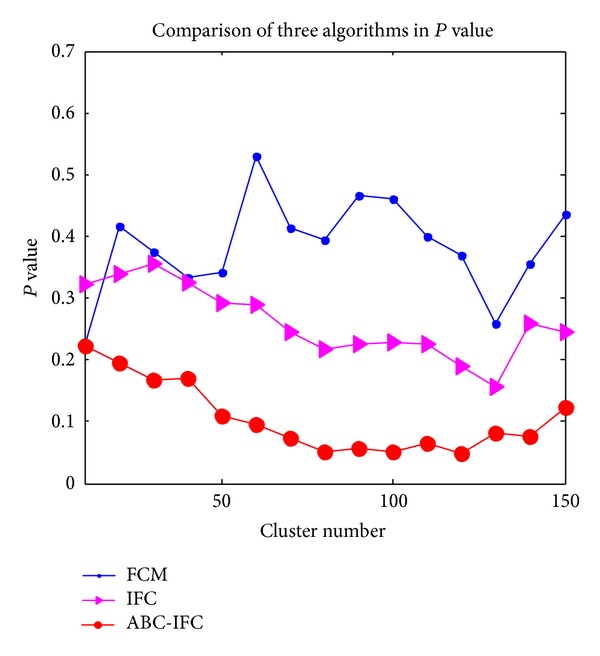
Comparison of three algorithms in Pvalue.
Comparison of f-measure among three algorithms is shown in Figure 6. f-measure of ABC-IFC is the highest among three algorithms and fluctuates slightly. Cluster results reach the best when the number of clusters changes from 80 to 90. f-measure of IFC is lower than ABC-IFC, in which f-measure tends to increase when the number of clusters increases, but the improvement is not obvious. f-measure of FCM increases with the clusters number increasing, but the values are far behind ABC-IFC. The cluster performance of IFC is better than FCM. However, ABC-IFC demonstrates excellent performance in terms of precision, recall, P value, and f-measure.
3.4. Cluster Results Analysis
Because it has a great impact on the algorithms, the number of cluster must be initialized first in ABC-IFC, IFC, and FCM algorithms. There is no rule to follow on determination of the number of clusters. Thus, the number of clusters tested was arranged from 10, 20, and 30 to 140 and 150. Table 2 shows the comparison of clustering results with different cluster numbers. In FCM algorithm, running time is very short. When the cluster number increases, recall decreases, the precision and f-measure increase. Although the running time is short, the values of both precision and f-measure are too small so that FCM algorithm is not feasible. IFC algorithm performs better than FCM in terms of precision; the recall value is lower than in FCM and the running time is not quite long. But precision, recall, P value, and f-measure are not well enough. The running time of ABC-IFC algorithm amplifies with the increase of cluster numbers. Precision, recall, and P value are better than the FCM and IFC algorithms; f-measure reaches the highest and ABC-IFC performs steady with various cluster numbers.
Table 2.
The comparison of three algorithms on different cluster numbers.
| Algorithm | Cluster number | Precision | Recall | Pvalue | F-measure |
|---|---|---|---|---|---|
| FCM | 10 | 0.0339 | 0.5814 | 0.2256 | 0.0641 |
| IFC | 10 | 0.3095 | 0.0606 | 0.3231 | 0.1014 |
| ABC-IFC | 10 | 0.6444 | 0.8373 | 0.2226 | 0.7283 |
|
| |||||
| FCM | 20 | 0.0409 | 0.5269 | 0.4166 | 0.0759 |
| IFC | 20 | 0.2924 | 0.1074 | 0.3383 | 0.1571 |
| ABC-IFC | 20 | 0.5741 | 0.6156 | 0.1964 | 0.5941 |
|
| |||||
| FCM | 30 | 0.0499 | 0.5080 | 0.3753 | 0.0909 |
| IFC | 30 | 0.3525 | 0.0883 | 0.3555 | 0.1412 |
| ABC-IFC | 30 | 0.5647 | 0.6789 | 0.1667 | 0.6166 |
|
| |||||
| FCM | 40 | 0.0581 | 0.5006 | 0.3322 | 0.1041 |
| IFC | 40 | 0.3288 | 0.1288 | 0.3253 | 0.1851 |
| ABC-IFC | 40 | 0.5559 | 0.5691 | 0.1698 | 0.5624 |
|
| |||||
| FCM | 50 | 0.0624 | 0.4905 | 0.3405 | 0.1107 |
| IFC | 50 | 0.3010 | 0.1172 | 0.2907 | 0.1687 |
| ABC-IFC | 50 | 0.5933 | 0.6452 | 0.1094 | 0.6182 |
|
| |||||
| FCM | 60 | 0.0675 | 0.4960 | 0.5303 | 0.1188 |
| IFC | 60 | 0.2628 | 0.2236 | 0.2893 | 0.2416 |
| ABC-IFC | 60 | 0.5254 | 0.7253 | 0.0510 | 0.6094 |
|
| |||||
| FCM | 70 | 0.0765 | 0.4920 | 0.4147 | 0.1324 |
| IFC | 70 | 0.2671 | 0.1343 | 0.2456 | 0.1787 |
| ABC-IFC | 70 | 0.5984 | 0.6864 | 0.0720 | 0.6394 |
|
| |||||
| FCM | 80 | 0.0831 | 0.4864 | 0.3930 | 0.1419 |
| IFC | 80 | 0.3057 | 0.1777 | 0.2171 | 0.2248 |
| ABC-IFC | 80 | 0.5665 | 0.8331 | 0.0954 | 0.6744 |
|
| |||||
| FCM | 90 | 0.0894 | 0.4861 | 0.4670 | 0.1510 |
| IFC | 90 | 0.2900 | 0.2068 | 0.2246 | 0.2414 |
| ABC-IFC | 90 | 0.6034 | 0.7331 | 0.0561 | 0.6620 |
|
| |||||
| FCM | 100 | 0.0938 | 0.4829 | 0.4597 | 0.1571 |
| IFC | 100 | 0.3136 | 0.1899 | 0.2279 | 0.2366 |
| ABC-IFC | 100 | 0.6081 | 0.6416 | 0.0508 | 0.6244 |
|
| |||||
| FCM | 110 | 0.1015 | 0.3337 | 0.3986 | 0.1557 |
| IFC | 110 | 0.3666 | 0.1956 | 0.2242 | 0.2551 |
| ABC-IFC | 110 | 0.6032 | 0.6785 | 0.0656 | 0.6386 |
|
| |||||
| FCM | 120 | 0.1073 | 0.4801 | 0.3685 | 0.1754 |
| IFC | 120 | 0.3193 | 0.1840 | 0.1903 | 0.2335 |
| ABC-IFC | 120 | 0.5873 | 0.6637 | 0.0479 | 0.6232 |
|
| |||||
| FCM | 130 | 0.1124 | 0.4819 | 0.2595 | 0.1823 |
| IFC | 130 | 0.2813 | 0.1849 | 0.1577 | 0.2231 |
| ABC-IFC | 130 | 0.6118 | 0.6734 | 0.0825 | 0.6411 |
|
| |||||
| FCM | 140 | 0.1192 | 0.4763 | 0.4354 | 0.1907 |
| IFC | 140 | 0.2818 | 0.2373 | 0.2576 | 0.2576 |
| ABC-IFC | 140 | 0.5622 | 0.7579 | 0.0750 | 0.6455 |
|
| |||||
| FCM | 150 | 0.1303 | 0.4793 | 0.4354 | 0.2049 |
| IFC | 150 | 0.2759 | 0.1886 | 0.2456 | 0.2240 |
| ABC-IFC | 150 | 0.7491 | 0.7537 | 0.0830 | 0.7514 |
Due to space limitations, Table 3 only listed the correctly and wrongly classified proteins in 8 clusters. It can be seen from Table 3 that the four clusters marked 1, 3, 6, and 8 are completely correct; clusters marked 2, 4, 5, and 7 are partly correct. Between the correctly and wrongly classified proteins, we can see that the proteins having the different functions provide a foundation for the research on the connection between different protein functional modules. The correctly classified proteins have the same function, which provides analysis basis for us to identify protein functional modules and predict protein function accurately.
Table 3.
The proteins classified correctly and wrongly in certain cluster.
| Ordinal cluster | The proteins classified correctly | The proteins classified wrongly | |||||
| 1 | YJL154c | YJL053w | YHR012w | — | |||
| 2 | YLR382c YKR052c |
YBR120c YDR194c |
YPR134w YIR021w |
YOR334w Q0120 |
YHR005c-a YDL044c |
YMR023c YGR222w |
YJL133w |
| 3 | YDR167w YPL254w YLR055c YHR099w |
YDR392w YCL010c YOL148c YDR145w |
YGR252w YDR176w YGL066w YBR198c |
YGL112c YDR448w YBR081c Y MR236w |
— | ||
| 4 | YNL151c YPR110c YOR116c |
YOR224c YHR143w-a YKL144c |
YOR210w YOR207c |
YPR190c YBR154c |
YNL113w | YPR187w | YNR003c |
| 5 | YPL218w YAL007c |
YIL109c YAR002c-a |
YPL085w YAL042w |
YML012w |
YGL200c YLR208w |
YPR181c |
YDL195w |
| 6 | YOR224c YOR210w YBR154c YPR187w |
YDL140c YIL021w YLR418c |
YOL005c YDR404c YGL070c YOR151c |
YJL140w YHR143w |
— | ||
| 7 | YDR167w YPL254w |
YDR392w YCL010c |
YGR252w | YGL112c | YDR176w YOL148c YHR099w YMR236w |
YDR448w YGL066w YDR145w |
YLR055c YBR081c YBR198c |
| 8 | YHR069c YDL111c |
YDR280w YGR095c |
YOL021c YCR035c |
YGR195w |
— | ||
4. Conclusions
In this paper, the fuzzy clustering algorithm has been used in PPI network clustering. Because there are some nodes unreachable in PPI network, we have redesigned the clustering objective function and proposed a novel clustering model combined with the optimization mechanism of artificial bee colony with the intuitionistic fuzzy clustering. The computational results on PPI dataset have shown that the algorithm could not only overcome the drawbacks of sensitivity to clustering center, but also have the highest accuracy and recall rate, the lowest P value, and the best f-measure among the competing algorithms. Meanwhile, the algorithm has a good effect on PPI network functional modules and also has great potential to solve other small-world and scale-free characterized complex network problems.
Acknowledgments
This paper is supported by the National Natural Science Foundation of China (nos. 61100164 and 61173190), Scientific Research Start-up Foundation for Returned Scholars, Ministry of Education of China ([2012]1707), and the Fundamental Research Funds for the Central Universities, Shaanxi Normal University (nos. GK201402035 and GK201302025).
Conflict of Interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
References
- 1.Graves PR, Haystead TAJ. Molecular biologist’s guide to proteomics. Microbiology and Molecular Biology Reviews. 2002;66(1):39–63. doi: 10.1128/MMBR.66.1.39-63.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Yang B, Liu D-Y, Liu J, Jin D, Ma H-B. Complex network clustering algorithms. Journal of Software. 2009;20(1):54–66. [Google Scholar]
- 3.Wang J, Li M, Deng Y, Pan Y. Recent advances in clustering methods for protein interaction networks. BMC Genomics. 2010;11(supplement 3, article S10) doi: 10.1186/1471-2164-11-S3-S10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hartigan JA, Wong MA. Algorithm AS 136: a K-Means clustering algorithm. Journal of the Royal Statistical Society C. 1979;28(1):100–108. [Google Scholar]
- 5.Luo F, Yang Y, Chen C-F, Chang R, Zhou J, Scheuermann RH. Modular organization of protein interaction networks. Bioinformatics. 2007;23(2):207–214. doi: 10.1093/bioinformatics/btl562. [DOI] [PubMed] [Google Scholar]
- 6.Li M, Wang J, Chen J. A fast agglomerate algorithm for mining functional modules in protein interaction networks. Proceedings of the International Conference on BioMedical Engineering and Informatics; May 2008; pp. 3–7. [Google Scholar]
- 7.Li M, Wang J, Chen J, Pan Y. Bioinformatics Research and Applications. Vol. 5542. Berlin, Germany: Springer; 2009. Hierarchical organization of functional modules in weighted protein interaction networks using clustering coefficient; pp. 75–86. (Lecture Notes in Computer Science). [Google Scholar]
- 8.Wang J, Li M, Chen J, Pan Y. A fast hierarchical clustering algorithm for functional modules discovery in protein interaction networks. IEEE/ACM Transactions on Computational Biology and Bioinformatics. 2011;8(3):607–620. doi: 10.1109/TCBB.2010.75. [DOI] [PubMed] [Google Scholar]
- 9.Palla G, Derényi I, Farkas I, Vicsek T. Uncovering the overlapping community structure of complex networks in nature and society. Nature. 2005;435(7043):814–818. doi: 10.1038/nature03607. [DOI] [PubMed] [Google Scholar]
- 10.Adamcsek B, Palla G, Farkas IJ, Derényi I, Vicsek T. CFinder: locating cliques and overlapping modules in biological networks. Bioinformatics. 2006;22(8):1021–1023. doi: 10.1093/bioinformatics/btl039. [DOI] [PubMed] [Google Scholar]
- 11.Li M, Chen J, Wang J, Hu B, Chen G. Modifying the DPClus algorithm for identifying protein complexes based on new topological structures. BMC Bioinformatics. 2008;9, article 398 doi: 10.1186/1471-2105-9-398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wang J, Liu B, Li M, Pan Y. Identifying protein complexes from interaction networks based on clique percolation and distance restriction. BMC Genomics. 2010;11(supplement 2, article S10) doi: 10.1186/1471-2164-11-S2-S10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ren J, Wang J, Li M, Wang L. Identifying protein complexes based on density and modularity in protein-protein interaction network. BMC Systems Biology. 2013;7, article S12 doi: 10.1186/1752-0509-7-S4-S12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Srihari S, Ning K, Leong HW. MCL-CAw: a refinement of MCL for detecting yeast complexes from weighted PPI networks by incorporating core-attachment structure. BMC Bioinformatics. 2010;11, article 504 doi: 10.1186/1471-2105-11-504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bu D, Zhao Y, Cai L, et al. Topological structure analysis of the protein-protein interaction network in budding yeast. Nucleic Acids Research. 2003;31(9):2443–2450. doi: 10.1093/nar/gkg340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sun PG, Gao L, Han SS. Identification of overlapping and non-overlapping community structure by fuzzy clustering in complex networks. Information Sciences. 2011;181(6):1060–1071. [Google Scholar]
- 17.Nabieva E, Jim K, Agarwal A, Chazelle B, Singh M. Whole-proteome prediction of protein function via graph-theoretic analysis of interaction maps. Bioinformatics. 2005;21(1):i302–i310. doi: 10.1093/bioinformatics/bti1054. [DOI] [PubMed] [Google Scholar]
- 18.Cho Y-R, Hwang W, Zhang A. Optimizing flow-based modularization by iterative centroid search in protein interaction networks. Proceedings of the 7th IEEE International Conference on Bioinformatics and Bioengineering (BIBE '07); January 2007; pp. 342–349. [Google Scholar]
- 19.Lei X, Tian J, Ge L, Zhang A. The clustering model and algorithm of PPI network based on propagating mechanism of artificial bee colony. Information Sciences. 2013;247:21–39. [Google Scholar]
- 20.Lei X, Huang X, Shi L, Zhang A. Clustering PPI data based on Improved functional-flow model through Quantum-behaved PSO. International Journal of Data Mining and Bioinformatics. 2012;6(1):42–60. doi: 10.1504/ijdmb.2012.045545. [DOI] [PubMed] [Google Scholar]
- 21.Lei X, Wu S, Ge L, Zhang A. Clustering and overlapping modules detection in PPI network based on IBFO. Proteomics. 2013;13(2):278–290. doi: 10.1002/pmic.201200309. [DOI] [PubMed] [Google Scholar]
- 22.Dunn JC. A graph theoretic analysis of pattern classification via Tamura’s fuzzy relation. IEEE Transactions on Systems, Man, and Cybernetics. 2000;4(3):310–313. [Google Scholar]
- 23.Bertoluzza C, Solci M, Capodieci ML. Measure of a fuzzy set. The α-cut approach in the finite case. Fuzzy Sets and Systems. 2001;123(1):93–102. [Google Scholar]
- 24.Ma J, Shao L. Optimal algorithm for fuzzy classification problem. Journal of Software. 2001;12(4):578–581. [Google Scholar]
- 25.Yuan X, Li H, Sun K. The cut sets, decomposition theorems and representation theorems on intuitionistic fuzzy sets and interval valued fuzzy sets. Science China Information Sciences. 2011;54(1):91–110. [Google Scholar]
- 26.Watts DJ, Strogatz SH. Collective dynamics of “small-world” networks. Nature. 1998;393(6684):440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- 27.Barabási A-L, Albert R. Emergence of scaling in random networks. Science. 1999;286(5439):509–512. doi: 10.1126/science.286.5439.509. [DOI] [PubMed] [Google Scholar]
- 28.Ruspini EH. A new approach to clustering. Information and Control. 1969;15(1):22–32. [Google Scholar]
- 29.Karaboga D, Basturk B. A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm. Journal of Global Optimization. 2007;39(3):459–471. [Google Scholar]
- 30.Karaboga D, Basturk B. On the performance of artificial bee colony (ABC) algorithm. Applied Soft Computing. 2008;8(1):687–697. [Google Scholar]
- 31.Karaboga D, Akay B. A comparative study of artificial bee colony algorithm. Applied Mathematics and Computation. 2009;214(1):108–132. [Google Scholar]
- 32.Srinivasa Rao R, Narasimham SVL, Ramalingaraju M. Optimization of distribution network configuration for loss reduction using artificial bee colony algorithm. International Journal of Electrical Power and Energy Systems Engineering. 2008;1(2)7092715 [Google Scholar]
- 33.Zhang YD, Wu LN, Wang SH, Huo YK. Chaotic artificial bee colony used for cluster analysis. Communication in Computer and Information Science. 2011;134:205–211. [Google Scholar]
- 34.Tasgetiren MF, Pan Q-K, Suganthan PN, Chen AH-L. A discrete artificial bee colony algorithm for the total flowtime minimization in permutation flow shops. Information Sciences. 2011;181(16):3459–3475. [Google Scholar]
- 35.Lei X, Huang X, Zhang A. Improved artificial bee colony algorithm and its application in data clustering. Proceedings of the 5th IEEE International Conference on Bio-Inspired Computing: Theories and Applications (BIC-TA '10); September 2010; Changsha, China. pp. 514–521. [Google Scholar]
- 36.Hadded OB, Afshar AMBO. MBO (Marriage Bees Optimization), a new heuristic approach in hydrosystems design and operation. Proceedings of the 1st International Conference on Managing Rivers in the 21st Century; 2004; pp. 499–504. [Google Scholar]
- 37.Güldener U, Münsterkötter M, Kastenmüller G, et al. CYGD: the comprehensive yeast genome database. Nucleic Acids Research. 2005;33:D364–D368. doi: 10.1093/nar/gki053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Mewes HW, Frishman D, Mayer KF, et al. MIPS: analysis and annotation of proteins from whole genomes in 2005. Nucleic Acids Research. 2006;34:D169–D172. doi: 10.1093/nar/gkj148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Zhang AD. Protein Interaction Networks. New York, NY, USA: Cambridge University Press; 2009. [Google Scholar]
- 40.Ucar D, Asur S, Catalyurek U. Knowledge Discovery in Databases: PKDD 2006. Vol. 4213. Berlin, Germany: Springer; 2006. Improving functional modularity in protein-protein interactions graphs using hub-induced subgraphs; pp. 371–382. (Lecture Notes in Computer Science). [Google Scholar]


