Mass univariate analysis of event-related brain potentials/fields I: A critical tutorial review

Abstract

Event-related potentials (ERPs) and magnetic fields (ERFs) are typically analyzed via ANOVAs on mean activity in a priori windows. Advances in computing power and statistics have produced an alternative, mass univariate analyses consisting of thousands of statistical tests and powerful corrections for multiple comparisons. Such analyses are most useful when one has little a priori knowledge of effect locations or latencies, and for delineating effect boundaries. Mass univariate analyses complement and, at times, obviate traditional analyses. Here we review this approach as applied to ERP/ERF data and four methods for multiple comparison correction: strong control of the family-wise error rate (FWER) via permutation tests, weak control of FWER via cluster-based permutation tests, false discovery rate control, and control of the generalized FWER. We end with recommendations for their use and introduce free MATLAB software for their implementation.

1. Introduction

A great methodological strength of the event-related brain potential (ERP) and magnetic field (ERF) techniques are their ability to track subtle differences in rapidly changing neurally generated electromagnetic fields at multiple spatial locations with millisecond resolution. These ERP/ERF data are comprised of vast numbers of observations with abundant non-zero correlations in space and time. Currently, the most common statistical analyses of ERPs/ERFs, a limited number of ANOVAs conducted on point measures such as mean or peak amplitude (Dien & Santuzzi, 2005), do not take full advantage of this wealth of information. Such analyses may detect the presence of an effect but typically provide relatively crude information as to when and where an effect occurs. However, advances in statistical theory, together with cheap, fast, computers, provide alternatives that do. In this article, we consider in depth one type of approach, mass univariate analyses (Woolrich, Beckmann, Nichols, & Smith, 2009) in which a large number of univariate tests, e.g., t-tests, can be properly used to compare ERPs/ERFs at an exhaustive number of time points and scalp locations. Crucial for this type of analysis are procedures that remove or mitigate the increased probability of false discoveries inherent in doing lots of hypothesis tests. Although versions of these methods have been introduced to EEG/MEG researchers previously (Blair & Karniski, 1993; Hemmelmann et al., 2004; Hemmelmann et al., 2005; Lage-Castellanos, Martinez-Montes, Hernandez-Cabrera, & Galan, 2010; Maris & Oostenveld, 2007), mass univariate analyses do not yet enjoy the widespread application in ERP/ERF research that they do in the analysis of fMRI data. This report presents a more comprehensive tutorial review than has appeared previously in connection with ERP/ERF research, followed by a critical evaluation and comparison of these procedures in light of important practical issues that have not been adequately discussed in the ERP/ERF literature. Moreover, in a companion paper (Groppe, Urbach, & Kutas, 2011), we report novel results evaluating the power and accuracy of these methods when applied to realistic simulated ERP data. Those simulations provide some sense of the relative utility of these different methods when applied to different types of ERP effects and of the accuracy of some methods when ERP data violate their assumptions. The aim of these reports is to show how mass univariate analyses are a valuable complement to and, in some cases, may even obviate the need for conventional ERP/ERF analyses.

To illustrate the mass univariate approach and its value, consider a typical ERP/ERF experiment, here a visual oddball paradigm (Groppe, Makeig, & Kutas, 2009, Experiment 3). In this experiment, participants were shown a series of words in uppercase (e.g., “BROWN”) or lowercase letters (e.g., “brown”) embedded in a series of the alternate case and instructed to silently count whenever one of those two categories of words appeared. The grand average ERPs elicited by the higher probability words (standards) and lower probability words (targets) are presented in Figure 1. Their difference is shown Figure 2-A. Typically, these ERPs would be analyzed in one or more time windows of interest based upon known ERP phenomena (e.g., a P2 window from 225 to 275 ms and a P3¹ window from 300 to 600 ms) by taking the mean ERP amplitude in those time windows and submitting them to repeated measure ANOVAs with two factors: stimulus type and electrode location.

Figure 1.

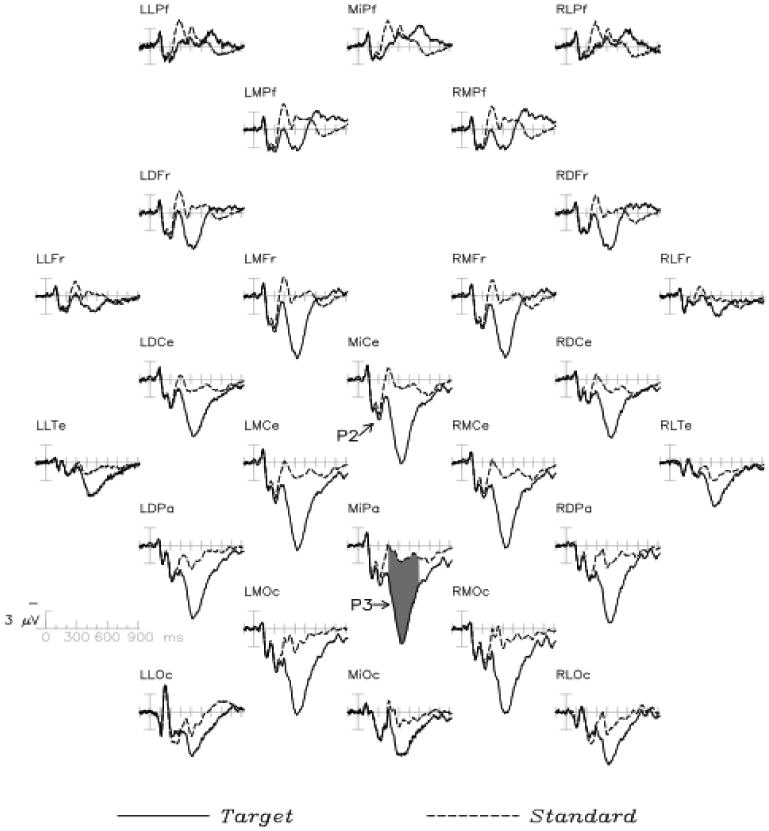
ERPs to targets and standards in a visual oddball task at 26 scalp electrodes. ERP figure locations represent corresponding electrode scalp locations. Up/down and left/right on the figure corresponds to anterior/posterior and left/right on the scalp, respectively. Shading indicates P3 effect time window (300 to 600 ms). Note that positive is visualized as down on the y-axes, a common convention in ERP research.

Figure 2.

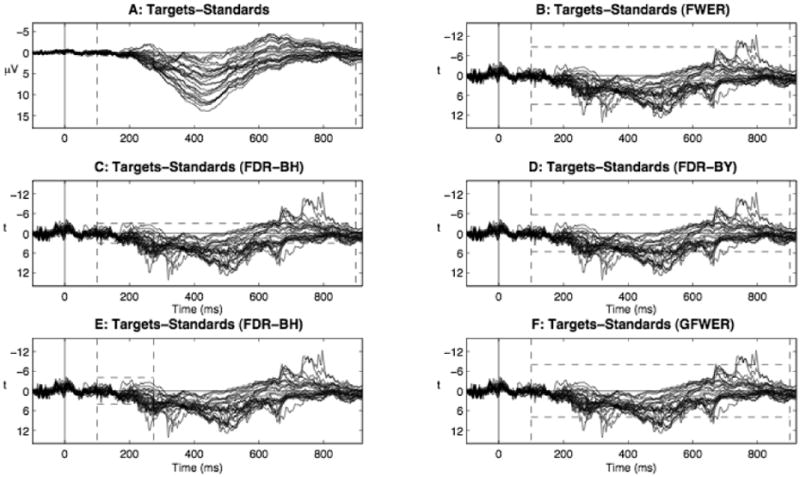
Butterfly plots illustrating difference waves in a visual oddball task. Each waveform in each plot represents the data at one of 26 scalp electrodes. All electrodes are visualized on the same axis for economy. Vertical dashed lines represent the time window analyzed (100 to 900 ms or 100 to 275 ms). Horizontal dashed lines represent critical t-scores derived from one of four analysis procedures. t-scores more extreme than critical t-scores indicate a significant difference between ERPs to targets and standards. FWER, FDR-BH, FDR-BY, and GFWER control was obtained via a t_max permutation test, the Benjamini and Hochberg (BH) FDR control procedure, the Benjamini and Yekutieli (BY) FDR control procedure, and Korn et al.'s GFWER control procedure (KTMS), respectively. Note that positive is visualized as down on the y-axes, a common convention in ERP research.

This approach has three obvious shortcomings. First, this analysis will miss any unexpected effects outside of the time windows of analysis. Indeed, inspection of the ERP waveforms in this case suggests some possible effects in addition to those in the P2 and P3 regions. At prefrontal electrodes, for instance, standard stimuli elicit a larger N2 on average than do targets, peaking around 300 ms and spanning the predetermined P2 and P3 analysis windows. Later in the epoch, after about 550 ms, the polarity of the oddball effect reverses with the ERPs to targets over prefrontal sites being more negative than those to standards. At other electrode locations, the standard and target waveforms begin to diverge somewhat before 300 ms and the resulting P3 effect appears to persist well beyond 600 ms. Of course, upon seeing these results, one could use conventional ANOVAs or t-tests to assess their significance (e.g., Hauk et al., 2006). However, such post hoc testing will overestimate the significance of differences to an unknown degree and thus cannot be trusted (Kriegeskorte, Simmons, Bellgowan, & Baker, 2009).

A related, additional shortcoming of this approach is that it requires investigators to know beforehand approximately when and where an effect will occur. For effects like the P3, whose latency can vary greatly across experimental paradigms (e.g., Bentin, Mouchetant-Rostaing, Giard, Echallier, & Pernier, 1999), this can be difficult. Finally, a third problem illustrated by conventional analysis of these data is that it provides a rather crude idea as to the timing and locus of effects. For example, with these data an ANOVA shows that the difference between targets and standards in the P3 time window is highly significant (main effect of stimulus type: F(1,7)=56.14, p=0.0001) and differs across electrodes (stimulus type by electrode interaction: F(25,175)=24.43, p<0.0001), but little about its onset, offset, or precisely at which electrodes the effect is reliably present. Follow up analyses at each electrode via a procedure such as Tukey's HSD could readily answer the latter question. However, determining the onset and offset of effects is much trickier. Some researchers have attempted to identify effect onsets by performing multiple tests at fixed intervals (e.g., every 100 ms--Revonsuo, Portin, Juottonen, & Rinne, 1998) without correcting for the multiple comparisons². This approach will tend to overestimate effect onsets to a potentially great degree due to the increased risk of false discoveries (i.e., “Type I errors”), depending on the number of comparisons. Alternatively, some researchers have defined the onset of effects as the first time point of a series of consecutive tests (e.g., 15 t-tests--Thorpe, Fize, & Marlot, 1996) each significant at an alpha level of 5%. This criterion is problematic in practice given that it is hard to know what the overall chance of error is and thus how many consecutive tests are required.

In contrast, the mass univariate approach to these data is illustrated in Figure 2-B, which shows the difference between ERPs to targets and standards at all electrodes and time points of interest as t-scores. Each t-score effectively shows the result of performing a t-test at each time point and electrode. The greater the t-score, the more reliably the ERPs to targets and standards differ. If we were to perform only a single two-tailed t-test, a t-score of +/-2.36 would correspond to an alpha level of 5% and a t-score more extreme than that would conventionally be considered a significant (i.e., reliable) difference³. However, given the large number of comparisons (5226 from 100 to 900 ms, our time window of interest) a t-score of +/-2.36 cannot serve as a significance threshold since this would very likely result in many differences that are due to noise being mistakenly identified as reliable. In fact, in this example, many t-scores before stimulus onset exceed +/-2.36. Given the experimental design, reliable differences between target and standard responses before their occurrence is nonsensical and a cause for interpretive concern.

Instead, therefore, we derive more conservative critical t-scores of +/- 8.73 via a permutation test procedure (see Section 2 below) that guarantees a 5% chance of making one or more false discoveries (i.e., the same degree of protection provided by Bonferroni correction or an a priori test window) in the entire set (i.e., “family”) of 5226 t-tests. One can see in Figures 2-B and 3 that there are several differences between standard and target responses. As expected, the ERPs to targets and standards differ in the P2 and P3 time windows at centro-medial and central-to-posterior electrodes, respectively. Moreover, we have precise lower bounds on when the effects begin and end, and know precisely where on the scalp the effect was detected. For example, the first and last significant t-scores for the P2 effect are at 252 and 272 ms, respectively, at electrode MiCe. And, although the P2 effect may begin earlier and/or last longer, we can say with 95% certainty that it begins by 252 ms and lasts until at least 272 ms. Finally, the other great advantage of this mass univariate procedure is that three unexpected effects outside of the P2 and P3 time windows were identified. Specifically, there is a left frontal N2-like effect from 316 to 360 ms, a posterior effect from 656 to 664 ms, and an apparent “slow wave” effect at medial prefrontal electrodes from 736 to 800 ms.

Figure 3.

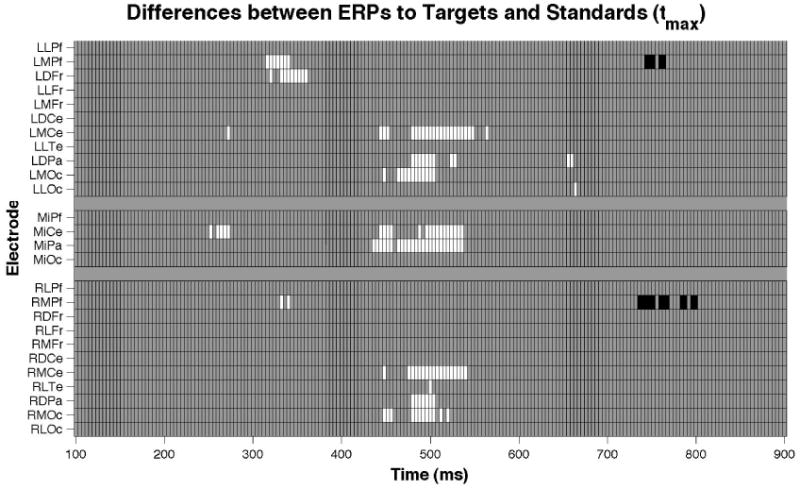
Raster diagram illustrating significant differences between ERPs to targets and standards from a visual oddball task according to a t_max permutation test. White and black rectangles indicate electrodes/time points in which the ERPs to targets are more positive and negative, respectively. Grey rectangles indicate electrodes/time points at which no significant differences were found. Note that the electrodes are organized along the y-axis somewhat topographically. Electrodes on the left (e.g., Left Lateral Prefrontal-LLPf) and right (e.g., Right Lateral Prefrontal-RLPf) sides of the head are grouped on the figure's top and bottom, respectively. Midline electrodes (e.g., Midline Central-MiCe) are shown in the middle. Within those three groupings, y-axis top-to-bottom corresponds to scalp anterior-to-posterior. Five effects are apparent: a P2 effect at MiCe around 250 ms, a left frontal effect around 325 ms, a P3 effect at central and posterior electrodes from 440-540 ms, a left posterior effect around 660 ms, and a slow wave effect at medial prefrontal electrodes around 750 ms.

For these data, the mass univariate approach clearly outperforms the conventional analysis in that it detected the expected effects with greater temporal and spatial detail and discovered several unexpected ERP effects. At the same time, however, the benefits of mass univariate analyses do come at the cost of less statistical power than a priori tests that do not require correction for multiple comparisons. In other words, mass univariate analyses are thus somewhat less likely to detect effects than conventional ANOVAs applied to a priori time windows. For example, the permutation test-derived critical t-scores of +/- 8.73 correspond to an alpha level of 0.005% for each t-test. Thus, our test is three orders of magnitude more conservative than if we had performed a single t-test on an a priori defined time point and electrode (or mean across time points and electrodes) using the same family-wise alpha level of 5%.

Many methods for correcting for multiple comparisons have been developed to counter the reduction in statistical power (for review see Farcomeni, 2008; Romano et al., 2008). In general, these various methods differ in the degree to which they increase statistical power by reducing the certainty that any single effect is reliable, the degree to which they can exploit possible dependencies between the multiple tests, and the set of circumstances in which the methods are guaranteed to work. In this article, we review and critically evaluate four such types of procedures. Each type of procedure is based on a different type of false discovery statistic that is explicitly controlled. The first method is a permutation test procedure which, like Bonferroni correction, “strongly” controls the family-wise-error rate (FWER), the probability that one or more false discoveries is made in the entire family of tests where family refers to all the tests related to a particular experimental contrast (e.g., targets vs. standards). The second method, cluster-based permutation tests, provides “weak” FWER control by grouping test results at nearby time points and sensors into clusters based on their statistical significance and proximity. Weak FWER control (Nichols & Hayasaka, 2003) means that FWER is only guaranteed to be controlled if there are no experimental effects (i.e., all the null hypotheses in the family of tests are true). The third method, false discovery rate (FDR) controls the mean proportion of ostensibly significant test results that are actually false discoveries in the family of tests. For example, if a family of hypothesis tests is corrected in such a way that the FDR is limited to 5%, that means that if the experiment were repeated an astronomical number of times, on average 5% or less of the rejected hypotheses would be rejected mistakenly (although in any particular experiment there might be more than 5% or less than 5%). The third method, generalized family-wise error rate (GFWER), is a relaxed version of strong FWER control. Instead of controlling the probability that no false discoveries are made, GFWER controls the probability that no more than some allowable, typically small, number of false discoveries is made.

We now turn to consider each of these approaches in more detail, each on its own merits, and in comparison with one another. We conclude with an overview and considerations governing the sound application of these methods to ERP/ERF data in practice.

2. Permutation Test Based Strong Control of the Family-Wise Error Rate

2.1 Introduction to Permutation Tests

Permutation tests date back to the early 20th century (Good, 2005) and are based on the insight that if two sets of samples are drawn from a single population of individuals the different observations are “exchangeable”. Exchanging a pair of observations is equivalent to swapping experimental condition labels. In a within-subjects design where each participant contributes a score to Condition A and a score to Condition B, the observations are exchanged by swapping the A and B condition labels within each participant S_i but not between participants. In a between-subjects design where participant S_i contributes a score to condition A and participant S_j contributes a score to condition B, observations are exchanged by swapping the A and B condition labels between the participants. In either case, a permutation testing procedure begins the same way as the usual parametric statistical test, i.e., by computing a sample statistic such as a t-score for the observed data in the A and B conditions, t_observed. Next, a permutation is constructed by exchanging one or more pairs of observations and a new t-score is recomputed for the A and B conditions under this rearrangement. This permutation process is repeated either exhaustively for all possible permutations or by randomly sampling a large number, e.g., 1,000 - 10,000, of the vast number of possible permutations and recalculating a t-score. Repeating this process many times results in a distribution of the possible t-scores for these data under the null hypothesis that observations are exchangeable, i.e., were sampled from the same population. The relative location of t_observed in this distribution provides the p-value for the observed data, indicating how probable such observations would be if the null hypothesis were true. For example, if t_observed is greater than or equal to 99% of the t-scores of the distribution, its p-value would be 2% for a two-tailed test (i.e., 2*1%-- see Supplemental Table 1 and Supplemental Table 2 for simple, concrete examples of how a within-subjects and between-subjects permutation test is executed). Permutation testing is thus similar to parametric hypothesis testing except that the latter uses a theoretical distribution of the test statistic derived by assuming that the population has a specific distribution (e.g., normal), whereas the former uses a distribution derived from permuting the observed scores.

For small sample sizes, it is possible to compute the null hypothesis distribution using all possible permutations. However, since the number of permutations grows quickly as a function of sample size, it is often too time consuming to compute all possible permutations in practice. When this occurs, one can very accurately approximate the distribution of all possible permutations from a large number (e.g., 5000) of random permutations. The number of permutations needed depends on the degree of precision required and on the alpha level of the test. More permutations are needed for greater precision and for smaller alpha levels. Small alpha levels require accurate estimation of the extreme tails of the null hypothesis distribution. Since values in the extreme tails are rare, a large number of permutations is necessary to observe them. As a general rule of thumb, Manly (1997) suggests using a minimum of 1000 permutations for a 5% alpha level and 5000 permutations for a 1% alpha level. Manly argues that these numbers should be generally sufficient to estimate p-values within +/- 2%. If greater precision is needed, one can easily use many more permutations with conventionally available computing power (e.g., 10,000--Blaire & Karniski, 1993). Moreover, one can quantify the accuracy of permutation test p-values with confidence intervals using techniques for estimating the expected value of binomial random variables (Manly, 1997).

2.2 Applying Permutation Tests to Simultaneous Multiple Comparisons

Critically, the above procedure can be generalized to a family of similar tests by computing the distribution of the most extreme statistic (e.g., t-score) across the entire family of tests for each possible permutation (Blair & Karniski, 1993). To illustrate, hypothetical ERP amplitudes at two electrodes from three participants in two experimental conditions are presented in Table 1 (Rows 2-3). We compute t-scores for each electrode (Table 1: Row 4, Column 5) and the most extreme of the two, “t_max” (Blair & Karniski, 1993), is 4.63. Note that t_max is the most extreme positive or negative value of the t-scores, and not necessarily the maximum value of the t-scores.

Table 1.

Within-participant permutation test calculations applied to hypothetical ERP amplitude data from two electrodes (Cz & Pz) in three participants.

	Participant 1 (Cz, Pz)	Participant 2 (Cz, Pz)	Participant 3 (Cz, Pz)
Condition A	2.9, 2.9 μV	1.1, 0.9 μV	3.2, 3.0 μV
Condition B	1.1, 1.2 μV	0.2, 0.3 μV	1.2, 1.5 μV	t-scores (Cz, Pz)	tmax
Observed Difference	1.8, 1.7 μV	0.9, 0.6 μV	2.0, 1.5 μV	t=4.63, 3.74,	4.63
Alternative Permutation 1	1.8, 1.7 μV	0.9, 0.6 μV	-2.0, -1.5 μV	t=0.20, 0.28	0.28
Alternative Permutation 2	1.8, 1.7 μV	-0.9, -0.6 μV	2.0, 1.5 μV	t=1.03, 1.18	1.18
Alternative Permutation 3	1.8, 1.7 μV	-0.9, -0.6 μV	-2.0, -1.5 μV	t=-0.32, -0.14	-0.32
Alternative Permutation 4	-1.8, -1.7 μV	0.9, 0.6 μV	2.0, 1.5 μV	t=0.32, 0.14	0.32
Alternative Permutation 5	-1.8, -1.7 μV	0.9, 0.6 μV	-2.0, -1.5 μV	t=-1.03, -1.18	-1.18
Alternative Permutation 6	-1.8, -1.7 μV	-0.9, -0.6 μV	2.0, 1.5 μV	t=-0.20, -0.28	-0.28
Alternative Permutation 7	-1.8, -1.7 μV	-0.9, -0.6 μV	-2.0, -1.5 μV	t=-4.63, -3.74	-4.63

We then calculate t_max for the remaining seven possible permutations of the data and derive a set of eight t_max scores. Note that when the voltage differences are permuted, the values from each participant change sign together, thereby preserving the within-participant relationships among electrode values across all permutations. The p-values for our original observations are derived from the t_max scores. Assuming a two-tailed test, the t-score for our observations at electrode Cz would be 0.125 because 1/8 of the t_max scores are greater than or equal to it. Likewise, the p-value for the observation at Pz would be 0.125.

This procedure cleverly corrects for multiple comparisons because the t_max distribution, from which the p-values of each comparison are derived, automatically adjusts to reflect the increased chance of false discoveries due to an increased number of comparisons. As more comparisons are added to the family of tests, there is an increased likelihood of getting more extreme observations by chance and the distribution extends outward (e.g., Figure 4: A & B), rendering the test more conservative. Moreover, the degree to which the t_max distribution extends adaptively reflects the degree of correlation between the multiple tests. For example, if the data at Cz and Pz were independent and the null hypothesis of no difference between conditions is true, controlling the family-wise alpha level at 0.05, requires a test-wise alpha level of approximately half that, 0.025. However, if the data at Cz and Pz were perfectly correlated, then there is effectively only a single test and the test-wise alpha level should equal the family-wise alpha level. Intuitively, if the correlation between Cz and Pz is somewhere between 0 and 1, the test-wise alpha level should be between .05 and .025, as is the case for the permutation procedure (Figure 4).

Figure 4.

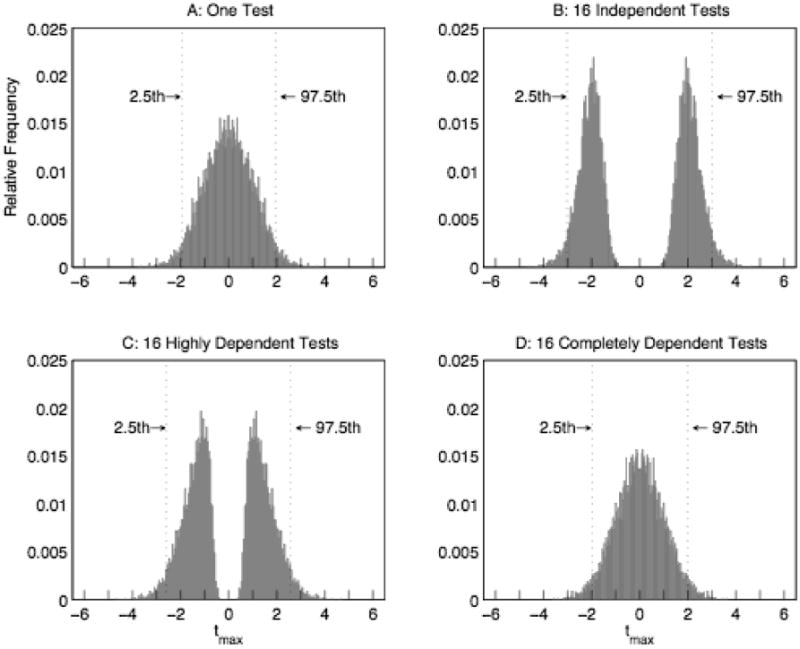
t_max distributions for permutation tests performed on a single test (Subplot A) or a family of 16 tests (Subplots B-D). Dotted lines indicate 2.5th and 97.5th percentiles (i.e., the critical t_max values corresponding to a family-wise alpha level of 0.05). The independent tests (Subplot B) are uncorrelated. The correlation between each pair of highly dependents tests is 0.80 (Subplot C). The correlation between each pair of completely dependent tests is 1 (Subplot D). All tests are based on a sample size of 100 generated from normally distributed random variables and 5000 random permutations.

It is also important to realize that statistics other than conventional t-scores can be used with this permutation test procedure. Using different statistics will affect the test's sensitivity to different types of departures from the null hypothesis (Groppe et al., 2011; Maris & Oostenveld, 2007; Hemmelmann et al., 2004).

2.3 Realistic Permutation Test Example

To provide a realistic example of permutation tests, we return to the example visual oddball ERPs introduced earlier. Again, Figure 1 displays the ERPs to rare target words and to the common standard words, while Figures 2-A and 2-B display the difference between the ERPs to targets minus standards in microvolts and t-scores, respectively. In Figure 2-A, the most pronounced ERP difference is a P3 effect peaking around 425 ms. Also visible are a P2 effect peaking around 250 ms and a “slow wave effect” peaking around 650 ms. The difference between ERPs in units of t-scores (Figure 2-B) provides a somewhat different perspective on the data. First, note the P3 effect is approximately the same magnitude as the P2 and slow wave effects, reflecting the fact that although the P3 effect is greater in amplitude than the other two effects, it is more variable across participants. Two additional effects become apparent in this representation: a positivity peaking around 325 ms and another peaking around 650 ms. This illustrates how simply visualizing data in units of a test statistic (e.g., t-scores, F scores) can help to reveal effects that might have been missed in a microvolt representation⁴.

To determine which, if any, of these apparent effects are reliable, the data were analyzed with a t_max permutation procedure at every time point and electrode from 100 to 900 ms post-stimulus onset. 5000 permutations were used to approximate the t_max distribution from all possible permutations and critical t-scores of +/- 8.73 were derived for a family-wise alpha level of 5.4%. Thus, all five effects (the P2, P3, slow wave, and the positivities at 325 and 650 ms) are significant (Figure 2-B). A raster diagram (Figure 3) shows exactly when and where differences are statistically reliable via the permutation method.

2.4 Permutation Test Pros & Cons

The great advantage of this permutation test procedure is that it guarantees strong control of FWER, the same degree of false discovery control as Bonferroni correction, but it is generally more powerful than Bonferroni (and other similar) procedures because it automatically adjusts to the degree of correlation between tests (Figure 4). Also advantageously the permutation method is non-parametric. In other words, unlike popular parametric tests like ANOVAs, the permutation method does not make specific assumptions about the shape of the population distribution from which the observations have been derived (e.g., that it is normal). It assumes only that observations are exchangeable. Although it is probably safe to assume that ERPs/ERFs are normally distributed enough for hypothesis tests that assume a normal population to provide accurate results, using a non-parametric test provides extra assurance, especially when the number of participants is small.

Permutation test control of FWER does, however, have some drawbacks. The most serious of these is that as the number of tests in the family grows, the power of the test can still be greatly weakened. As mentioned in Section 1, the t_max significance threshold in the visual oddball example corresponds to a test-wise alpha level of approximately 0.005%. Whereas this is five times less conservative than using a Bonferroni correction (i.e., 0.001%), it is nonetheless much worse than would be obtained from a handful of a priori tests.

Another limitation of permutation tests is that their accuracy is only guaranteed for simple analyses (e.g., comparing central tendencies of multiple experimental conditions, determining if multiple variables are correlated). For more complicated analyses like multiple regression or multifactor ANOVAs, permutation test results are not generally guaranteed to be accurate because testing individual terms in such models (e.g., partial correlation coefficients in multiple regression and interaction terms in multifactor ANOVAs) requires accurate knowledge of other terms in the model (e.g., the slope coefficients for all the other predictors in the multiple regression model or the mean of each factor in a multifactor ANOVA). Because such parameters have to be estimated from the data, permutation tests are only “asymptotically exact” for such tests (Anderson, 2001; Good, 2005). This means that as the sample size of the analysis increases, the true Type I error rate for the test approaches the nominal error rate (e.g., an alpha level of 5%). Thus for sufficiently large sample sizes the permutation test procedure will provide approximately accurate results, but it is not generally obvious just how large a sample size suffices.

An additional minor drawback of permutation tests is that the null hypothesis of exchangeability may be overly general for independent sample comparisons. This is an issue when a researcher wants to test a claim about a specific difference between two or more groups of participants (e.g., that the mean of some dependent measure is not equal across groups). Permutation tests test the null hypothesis that the distributions are exactly the same. As a consequence, if the groups came from populations with the same mean but different variances, this would violate the null hypothesis of the permutation test and potentially lead to significant differences that are mistakenly interpreted as differences in population means. Of course, this concern is not unique to permutation tests (e.g., the conventional independent samples t-test and ANOVA share it) and, as we show in simulation studies (Groppe et al., 2011), this problem can be mitigated by equating the numbers of participants in each group or by choosing test statistics that are less sensitive to such differences.

3. Cluster-Based Permutation Tests with Weak Control of the Family-Wise Error Rate

3.1 Introduction to Cluster-Based Permutation Tests

As mentioned previously, permutation tests are not limited to statistics like t-scores that are the basis of popular parametric tests, but can be based on an infinite variety of other statistics. Take, for example, “cluster-based” statistics computed by grouping together neighboring variables into clusters and deriving some value for the cluster from its constituents. One popular cluster-based statistic, “maximum cluster-level mass” (Bullmore et al., 1999), works as follows:

1. t-scores (or some other test statistic) are computed for every time point and sensor of interest.

2. All t-scores that do not exceed some threshold (e.g., the t-score corresponding to an uncorrected p-value of 5%) are ignored.

3. Of the remaining t-scores, all t-scores without a sufficient number (e.g., two) of adjacent above threshold t-scores are ignored. This step is optional⁵.

4. The remaining t-scores are formed into clusters by grouping together t-scores at adjacent time points and sensors.

5. The t-scores of each cluster are summed up to produce a cluster-level t-score. This is taken as the “mass” of the cluster.

6. The most extreme cluster-level t-score across permutations of the data is used to derive a null hypothesis distribution (just as the most extreme t-score across all tests is used to derive a null hypothesis distribution for the t_max procedure--Section 2.2).

7. The p-value of each cluster is derived from its ranking in the null hypothesis distribution and is thus adjusted for the multiple comparisons.

8. Each member of the cluster is assigned the p-value of the entire cluster and reflects an adjustment for multiple comparisons. The multiple comparison adjusted p-value of tests not assigned to a cluster is one.

Note that this procedure has a number of free parameters whose values can greatly affect the outcome of the test. The first of these is the definition of spatial neighbor, which can be set by a somewhat arbitrary distance threshold (e.g., all sensors within 4 cm of a sensor are its neighbor). The second free parameter is the t-score threshold for cluster inclusion. It is probably not advisable to use a threshold corresponding to a p-value of greater than 5%, since that could lead to significant test results that would not have been significant if no correction for multiple comparisons had been done. Making the threshold more extreme will generally produce more focal clusters (see next section). Finally, the optional step of requiring tests to have a certain number of above threshold neighbors (Step 3 above) will also tend to produce more focal clusters since it removes possible narrow links between larger clusters (http://fieldtrip.fcdonders.nl/tutorial/cluster_permutation_timelock?s).

This maximum cluster-level statistic is just one possible cluster-based statistic. Another is the “maximum cluster area” statistic, which is the number of members in a cluster (Bullmore et al., 1999), and can be used as above. The motivation for forming clusters of tests is that true ERP/ERF effects are generally more likely than ERP/ERF noise to occur coherently across multiple adjacent time points and sensors. Consequently, ERP/ERF effects will typically stand out more clearly from noise using cluster-based statistics. By the same token, however, cluster-based tests will be less likely to detect very focal ERP/ERF effects that are limited to a small number of time points and/or sensor sites (Groppe et al., 2011).

It is important to note that because p-values are derived from cluster level statistics, the p-value of a cluster may not be representative of any single member of that cluster. For example, if the p-value for a cluster is 5%, one cannot be 95% certain that any single member of that cluster is itself significant (e.g., Groppe et al., 2011). One is only 95% certain that there is some effect in the data. Technically, this means that cluster-based tests provide only weak FWER control (Maris & Oostenveld, 2007).

3.2 Cluster-Based Permutation Test Example

To illustrate this type of analysis, the maximum cluster-level mass procedure was applied to the visual oddball ERPs introduced earlier. An electrode's spatial neighborhood was defined as all electrodes within approximately⁶ 5.4 cm, resulting in 3.8 neighbors for each electrode on average. The t-score threshold for cluster inclusion was +/-2.36 (which corresponds to an uncorrected p-value of 5% for a single test) and t-scores were not required to have a minimum number of below threshold neighbors to be included in a cluster (i.e., Step 3 of the above procedure was omitted). As with the previous t_max permutation test example, all 26 scalp electrodes and time points between 100 and 900 ms were included in the analysis and the test was two-tailed.

The results of the test are visualized with a raster diagram in Figure 5-A. Because the significance threshold is cluster-based, the cluster test does not return a critical t-score beyond which individual test t-scores are significant (thus its results are not easily visualized with butterfly plots--Figure 2). The maximum cluster-level mass procedure returned one significant very broadly distributed cluster that begins at 208 ms at central and frontal electrodes and slowly shifts posteriorly to end at 752 ms at occipital electrodes (Figure 5-A). Thus, this procedure captures all the significantly positive results found by the previous t_max procedure (e.g., the P2 and P3 effects), and many more. Indeed, some of the significant t-scores have magnitudes as low as 2.37, which corresponds to an uncorrected p-value of approximately 5%. This shows how the cluster-based procedure is able to declare tests significant with relatively small uncorrected p-values if they are part of a massive neighborhood of t-scores. It also shows how functionally distinct ERP/ERF effects (i.e., the P2 and P3) can be captured in the same cluster. However, the cluster-based procedure misses the negative “slow wave” effect found by t_max because its neighborhood is not that massive, even though some members of the effect appear quite significant (t<-8).

Figure 5.

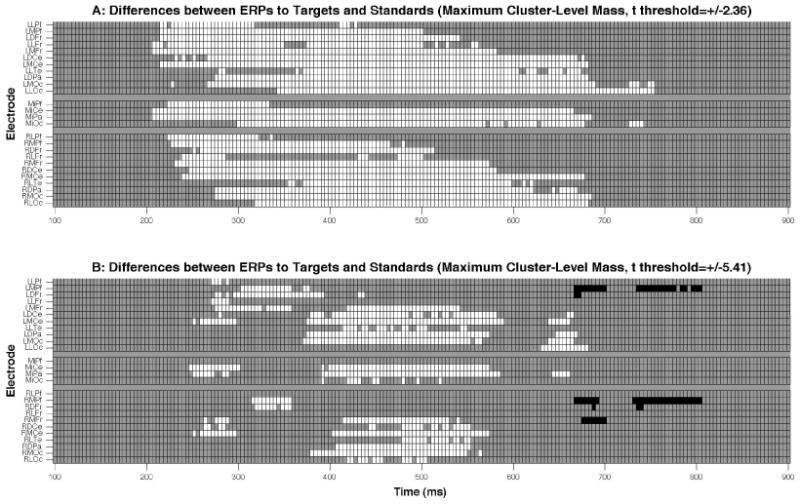
Raster diagrams illustrating significant differences between ERPs to targets and standards from a visual oddball task according to two different applications of a maximum cluster-level mass permutation test. The top raster (A) shows the test results when the t-score threshold for cluster inclusion is +/-2.36. The bottom raster (B) shows the test results when a more conservative t-score threshold for cluster inclusion, +/-5.41, is used. White and black rectangles indicate electrodes/time points in which the ERPs to targets are more positive and negative, respectively. Grey rectangles indicate electrodes/time points at which no significant differences were found. In the top raster, all significant effects belong to a single cluster. In the bottom raster there are four clusters: all significantly positive differences from 258 to 588 ms (this includes the P2 and P3 effect), all significantly positive differences from 632 to 680 ms, all negative differences from 668 to 700 ms, and all negative differences from 732 to 804 ms. The later positive cluster is an apparently novel effect and the negative clusters are presumably part of a slow wave effect. For more information on interpreting such raster diagrams see Figure 3.

If we repeat the cluster-based test but use a more conservative threshold for cluster inclusion, a t-score that corresponds to an uncorrected p-value of 0.1%, four, much more focal, significant clusters are returned (Figure 5-B). The first positive cluster lasts from 248 to 588 ms and includes the P2, P3, and a left frontal positivity that peaks around 325 ms. The other positive cluster consists of a left posterior effect that peaks around 650 ms. The earlier negative cluster lasts from 668 to 700 ms at frontal electrodes and is soon followed by the other negative cluster from 732 to 804 ms with a similar distribution. Members of all but the earlier negative cluster were also found by the t_max procedure (Section 2.3).

3.3 Cluster-Based Permutation Test Pros & Cons

By capitalizing on the fact that ERP/ERF effects typically span multiple neighboring time points and sensors, cluster-based permutation tests are remarkably good at capturing broad effects (Bullmore et al., 1999; Groppe et al., 2011, Maris & Oostenveld, 2007). Thus, given that the tests provide weak control of FWER, cluster-based tests are possibly the most powerful mass-univariate procedure for detecting the presence of such effects. Cluster-based tests also have the convenient properties of returning somewhat neater results than non-cluster-based tests and also exhibit the previously discussed general advantages of permutation tests: they exploit correlations between variables when correcting for multiple comparisons and are nonparametric (Section 2.4).

These advantages however come at the cost of uncertainty as to the reliability of an effect at a particular time point and sensor since cluster-based tests provide only weak FWER control. Maris and Oostenveld (Section 4.2.2, 2007) have argued that regardless of this shortcoming of cluster-based permutation tests, they are preferable to methods that provide strong control of FWER and thus a clear degree of certainty that an effect is present at an individual time point and sensor. Their rationale is that cluster-based tests should be more powerful than methods that provide strong control of FWER at detecting the presence of an effect, and that knowing whether or not an effect is present takes precedence over establishing exactly when and where the effect occurs⁷. While this may be true of some investigations, it is not true of all research questions, as when it is critical to establish lower bounds on ERP/ERF effect onsets (e.g., Groppe et al., 2010; Hillyard, Hink, Schwent, & Picton, 1973; Johnson & Olshausen, 2003).

Another shortcoming of cluster-based tests is that they are likely to miss narrowly distributed effects that occur across a limited number of time points and sensors (e.g., an N170 effect--Groppe et al., 2011), since their cluster mass or size will not differ much from that of noise clusters (Maris & Oostenveld, 2007). A less significant complication is that it is not clear how to set some of the parameters of the cluster test: the t-score (or other test-wise statistic) threshold for cluster inclusion, the definition of spatial neighbors, and the number of above threshold neighbors necessary for cluster inclusion. Choosing different values for these parameters will increase the power of the procedure for detecting some effects at the cost of missing or distorting others. Finally, these procedures are also subject to the shortcomings of permutation tests in general (Section 2.4), namely that they have less statistical power than a priori windows, they assume populations are exactly the same for independent samples tests, and they are only asymptotically exact for complicated analyses.

4. False Discovery Rate Control

4.1 Introduction to FDR Control

As already mentioned, while relatively powerful for families of highly correlated tests, permutation test-based strong control of FWER can sacrifice a great deal of power when the number of tests in a family is quite large. This problem and the increasing prevalence of large scale simultaneous hypothesis testing in many scientific disciplines has led to the development of weaker, but still useful alternatives to strong control of FWER. Perhaps the most popular of these is control of the “false discovery rate” (FDR--Benjamini & Hochberg, 1995), which is based on the “false discovery proportion” (FDP). FDP is the proportion of rejected null hypotheses that are mistaken (or 0 if no hypotheses are rejected):

$$\mathit{\text{FDP}}=\{\begin{array}{c}\frac{R_F}{R}\text{if}R>0\\ 0\text{if}R=0\end{array}$$ (1)

where R is the total number of rejected null hypotheses (i.e., tests with significant p-values) and R_F is the number of mistakenly rejected null hypotheses in the family of tests. FDR control limits the expected value (i.e., mean) of the FDP:

$$\mathit{\text{FDR}}=E(\mathit{\text{FDP}})$$ (2)

There are currently several algorithms for FDR control (Farcomeni, 2008; Romano, Shaikh, & Wolf, 2008); they differ in their statistical assumptions, the amount of computational labor, and their statistical power. Here we will consider what is probably the most popular algorithm, created by Benjamini and Hochberg (1995), as well as two more recent variants (Benjamini & Yekutieli, 2001; Benjamini, Krieger, & Yekutieli, 2006). These algorithms are quite simple, fast, and require only the computation of p-values for each of the tests in the family as inputs⁸.

The Benjamini and Hochberg (BH) procedure operates as follows:

1. Sort the p-values from the entire family of m tests (i.e., m is the total number of hypothesis tests) from smallest to largest (p_i refers to the ith smallest p-value).

2. Define k, as the largest value of i for which the following is true:

   $$p_i\le \left(\frac{i}{m}\right)\alpha$$ (3)

3. If at least one value of i satisfies this relationship, then hypotheses 1 though k are rejected, otherwise no hypotheses are rejected.

4. If the tests in the family are independent or exhibit positive regression dependency⁹ (Benjamini & Yekutieli, 2001), then the BH procedure guarantees the following:

   $$\mathit{\text{FDR}}\le \left(\frac{m_0}{m}\right)\alpha$$ (4)

   where m₀ equals the number of null hypotheses that are true. Since m₀/m takes a value between 0 and 1, the test results won't exceed the desired level of FDR for independent or positively regression dependent tests.

While simple and quite powerful, the BH procedure is not guaranteed to work for data with arbitrary dependence properties (e.g., normally distributed data with some negatively correlated variables). This led to a slight modification of the procedure by Benjamini and Yekutieli (BY--2001), who replaced Step 2 of the BH procedure is with the following:

2) Define k, as the largest value of i for which the following is true:

$$p_i\le \left(\frac{i}{m\sum _{j=1}^m\frac{1}{j}}\right)\alpha$$ (5)

This new procedure, BY, guarantees Equation 4 regardless of the dependency properties of the data, though it is generally much more conservative than the original BH procedure.

A problem with both of these FDR control procedures is that when a large proportion of hypotheses in the family of tests is false, m₀/m is small and the procedure is too conservative. Benjamini, Krieger, and Yekutieli (BKY--2006) correct for this via a “two-stage” version of the BH procedure. In the first stage, BKY estimates the proportion of hypotheses that are false and the estimate is used by the second stage to implement a more accurate, less conservative version of the BH algorithm. More specifically, the first stage of BKY is the same as BH, but instead of α, α′ is used:

$${\alpha }^{\prime }=\frac{\alpha }{1+\alpha }$$ (6)

The number of hypotheses rejected by the first stage, r₁, is the estimate of the number of false hypotheses. If r₁ is 0, the procedure stops and no hypotheses are rejected. If r₁ is m, then the procedure stops and all the hypotheses are rejected. Otherwise the BH procedure is run again with α″ instead of α′:

$${\alpha }^{″}=\left(\frac{m}{m-r_1}\right){\alpha }^{\prime }$$ (7)

and the resulting significance judgments are used. If the different tests in the family are independent, the BKY procedure guarantees the following:

$$\mathit{\text{FDR}}\le \alpha$$ (8)

4.2 FDR Control Example

To illustrate FDR control, Figure 2-C shows the results of applying the BH FDR procedure to the same data used to illustrate the t_max permutation test in Section 2.3. Again, t-tests were performed at every electrode and time point from 100 to 900 ms. In contrast to the t_max procedure, the BH FDR procedure is much less conservative and declares many more test results significant. Indeed, the critical t-scores of the BH FDR procedure (+/-3.00) correspond to a test-wise alpha level of approximately 2%, 383 times that of the t_max permutation procedure. The BY FDR procedure is considerably more conservative with critical t-scores of +/-5.65 (Figure 2-D), but it is still about 16 times less conservative than the t_max permutation test.

4.3 FDR Pros & Cons

The major benefit of FDR controls is that they are quite powerful methods of correcting for multiple comparisons, while still providing meaningful control of false discoveries in two ways. First of all, if all the null hypotheses in the family of tests are true (i.e., there are no effects), and FDR is controlled at level alpha, then FWER across the entire set of tests is also controlled at level alpha (i.e., FDR control provides weak FWER control). Thus, if an FDR procedure declares some results significant, then we can be as certain as if Bonferroni correction had been applied that there is indeed some effect in the data. Secondly, if the FDR procedure rejects some hypothesis using conventionally low alpha levels (e.g., 5%), we can be confident that the number of false discoveries is much smaller than the number of correct rejections.

Another key benefit of these FDR procedures is that they can be used with more complicated analyses (e.g., multiple regression) than permutation-based methods, and can be computed quite quickly.

On the downside, BH might not control FDR when some variables in the family are negatively correlated and BKY might not control FDR when some variables are negatively or positively correlated. Since EEG/MEG sources can project to multiple sensors and reverse polarity across sensors, such correlations will typically occur in ERP/ERF data sets (Groppe et al., 2011). Although other FDR procedures guaranteed to work for arbitrary test dependence relations exist, their utility is limited by their over-conservativeness (e.g., BY) or the fact that they only guarantee asymptotic FDR control (e.g., Troendle, 2000).

This shortcoming of the most popular FDR procedures, however, might not be that serious. Theoretical results show that when data come from relatively light-tailed distributions (e.g., a normal distribution), FDR control performs as if the tests were independent as the number of tests in a family increases (Clarke & Hall, 2009). Thus with a sufficient number of tests, FDR procedures guaranteed to work when the tests are independent should also provide accurate control of FDR for ERP/ERF data, which are generally likely to be approximately normally distributed. In fact, applications of BH and BKY FDR procedures to simulated ERP data sets have found that they do control FDR at or below the nominal level (Groppe et al., 2011).

Another potentially serious shortcoming of FDR methods is that the probability of a large proportion of false discoveries might be too high. This problem stems from the fact that FDR only controls the mean of the FDP distribution. Thus, even though the mean proportion of false discoveries might be controlled at a reasonable level (e.g., 5%), the proportion of false discoveries in any given analysis will vary from experiment to experiment and might be quite large with non-negligible probability. For example, Korn et al. (2004) found that when the BH procedure was applied to simulated data using an FDR level of 10%, there was a 10% chance that the true proportion of false discoveries was 29% or more for some simulation parameters. This potential problem with FDR procedures has led some statisticians to advise against their use (Korn et al., 2004; Troendle, 2008). Simulated ERP analyses, however, suggest this is not a problem for ERP data using the conventional alpha level of 5% (Groppe et al., 2011).

A final issue with FDR control that complicates the interpretation of its results is that reducing the number of tests included in the family can sometimes diminish the power of the analysis. For example, recall that applying the BH FDR procedure to the example oddball data from 100 to 900 ms leads to critical t-scores of +/-3.00 (Figure 2-C). However, when the same procedure is applied to the much smaller time window of 100 to 275 ms it becomes more conservative, with critical t-scores of +/-4.04 (Figure 2-E). This can occur because including highly significant tests in the family makes it possible to be less conservative when evaluating less significant tests. Indeed, procedure BKY at level α can lead to rejecting hypotheses with uncorrected p-values greater than α (Hemmelmann, Horn, Susse, Vollandt, & Weiss, 2005). This trait of FDR procedures runs counter to the statistical intuition that power should, if anything, increase as the number of statistical tests are reduced, and means that effects declared significant by FDR procedures might not replicate when tests are limited to that effect via a priori reasoning¹⁰.

5. Control of Generalized Family-Wise Error Rate (GFWER)

5.1 Introduction to GFWER Control

Since FDR control may lead to a sizable probability of a large proportion of false discoveries in any single experiment, some statisticians prefer methods that control the generalized family-wise error rate (GFWER--Hemmelmann et al., 2008; Korn et al., 2004). GFWER control guarantees that the number of false discoveries does not exceed a specified value, u, with probability 1-α or greater. If u is 0, then GFWER is equivalent to strong control of FWER. The benefit of GFWER over FWER is that by allowing a small number of false discoveries, the power of the analysis increases (Korn et al., 2004). Moreover, GFWER control provides a much better sense of the number of false discoveries than do FDR methods.

The GFWER method reviewed here is a permutation-based method developed by Korn, Troendle, McShane, & Simon (KTMS, 2004); others are available (Hemmelmann et al., 2008; Hommel & Hoffmann, 1987). The algorithm¹¹ works roughly as follows:

1. Sort the p-values from the entire family of m tests (i.e., m is the total number of hypothesis tests) from smallest to largest. p_i refers to the ith smallest p-value.

2. Automatically reject the u hypotheses with the smallest p-values (i.e., give them an adjusted p-value of 0).

3. For the remaining m-u hypotheses, obtain their adjusted p-values via a permutation test with the following modification: instead of using the most extreme test statistic (i.e., the test statistic with the smallest p-value) from each permutation, use the u+1th most extreme test statistic.

This procedure is guaranteed to control GFWER at the specified alpha level (indeed it is a bit overly conservative).

5.2 GFWER Example

To illustrate, Figure 2-F shows the results of applying the KTMS GFWER procedure with u set to 1 to the same data used to illustrate the t_max permutation test in Section 2.3. Again, t-tests were performed at every electrode and time point from 100 to 900 ms. Compared to the t_max procedure, the KTMS procedure is less conservative and declares a few more test results significant. Specifically, the critical t-scores of the KTMS procedure (+/-7.98) correspond to a test-wise alpha level of approximately 0.009%, almost twice that of the t_max permutation procedure.

5.3 GFWER Pros & Cons

To reiterate, the two main advantages of GFWER control are that it is more powerful than strong FWER control and it provides a clearer sense of the number of false discoveries than FDR control or cluster-based tests. Unlike the BH and BKY FDR procedures, the KTMS procedure is guaranteed to work for analyses in which a permutation test is appropriate regardless of the dependency structure of the data. Also, because KTMS is permutation-based, unlike the various Benjamini FDR methods, it exploits the correlations between variables to increase the power of the analysis.

Perhaps the greatest disadvantage of GFWER control is that it does not necessarily control FWER. Thus with GFWER control it may be less clear if there are any effects in the data than when FDR or FWER control is used. With the KTMS procedure, u null hypotheses are automatically rejected, such that if the number of false null hypotheses in the data are less than or equal to u, then the KTMS procedure's output will be effectively identical to that produced if there had been no false null hypotheses. Setting u to a small value (e.g., 1 or 2) can ameliorate this problem, albeit at the cost of decreased statistical power.

In addition to that general problem with GFWER control, the KTMS procedure has a few shortcomings due to the fact that it is permutation based. Thus, like permutation test-based control of FWER, the KTMS procedure is only guaranteed to work for simple analyses (e.g., t-tests, correlation--see Section 2.4) and when applied to independent samples analyses it will be sensitive to any (not just mean) differences between sampled populations (see Section 2.4). Finally, a further, minor problem, is that the KTMS procedure described here is somewhat overly conservative. However, this loss of power should not be significant except in situations where the number of false null hypotheses is large and a large number of false discoveries is allowed (Korn et al., 2004). Such a situation is unlikely to occur in practice but a more accurate, more computationally intensive version of the KTMS procedure is available in that eventuality (Procedure A in Korn et al., 2004).

6. Discussion

The primary purpose of this article is to provide a tutorial review and critical comparison of popular but under-utilized techniques for mass univariate analyses that are potentially of great value to ERP/ERF researchers. The mass univariate approach to data analysis consists of performing a massive number of univariate analyses (e.g., t-tests) with savvy corrections for multiple comparisons to remove or mitigate the increased probability of false discoveries inherent in doing lots of hypothesis tests. Mass univariate analyses allow ERP/ERF researchers to properly analyze their data with substantially fewer a priori assumptions and with much greater temporal and spatial resolution than conventional analyses in which mean time window measurements are subjected to ANOVAs. While these benefits come at the cost of some loss of statistical power and (sometimes) uncertainty as to the significance of any single effect, the power and certainty that remains may be more than adequate in many situations. Thus, mass univariate analyses serve as a valuable complement to and, in some cases, may obviate the need for conventional analyses.

More specifically, mass univariate analyses are preferable to conventional mean time window ANOVA analyses in the following situations:

• A researcher has little-to-no a priori belief as to when and where an effect will occur, as in the case of an exploratory study.

• A researcher has some a priori belief as to when and where a specific effect will occur but there may be additional effects at other latencies and/or sensors. For instance, a researcher might be interested in how some factor affects the P3, but there might be interesting, unexpected ERP effects preceding or following the P3.

• A researcher needs to establish precise lower bounds on the onset and offset of an effect or needs to identify specific sensors where an effect is reliable, e.g., delineating a lower bound on the time it takes the brain to discriminate between multiple categories of visual objects (Johnson & Olshausen, 2003; Thorpe et al., 1996).

In contrast, conventional ERP/ERF analyses are likely better when a researcher is testing hypotheses about well-studied ERP/ERF effects and knows a priori when and where such effects will occur. In these cases, averaging across time windows and/or sensors and performing ANOVAs should generally be more likely to detect effects. However, even in this case, a mass univariate analysis may still be sufficiently powerful.

6.1 Ways of Correcting for Multiple Comparisons

While it may be clear when a mass univariate analysis would be useful, there are important differences between the various procedures for correcting for multiple comparisons. In general, the key difference is how they negotiate the trade-off between statistical power (the ability to detect a real difference between conditions or real ERP/ERF correlates) and the degree of certainty one can have in the significance of any single test result. In this report we have evaluated four methods: (1) permutation test-based strong control of FWER, (2) cluster-based permutation tests with weak control of FWER, (3) three methods for FDR control invented by Benjamini and colleagues, and (4) a permutation-based method for control of GFWER. Of these, the method that provides the greatest certainty – the same degree as a priori tests and Bonferroni correction – is permutation test-based strong control of FWER and it is quite powerful relative to other methods of strong FWER control. Consequently, this method is well suited to situations where it is critical to avoid a false discovery (e.g., analysis of an experiment that is unlikely to be replicated) or when its power is likely to be adequate (e.g., when looking for a particularly robust effect or analyzing large sample sizes). Due to its maximal degree of certainty, permutation-based strong control of FWER is probably the best available method for establishing reliable lower bounds on the onset and offset of ERP/ERF effects when a priori boundaries an unavailable (e.g., Groppe et al., 2010). However, the conservatism of this procedure will tend to produce somewhat delayed measures of effect onsets and abbreviated measures of effect duration. Moreover, this procedure is particularly powerful relative to the other methods reviewed here when only a very small proportion of null hypothesis in an analysis are false (e.g., only a single, very narrowly distributed effect is present--Groppe et al., 2011).

In contrast, a related method, cluster-based permutation tests with weak control of FWER, is much more powerful than permutation-based strong control of FWER for detecting broadly distributed effects that span many time points and sensors (as many ERP/ERF phenomena do). However, this increased power comes with two potentially significant costs. The first is uncertainty as to the reliability of an effect at a single given time point and sensor. In other words, with the cluster-based test one only knows how likely it is that there is some effect in the analysis, but one does not know how likely that effect is to span a particular set of time points or sensors (in particular the test might be over-estimating the extent of the effect). Moreover, the procedure has very little power for detecting very focal effects that occur across a limited number of time points and sensors. To its credit, the simulation studies presented in our companion paper (Groppe et al., 2011) found that the maximum cluster mass permutation test is only as, or less, likely to produce false discoveries as the other methods reviewed here and that it is the most powerful at detecting broadly distributed effects. Thus cluster-based tests appear to be the best procedure to use when one is primarily interested in detecting somewhat to very broadly distributed effects.

Like cluster-based tests, false discovery rate controls are generally much more powerful than strong FWER controls but also provide no certainty as to the reliability of any single test result. Although some FDR algorithms are liable in principle to inflated rates of false discoveries when their assumptions are violated, our simulation studies (Groppe et al., 2011) found that this was not a problem for ERP data using a realistic number of comparisons and a nominal FDR level of 5%. Moreover, none of the FDR algorithms frequently produced an alarmingly high proportion of false discoveries and the BH and BKY procedures exhibited relatively good power regardless of ERP effect size. In light of all this, FDR methods are clearly well suited for exploratory studies because they can identify unexpected effects that can be followed up with further experimentation and they appear to have the best all-purpose power. These methods are also appropriate for confirmatory studies, especially when statistical power is limited (e.g., small sample sizes or weak effects) or it is critical to avoid missing effects (e.g., one is trying to find evidence in favor of the null hypothesis). In general the BH procedure is probably the best to use given its relatively good power, somewhat greater guarantees than BKY, and the fact that it produces FDR-adjusted p-values¹² (BKY simply indicates which tests are significant, which is not as informative). BKY is better to use when one expects a large proportion of false null hypotheses (e.g., greater than 35%--Hemmelmann et al., 2005) and BY is better to use when it is important to avoid making an unexpectedly large proportion of false discoveries. However, the greater uncertainty of all FDR control methods relative to a priori test windows should be kept in mind until their results are replicated, especially when an ostensible effect is a small proportion of the total number of rejected null hypotheses (and thus quite possibly entirely composed of false discoveries).

Finally, the KTMS algorithm for control of GFWER, represents a compromise between FDR and strong FWER control. By allowing (up to) a fixed number of false discoveries, GFWER is more powerful than strong FWER control, but unlike cluster-based tests and FDR control it provides a precise bound on the probability that the number of false discoveries exceeds a given number. GFWER is best suited to situations in which a researcher has some a priori hypothesis as to the number of effects to expect and lacks sufficient power to detect them using FWER control.

These recommendations for when to use each of these procedures are summarized in Table 2.

Table 2.

Situations in which each of the multiple comparison correction methods examined here are best suited.

Multiple Comparison Correction Procedure	Recommended Conditions of Use
Permutation-based strong control of FWER	Effects of interest are robust, sample size is large, or effect of interest is likely to only cover a small proportion of null hypotheses Strong control of FWER is necessary (e.g., purpose of analysis is to establish exactly when and where effects are reliable)
Cluster-based permutation test with weak control of FWER	Analyst is primarily interested in detecting somewhat to very broadly distributed effects Strong control of FWER is unnecessary
Benjamini & Hochberg FDR control	Exploratory studies of focally and/or broadly distributed effects Strong control of FWER is unlikely to be sufficiently powerful It is critical to avoid missing possible effects (i.e., making Type II errors) Analyst does not expect a large proportion (e.g., greater than 35%) of null hypotheses to be false
Benjamini & Yekutieli FDR control	A moderate to large proportion of null hypotheses are likely to be false It is important to minimize chances of making a larger than nominal proportion of false discoveries. Strong control of FWER is unlikely to be sufficiently powerful
Benjamini, Krieger, & Yekutieli FDR control	Useful under the same conditions as Benjamini and Hochberg FDR procedure and the analyst expects a large proportion (e.g., greater than 35%) of null hypotheses to be false.
Permutation-based control of GFWER	Analyst has some a priori expectation as to the number of false null hypotheses Strong control of FWER is unlikely to be sufficiently powerful

6.2 Other Practical Considerations

In addition to choosing a particular method for correction of multiple comparisons, there are a number of other practical issues to consider when performing mass univariate analyses:

• When one has some a priori hypotheses as to when and where effects will occur, one can perform a limited number of tests of these hypotheses and then perform a mass univariate analysis to detect any effects that might have been missed (e.g., Groppe et al., 2010). This approach optimizes one's power to detect expected effects and is an appropriate way to detect unexpected effects. If FDR control is used, one should probably not included expected effects in the mass univariate analysis, since large expected effects (e.g., a P3) will lead to a large proportion of false discoveries in other regions of the analysis where one is most uncertain about the presence of effects.

• To increase test power, it is best to exclude time points and sensors where no effect is likely to be present (e.g., before 100 ms poststimulus for visual stimuli).

• When using permutation-based strong FWER or GFWER control, it is probably best to downsample the data to around 100 Hz to decrease the number of comparisons and thus increase test power. Since ERP/ERF effects typically last at least 10 ms, all effects will generally still be detectable with a 100 Hz sampling rate. Changing the sampling rate is unlikely to have much effect on FDR control and cluster-based tests since it won't significantly change the proportion of false discoveries (Yekutieli & Benjamini, 1999) or cluster mass or size rankings.

• The magnitude of differences declared significant by a mass univariate procedure is likely to be over-estimated (Kriegeskorte, Lindquist, Nichols, Poldrack, & Vul, 2010). This is because multiple correction procedures increase the threshold for significance such that many small- or medium-sized effects must take fortuitously large values to reach significance. However, these large values are not representative of their true magnitude (Gelman & Weakliem, 2009).

• When performing independent samples tests, it is important to beware of tests that are sensitive to any difference between groups (e.g., differences in variance) and not just differences in central tendency (e.g., mean ERP amplitude). For parametric tests (e.g., t-tests and ANOVA) as well as permutation tests, using an equal number of participants per group provides a good measure of insensitivity to differences in group variance (Groppe et al., 2011; Zar, 1999). For permutation tests, insensitivity to differences in group variance can also be achieved by using unconventional test statistics (Groppe et al., 2011).

• When selecting the parameters of a mass univariate test (e.g., time window of interest, thresholds for cluster inclusion), it is inappropriate to tune them to produce more appealing test results. Test parameters should be justified by a priori reasoning that is independent of the particular contrasts being analyzed as doing otherwise will bias the results (Kriegeskorte et al., 2009). Moreover, researchers should explain the rationale for their choice of test parameters when reporting their results.

6.3 Conclusion

In conclusion, mass univariate analyses are a valuable addition to the statistical toolbox of the ERP/ERF methodology. They are ideally suited for the analysis of temporally or spatially unexpected effects and for questions that require a high degree of temporal or spatial resolution. We have covered some of the most common approaches for correcting for the large number of hypothesis tests that comprise a mass univariate analysis. Many other options for correcting for mass univariate analyses exist beyond those reviewed herein; among these are local false discovery rate control (Lage-Castellanos et al., 2010; Efron, 2004), random field theory (Kiebel & Friston, 2004), and false discovery exceedance control (for review see: Farcomeni, 2008; Romano et al., 2008). To help researchers apply these methods to their own data, we have provided freely available MATLAB software, called the “Mass Univariate ERP Toolbox.” The software is compatible with the EEGLAB toolbox (Delorme & Makeig, 2004) as well as the ERPLAB toolbox (http://erpinfo.org/erplab). The software, software documentation, and a tutorial, are available on the toolbox wiki (http://openwetware.org/wiki/Mass_Univariate_ERP_Toolbox). The EEGLAB toolbox and FieldTrip (Oostenveld, Fries, Maris, & Schoffelen, 2011) MATLAB software packages implement some of these procedures as well.