Abstract
The support vector machine (SVM) is a popular learning method for binary classification. Standard SVMs treat all the data points equally, but in some practical problems it is more natural to assign different weights to observations from different classes. This leads to a broader class of learning, the so-called weighted SVMs (WSVMs), and one of their important applications is to estimate class probabilities besides learning the classification boundary. There are two parameters associated with the WSVM optimization problem: one is the regularization parameter and the other is the weight parameter. In this paper we first establish that the WSVM solutions are jointly piecewise-linear with respect to both the regularization and weight parameter. We then develop a state-of-the-art algorithm that can compute the entire trajectory of the WSVM solutions for every pair of the regularization parameter and the weight parameter, at a feasible computational cost. The derived two-dimensional solution surface provides theoretical insight on the behavior of the WSVM solutions. Numerically, the algorithm can greatly facilitate the implementation of the WSVM and automate the selection process of the optimal regularization parameter. We illustrate the new algorithm on various examples.
Keywords: binary classification, probability estimation, solution surface, support vector machine, weighted support vector machine
1 Introduction
Frequently encountered in real applications is binary classification, in which we are given a training set {(xi, yi), i = 1, ···, n} of size n and the goal is to learn a classification rule. Here xi ∈ ℝp and yi ∈ {−1, 1} denote a p-dimensional predictor and a binary response (or class label), respectively, for the ith example. The primary goal of the binary classification is to construct a classifier which can be used for class prediction of new objects with predictors given. Among many existing methods for binary classification, the support vector machine (SVM) (Vapnik; 1996) is one of the most well known classifiers. It has gained much popularity since its introduction. It originates with the simple idea of finding an optimal hyperplane to separate two classes. The hyperplane is optimal in the sense that the geometric margin between these two classes is maximized. Later it was shown by Wahba (1999) that the SVM can be fit in the general regularization framework by solving
| (1) |
where H1(u) = max(1 −u, 0) is the hinge loss function, J(f) denotes the roughness penalty of a function f(·) in a function space
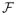 , and the sign of f(x) for a given predictor x will be used for class prediction. Here λ > 0 is a regularization parameter which balances data fitting measured by the hinge loss and model complexity measured by the roughness penalty. Lin (2002) shows that the Hinge loss is Fisher consistent. See Liu (2007) for a more detailed discussion on Fisher consistency of different loss functions. A common choice of the penalty is
. Other choices include the l1-norm penalty (Zhu et al.; 2003; Wang and Shen; 2007) and the SCAD penalty (Zhang et al.; 2006). In general, we set
, and the sign of f(x) for a given predictor x will be used for class prediction. Here λ > 0 is a regularization parameter which balances data fitting measured by the hinge loss and model complexity measured by the roughness penalty. Lin (2002) shows that the Hinge loss is Fisher consistent. See Liu (2007) for a more detailed discussion on Fisher consistency of different loss functions. A common choice of the penalty is
. Other choices include the l1-norm penalty (Zhu et al.; 2003; Wang and Shen; 2007) and the SCAD penalty (Zhang et al.; 2006). In general, we set
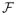 to be the Reproducing Kernel Hilbert Space (RKHS, Wahba; 1990)
to be the Reproducing Kernel Hilbert Space (RKHS, Wahba; 1990)
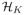 , generated by a non-negative definite kernel K(·,·). By the Representer Theorem (Kimeldorf and Wahba; 1971), the optimizer of (1) has a finite dimensional representation given by
, generated by a non-negative definite kernel K(·,·). By the Representer Theorem (Kimeldorf and Wahba; 1971), the optimizer of (1) has a finite dimensional representation given by
| (2) |
Using (2), it can be shown that the roughness penalty of f in
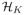 is
. Then the SVM estimates f(x) by solving
is
. Then the SVM estimates f(x) by solving
| (3) |
For the SVM (3), Hastie et al. (2004) showed that the optimizers b, θ1, ···, θn change piecewise-linearly when the regularization parameter λ changes and proposed an efficient solution path algorithm. From now on, we refer to this path as a λ-path.
Note that, in the standard SVM, each observation is treated equally no matter which class it belongs to. Yet this may not be always optimal. In some situations, it is desired to assign different weights to the observations from different classes; one such example is when one type of misclassification induces a larger cost than the other type of misclassification. Motivated by this, Lin et al. (2004) considered the weighted SVM (WSVM) by solving
| (4) |
where the weight πi’s are given by
with π ∈ (0, 1). Each point (xi, yi) is associated with one weight parameter πi, the value of which depends on the label yi. According to Lin et al. (2004), the WSVM classifier provides a consistent estimate of sign(p(x) −π) for any x, where p(x) is the conditional class probability p(x) = P (Y = 1|X = x). Using this fact, Wang et al. (2008) proposed the weighted SVM for probability estimation. The basic idea is to divide and conquer by converting a probability estimation problem into many classification sub-problems. Each classification sub-problem is assigned with a different weight parameter π, and these sub-problems are solved separately. Then the solutions are assembled together to construct the final probability estimator. A more detailed description is as follows. Consider a sequence of 0 < π(1) < ··· < π(M) < 1. For each m = 1, ···, M, solve the (4) associated with π(m) and denote the solution by f̂m(·). Finally, for any x, construct the probability estimator as p̂ (x) = {π(m+) + π(m−)}/2, where m+ = argmaxm f̂m(x) > 0 and m− = argminm f̂m(x) < 0. Advantages of the weighted SVM include flexibility and capability of handling large dimensional data.
One main concern about the probability estimation scheme proposed by Wang et al. (2008) is its computational cost. The cost comes from two sources: there are multiple sub-problems to solve, since the weight parameter π varies in (0, 1); each sub-problem is associated with one regularization parameter λ, which needs to be adaptively tuned in the range (0,∞). To facilitate the computation, the λ-path algorithm of the standard SVM (Hastie et al.; 2004) can be extended to the WSVM for any fixed π ∈ [0, 1]. In addition, Wang et al. (2008) developed the π-path algorithm for any fixed λ > 0. Both the λ-path and the π-path are piecewise-linear. However it is largely unknown how the WSVM solution fλ,π changes when both the regularization parameter λ and the weight parameter π vary together. The main purpose of our two-dimensional solution surface is to reduce the computation and tuning burden by automatically obtaining the solutions for all possible (π, λ) with an efficient algorithm.
One main motivation of this paper is to study the behaviors of the entire WSVM solutions and characterize them by a simple representation form through their relationship to π and λ. We use subscripts to emphasize that the WSVM solution f is a function of λ and π and sometimes omit the subscripts when they are clear from the context. Another motivation for the need of the solution surface is to automate the selection of the regularization parameter and improve the efficiency of searching process. Although Wang et al. (2008)’s conditional class probability estimator performs well as demonstrated by their numerical examples, its performance depends heavily on λ. They proposed to tune λ by using a grid search in their numerical illustrations. Yet, it is well known that such a grid search can be computationally inefficient and, in addition, its performance depends on how fine the grid is. The above discussions motivate us to develop a two-dimensional solution surface (rather than a one-dimensional path) as a continuous function of both λ and π in the analogous way that one resolved the inefficiency of the grid search for selecting the regularization parameter λ of the SVM by computing the entire λ-regularization path (Hastie et al.; 2004). From now on, we refer to the new two-dimensional solution surface of the WSVM as the WSVM solution surface.
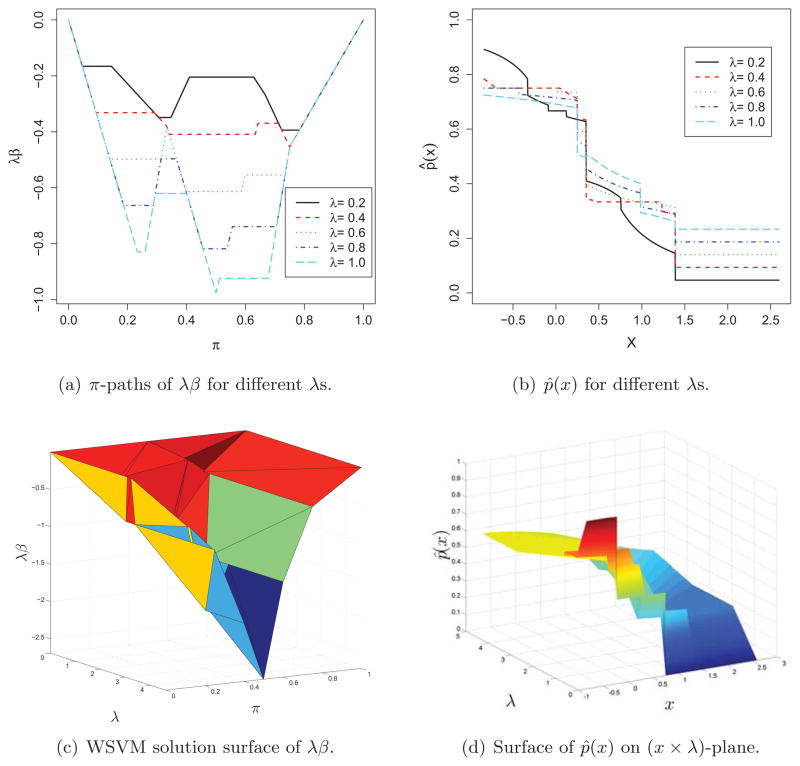
In order to show the difficulties in tuning the regularization parameter for the probability estimation (Wang et al.; 2008) and motivate our new tuning method based on the WSVM solution surface, we use a univariate toy example generated from a Gaussian mixture: xi is randomly drawn from the standard normal distribution if yi = 1 and from N (1, 1) otherwise, with five points from each class. The linear kernel (K(xi, xj) = xixj) is employed for the WSVM and its solution is then given by f(x) = b + βx with . In order to describe the behavior of f (x), we plot λβ based on the obtained WSVM solution surface (or path), since λβ, instead of β, is piecewise-linear in λ due to our parametrization. In Figure 1, the top two panels depict the solution paths of λβ for the different values of λ fixed at 0.2, 0.4, 0.6, 0.8, 1.0 (left) and the corresponding estimates of p̂ (·) as a function of x (right); the bottom two panels plot the entire two-dimensional joint solution surface (left) and the corresponding probability estimate p̂ (·) as a function of λ as well as x (right). We note that, although all the five π-paths are piecewise-linear in π they have quite different shapes for different values of λ (see (a)). Thus the corresponding probability estimates can be quite different even for the same x (see (b)), suggesting the importance of selecting an optimal λ. By using the proposed WSVM solution surface, we can completely recover the WSVM solutions on the whole (λ × π)-plane (see (c)), which enables us to produce the corresponding conditional probability estimators at a given x for every λ with very little computational expense (see (d)). We will shortly demonstrate that it is computationally efficient to extract marginal paths (λ-path or π-path) once the WSVM solution surface is obtained.
Figure 1.
Simulated toy example: the top two panels depict the solution λβ and the estimate p̂ (x) given by five marginal π-solution paths, with λ values fixed at 0.2, 0.4, 0.6, 0.8, 1.0. The bottom two panels plot the joint solution surface of λβ and the corresponding surface of p̂ (x). Notice that the horizontal axis of (b) is x. Similarly the surface in (d) lies on the (x × λ) plane.
In this example, we use a grid of five equally-spaced λs which is very rough. In practice, it is typically not known a priori how fine the grid should be or what the appropriate range of the grid is. If the data are very large or complicated, the grid one choose may not be fine enough to capture the variation of the WSVM solution and will lose efficiency for the subsequent probability estimation. The proposed WSVM solution surface provides a complete portrait for the WSVM solution corresponding to any pair of λ and π and therefore naturally overcomes this kind of practical difficulties, in addition to the gain in computational efficiency.
In this article, we show that the WSVM solution is jointly piecewise-linear in both λ and π and propose an efficient algorithm to construct the entire solution surface on the (λ × π)-plane by taking advantage of the established joint piecewise-linearity. As a straightforward application, an adaptive grid for tuning the regularization parameter of the probability estimation scheme (Wang et al.; 2008) is proposed. We finally remark that the WSVM solution surface has broad applications in addition to the probability estimation.
The rest of the article is organized as follows. In Section 2, the WSVM problem is formulated in details to develop the joint solution surface of the WSVM. In Section 3 we establish the joint piecewise-linearity of the WSVM solution on (λ × π)-plane. An efficient algorithm is developed to compute the WSVM solution surface by taking advantage of its piecewise-linearity in Section 4; its computational complexity is explored in Section 5. The proposed WSVM solution surface algorithm is illustrated by the kyphosis data in Section 6. It is then applied to the probability estimation problems in several sets of real data in Section 7. Some concluding remarks are given in Section 8.
2 Problem Setup
By introducing nonnegative slack variables ξi, i = 1, ···, n and using inequality constraints, the WSVM problem (4) can be equivalently rewritten as
The corresponding Lagrangian primal function is constructed as
| (5) |
where αi ≥ 0 and γi ≥ 0 are the Lagrange multipliers. To derive the corresponding dual problem, we set the partial derivatives of LP in (5) with respect to the primal variables to zero, which gives
| (6) |
| (7) |
| (8) |
along with the Krush-Kuhn-Turker (KKT) conditions
| (9) |
| (10) |
Notice from (6) that the function (2) can be rewritten as
| (11) |
By combining (6–10), the dual problem of the WSVM is given by
| (12) |
and this can be readily solved via the quadratic programming (QP) for any given λ and π. However, the two parameters λ and π may not be known in practice. A classical approach is to repeatedly solve the QP problem (12) for different pairs of (λ, π) in order to select the desired λ and π. This is very computationally intensive for large data set because the QP itself is a numerical method whose computational complexity increases polynomially in n.
For the standard SVM (equivalent to a special case of the WSVM with the weight parameter π = 0.5), Hastie et al. (2004) showed the piecewise-linearity of αi in λ and developed an efficient algorithm to compute the entire piecewise-linear solution path. The same idea can be extended straightforwardly to the WSVM with any fixed weight parameter or any fixed individual weights. In addition, Wang et al. (2008) showed the WSVM solutions αi are piecewise-linear in the weight parameter π while keeping the regularization parameter λ fixed. However it is largely unknown how the WSVM solution αi changes with respect to the two parameters jointly. In this article, we show that the WSVM solutions αis, as a function of both λ and π, form a continuous piecewise-linear solution surface on the (λ × π)-plane and propose an efficient algorithm to compute the entire solution surface.
Similar to the idea of Hastie et al. (2004), we categorize all the examples, i = 1, ···, n into the three disjoint sets as
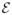 = {i : yif (xi) = 1, 0 ≤ αi ≤ πi} (elbow),
= {i : yif (xi) = 1, 0 ≤ αi ≤ πi} (elbow),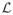 = {i : yif (xi) < 1, αi = πi} (left),
= {i : yif (xi) < 1, αi = πi} (left),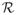 = {i : yif (xi) > 1, αi = 0} (right).
= {i : yif (xi) > 1, αi = 0} (right).
It is easy to see that the above three sets are always defined uniquely by the conditions (6)–(10). The set names come from the particular shape of the hinge loss function (Hastie et al.; 2004). Note that {αi, ∀i ∈
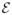 } contains most of the information on how the WSVM solution changes on the (λ × π)-plane, since the rest solutions {αi, i ∈
} contains most of the information on how the WSVM solution changes on the (λ × π)-plane, since the rest solutions {αi, i ∈
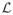 ∪
∪
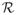 } are trivially determined by the definition of the sets.
} are trivially determined by the definition of the sets.
As λ and π change, the sets may change and, as long as this happens, we call it an event. All the solution surfaces for αi, i = 1, ···, n are continuous and hence no element in
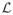 can move directly to
can move directly to
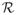 or vice versa. Therefore there are only three possible events to be considered as follows. The first event defines when one of αi, i ∈
or vice versa. Therefore there are only three possible events to be considered as follows. The first event defines when one of αi, i ∈
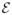 reaches πi and the corresponding index i exits from
reaches πi and the corresponding index i exits from
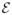 to
to
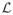 (event 1). Similarly, an αi, i ∈
(event 1). Similarly, an αi, i ∈
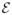 can reach the other boundary 0 and the index moves form
can reach the other boundary 0 and the index moves form
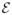 to
to
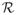 (event 2). The last event happens when one element i of
(event 2). The last event happens when one element i of
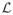 ∪
∪
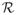 satisfies yif (xi) = 1 and enters to
satisfies yif (xi) = 1 and enters to
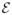 (event 3).
(event 3).
3 Joint piecewise-linearity
In this section, we study the behavior of the WSVM solutions from a theoretical point of view. One major discovery we have made is that, αi, i ∈
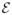 , hence all the αi, i = 1, ···, n changes in a jointly piecewise-linear manner when λ and π vary. The following theorem describes how αi moves as λ and π change. For simplicity, we define α0 = λb.
, hence all the αi, i = 1, ···, n changes in a jointly piecewise-linear manner when λ and π vary. The following theorem describes how αi moves as λ and π change. For simplicity, we define α0 = λb.
Theorem 1
(Joint Piecewise-Linearity) Suppose we have a point (λℓ, πℓ) in the (λ × π) plane. Let
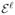 ,
,
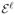 ,
,
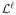 ,
, and
denote the associated sets and solutions obtained at (λℓ, πℓ), respectively. Now, we consider a subset
,
, and
denote the associated sets and solutions obtained at (λℓ, πℓ), respectively. Now, we consider a subset
 (of the (λ×π)-plane) which contains (λℓ, πℓ) such that no event happens within
(of the (λ×π)-plane) which contains (λℓ, πℓ) such that no event happens within
 . In other words, for all (λ, π) ∈
. In other words, for all (λ, π) ∈
 , the associated three sets,
, the associated three sets,
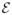 ,
,
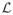 , and
, and
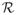 remain the same as
remain the same as
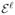 ,
,
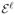 , and
, and
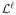 , respectively. Then the solution αi, i ∈ {0} ∪
, respectively. Then the solution αi, i ∈ {0} ∪
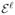 , denoted by α0,
, denoted by α0,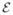 in a vector form moves in
in a vector form moves in
 as follows:
as follows:
| (13) |
where and Δ = (Δλ, Δπ)T = (λ − λℓ, π − πℓ)T. The gradient matrix, Gℓ is given by
| (14) |
where
; yℓ = {yi:i ∈
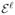 }T; |A| denotes the cardinality of a set A; and 1 is the one vector of length |
}T; |A| denotes the cardinality of a set A; and 1 is the one vector of length |
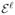 |.
|.
Proof
We can rewrite (11) as:
| (15) |
Moreover, in
 we have yif (xi) = yifℓ(xi) = 1, i ∈
we have yif (xi) = yifℓ(xi) = 1, i ∈
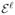 , which leads to
, which leads to
| (16) |
where
, ∀i ∈ {0}∪
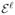 . In addition,
by definitions of the sets and the condition (7) gives
. In addition,
by definitions of the sets and the condition (7) gives
| (17) |
Finally, we have (|
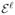 |+1) linear equations from (16), (17), which can be expressed in a matrix form as Aℓν= BℓΔ, where ν = {νi : i ∈ {0} ∪
|+1) linear equations from (16), (17), which can be expressed in a matrix form as Aℓν= BℓΔ, where ν = {νi : i ∈ {0} ∪
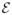 }T = α0,
}T = α0,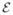 − α0,
− α0,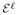 . Finally the desired result follows by assuming Aℓ to be invertible.
. Finally the desired result follows by assuming Aℓ to be invertible.
We remark that Aℓ is rarely singular in practice, and related discussions can be found in Hastie et al. (2004). It is worthwhile to point out that the joint piecewise-linearity of the solution guarantees the marginal piecewise-linearity as presented in Corollary 2, but not vice versa. Therefore, Theorem 1 implies the piecewise-linearity of the marginal solution paths as a function of either λ or π, which were separately explored by Hastie et al. (2004) and Wang et al. (2008).
Corollary 2
(Marginal Piecewise-Linearity) For a given π0, the solution, α0,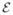 moves linearly in λ ∈ {λ : (λ, π0) ∈
moves linearly in λ ∈ {λ : (λ, π0) ∈
 } as follows.
} as follows.
Similarly, α0,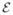 changes in π ∈ {π : (λ0, π) ∈
changes in π ∈ {π : (λ0, π) ∈
 } for a given λ0 as follows.
} for a given λ0 as follows.
where and denote the first and second column vectors of Gℓ in (14), respectively.
The classification function f(x) can be conveniently updated by plugging (13) into (15), which gives
| (18) |
where
and (gi1, gi2) denotes the row of Gℓ where i ∈ {0} ∪
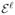 . We observe from (18) that f (x) is not jointly piecewise-linear in (λ, π) while it is marginally piecewise-linear in λ−1 and π, respectively.
. We observe from (18) that f (x) is not jointly piecewise-linear in (λ, π) while it is marginally piecewise-linear in λ−1 and π, respectively.
4 Solution Surface Algorithm
In this section, we propose an efficient algorithm to compute the entire solution surface of the WSVM on the (λ × π)-plane by using the joint piecewise-linearity established in Theorem 1.
4.1 Initialization
Denote index sets I+ = {i : yi = 1} and I− = {i : yi = −1}. We initialize the algorithm at π0 = |I+|/n. Notice that the π0 satisfies the so-called balanced condition that requires Σi∈I+ πi(π0) = Σi∈I− πi(π0). With π = π0 it is easy to verify that, for a sufficiently large λ, αi = π0 if i ∈ I+ and 1 − π0 otherwise. Following the idea of Hastie et al. (2004), the initial values of λ and α0 denoted by λ0 and , respectively are given by
where . The indices i+ and i− are defined as
It is possible to initialize the algorithm at any π between 0 and 1 rather than π0, however, we empirically observe that the initialized λ is the largest when π = π0. Notice that the corresponding solution is trivial as αi = πi for all i = 1, ···, n for any λ larger than λ0. Therefore, the proposed algorithm focuses only on the non-trivial solutions obtained at
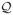 = {(λ, π) : 0 ≤ λ ≤ λ0, 0 ≤ π ≤ 1}. Finally, the three sets initialized at (λ0, π0) denoted by
= {(λ, π) : 0 ≤ λ ≤ λ0, 0 ≤ π ≤ 1}. Finally, the three sets initialized at (λ0, π0) denoted by
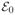 ,
,
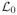 and
and
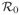 , respectively are given by
, respectively are given by
where φ denotes the empty set.
4.2 Update
Recall that, for any point (λℓ, πℓ), no event occurs if (λ, π) ∈
 and the WSVM solution can be updated by applying Theorem 1 for any (λ, π) ∈
and the WSVM solution can be updated by applying Theorem 1 for any (λ, π) ∈
 . Therefore, it is essential to know how to define
. Therefore, it is essential to know how to define
 as large as possible for any (λℓ, πℓ). We shall demonstrate next that the set
as large as possible for any (λℓ, πℓ). We shall demonstrate next that the set
 can be explicitly determined by some linear constraints.
can be explicitly determined by some linear constraints.
Note that event 1 happens when αi reaches πi for some i ∈
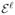 . Based on (13), we have the following inequality constraints to prevent event 1 from happening:
. Based on (13), we have the following inequality constraints to prevent event 1 from happening:
| (9) |
| (20) |
where and . In a similar way, we have the following inequalities to prevent event 2 :
| (21) |
In order to prevent event 3, we have yif (xi) < 1, ∀i ∈
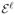 and yif (xi) > 1, ∀i ∈
and yif (xi) > 1, ∀i ∈
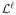 . Therefore, by noting (15), we have
. Therefore, by noting (15), we have
| (22) |
| (23) |
where
. We remark that the equalities do not need to be strict since an event is instant transition. Recall that it is enough to consider the solution on
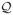 and hence the additional constraints 0 ≤ λ ≤ λ0 and 0 ≤ π ≤ 1 should be considered as well by default. In summary
and hence the additional constraints 0 ≤ λ ≤ λ0 and 0 ≤ π ≤ 1 should be considered as well by default. In summary
 can be defined by a subregion on the (λ × π)-plane that satisfies all the constraints (19)–(23). Figure 2 illustrates a
can be defined by a subregion on the (λ × π)-plane that satisfies all the constraints (19)–(23). Figure 2 illustrates a
 generated from the initial point (λ0, π0) for the toy example in Section 1. We remark that
generated from the initial point (λ0, π0) for the toy example in Section 1. We remark that
 forms a polygon which can be uniquely expressed by its vertices, since the constraints are all linear.
forms a polygon which can be uniquely expressed by its vertices, since the constraints are all linear.
Figure 2.
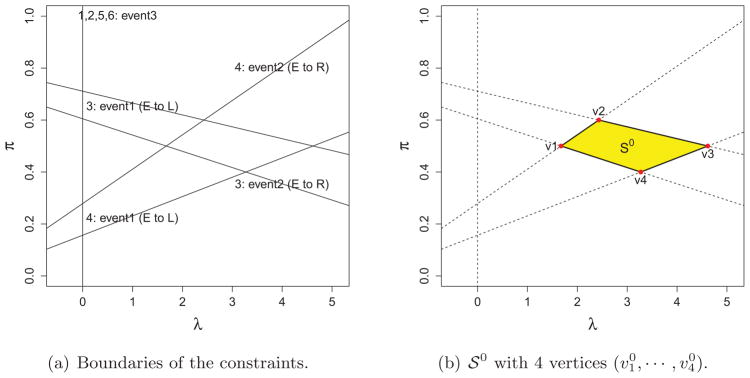
The illustration of defining
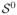 generated from the initial point (λ0, π0) for the toy example in Section 1: Each line in the left penal (a) represents a constraint boundary where an event occurs as labeled. For example, the upper right label represents the event: the fourth example moves from
generated from the initial point (λ0, π0) for the toy example in Section 1: Each line in the left penal (a) represents a constraint boundary where an event occurs as labeled. For example, the upper right label represents the event: the fourth example moves from
 to
to
 on the boundary. The set
on the boundary. The set
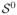 obtained from the boundaries in (a) is depicted in (b).
obtained from the boundaries in (a) is depicted in (b).
We describe next how to determine the vertices of
 in an efficient manner. First, compute all the pairwise intersection points of the boundaries of (19)–(23) then we have
intersection points, where nc denotes the number of constraints (19)–(23), n + |
in an efficient manner. First, compute all the pairwise intersection points of the boundaries of (19)–(23) then we have
intersection points, where nc denotes the number of constraints (19)–(23), n + |
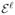 |. The left penal of Figure 2 shows all the intersections of the boundaries of the obtained constraints. Then, we can define the vertices by identifying the intersections that satisfy all the constraints (19)–(23) as illustrated in (b) of Figure 2. We denote the vertices of the
|. The left penal of Figure 2 shows all the intersections of the boundaries of the obtained constraints. Then, we can define the vertices by identifying the intersections that satisfy all the constraints (19)–(23) as illustrated in (b) of Figure 2. We denote the vertices of the
 as {
} where
, r = 1, … ; nv,.
as {
} where
, r = 1, … ; nv,.
There are a couple of issues we need to clarify here. First, based on our limited experience, we observe that nv is small and typically does not exceed eight. Hence it is not efficient to compute all the
intersections due to the involved computational intensity. Note also that some constraints are dominated by others on
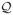 and are thus automatically satisfied if other constraints hold. Consequently, we can save a huge amount of computational time by excluding those constraints which are dominated by others, especially when n is large. We also need to order the vertices for set-updates which are discussed next. Here the ordering means that a vertex
, r = 1, ···, nv is adjacent to
and
, where we set
(see (b) in Figure 2). The updating of α1, ···, αn as well as α0 at vertices of
and are thus automatically satisfied if other constraints hold. Consequently, we can save a huge amount of computational time by excluding those constraints which are dominated by others, especially when n is large. We also need to order the vertices for set-updates which are discussed next. Here the ordering means that a vertex
, r = 1, ···, nv is adjacent to
and
, where we set
(see (b) in Figure 2). The updating of α1, ···, αn as well as α0 at vertices of
 provided is straightforward by Theorem 1.
provided is straightforward by Theorem 1.
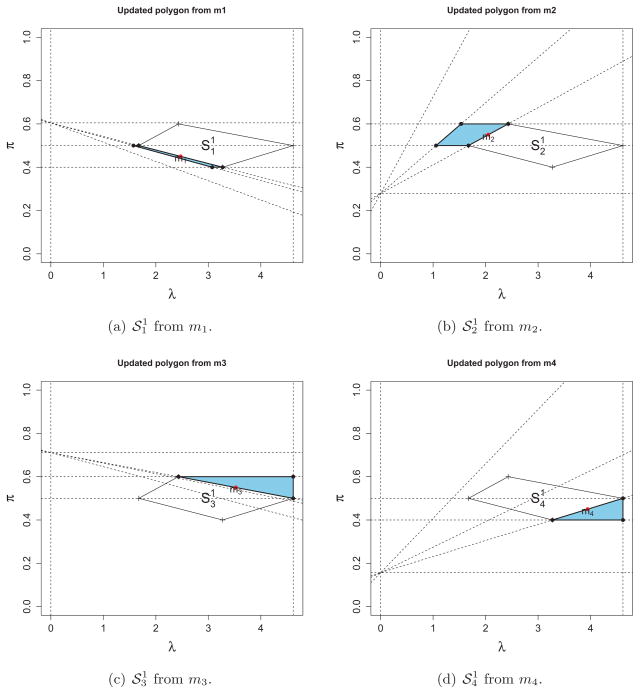
Figure 3 illustrates how to extend the polygons on
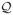 from current
from current
 in Figure 2-(b). Notice that the sides of
in Figure 2-(b). Notice that the sides of
 are determined by some boundaries of the constraints (19) – (23) and represent corresponding events. Each middle point of two adjacent vertices can be used as a new starting point, (λℓ+1, πℓ+1) in Theorem 1 to compute a new polygon
are determined by some boundaries of the constraints (19) – (23) and represent corresponding events. Each middle point of two adjacent vertices can be used as a new starting point, (λℓ+1, πℓ+1) in Theorem 1 to compute a new polygon
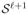 . Computing middle points and corresponding solutions denoted by
and
, respectively where r = 1, ···, nv is trivial due to the piecewise-linearity of the solutions. The bar sign in
is used to emphasize the quantities are obtained at middle points, not vertices. At each middle point, the corresponding three sets denoted by
, and
respectively can be updated based on which line the middle point mr is on. For example as shown in (a) of Figure 3, the three sets
, and
obtained at m1 are updated as
, and
. This is because
lies on the boundary which represents an event that the element 4 moves to the right set from the elbow set (see (a) in Figure 2). Now we have all the information required to generate a new polygon,
, from the middle point, m1 and
can be accordingly computed by treating m1 as a new updating point (This is the reason why we use a superscript ℓ + 1 to denote middle points). Figure 3 shows all the four newly-created polygons,
, r = 1, ···, 4 respectively from the four middle points m1, ···, m4 of the sides of
. Computing middle points and corresponding solutions denoted by
and
, respectively where r = 1, ···, nv is trivial due to the piecewise-linearity of the solutions. The bar sign in
is used to emphasize the quantities are obtained at middle points, not vertices. At each middle point, the corresponding three sets denoted by
, and
respectively can be updated based on which line the middle point mr is on. For example as shown in (a) of Figure 3, the three sets
, and
obtained at m1 are updated as
, and
. This is because
lies on the boundary which represents an event that the element 4 moves to the right set from the elbow set (see (a) in Figure 2). Now we have all the information required to generate a new polygon,
, from the middle point, m1 and
can be accordingly computed by treating m1 as a new updating point (This is the reason why we use a superscript ℓ + 1 to denote middle points). Figure 3 shows all the four newly-created polygons,
, r = 1, ···, 4 respectively from the four middle points m1, ···, m4 of the sides of
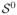 in Figure 2-(b). Notice that the right vertical line represents λ = λ0 and we do not have any interest beyond it. Finally, the proposed algorithm can be continued to extend the polygons being searched on
in Figure 2-(b). Notice that the right vertical line represents λ = λ0 and we do not have any interest beyond it. Finally, the proposed algorithm can be continued to extend the polygons being searched on
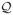 and is terminated when the complete solution surface is recovered on
and is terminated when the complete solution surface is recovered on
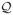 .
.
Figure 3.
The updated polygons
, r = 1, ···, 4 from the middle points m1, ···, m4 of the sides of
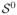 in Figure 2(b): Dotted lines in each subfigure depict the boundaries of constrains for obtaining the polygon.
in Figure 2(b): Dotted lines in each subfigure depict the boundaries of constrains for obtaining the polygon.
4.3 Resolving Empty Elbow
Note that either event 1 and or event 2 leads to the possibility that
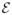 is empty, named empty elbow. This may cause a problem in the update described in Section 4.2, because Theorem 1 cannot be applied when
is empty, named empty elbow. This may cause a problem in the update described in Section 4.2, because Theorem 1 cannot be applied when
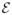 is empty.
is empty.
We suppose the empty elbow occurs at (λo, πo) and use a superscript ‘o’ to denote any quantity defined at (λo, πo). In order to resolve the empty elbow, we first notice that the objective function (4) is differentiable with respect to b and αi, i = 1, ···, n whenever the the elbow set is empty since in this case there is no example satisfying yif (xi) = 1. Taking derivative of (4) with respect to b and αi, we get two conditions to be satisfied under the empty elbow :i) , where and ii) αi are unique while α0 is not. Moreover, α0 can be any value in the following interval,
| (24) |
where
; and
, and
are similarly defined as
. Recall that α0 is continuous and hence the empty elbow can be resolved only by α0 touching one of the two boundaries aL and aU. Notice that the
is regarded as a starting point where the empty elbow begins and hence it must be one of aL and aU. Without loss of generality, we suppose
then the empty elbow should be resolved when it becomes the other boundary aU. Let
and
, then the
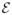 should be updated to {
}. The
should be updated to {
}. The
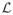 and
and
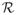 are accordingly updated as well since the updated index
enters to the
are accordingly updated as well since the updated index
enters to the
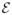 from one of the two sets. In case of
, we update in a similar way which leads to
.
from one of the two sets. In case of
, we update in a similar way which leads to
.
4.4 Pseudo Algorithm
Combining the previous several subsections, we now summarize our WSVM solution surface algorithm at Algorithm 1. We denote α = (α0, α1, ···, αn)T for simplicity. We note that the proposed algorithm computes the complete WSVM solution αs for any (λ, π) ∈
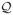 without involving any numerical optimization. We have implemented the algorithm in R language and the wsvmsurf package is available from the authors upon request (and will be available on CRAN soon).
without involving any numerical optimization. We have implemented the algorithm in R language and the wsvmsurf package is available from the authors upon request (and will be available on CRAN soon).
Algorithm 1.
WSVM solution surface of the WSVM
| Input: A training data set (xi, yi), i = 1, ···, n and a non-negative definite kernel function K(x, x′). |
Output : The entire (piecewise-linear) solution surface on
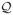 of αi, i = 0, ···, n, the optimizer of (4). of αi, i = 0, ···, n, the optimizer of (4). |
|
Table 1.
Empirical computing time based on 100 independent repetitions: the machine we used equips Intel Core (TM) i3 550 @ 3.20GHZ CPU with 4GB memory.
| n | Gaussian | Linear | ||||
|---|---|---|---|---|---|---|
|
| ||||||
| time(s) | piece | time/piece | time(s) | piece | time/piece | |
| 10 | 0.53 (0.01) | 164.3 (3.58) | 0.00325 | 0.44 (0.01) | 140.98 (2.70) | 0.00311 |
| 30 | 5.78 (0.08) | 2056.6 (27.16) | 0.00281 | 4.36 (0.06) | 1648.05 (21.24) | 0.00265 |
| 50 | 19.08 (0.22) | 6036.8 (55.29) | 0.00316 | 14.38 (0.16) | 4870.05 (52.40) | 0.00295 |
| 100 | 108.00 (1.07) | 25653.0 (193.50) | 0.00421 | 80.72 (0.67) | 20087.13 (148.05) | 0.00402 |
5 Computational Complexity
The essential part of the proposed algorithm involves several steps. First, we solve the linear equation system (14) of size 1 + |
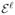 |, which involves O((1 + |
|, which involves O((1 + |
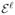 |)3) computations. We empirically observe that |
|)3) computations. We empirically observe that |
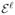 |, the number of support vector depends on n but is usually much less than n during the algorithm. Next, in order to determine the set
|, the number of support vector depends on n but is usually much less than n during the algorithm. Next, in order to determine the set
 , we compute constraints (19) – (23) and h1(xi) and h2(xi), which respectively requires O(n|
, we compute constraints (19) – (23) and h1(xi) and h2(xi), which respectively requires O(n|
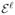 |) and O(n2) computations. Now we have nc = n + |
|) and O(n2) computations. Now we have nc = n + |
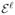 | constraints and need to find their intersection points which satisfy all the constraints (19)–(23) simultaneously. This is the most computationally expensive step since it requires to evaluate nc(nc − 1)/2 intersection points and check nc constraints for each point, which takes at least
computations in total.
| constraints and need to find their intersection points which satisfy all the constraints (19)–(23) simultaneously. This is the most computationally expensive step since it requires to evaluate nc(nc − 1)/2 intersection points and check nc constraints for each point, which takes at least
computations in total.
Our limited numerical experience suggests that the final vertices of
 is of size less than or equal to eight, which implies that most of the constraints are dominated by others. This leads us to suggest adding a refining step which removes those constraints dominated by others in the algorithm as follows. First, since all the constraints have a common linear form of αλ + bπ ≥ c for different values of a, b and c for different constraints, we can classify the constraints into two types depending on the sign of b, positive or negative, assuming b ≠ 0 for simplicity. See Figure 4-(a) for an illustration. If b < 0 for a constraint then the region represented by the constraint is below its boundary (dashed lines), otherwise it is above the boundary (dotted lines). For each type of constraints with either b > 0 or b < 0, we compute values of πs at λ = 0 and λ0 (vertical lines), then we can exclude most of, but not all dominated boundaries by sorting the π values obtained. The refining step requires at most
computations since it is based on the sorting algorithm, Shellsort variant. After the refining step, we have only ñc constraints to consider for computing the
is of size less than or equal to eight, which implies that most of the constraints are dominated by others. This leads us to suggest adding a refining step which removes those constraints dominated by others in the algorithm as follows. First, since all the constraints have a common linear form of αλ + bπ ≥ c for different values of a, b and c for different constraints, we can classify the constraints into two types depending on the sign of b, positive or negative, assuming b ≠ 0 for simplicity. See Figure 4-(a) for an illustration. If b < 0 for a constraint then the region represented by the constraint is below its boundary (dashed lines), otherwise it is above the boundary (dotted lines). For each type of constraints with either b > 0 or b < 0, we compute values of πs at λ = 0 and λ0 (vertical lines), then we can exclude most of, but not all dominated boundaries by sorting the π values obtained. The refining step requires at most
computations since it is based on the sorting algorithm, Shellsort variant. After the refining step, we have only ñc constraints to consider for computing the
 and ñc is much smaller than nc.
and ñc is much smaller than nc.
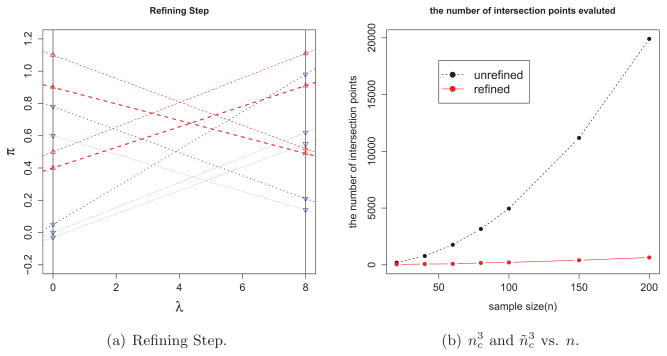
Figure 4.
Illustration of the refining step and its effect for simulated example: The left penal (a) shows all the boundaries of constraints. Dashed (red) lines represents boundaries of constraints with b < 0 and only two constraints (bold) are used to defined
 and the other two excluded are chosen by comparing π values at λ = 0 and λ0. Dotted (blue) lines are the ones with b > 0 and we can exclude dominated constraints in a similar manner. The right panel (b) shows dramatic saving in computation after use of the refining step by comparing the numbers of intersection points of unrefined constraints (nc) and refined ones (ñc) as functions of sample size, n.
and the other two excluded are chosen by comparing π values at λ = 0 and λ0. Dotted (blue) lines are the ones with b > 0 and we can exclude dominated constraints in a similar manner. The right panel (b) shows dramatic saving in computation after use of the refining step by comparing the numbers of intersection points of unrefined constraints (nc) and refined ones (ñc) as functions of sample size, n.
In order to demonstrate the benefit of the refining step, we consider the situations where the data sets from univariate Gaussian mixture for different sample size, n. Data are generated as xi ~ N (0, 1) if i ∈ I+ and xi ~ N (1, 1) otherwise with |I+| = |I−| = n/2. Employing Gaussian kernel
with σ = 1, Figure 4-(b) illustrates how effective the refining step is. We observe that only about 20% of the constraints are used to compute
 for relatively large n, suggesting a dramatic computational saving to evaluate
for relatively large n, suggesting a dramatic computational saving to evaluate
 (only about 0.23 = .8% computations is required, compared to the case when the refining step is not employed). The right panel (b) shows
(black dashed-line) versus
(red solid-line) for different n; the computational saving is substantial when n is large.
(only about 0.23 = .8% computations is required, compared to the case when the refining step is not employed). The right panel (b) shows
(black dashed-line) versus
(red solid-line) for different n; the computational saving is substantial when n is large.
In order to obtain the entire solution surface we need to iterate the aforementioned updating steps. It is quite challenging to rigorously quantify the number of required iterations as a function of n, since it depends on not only the data but also the kernel function employed (and hence its parameter). We instead evaluate empirical computing time for different sample size n based on 100 independent repetitions (Table 1). The data are simulated from a bivariate Gaussian mixture with the same number of observations from each class (i.e., |I+| = |I−| = n/2). In particular, if i ∈ I+ then xi is from N ((0, 0)T,
I2) and otherwise xi ~ N2 (2, 2)T,
I2 where I2 is the two-dimensional identity matrix. In Table 1, we report the average computing time, average number of pieces, and the computing time per piece for both the Gaussian kernel and the linear kernel. The kernel parameter σ of the Gaussian kernel is assumed to be fixed and set to be the median of pairwise distances between the two classes (Jaakkola et al.; 1999). Our limited numerical experience suggests that the computing time per a piece (
 ) does not depend severely on n while the entire time increases proportional to n2 since the number of polygons produced does. In Table 1, the numbers in parentheses are the corresponding standard errors.
) does not depend severely on n while the entire time increases proportional to n2 since the number of polygons produced does. In Table 1, the numbers in parentheses are the corresponding standard errors.
Finally, one may desire to extract the marginal path, either a λ-path or a π-path, from the WSVM solution surface. This can be easily done after obtaining all the polygons and the corresponding WSVM solutions. It is straightforward to interpolate the WSVM solution for any pair (λ, π) using the WSVM solutions corresponding to vertices of all those polygons produced from the WSVM solution surface. Let ‘d’ be the total number of vertices. As aforementioned, d is proportional to n2. Then it requires only O(d) computations to obtain the marginal solution paths, since the vertices of each polygon are properly ordered already.
6 Illustration
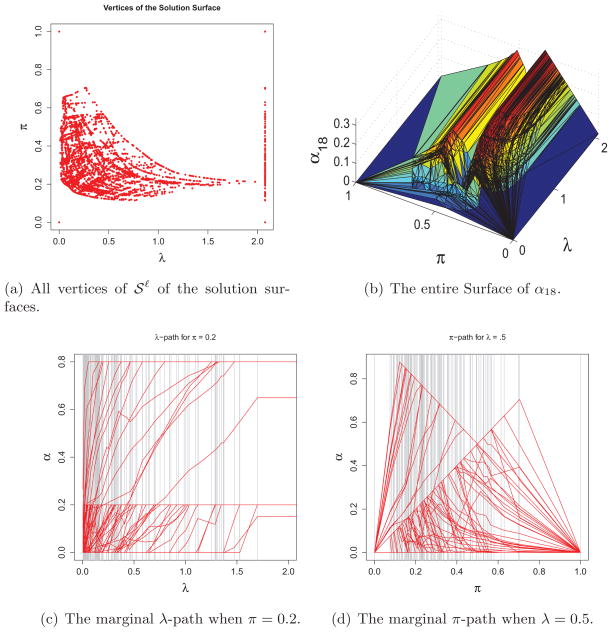
In this section, we illustrate how the proposed WSVM solution surface algorithm works by using the kyphosis data (Chambers and Hastie; 1992) available in R package rpart. The data contain the status (absence or presence of a kyphosis) of n = 81 children who had a corrective spinal surgery. The class variable yi is coded −1 for absence and +1 for presence of a kyphosis after the operation. Three predictors are recorded for each child (i.e., p = 3): age of a patient (in month), the number of vertebrae involved, and the number of the first vertebra operated on. The Gaussian kernel is used with kernel parameter σ set to be 0.01. The entire solution surface consists of 7,502 polygons (or pieces) and the total computing time is 34.90 seconds. In Figure 5, the panel (a) plots all the vertices of the polygons produced, (denoted by red dots), and the panel (b) depicts the entire surface of α18. There are 81 αi, i = 1, ···, 81-surfaces totally, one corresponding to each of the ith observation. For the purpose of illustration, we only show one of them for i = 18. The solution surfaces for the rest 80 αis can be visualized in a similar way. Once we have the entire two-dimensional solution surfaces, the marginal solution paths can be readily obtained for a fixed value of either λ or π. The two panels (c) and (d) represent the marginal regularization paths with a fixed π = 0.2 and the marginal paths with a fixed λ = 0.5, extracted from the WSVM solution surface, respectively. Notice that there are 81 observations in the data and hence each piecewise-linear path in (c) and (d) represents a marginal solution path of a αi where i = 1, ···, 81.
Figure 5.
Real data illustration on kyphosis data.
7 Applications to Probability Estimation
In this section, we revisit the motivating application of the proposed joint solution surface algorithm to the probability estimation (Wang et al.; 2008) introduced in Section 1. In Wang et al. (2008), the regularization parameter λ is selected by a grid search over the interval [10−3, 103] with ten equally-spaced points in each sub-interval (10j, 10j+1] where j = −3, ···, 2. In practice, it can be difficult to choose an appropriate range for parameter search or to determine the right level of grid coarseness. A general rule is: if the WSVM solution varies rapidly for different λ, we need a fine gird; otherwise, a coarse grid will be more appropriate in terms of computational efficiency. However, without a priori information available, a subjective choice of the range could be either too wide or too narrow, and the grid could be too fine or too rough. The proposed WSVM solution surface algorithm provides a natural and informative guidance to tackle these issues. We propose to use all the distinct λs obtained from the WSVM solution surface algorithm as the grid, namely the set of all λs corresponding to all vertices of those polygons obtained by the WSVM solution surface. We like to point out that the proposed grid of λ is adaptive to the solution variation, in the sense that we have a finer grid if the solution surface is complicated and a rough grid otherwise.
We compare these two grid search methods using two microarray datasets available at LIBSVM Data website (http://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary.html). For both of the datasets, the sample sizes are much smaller then the number of predictors. The Gaussian kernel is employed to train the WSVM and the associated kernel parameter σ is set to be the median distances between the two classes. In order to evaluate performance of the probability estimator using the two different grids, the fixed grid employed in Wang et al. (2008) and the proposed adaptive grid, the cross entropy error (CRE) is used. The CRE over a set of data {(xi, yi) : i = 1, 2, ···, n} is defined as follows.
| (25) |
Table 2 contains summarized information of the well-known microarray data sets used, Duke cancer and Colon cancer data. One merit of the proposed probability estimator is that it is not only distribution-free method but also free from the dimension of predictors p, since it exploits the kernel trick. For tuning λ, we employ the cross-validation (leave-one-out and 10-fold) instead of using independent tuning set since the data sets have relatively small sample sizes. Table 3 shows the test CREs for the microarray examples. We point out that clear improvements of the proposed adaptive grid are observed for the microarray examples compared to the fixed grid. This is because the joint solution surfaces of the microarray examples are complicated and the fixed grid fails to reflect this complicated pattern of the solutions.
Table 2.
Sources for the microarray data used for illustrations: The numbers of predictors (p) are all 7219 and much larger than the sample size (n).
| Name | train(n) | test(ñ) | p | Source |
|---|---|---|---|---|
| Duke Cancer | 38 | 4 | 7219 | West et al. (2001) |
| Colon Cancer | 40 | 22 | 2000 | Alon et al. (1999) |
Table 3.
Test CREs for Microarray data sets (p > n).
| data | tuning | fixed | adaptive | improve |
|---|---|---|---|---|
| Duke | LOCV | 0.4991 | 0.4794 | 3.94% |
| 10-fold | 0.4846 | 0.4729 | 2.42% | |
|
| ||||
| Colon | LOCV | 0.3058 | 0.2511 | 17.89% |
| 10-fold | 0.3058 | 0.2646 | 13.45% | |
8 Concluding Remarks
In this article, we first establish that the WSVM solution is jointly piecewise-linear in λ and π and then develop an efficient algorithm to compute the entire WSVM solution surface on the (λ × π)-plane by taking advantage of the joint piecewise-linearity. To demonstrate its practical value, we propose an adaptive tuning scheme for the probability estimation method based on the WSVM solution surface. Illustrations using real data sets show that the proposed adaptive tuning grid from the WSVM solution surface improves the performance of the probability estimator especially when the solution surfaces are complicated. We remark that the proposed solution surface provides the entire information of the WSVM solution for arbitrary pair of λ and π and therefore potentially contains wide applicability in various statistical applications.
The piecewise-linearity of the marginal λ-path or regularization paths has been well-studied in the literature. See Rosset and Zhu (2007) for a unified analysis under various models, where a general characterization of the loss and penalty functions to give piecewise-linear coefficient paths is derived. We would like to point out that it is possible to extend the notion of joint piecewise-linearity to more general problems beyond the weighted SVM. For example, we can show that the kernel quantile regression solution also enjoys the joint piecewise-linear property in terms of its regularization parameter and the quantile parameter. However, it is not yet clear what are general sufficient conditions for the joint piecewise-linearity to hold. We find that the sufficient conditions for the marginal (one-dimensional) piecewise-linearity, given in Rosset and Zhu (2007), generally do not imply the joint (two-dimensional) piecewise-linearity. For example, support vector regression (Vapnik; 1996) has piecewise-linear marginal paths, with respect to the regularization parameter or the intensity parameter, but its solution does not have the joint piecewise-linearity property. Based on our experience, the two-dimensional solution surface is much more complex than one-dimensional marginal paths, mainly due to the intricate roles played by two parameters and their relationship. This is an important topic and worth further investigation.
Acknowledgments
The authors would like to thank Professor Richard A. Levine, the associate editor, and two reviewers for their constructive comments and suggestions that led to significant improvement of the article. This work is partially supported by NIH/NCI grants R01 CA-149569 (Shin and Wu), R01 CA-085848 (Zhang), and NSF Grant DMS-0645293 (Zhang). The content is solely the responsibility of the authors and does not necessarily represent the official views of NIH or NCI.
Footnotes
Online Supplement: The online supplement materials contain the computer code and the instructions on how to build and install our newly developed R package wsvmsurf. All the files are available via a single zipped file “Supplement.rar”. After unzipping the file, one can retrieve one folder (“wsvmsurf”) and two text files (“example.R” and “readme.txt”). The folder “wsvmsurf” contains all the source files (which are properly structured) for building the R package “wsvmsurf”. The file “readme.txt” gives detailed instructions for installing the package. For windows machines, the package can be built by using R-tools available at www.r-project.org. For Linux machines, the installation can be done by using the R command R CMD build wsvmsurf. The file “example.R” contains the code to run two examples in the paper.
Contributor Information
Seung Jun Shin, Email: sshin@ncsu.edu, Department of Statistics, North Carolina State University, Raleigh, NC 27695.
Yichao Wu, Email: wu@stat.ncsu.edu, Department of Statistics, North Carolina State University, Raleigh, NC 27695.
Hao Helen Zhang, Email: hzhang@math.arizona.edu, Department of Mathematics, University of Arizona, Tucson, AZ 85718.
References
- Alon U, Barkai N, Notterman D, Gish K, Ybarra S, Mack D, Levine A. Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Cell Biology. 1999;96:6745–6750. doi: 10.1073/pnas.96.12.6745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chambers J, Hastie T. Statistical Models in S. Wadsworth and Brooks/Cole; Pacific Grove, CA: 1992. [Google Scholar]
- Hastie T, Rosset R, Tibshirani R, Zhou J. The entrie regularization path for the supprot vector machine. Journal of Machine Learning Reasearch. 2004;5:1931–1415. [Google Scholar]
- Jaakkola T, Diekhans M, Haussler D. Using the fisher kernel method to detect remote protein homologies. Proceedings of the Seventh International Conference on Intelligent Systems for Molecular Biology; Heidelberg, Germany: AAAI; 1999. pp. 149–158. [PubMed] [Google Scholar]
- Kimeldorf G, Wahba G. Some results on tchebycheffian spline functions. Journal of Mathematical Analysis and Applications. 1971;33:82–95. [Google Scholar]
- Lin Y. Support vector machines and the bayes rule in classification. Data Mining and Knowledge Discovery. 2002;6:259–275. [Google Scholar]
- Lin Y, Lee Y, Wahba G. Support vector machines for classification in nonstandard situations. Machine Learning. 2004;46:191–202. [Google Scholar]
- Liu Y. Fisher consistency of multicategory support vector machines. Proceedings of Eleventh International Conference on Artificial Intelligence and Statistics; Heidelberg, Germany: AAAI; 2007. pp. 289–296. [Google Scholar]
- Rosset S, Zhu J. Piecewise linear regularized solution paths. Annals of Statistics. 2007;35 (3):1012–1030. [Google Scholar]
- Vapnik V. The Natual of Statistical Learning. Springer-Verlag; 1996. [Google Scholar]
- Wahba G. Spline models for observational data; CBMS-NSF Regional Conference Series in Applied Mathematics; SIAM; 1990. [Google Scholar]
- Wahba G. Support vector machines, reproducing kernel hilbert spaces, and randomized gacv. In: Schölkopf B, Burges CJC, Smola AJ, editors. Advances in Kernel Methods: Support Vector Learning. MIT Press; 1999. pp. 125–143. [Google Scholar]
- Wang J, Shen X, Liu Y. Probability estimation for large-margin classifier. Biometrika. 2008;95 :149–167. [Google Scholar]
- Wang L, Shen X. On l1-norm multi-class support vector machines: methodology and theory. Journal of the American Statistical Association. 2007;102:595–602. [Google Scholar]
- West M, Blanchette C, Dressman H, Huang E, Ishida S, Spang R, Zuzan H, Jr, JAO, Marks J, Nevins J. Predicting the clinical status of human breast cancer by using gene expression profiles. Proceedings of the National Academy of Sciences. 2001;98:11462–11467. doi: 10.1073/pnas.201162998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang HH, Ahn J, Lin X, Park C. Gene selection using support vector machines with nonconvex penalty. Bioinformatics. 2006;22(1):88–95. doi: 10.1093/bioinformatics/bti736. [DOI] [PubMed] [Google Scholar]
- Zhu J, Rosset S, Hastie T, Tibshirani R. 1-norm support vector machines. Advances in Neural Information Processing Systems. 2003;16 [Google Scholar]