Facing acid–base disorders in the third millennium – the Stewart approach revisited

Abstract

Acid–base disorders are common in the critically ill. Most of these disorders do not cause harm and are self-limiting after appropriate resuscitation and management. Unfortunately, clinicians tend to think about an acid–base disturbance as a “disease” and spend long hours effectively treating numbers rather than the patient. Moreover, a sizable number of intensive-care physicians experience difficulties in interpreting the significance of or understanding the etiology of certain forms of acid–base disequilibria. Traditional tools for interpreting acid–base disorders may not be adequate for analyzing the complex nature of these metabolic abnormalities. Inappropriate interpretation may also lead to wrong clinical conclusions and incorrectly influence clinical management (eg, bicarbonate therapy for metabolic acidosis in different clinical situations). The Stewart approach, based on physicochemical principles, is a robust physiological concept that can facilitate the interpretation and analysis of simple, mixed, and complex acid–base disorders, thereby allowing better diagnosis of the cause of the disturbance and more timely treatment. However, as the concept does not attach importance to plasma bicarbonate, clinicians may find it complicated to use in their daily clinical practice. This article reviews various approaches to interpreting acid–base disorders and suggests the integration of base-excess and Stewart approach for a better interpretation of these metabolic disorders.

Introduction

Acid–base disorders frequently accompany critical illness and may, occasionally, be the only reason for admitting a patient to the intensive-care unit. Although such metabolic derangements can, occasionally, be life-threatening (eg, severe lactic acidosis in status asthmaticus),1 they are usually an accompanying manifestation in a large variety of clinical conditions such as sepsis, acute kidney injury, hemorrhage, trauma, severe metabolic dysregulation (eg, diabetic ketoacidosis), and different types of shock. Some acute disturbances of acid–base metabolism are generally self-limiting after management of the provoking insult (eg, lactic acidosis complicating seizures or severe asthma), while others may require aggressive treatment of the primary condition (eg, fluid resuscitation, vasopressor support, and antibiotics for septic shock). It should be stressed that interpretation of an acid–base disorder should not be undertaken without reference to the patient’s clinical condition.

When faced with acid–base disorders in their patients, many clinicians may feel anxious. This may be due to inexperience, lack of proper understanding of acid–base physiology, unfamiliarity with interpretation of results in relation to the underlying pathology, or lack of understanding about the significance of various parameters in arterial blood-gas results.2 Although meant to make interpretation easier, the situation is not helped by various tables and lists of causes of acidosis or alkalosis that accompany many textbook chapters written on this subject.3 Our purpose in this paper is to show how a combined Stewart and base-excess (BE) approach can be easy to apply at the bedside in the case of simple as well as complex acid–base disorders using simple mental mathematics.4

Acid–base knowledge – from the early times to the modern era

Definitions of acids and bases

The term “acid” is derived from the Latin word “acidus” meaning “sour taste”.5 Arrhenius defined acids as substances that, when dissolved in water, produce an increase in concentration of hydrogen ions (H⁺).6 Around the turn of the 20th century, Naunyn7 and others8 adopted Arrhenius’ definition of acids along with Faraday’s earlier description of cations (eg, sodium, Na⁺) as base forming and anions (eg, chloride, Cl⁻) as acid forming, and postulated that the acid–base status of body fluids was determined by its electrolyte composition, particularly of Na⁺ and Cl⁻. In the 1920s, Van Slyke embraced this concept in a definition carrying his name.9 The “modern” definition of acids – that is, as substances that can donate a proton (H⁺) – was proposed by Bronsted and Lowry in 1923.9 Since then, the notion of acids as H⁺ donors and bases as H⁺ acceptors has gained wide popularity.

The bicarbonate era

Although aware of the buffering power of non-carbonated species, Henderson10 was first to put significant emphasis on bicarbonate (HCO₃⁻) as an important alkali buffer in case of excess acid in body fluids (other than carbonic acid, measured as dissolved CO₂). He applied the law of mass action to the equilibrium reaction of carbonic acid and derived his landmark formula for calculating [H⁺] (Equation 1).10

$$[{\mathrm{H}}^{+}]=\frac{\mathrm{K}\times [{\mathrm{C}\mathrm{O}}_2]}{[{\mathrm{H}\mathrm{C}\mathrm{O}}_3{}^{-}]}.$$ (1)

With the introduction of the pH scale by Sörensen,11 Henderson’s equation was modified by Hasselbalch. Since then, generations of medical students and doctors have been taught the Henderson–Hasselbalch equation, a version of which is shown as Equation 2.

$$\text{pH}=\text{pK}+\log 10\frac{[{\mathrm{H}\mathrm{C}\mathrm{O}}^3]}{{\mathrm{S}\mathrm{C}\mathrm{O}}_2\times {\mathrm{Pa}\mathrm{C}\mathrm{O}}_2},$$ (2)

where “SCO₂” represents the solubility coefficient of CO₂ and “pK” the negative logarithm of the constant “K” in Equation 1.

According to this theory:

• the quantity of H⁺ added to or removed from the blood determines the final pH

• plasma membranes may be permeable to H⁺, thus intracellular as well as extracellular reactions will influence pH

• an analysis of the nonvolatile buffer equilibrium is not essential to describe the acid–base balance.

Although an easy concept, this approach has some major flaws, including sole dependence on HCO₃⁻, CO₂ and carbonic acid as well as completely ignoring the impact of weak acids on acid–base physiology.

In the 1950s, clinical chemists abandoned the Van Slyke definition of acids for the “modern” Bronsted–Lowry definition. This has been one of the important reasons for clinicians concentrating on H⁺ and its relationship with weak acids such as H₂CO₃, its conjugate anions (ie, HCO₃⁻), and their “role” in pH control. This widely used approach is based on the concept that the concentration of plasma H⁺ (and thus pH) is primarily determined by the H₂CO₃/HCO₃⁻ system. This “bicarbonate-centered” approach works reasonably well in stable clinical situations, thus has become the primary tool for interpreting acid–base abnormalities.

To better understand the acidosis accompanying diabetic coma, Van Slyke12 injected dogs with sulfuric acid and found that most of the acid was neutralized by hemoglobin (Hb) (about 30%) and tissue cells (about 40%), while only about 30% was buffered in the extracellular fluid by HCO₃⁻. He concluded that, despite the large acid load, blood pH was maintained at the expense of alkali consumption (HCO₃⁻ in this case), which he later described as “alkali deficit”. This useful concept had great clinical impact, because it permitted calculation of the amount of HCO₃⁻ needed to reverse a patient’s acidosis. However, it also created a problem: clinicians now began to associate HCO₃⁻ levels with acidosis and alkalosis without considering PaCO₂; this is prevalent to this day. This popular belief has also resulted in some confusion, with some physicians believing that acidosis or alkalosis is caused by a reduction or increase in HCO₃⁻ levels and associating acidosis with increased H⁺ thereby ignoring Naunyn’s concept of acid–base status being electrolyte dependent.7

Separating the metabolic and respiratory components in acid–base disorders: the BE era

Universal agreement exists that changes in PaCO₂ directly lead to changes in blood acid–base status,11 with a rise resulting in respiratory acidosis and a fall in respiratory alkalosis. However, qualification and quantification of the metabolic component of the acid–base disturbance (in particular, the role of HCO₃⁻) has been at the center of considerable debate for decades. For a long time, it has been recognized that a rise in PaCO₂ also causes plasma HCO₃⁻ to increase. In 1952, Danish physicians, unaware of the impact of raised PaCO₂ on HCO₃⁻ were puzzled by the “mysterious alkalosis” (measured as dissolved CO₂) that was killing polio victims13 until Bjørn Ibsen, a young Danish anesthetist, suggested that the rise in dissolved CO₂ was not caused by alkalosis but by respiratory acidosis due to CO₂ retention induced by respiratory muscle paralysis.14

The understanding that a rise in plasma CO₂ causes increased plasma HCO₃⁻ set the pace for the development of various refinements to quantify the metabolic component of acid–base disturbances. Even before the polio outbreak, Singer and Hastings had already advanced the concept of “buffer base” (BB),14 which is the sum of plasma buffer anions (ie, HCO₃⁻ and all nonvolatile weak acid buffers). In 1960, Astrup et al15 devised “standard bicarbonate” (SBic), which is measured plasma HCO₃ at a PaCO₂ of 40 mmHg (5.33 kPa). However, the most significant contribution to the science of acid–base physiology was made by Siggaard-Andersen et al when they introduced the BE concept in 1977.16 “BE” is defined as the amount of acid or base that must be added in vitro to a sample of whole blood to restore the pH to 7.40 while PaCO₂ is kept constant at 40 mmHg (5.33 kPa). Oxygenated blood at PaCO₂ 40 mmHg (5.33 kPa) and Hb 150 g/L has a BE of zero.17

Available tools for interpretation of acid–base disorders (from traditional to modern)

Many tools for interpreting acid–base disorders have been developed. They are briefly discussed below.

The CO₂/HCO₃⁻ (“Boston”) approach

Developed by Schwartz and Relman,18 this approach, entirely based on the Henderson–Hasselbalch equation, predicts the nature of acid–base disorders. It was derived from a large cohort of stable patients with known but “compensated” acid–base disturbances. H⁺ is related to CO₂ in respiratory, and to CO₂/HCO₃⁻ in metabolic, acid–base disturbances. This approach is easy to use in stable patients exhibiting simple acid–base disturbances, where the magnitude of increase in unmeasured anions parallels the drop in [HCO₃⁻]. However, as [HCO₃⁻] varies with changes in PaCO₂, the severity of the non-respiratory (metabolic) component of acid–base disorders and the nature of acids other than carbonic are difficult to assess. The CO₂/HCO₃⁻ approach is mostly applied to determine resting PaCO₂ in patients with chronic respiratory failure.19

The BE/deficit (“Copenhagen” or “Danish”) approach

Various refinements (BB, SBic, and BE) are suggested to allow better quantification of the non-respiratory (metabolic) component of acid–base disorders. BB increases in metabolic alkalosis and decreases in acidosis. However, Hb alterations cause changes in buffering that render the interpretation of BB erratic. SBic is not a measured but a calculated variable. BE, even though calculated, comes closest to being the parameter that is least influenced by changes in PaCO₂. As Hb is the main buffer in blood, changes in Hb can significantly affect BE. This error is considerably reduced if Hb is assumed to be 50 g/L instead of the normal 150 g/L (BE calculated this way is called “standard base excess” [SBE]). In practice, SBE is calculated by well-established formulae or derived from nomograms and not obtained by titration of blood with acid or base (as the definition would suggest).20 Nomograms are widely incorporated in blood-gas analyzer software and SBE calculated from variables like pH, HCO₃⁻, and Hb. Simple mathematical rules can be applied for using SBE in common acid–base disturbances.19,20 Thus, SBE does not change in acute respiratory acidosis or alkalosis. In metabolic acidosis, SBE decreases and becomes negative (⁻BE or base deficit), whereas it becomes positive in metabolic alkalosis (simply called BE or ⁺BE). However, calculating SBE is not without its pitfalls in the clinical arena. SBE can still vary with changes in PaCO₂, albeit only slightly, and may be unreliable in the presence of low albumin and/or phosphate (PO₄⁻) levels. Other drawbacks include inaccuracy due to in vitro measurement and that it does not take into account the respiratory status or the volume of distribution of bicarbonate.19

Anion-gap (AG) approach

Developed by Emmett and Nairns,21 this approach attempts to address the limitations of both the Boston and Copenhagen approaches. It is based on the principle of “electroneutrality” and calculated as:

$$\mathrm{A}\mathrm{G}=([{\mathrm{Na}}^{\text{+}}]+[{\mathrm{K}}^{+}])-([{\mathrm{Cl}}^{-}]+[{\mathrm{H}\mathrm{C}\mathrm{O}}_3{}^{-}]).$$ (3)

In this equation, “[ ]” represents the molar concentrations of ions. The sum of the difference in charge carried by commonly measured extracellular ions reveals a “gap” of about 12–16 mmol/L (depending upon local laboratory values). This value is usually positive and accounts for unmeasured anions (eg, lactate, ketones, sulfate, etc). In metabolic acidosis, an increase in AG is due to the accumulation of anions (like lactate or ketones that are not measured in Equation 3) and is termed “widened anion-gap acidosis”. If the AG remains within normal range, then metabolic acidosis is most likely caused by hyperchloremia.19 The AG approach is actually the principal method for detecting unmeasured anions as the cause of metabolic acidosis (eg, lactic acidosis, acidosis caused by specific poisons).22 A key issue, however, is deciding what constitutes a “normal” AG. Also, most critically ill patients have low albumin and phosphate concentrations, rendering the AG measurement less accurate. HCO₃⁻ represents another potential “unstable” variable in the AG equation, as it can potentially be influenced by certain therapeutic interventions (eg, deliberate hyperventilation in head injury).

Discussion

The methods discussed were essentially created to better comprehend the basic mechanisms of acid–base homeostasis in health and disease. They have been taught to generations of medical students and doctors and are applied daily at the bedside for optimizing treatment in a myriad of clinical situations. Unfortunately, these methods become less reliable in complex clinical conditions, especially at extremes of pH – for instance, in the critically ill. It must also be kept in mind that calculating BE, SBic, or actual plasma HCO₃⁻ only provides a “rough” estimate of a given metabolic disturbance but offers no in-depth insight into the underlying mechanism.23 Certain conditions (eg, hyperchloremic metabolic acidosis) are insufficiently explained with these methods.24 Finally, these methods lack sensitivity to unravel more complex acid–base disorders (see below).

Stewart (“modern” or “physicochemical”) approach

In 1981, Canadian physiologist Peter Stewart25,26 proposed a radically different approach toward understanding acid–base balance. Stewart re-emphasized previously overlooked principles of quantitative physical chemistry, thus clearing the way for a concept that could identify and explain simple as well as complex acid–base problems in different patient groups. Essentially, Stewart started with Arrhenius’ definition of acids and bases and discarded the Bronsted–Lowry definition, arguing that the latter created confusion because physicians associated acidosis with H^+.27 Stewart stated that “this latter concept leads us to suggest that [H⁺] is an independent variable and hinders us from calling CO₂ an acid, when both these statements are not true”. A detailed discussion of the Stewart approach is beyond the scope of this paper and is provided elsewhere.28 Here, we will only explore the basic principles of this interesting but still controversial approach.

Stewart applied the following laws of physical chemistry to complex body fluids:

• Law of electroneutrality – the sum of all positively charged ions (cations) must equal the sum of all negatively charged ions (anions) at all times.

• Law of conservation of mass – the amount of a substance in a solution remains constant unless it is added, removed, generated, or destroyed.

• Law of mass action – the dissociation equilibria of all incompletely dissociated substances must be met at all times.

Based on these principles, Stewart proposed three independent variables that determine pH:

1. Carbon dioxide. HCO₃⁻ and other carbon dioxide species now become dependent variables. The Henderson–Hasselbalch model is rejected.

2. Strong ions. More specifically, “strong ion difference” (SID), defined as the difference between strong cations (Na⁺, K⁺, Ca⁺⁺, Mg⁺⁺) and strong anions (Cl⁻, lactate, sulfate, ketones etc). Strong ions are fully dissociated at physiological pH.

3. Total nonvolatile weak acids (albumin, globulins, and inorganic phosphate). Referred to as “A_TOT” by Stewart. Weak acids are not fully dissociated at physiological pH.

CO₂ and the newly introduced SID and A_TOT are independent variables.

They remain unaffected by changes within the system or by other independent variables. Both H⁺ and HCO₃⁻ are defined as dependent variables that are directly and predictably affected by changes in the independent variables. Stewart constructed dedicated mathematical formulae to integrate this entirely novel way of looking at acid–base balance. However, the practical application of this exciting theoretical bench-work encountered grave difficulties. Sophisticated computer programs were required to address the complex formulae, limiting its bedside utility. In addition, traditional physiologists like Siggaard-Andersen and Fogh-Andersen29 openly criticized Stewart’s approach, condemning it as “absurd and anachronistic”. Because of this, the Stewart approach remained unknown to many clinicians for a long time. Over time, some adaptation has been made to make its bedside use simpler and easier. Initially, Stewart’s complex polynomial equations expressed pH value as a function of eight factors – three independent ones (CO₂, SID, and A_TOT) and five constants27 (these complex equations are not given here for the sake of brevity). Later work showed that changing two of the constants had no quantitative effect on pH.30 This generated a more workable six-factor equation that can be further simplified as follows:

$$\text{pH}=\text{pK}{\mathrm{l}}^{\prime }+\log \frac{\text{SID}-{\mathrm{A}}_{\text{TOT}}/(1+10\text{pKa}-\text{pH})}{{\mathrm{S}\mathrm{P}\mathrm{C}\mathrm{O}}_2}.$$ (4)

Stewart’s original polynomial equations showed that a change in pH was definitely indicative of a change in one or more independent variables. This implies an entirely different relationship of pH to PaCO₂ and HCO₃⁻ than the one expressed by the Henderson–Hasselbalch equation (which is one of association and not of cause).31 Though based on similar physical principles as the traditional approach, the Stewart approach is entirely different. One of the important differences is that H⁺ and HCO₃⁻ are not independent but determined by other variables. However, the most radical difference is that pH changes do not result from the generation or removal of H⁺ and/or HCO₃⁻ ions per se but from changes in other independent variables (CO₂, SID, and A_TOT). The Stewart approach remains controversial even today because it introduces new terms (independent and dependent variables and A_TOT); the approach also centers on water dissociation for acid-base status of body fluids rather than focusing on CO₂ and bicarbonate.32 Besides, Stewart treated plasma as “an isolated” one-compartment medium, thereby ignoring trans-membrane ionic traffic; however, real-life plasma is in equilibrium with other body compartments.32

SID can be measured in plasma as follows:

$$\text{SID}=([{\mathrm{Na}}^{+}]+[{\mathrm{K}}^{+}]+[{\mathrm{Mg}}^{\text{++}}]+[{\mathrm{Ca}}^{\text{++}}])-([{\mathrm{Cl}}^{-}]+[\text{lactate}]).$$ (5)

SID is always positive and its value is 38–44 mmol/L in normal individuals (depending on the local laboratory). At the bedside, values for K⁺, Mg⁺⁺, Ca⁺⁺, and, unless elevated, lactate are ignored, as their contribution to total SID is negligible. According to the Stewart approach, acids are considered in recognition of the fact that water is the (almost) infinite source of H⁺; the quantity of this H⁺, in turn, is determined by SID. If the sum of cations decreases relative to the sum of anions (eg, hyponatremia) or if the sum of anions exceeds that of cations (eg, hyperchloremia), electrical neutrality is upset. As an abundant H⁺ source, water hydrolysis restores this electrical neutrality. The hydrolysis process releases H⁺ while OH⁻ is taken up by cellular and Hb buffers. The opposite takes place when the sum of cations increases or that of anions decreases in relation to the sum of anions and cations, respectively.

The bulk of nonvolatile weak acids (A_TOT) mainly consists of albumin and inorganic phosphate. As these are “acids”, a decrease in concentration – as is often seen in the critically ill – will induce a moderate but significant alkalosis, whereas an increase in concentration will have the opposite effect (eg, hyperphosphatemia in chronic renal failure). Thus, three simple rules of thumb emerge:

1. When SID narrows, either by a relative decrease in cations or a relative increase in anions, metabolic acidosis develops.

2. When SID widens, either by a relative increase in cations or a relative decrease in anions, metabolic alkalosis ensues.

3. Hypoalbuminemia causes a moderate but relevant metabolic alkalosis and vice versa.

Alkalosis due to hypoalbuminemia, however, is not a “clinical condition” requiring treatment but one of the factors that affect SBE (see example below). Conversely, hyperalbuminemia will lead to metabolic acidosis.

SID measured by Equation 5 has been termed “apparent SID” (SID_a). When analyzing simple and complex acid–base disturbances, attention must be given to the electrolyte and albumin levels as both may affect the patient’s acid–base status at all times.

Strong ion gap

This concept has been advanced by some research groups.33 SID, calculated by Equation 5, is SID_a in its simplistic form. Under pathological conditions, various other unmeasured anions may exist that can change SID (effective SID [SID_e]). Along with this, account has to be taken of the role of weak acids. Therefore, confusion may arise since determination of the strong ion gap (SIG) requires calculation of SID_a and SID_e. SID_a is SID derived from the difference in measured strong cations and strong anions (Equation 5). SID_e, taking into account the role of weak acids (albumin and phosphate) and CO₂ charges in plasma water is calculated as shown in Equation 6.34

$$\begin{array}{l}{\text{SID}}_{\mathrm{e}}=(2.46\times 108\times \mathrm{P}\mathrm{C}{\mathrm{O}}_2/10\text{pH}+[\text{albumin in g}/\text{dL}]\\ \times [0.123\times \text{pH}-0.631]+[\mathrm{P}{\mathrm{O}}_4{}^{-}\text{ in mmol}/\mathrm{L}\\ \times \{\text{pH}-0.469\}]).\end{array}$$ (6)

SIG is the difference between SID_a and SID_e (SIG = SID_a − SID_e). HCO₃⁻ is not incorporated in the calculation that distinguishes SIG from the more familiar AG. One of the suggested equations for calculating SIG (which combines Equations 6 and 7) is35:

$$\begin{array}{l}\text{SIG}=([{\mathrm{Na}}^{\text{+}}+{\mathrm{K}}^{\text{+}}+{\mathrm{Mg}}^{++}+{\mathrm{Ca}}^{++}]-([{\mathrm{Cl}}^{-}+{\text{lactate}}^{-}])\\ -(2.46\times 108\times \mathrm{P}\mathrm{C}{\mathrm{O}}_2/10\text{pH}+[\text{albumin in g}/\text{dL}]\\ \times [0.123\times \text{pH}-0.631]+[\mathrm{P}{\mathrm{O}}_4{}^{-}\text{ in mmol}/\mathrm{L}\\ \times \{\text{pH}-0.469\}]).\end{array}$$ (7)

SIG has been found to be more sensitive than AG (corrected for albumin) in predicting mortality in critically ill children36,37 and other intensive-care unit populations. However, as can be seen in Equation 7, its bedside determination is cumbersome, as it requires a programmable calculator to determine its value rather than simple mental mathematics. Although a more accurate predictor of mortality in the critically ill, SIG not only measures the difference in anions but also the difference in all strong ions. Some studies have cast doubts about the clinical utility of SIG.38

Unifying BE and the Stewart approach at the bedside

The complexity of the equations devised by Stewart seriously thwart their bedside application. Therefore, Stewart’s original work has been modified over time. Researchers like Fencl, Figge, Gilfix, Story, Balasubramanian, and Kellum have considerably invested in Stewart’s original work,39 mainly by developing more convenient and practical bedside applications. For example, Gilfix et al40 elaborated an original concept of Fencl stipulating that changes in BE (being the net result of changes in SID and A_TOT) should be considered in the assessment of any acid–base disturbance. Studies have shown that the Stewart approach (either on its own or, more recently, in combination with the BE approach) is better at diagnosing hidden disturbances as well as unraveling complex acid–base disorders.22,31,41–43 However, these approaches have been criticized because they require more blood analysis (eg, serum electrolytes) than simple blood-gas analyzer results.44

Simple formulae that do not need computers or calculators have been devised to make the Stewart approach accessible in daily clinical practice. Evaluations of the SID and the A_TOT effect on BE (actually the SBE) are the most user-friendly clinical tools. They not only enable one to unmask and quantify an ongoing acid–base abnormality but also help to establish the probable cause. Applying a combined Stewart and BE approach necessitates routine withdrawal of arterial blood gases (ABGs) and basic biochemical variables (ie, Na⁺, Cl⁻, albumin, PO₄⁻). As K⁺, Ca⁺⁺, and Mg⁺⁺ only marginally contribute to the total sum of cations, SID, in simplified form, is best estimated as the difference between Na⁺ and Cl⁻ (and lactate, if elevated) (Figure 1). The following simple calculations can then be applied:

Figure 1.

Strong ion difference (SID) and plasma electroneutrality.

Abbreviations: alb, albumin; UA, unmeasured anion; Pi, phosphates.

• calculation of the SID effect on SBE: SBENaCl = {[Na⁺] − [Cl⁻]} − 38, where “38” is the average normal SID (Figure 2)4

• calculation of the A_TOT effect on SBE: SBE_ALB = 0.25 × (42 − measured albumin [ALB] in blood); where 42 is the normal plasma albumin value in g/L (Figure 2)

• SBE_NaCl + SBE_ALB = SBECorrection

• true SBE or base-excess gap (BEG): SBE − SBECorrection.

Figure 2.

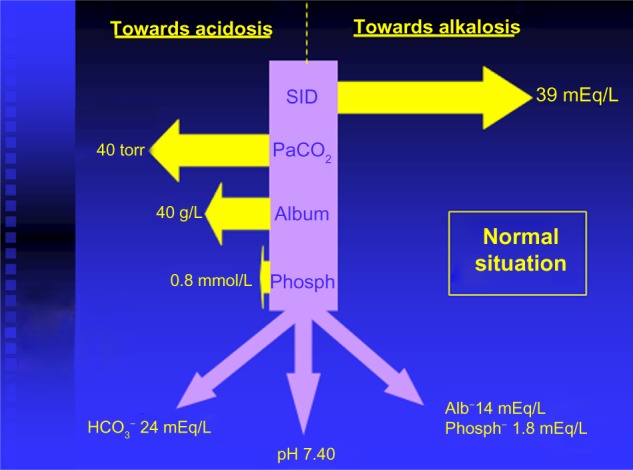
Apparent strong ion difference (SID_a) and effective strong ion difference (SID_e).

Abbreviations: alb/album, albumin; phosph, phosphates; SID, strong ion difference; Pa, partial pressure.

The above equations only require basic mental mathematics, thus are easy to use at the bedside for evaluation, treatment, and follow-up of simple as well as complex acid–base problems.

The following example illustrates how these formulae work in real life and underscores the superiority of the Stewart approach compared with traditional approaches in analyzing acid–base disturbances.

A 71-year-old female with chronic obstructive pulmonary disease was admitted to the general medical ward with acute pneumonia. Physical examination showed rapid shallow breathing, tachycardia, and expiratory crackles over the right lung base. She was treated with controlled oxygen by face mask, inhaled b-agonists, steroids and intravenous antibiotics. As congestive cardiac failure was suspected, a loop diuretic (furosemide) was also prescribed. ABG analysis on admission was compatible with acute hypocapnic respiratory failure with respiratory acidosis and compensatory metabolic alkalosis (pH =7.32, PaCO₂ =8 kPa [60 mmHg], PaO₂ =6.9 kPa [52 mmHg] and SBic 28 mmol/L on room air). On the fourth day after admission, she developed vague abdominal pain, accompanied by severe tachycardia, tachypnea, hypotension (blood pressure 86/45 mmHg) and oliguria. Fluid resuscitation with Hartmann’s solution was started and the patient was transferred for urgent surgery. Laparotomy confirmed perforated diverticular disease and severe peritonitis resulting in sepsis and septic shock. Repeated ABG evaluations, performed during the 4 days preceding surgery had shown a steadily increasing BE without any discernible effect on pH. The ABG results obtained immediately before transfer to the operating room are given in Table 1.

Table 1.

Arterial blood gases before transfer to operating room

Parameter	Result
pH	7.48
PaCO2	8.2 (60.2)
PaO2	8.9 (66.7) – on O2
SHCO3−	33.5
Base excess	+7.6

Note: Blood gas values are given in kPa (mmHg).

Abbreviation: Pa, partial pressure.

These ABG results obtained using traditional approaches reveal an obvious hypercapnic respiratory failure with concomitant metabolic alkalosis. If this metabolic alkalosis is considered “compensatory”, then “overcompensation” is certainly present. Another interpretation could be “primary” metabolic alkalosis with “compensatory” respiratory acidosis. However, being septic, hypotensive, and oliguric, it is surprising to observe metabolic alkalosis and not acidosis. Biochemical results were obtained in the blood sample withdrawn together with the first ABG (Table 2).

Table 2.

Main biochemical results

Parameter	Result
Na+	132 mmol/L
K+	3.4 mmol/L
Cl−	76 mmol/L
Albumin	18 g/L
Lactate	1.9 mmol/L

The AG (22.6–28.6, depending on calculation method) had not been calculated because metabolic acidosis was not detected by traditional methods of interpretation. Applying corrections for SID and A_TOT to SBE gave the following results:

$$\begin{array}{c}{\text{SBE}}_{\text{NaCl}}=\{132-76\}-38=56-38=+18({\text{ignoring K}}^{\text{+}}\text{ and locate values for simplification})\\ {\text{SBE}}_{\text{ATOT}}=0.25\times (42-18)=0.25\times 24=+6\\ {\text{SBE}}_{\text{Correction}}=18+6=24\\ \text{True BE or BEG}=7.6-24=-\mathrm{16.4.}\end{array}$$

The patient had moderately elevated PaCO₂, high serum bicarbonate, and slightly increased (“alkalotic”) pH – thus, apparent metabolic alkalosis. When both the SID effect and A_TOT effect on apparent metabolic alkalosis were calculated, a hidden metabolic acidosis was revealed (a true BE of −16.4) due to unmeasured anions, which was well in keeping with her clinical condition (sepsis and septic shock).45 This acidosis was masked by widened SID (due to hypochloremia, almost certainly diuretic induced) and lowered A_TOT (due to hypoalbuminemia). Traditional approaches failed to correctly identify metabolic acidosis in this patient. This example underpins that traditional approaches may adequately detect simple acid–base disorders in stable patients but fail to unravel complex disturbances. A combined Stewart and BE approach may solve this problem.

Measuring SIG may also perform better than traditional acid–base interpretation in the post-resuscitation phase of cardiac arrest.45–47 Continuous urinary acid–base analysis for SIG represents a new and exciting area of research.48

Conclusion

None of the approaches for interpreting acid–base homeostasis are without flaws. Siggaard-Andersen9 was the first to bring order to the chaos of definitions, terminologies, and formulae by introducing the concept of BE. However, BE is not a titrated but a calculated value, assuming normal, non-carbonated buffer. Stewart’s concept25,26 (essentially a modern version of the old BB concept of Singer and Hastings)20 has given a different insight into acid–base physiology. However, controversy exists around the validity of this approach. Stewart uses an older definition of acids and bases that was never widely adopted. Whether SID is an independent and HCO₃⁻ a dependent variable may or may not be justified. Also, the hypothesis that water dissociates into H⁺ and OH⁻ when SID, A_TOT, and CO₂ change, has not yet been confirmed. It cannot be denied, though, that the Stewart approach, as modified by Fencl, Gilfix, Figge, and others, offers better identification and cause-related diagnosis for complex acid–base problems. Its subsequent modification by other researchers,39 devising formulae that involve simple mental mathematics to evaluate the effect of SID and A_TOT on SBE (eg, BEG – BE_gap) make it very easy to use by the bedside. However, BEG has not been rigorously validated. One study found that BEG could not reliably quantify unmeasured anions in cardiac surgical patients.49 However, this was a retrospective study with only one assessment of acid–base status being made in these patients. Further, the study used an elevated reference for plasma chloride of 108 mmol/L, whereas the usual accepted reference is 102 mmol/L.4

Many clinicians feel uneasy with the Stewart approach. Stewart’s criticism of the importance of HCO₃⁻ and H⁺, classifying them as “dependent” variables, is felt a sacrilege by many physiologists as well as clinicians. To those skeptics and non-believers, we suggest that to fully appreciate Stewart’s work, HCO₃⁻ should be forgotten and “parked” in the back of the mind and practitioners should be more open-minded toward adapting the Stewart approach. We also suggest that the idea of the “compensation” of acidosis by concomitant alkalosis and vice versa, a concept that has been in vogue for years, be forsaken. This concept has been proposed and propagated by traditionalists to explain some of the changes observed during acid–base disturbances, but offers no explanation as to how a physiological derangement (alkalosis or acidosis) can logically be “corrected” or “compensated’” for by another physiological derangement.