Abstract
A recent viewpoint article (Improving the plausibility of success with inefficient metrics. ACS Med. Chem. Lett.2014, 5, 2–5) argued that the standard definition of ligand efficiency (LE) is mathematically invalid. In this viewpoint, we address this criticism and show categorically that the definition of LE is mathematically valid. LE and other metrics such as lipophilic ligand efficiency (LLE) can be useful during the multiparameter optimization challenge faced by medicinal chemists.
The utility of some ligand efficiency (LE) metrics has recently been challenged in a viewpoint article in ACS Medicinal Chemistry Letters.1 This article also argued that earlier seminal work by Lipinski2 has been misinterpreted and has led to an oversimplistic application of cut-offs for molecular properties such as MW < 500. The latter point is an interesting topic for debate that has been discussed in detail many times, not least because it appeals to the iconoclastic nature of medicinal chemists. However, the viewpoint article also incorrectly states that LE and related metrics “violate the quotient rule of logarithms” and “appear plausible but are mathematical impossibilities”.
The primary purpose of our viewpoint article is to correct these mathematical statements and prevent them from propagating through the literature. We also examine the behavior of LE and lipophilic ligand efficiency (LLE) for two matched chemical pairs and compare this with a simple example of fuel efficiency. Finally we briefly consider genuine deficiencies of LE metrics so as to put valid criticism into perspective.
Mathematical Validity
LE is usually defined as the average free energy of binding in kcal/mol per non-hydrogen atom:3,4
where HAC denotes the heavy atom count (i.e., number of non-hydrogen atoms), R is the ideal gas constant, and T is the temperature in Kelvin. At standard conditions of aqueous solution at 300 K, neutral pH and remaining concentrations of 1 M, −2.303RT approximates to −1.37 kcal/mol. Importantly, the equation converts Kd into an approximate free energy of binding meaning that ligand efficiency has units of (kcal/mol)/heavy atom.12
In ref (5), Shultz claims, “To be valid, LE must remain constant for each heavy atom that changes potency 10-fold” and “These metrics do not mathematically normalize size or potency because they violate the quotient rule of logarithms. To obey this rule and be a valid mathematical function HAC would be subtracted from pIC50 and rendered independent of size and reference potency.” In other words, Shultz takes issue with LE as defined by Hopkins et al. because he asserts that it violates the quotient rule of logarithms and is not a valid mathematical function.13
However, there is no requirement for LE to remain constant for each additional heavy atom that increases potency by 10-fold. LE is simply an average and, like any other average, is not required to remain constant for each additional data point that differs by a fixed amount.
The quotient rule of logarithms states that log(x/y) = log(x) – log(y). This relationship holds true for logarithms by definition. There is no general concept of a quotient rule of functions, so invoking the quotient rule of logarithms is not appropriate. LE is a simple and interpretable, mathematically well-defined function that divides a real number by an integer.14 It is perfectly valid mathematically to divide a real number by an integer.
Another frequently used metric is lipophilic ligand efficiency (LLE or LipE) defined as6
We agree with Shultz that LLE is a useful and mathematically valid metric but we would also make the following comment. It is essential to discriminate between views about the utility of efficiency metrics versus statements about their mathematical validity. The former is a subject for debate that most medicinal chemists can engage in, whereas unfounded assertions about mathematical validity stifle debate and need to be made carefully and accurately.
Expectations of Ligand Efficiency
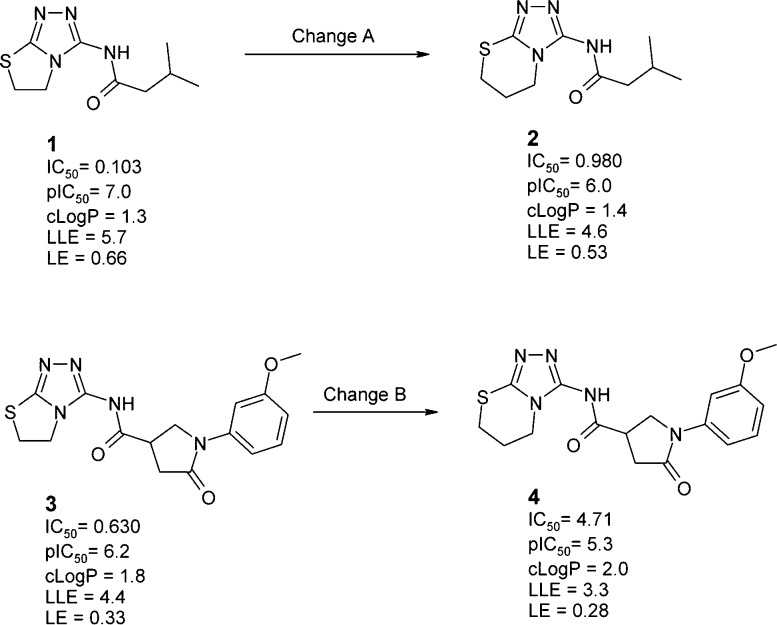
Ligand efficiency is a ratio of the free energy of binding to the size of the molecule. It is instructive to examine how one expects such a ratio to vary as changes are made to differently sized molecules. Figure 1 gives an example of four tankyrase inhibitors.5 The ring expansions of 1 to 2 (change A) and of 3 to 4 (change B) each cause an approximate 10-fold loss in affinity and a small (but similar) increase in lipophilicity. Change A and change B give a similar reduction in LLE. In contrast, the reduction in LE is significantly larger for change A than for change B. Shultz argues that one would expect a composite parameter (i.e., LE) that normalizes with respect to molecular size not to show size dependence of this kind.5 However, we believe that this is the expected behavior of any ratio.
Figure 1.
Tankyrase inhibitors where the same single atom addition (i.e, ring expansion) has been performed on molecules 1 and 3 that are of different sizes. Structures and data (including LE and LLE/LipE values) are taken from ref (5). IC50 is given in μM and LE is given in (kcal/mol)/heavy atom.
Figure 2 gives the familiar example of fuel efficiency, FE. Car journeys 1 and 3 have good FE associated with driving on the highway. The addition of the extra stage of town-driving causes a drop in FE for both journeys 2 and 4, but the drop in FE is largest for journey 2, the shorter one. The analogy with Figure 1 is clear: the same change to molecules 1 and 3 reduces potency in both cases but has more effect on the overall LE of the smaller molecule 2 than it does on the larger molecule 4.
Figure 2.
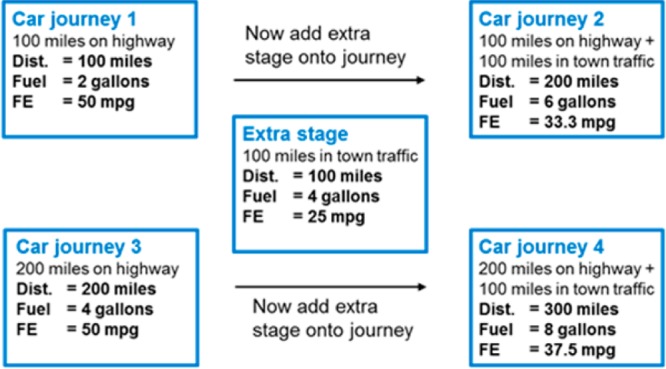
Effect on overall fuel efficiency (FE) of adding the same inefficient stage of 100 miles in town traffic to two fuel efficient journeys of different length.
The higher sensitivity of LE for small molecules is a direct result of the functional form of LE, and this behavior is shared by similar functions such as the fuel efficiency of car journeys. At very low numbers of heavy atoms there is the potential for potent molecules to have very large LE, but as a practical matter, medicinal chemists have little interest in extremely small fragments (e.g., molecular weight <75 Da). The behavior of LE as HAC tends toward zero is directly analogous to the behavior of fuel efficiency as the amount of fuel used in a journey tends toward zero. We agree that it is important that medicinal chemists are aware of this behavior but do not agree that this negates the usefulness of LE.
Limitations of Ligand Efficiency Metrics and When to Use Them
LE shows the expected behavior for a ratio of variables. We believe that it can be a very useful metric, but its simple and interpretable functional form ((kcal/mol)/heavy atom) means that it has deficiencies as well as strengths.
First, all non-hydrogen atoms are counted the same, so the introduction of a CH3, NH2, OH, F, Cl, or Br will cause the same change in HAC; no account is taken of the advantages and disadvantages of introducing polarity or charged species into a molecule. This highlights the risk of using LE in isolation without also considering other properties such as potency, cLogP, LLE, solubility, pharmacokinetics, etc.
More interestingly it has been observed across large numbers of compounds that the optimal or average LE is systematically higher for small ligands than for large ligands.4,7 This is a consequence of protein binding sites being limited in their size. Additionally the quality of fit inevitably degrades as the ligand gets larger because it becomes increasingly difficult to form optimal interactions with every site on the protein without introducing unfavorable ligand strain. Size-corrected and mathematically valid adjustments to LE, such as FQ7 and SILE,8 have been proposed. We have found both LE and its size-corrected versions to be useful when comparing molecules of different sizes and potencies, and for tracking progress during the optimization of hits into leads. It should be noted that at constant LE, potency is directly proportional to heavy atom count; hence, striving to maintain LE during optimization, when size often increases, can be a worthwhile tactic.9
The role of LE is to help control the molecular size of a series during optimization or to help decide whether one series is more suitable for progression than another. LE values vary for different targets;9 low LE values are expected for protein–protein interaction (PPI) targets and higher values are expected for more tractable targets such as kinases. In particular, LE will be less useful for highly tractable targets where obtaining small potent compounds is comparatively straightforward and where optimization will naturally focus on other properties (e.g., in vivo properties). The PARPs (such as tankyrase) are good examples of targets where obtaining high LE values is less challenging because a number of very small molecules have high potencies for their size (e.g., 3-methoxybenzamide has a potency of between 1 and 10 μM versus various PARPs).
Lipophilicity is an extremely important quantity to control during optimization, and Shultz rightly extols the virtues of LLE. LLE explicitly considers the balance of lipophilicity with potency and can be very useful in comparing HTS hits or during lead optimization. However, despite its strengths, it can be difficult to use LLE in comparing molecules of very different sizes and potencies. Also LLE will be less useful where the target requires very polar molecules. An example of this would be influenza neuraminidase where the first drug, zanamivir (cLogP = −5.6) was too polar for oral administration and the introduction of extra lipophilicity in oseltamivir (cLogP = 2.1) led to a more successful, orally bioavailable drug. LLE is a less important parameter for neuraminidase because, in contrast to most targets, producing potent molecules with low lipophilicity is not a major challenge.
We believe that obtaining a lead series with the right balance of potency, cLogP, and molecular size is a challenge for many biological targets, and we have previously observed that, for such challenging targets, drugs often have optimal combinations of LE and LLE values.9 Obtaining good in vivo properties is often facilitated by having the correct balance of potency and physical properties, but this is not a guarantee of success. We agree with Shultz about the inherent difficulties of multiparameter lead optimization, and we also agree that there is no one metric that correlates with success. However, we believe there are many biological targets where a consideration of efficiency metrics is helpful to the decision-making process.
Summary
The recent viewpoint article by Shultz summarizes a number of provocative opinions, many of which are interesting topics for debate and some of which we agree with. It is certainly true that many drugs are larger than 500 Da and that many drugs have high cLogP and poor solubility. Our belief is that compounds of this type are generally more difficult to optimize into candidates, take longer to develop, and have more chance of suffering attrition in clinical trials. A critical and balanced examination of the evidence supporting this belief is a welcome subject for debate. It is also interesting and important to question whether medicinal chemists have been overzealous in their adherence to physical property guidelines.
However, the tone of the viewpoint is sometimes unhelpful to effective debate and, more importantly, contains inaccuracies that hinder scientific inquiry. One can discuss the merits of LE and other metrics such as LLE, LELP, LLEAT, and FQ,10,11 but they are all mathematically valid. The functional form of LE gives the entirely expected behavior for a ratio of variables in that the LE of smaller molecules is more sensitive to changes than the LE of larger molecules.
Medicinal chemists are routinely faced with a highly challenging multiparameter optimization problem and an incomplete set of data to guide them to acceptable solutions. Heuristics such as LE are tools to help navigate the design space, but they are not intended to replace detailed consideration of the many in vitro and in vivo properties required in a successful drug. Our experience is that efficiency metrics can be useful to help the drug discovery process, and we encourage medicinal chemists to explore them on their own projects.
Glossary
ABBREVIATIONS
- LE
ligand efficiency
- MW
molecular weight
- LLE
lipophilic ligand efficiency (also called LipE, lipophilic efficiency)
- HAC
heavy atom count
- FE
fuel efficiency
- FQ
fit quality
- SILE
size independent LE
- PARP
poly ADP ribose polymerase
- HTS
high throughput screening
- LELP
lipophilicity corrected LE
- LLEAT
Astex LLE
Author Contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
Views expressed in this editorial are those of the author and not necessarily the views of the ACS.
The authors declare no competing financial interest.
References
- Shultz M. D. Improving the plausibility of success with inefficient metrics. ACS Med. Chem. Lett. 2014, 5, 2–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipinski C. A.; Lombardo F.; Dominy B. W.; Feeney P. J. Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings. Adv. Drug Delivery Rev. 2001, 46, 3–26. [DOI] [PubMed] [Google Scholar]
- Hopkins A. L.; Groom C. R.; Alex A. Ligand efficiency: a useful metric for lead selection. Drug Discovery Today 2004, 9, 430–431. [DOI] [PubMed] [Google Scholar]
- Kuntz I. D.; Chen K.; Sharp K. A.; Kollman P. A. The maximal affinity of ligands. Proc. Natl. Acad. Sci. U.S.A. 1999, 96, 9997–10002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The units arise directly from the conversion of an equilibrium constant (often approximated by the IC50) into a free energy of binding using one of the fundamental laws of chemistry (ΔG = −RT ln K).
- Shultz M. D. Setting expectations in molecular optimizations: Strengths and limitations of commonly used composite parameters. Bioorg. Med. Chem. Lett. 2013, 23, 5980–5991. [DOI] [PubMed] [Google Scholar]
- It is interesting to question if a number of fundamental physical equations, such as the Nernst equation, satisfy the criteria given in ref (5).
-
LE
is a mathematically well-defined function
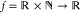 that maps the Cartesian product space domain of
reals and positive integers to the codomain of reals. For a definition
of a function, seeHaaser N. B.; Sullivan J. A.. Real Analysis; Dover: Mineola,
NY, 1991. [Google Scholar]
that maps the Cartesian product space domain of
reals and positive integers to the codomain of reals. For a definition
of a function, seeHaaser N. B.; Sullivan J. A.. Real Analysis; Dover: Mineola,
NY, 1991. [Google Scholar] - Leeson P. D.; Springthorpe B. The influence of drug-like concepts on decision-making in medicinal chemistry. Nat. Rev. Drug Discovery 2007, 6, 881–890. [DOI] [PubMed] [Google Scholar]
- Reynolds C. H.; Tounge B. A.; Bembenek S. D. Ligand binding efficiency: trends, physical basis, and implications. J. Med. Chem. 2008, 51, 2432–2438. [DOI] [PubMed] [Google Scholar]
- Nissink J. W. M. Simple size-independent measure of ligand efficiency. J. Chem. Inf. Model. 2009, 49, 1617–1622. [DOI] [PubMed] [Google Scholar]
- Hopkins A. L.; Keserü G. M.; Leeson P. D.; Rees D. C.; Reynolds C. H. The role of ligand efficiency metrics in drug discovery. Nat. Rev. Drug Discovery 2014, 13, 105–121. [DOI] [PubMed] [Google Scholar]
- Keserü G. M.; Makara G. M. The influence of lead discovery strategies on the properties of candidates. Nat. Rev. Drug Discovery 2009, 8, 203–212. [DOI] [PubMed] [Google Scholar]
- Mortenson P. N.; Murray C. W. Assessing the lipophilicity of fragments and early hits. J. Comput.-Aided. Mol. Des. 2011, 25, 663–667. [DOI] [PubMed] [Google Scholar]