Bayesian Hidden Markov Models to Identify RNA-Protein Interaction Sites in PAR-CLIP

Summary

The photoactivatable ribonucleoside enhanced cross-linking immunoprecipitation (PAR-CLIP) has been increasingly used for the global mapping of RNA-protein interaction sites. There are two key features of the PAR-CLIP experiments: The sequence read tags are likely to form an enriched peak around each RNA-protein interaction site; and the cross-linking procedure is likely to introduce a specific mutation in each sequence read tag at the interaction site. Several ad hoc methods have been developed to identify the RNA-protein interaction sites using either sequence read counts or mutation counts alone; however, rigorous statistical methods for analyzing PAR-CLIP are still lacking. In this study, we propose an integrative model to establish a joint distribution of observed read and mutation counts. To pinpoint the interaction sites at single base-pair resolution, we developed a novel modeling approach that adopts non-homogeneous hidden Markov models to incorporate the nucleotide sequence at each genomic location. Both simulation studies and data application showed that our method outperforms the ad hoc methods, and provides reliable inferences for the RNA-protein binding sites from PAR-CLIP data.

1. Introduction

The past decades have witnessed new discoveries of roles for RNA, which has come to be seen as a key player in gene regulation and cellular processes. RNA binding proteins (RBPs), which bind to RNA through RNA recognition motifs, modulate RNA processing, translation and functions, such as splicing, export, localization and stability. The functions of some RBPs are essential, and could cause some remarkable phenotype changes. For example, FUS protein (a member of FET family proteins) plays important roles in RNA editing and human cancers (Hoell et al., 2011; Neumann et al., 2011). AGO (Argonaute) proteins bind to small non-coding RNAs, such as siRNA and miRNA. They form an RNA-induced silencing complex (RISC), which is essential for RNA and small RNA interactions. Thus, the identification of RNA-RBP interactions is crucial to a systematic understanding of transcription, translation and other biological processes within cells, but there are still many unanswered questions (Licatalosi and Darnell, 2010; Sharp, 2009).

Recent developments in next-generation sequencing (NGS) technologies have resulted in genome-wide mapping of RNA-RBP interactions. One of the most established methods for genome-wide mapping of RNA-RBP binding sites is cross-linking immunoprecipitation coupled with high-throughput sequencing (CLIP-seq) technique. The general procedures of CLIP include covalently linking RNA with RBP, isolating the bound complex, removing the protein and converting RNA to cDNA for sequencing. There are a few variants of CLIP-seq that depend on the method being employed to cross-link RBP to RNA. The photoactivatable ribonucleoside enhanced CLIP (PAR-CLIP, Hafner et al., 2010) is a type of CLIP-seq, and it utilizes photoreactive analogs for incorporation into RNA at cross-linking sites. This cross-linking step is likely to induce a nucleotide specific mutation at the site of contact. For example, 4-thiouridine (4SU) introduces a thymine (T) to cytosine (C) mutation, while 6-thioguanosine (6SG) introduces a guanosine (G) to adenosine (A) mutation. PAR-CLIP has been successfully used for genome-wide identification of the RNA-RBP binding sites in many studies (Hafner et al., 2010; Hoell et al., 2011; Jaskiewicz et al., 2012; Kishore et al., 2011; Uniacke et al., 2012; Wen et al., 2011).

However, there are substantial challenges in analyzing PAR-CLIP data: (i) most genomic locations contain only a small number of mapped reads, which are likely to be noise resulting from unbound RNA to the target protein in sequencing samples; (ii) observed mutations in reads may not only be induced by cross-linking to the target protein, but also by sequencing errors (Zagordi et al., 2010) or single nucleotide polymorphisms (SNPs); and (iii) it is thought that the interactions are triggered through some motifs of nucleotide sequence structures. To overcome these challenges, a few methods that incorporate observed mutation counts into models have been proposed. For example, the cross-linking-induced mutation sites (CIMS) analysis was developed to identify the binding sites using mutation information alone (Zhang et al., 2010). The PARalyzer (Corcoran et al., 2011) utilizes kernel density estimations for mutations and non-mutations, and the wavClusteR (Sievers et al., 2012) employs nonparametric mixture models for mutation-to-read ratios to identify the binding sites. However, the underlying spatial dependence of genomic locations has not been taken into account by those studies, and no methods have established a probability model for joint distributions of observed read and mutation counts.

Spatial dependency in the read counts among neighboring locations has been observed in chromatin immunoprecipitation combined with massively parallel DNA sequencing (ChIP-seq) technique, which is designed to study protein-DNA interactions. Statistical methods (Keles, 2007; Xu et al., 2008; Gelfond et al., 2009; Mo and Liang, 2010; Qin et al., 2010; Mo, 2011) have been developed to account for the spatial correlations in ChIP-seq or ChIP-chip data. By modeling the spatial correlations, those methods greatly improve performance in identifying the protein-DNA binding sites from ChIP-seq data. However, compared to ChIP-seq data, PAR-CLIP data has two unique features: (1) it contains information about cross-linking induced mutation count at each location, which can be used as a marker for the protein-RNA interaction site; and (2) it can reach single-based pair resolution. No formal statistical methods have been developed before now which utilize these two features in PAR-CLIP data.

Here we propose Bayesian Hidden Markov models (HMMs, Rabiner, 1989) to account for the spatial dependency structure of neighboring genomic locations on both read and mutation counts. One of the novel characteristics in our model is to adopt non-homogeneous HMMs whose transition probabilities rely on nucleotide sequences, in order to account for the nucleotide-specific mutations in PAR-CLIP data. Incorporating the nucleotide sequence information allows the integrative model that considers mutation and read counts jointly in the HMM framework, which facilitates models to investigate the genome-wide spatial association of the binding sites at single-base pair resolution. An unobservable stochastic process that generates noise, read enrichment and mutation sites is translated into three hidden states. The biological interpretation associated with the state space allows for the development of suitable specifications for models and parameter space.

The results of both simulation studies and data application demonstrate that the proposed method provides consistently reliable estimations of the binding sites, and we validate that our model accurately captured the joint distribution of mutation and read counts in the data application. Our approach provides objective decision rules based on posterior probabilities of being binding sites for different genomic locations, which allows users without much statistical knowledge to easily interpret the results.

The paper is organized as follows. In Section 2, we briefly describe the PAR-CLIP data by Hoell et al. (2011) as a motivating example of this study. In Section 3, we specify the proposed model, and elucidate simulation-based posterior inference of the given model. Section 4 uses simulation studies to compare the prediction performances of our model with wavClusteR, a leading method for analyzing PAR-CLIP data. In Section 5, we implement our method on a published dataset, and the identified binding sites are supported by evidence from RNA secondary structures.

2. A Motivating Example

FUS protein is a highly conserved RBP involved in cancer biology and other diseases. It is abundant in cells and of great research interest for several reasons: (1) it is a fusion protein formed after chromosomal translocations in human cancer cells (Crozat et al., 1993); (2) it interacts with many nuclear hormone receptors and other important transcription factors (Powers et al., 1998); and (3) it could bind to RNA as well as DNA, and plays many roles in gene regulation (Wang et al., 2008). The binding targets of FUS protein were studied using PAR-CLIP (Hoell et al., 2011). The study discovered that FUS clusters are likely to contain secondary structures, suggesting that structural motifs may play an important role in protein-RNA recognition. In this study, 4SU was used for cross-linking and induced T → C mutations as the markers for the RNA-RBP binding sites. Hereafter, we use the term “mutation” only to refer to the characteristic mutation, which is T → C in this motivating example.

We downloaded the raw data generated by Hoell et al. (2011) from DRASearch (study number SRP003889). In this study, stable Flp-In T-REx HEK293 cell line with a stable and an inducible expression of Flag-HA-tagged protein was generated. Cell lines were grown for 12 to 16 hours in 4SU-supplemented medium and cross-linked RNAs were recovered from SDS-PAGE-purified FET protein immunoprecipitates. Then the converted cDNA libraries were sequenced by Solexa. Sequencing reads from the stable and inducible libraries were combined.

We preprocessed the raw reads using several steps. First, sequenced reads were aligned and mapped to corresponding genome sequences. Then, duplicates were defined as reads that map to the same chromosome, strand, start and end sites. Among duplicated reads, only one read with the maximum number of observed mutations was kept. Regions retaining at least two overlapped reads were formed into clusters, as in Khorshid et al. (2011). Then, our data was composed of read and mutation counts at each genomic location within the clusters.

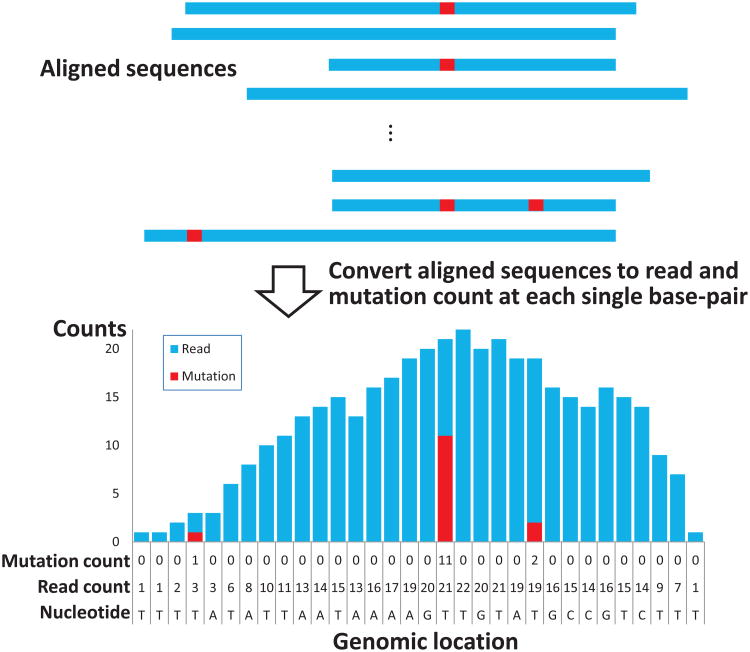
The graphical representation of the data is shown in Figure 1. Within the shown region, distributions of read counts can be approximately divided into unenriched and enriched regions. For the genomic locations with deep coverage of reads, the mutation/read ratios can be used as indicators of the binding sites. In the PAR-CLIP analysis, therefore, the genomic locations with high mutation/read ratios within read-enriched regions show strong evidence of being RBP binding sites. However, non-binding sites can have mutation counts due to random sequencing errors. Because the rate of these background random sequencing errors is not location specific, is much lower than the cross-linking induced mutation rate, and is unknown a priori, we developed Bayesian HMM models to separate the cross-linking induced mutations from the random sequencing errors based on the posterior probabilities.

Figure 1.

Illustration of the data construction. Observed mutations (1st line) and reads (2nd line) for each genomic location are given with the locations' nucleotide sequence (3rd line) in the bottom of a bar plot. This figure appears in color in the electronic version of this article.

As mentioned in Section 1, the key feature of PAR-CLIP is experimentally induced T → C mutations. Modeling the spatial association over genomic locations is impossible without incorporating the nucleotide sequence. In subsequent sections, we describe statistical models for the identification of the binding sites through modeling the spatial dependence structures.

3. Statistical Models

After the preprocessing of the PAR-CLIP data, we can derive the read count X_ij, mutation count M_ij, and nucleotide N_ij ∈ {A, C, G, T} at each genomic location i = 1, …, n_j within each region j = 1, …, J. In this study, we develop statistical models to pinpoint the RNA-RBP binding sites at single base-pair resolution.

3.1 Hidden Markov Models

The read enrichment tends to appear in contiguous genomic locations. The mutation sites are covered by consecutive enriched sites, and it is thought that the mutation sites may not be at the boundary of enriched regions, because neighborhoods of the mutation sites would also be involved in the RNA-RBP interaction, and hence covered by many reads.

To take account of such spatial dependence structure, we adopt a HMM with a Markov latent variable I_ij spanning three states as follows:

$$I_{ij}=\{\begin{array}{cc}1& \text{if unenriched}\&\text{non}-\text{mutation site};\\ 2& \text{if enriched}\&\text{non}-\text{mutation site};\\ 3& \text{if enriched}\&\text{mutation site}.\end{array}$$

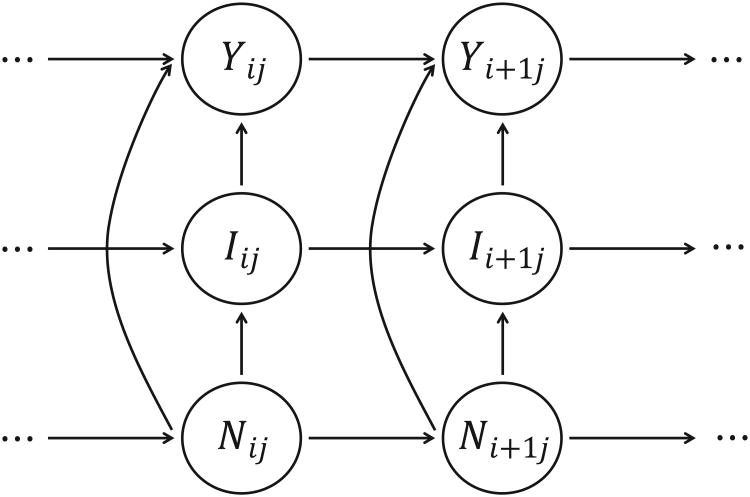
Genomic locations can receive mutation counts only if the underlying nucleotide is T. This property leads to non-homogeneous Markov transition probabilities relying on N_ij at transition sites, so we use the nucleotide sequences {N_ij} as covariates in the HMM to take heterogeneities in both likelihoods and state dynamics into consideration. A graphical representation of the dependence structure of non-homogeneous HMMs is shown in Figure 2. Given that regions are not in close proximity to one another, we assume that independent Markov chains are initiated in each region j.

Figure 2.

Graphical representation of the non-homogenous HMM, where {Y_ij} is the observable process, {I_ij} is the Markov chain, and {N_ij} is the nucleotide sequence (covariates). Independent Markov chains with identical transition rules are equipped for each region j.

Two Markov transition matrices K = (K_T, K_N) describe stochastic transition behaviors of I_i+1j relying on previous state I_ij and the nucleotide information at (i + 1, j) where the transition occurs. Let κ_T,rs denote the transition probability from r to s given that N_i+1j = T

$${\kappa }_{T,rs}:={\left[{\mathbf{K}}_T\right]}_{rs}=P(I_{i+1j}=s|N_{i+1j}=T,I_{ij}=r),$$

and let κ_N,rs denote the transition probability from r to s given that N_i+1j = A, C, or G

$${\kappa }_{N,rs}:={\left[{\mathbf{K}}_N\right]}_{rs}=P(I_{i+1j}=s|N_{i+1j}=A,C,\text{or}G,I_{ij}=r).$$

Given that true mutation sites cannot be on the boundaries of enriched regions, transitions between states 1 and 3 are prohibited. Also, the transition probabilities from state 1 to any states are assumed to be homogenous regardless of given one-step-ahead nucleotides. That is, κ_1s := κ_T,1s = κ_N,1s. The two transition matrices satisfying the assumptions above are presented as follows:

$${\mathbf{K}}_T=\left(\begin{array}{ccc}{\kappa }_{11}& {\kappa }_{12}& 0\\ {\kappa }_{T,21}& {\kappa }_{T,22}& {\kappa }_{T,23}\\ 0& {\kappa }_{T,32}& {\kappa }_{T,33}\end{array}\right)\text{and}{\mathbf{K}}_N=\left(\begin{array}{ccc}{\kappa }_{11}& {\kappa }_{12}& 0\\ {\kappa }_{N,21}& {\kappa }_{N,22}& 0\\ 0& 1& 0\end{array}\right).$$

For each row of the transition matrices, we choose independent Dirichlet priors with negligibly small hyperparameters. Let φ_T := (φ_T1, φ_T2, φ_T3) and φ_N := (φ_N1, φ_N2, 0) denote distributions of initial states whose nucleotides are T and {A, C, G}, respectively. The initial distribution φ := {φ_T, φ_N} is assumed to be independent of the transition kernels, so we put independent Dirichlet priors on φ. Details on the Dirichlet prior specification is given in Web Appendix A.

3.2 Likelihoods

Let Y_ij := (X_ij, M_ij) denote a pair of read and mutation counts. Observations Y = {Y_ij} are conditionally independent given I = {I_ij} and N = {N_ij}, and the joint density of Y can be decomposed into two parts.

$$\prod _{i,j}{p}_{\theta }({\mathbf{Y}}_{ij}|I_{ij},N_{ij})=\prod _{i,j}{p}_{\theta }(X_{ij}|I_{ij})p_{\theta }(M_{ij}|X_{ij},I_{ij},N_{ij}),$$

for some set of parameters θ.

To obtain the conditional density for the read count X_ij, we begin with the assumption that X_ij|(λ_s, I_ij = s) follows a Poisson distribution with mean λ_s, as this has been widely adopted in the literature. However, recent studies (Anders and Huber, 2010; Uren et al., 2012) have pointed out that more flexible models than Poisson mixtures would be appropriate to capture the overdispersion of read-count distributions.

Here, we expand the Possion model by introducing probabilities ω_s that genomic locations in state s are involved in RNA-RBP interactions. The ω_s can be viewed as a parameter which governs the reads-generating mechanism at sites in states s through the stochastic relation to λ_s. We assume λ_s has a exponential distribution with mean ω_s(1 − ω_s)⁻¹. To take account of the heterogeneity within ω_s, we assume ω_s follows a beta distribution. That is,

$${\lambda }_s|{\omega }_s~exp(\frac{{\omega }_s}{1-{\omega }_s})\text{and}{\omega }_s|{\mathrm{a}}_s,{\mathrm{b}}_s~\text{Ba}({\mathrm{a}}_s,{\mathrm{b}}_s),$$

where Ba(·, ·) denotes a beta distribution.

We follow the parametrization suggested by Weinberg and Gladen (1986), which involves a mean parameter μ_s = a_s · η_s and a shape parameter η_s = (a_s + b_s)⁻¹. The shape parameter η_s = 0 implies that there is no heterogeneity in ω_s. Then, by removing the conditioning on ω_s from the density p(X_ij|ω_s, I_ij = s) over the beta distribution, we obtain the beta geometric (BG) density.

$$p(X_{ij}=x|{\mu }_s,{\eta }_s,I_{ij}=s)=\frac{\mathrm{B}(\frac{{\mu }_s}{{\eta }_s}+x,\frac{1-{\mu }_s}{{\eta }_s}+1)}{\mathrm{B}(\frac{{\mu }_s}{{\eta }_s},\frac{1-{\mu }_s}{{\eta }_s})},$$

where B(·, ·) is the beta function. The BG distribution converges to the geometric distribution with a mean μ_s as η_s → 0. We find the mixture BG distribution fits the real data very well because of its capability of controlling tail thickness. The model assessment based on the posterior predictive distribution is shown in Section 5.2. Readers can find more details about the BG in Weinberg and Gladen (1986) and Wang (2011). Also, comparisons of likelihoods for modeling X_ij are available in Web Appendix G and H.

Genomic locations receiving small read counts are of little or no interest to researchers, since noise strengths dominate signal strengths in those locations. Considering those sites would dramatically increase the computation complexity, especially under the HMM framework, but provide very little gain in statistical inferences. So, we discard observations whose read counts ≤ c for some truncation point c. The truncated data consists of a set of observations such that {(X_ij, M_ij)|(i, j) ∈ R_c}, where R_c := {(i, j)|X_ij ≤ c}. Given that the data do not contain regions having no read-overlaps, the truncation cutoff c needs to be ≥ 1. Users may choose the smallest c that makes the analysis feasible within acceptable computational time limits. The left truncation is reflected on the likelihood of X_ij by shifting the BG to the right by c + 1.

In PAR-CLIP, mutations cannot be observed on a few positions in both read ends due to the preprocessing steps (the reads with mutations around the reads end are not mapped to the genome by the aligner). A few non-mutation sites (I_ij = 1 or 2) receive mutation counts while a majority of non-mutation sites receive zero mutations. To avoid underestimating noise strengths, we propose to use the zero inflated binomial for the mutation counts.

For each (i, j) ∈ R_c, let π_s denote the zero inflated probability which describes the probability that zero mutation counts (M_ij = 0) comes from a non-mutation state, and p_s denote the probability that a single read count yields a mutation when the location is in a binomial state. Noting that nonzero mutation counts can be observed only on T sites, we assume that the conditional distribution of M_ij given N_ij, X_ij, π_s, p_s, I_ij = s is

$$\begin{array}{l}p(M_{ij}|N_{ij},X_{ij},{\pi }_s,p_s,I_{ij}=s)\\ =\{\begin{array}{cc}\mathbf{1}(M_{ij}=0)& \text{if}{N}_{ij}\in \{A,C,G\};\\ \text{ZIB}(X_{ij},{\pi }_s,p_s)& \text{if}{N}_{ij}=T,\end{array}\end{array}$$

where ZIB(X_ij, π_s, p_s) denotes the zero inflated binomial distribution. That is,

$$\begin{array}{l}{M}_{ij}|N_{ij}=T,X_{ij},{\pi }_s,p_s,I_{ij}=s\\ ~\{\begin{array}{ccc}0& \mathrm{w}.\mathrm{p}.& {\pi }_s;\\ \text{Bin}(X_{ij},p_s)& \mathrm{w}.\mathrm{p}.& 1-{\pi }_s.\end{array}\end{array}$$

Let $\theta ={\{{\mu }_s,{\eta }_s,p_s,{\pi }_s\}}_{s=1}^3$ denote a set of parameters in the likelihood. For (i, j) ∈ R_c, the joint distribution of read and mutation counts given N_ij's and I_ij's can be written as

$$\begin{array}{c}P(\mathbf{X},\mathbf{M}|\mathbf{N},\theta ,\mathbf{I})=\prod _{i,j\in {\mathrm{R}}_c}p(X_{ij},M_{ij}|N_{ij},\theta ,I_{ij})\\ =\prod _{i,j\in {\mathrm{R}}_c}p(X_{ij}|\theta ,I_{ij})p(M_{ij}|N_{ij},X_{ij},\theta ,I_{ij})\\ =\prod _{i,j\in {\mathrm{R}}_c}{\text{BG}}_c(X_{ij}|{\mu }_{I_{ij}},{\eta }_{I_{ij}})\times \prod _{\begin{array}{c}i,j\in {\mathrm{R}}_c\\ N_{ij=T}\end{array}}\text{ZIB}(M_{ij}|X_{ij},{\pi }_{I_{ij}},p_{I_{ij}}).\end{array}$$

3.3 Priors

Since the three states have clear biological interpretations, we incorporate the biological knowledge into the priors, and in the interim we choose flexible priors to allow Bayesian learning. The parameters are restricted to be in the constrained parameter space C_θ to meet the biological interpretation of three hidden states.

First, the read-count distributions are identical in the enriched locations, which implies μ₂ = μ₃ and η₂ = η₃. Second, the first moment of BG_c(μ_s, η_s) is an increasing function of s ∈ {1, 2}. Third, η₁ = 0, which yields the geometric distribution for read counts in enriched regions instead of the BG. The second and third constraints ensure that the read-count distribution for unenriched regions to be concentrated on small values, whereas the read counts on enriched regions can be less dense on small values. That is, BG_c(X_ij|μ₁, η₁) > BG_c(X_ij|μ₂, η₂) for some small X_ij. Fourth, the signal strength on mutation sites would be greater than the noise strength. That is,

$$p_1,p_2<\epsilon -\delta ,\epsilon <p_3.$$ (1)

Last, the zero inflated probability for mutation sites is assumed to be 0. Combining all constraints above, we have

$$C_{\theta }=\{\theta |{\mu }_2={\mu }_3;{\eta }_2={\eta }_3;{\mu }_{1,1}<{\mu }_{1,2};{\eta }_1=0;p_1,p_2<\epsilon -\delta ;\epsilon <p_3;{\pi }_3=0\},$$ (2)

where μ_1,s denotes the first moment of BG(μ_s, η_s).

According to Zhang and Darnell (2011), the mutation-read ratio over 0.2 can be translated as evidence of the binding site. The small δ is chosen to insure the separability of error and true mutation probabilities. From extensive numeric studies, we found that choosing ε = 0.2 and δ = 0.01 typically provides stable posterior inference for small c ≤ 3. However, for large c ≥ 4 the posterior inference is not sensitive on the choice of ε and δ, and we often replace the constraint in (1) with {p₁, p₂ < p₃}.

We choose independent Gaussian priors on logit ${\mu }_s:=log\frac{{\mu }_s}{1-{\mu }_s}$ and logη_s, and independent beta priors on p_s and π_s. Together with the constrained parameter space, we have

$$p({\{logit{\mu }_s,log{\eta }_s\}}_{s=1}^3)=\prod _{s=1}^2\mathrm{N}(logit{\mu }_s|{\nu }_{{\mu }_s},{\sigma }_{{\mu }_s})\mathrm{N}(log{\eta }_s|{\nu }_{{\eta }_s},{\sigma }_{{\eta }_s}){\mathbf{1}}_{{\mathrm{C}}_{\theta }}({\{{\mu }_s,{\eta }_s\}}_{s=1}^3),p({\{p_s\}}_{s=1}^3)=\prod _{s=1}^3\text{Ba}(p_s|{\alpha }_{p_s},{\beta }_{p_s}){\mathbf{1}}_{{\mathrm{C}}_{\theta }}({\{p_s\}}_{s=1}^3),p({\{{\pi }_s\}}_{s=1}^3)=\prod _{s=1}^2\text{Ba}({\pi }_s|{\alpha }_{{\pi }_s},{\beta }_{{\pi }_s}){\mathbf{1}}_{{\mathrm{C}}_{\theta }}({\pi }_3),$$

where N(·|ν, σ) denotes the normal density with a mean ν and a standard deviation σ, and 1_Cθ(θ) is an indicator function that gives 1 if θ ∈ C_θ; 0 otherwise.

3.4 Posterior Inference

The Viterbi algorithm (Viterbi, 1967) can be implemented to estimate the most likely state sequences conditional on parameter estimated by the EM algorithm. However, there are needs for controlling the testing power to obtain higher confidence RNA-RBP binding sites. The false discovery rate (FDR, Benjamini and Hochberg, 1995) is commonly used for this purpose, which requires implementation of computationally intensive algorithms like the MCMC. Although the MCMC needs long computation times, additional computational costs are negligible compared to a few months of efforts required to generate and process the PAR-CLIP data.

Here we describe the simulation-based posterior inference for the proposed model. For the particle approximation of the posterior distribution, we draw samples from p(θ, I, K, φ, Z|N, Y) by employing the Metropolis within Gibbs sampler with the auxiliary variable Z. The full conditional distributions can be obtained as follows.

Given that p_s and π_s cannot be factorized in the ZIB part, we introduce unobserved random variables {Z_ij} to T sites, in order to achieve a computationally effective posterior sampler. This procedure is commonly known as data augmentation. The auxiliary variable Z_ij is defined on every T site, and Z_ij = 1 if zero mutation counts are generated from the zero state; otherwise Z_ij = 0. The conditional probability of Z_ij = 1 given X_ij, M_ij, p_Iij, π_Iij is (see Hall (2000) for more details)

$$P(Z_{ij}=1|N_{ij}=T,X_{ij},M_{ij},p_s,{\pi }_s,I_{ij}=s)=\{\begin{array}{cc}\frac{{\pi }_s}{{\pi }_s+{(1-p_s)}^{x_{ij}}(1-{\pi }_s)}& \text{if}{\mathit{M}}_{ij}=0;\\ 0& \text{if}{\mathit{M}}_{ij}\ne 0.\end{array}$$ (3)

Together with the auxiliary variables Z = {Z_ij}, the conditional posterior distribution of θ can be written as follows.

$$p(\theta |\mathbf{N},\mathbf{Y},\mathbf{I},\mathbf{Z})\propto \prod _{\begin{array}{c}{N}_{ij}=T\\ (i,j)∊R_c\end{array}}{\pi }_{I_{ij}}^{Z_{ij}}{[(1-{\pi }_{I_{ij}})\text{Bin}(M_{ij}|X_{ij},p_{I_{ij}})]}^{1-Z_{ij}}\times \prod _{(i,j)∊R_c}{\text{BG}}_c(X_{ij}|{\mu }_{I_{ij}},{\eta }_{I_{ij}})p(\theta )\propto \prod _{s=1}^2\text{Ba}({\pi }_s|{\alpha }_{{\pi }_s}+n_{z=1,s},{\beta }_{{\pi }_s}+n_{z=0,s}){\mathbf{1}}_{{\mathrm{C}}_{\theta }}({\pi }_3)$$ (4)

$$\times \prod _{s=1}^3\text{Ba}(p_s|{\alpha }_{p_s}+\sum _{\underset{z_{ij}=0}{I_{ij}=s}}{X}_{ij},{\beta }_{p_s}+\sum _{\underset{z_{ij}=0}{I_{ij}=s}}{X}_{ij}-M_{ij}){\mathbf{1}}_{{\mathrm{C}}_{\theta }}({\{p_s\}}_1^3)$$ (5)

$$\times p({\{logit{\mu }_s,log{\eta }_s\}}_1^3)\prod _{s=1}^3\prod _{I_{ij}=s}{\text{BG}}_c(X_{ij}|{\mu }_s,{\eta }_s),$$ (6)

where n_z=i,s denotes the number z_ij = i among locations satisfying I_ij = s and N_ij = T. It is easy to sample from (4), and the rejection sampling is used to draw particles from (5), but there is no clear way to sample from (6). Thus, we implement the Metropolis algorithm to obtain samples from (6), which is described in Web Appendix B.

The conditional distribution of hidden states I is

$$p(\mathbf{I}|\mathbf{N},\mathbf{Y},\theta ,\mathbf{K},\phi )\propto p(\mathbf{Y}|\mathbf{N},\theta ,\mathbf{I},\mathbf{K},\phi )p(\mathbf{I}|\mathbf{K},\phi ),$$

and the direct sampling from the above density is done by the forward-backward Gibbs sampler (FB Gibbs, Scott, 2002) as shown in Web Appendix C. Because we define the initial distributions φ to be independent of K, the posterior samples of K and φ can be drawn directly from Dirichlet distributions as described in Web Appendix D. For each MCMC iteration, we draw samples from the full conditional distribution described above. Then, the posterior probability of the mutation site p_ij = P(I_ij = 3|Y) is estimated as the average number of times that the MCMC sample $I_{ij}^{(t)}$ visits state 3 for some index set D. That is,

$${\widehat{p}}_{ij}=\sum _{t\in D}\frac{\#\{I_{ij}^{(t)}=3\}}{|\mathrm{D}|}.$$

4. Simulation Studies

In this section, we compare performances of our method with the wavClusteR on detecting the mutation site in the artificial data whose mutation counts are generated from the model established in the wavClusteR. All observations are simulated in Simulation Study 1, and real data with possible binding regions are used while regions with no binding sites are simulated in Simulation Study 2.

The wavClusteR (Sievers et al., 2012) provides the decision rule as a function of the mutation-to-read ratio M_ij/X_ij. A key assumption in the wavClusteR is that distributions of the ratios for the non-experimental induced mutations and 11 other types of substitutions (A→ G, T→ C, and so on) are approximately identical. They propose a nonparametric mixture modeling to filter out the non-experimental component from the mixture distribution of the ratios, and estimate the posterior density that describes which mutation-to-read ratios are more likely to be generated by the experimental component. Throughout this section, we use the term “substitution” to refer to the 11 types of substitutions other than the characteristic mutation (T → C).

4.1 Simulation Study 1

To simulate the artificial data, our model is used to generate the hidden state I_ij and read count X_ij, and the modeling assumption in the wavClusteR is used to generate mutations M_ij and other types of substitutions. The number of regions is set to be 400, and each region has 30 genomic locations. For 100 independent experiments, sampling distributions of parameters are chosen to mimic the empirical distribution obtained from the dataset in Section 5. The underlying nucleotides at each genomic location are independently drawn from {A, C, G, T} with probabilities {0.3, 0.2, 0.1, 0.4}. Initial distributions and transition matrices are chosen to generate 100 mutation sites on average. We generate read counts from BG₅ distribution, and the same truncation cutoff c = 5 is used in the wavClusteR.

The wavClusteR assumes heterogeneous mutation probabilities within states. Following the assumption, we generate mutation counts from

$$M_{ij}|N_{ij}=T,I_{ij}=s~\text{ZIB}(X_{ij},{\pi }_s,p_{s,ij}),$$

where π_s ∼ Ba(50, 50) for s = 1, 2 and π₃ = 0, and we draw random mutation probabilities p_s,ij at each i, j as follows.

$$\begin{array}{l}{p}_{s,ij}~\text{Ba}(1,9)\text{for}s=1,2,\\ p_{3,ij}~\text{Ba}(7,3).\end{array}$$

Substitutions are generated on non-mutation sites whose observed mutation is zero. Substitution counts are sampled from ZIB(X_ij, π_s, p_s,ij), and substitution types are chosen with equally likely probabilities given the nucleotide information. To be clear, these substitutions are used only in the wavClusteR, not in our method. Since we use identical distributions to generate substitutions and non-experimental induced mutations, the wavClusteR is expected to perform well in identifying mutation sites.

In our method, every hyperparameter except those for the BG is chosen as 0.01 to lessen its impact on the posterior inference. Hyperparameters for the beta geometric are chosen to have a mean 0 and a standard deviation 10¹⁰⁰. Posterior samples are drawn from the full conditional distribution in Section 3. For the simulation studies, we replace the constraint in (1) with {p₁, p₂ < p₃}, since posterior samples are not sensitive to the choice of ∊ and δ in our setting.

The simulations are coded in R and run on a Linux machine with a 2.66 GHz processor. The MCMC sequences of our method quickly reach approximate convergence within 500 iterations, so we simulate MCMC sequences with the length of 2,000, and burn in the first halves. The smoothed Receiver Operating Characteristic (ROC) curves are presented in Figure S2 in Web Appendix F. To provide more distinguishable ROC curves, true and false positive rates are computed based only on locations which receive at least one mutation count. The wavClusteR quickly picks up many false positives as the number of positives increases, and it fails to find some true positives at cutoffs near 0. Meanwhile, our method picks up almost all true positives at very small false positive rates.

The area under the ROC curve (AUC) can be used to compare the two methods. The average AUC of the HMM, the wavClusteR and the AUC difference between the two methods (AUC_HMM − AUC_WCR) over 100 experiments are 0.9643 (s.e. 0.0014), 0.8292 (s.e. 0.0052) and 0.1351 (s.e. 0.0053), respectively. The p-value of the Wilcoxon rank test with an one-sided alternative is less then 0.0001. Overall, our method outperforms the wavClusteR, and our model works well under the slight model mis-specification over the non-parametric mixture model.

4.2 Simulation Study 2

FMRP is a RNA-binding protein, and lack of FMRP results in human cognition and premature ovarian insufficiency. The identification of the RNA targets of FMRP was studied previously by Ascano et al. (2012), and a large scale simulation study is carried out here based on their dataset.

Enriched regions containing both motifs ACT[TG] and [AT]GGA with strong mutation signals are likely to include true binding sites. On these regions, locations with mutation-read ratios ≥ (0.4, 0.5) are assumed to be true binding sites. For each of the ratio cut-offs, 1,572 and 988 regions fulfill the criterion, and we randomly choose 500 of these regions for each experiment. On average, 630 and 590 binding sites are contained in artificial datasets, and 4,500 regions of length 40 are generated under the identical probability rules used in Section 4.1. The average AUC of the HMM, the wavClusteR and difference of AUCs between the two methods are presented in Table 1. The average AUC difference shows that our method identifies binding sites more effectively in the realistic signal strengths.

Table 1.

The average AUCs and standard errors of the HMM, the wavClusteR and differences between the two methods (Δ).

	HMM	Δ	wavClusteR
p ≥ 0.4	.9926 (.00009)	.0078 (.00023)	.9848 (.00020)
p ≥ 0.5	.9931 (.00010)	.0096 (.00024)	.9835 (.00020)

Since the wavClusteR utilizes nonparametric density estimations, its classification may not be as precise as ours when the truncated sample size is not large enough. Generally, the wavClusteR suggests choosing a high truncation cutoff c ≈ 20 for precise estimates of mutation-to-read ratios, which results in discarding many observations. To compensate this problem, Sievers et al. (2012) proposed another stage for the prediction, which is not considered here in our simulation studies.

5. Application to identify FUS protein binding sites

We implemented our method to analyze the FUS PAR-CLIP data in Section 2 and compared the performance of our method with the wavClusteR. The R package wavClusteR is used for this application. The truncation point c is 5, and regions whose lengths are less than 6 are discarded. Hyperparameters are chosen to be 0.01 for conjugate priors and a mean 0 and a standard deviation 10¹⁰⁰ for beta geometric parts as in Section 4.

5.1 Model checking and model diagnostics

The Gelman-Rubin statistics (Gelman and Rubin, 1992) are computed to check the MCMC convergence based on three chains with 20,000 samples initialized at different starting values. For the parallel chains of a scalar estimand, the statistic compares the between-chain variance with the within-chain variance as a proportion. Values significantly above 1 indicate that the chains do not escape the influence of initial values, and that more samples need to be simulated to improve the inference of the target distribution.

For all parameters in θ, the statistics are between 1 and 1.02. To summarize the convergence of joint density, we also compute the Gelman-Rubin statistic based on the log-posterior density log p(Y|θ^(t), I^(t), N), and we obtain 1. The acceptance ratio for proposed samples in the Metropolis algorithm is 0.72 for state 1, and 0.62 for state 2. Trace plots for each parameter are given in Figure S1 in Web Appendix E. The three chains mix well and they quickly reach the approximate convergence.

Assessing the plausibility of our model is carried out by computing the posterior predictive p-value. Let Y^rep denote the replicated observation generated from the posterior predictive distribution p(Y^rep|Y), and let T(Y, θ, I, N) := log p(Y|θ, I, N). The p-value P_T is defined as the probability that the replicated data could be as extreme as, or more extreme than, the observed data as follows:

$$P_T:=P(T({\mathbf{Y}}^{\mathit{\text{rep}}},\theta ,\mathbf{I},\mathbf{N})\ge T(\mathbf{Y},\theta ,\mathbf{I},\mathbf{N})|\mathbf{Y}).$$

The p-value can be viewed as the measure to assess the discrepancies between the model and data. More details about the posterior predictive checking (PPC) are given in Gelman et al. (1996).

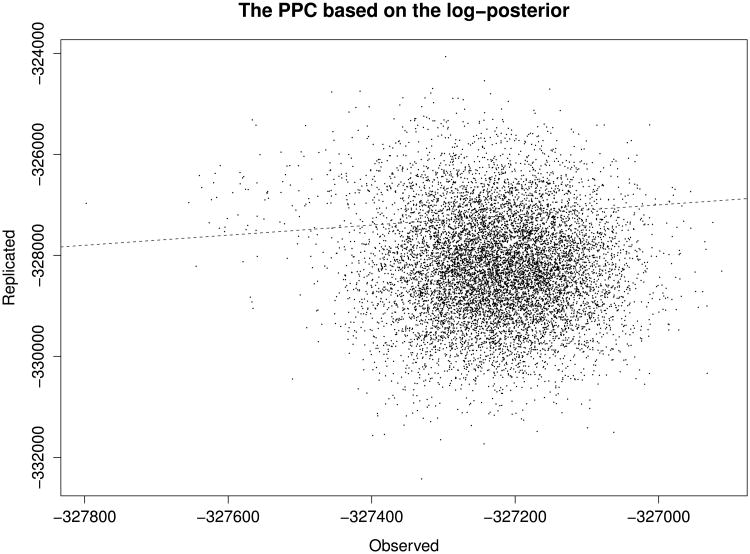
We estimate P_T using MCMC samples {[Y^rep]^(t), θ^(t), I^(t)}, and [Y^rep]^(t) is drawn from p(Y|θ^(t), I^(t), N). Figure 3 shows simulated paired values of T(Y, θ, I, N) and T(Y^rep, θ, I, N) based on the second half of the 20,000 MCMC samples. The estimated p-value is 0.1694, which suggests that the discrepancies between our model and the data are not significant. The PPC we performed in this section demonstrates that our modeling approach can be used to understand the mechanism to generate the read and mutation counts in PAR-CLIP.

Figure 3.

A scatter plot of log-posterior densities for the observed and replicated data. Based on the last 10,000 MCMC draws, the p-value is 0.1694. An identical line (y = x) is presented as a dashed line.

5.2 Results

The sequencing reads are aligned to the hg19 reference genome, resulting in 4,296,458 mapped reads. The sequencing depth is relatively smaller than expected in typical CLIP-seq studies, and saturation is not reached according to the authors' own calculation in Hoell et al. (2011). The identification of RNA-RBP binding sites is made by applying different values of cutoff τ on the posterior mean of p_ij. The FDR for each τ can be estimated from posterior probabilities p_ij (Newton et al., 2004) by

$$\mathit{\text{FDR}}(\tau )=\frac{\sum _{i,j}(1-p_{ij})\mathbf{1}(p_{ij}\ge \tau )}{\#\{p_{ij}\ge \tau \}}.$$

Table 2 summarizes numbers of binding sites identified by our method at different cutoffs. It shows that our approach identifies a reasonable number of high confidence binding sites with low FDR, which is beneficial to biologists who have limited resources to perform the experimental validation of RNA-RBP binding sites.

Table 2.

Numbers of sites identified by our method with different cut-offs τ on posterior prediction probabilities.

# of sites	τ	FDR
26	1.000	≈ 0
34	0.999	0.00007
35	0.995	0.00016
36	0.990	0.00037
37	0.975	0.00099
39	0.970	0.00244
40	0.965	0.00319
45	0.960	0.00694

Figure 4 shows the secondary structure containing one of the binding sites identified by our method. This site is in the top 26 binding sites identified by our method, but not in the top 26 identified by the wavClusteR. The secondary structure where the identified binding site resides is at the small loop of the secondary structure. The similar substructure resembling the small stem and loop in the figure is considered to be the binding motif in Hoell et al. (2011).

Figure 4.

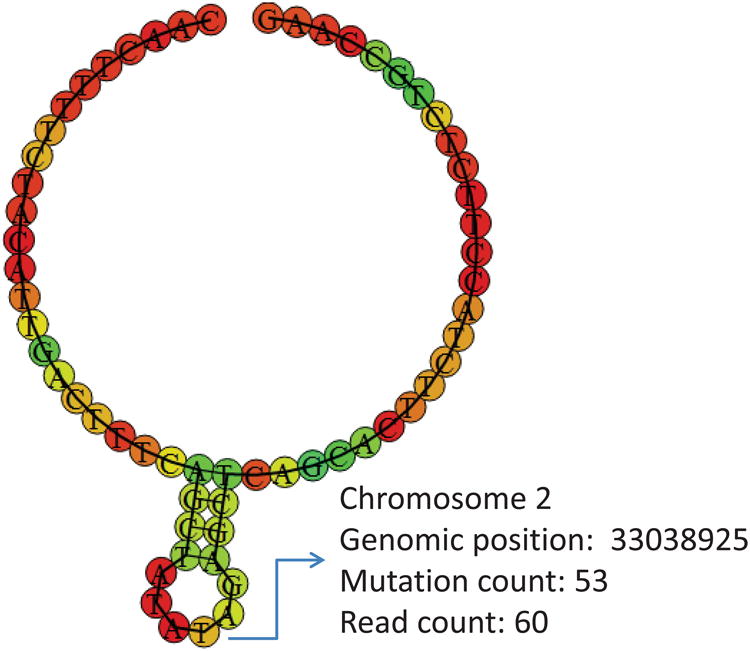
The secondary structure of the RNA-RBP binding site identified by our method. This figure appears in color in the electronic version of this article.

Our method identifies 36 binding sites with posterior probabilities > 0.99 and 45 binding sites with posterior probabilities > 0.95, whereas all sites received posterior probabilities < 0.8 in the wavClusteR. Further validation of the binding sites identified by the HMM approach is presented in Web Appendix I. We used the gene expression data from (Han et al., 2012), in which a novel chemical essay coupled with RNA-seq technique was used to study the FUS binding sites. In their study, FUS protein, together with its RNA binding targets, was precipitated upon exposure of lysates to the b-isox chemical. The read count ratios of RNA transcript in knockdown vs. control conditions were measured for all RNAs. For RNA targets of FUS, their ratios are likely to be less than 1. The validation demonstrates that our method leads to RNA targets with small expression ratios, which is consistent with what we expected from the biological knowledge.

6. Discussions

We developed a model-based approach to detect RNA-RBP binding sites in PAR-CLIP. Our method integrates models to identify enriched regions and high-confidence binding sites into one rigorous statistical model. An advantage of our integrative modeling is that the posterior probability of being a binding site is estimated based on data with less information loss, as compared with two-stage modeling approaches. This facilitates more accurate statistical inference, so our method would provide more reliable binding sites based on the FDR.

Main innovations of our framework are to adopt non-homogeneous HMMs and to employ BG distributions. Nucleotide specific mutation inductions are the key feature of PAR-CLIP data, and non-homogeneous HMMs successfully incorporate nucleotide sequences to investigate the spatial association among genomic locations. HMMs equipped with negative binomial emission distributions have been used to fit read count distributions in sequencing data. However, the PAR-CLIP data have empirical read count distributions with a dramatically decreasing density at small read counts and a heavy tail with slowly vanishing densities at large read counts, and such a shape is difficult to capture by the mixture of negative binomials. As demonstrated by the Bayesian posterior predictive checking on the real dataset, our modeling approach employing the BG successfully captures the read count distribution in PAR-CLIP.

One may be able to adopt other types of priors, but the computational efficiency obtained by the Dirichlet priors is an attractive characteristic under the Bayesian HMM of PAR-CLIP whose sample size can be a few million at least. Also, the Dirichlet priors have been widely adopted for studies in similar contexts. For example, modeling the copy number variation (Guha et al., 2008), genomic sequence and ChIP-Chip (Gelfond et al., 2009) and gene expression and sequence data (Xie et al., 2010). For the computational efficiency, we choose priors to have conjugate functional forms if possible while keeping hyperparameters minimally informative. The amount of information in hyperparameters is negligible in comparison to the numbers of sites (a few million), which is flexible enough to allow the Bayesian learning.

A large number of unenriched locations will be discarded for some large c, which makes the Bayesian learning less efficient in separating enriched regions from unenriched regions. Although the rank order of high-confidence binding sites is not sensitive to the choice of c ∈ [1,6], a large number of sites with unstable mutation-read ratios are introduced with small c ≤ 3, which makes the inference of p_s sensitive to the choice of ∊. To achieve accurate estimates of FDRs, users may choose the smallest c ≥ 4 that makes the analysis feasible within acceptable computational time limits.

The proposed method is tailored for the PAR-CLIP analysis, but our framework can be adapted to analyze other types of sequencing data with experiment-induced mutations. For example, the multinomial likelihood with random mutation probabilities can be considered to incorporate position-specific error rates into our model for the analysis of deletions, insertions, and substitutions in the high-throughput sequencing of RNA isolated by cross-linking immunoprecipitation (HITS-CLIP, Licatalosi et al., 2008).

In summary, this article presents the first successful attempt at integrative statistical modeling of mutation and read counts regarding the spatial dependence structure with the incorporation of nucleotide sequences. The high interpretability of our model leads to interesting biological insights, and introduces the method of non-homogeneous hidden Markov modeling and the beta geometric distribution into a new area of applications.