Reconstruction of normal and abnormal gastric electrical sources using a potential based inverse method

Abstract

The use of cutaneous recordings to non-invasively characterize gastric slow wave had limited clinical acceptance, primarily due to the uncertainty in relating the recorded signal to the underlying gastric slow waves. In this study we aim to distinguish and quantitatively reconstruct different slow wave patterns using an inverse algorithm. Slow wave patterns corresponding to normal, retrograde and uncoupled activity at different frequencies were imposed on a model of the stomach surface. Gaussian noise (10% peak-to-peak) was added to cutaneous potentials and the Greensite-Tikhonov inverse method was used to reconstruct the potentials on the stomach. The effectiveness of the number or location of electrodes on the accuracy of the inverse solutions was investigated using four different electrode configurations. Results showed the reconstructed solutions were able to reliably distinguish the different slow wave patterns and waves with lower frequency were better correlated to the known solution than those with higher. The use of up to 228 electrodes improved the accuracy of the inverse solutions. However, the use of 120 electrodes concentrated around the stomach was able to achieve similar results. The most efficient electrode configuration for our model involved 120 electrodes with an inter-electrode distance of 32 mm.

1. Introduction

Gastric electrical activity, or ‘slow wave’ activity is generated by the interstitial cells of Cajal (ICC) and conducts to the surrounding smooth muscle cells (SMC), coordinating patterns of motility. In the human stomach, gastric slow waves originate from a pacemaker region near the greater curvature in the corpus and then propagate towards the pylorus at a frequency of approximately 3 cycles-per-minute (cpm) (Koch and Stern 1994, O’Grady et al 2011). However, this activity is omni-present and is not always associated with peristaltic activity. Although the slow wave activity coordinates the peristalsis patterns, this only occurs in the presence of additional cooperating mechanisms (Huizinga and Lammers 2009).

Abnormalities in the patterns of slow wave propagation have been associated with several functional gastric motility disorders such as gastroparesis and functional dyspepsia (Bortolotti et al 1990, Leahy et al 2001, O’Grady et al 2012). Recently, high-resolution (HR) electrical mapping studies have further characterized gastric dysrhythmias. Two recent HR mapping studies (Lammers et al 2008, O’Grady et al 2011) in animal subjects have reported episodes of gastric dysrhythmia with spatiotemporal abnormalities. O’Grady et al (2012) also observed complex dysrhythmias in patients with gastroparesis and concluded that abnormalities of slow wave initiation and conduction often occur at the same frequency as normal activity.

Despite the detailed information HR serosal mapping provides, it has had limited application as a routine diagnostic tool due to its invasiveness. The ability to characterize slow wave activity reliably and non-invasively, e.g., electrogastrogram (EGG), would be beneficial for diagnosis of gastric motility disorders and for determining therapeutic strategies. EGG records the slow wave signals from the stomach using electrodes positioned on the skin surface and this non-invasiveness is a significant advantage. However, EGG has been hindered by the lack of standardized methodology (e.g., electrode configurations, recording periods, filtering techniques), a limited understanding of the organization of the electrical waves, and the signal attenuation caused by the volume conductor (Chang 2005), Mintchev and Bowes 1996, Bradshaw et al 2001, Kim et al 2012). These challenges have limited the application of EGG up to now as a clinical tool, despite the success of the 12-lead electrocardiogram (ECG).

A significant challenge now impeding the routine application of EGG is the relatively low amplitude signals of the gastric electrical activity, which makes separation of EGG from noise sources more challenging than standard ECG filtering. A number of different studies have investigated different methods for appropriately filtering EGG signals. These have included using high pass or adaptive filters, empirical mode decomposition, independent component analysis or neural networks, to separate EGG (3 cpm) from ECG (60 cpm) and intestinal slow waves (8–12 cpm) (Chang et al 2001, Chen et al 1989, Chen and Lin 1994, Liang et al 2000, Liang 2005, Tkacz and Mika 2010, Liang et al 1997). The use of breath holds during a recording period is routinely used when recording ECGs and EGGs for minimizing respiratory artifact (Pandey and Pandey 2005, Morton 1954).

The location or spatial resolution of body surface electrodes has an important role on obtaining sufficient information for reconstructing the underlying sources. In general, using a larger number of electrodes leads to better reconstruction of the underlying sources. But using an excessive number of electrodes is not practical and it is important to find the optimal placement and number of electrodes. The effect of the number of electrodes on the accuracy of source localization has been studied in several papers of electroencephalogram (EEG) (Spitzer et al 1989, Srinivasan et al 1998) and ECG (Li et al 2003). Spitzer et al (1989) and Srinivasan et al (1998) have shown that 30 mm inter-electrode distance was sufficient to characterize the brain’s electrical fields at the scalp surface. Li et al (2003) investigated the relationship between the number of electrodes on torso surface and the accuracy of estimating the tip of the pacemaker using 32, 64, 96 and 300 electrodes on the torso surface. The results indicated that there was a steep drop of error when using 64 from 32 electrodes but the errors remained almost the same when increasing from 96 to 300 electrodes, indicating the existence of optimal electrode configuration. However, studies suggested the optimal electrode configuration is not unique and can depend on the noise level (Ryynanen et al 2004), the resolution of the model (Li et al 2003), model geometry (Lux et al 1978, Dossel et al 1998, Laarne et al 2000) or the type of source model (Dossel et al 1998, Lantz et al 2003). In EGG studies typically four electrodes have been placed on the abdomen along the gastric axis (Chen et al 1999, Liang 2005, Du et al 2010). To date, no studies have investigated optimal inter-electrode distances in EGG recordings.

Recently, we have shown that by using potential based inverse methods we were able to resolve multiple gastric slow waves from body surface recordings (Kim et al 2012). In this follow up study, we aim to differentiate different slow wave patterns occurring in the stomach. EGG activity corresponding to a number of slow wave patterns representing normal and abnormal gastric activities at different frequencies were reconstructed using the Greensite-Tikhonov method. In addition, electrode configurations with different electrode densities and locations were used to investigate the most efficient electrode configuration for reconstructing the underlying slow wave activity in our model.

2. Methods

2.1 Geometric & Source Models

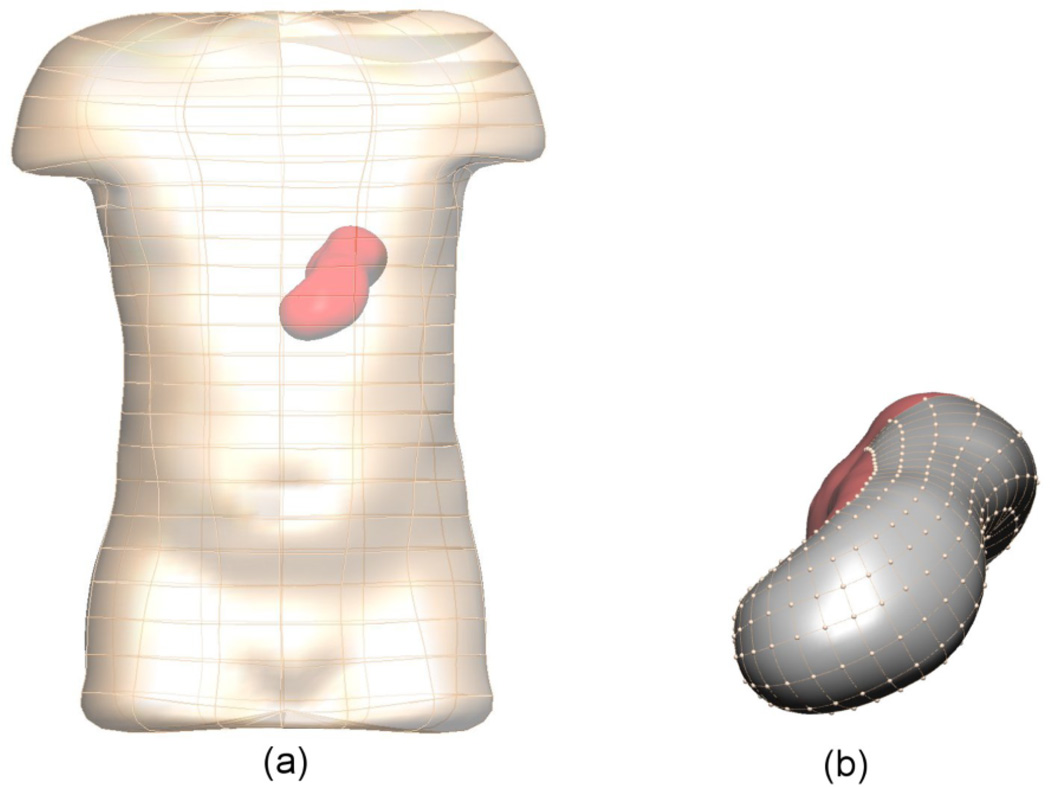
The anatomical model used in this study was derived from the Visible Human dataset (Spitzer et al 1996, Buist et al 2006). The model (shown in figure 1) consisted of two boundary element surface meshes, with the stomach surface mesh encased in the torso skin surface mesh. Both the torso and stomach conductivities were assumed to be homogeneous with a conductivity of 0.22 mS mm⁻¹ in the torso and 0.135 mS mm⁻¹ in the stomach (Kim et al 2012). The meshes were interpolated using cubic Hermite basis functions and the stomach and skin surfaces had 626 and 290 nodes, respectively. The shaded (grey) region on the stomach in figure 1(b) had 280 virtual electrodes and was used as the numerical comparisons of inverse solutions.

Figure 1.

Boundary element meshes of the skin and stomach surface. In (b) the shaded (grey) region on the stomach has 280 virtual electrodes and corresponds to the area represented in figures 4 and 6. The average distance between nodes is 6 mm.

Three different source models (shown in figure 2) were used to represent normal, retrograde and uncoupled activity. The activities were based on data obtained from HR human mapping studies (O’Grady et al 2011, 2012). The model setup was similar to a previous modelling study (Komuro et al 2010) but an updated biophysically based cell model (Corrias and Buist 2008) was used at each solution point on the stomach model to simulate the propagation of a slow wave. Equivalent dipole sources were derived from the transmembrane potential gradient of each element, resulting in a total of 608 dipoles. The dominant frequency was varied for each source model from 3 cpm to 2 or 4 cpm in order to investigate the effect of frequencies on the accuracy of the inverse solutions.

Figure 2.

Transmembrane potential distributions of the normal, retrograde and uncoupled source models shown at 2–3 time intervals. Shown are (a) normal slow wave activity originating in the corpus and propagating towards antrum, (b) retrograde slow wave activity originating in antrum region and propagating towards corpus, and (c) uncoupled activity where one wave originated at corpus region and propagated towards antrum and the other wave originated at antrum region and propagated towards corpus. In this case the two waves collided in the middle of stomach as indicated by the asterisk (*).

2.2 Forward and Inverse Solutions

Established methods (Pullan et al 2001) were used to solve the forward problem and simulate the resultant body surface potential field due to the gastric slow waves. After the introduction of 10% Gaussian noise to the simulated body surface potential field, gastric slow waves were reconstructed using the Greensite–Tikhonov inverse method (Greensite and Huiskamp 1998, Cheng et al 2003) with regularization levels determined using an L-curve method (Hansen and O’Leary 1993). For further information the readers should refer to the methods described in Kim et al (2012).

2.3 Surface Electrodes

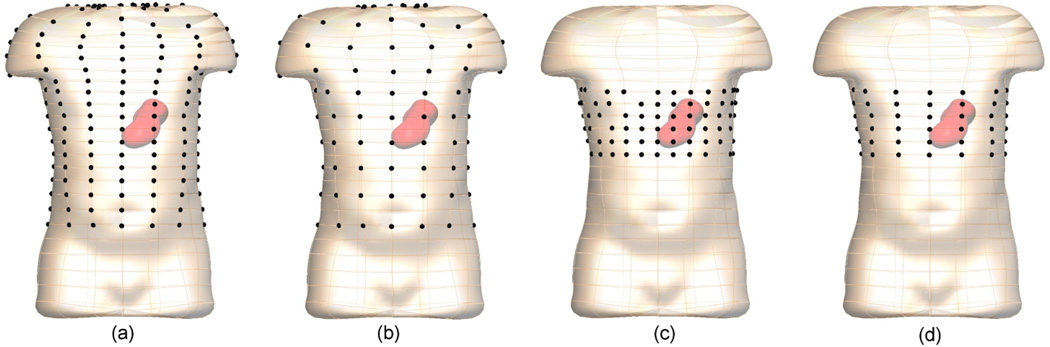
Electrogastrograms were simulated at four different surface electrode configurations, as shown in figure 3. The E228 and E120 had 228 and 120 electrodes around the body surface, respectively. The average inter-electrode distance was 63 mm for the E228 configuration and 118 mm for E120 configuration. The ED120 and E72 had 120 and 72 electrodes, respectively but were concentrated in the body-surface region above the stomach. The average inter-electrode distances of ED120 and E72 were 32 mm and 63 mm, respectively. For the ED120 configuration four electrodes were removed from each ‘ring’ of electrodes around the torso (24 in total) so that this configuration also had 120 electrodes.

Figure 3.

The body surface electrode configurations of (a) E228, (b) E120, (c) ED120 and (d) E72 comprising 228, 120 or 72 electrodes (dark spheres).

2.4 Comparison Methodology

The sensitivity of the reconstructed gastric slow waves was evaluated by comparing with the simulated ‘known’ slow waves derived from the dipole sources. Specifically, we compared the stomach potentials and derived entities such as activation times (ATs) and pacemaker location. The simulated slow wave traces were normalized over time and as such signal amplitudes were not explicitly considered. The ATs were defined as the points with greatest negative gradients and the AT map was constructed for one slow wave cycle.

Three metrics were used to compare the accuracy of the solutions: correlation coefficient (CC), root mean square (RMS) error and localization error. The CC error metric (1) provides a measure of the change in the pattern of potential or activation fields between known and reconstructed solution. This metric varies between 0 and 1, with a value of 1 indicating that the fields have the exact same pattern. This metric is independent of the magnitude of the fields; The RMS error (2) describes the average difference in the magnitudes of the potentials or activation times between the two fields. An RMS error of 0 s means there was on average no difference in the magnitude of the two fields; The pacemaker localization error metric is a distance measure between the site of initial activation in the forward and inverse solution. This measure is localized as it only compares the location of two points. A localization error of 0 mm indicates the same area was the site of initial activation. With the inverse solutions, the site of initial activation was often diffuse with a region having a similar activation time. The point of initial activation was therefore defined to be the centroid of this region.

$$CC=\frac{\sum _{i=1}^N{\tau }_F^i{\tau }_I^i-N{\overline{\tau }}_F{\overline{\tau }}_I}{N{\sigma }_F{\sigma }_I}$$ (1)

$$RMS=\sqrt{\frac{\sum _{i=1}^N{({\tau }_F^i-{\tau }_I^i)}^2}{N}}$$ (2)

where, ${\tau }_F^i\text{ and }{\tau }_I^i$ are for the values being compared from the forward and inverse solutions at node i, N is the total number of comparison sites, τ̄_F and τ̄_I are the means and σ_F and σ_I are the standard deviations of the fields.

3. Results

3.1 Effect of Slow Wave Patterns and Electrode Density

The accuracy of the inverse solutions from different slow wave patterns using four different electrode configurations as shown in figure 3 was initially investigated.

3.1.1 AT maps

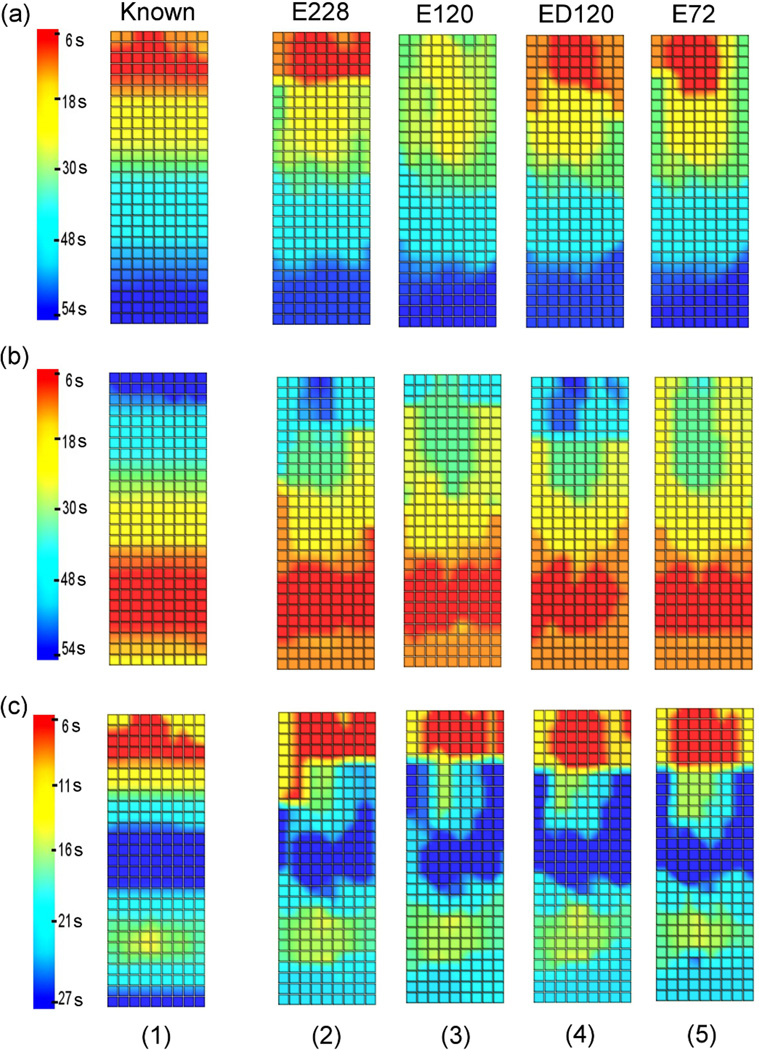
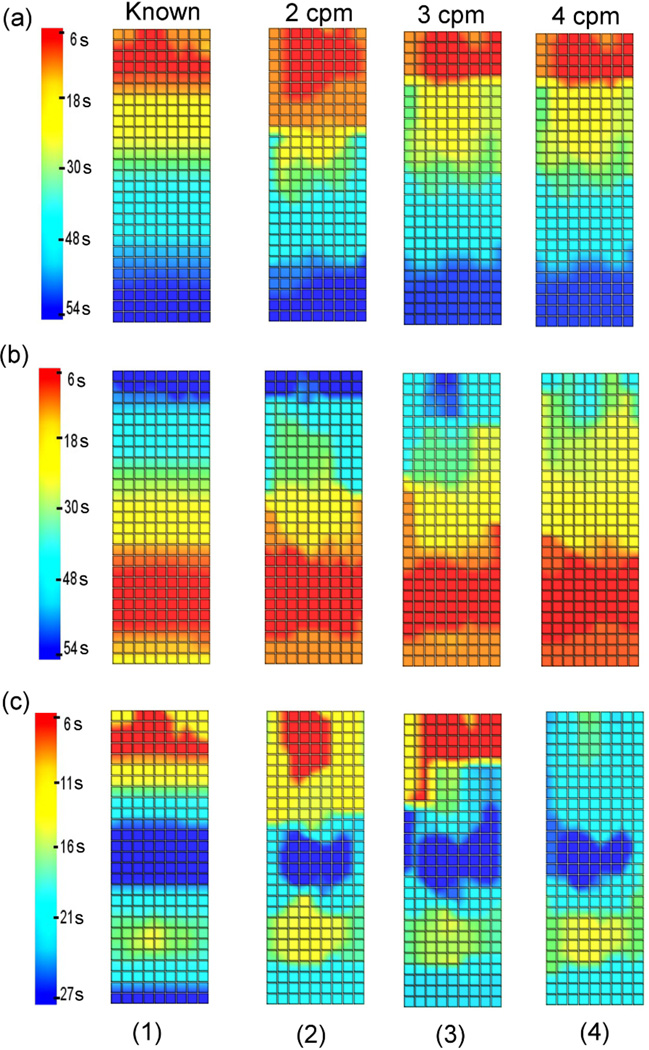
AT maps comparing the known and inversely reconstructed wave profiles on the stomach surface for a single cycle are shown in figure 4. The corners of the grids correspond to the electrodes on the stomach mesh in the area shaded grey in figure 1(b).

Figure 4.

AT maps for (1) the known solution and (2)-(5) inverse solutions using (2) E228, (3) E120, (4) ED120 and (5) E72 for (a) normal, (b) retrograde or (c) uncoupled activity. All slow wave patterns had a frequency of 3 cpm.

All reconstructed models were able to resolve normal, retrograde or uncoupled activity. Moreover, all inverse solutions were able to more accurately reconstruct the distal portion of the wave front than the proximal region. When reconstructing normal activity, the area of initial activation (red coloured, uppermost region) was not accurately reconstructed when the E120 electrode configuration was used (figure 4(a3)) since the activation time was initiated 21 s later than the known solution. When the retrograde activity was reconstructed using the E120 electrode configuration (figure 4(b3)) or the E72 electrode configuration (figure 4(b5)), the end of the slow wave cycle was not accurately resolved (dark blue coloured, uppermost region) since the activation time finished 18 s (E120) and 29 s (E72) earlier than the known solution. For the uncoupled activity, all reconstructed wave profiles were able to accurately determine the location where the two waves collided in the middle of stomach.

3.1.2 Numerical Comparisons

A series of simulations were conducted to investigate the stability and accuracy of the inverse solutions using the four different electrode configurations.

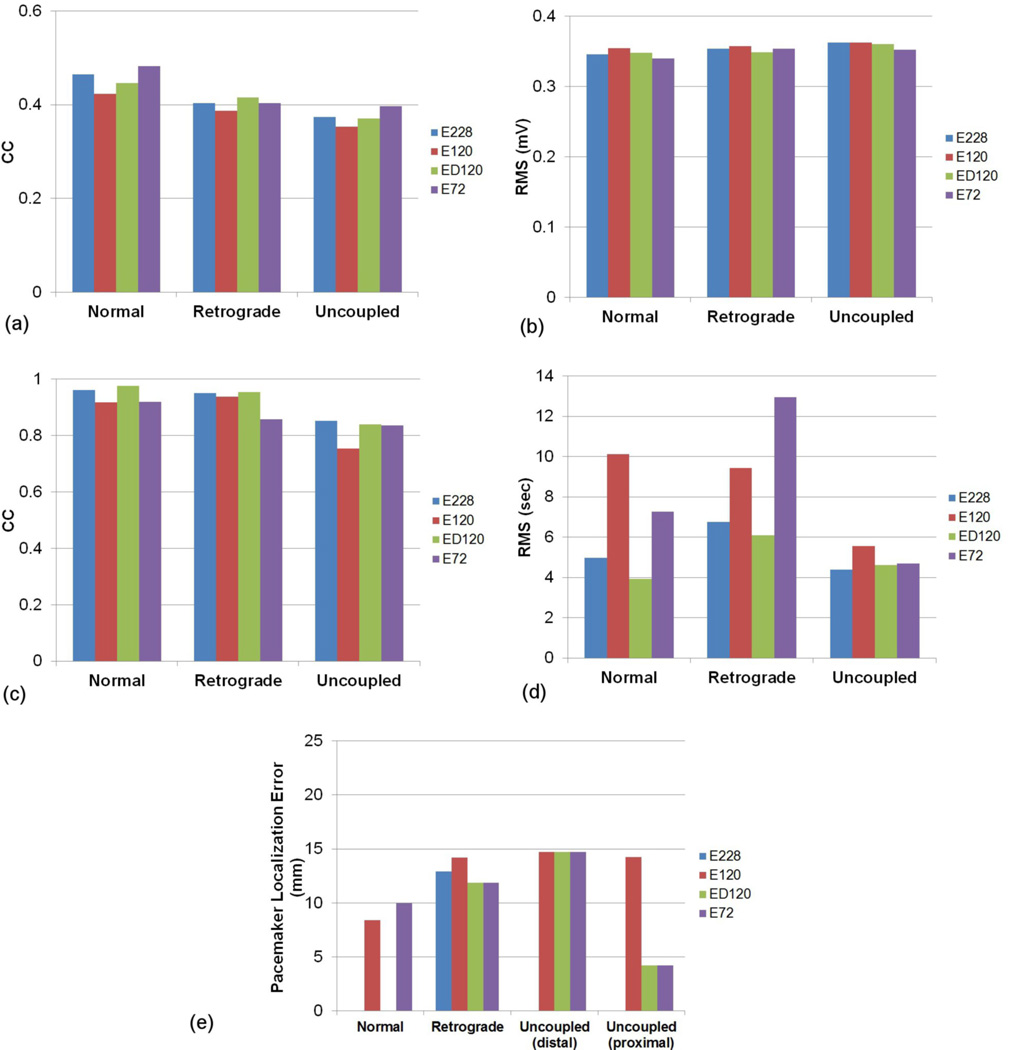
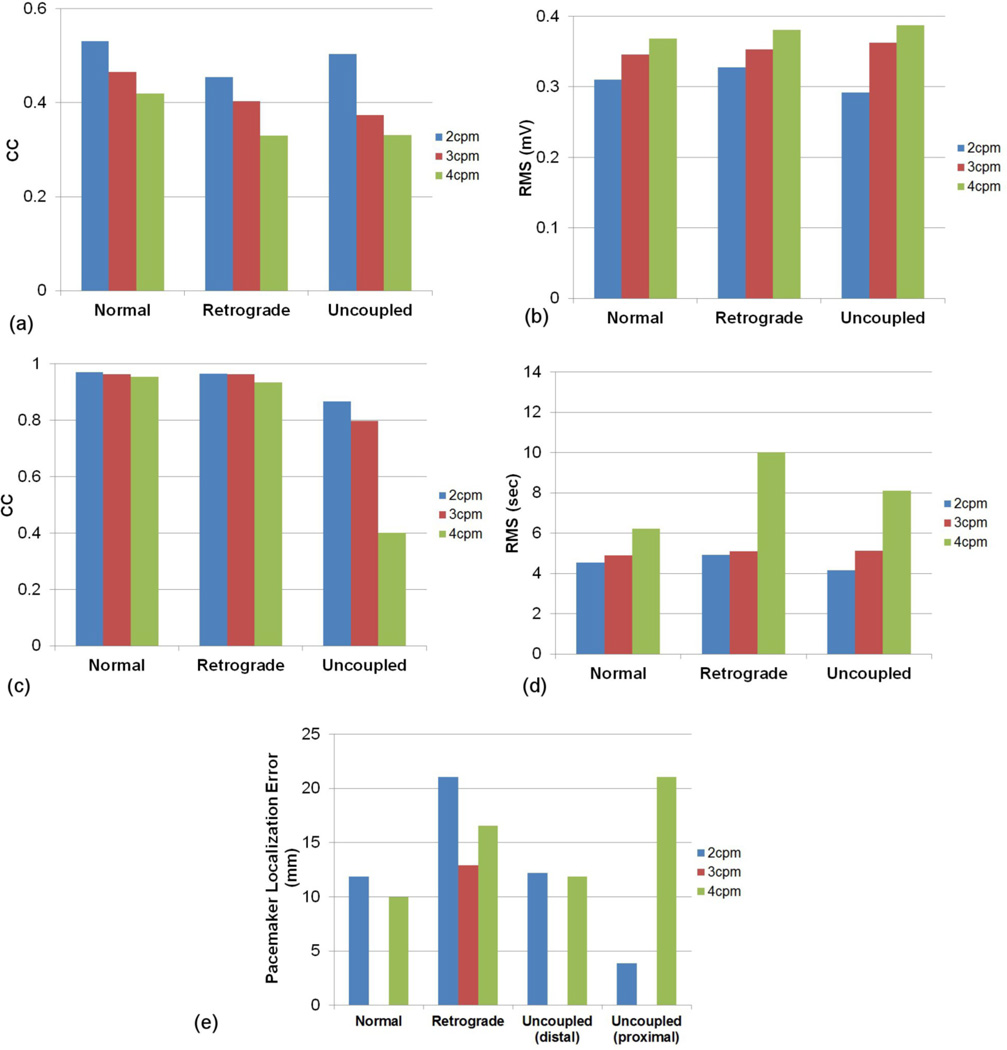
The CC values and RMS errors of potentials between the known and inverse solutions are illustrated in figures 5(a) and (b), respectively. The reconstructed slow waves were similar for all electrode configurations. The E120 reconstructed the worst inverse solutions for all types of slow wave sources. The CC values and RMS errors of ATs between the known and the inverse solutions are illustrated in figures 5 (c) and (d), respectively. The reconstructed ATs by E228 and ED120 were better correlated to the known solution than those by E120 or E72. The inverse solutions reconstructed using the E228 and ED120 configurations were similar, with a difference of less than 1% in CC and 1 s in the RMS error, even though the E228 configuration had almost twice as many electrodes. When E72 and E120 configurations were compared, E72 had the larger RMS error for the retrograde wave and smaller for the normal and uncoupled waves than E120. The localization error of the pacemaker region (figure 5 (e)) was less than 15 mm for all cases. In four cases (E228 configuration with normal and uncoupled activities and ED120 configuration with normal activity), the pacemaker was localized exactly, resulting in no visible entry on the bar graphs in figure 5 (e). Overall the ATs of inverse solutions for the normal and retrograde activity were more correlated to the known solution than those for the uncoupled activity. The average CC values were 94, 92 and 82% for normal, retrograde and uncoupled activity, respectively.

Figure 5.

Comparison of the accuracy of the activity reconstruction using the four different electrode configurations. The potential fields were compared using (a) CC and (b) RMS. The activation fields were also compared using (c) CC and (d) RMS. In addition, the accuracy of the (e) localization of pacemakers (mm) was compared.

3.2 Effect of Slow Wave Frequency

The effect of the frequency of the slow wave activity on the inverse solution accuracy was also investigated. A higher frequency tended to result in more number of waves as the space between successive cycles of activities shortened, and vice versa. We hypothesized that the presence of more simultaneous slow wave sources will result in greater error in the inverse solutions. For all cases, only the E228 electrode configuration was used to reconstruct inverse solutions.

3.2.1 Activation Time Maps

AT maps comparing the known and inversely reconstructed wave profiles on the stomach surface for a single cycle are shown in figure 6. Results showed that all reconstructed wave profiles were able to accurately reconstruct the direction of slow wave propagation. Moreover, the waves in the distal region were reconstructed more accurately than the proximal region of the stomach. Figure 6 also showed that the inverse solutions were able to reconstruct the solutions better with an underlying frequency of 2 or 3 cpm than when the frequency was 4 cpm. For the retrograde activity case with a frequency of 4 cpm, the end of the activity in the uppermost region (dark blue coloured) was not shown in the reconstructed inverse solution (figure 6(b4)) since the activation wave ended 22 s earlier than the known solution. When the uncoupled activity with 4 cpm was reconstructed (figure 6(c4)), the upper corpus region was again not accurately reconstructed (red and yellow coloured) since the activation time was initiated 12 s later than the known solution. However, for the uncoupled activity, all reconstructed wave profiles were able to accurately determine the location where the two waves collided in the middle of stomach.

Figure 6.

AT maps for (1) the known solution and (2)-(4) inverse solutions using slow wave patterns with a frequency of (2) 2 cpm, (3) 3 cpm and (4) 4 cpm for (a) normal, (b) retrograde or (c) uncoupled activity. For all cases, the E228 electrode configuration was used to reconstruct inverse solutions. The range of colour bar is the same for normal and retrograde activity (6–54 s) and reduced by half for the uncoupled activity (6–27 s).

3.2.2 Numerical Comparisons

A series of simulations were conducted to investigate the stability and accuracy of the inverse solutions for the waves with various frequencies such as 2, 3 or 4 cpm.

The CC values and RMS errors of the potential fields between the known and the inverse solutions are illustrated in figures 7(a) and (b), respectively. The results showed that the reconstructed waves of the lower frequency were more correlated to the known solutions and had lower RMS errors. When the AT maps were compared, figures 7(c) and (d) showed that inverse solutions with a frequency of 2 or 3 cpm had similar values of CC (96 % for normal and retrograde, 80% for uncoupled) or RMS errors (5 s), but the inverse solutions with a frequency of 4 cpm had a significantly lower CC (40 %) for the uncoupled activity and larger RMS errors, especially for the retrograde activity (10 s). The CC values of ATs of the uncoupled activity for all frequencies were lower than the CC values for the normal and the retrograde sources. The localization errors of pacemaker region (figure 7 (e)) were less than 22 mm for all cases. In three cases (normal and uncoupled activity with frequency of 3cpm), the pacemaker was localized exactly, resulting in no visible entry on the bar graphs in figure 7 (e). In general, the inverse solutions were reconstructed with more accuracy when the underlying activity had a lower frequency.

Figure 7.

Comparison of the accuracy of the inverse solutions when using the E228 configuration for the activities with a frequency of 2, 3 or 4 cpm frequency. The potential fields were compared using (a) CC and (b) RMS. The activation fields were also compared using (c) CC and (d) RMS. In addition, the accuracy of the (e) localization of pacemakers (mm) was compared.

4. Discussion

EGG provides a non-invasive way to characterize gastric slow wave activity. The most common method for interpreting EGG measurements has been to calculate the dominant frequency (Chen et al 1994, Lin et al 2000, Verhagen et al 1999). However, the uncertainty in relating EGG to slow wave spatial patterns has limited its clinical acceptance. Moreover, O’Grady et al (2012) concluded that abnormalities of slow wave initiation and conduction can occur close to the normal frequency of normal slow wave activity, which makes frequency-based analysis alone insufficient for detecting these dysrhythmia patterns. In this paper we have presented results showing that given appropriately filtered EGG signals with sufficient coverage of cutaneous electrodes, it is theoretically possible to resolve and differentiate different gastric slow wave patterns using the Greensite-Tikhonov inverse method.

The simulation study showed that the most efficient electrode configuration involved locating electrodes uniformly around stomach with an average inter-electrode distance of 32 mm (ED120). This configuration had a similar accuracy to using the E228 configuration that had coverage over a large proportion of the torso but at a lower inter-electrode distance. When using the E120 configuration (which covered the same area as E228 but with inter-electrode distance of 118 mm) the solution accuracy dropped. For all three slow wave patterns, on average the CC dropped from 92 to 87% and the RMS increased from 5.4 to 8.4 s for E228 and E120, respectively). When using 72 electrodes covering the same area as ED120 but with the inter-electrode distance of 63 mm the accuracy was similar to E120. Results showed that the accuracy of inverse solutions increased when additional electrodes were introduced. However, when we used up to 456 electrodes (result not presented) the solution accuracy was not improved upon that produced using the E228 configuration. The findings on inter-electrode distance agreed with previous studies in other fields (Spitzer et al 1989, Srinivasan et al 1998, Li et al 2003). Although the ED120 configuration had the same number of electrodes as the E120 configuration, the denser electrodes located near the stomach resulted in improved inverse solutions. Furthermore, our results indicated that locating the electrodes over the stomach with smaller inter-electrode distance (e.g., ED120 or E72) can have a similar accuracy to that covering larger area of body surface with larger inter-electrode distance (E228 or E120, respectively). This is likely due to the ability for these densely packed electrodes to capture the higher gradients in the potential fields on the skin surface located above the stomach. We conclude that both spatial density and coverage of electrodes play a significant role in the accuracy of inverse solutions, but an efficient electrode configuration can be achieved by locating electrodes in the area only covering stomach with appropriate inter-electrode distances.

The accuracy of the inverse solutions improved when sources with a lower frequency were being reconstructed. These results agreed with those shown by Chang et al (2005) that when the separation between two dipole sources was larger the rate for successful separation of the dipoles was improved.

In four situations the pacemaker was localized exactly (e.g., when using E228 for normal and uncoupled activities and ED120 for normal activity). However, this should not imply that E228 is the best electrode configuration for localizing the point of initial activation. It should be noted that all the reconstructed activation patterns were typically more diffuse and the site of initial activation was not well defined. We observed that the site of initial activation (with activation times less than 1 s) typically covered an area of approximately 20x30 mm. The centroid of this area was used to determine the site of initial activation and often this centroid was located at the same position as the site of initial activation. Rather than focusing on configurations with almost no error, it may be more pertinent to note that the maximum error was 15 mm for all configurations.

Overall, the inverse solutions were reconstructed more accurately for the normal and retrograde slow waves than uncoupled slow waves for all frequencies and electrode configurations. In general, the uncoupled activity was harder to reconstruct and more affected by changes in the electrode configuration and in frequency. The accuracy of the inverse solutions improved when the most distal wave front was located nearer to the antrum as we have previously observed (Kim et al 2012). This may be because the activity at the antrum of the stomach located closer to the recording electrodes may affect EGG recordings (Smout et al 1980, Yoshitomi et al 1996).

There are a number of assumptions and simplifications in this study. We have assumed that biological signals such as cardiac, respiratory and movement artifacts were filtered out and only Gaussian signal noise affected cutaneous potentials. Although it can be challenging to effectively separate EGG from noises, it has been shown to be possible in a number of previous studies (Chang et al 2001, Chen et al 1989, Chen and Lin 1994, Liang et al 2000, Liang 2005, Tkacz and Mika 2010). Our torso model did not include other organs such as the lungs and liver but only stomach. This may influence the accuracy of the inverse solutions when experimental data was used. However, previous studies have shown that the resultant body surface potentials were not significantly altered by the inclusion of such inhomogeneity (Bradley et al 2000, Cheng et al 2003b). Moreover, stomach movement and motility were ignored. However, despite these limitations, the inverse method applied in this study has shown the feasibility of differentiating different gastric activity patterns even if they had the same dominant frequencies.

The critical next step is to validate the inverse method experimentally, ideally by obtaining the stomach and body surface potentials simultaneously. Such experiments are both technically and logistically challenging. One way to obtain such data may measure stomach potentials using endoscopic mucosal sensors (Abell et al 2011, Coleski and Hasler 2004).

In conclusion, both normal and abnormal gastric slow waves were reconstructed from model-based potential measurements on the body surface in the presence of Gaussian noise using the Greensite- Tiknonov inverse method. The use of high-density EGG signals may allow inverse algorithms to provide a quantitative description of the underlying gastric slow wave activity. The simulation results in this study would ideally offer a predictive-step towards the critical experimental validation and clinical application of forward and inverse EGG recordings.