Multi-modal molecular diffuse optical tomography system for small animal imaging

Abstract

A multi-modal optical imaging system for quantitative 3D bioluminescence and functional diffuse imaging is presented, which has no moving parts and uses mirrors to provide multi-view tomographic data for image reconstruction. It is demonstrated that through the use of trans-illuminated spectral near infrared measurements and spectrally constrained tomographic reconstruction, recovered concentrations of absorbing agents can be used as prior knowledge for bioluminescence imaging within the visible spectrum. Additionally, the first use of a recently developed multi-view optical surface capture technique is shown and its application to model-based image reconstruction and free-space light modelling is demonstrated. The benefits of model-based tomographic image recovery as compared to 2D planar imaging are highlighted in a number of scenarios where the internal luminescence source is not visible or is confounding in 2D images. The results presented show that the luminescence tomographic imaging method produces 3D reconstructions of individual light sources within a mouse-sized solid phantom that are accurately localised to within 1.5mm for a range of target locations and depths indicating sensitivity and accurate imaging throughout the phantom volume. Additionally the total reconstructed luminescence source intensity is consistent to within 15% which is a dramatic improvement upon standard bioluminescence imaging. Finally, results from a heterogeneous phantom with an absorbing anomaly are presented demonstrating the use and benefits of a multi-view, spectrally constrained coupled imaging system that provides accurate 3D luminescence images.

1. Introduction

Bioluminescence imaging (BLI) is widely used for in vivo pre-clinical biomedical studies where the aim is to image distributed biological light sources, such as luciferase-tagged cancer cells, located inside a living animal. BLI images are often used to estimate the concentrations and spatial distributions of reporter molecules and thus to infer biological activity from measurements of the surface radiance. However, the quantitative accuracy is limited by the unknown, highly attenuating and scattering properties of biological tissue. This leads to ambiguous data and inaccurate analyses derived directly from captured two-dimensional images, particularly for deep sources[1].

The most frequently reported values of interest in studies involving BLI are the position, size and intensity of light source clusters which are then related to the concentration of reporter and underlying biological activity. In comparison with 2D BLI, 3D bioluminescence tomography (BLT) studies have shown that in some cases, most often when imaging optically homogeneous phantoms, individual luminescent sources can be reconstructed from surface fluence data with high accuracy in terms of spatial displacement, size and/or photon counting metrics thus improving upon BLI in terms of quantitative accuracy[2].

It is recognised that the accuracy of source reconstruction in BLT is strongly dependent on the availability and accuracy of prior knowledge of the internal distribution of optical properties within the imaged animal[3]. However, information regarding the optical properties is not generally known in advance, and there is currently no established non-invasive imaging technology available which can measure them effectively and simultaneously to infer not only attenuation properties, but also any related patho-physiological information which may be correlated with the bioluminescence data.

Here an all-optical, multi-modal imaging system is presented for performing quantitative volumetric and spatially resolved bioluminescence imaging via bioluminescence tomography alongside spectral diffuse optical tomography (DOT) for the reconstruction of molecular chromophore concentrations and spectrally and spatially resolved optical parameters. The purpose of the system is to provide several types of complimentary data, reconstructed in 3D for appropriate interpretation within the context of small animal imaging. The system provides information regarding the optical properties - the spectrally and spatially varying optical absorption and reduced scattering coefficients - of the domain being imaged, providing a detailed understanding of the behaviour of light travelling through the medium, hence allowing compensation for light attenuation in BLT reconstruction and providing accurate analysis in terms of parameters of interest, such as cell count and activity.

The present study demonstrates the use of spectrally-resolved DOT to improve BLT. The system is able to utilise the derived optical properties as prior information when performing BLT reconstruction. The system also demonstrates the application of a generalised optical surface capture approach which allows the subject surface topology to be measured from multiple views to assist with data co-registration as well as utilisation of a model-based approach for parameter reconstruction. The multi-modal system thus represents a novel combination of optical imaging modalities providing a fundamentally new methodology and resultant 3D imaging data set.

1.1. Overview of Imaging Systems

This section provides an overview of current developments of non-contact small animal imaging systems, mostly limited to 3D bioluminescence-based imaging but with some discussion of systems designed for fluorescence molecular tomography^‡ (FMT) which are conceptually closely related[4].

Whilst several commercial systems offer some form of BLT imaging (for a review of commercially available pre-clinical systems and their capabilities see Leblond[5]), there is a great deal of ongoing research looking at improving and validating tomographic methods.

The basic set-up for bioluminescence tomography studies which has been utilised by several investigators[6, 7, 8, 9] involves a highly-sensitive CCD camera in a fixed position pointing at a phantom or animal placed on a rotating platform. Multiple, typically four, distinct angularly-resolved views of the surface can then be captured in images acquired one-at-a-time following appropriate rotations of the subject providing data from all around the surface. Essentially the same set-up is used for fluorescence tomography with the addition of an excitation source[10, 11, 12, 13, 14, 15]. Whilst providing near-perfect surface coverage, such systems are limited in that multiple acquisitions are required in order to obtain a full data set. This limitation is significant because long exposure times are typically needed (on the order of minutes) in order to achieve adequate SNR when imaging deep bioluminescent sources and as such sequential imaging can result in infeasible experimental time requirements.

Furthermore, it has been shown that using multi-spectral data significantly improves the accuracy of BLT image reconstruction[16, 17] by increasing measurement information content and reducing the ill-posedness of the model inversion. Whilst the basic BLT imaging set-up can be extended to include filters and therefore collect multi-spectral as well as multi-view data sets this once again extends experimental time.

Kuo et al.[18] presented a single-view multi-spectral imaging system utilising a filter-wheel. This approach was extended by Chaudhari et al.[19] who devised a multi-spectral, multi-view system by incorporating mirrors positioned to provide four perpendicular views around the imaging subject, though this system required two differently focused images per wavelength owing to large optical path-length differences between views. Li et al.[20] later developed a multi-view system based on a conical mirror design with sequential spectral imaging. Wang et al.[21] developed a system capable of simultaneously acquiring multi-view and multi-spectral data within a single image by the use of a “rainbow” mouse-holder and four mirrors positioned around the subject. The mouse holder comprised three different filtering materials in a recurring pattern such that evenly spaced strips of the animal surface were visible at each wavelength. This approach worked well for three distinct spectral bands but if more wavelengths were required then too little of the surface might be visible at each spectral band. In addition the particular placement of the mirrors and the animal meant that large parts of the CCD remained unused[21]. More recently Wang et al.[22] devised a new method for collecting multi-spectral data in single images based on a digital spectral separation device.

BLT reconstruction methods all rely to some extent on knowing the shape of the imaged subject. Whilst simple phantoms with known geometry are often used to validate prototype BLT systems and methods, in general the subject shape is complex and unknown. As such it is necessary to measure the geometry within the scope of an imaging experiment. One solution to this problem is to image the subject using some separate structural imaging modality such as magnetic resonance imaging (MRI) or X-ray computed tomography (CT)[23, 9, 24]. Though this does increase experimental cost and also introduces a requirement for image registration, dual-modality visualisations can help put results into context and provide complementary data in imaging studies in addition to measuring the model geometry. Structural imaging modalities provide the opportunity to segment optically distinct regions to assign appropriate published optical property values. This has been shown to improve image reconstruction[23, 9, 24], but cannot account for optical property variations between individual imaged subjects and published values. Registration is required between modalities but this can be made easier by using a mouse-holder to keep the animal in the same pose[25, 23].

Liu et al.[26] developed a dual-modality microCT and BLT system in which microCT data was used to acquire geometry and additionally to assign approximate optical properties within a fixed system, Others, for example Schulz[27] and Yang[28], applied the same principle to FMT and microCT systems.

Kepshire et al.[29, 30] developed a highly sensitive time-resolved FMT microCT system in which photomultiplier tube (PMT) coupled fibers were used as photon counting detectors. Such multi-modal systems are advantageous over using separate imaging systems because the subject can stay in the same position between acquisitions making registration simpler and experimental time as well as time-based variations in e.g. anatomy or functional physiology can be minimised.

A significantly simpler and lower cost alternative is to measure the geometry via optical surface capture techniques (e.g. structured light techniques[31]). Deliolanis et al.[11] developed an FMT system that utilised multiple angularly resolved optical projections to reconstruct the geometry. This requires some added experimental time and complexity due to the need to rotate the sample and acquire many images. Li[20] utilised a laser line scanning system to capture geometric data. A method that is simpler and cheaper, based on sinusoidal structured light projection, was used by Kuo et al.[18] to capture the directly visible portion of the animal surface and a similar method has recently been developed by Basevi et al.[32] that can additionally capture surfaces visible in mirrors. These approaches are advantageous because neither optical components nor the animal have to move between images and in the latter case multiple surface-views are obtained simultaneously, making surface capture fast and simple[32].

Beyond secondary systems that provide structural priors for BLT, other multi-modality systems have been developed that provide complimentary imaging data for multi-modal studies thus providing enhanced scientific information.

Cao et al.[33] have developed a multi-modal single-photon emission computed tomography (SPECT), CT and optical system for BLT and FMT that utilises the geometric information from CT and uses SPECT to obtain prior information which informs FMT or BLT reconstruction. It was shown that reconstruction with SPECT priors was better than without. Alexandrakis et al.[34] proposed a system for combined optical and positron emission tomography (OPET) imaging which is designed so that the cylindrical (physically tomographic) detector array can detect both visible light and emitted gamma rays[35, 36].

It has been shown explicitly that BLT reconstruction performance is strongly improved by the use of accurate heterogeneous models of optical property distributions as opposed to assumptions of homogeneous or inaccurate properties[3, 26, 37]. Razansky et al.[38] showed that by utilising absorption measurement by integrated photo-acoustic tomography, FMT image reconstruction could be improved. It has been suggested that diffuse optical tomography (DOT) could be used to obtain optical property measurements and shown that this is effective in simulation[39, 40, 37].

Zhang et al.[40] showed that DOT using a single laser diode integrated within a basic BLT system improved reconstruction whilst Tan et al.[41] performed DOT alongside FMT using a single laser for both within a basic set-up. Pekar[42] developed a CT-DOT-BLT system utilising a laser diode source. Within this system, hard and soft prior approaches to DOT are carried out using CT-segmented regions building upon methods where this data is used to assign published properties to regions. A similar data flow concept was utilised by Yan et al.[43] who developed a gantry-based fully rotating multi-modality system comprising a CT system, an optical detection system and DOT sources in the form of two lasers. Within this system CT priors were again used and DOT reconstruction was performed at two wavelengths following which absorber concentration was deduced from maps of absorption based on the knowledge that only two absorbers were present. This method is an indirect approach to spectrally constrained DOT. However, this system carries the same disadvantage of the basic BLT system set-up[7] in that multi-view imaging is sequential and therefore time-consuming. In contrast to these methods using point-like excitation sources, Chen et al.[44] and Venugopal et al.[45] developed a small animal time-resolved DOT and FMT system based on a laser-coupled digital micromirror device (DMD) based wide-field illumination scheme allowing spatial patterns to be used and demonstrated that structured illumination and time-resolved detection improved upon standard methods. Multi-modality approaches have also been used to improve small animal DOT, for example Gulsen et al.[46] developed a DOT and MRI system and recent studies have shown that this fusion approach provides enhanced quantitative accuracy[47] and resolution[48].

In most cases where existing systems perform DOT to provide BLT with priors, they either reconstruct optical properties at particular wavelengths in which case this must be done for each wavelength for which BLT data is used, or do this and then fit the results to chromophore concentrations and scattering parameters after reconstruction[43]. The capacity for this second approach is limited in many existing systems due to the use of monochromatic sources.

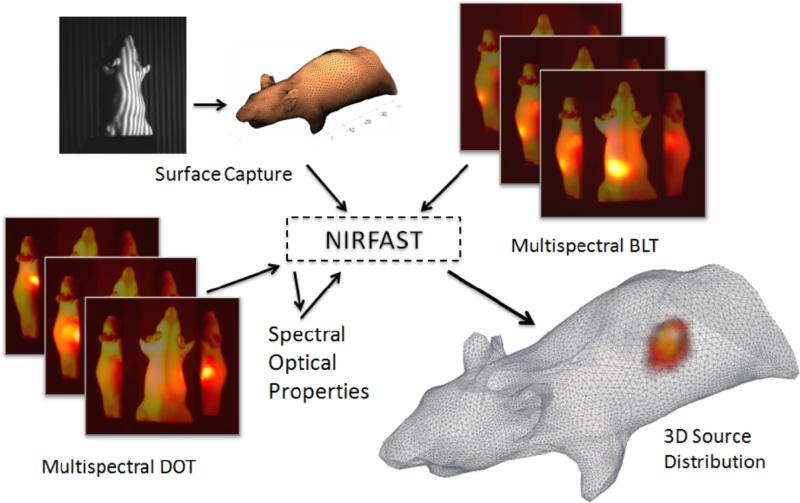
In the presented system, a novel combined multi-spectral DOT-BLT system is presented which additionally uses multi-view image acquisition and multi-view optical surface capture along with a wide-field illumination scheme. Building on current systems, an implementation of spectrally constrained DOT reconstruction within a non-contact small animal imaging system is demonstrated via a phantom study. A novel work-flow is proposed (figure 1) whereby optical surface capture is followed by spectral DOT and finally BLT providing two imaging end-points; a 3D functional image of chromophore concentration and a 3D luminescence image.

Figure 1.

Visual representation of the system concept. A mouse is surface captured to obtain its geometry and is then imaged in spectral luminescence and in spectral near-infrared trans-illumination modes. Using NIRFAST[49], DOT is used to reconstruct chromophore, scattering and subsequently functional parameters which are additionally used to inform reconstructions of bioluminescent source distributions.

2. System Design

The presented system follows the design and overall layout of many established in vivo optical imagers (e.g. that of Kuo et al.[18]) with a vertical light path and a horizontal stage to support the sample. The system is shown in figure 2. In a novel addition compared to most standard systems, two freely-positioned mirrors have been incorporated to expand the field of view of the camera and facilitate the imaging of three perpendicular views of the domain within a single acquisition. Mounted beneath the sample stage is a Digital Light Processing (DLP) unit coupled to a near-infrared (NIR) light source for injection of NIR light into the animal. The sample stage is mounted on an automated lab-jack which is used to change the focal plane without handling the lens and for geometric system calibration. In addition, the system includes two mini projectors, fixed above the sample, that are used for optical surface capture. The whole imaging system (except for the NIR source) is housed within a light tight box constructed from aluminum posts that form a cage-system (RS Components, Corby, UK) and aluminum panels which are painted matte black to minimise light reflection.

Figure 2.

(a) Labelled schematic and (b) photograph of the developed imaging system.

2.1. Optical Detection System

The optical detection system is composed of a Hamamatsu ImagEM-1K camera (Hamamatsu Photonics, Hamamatsu City, Japan), a 25mm fixed focal length VIS-NIR lens (Techspec, Edmund Optics, York, UK) and an FW102C automated filter wheel (Thorlabs, Ely, UK).

The ImagEM-1K is a back-thinned, electron-multiplying (EM-) charge-coupled device (CCD) camera. It is cooled to –55°C at which specifications indicate a dark current of 0.01e^–/pixel/s. The electron multiplication amplifies signals (nominally up to 1200×) before they are read out thus effectively reducing the read noise in low-light situations. The camera has a maximum read noise of 19 e^–/pixel and a minimum effective level of 1 e^–/pixel with sufficiently high EM gain. However, whilst in some imaging scenarios the EM gain provides an SNR increase, it also introduces a multiplication-related noise and is not as effective as increasing the exposure time when imaging conditions are stable and for this reason the EM-CCD mode in the present system is not used. In normal mode (without any EM gain) the CCD has a read noise of 10 e^–/pixel.

Each of the 1024 × 1024 pixels of the CCD are of size 13μm × 13μm and can be binned in hardware 1×, 2× or 4× creating effective imaging pixel areas of up to 2704μm² within a total detection area of approximately 13.3mm×13.3mm. The camera quantum efficiency is > 40% across the spectral range of interest (500nm – 900nm) and > 85% in the luminescence region (500nm – 700nm) where low-light conditions are expected.

The VIS-NIR lens has a variable aperture ranging from f/1.4 to f/17, which is always fixed within the system to f/1.4 (the largest possible) so as to collect the maximum signal possible under low light conditions and was chosen for its high transmittance in the visible and near-infrared (NIR) spectral regions. Its minimum working distance is 100mm and the field-of-view is 19.8°, which allows the full region of interest on the sample stage to fit into an image at a working distance of approximately 300mm.

The FW102c is a 6-position filter wheel that accommodates ø1″ circular filters. In the present system, 10nm full-width-half-maximum (FWHM) interference-based bandpass filters (Thorlabs, Cambridgeshire, UK) with central wavelengths in the range 500nm – 850nm are used. The FW102c allows the whole wheel to be quickly removed and replaced allowing for fast swapping of whole filter-sets, if required.

The back thread of the lens is screwed directly onto the camera whilst the front thread is coupled to a cage system that links the lens to the filter wheel with a short free-space coupling. This allows the focus of the lens to be manually adjusted if and when the lens system and its housing are physically extended. In the current set-up the front of the lens housing can move freely towards or away from the filter wheel without changing the position of the filter wheel.

2.2. Imaging platform

The sample stage consists of a 400mm × 300mm × 10mm black acetal sheet with a 30mm×50mm hole machined in the middle to allow the sample to be illuminated by the DLP projector underneath. Two 75mm right angle mirrors with enhanced aluminium coating (N-BK7; Edmund Optics, York, UK) are freely placed on the sample stage; there is no requirement to fix the mirrors to the stage since their locations are measured on-the-fly during imaging sessions (further details below). The mirror reflectance is high; R_mean > 95% in the luminescence region (500nm – 700nm) where low-light conditions are expected, and the size of the mirror allows the capture of the full length of a typical mouse body.

The imaging platform is mounted onto a motorised lab jack (L490MZ; Thorlabs, Ely, UK) by four 160mm vertical posts. The lab jack has a 51mm range of travel with a repeatability of 5μm.

2.3. NIR light source

The NIR light source consists of a DLP pocket projector (PK-102; Optoma, London, UK) mounted onto the labjack and coupled via a ø1000μm, 2m long optical fiber (QP1000-2-VIS-BX; Ocean Optics, Oxford, UK) to a tungsten-halogen lamp (HL-2000-FHSA, Ocean Optics, Oxford, UK). The use of the modified DLP projector as a source of wide-field illumination for small animal imaging follows a published design[44, 45] and allows the projection of point sources for excitation as well as spatially modulated light sources onto the underside of the animal within the region of illumination.

The DLP projector is modified in that its system of LEDs and dichroic mirrors that normally produce its light output were removed, and its housing was drilled and fitted with a fiber-adapter to allow the reception of the optical fiber. The fiber output consequently directly replaces the original sources in the pre-existing light path in which it is incident first upon a sgu)diffuser then a micro-mirror array, all within the unit. Using this setup, any desired pattern of NIR excitation can be selected using a graphical input which is then projected under the sample by the unit. The transmittance through the projector (i.e. the fiber-projector coupling efficiency) was measured at 650nm and found to be ≈ 15%.

2.4. Surface capture system

The surface capture system utilises the optical detection system in conjunction with two pocket projectors (MPro120; 3M, Bracknell, UK) to generate spatial patterns. The projectors are mounted onto the system cage and powered independently with their batteries removed, they are arranged so as to point roughly at the centre of the sample stage and angled so as to illuminate opposite sides of an imaged subject to allow maximum surface acquisition in conjunction with the use of the mirrors, as shown in figure 2.

2.5. Automated Acquisition

The camera, filter wheel, projectors and lab-jack are connected to a computer (Viglen Genie with Intel DQ67SW Motherboard, Intel Core i7 Processor i7-2600 (3.40GHz), Quad Core with 8MB Cache, 16GB of RAM and 2TB hard-disk drive) running 64-bit Windows 7 Enterprise (Microsoft). The computer has an NVIDIA GeForce GT520 graphics card installed so that in total (including the on-board graphics) it has 4 graphics outputs which are used to connect a monitor and the three system projectors. The filter wheel and lab-jack are connected via USB whilst the ImagEM camera is connected through a dedicated video capture card (PHOENIX-D24CL-PE1; Active Silicon Ltd, Iver, UK).

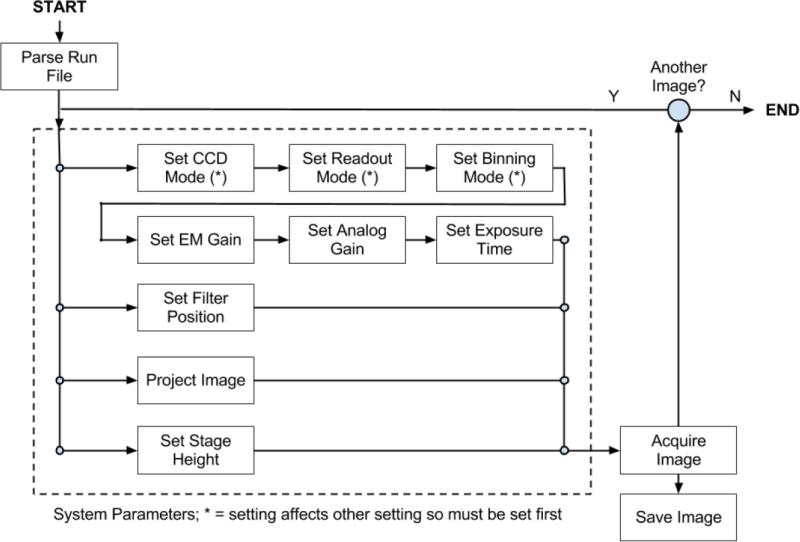
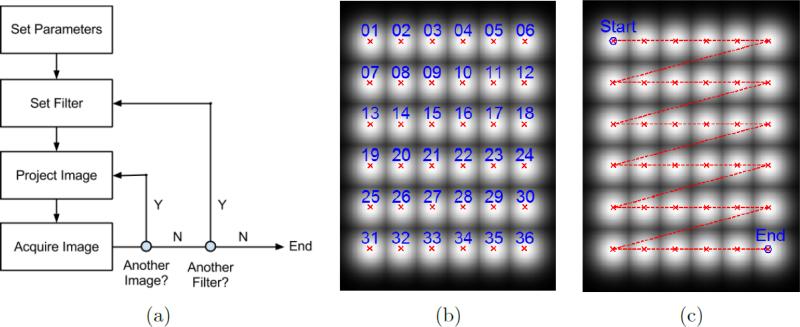
The system is controlled by a custom-made Labview program (National Instruments, Newbury, UK), which manages all aspects of data acquisition and on-line processing and is designed to be flexible and easy to use when imaging. Imaging runs are specified using run-files (simple .csv files adhering to a common pre-defined format) which specify system parameters for arbitrarily many images that will be acquired in the order specified. The adjustable fields include: CCD mode, readout mode, analogue gain, sensitivity gain, binning level, exposure time and projector image (NIR excitation pattern). The sequence of an example imaging run is shown in figure 3.

Figure 3.

General imaging run protocol. Note that whilst “Project Image” is only shown once, it represents a total of three parallel operations in which a projection is done with any or each of the three projectors in the system.

It is necessary that certain operations are performed in sequence in the order shown as several camera parameters (indicated by an asterisk (‘*’) in figure 3) affect the range of available values and the default value for other parameters. For example setting the CCD mode changes the applicability of the sensitivity gain feature, the range of possible exposure times, the range of possible readout modes and the current exposure time and readout mode. Imaging sessions consist of a simple loop in which parameters are set and images are acquired and subsequently saved. Images are saved in sequence and cleared from virtual memory so that long imaging sessions can be performed without exceeding system memory. The image management does introduce some temporal overhead and as such there is approximately 500 ms delay between successive image acquisitions (which is a small fraction of the time taken in most imaging runs, which is typically several tens of seconds per image).

Image data is saved as a matlab variable (.mat format) along with all corresponding imaging parameters which is useful for de-bugging, clarity and data processing and analysis. The .mat format was also found to be the most efficient lossless compression scheme as compared to .PNG and .TIFF formats for typical images acquired with the system.

3. Experimental materials and imaging methods

3.1. Physical phantom

A custom-made cylindrical phantom (Biomimic, INO, Quebec, Canada) is used that is approximately the same size as a mouse (ø25mm and 50mm in length), the body of which is made of a solid plastic with spatially homogeneous but spectrally varying absorption and scattering properties that have been characterised within the range of 500 to 850nm in terms of the absorption coefficient, μ_a ∈ [0.007, 0.012]mm^–1, and the reduced scattering coefficient, ${\mu }_s^{\prime }\in [1.63,1.79]{\mathrm{mm}}^{-1}$. The same phantom is used for both luminescence tomography and diffuse optical tomography examples presented here.

Within the phantom body there are two tunnels (ø6mm) at depths of 5mm and 15mm in which rods (cylindrical inclusions) can be inserted to either represent optical anomalies, such as organs or tumours, or to match the background effectively creating a solid homogeneous cylinder. In this study, bioluminescence is modelled by placing a light source half way along a tunnel enclosed between two rods of background matching material.

3.2. Surface capture

The geometry of the animal being imaged is important for two main reasons. Firstly, it must be known in order to build an accurate model with which to compute light propagation during image reconstruction. Secondly, it allows the visualisation of results within the correct physical context, i.e. 3D images can be rendered containing the surface as a reference thus allowing for clear and accurate biological interpretation.

To optically capture a model of 3D surface topology[32], a series of images are projected using each of the two upper projectors in the system (figure 2) in turn and images are collected of the sample under a series of illumination patterns. The projected patterns are sinusoidal fringes at 14 different spatial frequencies starting at 0.78125 fringes/image and increasing by a factor of √2 to a maximum of 70.7107 fringes/image which corresponds to a range of approximately 0.003 to 0.3 fringes/mm projected onto the stage. For each spatial frequency 6 evenly spaced phase shifts are used throughout the range 0 to 2π. In addition, “bright” and “dark” projections are used meaning a total of 86 (6 phases × 14 frequencies + 2 extras) images are collected for each projector. Examples of surface capture images are shown in figure 4.

Figure 4.

Surface capture raw data for a single data set: (a) maximum of bright images (full-field white projection from each projector); (b) highest frequency pattern projected with projector 1 and (c) with projector 2.

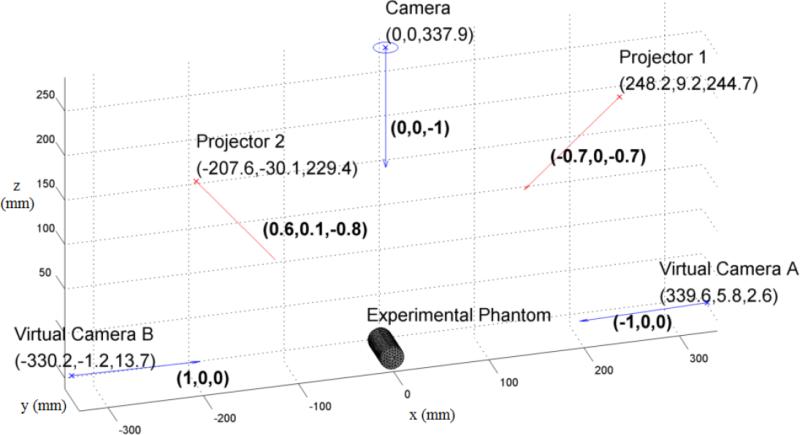
Applying the surface capture algorithm[32] to the acquired image set, the unwrapped phase is recovered which is converted, given knowledge of the system geometry, into a height map for points under observation. The system geometry in this case is deduced using a custom-made geometric calibration routine detailed in section 4.3. Figure 5 shows an example of component positions and view directions showing the scale of the system and provides an overview of the general set-up.

Figure 5.

The geometry of the imaging system illustrated in terms of the positions and view-directions of the two projectors used for surface capture and the camera used for detection along with accompanying virtual cameras which are the reflection of the camera in each of the mirrors. Note that z = 0 is the height of the stage when the labjack is fully retracted.

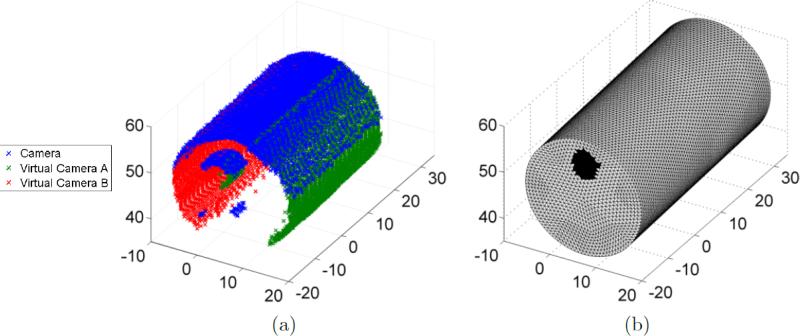
The surface capture algorithm has been described in detail and evaluated elsewhere[32], though an example of the result when applied to the cylinder phantom is shown in figure 6. The method places no restrictions on the position or orientation of components within the system which is advantageous for two reasons. Firstly, because it allows free placement of the projectors allowing maximum sample coverage with the two fields of view. Secondly, because it allows surface capture using mirror views, which is achieved by utilising two virtual cameras (effective camera locations given reflection in each mirror) with each projector as well as the direct view. This allows the capture of 3 partial point clouds in each acquisition (see figure 6), providing within the present system a greater surface coverage than has been achieved using similar previous methods. The dense point cloud is recovered with absolute 3D co-ordinates and can be used to create a surface or volume mesh for modelling or can be used to register pre-made meshes to the appropriate position in the system co-ordinate space.

Figure 6.

(a) Example surface capture point cloud in which points acquired at different views are indicated by different colours; and (b) FEM mesh following registration to the surface capture point cloud; black elements indicate the location of the rod that is left protruding slightly from the main cylinder and used as a reference for finding the correct rotation. The point cloud appears truncated compared to the mesh because the back portion of the cylinder was mounted into the rotation mount thus obscuring it from view.

In the present study, the system is tested using a cylindrically shaped phantom and as such obtaining a full surface is more difficult than it would typically be when imaging a mouse as there is significant curvature underneath that cannot be seen by the projectors. This effect can be seen in figure 4 in which the projection has not covered the lower part of the cylinder in the mirror views. Thus rather than using these points to create a mesh we register a pre-made cylindrical mesh to the point clouds obtained by the surface capture, as detailed in the next section (section 3.3).

For surface capture imaging, the camera parameters are: EMCCD mode; read mode 3; exposure time 0.12 seconds; no binning. These modes provide the fastest imaging possible on the camera without binning which is important due to the relatively large number of images that need to be taken. With these modes, surface capture takes approximately 40 seconds per projector including overhead (from saving images and driving devices). The lack of binning means that the point-cloud is more spatially dense and therefore accurate for acquiring the curvature of the imaged sample.

3.3. Finite-element model creation and registration

The 3D volume is modelled using a tetrahedral mesh which is suitable for use with the finite element method to simulate diffuse light propagation for image reconstruction. Meshes are created using NIRFAST[49, 50].

In this work, a cylindrical mesh is first made of the appropriate dimensions so as to match the physical cylinder phantom (50mm long with ø25mm), then registered to each set of surface capture points acquired (i.e. for each distinct experiment).

The registration is achieved by first fitting for the position of the cylinder mesh by minimising the total distance of all surface capture points to the nearest point on the model surface and secondly finding the best rotation of the mesh such that surface capture points visible on an inclusion rod (one of which is left protruding from the cylinder body for this purpose; visible in figure 4 and illustrated in figure 6) are nearest to the known possible inclusion rod locations.

Whilst this particular registration method is applicable only to the cylindrical geometry, it has previously been shown that surface capture point clouds can be used to register mouse-shaped meshes when imaging a mouse-shaped phantom of known geometry[51] and with this example it was shown that the combined operations of surface capture point production and registration of the known geometry to the point set result in discrepancies between the registered geometry and the points of around 100 to 200μm[32]. In the general case, it is anticipated that it will be possible in animal studies to build a mesh directly from the surface capture points and surface mesh generation from surface capture points has been previously demonstrated on a real animal[32].

3.4. Lens Model

Measurements made on the CCD are non-trivially related to the amount of light leaving the surface of the imaged object because of the presence of a complex lensing system acting as a non-linear function dependant upon several factors including the focal length, the distance of the focal plane from the surface and the orientation of the part of the surface under observation. Ripoll et al.[52] formulated a rigorous treatment of this problem and described this mapping under several conditions such as when the object is perfectly in focus and when the exitance is Lambertian. This model has been extended by Chen et al.[53] to describe explicitly any lens system under a thin lens model making use of the Lambertian surface assumption. Equation 1, (adapted from Chen et al.[53]), describes the resulting relationship obtained between surface and CCD captured image.

$$P\left({\mathbf{r}}_d\right)=\frac{1}{\pi }{\int }_S{J}_n\left(\mathbf{r}\right)\xi (\mathbf{r},{\mathbf{r}}_d)\frac{\text{cos}{\theta }_s\text{cos}{\theta }_d}{{\mid {\mathbf{r}}_{vd}-\mathbf{r}\mid }^2}d{A}_{vd}dS$$ (1)

Here, P(r_d) is the total power incident upon the detection element centred at point r_d on the CCD with corresponding virtual detection point r_vd situated in the focal plane with area dA_vd; r is a point on the imaged surface S; θ_s is the angle between the surface normal at point r and the outgoing ray that passes through r and r_vd; θ_d is the angle between the normal to the detection element (the view direction of the system) and the same ray; ξ is a visibility term which is either 0 or 1 and serves to either discount or include parts of the surface that are physically visible due to the lens system.

In this work, a variant of the method of Chen et al.[54] is used to map CCD measurements onto the surface. This involves solving the inverse light mapping problem using a regularised non-negative least squares optimisation method having first obtained the relationship between surface flux and detector irradiance by applying Equation 1 to discretised models of the imaged surface and detection system for the imaging geometry shown in figure 5.

3.5. Bioluminescence Imaging (BLI)

For luminescence imaging, filters in the range 500 to 650nm were loaded into the filter wheel and the phantom was placed on the imaging stage in the centre of the camera field-of-view. The mirrors were then positioned around the sample and the surface capture method above was used to obtain a point cloud of the surface. An auto-expose routine was then run to acquire exposure times that maximised the signal received up to a target value of 60000 counts (out of a possible 65535) with a maximum exposure time of 10 minutes which was set as a cut-off point to avoid infeasibly long experimental time. A single image was then acquired for each loaded filter creating a multi-spectral data set of phantom images. The total acquisition time for BLI was dependent on the level of signal available, and subsequently upon source depth and external perspective, but by way of example the total imaging time for the case presented in figure 12(a) was 8.15 minutes.

Figure 12.

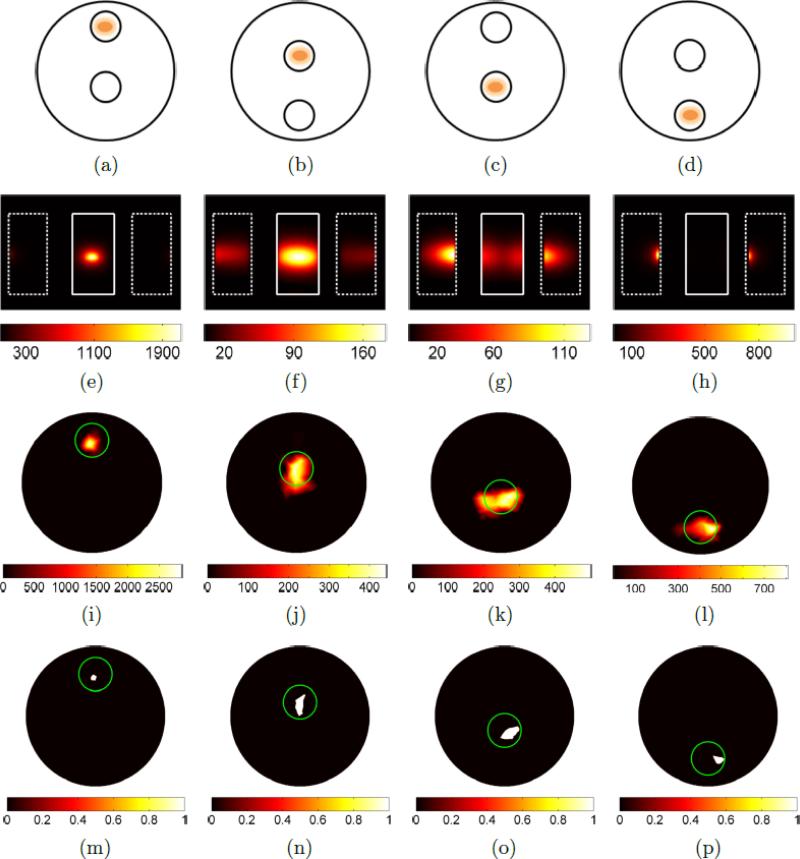
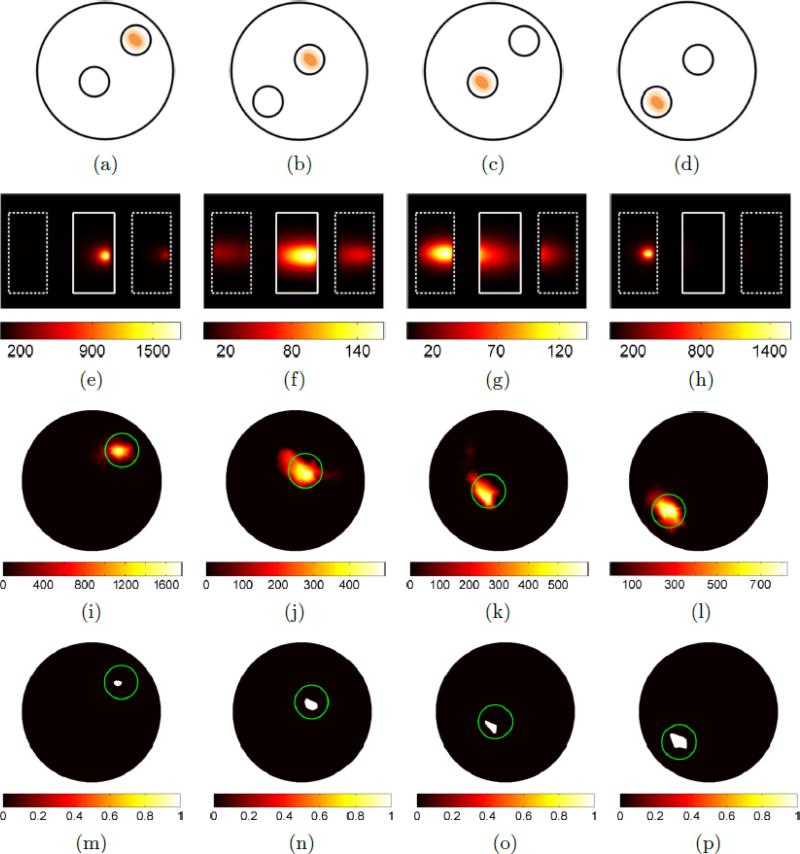
Summary of on-axis, homogeneous BLT experiment results showing: (a-d) schematics of source experimental locations in 2D projection; (e-h) BLI images (CCD measurement e^–/s) of the phantom at λ = 600nm with approximate phantom outlines; (i-l) slices through corresponding BLT reconstructions at the axial offset corresponding to the centre-of-mass of the reconstruction; and (m-p) the slice images thresholded at 75% of the maximum value.

To mimic in vivo bioluminescence experiments, a small (0.9×2.5mm) self-sustained tritium-based light source (Trigalight Orange III; MB-Microtec, Niederwangen, Switzerland) was used as an artificial bioluminescence source. The emission spectrum of the tritium-based light source is a Gaussian-like curve with a central peak at 606nm and a full-width-half-maximum of approximately 100nm, meaning that it is similar to the spectral output of a bioluminescent reporter[55, 56].

The light source was placed at one of two depths (5 or 15mm) inside the cylinder phantom which was then rotated by either 0, 45, 90 or 135 degrees in order that the effective target source location was one of 8 (2 depths × 4 rotations) possible positions appearing as either 4 different depths along the central axis of the cylinder (figure 9) or as the same positions following 45 degree rotations (figure 10). These sets of 4 experiments will hereafter be referred to as the on-axis and off-axis data sets respectively.

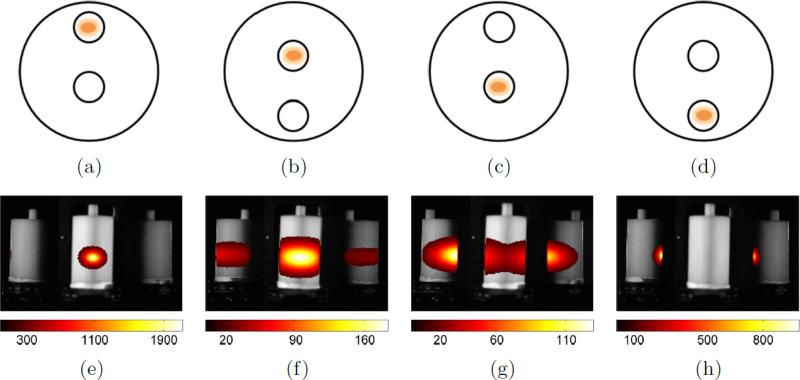
Figure 9.

Bioluminescence phantom imaging results for the on-axis data set: (a-d) phantom schematics; and (e-h) luminescence images at λ = 600nm shown overlaid on maximum-signal images from surface capture data sets as a spatial reference. Luminescence images are set as completely transparent at all points where the value is less than 10% of the maximum value in the image.

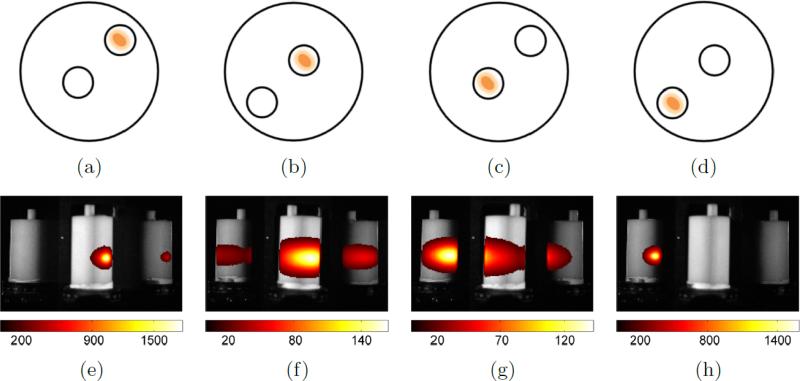
Figure 10.

Bioluminescence imaging results for the off-axis data set at λ = 600nm.

When put into the phantom, the luminescent source was held in a central position in one of the tunnels, supported between two half-length rods with background-matching properties. The other tunnel was filled with background-matching rods to make the cylinder effectively homogeneous.

To provide accuracy in fixing the rotation of the phantom and consistency between data sets, it was fixed in a rotation mount that was mounted directly to the sample stage. The rotation mount shows the turned angle in units of single degrees. Between experiments, the phantom was removed from the mount so as to change the source position when required but was marked to return it to the same position when remounting.

3.6. Bioluminescence Tomography (BLT)

For BLT, imaging was first performed as outlined above. CCD measurements were converted from digitised image counts into maps of irradiance (on the CCD) in terms of electrons per second according to the method in section 4.2. CCD irradiance was then used in conjunction with a model of the free-space propagation of light (section 3.4) in the imaging system to calculate maps of surface irradiance at ~1000 evenly spaced locations on the phantom surface. For this step, each view was dealt with independently and subsequently scaled by a term that compensates for the mirror reflectance before all multi-view data was scaled by the known system-response-source-emission which was measured in a calibration experiment (section 4.1).

The phantom volume and surface were represented using a tetrahedral mesh which was registered to the correct position in the imaging system co-ordinate space (section 3.3). 3D image reconstruction was then performed using a compressed-sensing based conjugate gradient (CSCG) algorithm[57]. The algorithm was applied in conjunction with the finite element method (FEM) of modelling the propagation of diffuse light. Working within this framework, the forward model of light transport from luminescent sources to boundary measurements was provided by NIRFAST[16, 17, 49]. The model is based on the diffusion approximation to the radiative transport equation:

$$-\nabla \cdot \kappa \left(r\right)\nabla \Phi \left(r\right)+{\mu }_a\left(r\right)\Phi \left(r\right)=B\left(r\right)$$ (2)

Where B(r) is the bioluminescent source at position r; Φ is photonic fluence rate; κ is the diffusion coefficient defined as $1∕\left(3({\mu }_a+{\mu }_s^{\prime })\right)$; μ_a is the absorption coefficient; and ${\mu }_s^{\prime }$ is the reduced scattering coefficient. By utilising the above model in which the fluence is linear with respect to source assuming fixed μ parameters, the spectral Jacobian (or sensitivity) matrix that relates source to measured boundary data was calculated.

$$y=Wb$$ (3)

Where y is the spectral boundary measurements, W is the spectral sensitivity matrix. and b is the source term for each node in the finite element mesh used for the model.

The CSCG solver[57] calculates an estimate of b by minimising

$$x=min{\Vert y-Wx\Vert }_2^2+\gamma {\Vert x\Vert }_1$$ (4)

where x is the estimate of b and γ is a parameter controlling the relative weighting of two objectives; the fit between predicted and observed measurements $\left({\Vert y-Wx\Vert }_2^2\right)$ and the sparsity of the source distribution (∥x∥₁) that is recovered within the spatial domain.

3.7. NIR Diffuse Trans-Illumination Imaging

For diffuse trans-illumination imaging, the cylindrical phantom was placed on the platform directly above the NIR projector source. Images were then acquired in the same manner as described for luminescence imaging with the additional feature that for each filter, 36 different patterns were projected from the NIR source projector so as to mimic the raster scanning of a point source such as a fiber-bundle illuminating the phantom from underneath. Each of the trans-illumination patterns contained a single 2D Gaussian distribution with a maximum intensity equal to the maximum projectable intensity and a standard deviation of approximately 2mm on sample (40 pixels in the original projection image). The Gaussians sources were positioned to form a 6 × 6 grid as shown in figure 7.

Figure 7.

(a) Diffuse imaging protocol; (b) source grid illustrated in the form of the maximum intensity through the stack of all projected images with each Gaussian centrepoint labelled by the order of appearance in the imaging protocol; (c) the same image showing the effective raster scan order for the source patterns.

In addition, for each wavelength a dark image was acquired i.e. an image where the projector is projecting the darkest possible level at all pixels. This was required because the projector always has some non-zero light output even when the projection image is at 0 and as such this intensity must be treated as a baseline to be subtracted from data.

To set the exposure time for diffuse imaging the brightest of the sources is first established at a single wavelength via a short-exposure image of each source being acquired at a single wavelength. The auto-expose routine is then applied to each wavelength for that source only. The subsequently calculated filter-resolved exposure times are used for all sources. In this case there is a maximum possible exposure time of 30s set to limit experimental time. In practice, in all cases presented this value of 30s was used leading to a total diffuse image acquisition time of ≈ 1.5hours (37 source images × 5 wavelengths × 30s).

3.8. Diffuse Optical Tomography (DOT)

Following diffuse imaging, the acquired data set contains 37 images at each wavelength (36 source patterns plus a background image). These images are first converted into units of e^–/s as detailed in section 4.2 and then the background image is subtracted from all other images for each wavelength. The acquired multi-source, multi-spectral data set is then mapped onto the phantom surface according to the method described in section 3.4 providing transmitted boundary data. Data is calibrated on a per-source, per-wavelength basis with scaling factors based on a reference data set acquired for a homogeneous phantom which compensates for spatial variation in the input source intensity as well as the detection-system efficiency. The FEM approach is then used for image reconstruction.

Spectral diffuse optical tomography image reconstruction was carried out using NIRFAST in which the formulation of the light-transport problem within the volume is also based on the diffusion approximation:

$$-\nabla \cdot \kappa \left(r\right)\nabla \Phi \left(r\right)+{\mu }_a\left(r\right)\Phi \left(r\right)=q_0$$ (5)

Where q₀ is now the known source term in each case and

$${\mu }_a\left(\lambda \right)=\sum _{i=1}^{n_c}{∊}_i\left(\lambda \right)C_i$$ (6)

and

$${\mu }_s^{\prime }=a{\lambda }^{-p}$$ (7)

where ε_i is the molar absorption coefficient of the i^th absorbing chromophore present in the volume with molar concentration C_i and a and p are the scattering amplitude and power respectively under an approximation to Mie theory[49].

The Jacobian matrix J is calculated, which relates the entities C, a, and p to the boundary measurements φ_dot given an initial guess of μ = [C, a, b] which is now a vector representing node-wise chromophore concentrations and scattering parameters throughout the FEM mesh. The reconstruction is undertaken by use of an iterative Tikhonov-regularised Levenberg-Marquardt type update term.

$$J^T{(J{J}^T+\rho I)}^{-1}\delta {\varphi }_{dot}=\delta \mu$$ (8)

Where ρ is a regularisation parameter. By stopping the algorithm after a certain number of iterations, we then obtain μ.

By utilising spectral DOT, the concentration of absorbers and the scattering properties within the medium are computed directly rather than solving for μ at multiple wavelengths and then curve fitting. This serves to constrain the solution space given the spectral characteristics of the finite set of known absorbers assumed to be present.

3.9. Combined DOT and BLT

As well as pursuing DOT as a complimentary modality to BLT, its application as a precursor providing prior information that can be utilised to improve luminescence image reconstructions was also investigated. In this case the scattering properties and chromophore concentrations obtained by DOT are used to calculate absorption and reduced scattering coefficients at wavelengths at which luminescence measurements are acquired, which are then used for BLT reconstruction.

4. Data processing and System Characterisation

4.1. Detection System Spectral Response

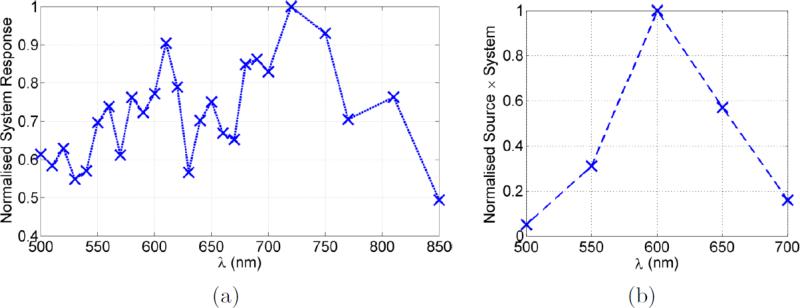
The relative spectral response of the detection system was measured in a set of experiments in which the (unfiltered) tungsten halogen source was re-mounted above the stage and set incident upon a spectralon reflectance standard (99%, Labsphere, NH, USA) on the sample stage. This was imaged several times through each of the bandpass filters and the mean reflected values were divided by the known source spectrum to obtain the system response function.

Additionally, the Trigalight luminescent source emission multiplied by the system response was measured directly as a single quantity by imaging the source directly on the sample stage through each of the filters used in the BLT study. Figure 8 shows the measured spectral response and the measured luminescence source-system spectral response.

Figure 8.

Normalised spectral system response functions: (a) system response for the NIR source; (b) system response for luminescent source.

The system response is more variable than might be expected and non-smooth since the dominant factor is the filter transmittance which is somewhat variable between filters in terms of both FWHM and peak height.

4.2. Conversion from image grey-levels to real-world units

The number of photons irradiating each pixel on the CCD can be calculated by:

$$p=\frac{c}{\left(asQ\right)}(I-D-d)$$ (9)

where c (e^–/counts) is a constant, camera-dependent conversion factor which for our camera is 0.6 in normal mode and 6.3 in EMCCD mode, a (no units) is the analogue gain applied which is always set to 1, Q (e^–/photons) is the quantum efficiency of the camera, s (no units) is the sensitivity (or EM-) gain applied which is also always 1 in this study, I (counts) is the image, D (counts) is the digitiser offset and d (counts) is the dark signal which together define the counts that are present not due to incident light. The digitiser offset is a property of the camera that is dependent on read-mode, CCD mode and binning mode. By taking many repeated images with the lens cap on, it was measured in each mode and committed to a library for recall and subtraction. The quantum efficiency is not known explicitly so is set to 1 in this study and measurements that result from the above conversion are in units of e^– read out from the CCD until further calibrations are applied dependant on the imaging mode.

4.3. Geometric calibration

The geometry of the imaging system is characterised assuming a thin lens model for the camera and two upper projectors. The location of a single pupil point and the directions corresponding to the trajectory of light emerging from each pixel for each of these components was determined using a custom-made automated calibration method. The method uses images of a regular grid obtained at several known distances by placing a printed grid on the sample stage and moving the lab jack vertically by known amounts. The grid co-ordinates are used to solve for the location of the camera. A similar approach is then used to calibrate the projectors whereby a regular grid is projected and its reflection imaged on the stage at various heights again separated by known distances. The camera model is used to extract 3D co-ordinates in the camera co-ordinate system of the projected grid and these are then used to solve for the projector parameters.

The above calibration only needs to be done once, assuming components remain fixed. In contrast, it is assumed the mirrors are not fixed between experiments and their location is measured on-the-fly using an extension to the surface capture imaging protocol (section 3.2) that is based on dual-photography. This involves the addition of another set of patterns to the routine with pattern-direction perpendicular to the original set. This provides a unique pixel-wise encoding for each projector meaning that projected pixels visible in the mirror can be identified also in the main view. Using the geometric model and a set of derived pairs of points, the location of the mirror surface can be determined that best fits the observations.

A reduced depiction of the system geometry comprising the pupils and principal view-directions of components is shown in figure 5.

4.4. DOT source model

Whilst Gaussian sources are projected onto the phantom for DOT (section 3.7), these are modelled with NIRFAST as point sources. The location of each of the point sources was established using a simple experiment in which each projection was imaged in turn through each filter used for DOT onto white paper. The resultant images were used in conjunction with the system geometric model (section 4.3) to establish a 3D source position in the plane of the sample stage. These co-ordinates are used explicitly as the FEM source positions following their movement to the nearest point lying one scattering length inside the surface within NIRFAST[58]. This experiment could have also been used to establish the relative brightness of different sources as seen by the camera but in the present study this step has been omitted in favour of calibrating the data directly with a reference data set.

5. Results and discussion

5.1. BLI

To evaluate the system, several experiments were performed using a cylindrically shaped phantom. First, the phantom was set-up in eight different configurations each of which modelled a different BLI scenario in terms of the target source position and depth. The source was placed at one of four depths in a central position axially and these four scenarios were then duplicated with the addition of a 45° rotation to the phantom within the system to provide both on-axis and off-axis data sets. The phantom was then imaged according to the protocol outlined in section 3.5 using 500, 550, 600, 650, and 700nm filters. The results of the imaging sessions are shown in figures 9 and 10 in a format similar to that often used to present results in biomedical studies (see for example Contag[55]). These figures also show a schematic diagram of a 2D cross section through the phantom volume along with a representative image (at 600nm, near the peak emission wavelength of the source) taken from the acquired 5 wavelength image stack for each experimental scenario.

The surface flux distribution is clearly visible and interpretable in the images, although it is worth considering the diversity of apparent image features given that the actual source being imaged is known to be identical in each case, merely situated at different depths within the phantom and within the system. It can be seen that even in this, a homogeneous phantom, the qualitative appearance of the images changes drastically for example appearing as a tightly packed source in the shallowest case (figure 9(e)) and as two intuitively separable blurred surface flux structures in a deeper case (figure 9(g)). Quantitatively, it can be seen that the signal drops by approximately a factor of 10 between the first and second scenarios in both the on and off-axis data sets and that whilst the use of mirrors allows access to previously invisible signals (e.g. figure 9(h)) this also confuses matters under naive interpretation in that a deeper source with respect to the camera view-point can be seen to appear quantitatively more intense in a mirror view due it being shallow with respect to the nearest visible surface point; in this case a point visible through a mirror. It is therefore not possible to accurately deduce a count (or cell-count in a biological study) directly from this type of data when the source is a collection of bioluminescent or fluorescently-labelled markers. These results are a clear indication of the need for more advanced tomographic image recovery.

5.2. BLT

The BLI image data presented in the previous section was used as input for BLT, along with surface capture data taken prior to imaging in each experiment. The methods presented in sections 3.4 and 3.6 were used to produce 3D BLT images of reconstructed source distributions in each case. The 3D cylindrical FEM mesh that was created and used for image reconstruction contained approximately 11, 000 nodes and 47, 000 linear tetrahedral elements. Figure 11 shows a single luminescence reconstruction (corresponding to the example in figure 9(a)), rendered in 3D using Paraview (Kitware, NY, USA) and sliced through the volume at the axial depth corresponding to the axial displacement of the centre-of-mass of the reconstructed source. All further visualisations are presented in this slice format for ease of interrogation with reference to the 2D cross-sectional target diagrams. Experimental results are shown in figures 12 (on-axis set) and 13 (off-axis set).

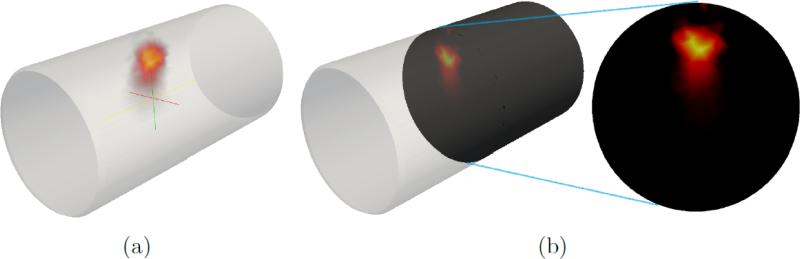
Figure 11.

Visualisation of (a) 3D reconstruction for the data set with the most shallow source (see figure 12(a)) along with (b) indication of how the following 2D slice representations of results are obtained

Figure 13.

Summary of off-axis, homogeneous BLT experiment results showing: (a-d) schematics of source experimental locations in 2D projection; (e-h) BLI images (CCD measurement e^–/s) of the phantom at λ = 600nm with approximate phantom outlines; (i-l) slices through corresponding BLT reconstructions at the axial offset corresponding to the centre-of-mass of the reconstruction; and (m-p) the slice images thresholded at 75% of the maximum value.

In the on-axis data set (figure 12), it can be seen that qualitatively the reconstructed images are accurate and clear; in contrast to the results of BLI, it is easy to interpret the images as showing a single source in the correct location. It can also be seen that in the cases where the source is farthest from the surface (figure 12(j) and figure 12(k)) the reconstructed distributions are slightly broader than in other cases and in the case where the source is farthest from the detector and least visible in recorded images (figure 12(l)) the recovered distribution appears qualitatively less well-localised.

In the off-axis data set (figure 13) the results are very similar, with the images once again qualitatively clear and accurate in terms of showing a single source in the correct location in each case. There is a qualitative improvement in the image of the deepest source (figure 13(l)) compared to the on-axis set primarily due to the improved signal level and surface flux visibility in the rotated case; it is expected that the deepest case in the on-axis experiment would be the most challenging problem since the source is most difficult to see from all three views and is therefore a worst case scenario.

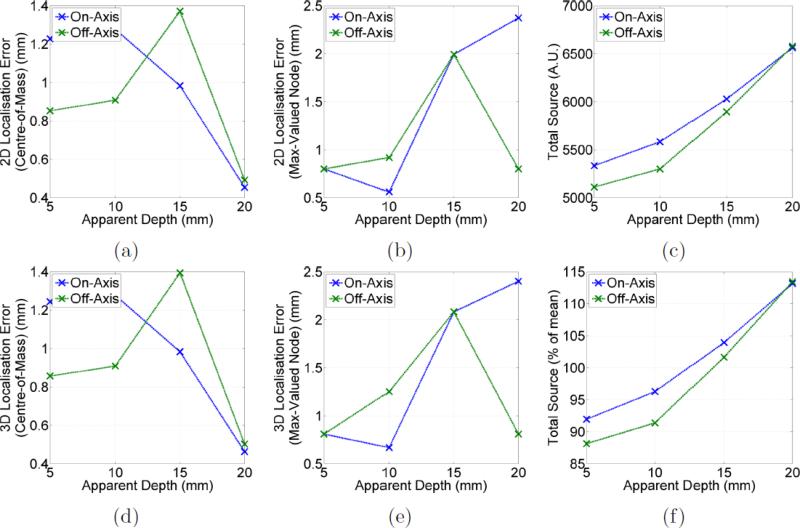
Figure 14 shows a quantitative analysis of the reconstructed luminescent source distributions for both the on-axis and off-axis sets. Firstly, it shows the localisation error measured in 2D (in the presented slice only) and in 3D by two distinct metrics. By the first metric (figure 14(a)) the position of the reconstructed source distribution is considered to be its centre-of-mass:

$$c_b=\frac{{\sum }_{i=1}^n{\mathbf{x}}_i{b}_i}{{\sum }_{i=1}^n{b}_i}$$ (10)

where n is the number of nodes in the mesh, x_i and b_i are the position and reconstructed source intensity respectively at the i^th node. By the second metric the position of the reconstructed source is assumed to be the position of the maximum-valued node. The positional error is then the Euclidean distance between the expected source location (assumed to be the centre of the appropriate tunnel) and the recovered source location. The reason for showing both 2D and 3D metrics is that the axial depth of the source was difficult to control in the experiment but was estimated to be approximately central, as such it is not clear which metric is necessarily most appropriate and both are shown for completeness. The figure also shows the total reconstructed source (i.e. the sum across all nodes of the recovered source value) in absolute terms (arbitrary but consistent units) and as a percentage of the mean value across both sets.

Figure 14.

Summary of BLT results in quantitative terms for both the on-axis and off-axis (45° rotated) experiments ordered versus effective depth w.r.t. the top of the phantom: (a) the 2D error in reconstructed source position based on the centre-of-mass metric; (b) the 2D position error based on the max-valued node metric; (c) the total (summed) reconstructed source shown in arbitrary units; (d) and (e) the 3D versions of (a) and (b) respectively; and (f) the values of (c) shown as a percentage of the mean value across both sets.

It can be seen from the graphs that by the metrics of accuracy presented the localisation error is less than 2.5mm. The error is less than 1.5mm in all cases using the centre-of-mass metric which is consistent with the best previously published BLT results[59, 60, 17, 61]. Using the max-valued node error metric it can be seen that there is less accuracy as the depth increases in the on-axis set, which is indicative of the source becoming less well focused (i.e. more diffuse) whilst remaining centred in approximately the correct location. It can be seen that the reconstructed source intensity is consistent across both sets, within 15% either side of the mean value. This is very encouraging as it shows quantitative stability in the reconstruction with respect to a diverse variety of source locations and depths. This is a dramatic improvement on the quantitative variation within bioluminescence images (section 5.1) and suggests that in the case where optical properties are known, and assuming the diffusion equation holds sufficiently well, the presented BLT approach could be effectively applied to cell-counting applications and would offer a substantial improvement upon BLI.

5.3. Diffuse trans-illumination imaging and DOT

In order to test the DOT methodology and to perform a proof of concept for the use of DOT to provide prior information for BLT reconstruction, a single DOT experiment was performed using the cylindrical phantom. The phantom was first imaged in accordance with the diffuse trans-illumination imaging protocol (section 3.7) following the insertion of a double-absorbing rod anomaly into the shallower inclusion tunnel. Images were acquired with 650, 700, 750, 810 and 850nm filters.

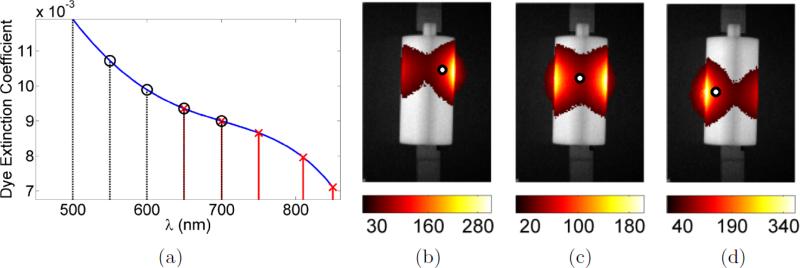
The spectral DOT reconstruction method (section 3.8) was then applied to the trans-illumination data. For reconstruction, the regularisation parameter within NIRFAST was set to ‘automatic’ and the reconstruction was terminated after 7 iterations. In this instance it was assumed that scattering was known, with scatter amplitude and scatter power being fixed at a = 1.6160 and p = 0.1543 (eq. 7). The only chromophore considered was a single dye which was assumed to be the main absorber within the phantom and was assigned spectral extinction coefficients equal to the known background absorption coefficient spectrum. To model the extinction coefficient, a curve was fit to the manufacturer-measured data over the range 500 to 850nm, as shown in figure 15. Also marked in this figure are the central wavelengths of the filters used for spectral diffuse imaging and spectral BLI. It can be seen that diffuse imaging and BLI were performed in the NIR and the visible parts of spectrum respectively with only partial overlap requiring that the spectral method was used (as opposed to performing multiple single-wavelength reconstructions) in order to calculate absorption properties at BLT wavelengths from DOT results.

Figure 15.

(a) Spectral dye extinction coefficient. Spectral sampling is shown both in terms of where DOT data was acquired (red lines and crosses) and where the BLT data was acquired (black dashed lines and circles); (b-d) diffuse trans-illumination images at 750nm with NIR source positions 1, 15 and 36 repectively, visualised in the same manner as the BLI images in figures 9 and 10 with approximate source location (under the phantom) shown by the overlaid white circle.

Figure 15 also shows three diffuse trans-illumination images at λ = 750nm each for a different NIR source (section 3.7) numbered here according to the grid shown in figure 7. It can be seen that as the source position changes the surface distribution of light as measured on the CCD also changes in an intuitively logical way. It can also be seen that, owing to the shape of the cylinder and the path-lengths associated with this geometry, the signal is significantly stronger at the far sides of the cylinder rather than through the centre. This is the factor that underpins the choice not to use mirrors for DOT at the present time, namely that the dynamic range across the surface is such that to collect signals further around the cylinder surface would overwhelm those visible through the top view, thus the acquired data would not have adequately probed the whole volume and would be inappropriate for tomography. This issue has previously been noted by Venugopal et al.[62] who have looked at the optimisation of patterns in order to minimise dynamic range and maximise volume inspection by optimisation of spatial input. This is a future direction for the present system.

Figures 16 and 17 show the results of performing spectral DOT reconstruction. It can be seen that the dye concentration anomaly is reconstructed in the correct spatial location with some blurring and at the correct concentration. It can also be seen that there are image artefacts on either side of the anomaly where the background concentration is underestimated in two places. Isolation of the cause of these artefacts and improvement of image quality are subjects for future work. However, it is considered that one potential cause could be that the placement of sources onto the FEM mesh assumes a simple direct mapping of source positions onto the mesh at the nearest point. Whilst this mechanism is appropriate for very short distance corrections particularly in contact mode imaging, in this case the projector source-projection method in conjunction with the curvature of the cylinder means that the actual source is likely to be different in each projected case. In order to account for this process effectively a model of the lower projector would also be required, which is challenging because of the very short working distance. However, it is expected that this effect would be somewhat minimised when imaging an object flush with the stage such as a sedated mouse, and that in this sense the cylindrical shape of the phantom may have caused difficulty for DOT. This will be tested in the future with phantoms with a flat bottom face.

Figure 16.

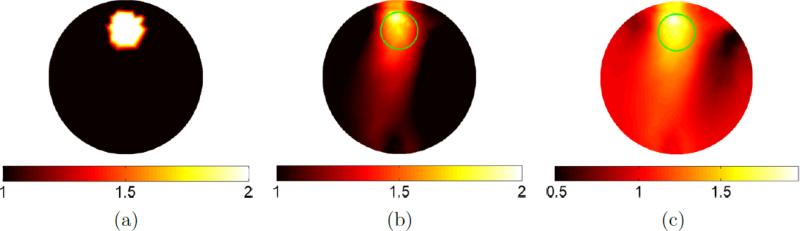
Spectral DOT results shown as slices through the 3D reconstruction at an axial offset equal to the location of the centre of the NIR source grid: (a) target absorber concentration showing rod anomaly; (b) reconstructed absorber concentration scaled to the same color-scale as the target; (c) reconstructed absorber concentration scaled to its own extremal values.

Figure 17.

3D renderings of a cropped section of the cylinder (approximately 20mm long centred axially around the centre of the source grid: (a) the target dye concentration anomaly location; and (b) the reconstructed concentration thresholded at 1.45

5.4. Combined DOT-BLT

In order to test the concept of utilising DOT results as a priori data to aid BLT image reconstruction, the Trigalight luminescent-like source was placed in the lower tunnel between background-matching rods, whilst the absorption anomaly remained in place in the upper rod. The phantom was then replaced in the system and imaged in luminescence mode. Two BLT reconstructions were then performed, one that assumed homogeneous background material throughout the volume, and one that assume the concentration values reconstructed using DOT. BLT reconstructions used the same FEM mesh and algorithm parameters as were used in the homogeneous phantom BLT studies. Slices through the resulting reconstructions, along with a schematic diagram of the phantom, are shown in original and thresholded formats in figure 18.

Figure 18.

Reconstructions of luminescence source distribution in the case where the target is in the lower tunnel with an anomaly in the upper tunnel: (a) schematic of target slice showing anomaly and source positions; (b) BLT reconstruction where the absorber concentration is assumed to be the background level throughout the volume; (c) BLT reconstruction where the absorber concentration is assumed to be that obtained via DOT; (d) and (e) 75% thresholded versions of (b) and (c).

Qualitatively, the reconstructed images appear different, with the image based on the a priori DOT data being well-recovered and positioned in terms of the expected distribution in a manner consistent with the homogeneous BLT studies (section 5.2). The reconstruction based on the assumption of homogeneity appears qualitatively poorer being more spread out and focused in a position further towards the edge of the expected region as opposed to being centrally localised. In terms of the previously applied quantitative metrics (section 5.2), the results of the DOT-BLT experiment are shown in table 1.

Table 1.

Table showing quantitative results of BLT-DOT experiment.

3-View Reconstructions	Homogeneous	DOT Prior
2D Position Error (mm; centre-of-mass)	1.23	1.20
3D Position Error (mm; centre-of-mass)	1.23	1.20
2D Position Error (mm; max-valued node)	1.99	1.99
3D Position Error (mm; max-valued node)	2.08	2.08
Total Source (A.U.)	5791	6677
Total Source (% of BLT experiment mean)	100%	115%

There is little to choose between the quantitative results of the two reconstructions. Although position error judged by the centre-of-mass approach is slightly less in the prior case this is only a 2.5% improvement and the equal max-valued localisation errors reveal that despite differences in qualitative appearance, the max-values node was the same in each case. Given the qualitative change in the reconstructed images themselves, it is considered that these metrics may not be capturing the distribution of the sources effectively. The total source reconstructed is actually closer to the BLT experiment mean value (treated as a reference point in figure 14) in the homogeneous-assumption case although it is perhaps worth noting that in the equivalent homogeneous experiment in terms of source location (the on-axis experiment at depth 15mm; figure 14(f)), the reconstructed source was above 100% and the reconstruced source generally increased with depth indicating that possibly the mean across all depths might not be the most appropriate bench-mark for evaluating the single BLT-DOT result.

Despite the lack of substantial quantitative improvement judged by these metrics, the qualitative image improvement when using the prior information provided by DOT suggests that this is a useful technique to pursue. It is additionally not surprising that in this experiment the homogeneous reconstruction worked reasonably well as the multiple-view approach combined with the source position means that the highest signal for this data set was obtained in the side-views and therefore would be affected relatively little by the presence of the anomaly positioned between the source and the already less sensitive top-view.

To investigate further whether the good quality of the homogeneous reconstruction was due to the enhanced coverage made available by the multi-view set-up and whether it was this that was overcoming the lack of anomaly knowledge in this experiment, a final pair of reconstructions were performed that used only the top-view (non-mirror) data from the above experiment. Again one reconstruction assumed background, homogeneous properties and one utilised the DOT prior information. The results are shown in figure 19 and quantitative results are summarised in table 2.

Figure 19.

Reconstructions of luminescence source distribution in the case where the target is in the lower tunnel with an anomaly in the upper tunnel, with reconstruction performed using top-view (direct) data only: (a) schematic of target slice showing anomaly and source positions; (b) BLT reconstruction where the absorber concentration is assumed to be the background level throughout the volume; (c) BLT reconstruction where the absorber concentration is assumed to be that obtained via DOT; (d) and (e) 75% thresholded versions of (b) and (c).

Table 2.

Table showing quantitative results of BLT-DOT experiment.

Top-Only (1-View) Reconstructions	Homogeneous	DOT Prior
2D Position Error (mm; centre-of-mass)	5.17	0.78
3D Position Error (mm; centre-of-mass)	5.21	0.81
2D Position Error (mm; max-valued node)	3.39	0.56
3D Position Error (mm; max-valued node)	3.57	0.67
Total Source (A.U.)	21525	5476
Total Source (% of BLT experiment mean)	371%	94%

It can be seen that in the case where side-view data is not used the effects of making the homogeneous assumption are far more significant. Qualitatively the DOT-prior reconstruction looks quite similar to the multi-view version albeit a little less well-focused whilst the homogeneous reconstruction is no longer recognisable as a small source cluster in the right location, rather it is very broad and blurred, and somewhat deeper than the true source location.

The quantitative metrics now show that the homogeneous reconstruction also contains around 3 to 4 times the expected total source as well as being clearly in the wrong position. The quantitative accuracy of the DOT-prior top-only reconstruction is actually better than in the 3-view case which could be due to a diminished influence of the DOT artefacts (located towards the sides) although this may merely be due to limitations in the metrics used.

6. Conclusion

A novel imaging system for performing multi-modal optical tomography for application in small animal imaging has been presented in which the key novelties are: the physical system design; the combination of spectral DOT, optical surface capture and BLT, performed with a single system and within an integrated methodology; and the first application of the multi-view surface capture technique as part of the multi-modal workflow.

It has been shown that in eight separate experiments, with distinct scenarios in terms of target source location, that the system and algorithms produce reliable BLT results in terms of quantitative stability, with the total reconstructed source varying by less than ±15%, and spatial localisation with errors always being less than 1.5mm when measured using the reconstructed centre-of-mass. These results suggest that the BLT methodology works effectively when the diffusion equation holds and the optical properties are known. It has been shown explicitly that the same signals when viewed directly in BLI image data are spatially diverse, ambiguous and vary by several orders of magnitude, highlighting that the proposed BLT method provides a strong improvement in quantitative image evaluation.

Spectrally constrained DOT has demonstrated the accurate detection of an optical anomaly in the form of a single chromophore concentration change. Qualitatively this reconstruction was accurate in terms of the spatial position and size of the reconstructed anomaly and whilst the DOT utilised an initial guess of the background level of concentration and the scattering properties were known, in general this will not always be necessary as methods exist for estimating bulk parameters from measurements[63] and these will be investigated in future studies.

Although there was some blurring and artefacts in the DOT reconstruction, it is anticipated that the image quality will be improved with more convenient object geometry (having a flat as opposed to a curved lower surface, which is a realistic assumption in animal studies) and/or with a better model of the source projection. Additionally, the use of multi-view data can be made possible with investigations of optimised wide-field NIR source patterns as a mechanism for better probing the medium[62] and this should result in improved DOT results.

It is proposed that the method of recovering chromophore concentrations will be extended to investigations of functional parameters in vivo, for example measuring blood oxygenation level within small animals by reconstructing oxy- and deoxy- haemoglobin concentrations throughout the volume, and that this will provide fundamentally new and useful complimentary physiological data in biomedical luminescence imaging studies. This is an idea that has been successfully exploited in other domains such as human breast DOT in which tumours have been shown to have optical contrast in the form of distinct blood oxygenation and water content characteristics[64, 65, 66].

Finally, a proof of concept has been presented for the use of spectral DOT results as prior information for BLT reconstruction and has shown that qualitative image accuracy is improved when using DOT-BLT rather than naive BLT. It was found that this effect was amplified greatly when reconstruction was performed using single-view data only, which is likely to be related to the particular optical anomaly location in this case. This suggests that in general, in more complex optically spatially varying media such as small animals, the use of multi-view DOT-BLT will improve image reconstruction.

Optimisation of the protocol in terms of imaging time was not a major priority of the presented work, although it has been noted that the time achieved would have been three-fold worsened if multi-view/rotational approaches had been used to acquire three views instead of the mirror approach. The total acquisition time for the whole imaging protocol was at best approximately 1.6 hours which is quite high compared to that typically used in current bioluminescence imaging systems. However, the vast majority of this time is spent on the diffuse imaging and is largely due to the high number of distinct illumination patterns used at each wavelength. It is anticipated that by use of wide-field illumination[45, 44] schemes, providing higher signal and with less patterns required, this could be substantially reduced. Additionally, improved hardware such as a larger optical sensor, filters with higher transmittance and a micro-mirror device with higher coupling efficiency (such as a more expensive DMD) could further improve the time required and make routine pre-clinical imaging more favourable. These optimisations are considered future work.

Further future directions include working towards simultaneous DOT and BLT imaging involving the addition of a second detection system to the current set-up and the use of fully distinct spectral ranges for each modality as opposed to the partially distinct bands used here in addition to advanced methods such as the spectral derivative approach to DOT[67]. The DOT also will be more rigorously tested with further phantoms in a manner similar to the BLT imaging performed in this study once mutliple views are utilised as in order for the system to be generalised and independent it will be necessary to obtain full volume sensitivity in the manner shown here for BLT.

In summary, the novel multi-view, spectral DOT-BLT system with optical surface capture provides clear quantitative imaging improvements over standard BLI by stabilising light source counts to within 15% either side of the mean rather than several orders of magnitude. It also allows interpretable accurate 3D images to be produced of optical parameters and light source distributions within the volume. Furthermore combined DOT and BLT improves BLT image reconstruction.