Visual and Proprioceptive Contributions to Compensatory and Pursuit Tracking Movements in Humans

Abstract

An ongoing debate in the field of motor control considers how the brain uses sensory information to guide the formation of motor commands to regulate movement accuracy. Recent research has shown that the brain may use visual and proprioceptive information differently for stabilization of limb posture (compensatory movements) and for controlling goal-directed limb trajectory (pursuit movements). Using a series of five experiments and linear systems identification techniques, we modeled and estimated the sensorimotor control parameters that characterize the human motor response to kinematic performance errors during continuous compensatory and pursuit tracking tasks. Our findings further support the idea that pursuit and compensatory movements of the limbs are differentially controlled.

I. Introduction

Successful interaction with the environment is predicated on the brain’s ability to use sensory information to guide performance of motor tasks. Everyday tasks can be divided into two types: compensatory tasks, which involve holding an object steady against an external perturbation, and pursuit tasks, which involve moving an object from place to place or intercepting an object in space (such as catching a ball). That most of us can do these things without much difficulty is indisputable; however, the conscious and unconscious processes controlling such actions are not yet fully understood.

Previous studies exploring the mechanisms underlying goal-directed movement have demonstrated that motor control can be modeled – to a first approximation - as a linear, closed-loop system informed by multi-sensory (i.e. visual and proprioceptive) estimates of position [1,2,3,4]. The relative contributions of these estimates can be characterized using systems identification techniques [1,2,3,4]. We have recently extended these techniques to additionally characterize the delays, noise sources, and system gains involved in compensatory and pursuit tracking tasks using the wrist [1,2]. Recent experimental evidence suggests that separate and distinct control processes are invoked during stabilization and pursuit movements [5,6,7,8], although those studies only noted the possible differences in control mechanisms. The present study seeks to quantify the differences in control mechanisms for pursuit and compensatory tracking tasks.

II. Methods

A. Model Description

Inspired by Peterka 2002 [3], we modeled sensorimotor control of the wrist as a “dual feedback” system. The model consists of a forward motor control path informed by two sensory (visual and proprioceptive) feedback paths. In the forward path, the neural processing associated with correction of errors between desired (θ_d) and realized (θ_r) wrist position is modeled generically as a PID (proportional, integral, derivative gain) controller. Delays in the forward path (due to synaptic transmission delays in the CNS and excitation/contraction coupling) are modeled by a lumped forward delay (T_ff). A novel aspect of our model is that multiplicative motor noise (α) degrades the generation of torque. Torque is converted into angular position using a 2^nd order model of the wrist characterized by its inertia, viscosity, and stiffness. In each feedback path, sensory perception of wrist position is delayed (T_v and T_p) and weighted (K_vf and K_pf). The two estimates are then summed together with an internal sensory noise (σ_s²) to provide a sensory estimate of wrist position. The forward model (noiseless feedback prediction) provides predictive compensation for the wrist dynamics and system delays.

B. Subjects

Four healthy volunteers (4 female; ages 25.8±1.9 yrs) participated in both the compensatory and pursuit tasks. All were right handed, according to the Edinburgh handedness inventory. Written informed consent was obtained from each subject in accordance with institutional guidelines approved by Marquette University and the experiments were performed in accordance with the Declaration of Helsinki.

C. Experimental Setup

The experimental setup is shown in Fig. 2. Subjects were seated in front of a monitor on which a target (filled circle) and a cursor (ring) were displayed. Subjects used a custom 1-D robotic manipulandum, which allowed for smooth rotation about the wrist joint, to control the location of the cursor. The arm was held in place using three rigid supports. Direct view of the hand was blocked, so that only the cursor provided visual information about wrist angle. We recorded joint angle, velocity, and torque information from the robot.

Figure 2.

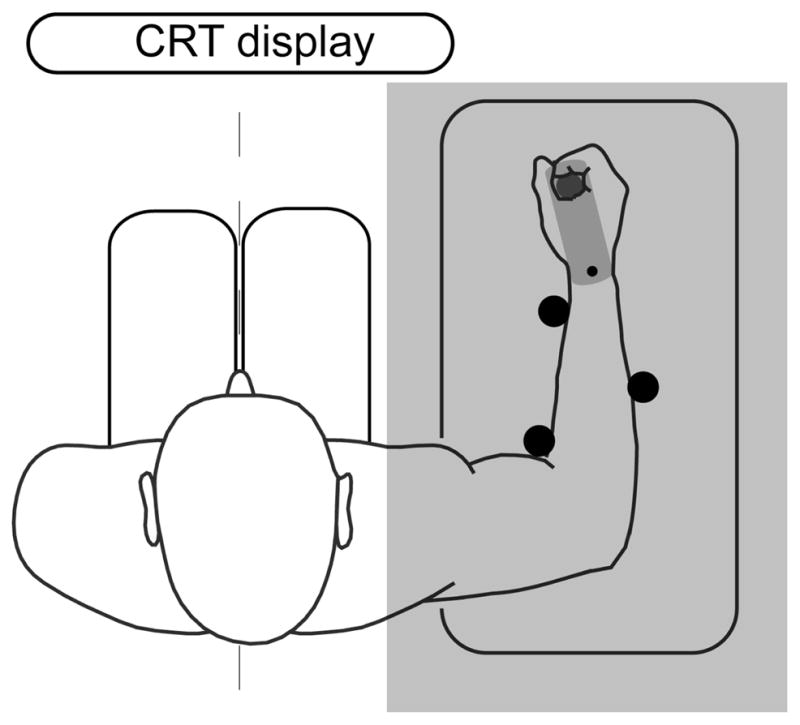
Experimental setup. The subject was seated with their arm resting on the robot. The subject used the manipulandum to control a cursor presented on a computer display.

D. Description of Experiments and Analyses

Subjects performed a series of five experiments (order counterbalanced across subjects) in which they were to maintain the cursor on the target while the target was either moving (pursuit) or stationary (compensatory). Closed-loop control was interrogated by randomly displacing either the position of the cursor/target (visual) or the position of the manipulandum handle (proprioceptive).

1) System Delays

The first experiment consisted of three separate tasks designed to estimate the sensory delays and the effective forward delay. To measure the open loop sensory delays, a continuous, low frequency (0–.5Hz), pseudorandom perturbation was applied to either the cursor (compensatory) or target (pursuit) (Task 1: visual) or the manipulandum (Task 2: proprioceptive) positions. 10 trials of 20 seconds each were collected for each condition. Subjects were asked to correct for the perturbations as quickly and accurately as possible. Open loop sensory delays were estimated by finding the peak of the cross correlation between the perturbation and the subject’s position response. To measure the effective feedforward delay (Task 3), subjects performed a low-frequency (0.5Hz) sinusoidal pursuit task. The stimulus was designed to be deterministic to allow subjects to predict the location of the target over time. Subjects were instructed not to lead the target in order to characterize the residual delay not accounted for by internal prediction mechanisms. Again, the forward delay was estimated from the peak of the cross correlation between the perturbation signal and the subject’s response.

2) Feedforward Motor Noise

Subjects performed 25, 10 second isometric wrist flexion trials, during which they were to move the cursor (under torque control) to capture a static, displaced target. Five trials at each of five different required torque levels were tested. The average within-trial standard deviation of torque for each level of activation was calculated, and the scaling factor on the noise was linearly fit across levels.

3) Passive Wrist Dynamics

Subjects performed 10 trials lasting 32 seconds each. Here, subjects were to hold the manipulandum with the same grip force as used in the previous experiments, but instructed not to resist the movements of the manipulandum (a “do not intervene” test). The manipulandum was continuously displaced using a pseudorandom perturbation (0–30Hz). For each set of trials, the frequency response function (FRF) was calculated and then the set of FRFs was averaged to provide a single estimate of the frequency response. The model parameters were then fit, using a least squares curve fit, to a 2^nd-order model of wrist dynamics (Eq. 1)

$$P(s)=\frac{1}{{Js}^2+Bs+K}$$ (Eq. 1)

where J, B, and K correspond to the moment of inertia, viscous damping, and spring constant of the wrist, respectively.

A bootstrapping analysis was used to characterize the uncertainty in the least squares fit and to provide an estimate of the statistical certainty to compare parameter estimates between subjects. To do this, the data set was resampled with replacement ten thousand times. Each resampled data set was fit using randomized initial conditions, to obtain a distribution of estimates for each parameter. The mean and standard deviation of the resulting distributions were calculated for subsequent analysis.

4) Sensory Gains, Neural Controller Gains

This experiment consisted of 20, 32 second trials, arranged in two sets of 10. A high frequency (0–10Hz, 2^nd order zero-phase Butterworth filter) pseudorandom perturbation was applied to the cursor position. Subjects were asked to correct for the perturbations as quickly and accurately as possible. The FRF was calculated from the data on a trial-by-trial basis, then averaged across trials. We then fit the model transfer function, using the perturbation (D_ext for compensatory movements and θ_d for pursuit movements) as the input, and subject position as the output, for stabilization (Eq. 2) and pursuit (Eq. 3) respectively. We then used a least squares curve fit of the FRF of the data to the transfer function using the same method described in Experiment 3.

$${\theta }_r=\frac{K_{vf}{e}^{-T_{v_{ol}}s}{\mathit{CsD}}_{\mathit{ext}}}{\frac{s}{P}+Cs[1+(K_{vf}-K_v)e^{-T_{v_{ol}}s}+(K_{pf}-K_p)e^{-T_{p_{ol}}s}]}$$ (Eq. 2)

$${\theta }_r=\frac{e^{-T_{v_{ol}}s}Cs{\theta }_d}{\frac{s}{P}+Cs[1+(K_{vf}-K_v)e^{-T_{v_{ol}}s}+(K_{pf}-K_p)e^{-T_{p_{ol}}s}]}$$ (Eq. 3)

where P is the frequency response function of the plant (Eq. 1) and C is the transfer function of the neural PID controller (derivative gain: K_d; proportional gain: K_pr; integral gain:K_i) (Eq. 4)

$$C=K_{d}s+K_{pr}+\frac{K_i}{s}$$ (Eq. 4)

5) Model Validation

The final experiment was designed to test the model’s ability to predict subjects’ performance. The task was the same as that used to estimate the visual delay, and consisted of 10 trials of 20 second duration. Pursuit trials were used to validate the pursuit condition, and compensatory trials were used to validate the compensatory condition. The parameters estimated from the previous experiments were used to model subjects’ individual performance on the task. The simulated response of the subject was then compared to the actual response generated by the subject.

III. Results

Passive wrist inertia, feedforward delay, feedforward motor noise, and proprioceptive delay were all assumed to be invariant between testing conditions. Initially, we also anticipated that the visual delays would be invariant between conditions, although within-subject comparisons found that the visual delay was lower in pursuit tracking than in compensatory tracking (t<−2.0; p<0.05 for all subjects).

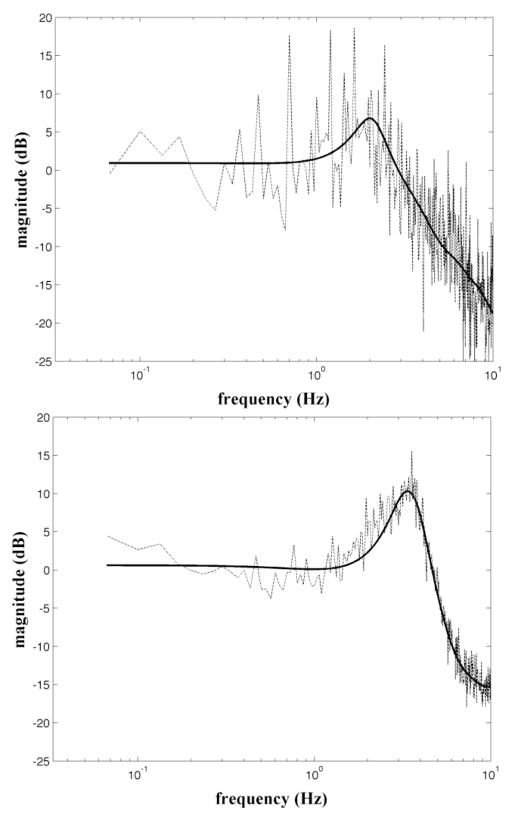
Fig. 3 shows the frequency response functions obtained from Exp. 4 during compensatory and pursuit conditions for a representative subject. Note the higher cutoff frequency for the pursuit condition (4.8±1.3Hz; mean±SD, here and elsewhere) than for the compensatory condition (3.9±1.1Hz). Additionally, the resonance is higher in the pursuit condition (12.2±2.7dB) than in the compensatory condition (6.6±3.8dB). Finally, the pursuit condition has a much sharper cutoff than that of the compensatory condition.

Figure 3.

Magnitude of the frequency response of the compensatory (top) and pursuit (bottom) to a high frequency (0–10Hz) visual perturbation

Between-subject comparisons of the controller gains showed consistent differences between pursuit and compensatory tasks. Across subjects, the best-fit integral gains, K_i, were consistently estimated as zero for the compensatory task but not for pursuit (K_i=1.5±2.1). Additionally, the proportional gain, K_pr, was consistently higher for pursuit (0.068±0.010) than compensatory (0.025±0.015). However, we found no consistent difference between derivative gains for pursuit (0.00086±0.0011) and compensatory (0.00056±0.00050). Estimates of controller gains across subjects are shown in Fig. 4.

Fig. 4.

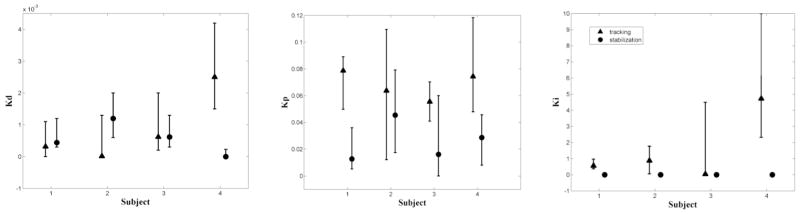
Comparison of neural controller gains with 95% confidence bounds. Triangles: pursuit tracking; circles: compensatory tracking.

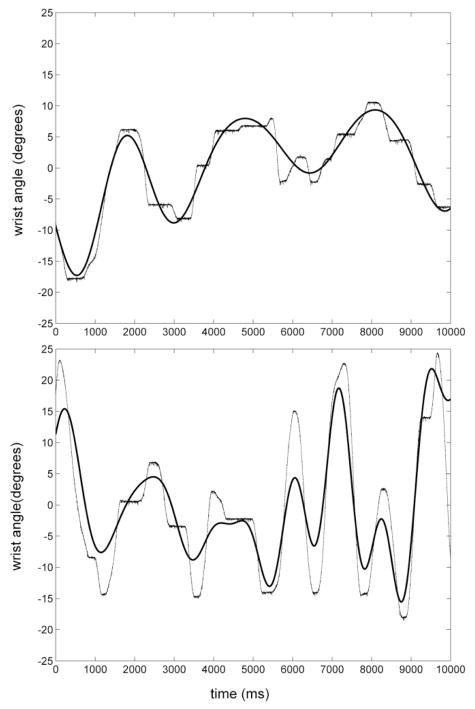
Fig. 5 shows sample time series of wrist position data obtained in Experiment 5 for a representative subject. The variance accounted for (VAF) by the best-fit model obtained in experiments 1–4 was quantified for each subject by comparing the model predictions of wrist angle to actual subject performance in each trial of Experiment 5. For the compensatory experiment, the solid line shows the perturbation applied to the cursor; for the pursuit experiment, the solid line shows the target position – the desired position of the hand. The VAF decreased slightly during the pursuit condition.

Figure 5.

Sample time courses for one subject (a) during compensatory tracking of visual displacements of the cursor and (b) during continuous pursuit of the target. The dashed lines show the subject response; solid lines show the model response to the same inputs.

IV. Discussion

Here, we have used a single lumped-parameter model of neuromotor control (Fig. 1) to characterize how sensory feedback is used to guide control of wrist position in both postural compensatory and target pursuit tasks. Despite the fact that the only conceptual difference between testing conditions is that pursuit tracking requires the desired wrist angle θ_d to vary as a function of time, whereas θ_d remains constant in compensatory tracking, our model found significant differences between estimated control parameters for the two conditions. These findings provide compelling support to the idea that the neural mechanisms governing limb posture and movement are at least partially distinct.

Figure 1.

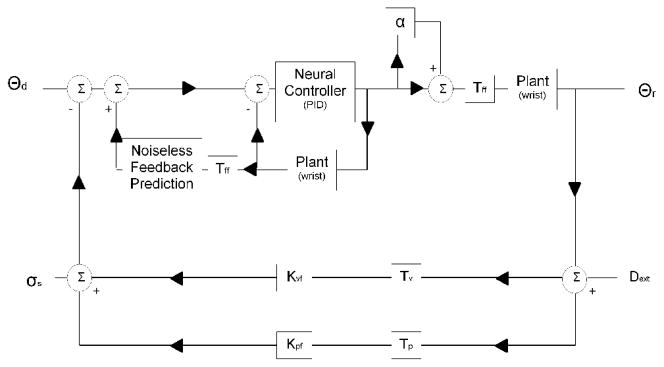
Control system model of sensorimotor control of movement. The inputs are the desired position of the wrist (Θ_d) and the perturbation (D_ext) applied to either the visual or proprioceptive sensory feedback pathways. The system output is the physically realized wrist position (Θ_r)

The difference in visual delays between compensatory and pursuit tasks was particularly surprising because it is commonly assumed that the visual delay is dominated by physiological factors not subject to neural modification. However, pilot data (not presented here) has shown that the visual delay can indeed increase as higher frequency components are added to the perturbation. This frequency dependence may be due to an increased ability to predict perturbations when they occur more slowly. This may also have contributed to the lower VAF for pursuit tracking; since the signal used for pursuit had higher frequency content (0–1Hz for pursuit; 0–.5 Hz for compensatory).

Additional support for the idea that the brain uses categorically different control mechanisms for compensatory and pursuit movements comes from differences in both the proportional and integral gain parameters of our generic PID model of the feedforward controller. In particular, we note that an integral gain was present in the target pursuit condition but was negligible during compensatory tracking.

V. Conclusion

A growing body of experimental research has shown that the control of limb posture and movement may be differentially impaired by neuromotor diseases [7,8,9]. By applying the techniques we developed here to populations with sensorimotor deficits, we expect to gain a better understanding of how these processes can be affected by neurological impairment. Such information could facilitate future development of rehabilitation strategies individualized for patients whose neural impairments may be limited to certain aspects of control (eg. limb postural regulation, integration of visual and proprioceptive feedback, etc.), thereby increasing the potential effectiveness of therapy and the quality of life for people with motor disabilities.