Modeling-error robustness of a viral-load preconditioning strategy for HIV treatment switching

Abstract

In previous work, we have developed optimal-control based approaches that seek to minimize the risk of subsequent virological failure by ”pre-conditioning” the viral load during therapy switches. In this paper, we use Monte-Carlo methods to evaluate the sensitivity of an open-loop implementation of these approaches to modeling errors. To account for hidden parameter dependencies, we use parameter distributions obtained from the convergence of Bayesian parameter estimation techniques applied to sets of clinical data obtained during serial therapy interruptions as the distribution from which the Monte-Carlo method samples.

I. INTRODUCTION

Modern combination therapy for HIV successfully suppresses the virus in a majority of cases. Treatment with a particular antiviral combination therapy often fails, however, due to a variety of factors, including adverse reactions and drug-resistant virus. Drug resistance in particular develops in up to 30 to 50% of all individuals being treated with highly active antiretroviral therapy (HAART) [1]. Drug resistance which occurs early in treatment is usually due to pre-existing resistant strains, whereas resistance emerging later is usually associated with poor compliance to the treatment schedule [2].

When resistance develops to a particular antiviral regimen, the patient must be transitioned to a new regimen. Resistance renders all components of the previous regimen useless for future regimens, as the function of multiple antiviral components in long-term control is to raise the mutational barrier to resistance, and resistant virus remains in the patient's viral reservoirs forever, erasing this barrier [3]. The new regimen must consist entirely of novel antiretrovirals, without established cross-resistance. 23 unique antiretrovirals are currently approved for the treatment of HIV infection [4], with several more being tested; however, the known patterns of cross-resistance mean that sequentially applied, only 6-7 combination therapies are available. There is a significant risk of a patient developing resistance to all available combinations; it is critical, therefore, to prevent the emergence of resistance to remaining antiretrovirals if possible [1].

A number of approaches are being explored to accomplish this goal. The International AIDS Society-US Panel now recommends resistance testing as part of the initial patient assessment, due to the prevalence of resistant strains in the population [5] [6] [7]. This is done in order to exclude from regimens those antiretrovirals to which resistance in known to exist, thus preserving the remaining antiretrovirals. A large body of research has focused on identifying viral strains exhibiting cross-resistance to one or more antiretroviral drugs [8] [9] [10] [11], allowing a more informed choice of new regimen based on the likely patterns of cross-resistance. More recent research has attempted to use this data to develop optimal treatment sequences, which are designed such that failure to combinations early in the sequence is unlikely to have broad cross-resistance with the remaining treatment options [12].

In our previous work [13],[14],[15],[16], we have developed optimal treatment scheduling algorithms which seek to minimize the risk of subsequent virological failure by ”pre-conditioning” the viral load prior to introducing a novel antiretroviral combination. This is accomplished by exploiting the residual efficacy of the failed antiretrovirals, either through interrupted therapy or through the use of novel combinations. We are exploiting the observation of Bonhoeffer and Ribeiro [2], [17], who show that resistant virus is most likely to emerge immediately following a therapy switch, and that the risk of resistance is proportional to the total viral load at the introduction of the new therapy.

In this paper, we test the robustness of this method to model parameter errors. Models of virus competition are only approximate descriptions of the system behavior, and parameters will likely change from patient to patient, and likely drift over time for the same patient. A method which is highly sensitive to model inaccuracies would be useless in practice. We have used a distribution of model parameters generated using Bayesian estimation techniques from patient data from an interruption trial reported in [18],[19]. This distribution was used for Monte-Carlo analysis of the performance of our algorithm using nominal parameter values.

In section II we revisit the model introduced in previous work, and describe the parameter estimation technique used to generate the parameter distribution. We also discuss the experiment from which the data were generated. In section III, we describe the algorithm for optimal treatment switching. In section IV, we introduce a performance metric to determine success or failure of the algorithm, present the results of the algorithms performance across our parameter distributions, and discuss the patterns of robustness and sensitivity observed. In section V, we discuss the implications of these results for clinical implementation of this method, and briefly discuss future works.

II. MODEL IDENTIFICATION

A. Viral strain competition model

The dynamics of HIV competition are represented in our work by an ordinary differential equation model first presented in [13]:

$$\begin{array}{cc}\hfill & \stackrel{.}{x}=\lambda -dx-{\beta }_w(1-u_1)(1-u_2)x{v}_w-{\beta }_r(1-u_2)x{v}_r\hfill \\ \hfill & {\stackrel{.}{y}}_w={\beta }_w(1-u_1)(1-u_2)x{v}_w-a_w{y}_w+{\lambda }_w\hfill \\ \hfill & {\stackrel{.}{y}}_r={\beta }_r(1-u_2)x{v}_r-a_r{y}_r+{\lambda }_r\hfill \\ \hfill & {\stackrel{.}{v}}_w=k_w{a}_w{y}_w-u_w{v}_w\hfill \\ \hfill & {\stackrel{.}{v}}_r=k_r{a}_r{y}_r-u_r{v}_r\hfill \end{array}$$

describing the dynamics of multiple species of HIV virus v_i, their respective infected cell populaitons y_j, their relative susceptibility to antiviral regimens u_k, and the healthy target cell population x. The equations above are for a single wild-type and a single resistant virus strain, but the equations are arbitrarily scalable to any number of species. The contribution of reservoir dynamics is approximated here as a small constant influx.

B. Parameter estimation

To apply the system of equations describing the evolution of viral loads and CD4+T cells to a specific individual, the parameters of the nonlinear differential equations need to be estimated. Using patient data from the AutoVac study [19], we have used Bayesian estimation techniques (specifically, the MCMC method) to identify parameters from this model. The AutoVac study took viral load measurements at 1-day intervals during a series of on-off treatment switches for a number of patients. The data available for estimation is limited to a few values of viral loads after an interruption of medication and reintroduction. In this work, we follow the approach of Huang [20] in applying a Bayesian nonlinear mixed-effects model. There are six parameters to estimate: λ, the generation rate of the target cells, d, the death rate of the target cells, β, the infection rate for the wild type virus, a, the death rate of the cells infected with the wild type virus, k, the number of viral particles emitted per infected cell, and u, the death rate of viral particles. The generation rates for the wild and resistant virus from long-term reservoirs are assumed to be a small, known constant. Since the data is so limited, the parameters for the resistant virus is assumed to be known from the parameters of the wild type virus. The beta for the resistant type virus is assumed to be the same for the resistant virus. The death rate for the resistant virus is assumed to 2.5 times the death rate of the wild type virus. The number of viral particles per infected cell and the death rate of viral particles are assumed to be the same for both the wild and resistant virus.

Assume that there are n subjects and for the i^th subject, we have m_i measurements of viral load. We denote the mean of the parameters as:

$$\begin{array}{cc}\hfill & \mu ={[\text{log}\left(\lambda \right),\text{log}\left(d\right),\text{log}\left(\beta \right),\text{log}\left(a\right),\text{log}\left(k\right),\text{log}\left(u\right)]}^T\hfill \\ \hfill & {\theta }_i={[\text{log}\left({\lambda }_i\right),\text{log}\left(d_i\right),\text{log}\left({\beta }_i\right),\text{log}\left(a_i\right),\text{log}\left(k_i\right),\text{log}\left(u_i\right)]}^T\hfill \\ \hfill & ϴ=\{{\theta }_i,i=1,\cdots ,n\}\hfill \\ \hfill & {ϴ}_{\left\{i\right\}}=\{{\theta }_l,l\ne i\}\hfill \\ \hfill & Y=\{y_{ij},i=1,\cdots ,n;j=1,\cdots ,m_i\}\hfill \end{array}$$

The logarithm is used to ensure that all estimates of the parameters are positive. The vectors,μ and θ_i are the mean of the parameters and the parameters for the i^th individual respectively. The matrices Θ, Θ{i} and Y are the matrix of the parameters where the i^th column is the parameter for i^th patient, the matrix of parameters with the i^th column deleted and the matrix of available measurements for all the patients. Let V(t) denote the solution of the differential equation and V_ij(θ_i,t_j) is the value of V(t) for the i^th patient using parameters θ_i at time t_j. Finally, y_ij(t_j) is the logarithms of the measurements of viral load for patient i at time t_j and e_i(t_j) is the measurement error for the i^th individual at time t_j and is assumed to be zero mean.

Following the three stage development of [21] [22] [20], the Bayesian nonlinear, mixed-effects model can be written as:

1. The variation within a single subject obeys: y_i = f_i (θ_i)+e_i with the components of being independent with 0 mean and equal variance σ².

2. The between subject variation is given by, θ_i = μ + b_i with b_i ~ N 0,Ξ^–1) with N being the normal distribution.

3. The hyper-distributions on the prior parameters are: σ^–2 ~ Ga(a,b),μ ~ N (η,Λ),Ξ^–1 ~ Wi(Ω,ν) with Ga being the gamma distribution and Wi is the Wishart prior distributions. All the hyper-parameters, a,b,η,Λ,Ωandν are known.

The hyper-parameters are defined as:

$$\begin{array}{cc}\hfill & {\sigma }^{-2}\sim Ga\left(a+\frac{\sum _{i-1}^n{m}_i}{2},A^{-1}\right)\hfill \\ \hfill & \mu \sim N(B^{-1}C,B^{-1})\hfill \\ \hfill & {\Xi }^{-1}\sim Wi(D-1,n+\nu )\hfill \end{array}$$

with $A=b^{-1}+\frac{1}{2}{\sum }_{i=1}^n{\sum }_{j=1}^{m_i}{\mid y_{ij}-f_{ij}({\theta }_i,t_j)\mid }^2,B=n{\Xi }^{-1}+{\Lambda }^{-1}$, $C={\Xi }^{-1}{\sum }_{i=1}^n{\theta }_i+{\Lambda }^{-1}\eta$ and $\mathrm{D}={\Omega }^{-1}+{\sum }_{i=1}^n({\theta }_i-\mu ){({\theta }_i-\mu )}^T$.

To obtain reasonable results from the MCMC method, good initial estimates of θ_i are needed. A constrained least squares approach is used to get an initial estimate. The parameters are constrained so that basic reproduction ratio, R₀ is greater than 1. If it were less than 1, the virus would eventually be eliminated, but because of long-lived reservoirs, the virus is never totally eradicated. Another constraint is that the equilibrium of CD4 cell (x) count is less than 1500. This constrained non-linear least square provides the initial estimates for the MCMC approach described above.

The above procedure was applied to the data for 12 patients. The MCMC procedure produced 200,000 possible combinations of data that are consistent with the patients’ data. From this result, the marginal probability densities for of the six parameters can be established.

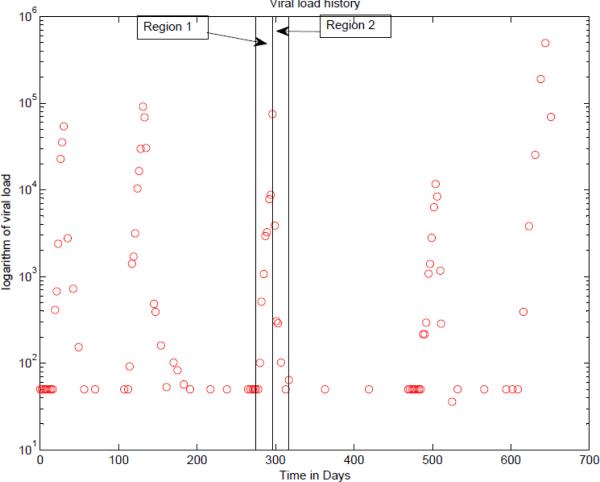
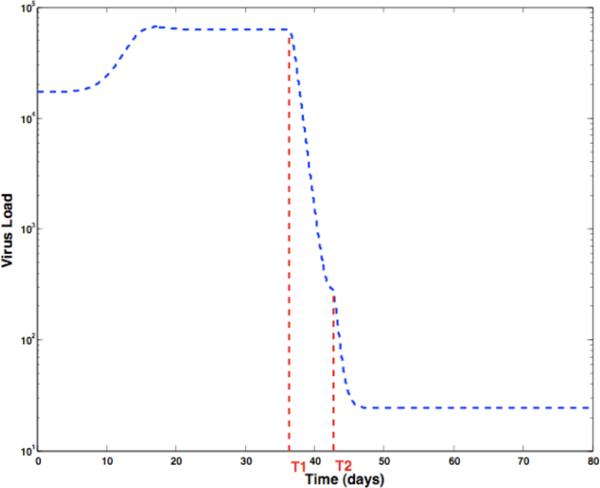
Models were generated for each of 12 patients. For each patient, treatment was interrupted and after a period of time, the treatment was restarted. This cycle of interruption and reinstating the treatment is repeated 3 or 4 times. Shown in Fig.1 is a plot of the logarithm of the viral load for a particular patient versus time in days. There are 5 interruptions in treatment, and in four cases, the treatment was reinitiated. For the purpose of fitting the data, one of the pulses, say the third one in the figure is used for parameter estimation. The data in region 1 in which the treatment is interrupted is used to estimate the 6 parameters, λ,d,β,a,k and u, using a constrained nonlinear least squares. The data in region 2 contains information concerning the drug efficiency. With the value of the six parameters fixed to those values found by least squares in region 1, the data of region 2 is used to estimate the drug efficiency.

Fig. 1.

The logarithm of the viral load for Patient 1

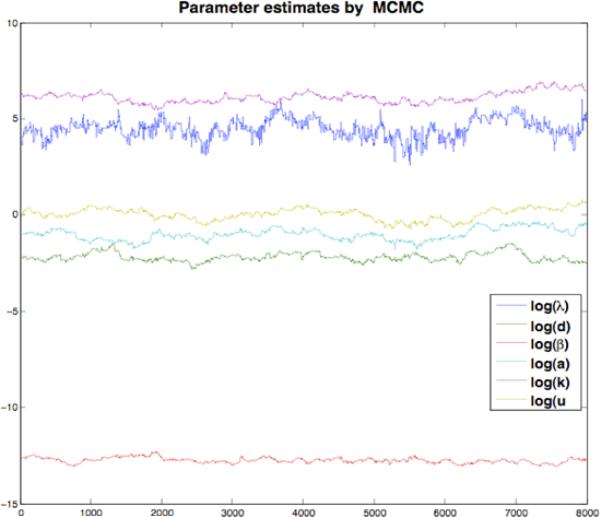
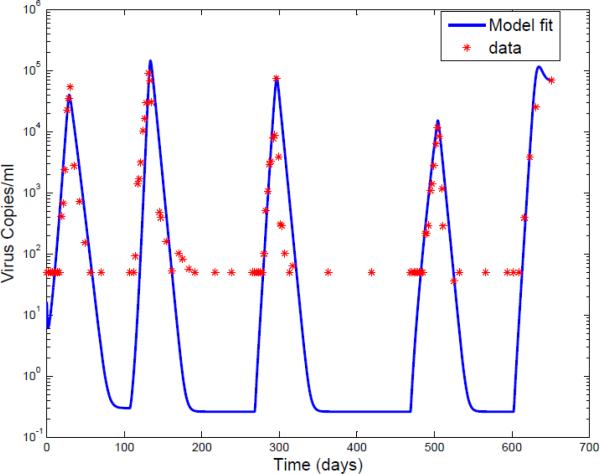
For each of the other pulses, the parameters λ,d,β,a,k and u, are held to their estimated values. Since drug efficiency can be time varying, the data after the reintroduction of the drug is used to estimate the drug efficiency. Results of a particular patient by using this identification method are shown in Fig.2 and Fig.3.

Fig. 2.

Convergence of parameter estimates for a single patient over first 8000 samples using Metropolis-Hastings Algorithm

Fig. 3.

The logarithm of the viral load for Patient 1

III. OPTIMAL TREATMENT SWITCHING

Normally, at the beginning of antiretroviral treatment, the amount of HIV in patients’ body goes down dramatically. The reason for this is most of the virus is wild-type. Just as wild-type virus is the most fit and most able to replicate without any treatment, it's also the most sensitive to antiretroviral treatment. The negative side of wild-type virus's sensitivity to antiretroviral drugs is that when treatment begins, the viruses with certain mutations in the reverse transcriptase or protease enzymes have a survival advantage. The drug cannot stop these kinds of viruses from reproducing. Drug-resistant virus is able to replicate despite the presence of the drug and will become the dominant strain over time. But the competition relationship between wild-type virus and resistant virus offers a possible way to control drug-resistance risk. In the previous works [13],[14],[15],[16], we proposed a novel idea to control drug-resistance risk by using structured treatment interruptions (STIs) properly.

Since the late 1990s, Various STIs have been studied for the following reasons: interruptions are worthy to study are:

1. to reinvigorate the immune response.

2. to help people from treatment fatigue.

3. to deal with drug side effects.

4. to wait some new drugs.

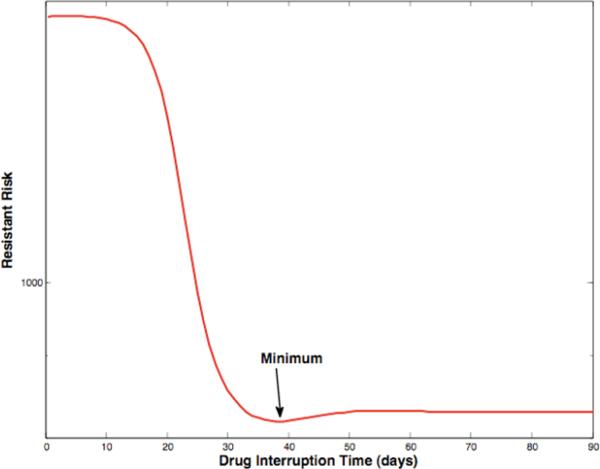
We have developed scheduling algorithms for optimally switching from a failing antiviral regimen to a naive antiviral regimen. These schedules consist of an optional interruption of length T1, to sensitize the virus, followed by either the re-introduction of the failing regimen or the introduction of a permutation of previously failed antiviral regimen components, resulting in transient suppression of the sensitized viral load. Before viral load rebound occurs, the naive antiviral regimen is introduced at time T2, resulting in a greatly reduced risk of subsequent virological failure. The optimal time for introduction of the naive regimen is fixed by the initial conditions at time T1. The optimal interruption length T1 changes as a function of parameters; there may be a true optimum, as shown in Fig.4, or the optimal time may be infinite. In the second case, a knee in the curve, where increased interruption time yields only marginal benefit, dictates the switching time. Fig.5 shows the associated optimal switching schedule, with viral load as a function of time.

Fig. 4.

Achievable risk reduction as a function of interruption length; in this case, a true minimum exists.

Fig. 5.

Optimal switching schedule. Treatment is interrupted at time 0, and reintroduced at time T1. At time T2, naive treatment is introduced, yielding an 2 order-of-magnitude reduction in risk.

IV. ROBUSTNESS TO MODELING ERROR

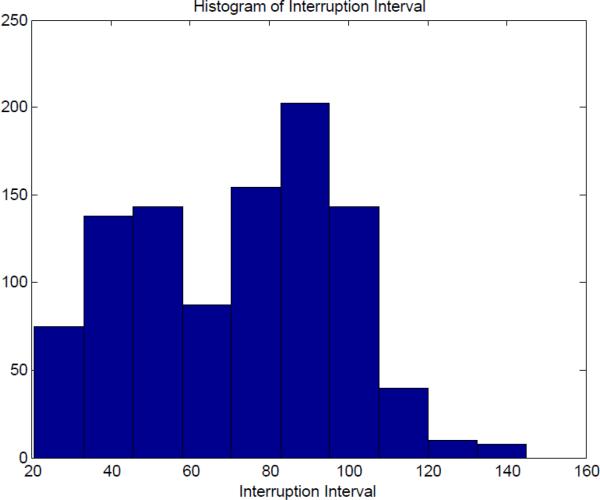
The MCMC algorithm produced 200,000 possible parameters estimates. Any solution to the estimation problem would be a sample from this multivariate distribution. To test the robustness of our method, we randomly sampled with replacement from the database of parameter values. For each we computed the optimal switching time to reintroduce the HIV cocktail of drugs. Furthermore, we assumed that the mean of the distribution was the true value for that individual. From the risk or viral load vs. switching time curve, the optimal switching time and minimum risk or minimum viral load can be found. Fig.6 shows the distribution of the optimal interruption interval for 1000 samples from the 200,000 possible values. The optimal switching time are very sensitive to the parameter values. To see the effect of parameters that are not optimal, the risk beyond the optimal value was generated for these samples. Fig.7 is the histogram of the actual risk for the 1000 samples based on the proposed algorithm.

Fig. 6.

Histogram of Interruption Interval

Fig. 7.

Histogram of Actual Risk

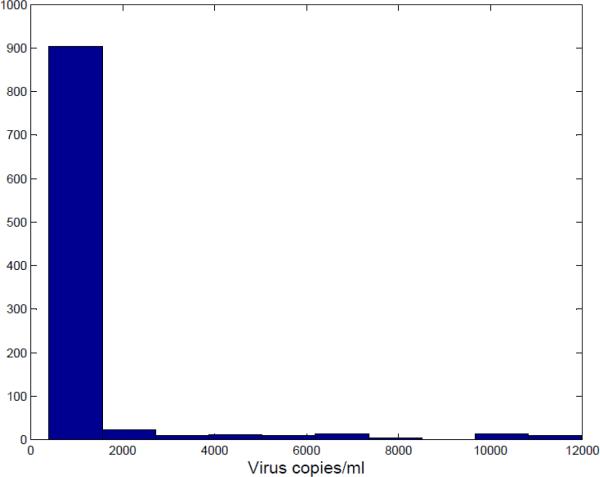
Guidelines for the Use of Antiretroviral Agents in HIV-1-Infected Adults and Adolescents [23] states:” There is no consensus on the optimal time to change therapy for virologic failure. The most aggressive approach would be to change for any repeated, detectable viremia (e.g., two consecutive HIV RNA geater than 50 copies/mL after suppression to less than 50 copies/mL in a patient taking the regimen). Other approaches allow detectable viremia up to an arbitrary level (e.g., 1000-5000 copies/mL)”. In this paper, values of 2500 or less for actual risk is viewed as being acceptable in this paper. In this case, 92.5% or 925 out of 1000 sets of parameter estimates produced values with an excess risk less than 2000. That means for each of these models would produce a risk to patient that is significantly less than what the patient would experience if there was no delay in switching. For the 75 or 7.5% of the exemplars for which the value exceeds 2000, the fit to the training data was poor and would most likely have been rejected.

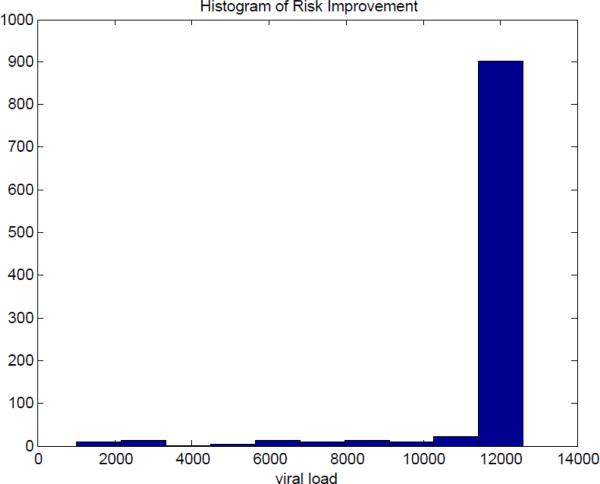
Although the guidelines [23] [24] suggests to change drugs when virus load exceeds some threshold values (e.g., 1000-5000 copies/mL), it has a little probability to find the exact timing for viral load just reaching the threshold, because a patient during therapy routinely tests viral load every 3 or 4 months. Therefore, it is reasonable to choose equilibrium of viral load as the comparison benchmark. In this case, even for the case of poor fits to the data, the solutions are still much better than would have happened without the interruption. Fig.8 shows the histogram of the risk improvement, compared with the situation without STIs, for these 1000 samples. Here are some important statistics on the improvement in risk: the average improvement is 12,028, the median is 12,600 and the minimum improvement is 1,022.

Fig. 8.

Histogram of Risk Improvement

V. CONCLUSIONS AND FUTURE WORKS

A. CONCLUSIONS

In this paper, we have developed a Monte-Carlo technique for testing the robustness of our previously proposed viral-load preconditioning procedure [13],[14],[15],[16] to likely variations in patient dynamics. In order to implicitly account for important parameter dependencies, we use the stochastic distribution of parameters generated by MCMC parameter identification applied to data from 12 HIV patients as the set from which parameter sets are randomly chosen.

For each Monte-Carlo trial, we measured the performance obtained by applying an optimal control schedule generated using a nominal parameter set to a system with a stochastically varying parameter set. The true optimal schedule was also obtained for each stochastically varying parameter set. For each case, we measured the achieved minimal viral load, the theoretically obtainable viral load (if the true parameters were known), and the difference in optimal switching time.

Optimal switching time was very sensitive to model variation. However, the achieved minimum viral load was not. As shown in the histogram Figure 7, even with significant variation in parameter values, the nominal parameter set achieved significant viral load suppression to below 2500 copies/mL in 92.5% of the cases. As most widely used treatment recommendations do not suggest switching treatment until viral load reaches 5000 copies/mL, this represents a 50% reduction in the risk of subsequent virological failure due to pre-existing resistant strains, when compared to state of the art treatment. Furthermore, current guidelines for viral load monitoring during long-term suppression allow infrequent enough measurement that the resistant strain is likely to have reached equilibrium before it is detected. This would represent a baseline viral load as high as 50,000 copies/mL, and a 96% reduction in risk.

The mathematical models which describing HIV dynamics can be valuable tools for assisting in the design of clinic treatment strategies, because of the wealth of research on HIV pathogenesis and HIV dynamic models formalizing description of its underlying processes. However, it is relatively difficult to get the accurate values for the parameters. In this paper, it has been demonstrated that even a nominal model is sufficient to obtain significant improvement over state of the art care, and that sensitivity to model inaccuracy does not present a significant problem to implementation of this procedure.

B. FUTURE WORKS

The parameter distributions which are used in this work were generated from a relatively small sample of patients. In order to gain greater confidence in the parameter distributions, we will be use the parameter estimation approaches on a larger set of patient data.

The ratio of wild-type virus parameters to resistant virus parameters was assumed to be fixed in this paper. This is due to a lack of reliable in vivo data on resistant virus dynamics. We intend to use in vitro viral fitness data, correlated to our in vivo parameter estimates, to obtain a better estimate of parameter values as a function of viral strain.

The results of this paper suggest that our method can be implemented in a ”model-free” form; that is, a heuristic equation based on a nominal model will provide adequate results. To implement this, however, we need a closed-loop measurement method to detect the viral load minimum. We are developing methods for detecting the minimum which use a minimal number of viral load measurements, to minimize cost and risk to the patient.

Finally, we are developing predictive models of viral load composition, to be able to estimate, based on the patient's history of antiviral use and failure, which resistant virus populations are likely established in the patient. This will allow us to directly calculate the risk of particular strains emerging, which will allow us to further optimize treatment.