Optimal Retirement with Increasing Longevity

Abstract

We develop an optimizing life-cycle model of retirement with perfect capital markets. We show that longer healthy life expectancy usually leads to later retirement, but with an elasticity less than unity. We calibrate our model using data from the US and find that, over the last century, the effect of rising incomes, which promote early retirement, has dominated the effect of rising lifespans. Our model predicts continuing declines in the optimal retirement age, despite rising life expectancy, provided the rate of real wage growth remains as high as in the last century.

I. Introduction

The improvement in life expectancy and living standards over the last 150 years constitutes a dramatic increase in human welfare. Theseimprovements have not only resulted in a large direct gain in welfare (Nordhaus, 2003; Becker et al., 2005) but have also had a profound influence on economic life-cycle behavior by changing people’s time horizons (Hamermesh, 1985).

In this paper, we extend the Blanchard—Yaari—Weil model of consumption with finite lives and perfect annuity markets to endogenously determine retirement, as well as the time path of consumption. We use the model to show how optimal retirement decisions respond to changes in wage levels and life expectancy. Following Auerbach and Kotlikoff (1987), we explain that the retirement of older workers is a result of the decline in health that comes with age, which increases the disutility of labor and reduces the productivity of working.

While health declines with age, longer lifespans have been accompanied by improved age-specific health status (i.e., we are living both longer and healthier lives). The “compression of morbidity” hypothesis (Fries, 1980) maintains that the average age at first infirmity, disability, or other morbidity is postponed to such an extent that the period of ill health at the end of life is compressed. Increases in life expectancy in the US over the last two centuries have indeed been associated with reductions in the age-specific incidence of disease, disability, and morbidity (Fogel, 1994, 1997; Crimmins et al., 1997; Costa, 2002; Freedman et al., 2002). We model the compression of morbidity by assuming that the age of onset of disability rises proportionately with life expectancy.¹ The compression of morbidity means that it is plausible that people respond to longer life expectancy by raising their retirement age.

Increases in both wages and lifespan have wealth effects, in that they enlarge the budget set. They also have incentive and substitution effects by changing the rewards for working. Our model shows that, under standard assumptions on preferences, particularly the intertemporal elasticity of substitution, higher wage levels lead to earlier retirement. However, we show that an increase in life expectancy leads to a rise in retirement age, but less than proportionately. The intuition for the less than proportional rise in retirement age is that later retirement allows a longer period of compound interest on savings, making people richer at retirement than previously, which encourages earlier retirement. We calibrate the size of the effect of lifespan increase versus the effects of higher wages using data from the US, showing that over the last century the effect of higher wages has dominated, leading to earlier retirement.

While increases in life expectancy usually lead to later optimal retirement, in theory it is possible for the reduction in age-specific mortality rates at young ages to lead to earlier retirement (D’Albis et al., 2012). We focus on whether the rise in retirement age will be more or less proportional to the increase in life expectancy. We derive a simple condition on the change in the survival function, which we show is verified empirically, under which the changes in expectancy lead to a less than proportional increase in retirement age.

While we concentrate on the effects of greater longevity on retirement age, we also show that longer lifespans tend to reduce the rates of saving. This generalizes the results on savings in Bloom et al. (2007), who assumed log utility of consumption and age-independent mortality rates, because we assume only a concave utility function over consumption, and allow general age-specific mortality rates. Our savings results differ from those in previous theoretical papers (Chang, 1991; Kalemli-Ozcan and Weil, 2010), where it was argued that increased longevity will increase rates or saving. The major difference is that we allow for the compression of morbidity, which encourages longer working lives, and we assume complete annuity markets, which compensate savers for the risk that savings could be wasted because of early mortality.

Our theoretical model predicts countervailing forces on retirement age from the secular rise in wage levels and healthy life expectancy. We resolve this by calibrating the model using data from the US over the last century. Over this period, our calibration suggests that the magnitude of the effect of higher wage levels on retirement has been twice as large as the effect of longer lifespans, so that, overall, our model predicts a movement towards earlier retirement. The calibrated decline in retirement age is consistent with the observed evolution of earlier retirement over the last century (Costa, 1998a, 1998b). Our model assumes rational agents and perfect annuity markets.

Our paper does not take into account the role of social security systems that produce incentives known to be important for retirement decisions (Gruber and Wise, 1999). Rather than think of social security systems as distortions that move behavior away from the optimum, we can think of them as mechanisms aimed at overcoming suboptimal outcomes due to myopia in savings decisions and failures of the annuity market. If social security systems are designed to overcome bounded rationality and market failures, and to mimic the optimal outcomes that would occur if people were rational and markets were perfect, our model should predict actual behavior. Our calibration exercise can therefore be regarded as a test of whether actual outcomes — where forced saving and the retirement incentives due to social security offset the effect of bounded rationality and market failures — mimic what would happen with optimal behavior.

We present our model in Section II. In Section III, we show how the dynamic programming problem that agents face generates a set of equations that determine the optimal retirement age and consumption profile, and we use the model to investigate the theoretical effect of increases in healthy lifespan and wages on retirement behavior. In Section IV, we calibrate the model to 20th-century US data. In Section V, we give some concluding remarks.²

II. The Model

Our formal life-cycle model makes a number of simplifying assumptions. We assume that the mortality schedule is exogenous, ignoring the possibility of using consumption and health services to extend longevity (Ehrlich and Chuma, 1990), or the possibility of a reverse link from labor supply to health status and life expectancy. In the interests of simplicity, we also start our analysis at adulthood, following the conclusion of full-time education. In principle, schooling is endogenous and longer lifespans might increase the incentive to invest in education (De la Croix and Licandro, 1999), although it is really only the duration of working life that earns a return to education (Echevarría and Iza, 2006; Hazan, 2009). We avoid this issue by starting our analysis after schooling has been completed, and we assume that people make decisions only about labor supply and consumption.

We begin by modeling age-specific mortality. In principle, we could have changes in the mortality rate at any age, with other mortality rates being fixed, as D’Albis et al. (2012) assume. However, in practice, age-specific mortality rates within a country tend to move together in the same direction over time. This assumption lies behind common methods of modeling age-specific mortality rates, such as model life tables (Murray et al., 2000) and the model of Lee and Carter (1992). Under this assumption, we have a one-to-one mapping from life expectancy to a survival schedule.³ We denote the probability of survival to age t when life expectancy is z by s(t,z). The mortality rate at age t is

$$m(t,z)=-\frac{(\mathrm{d}s∕dt)(t,z)}{s(t,z)}.$$ (1)

We assume that there is a biological maximum, T , to the length of life (Carnes et al., 2003). Analytically, this ensures that that there is no possibility of an infinite working life and retirement age.

An important feature of our model is the health scheduleh(t,z), which, as in Bloom et al. (2007), depends on age and life expectancy. We assume that health declines with age t, but that health at age t depends on life expectancy z. If health is independent of z, it implies that increases in life expectancy are not associated with general health improvements in the form of reductions in morbidity (sickness), which in turn implies that population aging is associated with an increasingly large proportion of unhealthy people.

However, the evidence points in the opposite direction. Not only are people living longer, but age-specific disability is also falling. Cutler (2001) attributes reductions in disability at older ages to the long-term protective effects of reduced disease exposure in childhood, the rising levels of education and socioeconomic status, improved health-related behavior (such as the reduction in smoking), improved medical care, and the use of special aids to reduce disability for a given state of health. Manton et al. (2006) estimate that between 1935 and 1982, both life expectancy and (disability-free) active life expectancy at age 65 increased in the US, keeping the proportion of disability-free life after 65 relatively steady at around 73 per cent. However, between 1982 and 1999, life expectancy at age 65 rose from 16.9 to 17.7 years, while active life expectancy rose from 12.3 to 13.9 years. This implies a rise in the proportion of disability-free life to over 78 per cent, and a reduction in the absolute time spent in disability from 4.6 to 3.8 years. The compression of morbidity, either absolute or relative, appears to hold in most developed countries (Mor, 2005). Although time-series evidence in developing countries is scarce, Mathers et al. (2001) show that, across countries, health-adjusted life expectancy (each life year weighted by a measure of health status) increases as rapidly as total life expectancy, implying a rising ratio of healthy to total life expectancy as the latter increases.

While there is strong evidence for a long-term compression of morbidity in the US, the picture for the future and the very recent past might be less clear, perhaps because of rising obesity (Olshansky et al., 2005; Crimmins and Beltrán-Sánchez, 2011). Although the compression of disability in the US, at least in the past, seems evident, and although disability is a cause of retirement (Gordo, 2011), most people retire before the onset of severe disability. Despite the fact that they might still be physically capable of working, people with moderate ill health that does not amount to disability might be deterred from participating in the labor force. The “dynamic equilibrium” hypothesis suggests that the compression of time spent in severe disability might be the result of reducing the transition rate from low or moderate ill health to severe disability. In turn, this might result in an increase in the prevalence of less severe disability states (e.g., Graham et al., 2004).

To examine the effect of the compression of morbidity, we take as our benchmark the case where healthy lifespan increases proportionately to overall lifespan. This assumption (i.e., that the relative proportion of lifetime spent in disability is constant) seems weaker than the assumption that the absolute number of years lived with disability declines. Technically, this implies that the health schedule is homogeneous of degree zero, so that health at each age depends only on the age relative to life expectancy:

$$h(\rho t,\rho z)=h(t,z)\text{for}\rho >0\Rightarrow h(t,z)=h[(t∕z),1].$$ (2)

We denote labor supply at time t by X_t, which is assumed to lie in the closed interval [0,1]. Felicity is assumed to be strongly separable in goods and leisure⁴ and is given by⁵

$$u\left[c\left(t\right)\right]-\chi \left(t\right)v\left[h(t,z)\right],$$ (3)

where c t(t) is consumption at age t and v[h(t,z)] is the disutility of working given the health state h(t,z). We assume that u is twice differentiable with u′(c > 0,u″(c) < 0, and that the disutility function v satisfies v′(h) < 0, so that the disutility of work (and the relative utility of leisure) is higher when health is lower. Lifetime expected utility is

$$U={\int }_0^T{\mathrm{e}}^{-\delta t}s(t,z)\{u\left[c\left(t\right)\right]-\chi \left(t\right)v\left[h(t,z)\right\}\mathrm{d}t,$$ (4)

where δ is the subjective rate of time preference, and T is the biological maximum lifespan. The wage earned by a worker with health h is given by

$$w(t,h)=A\left(t\right)w_h\left[h(t,z)\right].$$ (5)

The term A(t)captures the change in wages over time as workers age due to exogenous forces (e.g., technical progress) and age effects, and w_h[h(tt,z)] captures the fact that worker productivity depends on health, which is a function of age relative to life expectancy.⁶ We assume A′(t) ≥ 0 and w′_h(h) ≥ 0, so that wages are increasing over time due to exogenous forces and wages are higher for workers with better health. The multiplicative functional form implies that the health effect on log wages is additive, which is consistent with a Mincer wage equation that includes health as a form of human capital, as in Schultz (1999). We can, in principle, capture the observable inverted U-shape of productivity with age (Skirbekk, 2003) if we assume that the A(t) term dominates initially, but overall productivity eventually declines because of the health-related component.⁷ Chang (1991) and Kalemli-Ozcan and Weil (2010) have exogenous ageμ̵wage schedules that do not change as life expectancy varies; we allow for an effect of life expectancy on wages through improved health.

Wealth W evolves according to

$$\frac{\mathrm{d}W}{\mathrm{d}t}=\chi \left(t\right)A\left(t\right)w_h\left[h(t,z)\right]+[m(t,z)+r]W\left(t\right)-c\left(t\right).$$ (6)

If the agent works at time t, he or she earns the wage A(t)W_h[h(t,z)], and this is added to wealth. Consumption c(t reduces wealth, while the stock of wealth earns a return, m(t,Z)+ r. We assume that wealth can be transferred from one period to another by saving or borrowing from the competitive financial sector. This sector can borrow or lend freely at the interest rate r. Agents are paid an effective interest rate m(t,Z) + r on their savings, which is larger than r, to compensate them for the fact that they might die before withdrawing their savings. Similarly, agents who borrow pay the rate m(t,Z + r to compensate the bank for the fact that they might die before repaying their borrowings. This is equivalent to treating all savings as annuity purchases, while assuming that all borrowing has to be accompanied by an actuarially fair life insurance contract for the amount of the loan. Provided that there is a continuum of agents, the financial sector can avoid all risk by aggregating over individuals, thereby earning zero profits.

The transfer of wealth to the financial sector from those who die exactly compensates deposit-taking institutions for the fact that they pay an interest rate m(t,z)+ r on deposits that exceed the risk-free rate r, and rules out the need to consider unintended bequests.

The budget constraint for the agent is

$${\int }_0^T{\mathrm{e}}^{rt}s(t,z)c\left(t\right)\mathrm{d}t={\int }_0^r{\mathrm{e}}^{-rt}s(t,z)\chi \left(t\right)A\left(t\right)w_h\left[h(t,z)\right]\mathrm{d}t.$$ (7)

The control variables for the agent’s optimization problem are cX . Agents must decide when to work and what their consumption stream should be.⁸

We assume the following boundary conditions:

$$\begin{array}{cc}\hfill & A\left(0\right)w_h\left[h(0,z)\right]u^{\prime }\left[c\left(0\right)\right]>v\left[h(0,z)\right];\hfill \\ \hfill & A\left(T\right)w_h\left[h(T,z)\right]u^{\prime }\left[c\left(T\right)\right]<v\left[h(T,z)\right].\hfill \end{array}$$ (8)

The first boundary condition implies that the disutility of working at age zero is low enough to ensure that the agent always prefers to work at the start of life, rather than to live with no work and no consumption. The second boundary condition implies that the disutility of working at the maximum possible age is high enough that the agent always prefers to retire.

In what follows, we assume that the rate of interest r is positive and equals the rate of time preference δ . Our theory is developed for the case where the growth rate of the exogenous component of wages is moderate. If wage growth is very rapid, then a retired worker might re- enter the labor market to take advantage of the high wages when older. To rule this out, we assume that, for every life expectancy, the rate of growth of the disutility of labor with age exceeds the exogenous component in the rate of growth of wages at each point in time:

$$\frac{\stackrel{.}{A}}{A}<\frac{\stackrel{.}{v}}{v}.$$ (9)

We show that this condition implies that retirement occurs only once and is never reversed. In this case, we can label the retirement age R .

III. Optimal Retirement and Consumption Decisions

The Hamiltonian for the problem of maximizing lifetime utility subject to the budget constraint is

$$\begin{array}{cc}\hfill H=& {\mathrm{e}}^{-\delta t}s(t,z)\{u\left[c\left(t\right)\right]-\chi \left(t\right)v\left[h(t,z)\right]\}\hfill \\ \hfill & +\varphi \left(t\right)\{\chi \left(t\right)A\left(t\right)w_h\left[h(t,z)\right]+[m(t,z)+r]W\left(t\right)-c\left(t\right)\}.\hfill \end{array}$$ (10)

The first-order conditions are reported in the Online Appendix and can be shown to yield the following:⁹

$$\frac{\stackrel{.}{c}}{c}=(r-\delta )\frac{u^{\prime }\left(c\right)}{-c{u}^{″}\left(c\right)};$$ (11)

$$\begin{array}{cc}\hfill u^{\prime }\left[c\left(t\right)\right]A\left(t\right)w_h\left[h(t,z)\right]>v\left[h(t,z)\right]\Rightarrow & \chi \left(t\right)=1;\hfill \\ \hfill u^{\prime }\left[c\left(t\right)\right]A\left(t\right)w_h\left[h(t,z)\right]=v\left[h(t,z)\right]\Rightarrow & \chi \left(t\right)\in [0,1];\hfill \\ \hfill u^{\prime }\left[c\left(t\right)\right]A\left(t\right)w_h\left[h(t,z)\right]<v\left[h(t,z)\right]\Rightarrow & \chi \left(t\right)=0.\hfill \end{array}$$ (12)

The concavity of the utility function u in consumption implies that the Hamiltonian is concave in the two control variables Hence, these first-order conditions give a global maximum of the Hamiltonian in the control variable, c and X. The Hamiltonian is jointly concave¹⁰ in the two control variables and the state variable, wealth, and hence satisfies the Mangasarian condition for our set of equations to give a maximum for the dynamic programming problem (see Sydsaeter et al., 2000).

Equation (11) is the standard finding of consumption smoothing over the life cycle. Given our assumption that r=δ, optimal consumption is constant over time.¹¹ The risk of death does not affect consumption decisions because annuities insure perfectly against financial losses due to death. Equation (12) implies that agents work at time t as long as the utility gain from the consumption purchased by the wage they earn (marginal utility of consumption χ wage) exceeds the disutility of working. We would emphasize the bang-bang nature of the work decision. At most ages, individuals either choose to work full time X(t)=1, or not to work at all X(t)=0. The agent is indifferent between working and not working only when the marginal utility of consumption χ the wage exactly equals the disutility of working.

Proposition 1. (a) In the optimal plan, retirement occurs once and is not reversed. (b) The retirement age and consumption stream that maximize expected lifetime utility are unique. (See the Online Appendix for proof.)

First, we prove that any optimal plan has a single and irreversible retirement age. We then prove that this optimal plan is unique. Note that retirement emerges endogenously from our model. In our framework, a lack of health effects on the disutility of labor and wages, combined with exogenous wage growth, would tend to produce leisure during youth when wages are low, and work when older and wages are high; the health effects are essential for our model to produce retirement. The assumption that r=δ, simplifies the proof of uniqueness of the retirement age but is not essential. However, if r=δ, consumption falls over time and older people choose to go back to work after retirement because the high marginal utility of consumption makes working and earning money attractive. We would need to add an assumption that implies that this effect was not too large to ensure the non-reversal of retirement decisions.

Given Proposition 1, we can rewrite the budget constraint as

$${\int }_0^T{\mathrm{e}}^{-rt}s(t,z)c\left(t\right)\mathrm{d}t={\int }_0^R{\mathrm{e}}^{-rt}s(t,z)A\left(t\right)w_h\left[h(t,z)\right]\mathrm{d}t.$$ (13)

In what follows, the choice variables are consumption level and retirement age, chosen to maximize utility subject to equation (13). The key equation that retirement age must solve is

$$u^{\prime }\left[c\left(R\right)\right]A\left(R\right)w_h\left[h(R,z)\right]=v\left[h(R,z)\right].$$ (14)

At the optimal retirement age, the marginal utility of consumption χ wage equals the disutility of working.

In practice, each succeeding cohort tends to have high life expectancy, better health, and higher wages than its predecessor, and optimal retirement decisions for different cohorts will reflect changes in both age-specific wages A(R) and life expectancy z. In Section IV, we calibrate what our model predicts as the retirement behavior for cohorts born during the last century, given observed and expected changes in life expectancy, health, and wages. In this section, however, we first derive some theoretical results on the sign and magnitude of the effect of improvements in life expectancy and wages, taken separately, on the optimal retirement age. These theoretical results will help us to understand the results of the calibration exercise.

First, we consider what happens if life expectancy increases and we have a proportional decline in morbidity. Lee and Goldstein (2003) argue that a natural benchmark for responding to an increase in life expectancy is to adjust the timing of all life choices proportionately. Bloom et al. (2003) show that in the case of a fixed lifespan, with no mortality previously, the optimal response to an increase in lifespan and health is to increase working life proportionately, keeping consumption unchanged, provided that interest rates, time preference rates, and exogenous wage growth are all zero. In our framework, however, it is not clear that such a proportional response is even feasible. Consider an initial life expectancy z₀ and let the optimal retirement age and the optimal consumption level be R^*₀ and c^*₀, respectively, with this life expectancy. Let the optimal retirement age at the longer life expectancy Z₁ be R^*₁ and let the optimal consumption level be. We require the old consumption stream to be affordable at the new survival schedule, provided retirement is postponed in line with life expectancy.¹² We call this the proportionality condition:

$${\int }_0^T{\mathrm{e}}^{-rt}s(t,z_1)c_0^{\ast }\mathrm{d}t\le {\int }_0^{R_0^{\ast }{z}_1∕z_0}{\mathrm{e}}^{-rt}s(t,z_1)A\left(t\right)w_h\left[h(t,z)\right]\mathrm{d}t\text{for}{z}_1>z_0.$$ (15)

This means that the extra income from working proportionately longer is sufficient to finance expected consumption, given the likelihood of survival to older ages when life expectancy rises.

In practice, this condition is satisfied in historical data and future projections for the US. In the Online Appendix, we examine cohort survival schedules for the US (the survival curve faced by the cohort) for different birth years. We use data from the US because we have projections on future mortality rates for cohorts born after 1900, while for other countries we only have the observed completed survival schedules for cohorts born before 1900, without projections. Using long-run averages for the real interest rate and wage growth, we show that moving from the survival schedule of those born in 1900 to those born in 1925, 1950, 1975, or 2000 (based on historical cohort survival rates and projected future rates), with an increase in the retirement age proportional to the increase in life expectancy, would in each case allow consumption to increase. This means that it has been feasible to keep the working life proportional to life expectancy with consumption unchanged.

While we are primarily interested in the effects on retirement age, it is useful to know what happens to consumption when we increase life expectancy. The result for consumption, given in Proposition 2, is useful in the proof of Proposition 3, where we examine the effect of life expectancy on retirement age

Proposition 2. If changes in the survival schedule satisfy the proportionality condition, the optimal response to an increase in life expectancy requires consumption to remain the same or increase. (See the Online Appendix for proof.)

The intuition for this result is that it is possible for the agent to increase working life proportionately but to keep consumption unchanged. In general, the agent will do better than this. If both leisure and consumption are normal goods, then the agent will take some of the additional welfare in the form of consumption and some in the form of increased leisure.

Proposition 3. If changes in the survival schedule satisfy the proportionality condition and there is no exogenous wage growth, the optimal response to an increase in life expectancy requires the retirement age to rise less than proportionately with life expectancy. (See the Online Appendix for proof.)

The condition on wages is to guard against the possibility that wages are rising so rapidly over time that the substitution effect dominates the wealth effect and that workers increase the proportion of life spent working to take advantage of higher wages later in life.

We now turn to the issue of how retirement and consumption are affected by a change in the exogenous component of the wage schedule. We consider what happens when the level of wages rises; we think of the wage schedule A(t) moving up proportionately at every age. We find that what happens depends crucially on the intertemporal elasticity of substitution, which in our model is the inverse of the coefficient of relative risk aversion because of the assumption of time-separable utility.

Proposition 4. When the level of wages rises, the optimal responses of the agent are: (a) to keep retirement unchanged and to increase consumption proportionately with wages, if the utility function has a local intertemporal elasticity of substitution of unity; (b) to raise the age of retirement and to increase consumption more than proportionately with wages, if the utility function has a local intertemporal elasticity of substitution greater than unity; (c) to lower the age of retirement and to increase consumption less than proportionately with wages, if the utility function has a local intertemporal elasticity of substitution less than unity. (See the Online Appendix for proof.)

A change in wages has both income and substitution effects on retirement. With higher lifetime income, there will be a greater demand for leisure, if leisure is a normal good, leading to earlier retirement. However, a higher wage gives a greater incentive to work — a substitution effect. The pivotal case where these two effects exactly balance, and there is no effect on retirement, occurs where there is relative risk aversion that is locally unity. We state this as part of Proposition 4 to show that this general result applies to our model. The long-term decline in retirement age is consistent with an intertemporal elasticity of substitution less than unity (which, in our model, implies a coefficient of relative risk aversion that exceeds 1), in which case the income effect of higher wages, which increases the demand for leisure, is larger than the substitution effect, which increases the incentive to work.

We focus on the effects of changes in life expectancy and the level of wages on retirement decisions. Bloom et al. (2004) have also investigated the effects of changes in the interest rate, the rate of time preference, and the rate of wage growth under more restrictive functional forms for utility and mortality.

IV. Calibration

We now perform a calibration exercise. We solve the model numerically using explicit functional forms and plausible values of the parameters. We assume that we have iso-elastic utility¹³

$$u\left(c\right)=k+\frac{c^{1-\beta }}{1-\beta }.$$ (16)

For the calibration, we take β=2. Studies on labor supply that look across countries, or over long periods of time, find that labor supply is lower when wages are higher and give estimates that are close to β=2 (Chetty, 2006). Studies that look at shorter-term variation in wages find a lower response of labor supply to wage charges and are often compatible with values of β equal to 1; for example, McGrattan and Rogerson (2004) have looked at the effect of wage variations on hours worked. In some cases, values of β less than 1 are found; for example, Browning et al. (1999) have argued that their best estimate of β is 0.8. Because we are concerned with changes in labor supply over a very long time period, we prefer to use the estimate β=2, which comes from comparing situations with very different wage levels. However, it should be noted that the ability of our model to explain the long-term movement towards earlier retirement, which preceded the introduction of social security (Costa, 1998a, 1998b), depends crucially on the assumption that β exceeds 1.

Our utility function implies that optimal consumption at each age t satisfies

$$\frac{\stackrel{.}{c}}{c}=(r-\delta )\frac{u^{\prime }\left(c\right)}{-c{u}^{″}\left(c\right)}=\frac{(r-\delta )}{\beta },c\left(t\right)=c\left(0\right)\exp \left[\frac{(r-\delta )}{\beta }t\right]=c\left(0\right)\text{for}r=\delta .$$ (17)

We assume that the survival function s(t) has a Gompertz—Makeham shape, which is a good approximation to empirical mortality schedules for adults in the US (Bebbington et al., 2012), so that the survival curve and the associated mortality schedulem(t) can be written as

$$\mathrm{s}\left(t\right)=\exp \left[-\rho t-\frac{a}{b}({\mathrm{e}}^{bt}-1)\right],m\left(t\right)=\rho +a{\mathrm{e}}^{bt}.$$ (18)

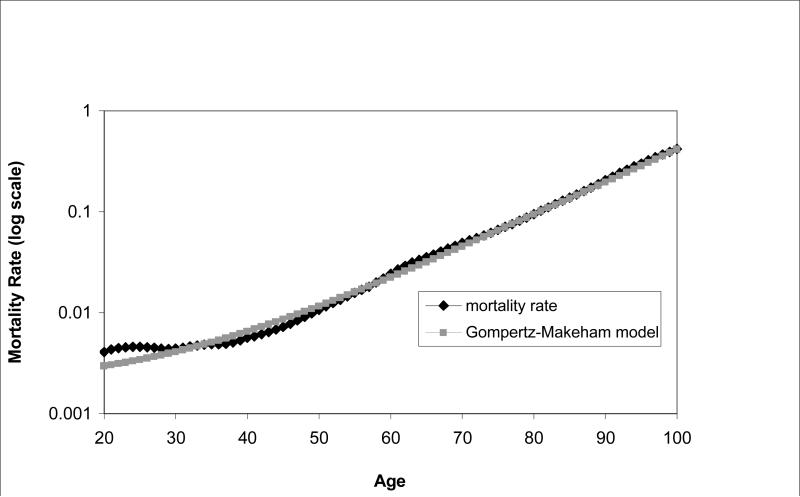
Different birth cohorts, with different life expectancies, will have different values of the parameters ρ, a, and b. Table 1 gives the estimated values of ρ, a, and b for mortality schedules for people aged 20 and over in the US for cohorts born in 1901, 1951, and 1996, based on data and projections from the Berkeley Mortality Database.¹⁴ The values of the parameters ρ, a, and b are estimated to fit the empirical mortality schedule using non-linear least-squares. Figure 1 shows the empirical mortality schedules and the fitted values based on our Gompertz—Makeham function estimates for the 1901 birth cohort, where we have actual (rather than projected) mortality rates at all ages. Figure 1 shows that the Gompertz—Makeham function provides a reasonable fit to the observed data.

Table 1.

Estimated Gompertz–Makeham mortality parameters

	Birth cohort 1901	Birth cohort 1951	Birth cohort 1996
ρ × 100	0.195** (0.045)	–0.134 (0.078)	–0.171** (0.065)
a × 100	0.103** (0.004)	0.059** (0.005)	0.051** (0.004)
b	0.075** (0.0005)	0.080** (0.001)	0.079** (0.001)
N	80	80	80
R 2	0.999	0.997	0.997

Notes: Based on mortality rates at ages 20–100 from the Berkeley Mortality Database. Mortality at later ages for the 1951 cohort and at all ages for the 1996 cohort are projected. ***, **, and * denote significance at the 1, 5, and 10 per cent levels, respectively.

Fig. 1.

Adult mortality rates of the 1901 birth cohort in the US

Source: Berkeley Mortality Database

We assume that the disutility of labor at each age is proportional to mortality at that age,

$$v\left(t\right)=dm\left(t\right)=d(\rho +a{\mathrm{e}}^{bt}),$$ (19)

so that reductions in mortality, and increases in life expectancy, are associated with a lower age-specific disutility of working. The parameter d, which denotes the weight given to the disutility of working in the utility function, is calibrated so that optimal retirement of the cohort born in 1900 is 65. This gives us a value of d = 0.87.

We normalize the real wage to be 100 in 1921, when the cohort born in 1901 is assumed to start work. We take the long-run real rate of interest and therefore the rate of time preference to be 3 per cent. The Congressional Budget Office (2004) uses a value of the long-run rate of real wage growth of σ=1.27 per cent per annum.¹⁵ This means that real wages were 189 in 1971 (when the cohort born in 1951 started work) and will rise to 334 in 2016 (when the cohort born in 1996 starts work). Table 2 summarizes the parameter values that we use in the calibration. In this calibration, wages for the worker rise at 1.27 per cent per annum; we ignore the effect of health on wages.

Table 2.

Parameters used in calibration

Interest rate	r	0.03
Wage growth rate	σ	0.0127
Rate of time preference	δ	0.03
Disutility of work	d	0.87
Coefficient of relative risk aversion	β	2

The first-order condition for retirement is that the disutility of working is equal to the wage χ the marginal utility of consumption (R)=w(R)′[c(R)]. Hence, we require

$$d(\rho +a{\mathrm{e}}^{bR})=w\left(0\right){\mathrm{e}}^{\sigma R}{\left\{c\left(0\right)\exp \left[\frac{(r-\delta )}{\beta }R\right]\right\}}^{-\beta }=w\left(0\right){\mathrm{e}}^{(\sigma +\delta -r)R}c{\left(0\right)}^{-\beta }.$$ (20)

In order to solve equation (20) for the optimal retirement age R, first we need to solve for the initial level of consumption c(0). To find this, we apply the budget constraint

$${\int }_0^T{\mathrm{e}}^{-rt}\mathrm{s}\left(t\right)c\left(t\right)\mathrm{d}t={\int }_0^R{\mathrm{e}}^{-rt}\mathrm{s}\left(t\right)w\left(t\right)\mathrm{d}t,$$ (21)

which implies

$$c\left(0\right){\int }_0^{\infty }\exp \left\{-\left[r+\rho -\frac{(r-\delta )}{\beta }\right]t-\frac{a}{b}({\mathrm{e}}^{bt}-1)\right\}\mathrm{d}t=w\left(0\right){\int }_0^R\exp \left[-(\rho +r-\sigma )t-\frac{a}{b}({\mathrm{e}}^{bt}-1)\right]\mathrm{d}t.$$ (22)

We have two equations (20) and (22) with two unknowns, retirement age and consumption level, R and c(0). In the Online Appendix, we show how equations (20) and (22) can be combined to give a closed-form solution for c(0). This allows us to construct an implicit function for retirement age alone, which we then solve numerically. We have written equations (20) and (22) for general values of rand δ so that, in principle, the two equations could be solved for initial consumption c(0) and R for arbitrary values of r and δ, with the time path of consumption then being determined as in equation (17). However, for simplicity, we carry out the calibration only for r=δ.

Table 3 gives the calibrated retirement age that solves equations (20) and (22) for different mortality schedules (after age 20) and initial wage levels. Moving along the first row of Table 3, we see the effect of changing the initial wage level, holding the survival schedule steady at that experienced by the 1901 birth cohort. By 1951, initial wages were 1.89 times greater than in 1921, while in 2016 they will be 3.34 times greater (assuming a constant long-run growth rate of wages). In Table 3, we see that higher lifetime incomes and consumption lead to earlier retirement. We estimate that the effect of rising income levels, holding life expectancy constant, would have reduced the retirement age to 59.3 for the cohort born in 1951, and will reduce it further to 54.5 for the cohort born in 1996. These estimates imply that a doubling of wages reduces retirement age by just over five years.

Table 3.

Calibrated retirement ages

Cohort birth year	Life expectancy at age 20	Wage index at age 20
		100	189	334
1901	41.9	65.1	59.3	54.5
1951	49.4	68.1	62.3	57.6
1996	54.3	70.3	64.4	59.5

Notes: Life expectancy at age 20 is based on data and projections from the Berkeley Mortality Database. We assume that each cohort starts working at age 20. Wages in 1921 are indexed to 100. Wages in 1971, and projected wages in 2016, relative to 1921, are based on a long-run rate of wage growth of 1.27 per cent per annum, and are 189 and 334, respectively. The calibrated retirement age is the retirement age predicted by our model for that life expectancy and wage at age 20 with wage growth of 1.27 per cent per annum.

If, instead, we start with the 1901 survival schedule and the 1921 real wages of 100 and then move down along the first column of Table 3, we see the effect of longer lifespans. At the 1901 survival schedule, total life expectancy conditional on reaching age 20 was a further 41.9 years. At the 1951 survival schedule, life expectancy conditional on survival to age 20 rises to 49.4 years, a gain of 7.5 years. We estimate that this gain in life expectancy would lead to a rise in the retirement age of three years, to 68.1. We further estimate that a person living with the 1996 cohort survival schedule but 1901 cohort income (i.e., based on 1921 wages) would have a life expectancy conditional on reaching age 20 of 74.3 years, and would raise his or her retirement age to 70.3. These results imply that each increase in a year of life expectancy at age 20 raises retirement age by about 0.4 years. This is consistent with our result that rising life expectancy raises retirement age but less than proportionately.

Moving along the rows of Table 3 gives the effect of increases in income, while moving down a column gives the effect of longer lifespan. The diagonal elements (in bold) give the overall effect on the optimal retirement age for different cohorts that have experienced differences in both survival schedules and income levels. As can be seen, as we move to later cohorts, the net effect of increases in wages and longer life expectancies is to reduce the optimal retirement age.

Table 4 gives the actual median retirement age over the period 1960–2010 based on data from Gendell and Siegel (1992) and Gendell (2008). This is a mixture of the retirement behavior of different cohorts in the year, but the value for 1960–1965 corresponds roughly with the 1901 birth cohort, while the value for 2005–2010 reflects the behavior of the 1951 birth cohort. The calibrated reduction in retirement age for the 1951 birth cohort relative to the 1901 cohort matches closely the observed reduction in age of retirement.

Table 4.

Median retirement age for men

1960–1965	65.2
1965–1970	64.2
1970–1975	63.4
1975–1980	63.0
1980–1985	62.8
1985–1990	62.6
1990–1995	62.4
1995–2000	62.0
2000–2005	61.6
2005–2010	61.6

Sources: Gendell and Siegel (1992) and Gendell (2008)

V. Conclusion

Our model demonstrates two major, long-term influences on the optimal age at retirement. First, at higher levels of lifetime wages, the desire for increased leisure leads to early retirement. Second, longer lifespans and healthier lives lead to a less than proportional increase in working life. Calibration results indicate that, historically, the effect of higher wages has dominated, leading to a secular trend towards early retirement.

Clearly, the model is idealized and has a number of limitations. It is strictly a partial equilibrium model: there is no production sector, which means that the demand for labor is not modeled and wages are exogenous. Although the theory improves on the existing body of literature by specifying an arbitrary concave utility function over consumption, leisure is additively separable. In addition, the intertemporal utility function is strongly separable: this is not innocent, because it imposes the restriction that the coefficient of relative risk aversion is the inverse of the intertemporal elasticity of substitution. More immediately, our assumption that the rate of interest equals the rate of time preference could be adjusted, which would allow for consumption growth over time. Our preliminary investigations suggest that our propositions would hold substantially, albeit in a more restrictive form. At a practical level, capital markets are not perfect, as required by the model, and there are other distortions in reality, such as taxes and social security.

However, despite these limitations, our model provides a benchmark against which the impact of increases in life expectancy on retirement can be evaluated. Our main result is that the effect of increasing life expectancy should be to increase optimal retirement ages, but only to a modest extent. Our calibration exercise suggests that this effect has been outweighed over the last century by the effect of rising wages, leading to an increased demand for leisure and lower retirement ages, which is consistent with the historical record of retirement ages for the US. Calibration will likely give similar results for other developed countries.

We leave for future research the issue of how the results of our model will change with more general utility functions and the relaxation of the other strict assumptions of the model.