Abstract
PURPOSE
To test the hypothesis that spatially selective corneal stromal stiffening can alter corneal astigmatism and assess the effects of treatment orientation, pattern, and material model complexity in computational models using patient-specific geometries.
SETTING
Cornea and Refractive Surgery Service, Academic Eye Institute, Cleveland, Ohio, USA.
DESIGN
Computational modeling study.
METHODS
Three-dimensional corneal geometries from 10 patients with corneal astigmatism were exported from a clinical tomography system (Pentacam). Corneoscleral finite element models of each eye were generated. Four candidate treatment patterns were simulated, and the effects of treatment orientation and magnitude of stiffening on anterior curvature and aberrations were studied. The effect of material model complexity on simulated outcomes was also assessed.
RESULTS
Pretreatment anterior corneal astigmatism ranged from 1.22 to 3.92 diopters (D) in a series that included regular and irregular astigmatic patterns. All simulated treatment patterns oriented on the flat axis resulted in mean reductions in corneal astigmatism and depended on the pattern geometry. The linear bow-tie pattern produced a greater mean reduction in astigmatism (1.08 D ± 0.13 [SD]; range 0.74 to 1.23 D) than other patterns tested under an assumed 2-times increase in corneal stiffness, and it had a nonlinear relationship to the degree of stiffening. The mean astigmatic effect did not change significantly with a fiber- or depth-dependent model, but it did affect the coupling ratio.
CONCLUSIONS
In silico simulations based on patient-specific geometries suggest that clinically significant reductions in astigmatism are possible with patterned collagen crosslinking. Effect magnitude was dependent on patient-specific geometry, effective stiffening pattern, and treatment orientation.
Astigmatism is a common refractive abnormality that arises primarily from rotational asymmetry of corneal curvature. Surgical methods for correcting astigmatism include photoablative refractive procedures, such as laser in situ keratomileusis (LASIK) or photo-refractive keratectomy (PRK); femtosecond-shaped lenticule extraction techniques; and incisional procedures, such as astigmatic keratotomy (AK), that involve placement of paired peripheral corneal arcuate incisions along the steep axis of astigmatism to flatten the steeper axis. Astigmatic keratotomy is a convenient method of astigmatism correction that is inexpensive to implement and easily combined with cataract surgery. However, it is less predictable than photoablative surgery, has a limited range of effect, can induce corneal higher-order aberrations (HOAs) that reduce visual acuity,1,2 and can destabilize the cornea due to its dependence on deep disruption of collagen lamellar continuity. All the above techniques probably involve some degree of corneal material weakening either as a mechanism for inducing refractive effect or as a byproduct of treatment.
Corneal collagen crosslinking (CXL) is an emerging treatment for corneal ectasia that augments corneal material strength with the primary goal of stabilizing progressive disease.3 Treatment generally first involves corneal exposure to a photosensitizing chemical agent, such as riboflavin, followed by ultraviolet-A (UVA) light exposure, in which the interaction of the agent, light, oxygen, and collagenous tissue leads to increased corneal tensile strength.4 Because the stiffening effect associated with riboflavin–UVA CXL does not occur in the presence of riboflavin alone,4 which diffuses throughout the tissue and requires the addition of UVA light that can be delivered in a spatially selective manner, focal stiffening is feasible from a practical standpoint. A previous computational modeling study by Roy and Dupps5 simulated keratoconus progression and its treatment with standard broad-beam CXL treatments but also evaluated modified patterns that were more effective than standard treatments in reversing topographic steepening and regularizing corneal geometry. In this study, we applied a similar simulation-based approach to developing new approaches to the treatment of refractive error, specifically astigmatism.
The goals of this computational simulation study were to test the hypothesis that spatially selective corneal stiffening can alter corneal astigmatism; to assess the effects of treatment pattern, orientation, and stiffening magnitude on patient tomography-driven finite element models; and to compare simulation results for 2 material property formulations.
PATIENTS AND METHODS
Patient Tomography Samples
Ten eyes of 10 patients with corneal astigmatism were selected by retrospective review of corneal tomography under an institutional review board (IRB)–approved research protocol (Cleveland Clinic IRB protocol #13-213). Patients from the Cole Eye Institute Cornea and Refractive Surgery services were selected based on the presence of astigmatic anterior corneal curvature patterns measured with a Scheimpflug-based anterior segment imaging system (Pentacam, Oculus Optikgeräte GmbH). A variety of magnitudes and patterns of astigmatism (horizontal, vertical, oblique, regular, and irregular) were included to create a test group representative of a range of naturally occurring corneal astigmatism patterns. Only data from unoperated corneas were analyzed, and no eyes with frank keratoconus were included.
Model Preprocessing and Pre-Strain Calculations
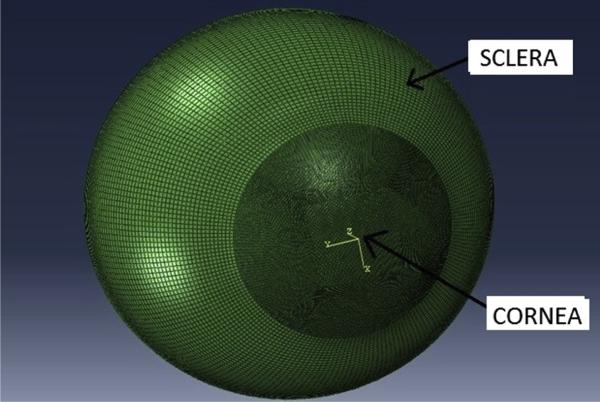
Anterior and posterior corneal elevation data were exported to construct patient-specific 3-dimensional (3-D) geometries. The points composing each surface were fit to a 12th-order Zernike polynomial.6 A Python script routine was developed to extrapolate and complete the whole corneal geometry based on the Zernike polynomial. The extrapolated data were imported into Solidworks software (version 2011, Dassault Systems) using 25 anterior and 25 posterior concentric point clouds to construct the 3-D geometry. To avoid nonphysiologic constraints on the motion of the corneoscleral limbus,7 a spherical anterior half sclera with a uniform thickness of 1.0 mm and outer radius of 10.5 mm was attached to the cornea at the limbus.8 The resulting 3-D cornea–scleral geometry was meshed using a commercial mesh generator (Truegrid, version 2.4) with 18 000 hexahedral brick elements (Figure 1). Finite element analyses were run in a commercial finite-element solver (Abaqus version 6.11, Simulia, Dassault Systems).
Figure 1.
Example of a corneoscleral 3-D finite element mesh derived from patient-specific clinical Scheimpflug tomography and coupled to a standardized sclera.
Corneal geometries acquired in living eyes under physiologic loading are different from those that would be obtained in a zero intraocular pressure (IOP) state. Because assumptions about zero-load geometry can influence model results,9,10 an inverse iterative method for estimating the zero-load state was applied based on a previous approach to this problem.11 A negative IOP was applied to the loaded model before procedure simulations were performed to bring the cornea to the no-load state. These no-load conditions were taken as a reference for the initial conditions, and the node positions and stresses were calculated iteratively until the difference between the imaged node positions and the predicted node positions in the model approached the acceptable limit of error. Elsheikh et al.12 suggest that 3 to 4 iterations are sufficient to estimate the correct no-load geometric conditions. Six iterations were performed in the current study before CXL procedures were modeled.
Material Models
For the first 2 aims of this study, an isotropic hyperelastic incompressible material model was adopted from previous work.8 The material constants were obtained by fitting the stress–strain measurement data obtained experimentally by Wollensak et al.13 The strain energy equation for such models includes the following basic components:
| (1) |
| (2) |
| (3) |
where W is the total strain, the subscripts indicate the isotropic and the volumetric (incompressible) components of the total strain energy, J and is the determinant of the deformation tensor F, which is explained below in detail. The material constants C10 and C20 are linearly scaled by the stiffening multiplier to increase the stiffness of the material within the spatially selected zones.8
As an alternative material formulation, an anisotropic, hyperelastic, depth-dependent, and incompressible material model was used for the comparison posed in the last aim of this study. The strain energy equation for this model includes an additional fiber component, where the strain energy equation is
| (4) |
where Wground is the isotropic part of the equation, which was defined above and does not consider fiber directions. This portion of the equation was defined by a reduced polynomial model above. However, it is defined as a neo-Hookean material model that still accounts for the first 3 material strain invariants (I1, I2, I3) in this strain energy equation by simply omitting the second portion of the reduced polynomial formulation. Wfiber accounts for fiber directions by computing the fourth and sixth strain invariants, which include 2 orthotropic fiber directions (nasal–temporal and superior–inferior). The IOP was specified as 15 mm Hg.
In continuum mechanics deformation, stress and strain tensors are decomposed to explain the isochoric (volume-conserving) behavior of the material:
where F is the deformation gradient and J = det (F) defines the compressibility of the material (det is the determinant). The right Cauchy-Green strain tensor (C) is calculated as
The modified C (C̄) is calculated as
The total strain energy is separated into 3 components described by the following equations:
| (5) |
| (6) |
where C10 is isotropic material constant and k14, k24, k16, and k26 are anisotropic material constants. The values of these variables were set to 50000, 1.0e −05, 234000, and 29.917, respectively.14,15 The definitions of the strain invariants Īi, Ī4, and Ī6 can be found in a previous publication from this laboratory.2
To incorporate the effect of depth dependency of the material properties of the stroma, the cornea was separated into 5 depth regions with each region comprising 20% of the patient-specific thickness. Using a modification of a prior approach,16 the depth dependency was implemented by linearly scaling the general ground strain energy equation (equation 7) with an additional scaling variable α that scaled the material properties and their approximate spatial transition according to previously published depth-dependent cohesive strength studies in human corneas.17 The value of α was changed from 2.0 to 1.2 linearly from anterior to posterior cornea, respectively.
| (7) |
Collagen Crosslinking Treatment Simulation
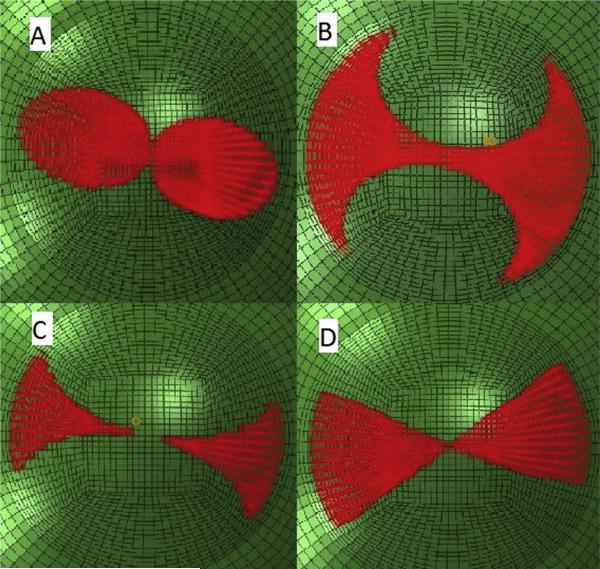
To simulate the material effect of CXL, the corneal tissue encompassed by the candidate CXL treatment pattern was assigned a greater stiffness than the surrounding cornea. To implement this material change, the isotropic portion of the strain energy equation was multiplied by a factor of 2 for all material formulations, except where stated otherwise. Four candidate patterns were studied as follows: (1) rounded bow-tie, (2) butterfly, (3) center-sparing butterfly, and (4) linear bow-tie (Figure 2).
Figure 2.
Four candidate treatment patterns for reducing corneal astigmatism through stromal stiffening. A: Rounded bow-tie. B: Butterfly. C: Center-sparing butterfly. D: Linear bow-tie.
The rounded bow-tie pattern was created as 2 symmetrical ellipses with respect to the steep axis with a major diameter of 4.5 mm and a minor diameter of 3.0 mm. The major diameters of the ellipses are congruent with the flat corneal meridian.
The butterfly patterns were created by subtracting 2 symmetrical circles with diameters of 3.5 mm in pattern 2 (butterfly) and 4.5 mm in pattern 3 (center-sparing butterfly) with respect to the steep meridian from a central circle with a diameter of 9.0 mm.
The linear bow-tie pattern was specified as 2 symmetrical 60-degree circle segments with respect to the steep axis of the astigmatism. A 60-degree width was selected based on a separate width sensitivity analysis not presented here.
The element centroids were calculated and the elements with centroids that were to be included in the treatment pattern were selected with a custom Python script. The effective depth of stromal CXL treatment was assumed to be 300 mm based on published experimental data.18–20 Due to the pattern of the finite-element mesh and the method of assigning increased material properties within specified elements of the mesh, the depth of the treatment increased slightly in the periphery as a function of local corneal thickness. The stiffening effect was modeled as a uniform increase across the lateral extent of the pattern and through the depth of the treatment.
Simulated keratometry (K) values were derived from pre-treatment and posttreatment geometries, and the differences in corneal astigmatism (the difference between steep and flat simulated K values) were compared by the paired t test. Corneal lower-order aberrations (LOAs) and HOAs were derived from Zernike fits to the anterior corneal geometries (VolCT, Sarver & Associates) before and after simulated treatment and expressed as root-mean-square values representing the 2nd-order and lower polynomial terms (LOAs) and 3rd-order through 12th-order terms (HOAs) using a 4.0 mm simulated pupil diameter. Third-order aberration values, including coma, trefoil, and spherical aberrations, were further analyzed using 3.0 mm, 6.0 mm, and 9.0 mm simulated pupil diameters. In addition to the core analyses, sensitivity analyses were performed by running multiple models to assess the effect of treatment pattern orientation using 1 patient model and the impact of the stiffening magnitude on the astigmatic effect with 1 pattern (rounded bowtie) in all 10 modeled patients. In the latter analysis, stiffness multipliers of 2, 4, and 6 were studied.
The pattern that showed the highest correction was further modeled with a hyperelastic anisotropic depth-dependent model with the stiffness multiplier of 2 and the same effective depth of stiffening. Implementation of stiffening in the material model was as described above. Material orientations were assigned to each 10 000 corneal brick elements based on their spatial coordinates and preferred fiber-orientation data, which were obtained from x-ray diffraction results reported by Meek and Boote.21 Vector analysis of surgically induced astigmatism (SIA)22 in the pattern 4 group was also performed to determine whether rotation of the astigmatic vector altered the net magnitude of astigmatic effect.
RESULTS
Tomographic characteristics of the 10 modeled astigmatic patients included the following values: mean maximum curvature (maximum K), 45.28 diopters (D) ± 1.62 (SD); mean apical corneal thickness, 565.2 ± 22.4 mm; mean minimum corneal thickness, 562.1 ± 21.8 mm; and Scheimpflug-derived inferior– superior anterior curvature discrepancies of less than 1.0 D consistent with nonkeratoconic corneas. As an initial assessment of the effect of pattern orientation on astigmatic outcome, 2 simulations of the linear bow-tie pattern were compared in patient 2, 1 simulation with the major axis oriented on the steep axis of astigmatism and the other with the major axis perpendicular to the steep axis. Treatment on the flat axis of astigmatism reduced preoperative astigmatism from 2.20 D to 0.88 D, whereas treatment on the steep axis increased astigmatism to 2.60 D.
Figure 2 shows 4 candidate treatment patterns oriented on the flat meridian simulated independently in each of the 10 study eyes (Table 1) with fiber-independent material properties. Statistically significant mean reductions in corneal astigmatism were achieved with each of the 4 patterns using a stiffness multiplier of 2 (all P < .001, paired Student t test). With a corneal stiffening factor of 2, the linear bow-tie pattern produced the largest magnitudes of correction of all investigated patterns.
Table 1.
Pretreatment and posttreatment corneal astigmatism in computational simulations of 4 candidate stiffening patterns. All values are derived from simulated K values.
| Posttreatment Astigmatism (D) |
Change (D) |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | Pretreatment Astigmatism (D) | Rounded Bow-tie (Pattern 1) | Butterfly (Pattern 2) | Center-Sparing Butterfly (Pattern 3) | Linear Bow-tie (Pattern 4) | Pattern 1 | Pattern 2 | Pattern 3 | Pattern 4 |
| Patient | |||||||||
| 1 | 2.69 | 1.70 | 1.77 | 2.21 | 1.59 | –0.99 | –0.92 | –0.48 | –1.10 |
| 2 | 2.21 | 1.11 | 1.17 | 1.64 | 1.09 | –1.10 | –1.04 | –0.57 | –1.12 |
| 3 | 3.92 | 2.91 | 2.93 | 3.39 | 1.97 | –1.01 | –0.99 | –0.53 | –1.12 |
| 4 | 3.07 | 2.02 | 2.05 | 2.52 | 2.8 | –1.05 | –1.02 | –0.55 | –1.10 |
| 5 | 1.22 | 0.67 | 0.43 | 0.82 | 0.35 | –0.55 | –0.79 | –0.40 | –0.92 |
| 6 | 2.75 | 2.32 | 2.35 | 2.49 | 1.66 | –0.43 | –0.40 | –0.26 | –1.09 |
| 7 | 2.38 | 2.28 | 2.24 | 2.29 | 1.64 | –0.10 | –0.14 | –0.09 | –0.74 |
| 8 | 2.10 | 0.97 | 1.03 | 1.52 | 0.95 | –1.13 | –1.07 | –0.58 | –1.15 |
| 9 | 2.79 | 2.00 | 2.01 | 2.34 | 1.69 | –0.79 | –0.78 | –0.45 | –1.10 |
| 10 | 1.37 | 1.05 | 1.08 | 1.03 | 0.17 | –0.32 | –0.29 | –0.34 | –1.23 |
| Statistic | |||||||||
| Mean | 2.45 | 1.70 | 1.71 | 2.03 | 1.25 | –0.75 | –0.74 | –0.43 | –1.20 |
| SD | 0.79 | 0.73 | 0.76 | 0.77 | 0.7 | 0.37 | 0.34 | 0.16 | 0.45 |
| P value* | — | — | — | — | — | <.001 | <.001 | <.001 | <.001 |
Student t test of pretreatment to posttreatment change in astigmatism
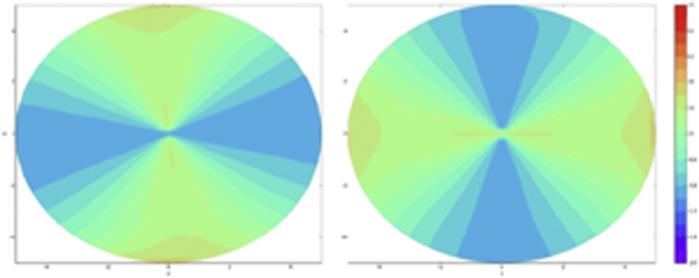
Table 2 shows detailed individual responses of steep and flat simulated K values and corneal LOAs and HOAs for the most effective candidate treatment pattern (pattern 4). The astigmatic effect resulted from statistically significant increases in curvature along the flat (treated) meridian coupled with statistically significant decreases in curvature along the steep (untreated) meridian. The mean coupling ratio, expressed as the ratio of steepening to flattening effects based on clinical convention, was 0.86. Corneal LOAs first-surface aberrations decreased significantly, and much smaller clinically insignificant but statistically significant increases in HOAs were observed. An additional comparison of pretreatment and posttreatment LOA and HOA values for the 2 bow-tie-configuration patterns (1 and 4) showed that LOAs were more effectively reduced with the linear bow-tie pattern than by the rounded bow-tie pattern. Similarly, increases in HOAs were less with the linear bow-tie pattern than with the rounded bow-tie pattern. The vector analysis suggested insignificant amounts of rotation of the axis of astigmatism, with less than a 0.05 D difference in the SIA measured by simulated K and by vector magnitude in any given modeled patient. Figure 3 and Figure 4 show the effects of flat-axis linear bow-tie stiffening patterns on axial topography in 2 modeled patients (patients 1 and 2) with regular astigmatism and 1 patient (patient 10) with irregular astigmatism, respectively. Figure 5 shows axial curvature difference maps showing the effect of simulated astigmatic CXL in patient 1 and patient 2.
Table 2.
Astigmatism and anterior corneal aberration values in 10 patient models before and after simulated refractive CXL using a linear bow-tie treatment (pattern 4) with 2x corneal stiffening aligned on the flat axis of astigmatism.
| Pretreatment |
Posttreatment |
Change |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ksteep (D) |
Kflat (D) |
LOA RMS (μm) |
HOA RSM (μm) |
Ksteep (D) |
Kflat (D) |
LOA RMS (μm) |
HOA RSM (μm) |
Ksteep (D) |
Kflat (D) |
LOA RMS (μm) |
HOA RSM (μm) |
|
| Patient | ||||||||||||
| 1 | 42.79 | 40.10 | 1.19 | 0.06 | 42.13 | 40.54 | 0.56 | 0.11 | –0.66 | 0.44 | –0.63 | 0.05 |
| 2 | 44.12 | 41.91 | 0.96 | 0.14 | 43.48 | 42.39 | 0.34 | 0.16 | –0.64 | 0.48 | –0.62 | 0 |
| 3 | 47.96 | 44.04 | 1.99 | 0.22 | 47.37 | 44.57 | 1.45 | 0.23 | –0.59 | 0.53 | –0.54 | 0 |
| 4 | 44.18 | 41.11 | 1.26 | 0.18 | 43.55 | 41.58 | 0.78 | 0.23 | –0.63 | 0.47 | –0.48 | 0.05 |
| 5 | 43.91 | 42.64 | 0.64 | 0.16 | 43.5 | 43.15 | 0.20 | 0.16 | –0.41 | 0.51 | –0.44 | 0 |
| 6 | 43.11 | 40.36 | 1.18 | 0.06 | 42.34 | 40.68 | 0.61 | 0.10 | –0.77 | 0.32 | –0.57 | 0.04 |
| 7 | 45.40 | 43.02 | 1.40 | 0.24 | 44.94 | 43.3 | 1.24 | 0.25 | –0.46 | 0.28 | –0.16 | 0 |
| 8 | 44.07 | 41.97 | 0.91 | 0.20 | 43.42 | 42.47 | 0.43 | 0.22 | –0.65 | 0.50 | –0.48 | 0.02 |
| 9 | 44.00 | 41.21 | 1.11 | 0.21 | 43.38 | 41.69 | 0.67 | 0.25 | –0.62 | 0.48 | –0.44 | 0.04 |
| 10 | 46.20 | 44.80 | 0.68 | 0.21 | 45.74 | 45.57 | 0.29 | 0.21 | –0.46 | 0.77 | –0.39 | 0.00 |
| Statistic | ||||||||||||
| Mean | 44.57 | 42.12 | 1.13 | 0.17 | 43.99 | 42.59 | 0.66 | 0.19 | –0.59 | 0.48 | –0.48 | 0.02 |
| SD | 1.55 | 1.53 | 0.39 | 0.06 | 1.60 | 1.61 | 0.41 | 0.06 | 0.11 | 0.13 | 0.14 | 0.02 |
| P value* | — | — | — | — | — | — | — | — | <.001 | <.001 | <.001 | <.001 |
HOA RMS = higher-order root-mean-square aberrations calculated for a 4.0 mm pupil; Kflat = simulated keratometry value for flat meridian; Ksteep = simulated keratometry value for steep meridian; LOA RMS = lower-order root-mean-square aberrations
Student t test on pretreatment – posttreatment values
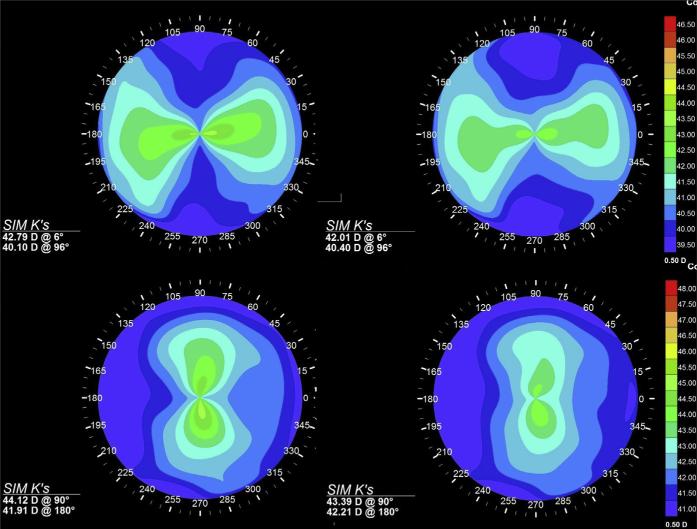
Figure 3.
Axial curvature maps and simulated K values (Sim K's) for patients with regular against-the-rule astigmatism (patient 1, top row) and with-the-rule astigmatism (patient 2, bottom row) before (left) and after (right) simulated corneal CXL with a linear bow-tie treatment pattern oriented along the flat axis and assuming a 2-times increase in stromal stiffness in the treatment zone. Reductions in overall astigmatism are observed through steep-ening of the treated axis and flattening of the orthogonal axis.
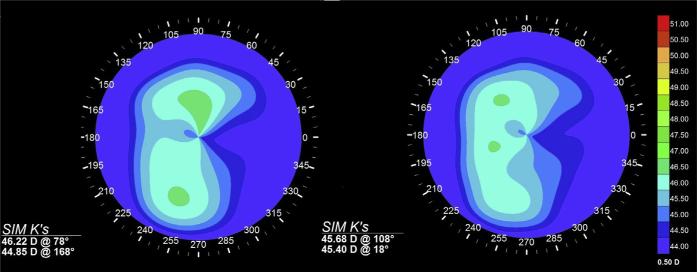
Figure 4.
Axial curvature maps and simulated K values (Sim K's) for a patient with irregular astigmatism (patient 10) before (left) and after (right) simulated 2-times stromal stiffening with a linear bow-tie treatment pattern oriented along the flat axis (168 degrees).
Figure 5.
Pretreatment to posttreatment axial curvature difference maps (diopters) for simulations of patient 1 (left) and patient 2 (right).
Table 3 shows the dependence of astigmatic effect on the magnitude of stiffening based on the results of the pilot sensitivity analysis in which the stiffness multiplier was varied for 10 eyes treated virtually with pattern 1 (the rounded bow-tie). A stiffness increase from 2- to 4-times over pretreatment values favored an insignificant trend toward an increased astigmatic effect (mean from –0.75 ± 0.43 D to –0.98 ± 0.84 D) (P = .1, paired t test). A further increase in modeled stiffening effect to 6 times not only did not increase the astigmatic effect but favored an insignificant paradoxical reduction in the mean astigmatic effect and greater intersubject variability (–0.86 ± 1.01 D) (P = .4).
Table 3.
Astigmatism values for 10 patient models before and after simulated refractive CXL using a rounded bow-tie treatment (pattern 1) with 2-times, 4-times, and 6-times corneal stiffening aligned on the flat axis of astigmatism.
| Pretreatment (D) |
Posttreatment, 2X Stiffening (D) |
Posttreatment, 4X Stiffening (D) |
Posttreatment, 6X Stiffening (D) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | Ksteep | Kflat | Astig | Ksteep | Kflat | Astig | Ksteep | Kflat | Astig | Ksteep | Kflat | Astig |
| Patient | ||||||||||||
| 1 | 42.79 | 40.10 | 2.69 | 41.72 | 40.02 | 1.70 | 40.99 | 39.8 | 1.19 | 40.73 | 39.66 | 1.07 |
| 2 | 44.12 | 41.91 | 2.21 | 43.05 | 41.94 | 1.11 | 42.27 | 41.83 | 0.39 | 41.96 | 41.72 | 0.24 |
| 3 | 44.18 | 41.11 | 3.07 | 43.17 | 41.15 | 2.02 | 42.47 | 41.06 | 1.41 | 42.2 | 40.96 | 1.24 |
| 4 | 47.96 | 44.04 | 3.90 | 47.05 | 44.14 | 2.91 | 46.5 | 44.02 | 2.48 | 47.96 | 44.04 | 3.9 |
| 5 | 43.91 | 42.64 | 1.27 | 43.12 | 42.45 | 0.67 | 42.84 | 42.07 | 0.77 | 42.74 | 41.86 | 0.88 |
| 6 | 43.11 | 40.36 | 2.75 | 42.27 | 39.95 | 2.32 | 41.82 | 39.48 | 2.34 | 41.67 | 39.28 | 2.39 |
| 7 | 45.4 | 43.02 | 2.38 | 44.85 | 42.57 | 2.28 | 44.69 | 42.03 | 2.66 | 44.59 | 41.75 | 2.84 |
| 8 | 44.07 | 41.97 | 2.10 | 43.00 | 42.03 | 0.97 | 42.25 | 41.95 | 0.30 | 41.96 | 41.86 | 0.10 |
| 9 | 44.00 | 41.21 | 2.79 | 43.09 | 41.09 | 2.00 | 42.55 | 40.81 | 1.74 | 42.38 | 40.67 | 1.71 |
| 10 | 46.22 | 44.85 | 1.37 | 45.88 | 44.83 | 1.05 | 45.96 | 44.50 | 1.46 | 46.00 | 44.40 | 1.60 |
| Statistic | ||||||||||||
| Mean | — | — | 2.45 | — | — | 1.70 | — | — | 1.47 | — | — | 1.60 |
| SD | — | — | 0.78 | — | — | 0.73 | — | — | 0.84 | — | — | 1.18 |
Astig = astigmatism; Kflat = keratometry in flat meridian; Ksteep = keratometry in steep meridian
Pattern 4 was further modeled in each of the 10 patients with a fiber- and depth-dependent material model. The mean astigmatic reduction was slightly decreased in the fiber-dependent model from –1.08 ± 0.13 to –1.03 ± 0.1. The mean difference in astigmatic effect between the 2 models was not significant (P = .6). However, the mean coupling ratio decreased from 0.86 to 0.52 with the fiber-dependent material formulation. Table 4 compares the individual corneal astigmatism responses for each material formulation. Table 5 shows the mean values of spherical aberration, coma, and trefoil for all patients after simulation of stiffening with pattern 4 for 3.0 mm, 6.0 mm, and 9.0 mm simulated pupil diameters.
Table 4.
Astigmatism in 10 patient models with fiber-independent and fiber dependent material formulations before and after simulated refractive crosslinking using a linear bow-tie treatment (pattern 4) with 2x corneal stiffening aligned on the flat axis of astigmatism.
| Fiber-Independent Material Model |
Fiber-Dependent Material Model |
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pretreatment (D) |
Posttreatment (D) |
Change (D) |
Posttreatment (D) |
Change (D) |
||||||||||
| Parameter | Ksteep | Kflat | Ksteep | Kflat | Ksteep | Kflat | Astig | Ratio | Ksteep | Kflat | Ksteep | Kflat | Astig | Flattening Ratio |
| Patient | ||||||||||||||
| 1 | 42.79 | 40.10 | 42.13 | 40.54 | –0.66 | 0.44 | –1.10 | 0.66 | 42.01 | 40.4 | –0.78 | 0.30 | –1.08 | 0.38 |
| 2 | 44.12 | 41.91 | 43.48 | 42.39 | –0.64 | 0.48 | –1.12 | 0.75 | 43.39 | 42.21 | –0.73 | 0.30 | –1.03 | 0.41 |
| 3 | 47.96 | 44.04 | 47.37 | 44.57 | –0.59 | 0.53 | –1.12 | 0.89 | 47.32 | 44.36 | –0.64 | 0.32 | –0.96 | 0.50 |
| 4 | 44.18 | 41.11 | 43.55 | 41.58 | –0.63 | 0.47 | –1.10 | 0.74 | 43.53 | 41.41 | –0.65 | 0.30 | –0.95 | 0.46 |
| 5 | 43.91 | 42.64 | 43.5 | 43.15 | –0.41 | 0.51 | –0.92 | 1.24 | 43.28 | 42.9 | –0.63 | 0.26 | –0.89 | 0.41 |
| 6 | 43.11 | 40.36 | 42.34 | 40.68 | –0.77 | 0.32 | –1.09 | 0.41 | 42.3 | 40.69 | –0.81 | 0.33 | –1.14 | 0.40 |
| 7 | 45.40 | 43.02 | 44.94 | 43.3 | –0.46 | 0.28 | –0.74 | 0.60 | 44.62 | 43.45 | –0.78 | 0.43 | –1.21 | 0.55 |
| 8 | 44.07 | 41.97 | 43.42 | 42.47 | –0.65 | 0.50 | –1.15 | 0.76 | 43.37 | 42.27 | –0.70 | 0.30 | –1.00 | 0.42 |
| 9 | 44.00 | 41.21 | 43.38 | 41.69 | –0.62 | 0.48 | –1.10 | 0.77 | 43.34 | 41.51 | –0.66 | 0.30 | –0.96 | 0.45 |
| 10 | 46.20 | 44.80 | 45.74 | 45.57 | –0.46 | 0.77 | –1.23 | 1.67 | 45.68 | 45.4 | –0.52 | 0.60 | –1.12 | 1.15 |
| Statistic | ||||||||||||||
| Mean | 44.57 | 42.12 | 43.99 | 42.59 | –0.59 | 0.48 | –1.07 | 0.85 | 43.88 | 42.46 | –0.69 | 0.34 | –1.03 | 0.52 |
| SD | 1.55 | 1.53 | 1.60 | 1.61 | 0.11 | 0.13 | 0.14 | 0.36 | 1.59 | 1.60 | 0.09 | 0.10 | 0.10 | 0.23 |
| P value* | — | — | — | — | <.001 | <.001 | — | — | — | — | <.001 | — | .5 | — |
Astig = asigmatism; Kflat = keratometry in flat meridian; Ksteep = keratometry in steep meridian
Student t test on pretreatment – posttreatment values
Table 5.
Changes in 3rd-order aberrations after simulation of stiffening with pattern 4 for 3.0 mm, 6.0 mm, and 9.00 mm pupil diameters.
| Mean (μm) ± SD |
|||||||
|---|---|---|---|---|---|---|---|
| 3.0 mm Pupil |
6.0 mm Pupil |
9.0 mm Pupil |
|||||
| Value | Preop | Postop | Preop | Postop | Preop | Postop | Change |
| Horizontal coma | –0.03 ± 0.11 | 0.00 ± 0.03 | –0.02 ± 0.14 | –0.02 ± 0.15 | 0.02 ± 0.60 | –0.08 ± 0.43 | –0.02 ± 0.06 |
| Trefoil 1 | 0.06 ± 0.25 | –0.01 ± 0.02 | 0.00 ± 0.01 | 0.00 ± 0.06 | 0.05 ± 0.35 | 0.01 ± 0.32 | –0.03 ± 0.03 |
| Trefoil 2 | 0.05 ± 0.13 | 0.00 ± 0.04 | 0.00 ± 0.08 | 0.01 ± 0.07 | 0.08 ± 0.23 | 0.06 ± 0.22 | –0.02 ± 0.03 |
| SA | 0.12 ± 0.30 | 0.02 ± 0.03 | 0.27 ± 0.1 | 0.27 ± 0.11 | 2.10 ± 3.25 | 1.14 ± 0.26 | –0.35 ± 0.53 |
SA = spherical aberration
DISCUSSION
This study evaluated a simulation-based approach to development of a new corneal refractive treatment for astigmatism and included initial optimization studies to guide rational treatment-pattern decisions for future clinical trials. The treatment of astigmatism has been studied using analytic and computational models of AK.23,24 This includes a recent study in a 3-D, whole eye fiber-dependent model designed to assess the effect of different surgical variables on astigmatic outcomes.5 In the current study, using a modeling approach that incorporated the fiber-dependent behavior of the cornea; nonlinear, hyperelastic, and anisotropic considerations5,7,9,10; and contributions of scleral properties to the corneal response,8 we performed a series of experiments simulating the effects of candidate collagen stiffening treatments on corneal astigmatism in a series of models derived from clinical tomography.
This study shows the potential for CXL-based treatments to produce targeted astigmatic effects of clinically significant magnitude. Candidate treatment patterns leverage the tendency of CXL to produce localized corneal flattening and compensatory steep-ening elsewhere with relative conservation of overall corneal curvature, a principle that was shown in our previous simulations of focal CXL for keratoconus.5 For pattern 4 in our study, increasing the width of the stiffening pattern toward the corneal periphery flattened the peripheral cornea and steepened the central cornea in the treated meridian. Because of this mechanism of action, such a treatment must be aligned on the flat meridian to reduce astigmatism. Two material formulations for representing the corneal stroma produced similar mean changes in astigmatism; however, the fiber-dependent, depth-dependent approach led to more flattening of the steep axis than steepening of the flat axis.
With a linear bow-tie pattern, a mean reduction of 1.08 D (range 0.74 to 1.23 D) was achieved with a specified increase in elastic strength of 2 times, which was taken as a conservative estimate of the magnitude of corneal stiffening that could be consistently achieved with current CXL methods.5,25 The argument that doubling of stiffness is clinically feasible is also supported by a patient-specific inverse finite-element analysis study from our group that estimated a mean stiffening effect greater than 2 times across all postoperative time points in a 16-patient series from the first U.S. Food and Drug Administration CXL trial for keratoconus and corneal ectasia.8 Although data on the relative mechanical efficacy of various CXL approaches are scarce, an in vivo rabbit study26 showed that a transepithelial CXL approach with the adjuvants benzalkonium chloride and ethylenediaminetetraacetic acid produced at least as much stiffening as epithelium-off CXL as measured by optical coherence elastography. Even greater stiffening magnitudes are likely to be achieved using strategies such as higher fluence UVA exposures27 and optimization of oxygen-dependent reaction kinetics.28 The nonlinear relationship between the stiffening dose and the topographic effect observed with the rounded bow-tie treatment pattern and the increases in interindividual variability at higher stiffening levels suggest that individual analysis of the optimum stiffening dose is important for clinical treatment planning. Sensitivity to stiffening effect was assessed in 1 treatment pattern only. The stiffness sensitivity of the more generally effective pattern, pattern 4, and the upper limits of treatment remain to be determined.
Because of the nonorthogonal angle of incidence, some decrease in UVA delivery to the corneal stroma in the peripheral cornea is likely with a homogenous UVA source. In previous studies,5,8 we modeled the potential impact of tapered or attenuated treatment profiles and saw slight differences in the resultant topographic effects. Modulation of the spatial intensity of the exposure is another parameter that could be varied to further customize the curvature change. The current study modeled the manifest stiffening effect at the level of the tissue and, in this case, assumed a homogenous UVA absorption profile. The actual irradiance profiles at the UVA source required to deliver the modeled stiffening effect at the tissue level are not worked out here but could be derived from experimental data, estimated by calculation, or both.
Many potential applications exist for a CXL-based corneal treatment for astigmatism. Residual postoperative astigmatism after cataract surgery with routine or premium intraocular lens (IOL) implantation is a major source of reduced retinal image quality and patient dissatisfaction.29 Zheleznyak et al.30 found that the negative impact of residual astigmatism on through-focus image quality and depth of focus was significant for all tested IOL designs but was greatest for multifocal IOLs. The same study determined that residual astigmatism greater than 0.75 D significantly diminished the depth-of-focus benefit of multifocal IOLs. A CXL-mediated treatment for astigmatism might also be attractive in virgin corneas due to the absence of tissue ablation, extraction, or incision. By the same reasoning, a CXL approach would be particularly attractive in phakic IOL patients (especially those with thinner corneas not amenable to photoablative refractive surgery), post-LASIK patients when there is a concern of post-refractive surgery ectasia, in post-PRK patients with thin corneas not amenable to photoablative enhancement, and in post-refractive lenticular extraction procedures in which femtosecond creation of a very fine astigmatic lenticule and the requisite opening of a side-cut incision (and the associated induction of astigmatism) could potentially be avoided. The patient-to-patient variation in response to identical patterns summarized in Tables 1 to 3 along with the observation that no single pattern was most effective for all corneal geometries reinforces that patient-specific 3-D geometry and related structural mechanics are important design variables in the treatment of astigmatism. The modeling approach presented here provides a strategy for developing individualized treatment algorithms that explicitly account for these variables.
The mechanism of action of CXL-mediated astigmatic treatment is different from that of corneal relaxing incisions, which flatten the central cornea and are oriented on the steep meridian. Like AK, astigmatic CXL treatment has a coupling effect. Unlike AK, the coupling ratio for CXL-based treatment in this study favored a mild tendency toward net corneal steep-ening, which could make it a more attractive option than AK for phakic or pseudophakic presbyopic patients or any patient with mixed or hyperopic astigmatism because CXL would likely favor a shift toward emmetropia. Simulated CXL-based treatments also appear to reduce astigmatism without inducing the 4- to 6-fold increases in HOAs that have been associated with relaxing incisions.2 In the current simulations, no consistent increases in spherical aberration, coma, or trefoil were noted. In practice, AK and CXL-mediated astigmatic treatments could easily be combined because the treatments involve orthogonal axes. In a separate 1-patient computational modeling study, we found that a combination of AK in the steep meridian and linear bow-tie pattern CXL in the flat meridian corrected higher levels of astigmatism than could be corrected with either modality alone.31
The astigmatic effects of the simulated treatments in this study were measured solely on the basis of anterior corneal changes. Future implementations of the modeling process will include more complete optical representations of refractive effect that include posterior corneal effects and corneal elevation relative to a specified retinal image plane. For the primary purposes of generating proof of concept and development of candidate patterns for treatment of corneal astigmatism via stroma stiffening, the corneal epithelium was not included in the models and was therefore assumed to be unaltered by whichever clinical CXL method would be used to generate corneal stiffening. This assumption could introduce a nominal error in the modeling of such treatments in eyes in which the final posttreatment corneal epithelial thickness profile differs from the pretreatment thickness profile. Eventually, clinical characterization of changes in the corneal epithelial thickness with optical coherence tomography or very-high-frequency ultrasound imaging can be explicitly incorporated into the model. Another limitation of the study is that assigned material properties were derived from ex vivo data and were standardized across patient models. Although this provides a reasonable starting point for the aim of treatment discovery, incorporation of patient-specific material properties is likely to support higher fidelity simulations and lower prediction error for individual cases. Studies to validate model predictions against ex vivo corneal experiments are underway, and validation in parallel with future clinical trials is planned. The effect of gradient stiffening patterns are also being explored and will be compared with the results of the uniform stiffening patterns to inform further pattern optimization.
In summary, this in silico study presents a new noninvasive alternative for corneal refractive correction of astigmatism. The results show proof of concept that selective stiffening of the cornea is capable of reproducibly reducing corneal astigmatism with minimal induction of HOAs and with augmentation of rather than a reduction in corneal biomechanical integrity.
WHAT WAS KNOWN
Corneal CXL in ectatic corneas has been shown not only to halt progressive topographic steepening but also to reduce corneal curvature in the majority of treated eyes.
Cornea-based treatments for astigmatism typically involve incisional or ablative approaches that reduce corneal biomechanical strength as the mechanism of action or as a byproduct of treatment.
WHAT THIS STUDY ADDS
Proof of concept is presented for the selective alteration of corneal astigmatism with patterned collagen stiffening treatments.
Candidate patterns for a new nonincisional nonablative treatment of astigmatism are described and compared using a simulation-based approach to treatment design.
Differences in the mean astigmatic effect of 2 different material formulations were clinically and statistically insignificant; however, the local topographic changes and coupling ratio were affected by the incorporation of fiber-dependent anisotropy.
Biography

First author: Ibrahim Seven, MS
Cole Eye Institute, Ocular Biomechanics and Imaging Laboratory, Cleveland, Ohio
Footnotes
Marc Friedman, PhD, Evan Sherr, MS, Satish Herekar, MSEE, and David Muller, PhD, Avedro, Inc. provided input on treatment pattern simulations.
FINANCIAL DISCLOSURES
Drs. Roy and Dupps hold intellectual property through Cleveland Clinic Innovations related to computational modeling and have received royalties for use of the model in sponsored research from Avedro, Inc., Carl Zeiss Meditec AG, and Topcon Medical Systems, Inc. Mr. Seven has no financial or proprietary interest in any material or method mentioned.
REFERENCES
- 1.Kohnen T, Bühren J. Corneal first-surface aberration analysis of the biomechanical effects of astigmatic keratotomy and a micro-keratome cut after penetrating keratoplasty. J Cataract Refract Surg. 2005;31:185–189. doi: 10.1016/j.jcrs.2004.09.048. [DOI] [PubMed] [Google Scholar]
- 2.Montés-Micó R, Muñoz G, Albarrán-Diego C, Rodríguez-Galietero A, Alió JL. Corneal aberrations after astigmatic keratotomy combined with laser in situ keratomileusis. J Cataract Refract Surg. 2004;30:1418–1421. doi: 10.1016/j.jcrs.2003.11.057. [DOI] [PubMed] [Google Scholar]
- 3.Wollensak G, Spoerl E, Seiler T. Riboflavin/ultraviolet-A–induced collagen crosslinking for the treatment of keratoconus. [March 14, 2014];Am J Ophthalmol. 2003 135:620–627. doi: 10.1016/s0002-9394(02)02220-1. Available at: http://grmc.ca/assets/files/collagen_crosslinking_2003_wollensak.pdf. [DOI] [PubMed] [Google Scholar]
- 4.Spoerl E, Huhle M, Seiler T. Induction of cross-links in corneal tissue. Exp Eye Res. 1998;66:97–103. doi: 10.1006/exer.1997.0410. [DOI] [PubMed] [Google Scholar]
- 5.Roy AS, Dupps WJ., Jr Patient-specific computational modeling of keratoconus progression and differential responses to collagen cross-linking. [March 14, 2014];Invest Ophthalmol Vis Sci. 2011 52:9174–9187. doi: 10.1167/iovs.11-7395. Available at: http://www.iovs.org/content/52/12/9174.full.pdf. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Smolek MK, Klyce SD. Goodness-of-prediction of Zernike polynomial fitting to corneal surfaces. J Cataract Refract Surg. 2005;31:2350–2355. doi: 10.1016/j.jcrs.2005.05.025. [DOI] [PubMed] [Google Scholar]
- 7.Roy AS, Dupps WJ., Jr Effects of altered corneal stiffness on native and postoperative LASIK corneal biomechanical behavior: a whole-eye finite element analysis. J Refract Surg. 2009;25:875–887. doi: 10.3928/1081597X-20090917-09. [DOI] [PubMed] [Google Scholar]
- 8.Sinha Roy A, Rocha KM, Randleman JB, Stulting RD, Dupps WJ., Jr Inverse computational analysis of in vivo corneal elastic modulus change after collagen crosslinking for keratoconus. Exp Eye Res. 2013;113:92–104. doi: 10.1016/j.exer.2013.04.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pinsky PM, van der Heide D, Chernyak D. Computational modeling of mechanical anisotropy in the cornea and sclera. J Cataract Refract Surg. 2005;31:136–145. doi: 10.1016/j.jcrs.2004.10.048. [DOI] [PubMed] [Google Scholar]
- 10.Pandolfi A, Holzapfel GA. Three-dimensional modeling and computational analysis of the human cornea considering distributed collagen fibril orientations. J Biomech Eng. 2008;130:061006. doi: 10.1115/1.2982251. [DOI] [PubMed] [Google Scholar]
- 11.Sinha Roy A, Dupps WJ., Jr Patient-specific modeling of corneal refractive surgery outcomes and inverse estimation of elastic property changes. J Biomech Eng. 2011;133:011002. doi: 10.1115/1.4002934. [DOI] [PubMed] [Google Scholar]
- 12.Elsheikh A, Whitford C, Hamarashid R, Kassem W, Joda A, Büchler P. Stress free configuration of the human eye. Med Eng Phys. 2013;35:211–216. doi: 10.1016/j.medengphy.2012.09.006. [DOI] [PubMed] [Google Scholar]
- 13.Wollensak G, Spoerl E, Seiler T. Stress-strain measurements of human and porcine corneas after riboflavin–ultraviolet-A-induced cross-linking. J Cataract Refract Surg. 2003;29:1780–1785. doi: 10.1016/s0886-3350(03)00407-3. [DOI] [PubMed] [Google Scholar]
- 14.Hoeltzel DA, Altman P, Buzard K, Choe K-i. Strip extensiometry for comparison of the mechanical response of bovine, rabbit, and human corneas. [March 14, 2014];J Biomech Eng. 1992 114:202–215. doi: 10.1115/1.2891373. Available at: http://www.buzard.info/StripExtensiometry.pdf. [DOI] [PubMed] [Google Scholar]
- 15.Holzapfel GA, Gasser TC, Ogden RW. A new constitutive framework for arterial wall mechanics and a comparative study of material models. [March 14, 2104];J Elasticity. 2000 61:1–48. Available at: http://hallf-dom.hallf.kth.se/cv/papers/report-8.pdf. [Google Scholar]
- 16.Sinha Roy A, Dupps WJ, Jr, Roberts CJ. Comparison of biomechanical effects of small-incision lenticule extraction and laser in situ keratomileusis: finite element analysis study. J Cataract Refract Surg. 2014;40 doi: 10.1016/j.jcrs.2013.08.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Randleman JB, Dawson DG, Grossniklaus HE, McCarey BE, Edelhauser HF. Depth-dependent cohesive tensile strength in human donor corneas: implications for refractive surgery. J Refract Surg. 2008;24:85–89. doi: 10.3928/1081597X-20080101-15. [DOI] [PubMed] [Google Scholar]
- 18.Spoerl E, Raiskup F, Kampik D, Geerling G. Correlation between UV absorption and riboflavin concentration in different depths of the cornea in CXL [letter]. Curr Eye Res. 2010;35:1040–1041. doi: 10.3109/02713683.2010.506969. reply by AP Søndergaard, J Hjortdal, T Breitenbach, A Ivarsen, 1042–1043. [DOI] [PubMed] [Google Scholar]
- 19.Spoerl E, Mrochen M, Sliney D, Trokel S, Seiler T. Safety of UVA–riboflavin cross-linking of the cornea. Cornea. 2007;26:385–389. doi: 10.1097/ICO.0b013e3180334f78. [DOI] [PubMed] [Google Scholar]
- 20.Mazzotta C, Caporossi T, Denaro R, Bovone C, Sparano C, Paradiso A, Baiocchi S, Caporossi A. Morphological and functional correlations in riboflavin UV A corneal collagen cross-linking for keratoconus. [March 14, 2014];Acta Ophthalmol. 2012 90:259–265. doi: 10.1111/j.1755-3768.2010.01890.x. Available at: http://onlinelibrary.wiley.com/doi/10.1111/j.1755-3768.2010.01890.x/pdf. [DOI] [PubMed] [Google Scholar]
- 21.Meek KM, Boote C. The use of X-ray scattering techniques to quantify the orientation and distribution of collagen in the corneal stroma. Prog Retin Eye Res. 2009;28:369–392. doi: 10.1016/j.preteyeres.2009.06.005. [DOI] [PubMed] [Google Scholar]
- 22.Alpins NA. A new method of analyzing vectors for changes in astigmatism. J Cataract Refract Surg. 1993;19:524–533. doi: 10.1016/s0886-3350(13)80617-7. [DOI] [PubMed] [Google Scholar]
- 23.Pinsky PM, Datye DV. Numerical modeling of radial, astigmatic, and hexagonal keratotomy. Refract Corneal Surg. 1992;8:164–172. [PubMed] [Google Scholar]
- 24.Hanna KD, Jouve FE, Waring GO, III, Ciarlet PG. Computer simulation of arcuate keratotomy for astigmatism. Refract Corneal Surg. 1992;8:152–163. [PubMed] [Google Scholar]
- 25.Knox Cartwright NE, Tyrer JR, Marshall J. In vitro quantification of the stiffening effect of corneal cross-linking in the human cornea using radial shearing speckle pattern interferometry. J Refract Surg. 2012;28:503–507. doi: 10.3928/1081597X-20120613-01. [DOI] [PubMed] [Google Scholar]
- 26.Armstrong BK, Lin MP, Ford MR, Santhiago MR, Singh V, Grossman GH, Agrawal V, Sinha Roy A, Butler RS, Dupps WJ, Wilson SE. Biological and biomechanical responses to traditional epithelium-off and transepithelial riboflavin-UVA CXL techniques in rabbits. J Refract Surg. 2013;29:332–341. doi: 10.3928/1081597X-20130415-04. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wernli J, Schumacher S, Spoerl E, Mrochen M. The efficacy of corneal cross-linking shows a sudden decrease with very high intensity UV light and short treatment time. [March 14, 2014];Invest Ophthalmol Vis Sci. 2013 54:1176–1180. doi: 10.1167/iovs.12-11409. Available at: http://www.iovs.org/content/54/2/1176.full.pdf. [DOI] [PubMed] [Google Scholar]
- 28.Kamaev P, Friedman MD, Sherr E, Muller D. Photochemical kinetics of corneal cross-linking with riboflavin. [March 14, 2014];Invest Ophthalmol Vis Sci. 2012 53:2360–2367. doi: 10.1167/iovs.11-9385. Available at: http://www.iovs.org/content/53/4/2360.full.pdf. [DOI] [PubMed] [Google Scholar]
- 29.de Vries NE, Webers CAB, Touwslager WRH, Bauer NJC, de Brabander J, Berendschot TT, Nuijts RMMA. Dissatisfaction after implantation of multifocal intraocular lenses. J Cataract Refract Surg. 2011;37:859–865. doi: 10.1016/j.jcrs.2010.11.032. [DOI] [PubMed] [Google Scholar]
- 30.Zheleznyak L, Kim MJ, MacRae S, Yoon G. Impact of corneal aberrations on through-focus image quality of presbyopia-correcting intraocular lenses using an adaptive optics bench system. J Cataract Refract Surg. 2012;38:1724–1733. doi: 10.1016/j.jcrs.2012.05.032. [DOI] [PubMed] [Google Scholar]
- 31.Seven I, Dupps JW., Jr Patient-specific finite element simulations of standard incisional astigmatism surgery and a novel patterned collagen crosslinking approach to astigmatism treatment. J Med Devices. 2013;7(4):040913. doi: 10.1115/1.4025980. [DOI] [PMC free article] [PubMed] [Google Scholar]