Abstract
Much research supports the existence of an Approximate Number System (ANS) that is recruited by infants, children, adults, and non-human animals to generate coarse, non-symbolic representations of number. This system supports simple arithmetic operations such as addition, subtraction, and ordering of amounts. The current study tests whether an intuition of a more complex calculation, division, exists in an indigene group in the Amazon, the Mundurucu, whose language includes no words for large numbers. Mundurucu children were presented with a video event depicting a division transformation of halving, in which pairs of objects turned into single objects, reducing the array's numerical magnitude. Then they were tested on their ability to calculate the outcome of this division transformation with other large-number arrays. The Mundurucu children effected this transformation even when non-numerical variables were controlled, performed above chance levels on the very first set of test trials, and exhibited performance similar to urban children who had access to precise number words and a surrounding symbolic culture. We conclude that a halving calculation is part of the suite of intuitive operations supported by the ANS.
Introduction
Infants, children, adults, and many non-human animals are able to represent large numbers of objects, sounds, and events in an imprecise fashion, using the Approximate Number System (ANS; Cordes, Gelman, Gallistel & Whalen, 2001; Dehaene, 1997; Gallistel, 1990; Lipton & Spelke, 2004; van Loesbrook & Smitsman, 1990; Meck & Church, 1983; Platt & Johnson, 1971; Starkey & Cooper, 1980; Starkey, Spelke & Gelman 1990; Wood & Spelke, 2005; Xu & Spelke, 2000). The ANS supports these computations without the use of symbols such as Arabic numerals; its signature is the imprecise representation of number, in which the discrimination of two quantities is determined by their ratio and not absolute difference (e.g. 10/20 and 100/200 are equally discriminable; see Izard & Dehaene, 2008). Studies performed on infants, children, adults, and non-human primates suggest that the ANS also supports simple non-symbolic arithmetic operations including addition, subtraction, and ordering (Barth, La Mont, Lipton & Spelke, 2005; Barth, La Mont, Lipton, Dehaene, Kanwisher & Spelke, 2006; Brannon, 2002; Brannon, Wusthoff, Gallistel & Gibbon, 2001; Cantlon & Brannon, 2006; Cantlon & Brannon, 2007; Capaldi & Miller, 1998; Cordes, Gallistel, Gelman & Latham, 2007; Gilmore, McCarthy & Spelke, 2007; McCrink & Wynn, 2004, 2009; Pica, Lemer, Izard & Dehaene, 2004).
The potential for the ANS to underlie the operations of multiplication and division is unclear. Work on the neuroscience of number has revealed a consistent difference in neural activation patterns for addition/subtraction and multiplication/division, but this finding may be due to a distinction between rote and on-line computation. For example, there is a bilateral activation pattern in the horizontal segment of the intraparietal sulci (HIPS) during tasks which require recruitment of the semantic representation of quantity (Thioux, Pesenti, Costes, De Volder & Seron, 2005; Dehaene, 1996; Naccache & Dehaene, 2001), with activation increasing during calculation tasks such as subtraction, approximate addition, or numerical comparison (Chochon, Cohen, van de Moortele & Dehaene, 1999; Dehaene, Spelke, Pinel, Stanescu & Tsivkin, 1999; Menon, Rivera, White, Glover & Reiss, 2000). In contrast, the left angular gyrus (AG) exhibits greater activation during a multiplication task compared to a number comparison or subtraction task (Chochon et al., 1999; Lee, 2000). Dehaene, Piazza, Pinel and Cohen (2003) suggested that the HIPS and AG are distinct parietal circuits that underlie different calculation tasks, with the left AG responsible for exact calculations drawing upon rote verbal facts. This distinction is also supported by cases of patients with brain lesions in the parietal lobe, in which one observes a double dissociation between performance on subtraction and multiplication tasks, especially those problems that differ in terms of memorization or verbal encoding (e.g. readily recalled multiplication-table problems; Cohen & Dehaene, 2000; Dehaene & Cohen, 1997; Delazer & Benke, 1997; Lampl, Eshel, Gilad & Sarova-Pinhas, 1994; Van Harskamp & Cipolotti, 2001).
One likely reason that scaling processes such as multiplication and division appear to rely on distinct verbal-numerical regions such as the AG is because of the tendency to provide multiplication problems to subjects in a way that allows or encourages the use of rote-learned, exact calculation based on memorized tables (e.g. 9*4=x). Outcomes to subtraction problems, on the other hand, tend to not be memorized (e.g. 9−4=x), and therefore are more likely to activate semantic representations of number. When methods that do not emphasize written, tabular multiplication problems are used, and instead the presence of scaling calculations can be indirectly inferred, there is evidence that the ANS is active. In one recent series of studies, adults who are shown a particular proportion (1/2, 2/4, 3/6) repeatedly, and then shown an ‘oddball’ proportion (e.g. 3/5), exhibit activation patterns traditionally associated with a semantic representation of number (Jacob & Neider, 2009a, 2009b). Using an fMRI adaptation procedure in which proportions of one type were repeatedly presented, interspersed with deviant proportions, the authors found that areas associated with encoding of absolute number (the intraparietal sulcus, or IPS) exhibited a rebound in activation to deviant proportions, and this activation increased as the discrepancy between the two proportions increased. Further, the effect was robust to format, indicative of the highly conceptual nature of the proportions. It was found for spatial proportions in addition to numerical proportions (lines of different lengths; Jacob & Nieder, 2009a) and when the adaption stimuli were Arabic numerals (e.g. 1/4), but deviants were presented as words such as one-half (Jacob & Neider, 2009b). (See Jacob, Vallentin & Nieder, 2012, for a recent review of the neuroscience of proportional reasoning.)
A form of implicit reasoning about proportions has been studied for several decades by developmental psychologists who aimed to establish the arithmetic intuitions guiding children’s early division reasoning (Goswami, 1989; Jeong, Levine & Huttenlocher, 2007; Mix, Levine & Huttenlocher 1999; Spinillo & Bryant, 1991; Sophian, 2000; Piaget & Inhelder, 1956). In these studies, children as young as 3 years of age are presented with one or more arrays that exhibit a particular proportion (e.g. a rectangle, square, and diamond that all have shading on three-quarters of their surface area), and then must select a test stimulus that exemplifies that same proportion of shaded area (e.g. a three-quarters shaded diamond). Despite some early evidence by Piaget and Inhelder (1956) that children perform poorly until 7 or 8 years of age, later work with more sensitive measures revealed that even preschoolers can extract and identify a common proportional relationship between test and standard (Sophian, 2000). Further, the proportion of one-half appears to hold a privileged place in the child’s mind; children can most readily grasp this particular proportion, and use it as a boundary to establish whether two proportions are discriminable (Ball, 1993; Mix et al., 1999; Spinillo & Bryant, 1991), leading some to propose that the process of equal splitting is a conceptual primitive (Confrey, 1994).
These methods demonstrate a sensitivity to numerical proportions, but they have several limitations. First, the above proportional analogy tasks do not preserve the serial, step-by-step format of whole-number multiplication and division problems as presented during schooling (a number a, acted upon by some factor b, yields outcome c). Tasks that follow this step-by-step structure can support understanding of arithmetic in a school-based setting. For example, Gilmore et al. (2007) found that 5- and 6-year-old children who have no formal arithmetic knowledge performed well when presented with visualized, narrated depictions of an addition or subtraction scenario such as the following: ‘Sarah has 15 candles and she gets 19 more, John has 51 candles. Who has more?’ Their performance was dictated by the ratio of the actual outcome (Sarah’s total) and comparison amount (John’s total), suggesting that kindergarten children recruit the ANS when presented with challenging addition and subtraction problems in a symbolic format.
Second, with few exceptions (McCrink & Wynn, 2007), these proportional analogy and probability tasks tap into subjects’ conceptions of space and spatial variables (mainly, area) instead of abstract representations of number. For example, Sophian (2000) presented children with pictures of a sketched figure with a particular proportion of head:body, and then had children choose from two smaller test stimuli the picture which exemplified the same proportion. Such a proportional homology task is a calculation that – at some level – must involve a division-based process, and it is impressive that preschoolers with no formal education can make this inference. However, this inference does not speak to reasoning about numerical magnitudes as distinct from other types of quantity, and it does not preserve the serial, explicit nature that may assist in formal education later in life.
Studies of infants and young children, using video-based events in which non-symbolic arrays of objects are added to, and subtracted from, other arrays of objects, suggest an alternative means to depict these operations (Barth et al., 2005, 2006; McCrink & Wynn, 2004, 2009). This method has been adapted to convey the operations of multiplication and division in a concrete, serial, non-symbolic fashion in which children compute over explicitly numerical representations from the ANS, controlling for co-varying non-numerical factors (Barth, Baron, Spelke & Carey, 2009; McCrink & Spelke, 2010, submitted). In these studies, 5–7-year-old Western children who have no formal education in multiplication or division were able to scale an estimated non-symbolic amount by a multiplicative or divisive factor. The children were able to halve, double, quadruple, quarter, and even multiply by an uneven factor of 2.5 a series of large, approximate numerical values such as 12 or 24, suggesting that this fundamental core scaling ability is supported by the ANS alongside addition and subtraction.
Although this scaling process was not taught in school, it is unclear to what extent children’s performance depended on count lists and other precise mechanisms for tracking and reasoning about number. Although the children who have shown this ability were screened to have no formal education in multiplication and division, and the arrays were designed to be uncountable given time constraints, there is an emphasis on mathematics from a very early age in American culture. Parental coaching, books, and even television shows (e.g. ‘Sesame Street’) geared towards infants and preschoolers highlight counting, repeated set adding, and proportional equivalence across objects and arrays. Thus, the previous research leaves open the possibility that education or enculturation, rather than intuitive number sense, is responsible for young children’s competence with approximate multiplication and division. In the present research, we therefore sought to determine whether intuitions of approximate division over non-symbolic, estimated quantities would be available to children in an indigenous Amazonian tribe, who speak the Mundurucu language and have limited and variable access to formal schooling. The Mundurucu language has unique number words only for the numbers 1 through 5. Mundurucu children have highly variable access to education, rulers, graphs, and other measurement devices. However, the Mundurucu do possess intuitive concepts of number, and they share foundational arithmetic capacities with Westernized populations, despite lacking overt and precise symbols for large numbers or mathematical operations (Dehaene, Izard, Spelke & Pica, 2008; Pica et al., 2004). If the ability to scale large numerical quantities is a fundamental capacity operating over ANS representations, it should be present in Mundurucu subjects.
Method
The subjects were shown videotaped events depicting a non-symbolic scaling factor of one-half. In order to establish the scaling factor, rectangles were shown which, after a wave of a computerized wand, coalesced into a single rectangle which grew, shrank, and moved independently after the transformation. Arrays of various large quantities of rectangles were then shown, occluded, and transformed. After a comparison array appeared on the other side of the screen, the subjects indicated whether this array, or the occluded transformed array, was more numerous (see Figure 1 for a schematic). This comparison array differed from the correct outcome by a factor of 1.5 or 2.0 (the Weber ratio, or WR). If these individuals were able to mentally transform the initial array, they would be above chance at choosing which was more numerous. For the initial set of training trials, cues to continuous extent (such as area and contour length) were confounded with number; for the final set of testing trials, these cues were controlled such that only numerical division of the initial array would yield above-chance performance. Both the manipulation of WR and control of co-varying perceptual factors to ensure numerical calculations per se were included in order to test the specific hypothesis that the ANS in particular is underlying the numerical representations and calculations necessary to complete this task. Given previous work on the nature, function, and theory of the ANS, we predicted that (a) performance will decrease as the Weber ratio decreases, and (b) children will still succeed in this task even when non-numerical variables are unavailable for computation.
Figure 1.

A schematic of the experimental procedure during the training trials. Testing trials were identical except that (a) no transformed outcome was shown, and (b) the comparison arrays were controlled for area and contour length instead of density and item size.
Subjects
Fifteen Mundurucu children participated in this experiment (age range 7–11 years, mean age 9 years). These subjects were all native speakers of Mundurucu. They had varying degrees of education, with seven subjects possessing some level of schooling (two subjects were in Year 1, three in Year 2, and two in Year 3). The experiment was conducted in the Mundurucu language to minimize the effects of this schooling, and the subjects had not yet learned any terms for division or multiplication in their schooling. Years 1 and 2 are devoted to reading and writing single letters, and formulating words and basic sentences, respectively. In Year 3 they are introduced to words and symbols for precise large numbers. Recent work by Piazza, Pica, Izard and Dehaene (in press) has established that the third year, when rudiments of formal arithmetic are introduced, leads to substantial improvements in ANS acuity, relative to uneducated Mundurucu speakers.
Displays and procedure
Scaling factor introduction
The child and experimenter watched the video displays on a Macintosh laptop computer. The children first viewed a display consisting of two blue rectangles, which grew and shrank for several seconds before becoming stationary. An animated wand appeared and, after several seconds of waving, the two rectangles became comparably sized and joined into one rectangle. When testing children from the United States in this paradigm, we invoke the concept of a magic wand. For the Mundurucu speakers it was accompanied by the spoken term ‘motion’, as we discovered during conversations before testing that there is no such thing as a ‘magic wand’ in their culture. The experimenter exclaimed ‘Look! ‘ and directed the child’s attention to the screen. The child then saw a video that was identical to the previous video, but now the rectangles were occluded during the waving of the wand. In this way the child saw the actual merging of the rectangles via the wand, and saw an example of that merging occurring under occlusion.
Training block
During training, children saw a large number of blue rectangles on the left side of the screen. After several seconds, an occluder covered the array. The wand then came out and waved over the occluded array, while the experimenter exclaimed ‘Look!’ to direct the child’s attention to the screen. A comparison array composed of pink squares came down on the right side of the screen. These squares were of identical size and density (1 cm2 area, 4 cm contour length, 25 squares per 100 cm2 area across all training trials). The children were asked to point where they thought there were more rectangles, the experimenter recorded their answers, and then the screen dropped and the children learned whether they answered correctly. To control for experimenter bias, the experimenter sat next to the child and several feet away from the screen, and phrased the question neutrally (‘Where are there more now?’). In these training trials, the area of the comparison array and the number of objects were confounded. For example, the subject would see an array of 24 objects (~27 cm2 area, ~120 cm contour length) become occluded and transformed, then a comparison array of six squares would appear on the right side of the screen (6 cm2 area, 24 cm contour length, density of ~25 squares per 100cm2 envelope). After a response was given, the occluder dropped to reveal the outcome of 12 rectangles (the original outcome array, with each object coalesced with another comparably sized object, for a total of ~27 cm2 area, ~100 cm contour length due to the joining of objects). In this way, the size of the comparison array in terms of overall area and contour length differed along with numerical quantity: the comparison arrays that were least numerous were physically also the smallest.
Testing block
The test trials were similar to the training trials, except that (a) subjects did not see the final outcome, and they were not told whether they answered correctly (e.g. the screen covering the outcome never dropped to show the correct answer), (b) area and contour length of the comparison arrays was no longer confounded with number, so correct responses could only be based on numerical variables per se, and (c) new values were used to avoid any rote learning that may have carried over from training. For example, a subject might see an initial array of 16 objects (~28 cm2 area, 130 cm contour length), and then a comparison array of four objects (~35 cm2 area, 100 cm contour length). On a later trial, they would see a similar initial array of 16 objects, slightly rotated or reconfigured, and then a comparison array of 12 objects (also ~35 cm2 area, 100 cm contour length). The extent dimensions for the comparison arrays, which were identical across all distance types (correct outcome*2,*1.5,/1.5, and /2), were chosen to be similar to the imagined occluded amount. In this way, even subjects who were visualizing the outcomes behind the screen could not use area or contour length to guide their judgments, and must use only the number of objects in the comparison array relative to the calculated outcome. The method of controlling for use of non-numerical variables was modeled after McCrink and Spelke (2010, submitted).
Design
There were 12 training trials and 16 test trials. On equal numbers of trials in each category, the comparison array differed from the outcome by a Distance factor of /2 (i.e. it presented half the correct outcome), /1.5, *1.5, or *2 (i.e. it presented twice the correct outcome). The initial array values for training trials were: 24, 44, and 56 objects. The initial array values for testing trials were: 16, 32, 48, and 64 objects. These testing values were chosen to examine whether children would only be able to interpolate the transformation (e.g. succeed only on initial arrays of 32 and 48, which are in the same range as training) or could extrapolate the transformation as well (e.g. succeed on initial arrays of 16 and 64, which are outside the range of training). See Table 1 for the specific values used. We included a large number of training trials (12, along with 16 testing trials) for several reasons. Even though we knew from previous work that this relationship was readily grasped by US children, we wanted to give the Mundurucu children the same opportunity to extract the proportion. This allows us to look for any potential learning effects across the course of training, and yields identical data for comparison to those found in McCrink and Spelke (submitted). Previous work in the villages of the Amazon has also found that Mundurucu speakers are less interested in these tasks than a US population; building in extra time and opportunity to learn critical components of the task is one solution to this problem.
Table 1.
Specific values used during the training and testing trials
| Training | Testing |
|---|---|
| 24/2 vs. 6 | 16/2 vs. 4 |
| 24/2 vs. 8 | 16/2 vs. 5 |
| 24/2 vs. 18 | 16/2 vs. 12 |
| 24/2 vs. 24 | 16/2 vs. 16 |
| 44/2 vs. 11 | 32/2 vs. 8 |
| 44/2 vs. 15 | 32/2 vs. 11 |
| 44/2 vs. 33 | 32/2 vs. 24 |
| 44/2 vs. 44 | 32/2 vs. 32 |
| 56/2 vs. 14 | 48/2 vs. 12 |
| 56/2 vs. 19 | 48/2 vs. 16 |
| 56/2 vs. 42 | 48/2 vs. 36 |
| 56/2 vs. 56 | 48/2 vs. 48 |
| 64/2 vs. 16 | |
| 64/2 vs. 21 | |
| 64/2 vs. 48 | |
| 64/2 vs. 64 | |
Results
Each subject was given an average score composed of his or her performance on training and testing trials whose comparison arrays were a particular distance from the correct outcome (correct outcome/ 2,/1.5, *1.5, or *2), a measure which captures both Weber ratio (a psychophysical measure, defined here as the ratio of the greater:lesser of the calculated outcome and the comparison array) and comparison array type (whether it was larger, or smaller than the correct outcome of the transformation). Overall performance during training (85%) and testing (73%) was significantly above chance (one-sample t-tests; ts(13) = 12.59, 6.23, both ps < .001, two-tailed). Using a test proportion of 67.8% (19/28 trials with an alpha level of .05), we also calculated the number of children whose individual performance was above chance; 13 of 15 children met this criterion (13 observed successes with a total N of 15, binomial sign test with an alpha of .05, p < .01).
A repeated-measures ANOVA with block (training block, testing block), Weber ratio (1.5, 2.0) and comparison array type (smaller than outcome, larger than outcome) as within-subject factors was performed over the subjects’ scores.1 There was a significant main effect of block (F(1, 14) = 7.92, p = .01, η2 = .36); the subjects performed better during training (85%), when both continuous variables and numerical variables were available, than during testing (73%), when only numerical variables could drive performance. There was no main effect of Weber ratio (F(1, 14) = 2.38, p = .14, η2 = .15); subjects scored 76% correct for 1.5 WR and 82% correct for the 2.0 WR. There was a marginal main effect of comparison array type (F(1, 14) = 4.14, p = .06, η2 = .23); subjects answered correctly 86% of the time when the comparison array was smaller than the computed outcome, vs. 72% when it was larger. Performance was worst at the correct*1.5 comparison distance trials (71%), better for the *2 (74%) and /1.5 trials (85%), and best for /2 (93%). This pattern, along with the higher performance for trials in which the comparison array was smaller than the outcome, indicates a tendency to overestimate the outcomes. We also examined overall performance as a function of only the Weber ratio of the trial. Subjects’ scores were collapsed into a Weber ratio of 2:1 (/2 and *2 comparison arrays) and 1.5:1 (/1.5 and *1.5 comparison arrays) for both the training and testing trials. For both training and testing individually, both Weber ratio trial types were above chance (one-way t-tests against chance, all ps < .01). Studies on the ANS consistently find a decrease in performance as the Weber ratio of two values approaches 1.0, and it is considered a hallmark of this system. We assigned each child a score for their training and test items at either the 1.5 WR or 2.0 WR. Here, as predicted within the ANS framework, this analysis indicates that performance was lower for the Distance 1.5:1 trial than the Distance 2:1 trial types (paired-samples one-tailed t-test, t(29) = 1.9, p = .034; see Figure 2).
Figure 2.
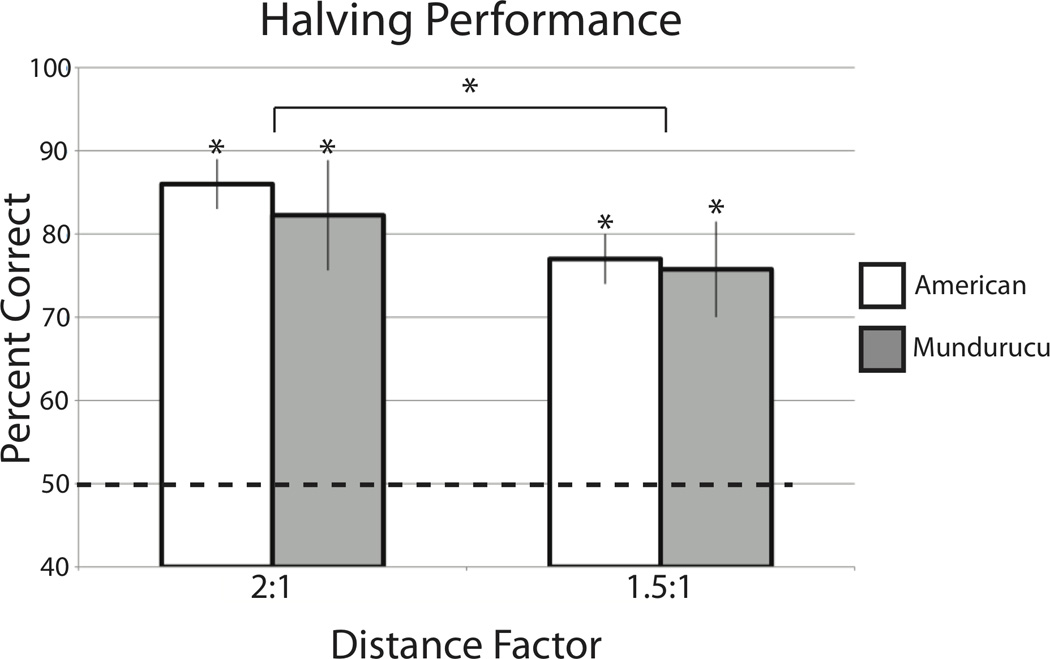
Performance on the halving task across both blocks for the American children in McCrink and Spelke (submitted) and the present Mundurucu sample. The children’s ability to correctly determine which array is more numerous is plotted as a function of the ratio of comparison array:correct transformed outcome (2:1 or 1.5:1). Asterisks convey a p-value of < .05. Chance is indicated with a dashed line at 50%.
Independent-subjects t-tests on training and testing performance between the genders reveal no significant differences (Training: 87% female, 83% male; Testing: 70% female, 77% male; ts(13) = .67, .96, both ps > .05). Linear regressions on training and testing performance scores reveal no significant impact of grade on training performance (R2 = .05, F(1, 14) = .62, p > .05). However, there was a significant impact of grade during the testing block (R2 = .47, F(1, 14) = 11.47, p < .01), during which numerical variables and continuous extent variables such as area and contour length are unconfounded. A follow-up one-way ANOVA of overall performance × grade shows no significant differences between the grades individually but rather a significant linear trend (F(1, 11) = 6.20, p = .03). Importantly, as predicted, even those subjects who are not schooled (n = 8) were above chance for overall performance (73%), training (82%), and testing (66%; one-sample one-way t-tests against chance, all ps < .05).
In order to tease apart the relative contributions of schooling and maturation, we examined whether the age of the child impacted their overall performance in the same way. Linear regressions on training performance and testing performance reveal no significant change over age (R2 = .09, .15, respectively, Fs(1, 14) = 1.32, 2.37, both ps > .05). Overall, we found that the children were quite variable, and older children did not outperform younger ones (one-way ANOVA of overall performance × age, F(1, 10) = 2.88, p = .12).
To test whether the subjects learned this scaling relationship over the course of training, we tabulated each subject’s percentage of correct responding for the first and last trials at each Distance trial type (correct/2,/1.5, *1.5, *2) during the training block. Performance was above chance for both the first set and the last set of trials of each type (85% and 83%, respectively; one-sample t-tests against chance yield ts (14) = 7.36, 7.14, both ps < .005, one-tailed), indicating that children did not require much training to understand and apply the halving transformation. There was no significant improvement from the first set of trials to the last set of trials (paired-sample t-test, t(14) = .29, p = .77). In addition, the subjects were able to extrapolate to initial array values outside the range they learned in training. While training was restricted to the range 24–56 objects, performance on halving 16-object and 64-object arrays during testing was significantly above chance (73% and 68%, respectively; two-tailed one-sample t-test against chance, ts(14) = 4.5, 2.95, ps < .05).
Range analyses
Barth et al. (2009) found that American children, viewing a similar paradigm, sometimes resorted to range-based strategies in order to make their comparisons. If subjects realize that the comparison arrays fall within a certain range (e.g. a minimum of six objects and a maximum of 56 objects), they may use the extremities of this range in order to guide their response. For example, when given a problem of 16/2 vs. a comparison array of four, subjects may respond that the occluded outcome is larger simply because they realize that four is a small number – and therefore likely to designate the smaller quantity. We tabulated subjects’ percentages correct for problems whose comparison arrays fell within the extremities of the possible range (with values of 4, 5, 8, 11, 36, 48, 48, 64) vs. the middle of the possible range (with values of 12, 12, 16, 16, 16, 21, 24, and 32). Children’s mid-range performance was significantly above chance (72%, one-sample t-test against chance, t(14)= 4.52, p < .001). There was no significant difference between mid-range performance (72%) vs. end-range performance (75%; paired-sample t-test, t(14) = .64, two-tailed p = .54), suggesting that Mundurucu children did not use this strategy. Moreover, children’s responses to the comparison arrays that lay in the middle of the range were modulated by the Weber ratio of the comparison array and outcome array. Specifically, the comparison array values of 12 and 48 each had one trial in which they were relatively distinct from the outcome (e.g. differed by a factor of 2.0) and one in which they were relatively close to the outcome (e.g. differed by a factor of 1.5). The children performed significantly better on the Distance 2.0 trials of the same value, compared to the Distance 1.5 trials (77% vs. 53%, t(14) = 2.17, p = .048).
Cross-cultural comparisons
In order to compare performance among the Mundurucu to that of an urban population, we compared the current dataset to that of McCrink and Spelke (submitted), which uses a similar paradigm and identical stimulus set, albeit with a slightly younger group of US children (5–7 years of age). One-way ANOVAs examining overall performance during training and testing with ethnicity as a between-subjects variable (Mundurucu, American) reveal no significant differences as a function of ethnicity (Training: 85% Mundurucu vs. 81% US children; Testing: 73% Mundurucu vs. 82% US children; Fs(1, 30) = .74, 3.55, both ps > .05). There was also no effect of ethnicity on performance on the very first trials after the single exemplar video for the Mundurucu and US children (85% vs. 73%; one-way ANOVA F(1, 29) = 2.59, p > .05). To best examine the relative performance of each group overall and as a function of task specifics, we performed an omnibus ANOVA over both groups’ data with Weber ratio (1.5, 2.0), comparison array type (smaller than outcome, larger than outcome) and Block (Training, Testing) as within-subjects factors, and ethnicity as a between-subjects factor. There were no significant main effects of block, ethnicity, and no interactions of ethnicity with Weber ratio or comparison array type. There was a significant main effect of comparison array type (F(1, 29) = 12.78, p < .01, η2 = .31), with children performing significantly better when the comparison array was smaller than the correct outcome rather than larger (88% vs. 73%), again indicative of both populations systematically overestimating the quotients. We also found a highly significant main effect of Weber ratio (F(1, 29) = 8.47, p < .001, η2 = .23). There was a marginal interaction of ethnicity and block (F(1, 29) = 3.99, p = .055, η2 = .12); although their overall performances are statistically comparable, the Mundurucu children did slightly better in training compared to testing (85% vs. 73%), whereas the American children performed at essentially the same level in both (81% vs. 82%).
In contrast to the Mundurucu children, the American children exhibited a tendency to use range information in addition to actually computing the outcome; they performed significantly above chance for both mid-range and end-range, but slightly better for end- than mid-range problems (86% vs. 78%). To quantify this difference, we performed one-way ANOVAs over children’s mid- and end-range performance with a between-subjects factor of ethnicity. Mundurucu and American children were comparable on mid-range problems (72% vs. 78%, F(1, 30) = 1.3, p > .05), but American children outperformed the Mundurucu on end-range problems (75% vs. 86%, F(1, 30) = 4.23, p = .047).
Discussion
In this study, Mundurucu children performed a serial, non-symbolic division task in which they viewed a set of objects and mentally transformed this set into another of half the numerical magnitude. Subjects were able to intuit a halving relationship between two objects and one object with very little training, and they generalized this relationship to much larger, new amounts, both within and outside the range of the training problems. They did so even though continuous variables that normally co-vary with number (density, item size, area, and contour length) were uninformative as input to the halving calculation. Age of the child (from 7 to 11 years) did not have a significant impact on overall performance. Finally, even subjects without formal education succeeded in this task, although education did improve performance.
We propose that the Mundurucu people mentally transformed large numbers by a factor of one-half with the support of an imprecise, untrained number system that is independent of numerical language and can make calculations over number per se independent from co-varying spatial extent dimensions. Although we believe this system to be the Approximate Number System, as detailed in the Introduction, we must be cautious with this interpretation. One of the hallmarks of this particular system is a decrease in performance when the comparison value was relatively close in number to the outcome, characteristic of the Weber ratio (in which the ratio of two amounts determines their discriminability). We saw modulation according to Weber ratio with a simple analysis, but the more complex model indicated that this modulation was trumped by the children’s tendency to overestimate. The implemented design, which controlled for the non-numerical quantity information oftentimes confounded with numerical magnitude, required that subjects rely on numerical magnitudes per se as the manipulated variables in this visual equation. Above all, the Mundurucu language has no words for the precise numerical quantities over which children calculated, and the children in these studies had little to no training in counting, tabulation, or arithmetic procedures.
A comparison of the Mundurucu children with children studied in an affluent Boston suburb (McCrink & Spelke, submitted) highlights several shared aspects of performance on this task. First, both the Mundurucu and the US children showed similar and above-chance responding on the very first set of trials. Second, performance during the training and testing trials was statistically comparable across both groups. Third, both English and Mundurucu speakers exhibited a similar performance profile for both Weber ratio and comparison array type, with a tendency towards overestimation (as reflected by poorer performance on trials in which the comparison array was larger than the outcome). It is difficult to tease apart exactly what is driving this overestimation effect, but we propose two candidates that may underlie it. It could be due to an anchoring heuristic, with the initial array drawing children to a higher outcome tally – thus leading to confusion between the subjective outcome, and comparison arrays which are larger than the objective outcome. Alternatively, it may be due to a directional miscalculation of scaling factor (scaling by a factor closer to .67 than .50), a phenomenon that appears to be present when children perform a similar multiplication task (McCrink & Spelke, 2010). Either way, these commonalities suggest that halving of numerical arrays is equally intuitive for children in both these cultures, and that whichever mental process is responsible for this calculation is operating in a similar fashion in both groups.
The groups did not behave identically, however. American children were more likely than Mundurucu children to use range-based strategies, and the Mundurucu – especially those without any education – showed a decrease in performance when additional cues to quantity (e.g. area, contour length) were unavailable. We speculate on several potential reasons for this. First, the US children may be more accustomed to a testing scenario in which one must dedicate sustained attention, and focus on number as an abstract concept. Second, US children may be more aware of how tests are crafted given their experience with everyday mathematics, and likely to seek out alternate methods for solving problems. Third, the US children’s experience with media may lead to faster (but not better) processing, leaving time to ferret out alternative patterns in the data. Finally, and more fundamentally, there could be differences in working memory due to practice with sustained attention and the culture of education found in the US, which lead to faster encoding and leftover processing capacity for alternative strategies. In addition, although there were no significant differences between the Mundurucu and US children in terms of general trends in Weber ratio differences, the modulation of performance with ratio was significant only for the US children (a 9% performance change as a function of ratio) and not for the Mundurucu children (with a 6% change). These differences, taken with the noted continuities, suggest that core knowledge and culture interact to modulate children's performance. The frequent use of symbols, an understanding of precise counting, and a cultural emphasis on enumeration – none of which are present in this Amazon population – are not needed to perform this core scaling process, but they may encourage the use of multiple strategies to problem solving.
This conclusion is also supported by the significant impact of school level on the performance of the Munduruku children. Adolescents and children in this population enter school sometime around the age of 8 or 9, though many children do not know their age and enter school at variable times (among 11-year-old children, for example, several had no schooling whereas two had 3 years of schooling). Piazza et al. (in press) found that in the third year of schooling, precise number words are introduced (in Portuguese) along with additional schooling in mathematics (e.g. estimation tasks, rudimentary adding and subtracting), and this third year sees a marked increase in the pupils’ ANS acuity. Individuals with no schooling still performed at above-chance levels on the current task, but as the level of schooling increased so did performance, likely due to increased ANS acuity. This speculation is supported by the finding of a linear relationship between schooling and performance only during testing trials; it is in these trials that area and contour length (two very commonly confounded cues to numerosity which are available for use in the training trials) were decorrelated with numerical magnitude, requiring subjects to compute the halving calculation over number per se.
Equally notable is the fact that age did not have a significant impact on the subjects’ performance on the task. Although one should be cautious of over-interpreting this lack of a maturation effect due to the small sample size (n = 15), small age range (7–11 years old), and less-than-reliable age data, the Mundurucu people are a rare opportunity to tease apart the relative contributions of biological maturation and schooling to the development of the ANS because children enter school at variable times in their development and thus have varying amounts of education at any given age. In industrialized cultures, one sees a rapid increase in ANS acuity during infancy (Lipton & Spelke, 2003), and then growing precision of the ANS throughout early childhood and even into adulthood (Halberda & Feigenson, 2008). However, because there is a confluence of maturation and education, one cannot determine the driver of this increasing precision. The current finding that education, but not age, impacts performance suggests a major role for education and enculturation on the development of this core number system in late childhood.
The capacity shown here to compute and equate a one-half relationship holds a special place in the literature on proportional analogical reasoning. Although the vast majority of previous studies use space, and not number, to probe proportional reasoning, and do so in a more implicit fashion than the serial paradigm used here, both types of studies rely on the child to recognize proportional analogies. In addition, there are several experiments in which young children show a particular facility with proportions equivalent to one-half (Goswami, 1989; Mix et al., 1999; Singer-Freeman & Goswami, 2001). However, recent research by McCrink and Spelke (submitted) illustrates that the division shown by children here is flexible and extends to scaling by one-quarter. Young children with no training on multiplication or division are also able to multiplicatively scale by a factor of 2, 4, and even 2.5, although performance decreased as the scaling factor increased (McCrink & Spelke, 2010). In addition, Huttenlocher, Levine and colleagues (Boyer, Levine & Huttenlocher, 2008; Boyer & Levine, 2012; Jeong et al., 2007), utilizing a proportional analogy task in which children must examine some standard (say, a beak filled with x units juice : y units water) and choose which of two test stimuli exemplify this same proportion, have also found flexible scaling at many factors with a decrement in performance as the factor increased. Future research with the current population of Mundurucu speakers will aim to discover whether this core division extends beyond the especially intuitive case of division by two, and whether one finds a similar capacity in the domain of spatial proportions.
Gallistel and colleagues (Balsam, Drew & Gallistel, 2010; Gallistel, 1990; Gallistel & Gibbon, 2000) have argued, based on research on animals, that proportional calculations over purely numerical variables – as well as spatial and temporal variables – form the bedrock for cognitive processes essential to survival. The calculation of rate of reward (perceived number of rewards divided by the temporal interval) in a foraging scenario predicts animal behavior in both naturalistic (Harper, 1982) and laboratory experiments (Gallistel, Mark, King & Latham, 2001, Leon & Gallistel, 1998). These calculations are also proposed to underlie a spontaneous appreciation of risk and optimal switching behavior (Balci, Freestone & Gallistel, 2009; Gallistel, 2008), and are found in experimentally naïve mice (Gallistel, King, Gottlieb, Balci, Papachristos, Szalecki & Carbone, 2007) – bolstering the claim that complex scaling abilities are innately present. In their review on the topic, Jacob et al. (2012) propose that our minds are able to represent numerical values of proportional relationships in much the same way that they represent absolute magnitudes. This sense of proportion is automatic and independent of language and presentation format (Jacob & Nieder, 2009a, 2009b), early-developing (McCrink & Wynn, 2007), and encoded by the same brain regions as absolute quantity (Vallentin & Nieder, 2008, 2010).
Further support for Jacob et al.’s (2012) proposition are the findings that infants, who cannot rely upon memorized number facts or division procedures, also show competence when tasks probe implicit calculations of ratios (Denison & Xu, 2010a, 2010b; Duffy, Huttenlocher & Levine, 2005; McCrink & Wynn, 2007; Xu & Garcia, 2008). McCrink and Wynn (2007) found that after habituation to several exemplars of the same numerical ratio of object A:object B (e.g. 8:4, 38:19, 22:11, …), 6-month-old infants dishabituated selectively to a new ratio (e.g. 40:10) compared to a new example of an old ratio (e.g. 20:10). Téglás et al. (Téglás, Girotto, Gonzalez & Bonatti, 2007; Téglás, Vul, Girotto, Gonzalez, Tenenbaum & Bonatti, 2011) showed 12-month-old infants either a probable (a yellow ball coming out of a container which contains three yellow balls and one blue ball) or improbable (a yellow ball coming out of a container which contains one yellow ball and three blue balls) event. The infants looked longer to improbable events than probable ones, indicating an appreciation for the inherently proportional base-rate of occurrence of each event. Xu and colleagues (Denison & Xu, 2010a, 2010b; Xu & Denison, 2009, Xu & Garcia, 2008) have established that infants can compute proportional information about an array to gauge the probability of an event, and even use this information to guide their behavior (e.g. choosing a lollipop that was drawn from a container that contained a higher proportion of their favored-colored lollipop).
The current paradigm represents a step forward in studying proportional relationships because it requires the subject to scale a magnitude in a serial, explicit fashion in order to arrive at the correct outcome. Whereas the vast majority of studies of proportional reasoning rely on a match-to-sample task in which participants view some standard and then choose a match or deviant, the children in the present study viewed math problems unfolding in real time; x / y = z, wherein the participant must represent x behind an occluder, generate y from the familiarization movie, and calculate outcome z. This task therefore provides a link between the analogical nature of previous studies (e.g. Jacob & Nieder, 2009a, 2009b) and the serial and generative nature of step-by-step problems that children must learn in school. Given work by Gilmore et al. (2007) showing that children utilize their ANS at the beginning of their symbolic instruction on addition and subtraction problems, we speculate that the format presented here could provide a scaffold for reasoning about a relatively difficult concept (fractional understanding) in a concrete, transparent fashion.
Overall, the current findings accord with and extend research on the evolution of intuitive proportional reasoning in both non-human populations (e.g. the rate-matching foraging done by non-human animals; see Gallistel, 1990, for a review) and statistical and ratio-based reasoning in infancy (McCrink & Wynn, 2007; Téglás et al., 2007, 2011; Xu & Denison, 2009). They reveal a remarkable capacity for proportional reasoning in a population that has little in the way of symbols or precise counting. These Mundurucu speakers were able to mentally transform a large numerical array into half that amount using only their ‘number sense’.
Research highlights.
Mundurucu children, even those who have no schooling or number words for amounts larger than 5, can divide non-symbolic magnitudes in half.
Performance for Mundurucu and American children is comparable.
Education, but not age, increased performance as well as non-numerical strategy use.
Footnotes
Because the small number of subjects in this population leads to a very small number of subjects for some cells in an omnibus ANOVA, we performed a repeated-measures ANOVA over the within-subjects factors only, followed by independent t-tests for gender, and regressions for age and education.
References
- Balci F, Freestone D, Gallistel CR. Risk assessment in man and mouse. Proceedings of the National Academy of Sciences, USA. 2009;106(27):11424–11425. doi: 10.1073/pnas.0812709106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ball D. Halves, pieces, and twoths: constructing and using representational contexts in teaching fractions. In: Carpenter TP, Fennema E, Romberg TA, editors. Rational numbers: An integration of research. Hillsdale, NJ: Lawrence Erlbaum; 1993. pp. 157–195. [Google Scholar]
- Balsam P, Drew M, Gallistel CR. Time and associative learning. Comparitive Cognition and Behavior Reviews. 2010;5:1–22. doi: 10.3819/ccbr.2010.50001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barth H, Baron A, Spelke L, Carey S. Children’s multiplicative transformations of discrete and continuous quantities. Journal of Experimental Child Psychology. 2009;103:441–454. doi: 10.1016/j.jecp.2009.01.014. [DOI] [PubMed] [Google Scholar]
- Barth H, La Mont K, Lipton J, Dehaene S, Kanwisher N, Spelke E. Nonsymbolic arithmetic in adults and young children. Cognition. 2006;98:199–222. doi: 10.1016/j.cognition.2004.09.011. [DOI] [PubMed] [Google Scholar]
- Barth H, La Mont K, Lipton J, Spelke E. Abstract number and arithmetic in preschool children. Proceedings of the National Academy of Sciences, USA. 2005;102(39):14117–14121. doi: 10.1073/pnas.0505512102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyer T, Levine SC, Huttenlocher J. Development of proportional reasoning: where young children go wrong. Developmental Psychology. 2008;44(5):1478–1490. doi: 10.1037/a0013110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyer TW, Levine SC. The development of proportional scaling: is 1/3 = 2/6 = 3/9 = 4/12? Journal of Experimental Child Psychology. 2012;111:516–533. doi: 10.1016/j.jecp.2011.11.001. [DOI] [PubMed] [Google Scholar]
- Brannon E. The development of ordinal numerical knowledge in infancy. Cognition. 2002;83(3):223–240. doi: 10.1016/s0010-0277(02)00005-7. [DOI] [PubMed] [Google Scholar]
- Brannon E, Wusthoff C, Gallistel CR, Gibbon J. Subtraction in the pigeon: evidence for a linear subjective number scale. Psychological Science. 2001;12(3):238–243. doi: 10.1111/1467-9280.00342. [DOI] [PubMed] [Google Scholar]
- Capaldi E, Miller D. Counting in rats: its functional significance and the independent cognitive processes that constitute it. Journal of Experimental Psychology: Animal Behavior Processes. 1988;14(1):3–17. [Google Scholar]
- Cantlon J, Brannon E. Shared system for ordering small and large numbers in monkeys and humans. Psychological Science. 2006;17(5):401–406. doi: 10.1111/j.1467-9280.2006.01719.x. [DOI] [PubMed] [Google Scholar]
- Cantlon JF, Brannon EM. Basic math in monkeys and college students. PLoS Biology. 2007;5(12):e328. doi: 10.1371/journal.pbio.0050328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chochon F, Cohen L, van de Moortele PF, Dehaene S. Differential contributions of the left and right inferior parietal lobules to number processing. Journal of Cognitive Neuroscience. 1999;11(6):617–630. doi: 10.1162/089892999563689. [DOI] [PubMed] [Google Scholar]
- Cohen L, Dehaene S. Calculating without reading: unsuspected residual abilities in pure alexia. Cognitive Neuropsychology. 2000;17:563–583. doi: 10.1080/02643290050110656. [DOI] [PubMed] [Google Scholar]
- Confrey J. Splitting, similarity, and rate of change: a new approach to multiplication and exponential functions. In: Harel G, Confrey J, editors. The development of multiplicative reasoning in the learning of mathematics. Albany, NY: State University of New York Press; 1994. pp. 291–330. [Google Scholar]
- Cordes S, Gallistel CR, Gelman R, Latham P. Nonverbal arithmetic in humans: light from noise. Perception & Psychophysics. 2007;69(7):1185–1203. doi: 10.3758/bf03193955. [DOI] [PubMed] [Google Scholar]
- Cordes S, Gelman R, Gallistel CR, Whalen J. Variability signatures distinguish verbal from nonverbal counting for both large and small numbers. Psychonomic Bulletin & Review. 2001;8(4):698–707. doi: 10.3758/bf03196206. [DOI] [PubMed] [Google Scholar]
- Dehaene S. The organization of brain activations in number comparison: event-related potentials and the additive-factors method. Journal of Cognitive Neuroscience. 1996;8:47–68. doi: 10.1162/jocn.1996.8.1.47. [DOI] [PubMed] [Google Scholar]
- Dehaene S. The number sense. New York and Cambridge: Oxford University Press, Penguin Press; 1997. [Google Scholar]
- Dehaene S, Cohen L. Cerebral pathways for calculation: double dissociation between rote verbal and quantitative knowledge of arithmetic. Cortex. 1997;33(2):219–250. doi: 10.1016/s0010-9452(08)70002-9. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Izard V, Spelke E, Pica P. Log or linear? Distinct intuitions of the number scale in Western and Amazonian Indigene cultures. Science. 2008;320(5880):1217–1220. doi: 10.1126/science.1156540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehaene S, Piazza M, Pinel P, Cohen L. Three parietal circuits for number processing. Cognitive Neuropsychology. 2003;20:487–506. doi: 10.1080/02643290244000239. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Spelke ES, Pinel P, Stanescu R, Tsivkin S. Sources of mathematical thinking: behavioral and brain-imaging evidence. Science. 1999;284:970–974. doi: 10.1126/science.284.5416.970. [DOI] [PubMed] [Google Scholar]
- Delazer M, Benke T. Arithmetical facts without meaning. Cortex. 1997;33:697–710. doi: 10.1016/s0010-9452(08)70727-5. [DOI] [PubMed] [Google Scholar]
- Denison S, Xu F. Twelve- to 14-month-old infants can predict single-event probability with large set sizes. Developmental Science. 2010a;13:798–803. doi: 10.1111/j.1467-7687.2009.00943.x. [DOI] [PubMed] [Google Scholar]
- Denison S, Xu F. Integrating physical constraints in statistical inference by 11-month-old infants. Cognitive Science. 2010b;34:885–908. doi: 10.1111/j.1551-6709.2010.01111.x. [DOI] [PubMed] [Google Scholar]
- Duffy S, Huttenlocher J, Levine S. How infants encode spatial extent. Infancy. 2005;8(1):81–90. doi: 10.1207/s15327078in0801_5. [DOI] [PubMed] [Google Scholar]
- Gallistel CR. The organization of learning. Cambridge, MA: MIT Press; 1990. [Google Scholar]
- Gallistel CR. The neural mechanisms that underlie decision making. In: Glimcher PW, Camerer CF, Fehr E, Poldrack RA, editors. Neuroeconomics: Decision making and the brain. New York: Elsevier/Academic; 2008. pp. 419–424. [Google Scholar]
- Gallistel CR, Gibbon J. Time, rate, and conditioning. Psychological Review. 2000;107:289–344. doi: 10.1037/0033-295x.107.2.289. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, King AP, Gottlieb D, Balci F, Papachristos EB, Szalecki M, Carbone KS. Is matching innate? Journal of the Experimental Analysis of Behavior. 2007;7(2):161–199. doi: 10.1901/jeab.2007.92-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallistel CR, Mark TA, King AP, Latham PE. The rat approximates an ideal detector of changes in rates of reward: implications for the law of effect. Journal of Experimental Psychology: Animal Behavior Processes. 2001;27:354–372. doi: 10.1037//0097-7403.27.4.354. [DOI] [PubMed] [Google Scholar]
- Gilmore C, McCarthy S, Spelke ES. Symbolic arithmetic knowledge without instruction. Nature. 2007;447:589–591. doi: 10.1038/nature05850. [DOI] [PubMed] [Google Scholar]
- Goswami U. Relational complexity and the development of analogical reasoning. Cognitive Development. 1989;4:251–268. [Google Scholar]
- Halberda J, Feigenson L. Developmental change in the acuity of the ‘number sense’: the approximate number system in 3-, 4-, 5-, 6-year-olds and adults. Developmental Psychology. 2008;44(5):1457–1465. doi: 10.1037/a0012682. [DOI] [PubMed] [Google Scholar]
- Harper D. Competitive foraging in mallards: ‘ideal free’ ducks. Animal Behaviour. 1982;30(2):575–584. [Google Scholar]
- Izard V, Dehaene S. Calibrating the mental number line. Cognition. 2008;106(3):1221–1247. doi: 10.1016/j.cognition.2007.06.004. [DOI] [PubMed] [Google Scholar]
- Jacob S, Nieder A. Tuning to non-symbolic proportions in the human frontoparietal cortex. European Journal of Neuroscience. 2009a;30:1432–1442. doi: 10.1111/j.1460-9568.2009.06932.x. [DOI] [PubMed] [Google Scholar]
- Jacob S, Nieder A. Notation-independent representation of fractions in the human parietal cortex. Journal of Neuroscience. 2009b;29:4652–4657. doi: 10.1523/JNEUROSCI.0651-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacob S, Vallentin D, Nieder A. Relating magnitudes: the brain’s code for proportions. Trends in Cognitive Sciences. 2012;16:157–166. doi: 10.1016/j.tics.2012.02.002. [DOI] [PubMed] [Google Scholar]
- Jeong Y, Levine SC, Huttenlocher J. The development of proportional reasoning: effect of continuous vs. discrete quantities. Journal of Cognition and Development. 2007;8(2):237–256. [Google Scholar]
- Lampl Y, Eshel Y, Gilad R, Sarova-Pinhas I. Selective acalculia with sparing of the subtraction process in a patient with left parietotemporal hemorrhage. Neurology. 1994;44(9):1759–1761. doi: 10.1212/wnl.44.9.1759. [DOI] [PubMed] [Google Scholar]
- Lee K. Cortical areas differentially involved in multiplication and subtraction: a functional magnetic resonance imaging study and correlation with a case of selective acalculia. Annals of Neurology. 2000;48(4):657–661. [PubMed] [Google Scholar]
- Leon M, Gallistel CR. Self-stimulating rats combine subjective reward magnitude and subjective reward rate multiplicatively. Journal of Experimental Psychology: Animal Behavior Processes. 1998;24(3):265–277. doi: 10.1037//0097-7403.24.3.265. [DOI] [PubMed] [Google Scholar]
- Lipton JS, Spelke ES. Origins of number sense: large number discrimination in human infants. Psychological Science. 2003;14(5):396–401. doi: 10.1111/1467-9280.01453. [DOI] [PubMed] [Google Scholar]
- Lipton J, Spelke E. Discrimination of large and small numerosities by human infants. Infancy. 2004;5(3):271–290. [Google Scholar]
- McCrink K, Spelke E. Core multiplication in childhood. Cognition. 2010;116:204–216. doi: 10.1016/j.cognition.2010.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCrink K, Spelke E. Core division in childhood. (submitted) [Google Scholar]
- McCrink K, Wynn K. Large-number addition and subtraction by 9-month-old infants. Psychological Science. 2004;15:776–781. doi: 10.1111/j.0956-7976.2004.00755.x. [DOI] [PubMed] [Google Scholar]
- McCrink K, Wynn K. Ratio abstraction by 6-month-old infants. Psychological Science. 2007;18:740–746. doi: 10.1111/j.1467-9280.2007.01969.x. [DOI] [PubMed] [Google Scholar]
- McCrink K, Wynn K. Operational momentum in large-number addition and subtraction by 9-month-old infants. Journal of Experimental Child Psychology. 2009;104:400–408. doi: 10.1016/j.jecp.2009.01.013. [DOI] [PubMed] [Google Scholar]
- Meck WH, Church RM. A mode control model of counting and timing processes. Journal of Experimental Psychology: Animal Behavior Processes. 1983;9(3):320–334. [PubMed] [Google Scholar]
- Menon V, Rivera S, White C, Glover G, Reiss A. Dissociating prefrontal and parietal cortex activation during arithmetic processing. NeuroImage. 2000;12:357–365. doi: 10.1006/nimg.2000.0613. [DOI] [PubMed] [Google Scholar]
- Mix K, Levine SC, Huttenlocher J. Early fraction calculation ability. Developmental Psychology. 1999;35(5):164–174. doi: 10.1037//0012-1649.35.1.164. [DOI] [PubMed] [Google Scholar]
- Naccache L, Dehaene S. The priming method: imaging unconscious repetition priming reveals an abstract representation of number in the parietal lobes. Cerebral Cortex. 2001;11:966–974. doi: 10.1093/cercor/11.10.966. [DOI] [PubMed] [Google Scholar]
- Piaget J, Inhelder B. The child’s conception of space. New York: Norton; 1956. [Google Scholar]
- Piazza M, Pica P, Izard V, Dehaene S. Education enhances the acuity of the approximate number system. Psychological Science. doi: 10.1177/0956797612464057. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pica P, Lemer C, Izard V, Dehaene S. Exact and approximate arithmetic in an Amazonian indigene group. Science. 2004;306(5695):499–503. doi: 10.1126/science.1102085. [DOI] [PubMed] [Google Scholar]
- Platt JR, Johnson DM. Localization of position within a homogeneous behavior chain: effects of error contingencies. Learning and Motivation. 1971;2:386–414. [Google Scholar]
- Singer-Freeman K, Goswami U. Does half a pizza equal half a box of chocolates? Proportional matching in an analogy task. Cognitive Development. 2001;16(3):811–829. [Google Scholar]
- Sophian C. Perceptions of proportionality in young children: matching spatial ratios. Cognition. 2000;75:145–170. doi: 10.1016/s0010-0277(00)00062-7. [DOI] [PubMed] [Google Scholar]
- Spinillo A, Bryant P. Children’s proportional judgments: the importance of ‘half’. Child Development. 1991;62(3):427–440. [Google Scholar]
- Starkey P, Cooper R. Perception of number by human infants. Science. 1980;210(4473):1033–1035. doi: 10.1126/science.7434014. [DOI] [PubMed] [Google Scholar]
- Starkey P, Spelke ES, Gelman R. Numerical abstraction by human infants. Cognition. 1990;36(2):97–127. doi: 10.1016/0010-0277(90)90001-z. [DOI] [PubMed] [Google Scholar]
- Téglás E, Girotto V, Gonzalez M, Bonatti LL. Intuitions of probabilities shape expectations about the future at 12 months and beyond. Proceedings of the National Academy of Sciences, USA. 2007;104(48):19156–19159. doi: 10.1073/pnas.0700271104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Téglás E, Vul E, Girotto V, Gonzalez M, Tenenbaum JB, Bonatti LL. Pure reasoning in 12-month-old infants as probabilistic inference. Science. 2011;332:1054–1059. doi: 10.1126/science.1196404. [DOI] [PubMed] [Google Scholar]
- Thioux M, Pesenti M, Costes N, De Volder A, Seron X. Task-independent semantic activation for numbers and animals. Cognitive Brain Research. 2005;24(2):284–290. doi: 10.1016/j.cogbrainres.2005.02.009. [DOI] [PubMed] [Google Scholar]
- Vallentin D, Nieder A. Behavioral and prefrontal representation of spatial proportions in the monkey. Current Biology. 2008;18:1420–1425. doi: 10.1016/j.cub.2008.08.042. [DOI] [PubMed] [Google Scholar]
- Vallentin D, Nieder A. Representations of visual proportions in the primate posterior parietal and prefrontal cortices. European Journal of Neuroscience. 2010;32:1380–1387. doi: 10.1111/j.1460-9568.2010.07427.x. [DOI] [PubMed] [Google Scholar]
- Van Harskamp NJ, Cipolotti L. Selective impairments for addition, subtraction and multiplication: implications for the organisation of arithmetical facts. Cortex. 2001;37:363–388. doi: 10.1016/s0010-9452(08)70579-3. [DOI] [PubMed] [Google Scholar]
- van Loesbrook E, Smitsman A. Visual perception of numerosity in infancy. Developmental Psychology. 1990;26(6):916–922. [Google Scholar]
- Wood JN, Spelke ES. Infants’ enumeration of actions: numerical discrimination and its signature limits. Developmental Science. 2005;8(2):173–181. doi: 10.1111/j.1467-7687.2005.00404.x. [DOI] [PubMed] [Google Scholar]
- Xu F, Denison S. Statistical inference and sensitivity to sampling in 11-month-old infants. Cognition. 2009;112:97–104. doi: 10.1016/j.cognition.2009.04.006. [DOI] [PubMed] [Google Scholar]
- Xu F, Garcia V. Intuitive statistics by 8-month-old infants. Proceedings of the National Academy of Sciences of the United States of America. 2008;105(13):5012–5015. doi: 10.1073/pnas.0704450105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu F, Spelke E. Large number discrimination in 6-month-old infants. Cognition. 2000;74(1):B1–B11. doi: 10.1016/s0010-0277(99)00066-9. [DOI] [PubMed] [Google Scholar]


