Corticospinal Signals Recorded with MEAs can Predict the Volitional Forearm Forces in Rats

Abstract

We set out to investigate if volitional components in the descending tracts of the spinal cord white matter can be accessed with multi-electrode array (MEA) recording technique. Rats were trained to press a lever connected to a haptic device with force feedback to receive sugar pellets. A flexible-substrate multi-electrode array was chronically implanted into the dorsal column of the cervical spinal cord. Field potentials and multi-unit activities were recorded from the descending axons of the corticospinal tract while the rat performed a lever pressing task. Forelimb forces, recorded with the sensor attached to the lever, were reconstructed using the hand position data and the neural signals through multiple trials over three weeks. The regression coefficients found from the trial set were cross-validated on the other trials recorded on same day. Approximately 30 trials of at least 2 seconds were required for accurate model estimation. The maximum correlation coefficient between the actual and predicted force was 0.7 in the test set. Positional information and its interaction with neural signals improved the correlation coefficient by 0.1 to 0.15. These results suggest that the volitional information contained in the corticospinal tract can be extracted with multi-channel neural recordings made with parenchymal electrodes.

I. Introduction

Multiple cortical and subcortical areas of the brain contribute to the control of the limbs. Brain-computer interfaces face a challenge that the activity in all these brain areas needs to be accessed simultaneously in order to predict the limb trajectories with high accuracy. On the other hand, motor signals descending in the spinal cord contain the output signals that are formed after respective contributions of various brain centers. The axons carrying these descending signals are tightly bundled together in the spinal cord tracts that provide the volitional control signals to the spinal cord neural circuitry in each segment that innervate the skeletal muscles of the body. Thus, neural signals recorded from the spinal cord white matter tracts must be richer in terms of their volitional information than those obtained from the cerebrum.

The spinal cord contains two major descending systems: the lateral and the medial systems. The medial descending system is mainly involved in posture related activities by integrating vestibular, visual, and somatosensory information [1]. The lateral system, consisting of the corticospinal tract (CST) and the rubrospinal tract (RST), is involved in producing skilled forelimb movements and constitutes the main pathways for motor control across species [2]). In the rat, unlike the humans, the major component of the CST travels separately from the RST in the ventral-most portion of the dorsal funiculus of the spinal cord [3].

In this study, we recorded descending signals in the corticospinal tract (CST) at the cervical level in the rat spinal cord during the lever pressing task. Our objective was to investigate if volitional signals could be extracted from the CST using multi-electrode arrays. We took advantage of the fact that in the dorsal column the fibers travel in the rostrocaudal direction are more or less parallel to each other, and therefore, a flexible, planar structure like a polyimide electrode substrate can be inserted between those axons with minimal trauma to the cord. The results confirm the feasibility of the approach, at least for short term studies.

II. Methods

A. Hardware and Software

A Novint Falcon Device was adapted for the study. A custom handle was designed to house a force/torque sensor (Nano-17, ATI). A rigid lever with an enlarged contact area was mounted to the force sensor. The configuration of force fields simulated by the haptic device was defined in a series of text files. Simultaneous image logs were collected using three high speed infrared cameras (Optitrack, Natural Point). These cameras could also provide tracking for reflective markers in 3D space if desired. The cage was constructed from transparent Plexiglas to facilitate imaging. Neural signals were amplified using a 30-channel wireless neural recording system (TBSI systems) and digitized by a National Instruments Board (PCI 6225). A Visual C++ program controlled the experiment by synchronizing the data acquisition, providing feedback to the haptic device to modify its dynamic parameters such as viscosity and spring constant during the trial, and signaling to the rat to start each trial.

B. Experimental Protocol

Food restricted Long Evans rats were trained to press the lever connected to the haptic interface to receive sugar pellets. The starting height of the lever was gradually increased once animals began to perform the task. The roof of the cage was incrementally lowered after the lever reached its intended height of 20mm above the window where the sugar pellets were delivered. Training was considered complete when the animal pressed the lever by elbow and shoulder movements alone with minimal trunk involvement.

A dorsal laminectomy was performed on the animal at C4 level. A polyimide flexible substrate electrode (15μm thickness) array in 4×8 configuration with Au contacts coated with PEDOT (each f15μm and 80μm pitch) was inserted into the spinal cord near the central sulcus. The short edge of the array was in the rostrocaudal direction and the contacts were facing the trained arm side. The connector for the array was kept directly above the implant site protruding through the skin anchored by a stainless steel wire frame attached to the second vertebra using non-absorbable suture. Polyimide ribbon cable between the array and the connector (15mm) had a slack to avoid any pulling on the array. After the animal recovered from surgery, the wireless amplifier/transmitter was inserted into the connector and held by stainless steel screws secured into the acrylic around the connector and remained secured for duration of the study.

C. Data Processing

PCA Principle Component Analysis (PCA) was carried out on raw neural signals. Thefirst ten principle components were removed from each channel since these components were contaminated by non-neural sources. If the raw value of any channel exceed the input range of the data acquisition board, these data points and all the data points within 8ms windows on either side of the saturation segment were excluded from the analysis.

Mean power was calculated for every frequency of every channel by calculating the FFT for each channel in a sliding window of 16ms moving in steps of 1ms. Power amplitudes at frequencies between 90 and 1500Hz were included in further processing. Force and power data were filtered using a 3rd order Butterworth filter with a cutoff of 16Hz. The filter was run through the signals both forward and backward in time to eliminate group delay.

A second PCA was carried out on all powers from all channels over time, position and velocity of the lever, as well as interaction between vertical position and powers. This generated 1386 uncorrelated components. The magnitude of the measured force was regressed on these principle components.

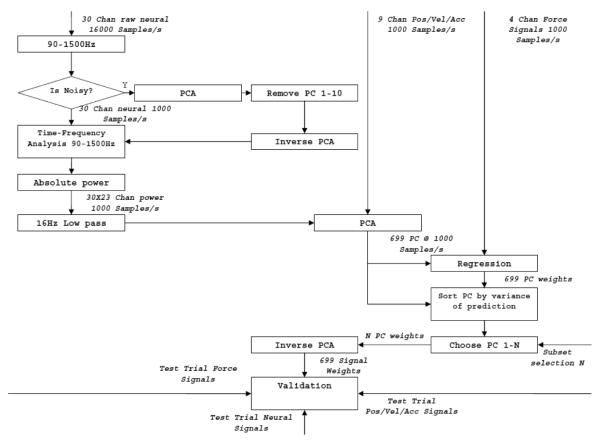
Subsets of regressed weights were divided by the respective subsets of PCA scores to generate weights for powers. The first subset contained only the largest component, and the next subset contained it and the next largest component, and so on. A transfer functions was estimated for each set of weights by applying inverse Fourier Transform to the ratio between the Fourier transform of measured and predicted force. (Fig. 5)

Figure 5.

Flow Chart of the data processing algorithm for a single PC subset, without interactions.

Each set of weights and associated transfer functions were tested on a different set of trials. Correlation coefficients and coefficients of determination (see Appendix) between the measured and predicted force for the test set were plotted against the number of principle component used. The mean of the correlation and coefficients of determination was used as the criteria for choosing the best weights.

III. Results

A. Dependence on number of components and trials

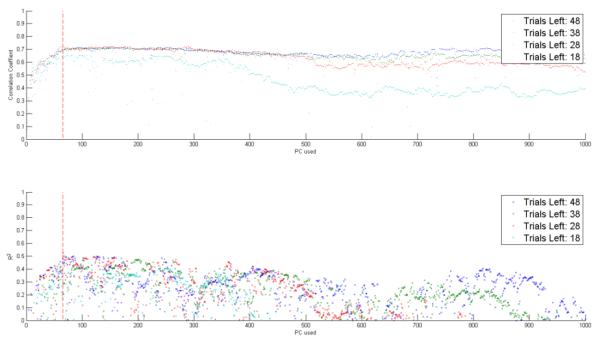
Increasing the number of components used first lead to an improvement of the reconstruction, then deterioration due to over-fitting (Fig. 3). The optimal number of components depended on trials included. Generally speaking, the quality of reconstruction increased as a function of number of trials used in the estimation up to a value limited by the quality of data. Typically it took at least 20 trials to reach this point. Increasing the amount of data used for estimation also reduced the steepness of decline caused by over-fitting.

Figure 3.

Weight and transfer function tests of the same session as in Fig. 2:

Each point indicates one test result. Each test uses one additional principle component to the test to its left. Outliers and instability in coefficient of determination are caused by errors in estimated transfer functions. The vertical line marks the set of weights and transfer function used in Fig. 2.

B. Contribution of Interactions

Introducing interaction of force and position into the model caused a decrease in reconstruction accuracy when data was insufficient for estimation of weights for the additional terms. Accuracy was observed to increase with the addition of interaction terms when sufficient data were available. Interaction between neural signals did not appear to play a significant role.

C. Order of Components

Ordering components in an order of descending variance produced the best results. Ordering components by descending correlation with force produced estimates with low Coefficients of Determination and vice versa. Ordering components by standard deviation of weights across trials produced results comparable to ordering by variance.

IV. Discussions

A. Contribution from Hand Position

Correctly scaled position improved reconstruction when it served as an input signal. This is pertinent because the haptic system was not programmed to act as a simple spring. The observation could be interpreted as a displacement of a limb under constant command signal generateing a force proportional to the displacement (2). This is consistent with predictions of Equilibrium Control Theory and results of physiological studies in humans. [4]

B. Implications of Interaction

Similarly, introducing interaction terms in the mathematical model between position and force further improved reconstruction beyond the results achieved without the interaction (3). This can be seen as dependence of control signal transformation from neural to force signals on posture. One possible explanation is that the command signal is encoded in joint or muscle coordinates and identical command signals generate different end effector forces as a consequence of mechanics. Alternatively, it is possible for descending signal to encode weights of attractors in end effector coordinates and the interaction accounts for the modulation of restorative force by neural signals.

C. Interpretation of Weights

Regression weights of power elements showed two patterns: correlated activity for all elements of the same channel and power elements with large weights. It is possible the latter reflects contributions from nearby fibers with specific firing rate and binary activity.

V. Conclusions

This study illustrates the effectiveness of separation of field potentials into constituent powers as an effective method of analysis of spinal motor commands. It also demonstrates the importance of non-neural parameters and interactions in the analysis of neural signals. This method may find other applications in interpreting other motor and sensory signals carried by the spinal cord.

Figure 1.

Photo of the Experimental Apparatus: The Falcon device with custom mount for the force sensor is visible at the center. Two of the three cameras are visible to its right. The lever is curved to facilitate positioning of the cameras.

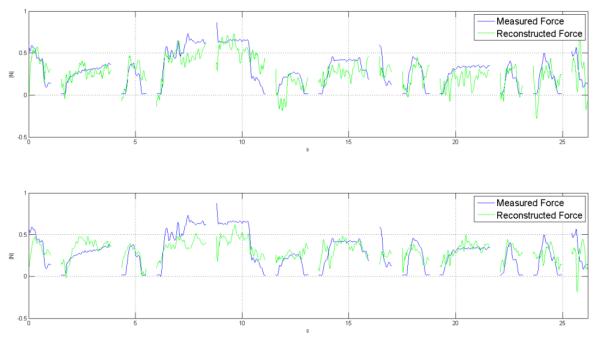
Figure 2.

Reconstruction with highest correlation coefficient:

Reconstruction of test trials. Blue: Measured force, Green: Reconstructed force. Each separate segment is a different trial. Test trials were randomly selected as one of the five trials and were not consecutive. (Trials used: 28, Components used 66, Correlation Coefficient 0.73, R squared 0.52)

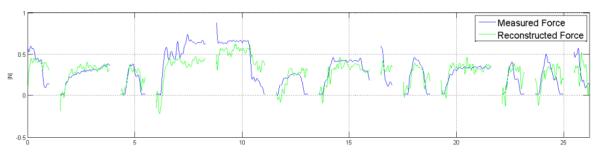
Figure 4.

Reconstruction of the same session without interactions: Top plot: Optimal reconstruction without interactions (2). (Correlation coefficient 0.69, R-squared 0.41) Bottom plot: Optimal reconstruction using only neural signals (1). (Correlation coefficient 0.630, R-squared 0.39)

VI. Appendix

Coefficient of Determination is defined as follows in this paper:

$$R^2=1-\frac{{\Sigma }_t{(F-\widehat{F})}^2}{{\Sigma }_t{(F-\overline{F})}^2}$$ (0)

Where the numerator is the sum of squares of prediction errors and the denominator is the variance of the force. The following models were tested in this study:

$${\widehat{F}}_1\left(t\right)=K\left(t\right)\otimes \langle \mathit{wN}\left(t\right)\rangle$$ (1)

$$\widehat{F_2}\left(t\right)=K\left(t\right)\otimes \left[\mathit{cx}\right(t)+w\cdot N(t\left)\right]$$ (2)

$$\widehat{F_3}\left(t\right)=K\left(t\right)\otimes \left[\mathit{cx}\right(t)+w\cdot N(t)+z\cdot x(t\left)N\right(t\left)\right]$$ (3)

The basic model considers neural information. The second model also considers positional information. The last model considers neural activity, position, and their interaction.