Sampling Strategies to Evaluate the Performance of Unknown Predictors

Abstract

The focus of this paper is on how to select a small sample of examples for labeling that can help us to evaluate many different classification models unknown at the time of sampling. We are particularly interested in studying the sampling strategies for problems in which the prevalence of the two classes is highly biased toward one of the classes. The evaluation measures of interest we want to estimate as accurately as possible are those obtained from the contingency table. We provide a careful theoretical analysis on sensitivity, specificity, and precision and show how sampling strategies should be adapted to the rate of skewness in data in order to effectively compute the three aforementioned evaluation measures.

1 Introduction

One of the important challenges of machine learning and data mining research is the evaluation of models or hypotheses with the help of data. The typical and the easiest approach to this problem is to draw a sample randomly from the underlying sample distribution. However, this approach may not be the best solution if each example in the sample comes at a cost that is associated, for example, with the example extraction or annotation of examples by a human expert. In such a case, one seeks a sampling solution that maximizes the benefits of the sample for the evaluation task, while minimizing its size.

As an example, consider the problem of assessment of the quality of a diagnostic model in Medicine, that decides whether a patient suffers from a certain disease. The typical statistics of interest when building such models are the sensitivity, the specificity and the precision of the model. Assuming the disease prevalence is low, the random selection of patient examples may lead to a large number of negative and a small number of positive examples, which may prevent us from accurately estimating the sensitivity and the precision of the model. To assure an accurate assessment of sensitivity, the random sample would have to be much larger which would make the evaluation process very costly.

The focus of our work is on the analysis of methods for cost-effective evaluation of classification models and their key statistics (e.g. sensitivity, specificity and precision) when the prevalence of the two classes is unequal and highly biased toward one of the classes. Our goal is to design strategies for choosing examples such that they can be used to evaluate accurately a large set of classification models or rules one may want to experiment with, and not just one model. The setting of our problem fits any problem for which we expect to build a benchmark set of examples, programs, images, documents, objects that need to be labeled for evaluating the performance of multiple designs and assess their performance. Here are a few examples:

• Consider the problem of evaluation of many possible diagnostic models in Medicine. Such models may originate from different sources; they can be proposed either by different experts, or automated algorithms, or some other model building processes. We want to get a small set of examples to evaluate as accurately and cost-efficiently as possible all these models and compute their key classification (diagnostic) statistics.

• Assume we are interested in developing an inexpensive test (assay) to accurately diagnose a disease from blood samples. The current state-of-the art is a very expensive but an accurate test. To assess how good the potential inexpensive test or tests are, we use a set of stored and labeled blood samples that can be used to run the new assay and evaluate how well it performs. We are interested in obtaining a small sample to be stored and labeled with an expensive test. The sample should be as small as possible and capable of assessing the quality of any test.

• Assume the goal of a company is to develop a system for classification of satellite (microscope) images. It considers and studies multiple designs. To test and assess the quality of the system a benchmark set of images must be selected and assesses by experts so that different designs can be readily evaluated. The question is how to select a small set of benchmark images sufficient for these evaluations.

Whilst our work bears some resemblance to the active learning framework, we would like to stress that it is very different in its goals and hence the methodology does not transfer to our task. The key difference is that active learning relies on an underlying model (classification, distribution model) it aims to optimize (or learn) from data, and its sample selection strategy makes an attempt to learn the pre-selected model as efficiently and with as small sample size as possible. Hence, the primary output of the active learning is the model it learns. In our work, we do not pre-select and learn (optimize) the model, instead we want a sample that can help us to evaluate any classification model, regardless of its origin. Therefore, our primary output is the sample itself. Another difference is that we are interested in evaluating every possible model with a broader range of classification statistics (sensitivity, specificity, precision) while the active learning framework typically narrows its focus to only one statistics.

One might argue that active learning framework can be used to accurately label all the unlabeled examples by constructing a very good classifier. However, the active learning framework cannot guarantee a classifier that has controlled generalization ability when the labeling budget is very limited. The only guarantee (to a certain degree) is that the model constructed using active learning procedure is better than the one constructed using the passive selection of examples. Therefore, relying on the labels of examples obtained using a model can be very risky and lead to a poor evaluation of the future models (rules). Moreover, for the problems that we consider in this paper (e.g. diagnosing models in medicine), the construction of an accurate model is a challenging task and subject to future model construction. This continuous effort on model construction has been our main motivation to obtain a sample that allows us to evaluate the future models constructed by different procedures.

We start this paper by analyzing what types of examples we need to include in the evaluation set when the priors of the two classes changes. To get some insights to the types of analysis in this paper, let us consider two extreme cases: one that has classes of balanced sizes and the other one that is very unbalanced. Intuitively, when the two classes are balanced, a random selection of examples is likely to perform well in calculating all the interesting evaluation measures (i.e. precision, sensitivity, and specificity). However, a random selection of examples will lead to a poor evaluation of precision and sensitivity of the rules when the classes are unbalanced (suppose the positive class is the minority class). This is because the number of positive examples in the sample will be very limited and the overlap of these positive examples and the positive examples returned by the rule can be very small that leads to high uncertainty in evaluating these rules. The smaller the positive rate of the rule (the number of positive examples returned by the rule) is, the smaller this overlap and the higher the uncertainty will be. Therefore, intuitively, the rule of thumb is to sample more positive examples when the positive rate of the rule is small or the positive class is rare. However, the question is how qualitatively the positive rate of the rule and the unbalance ratio of classes on one hand and the number of positive examples on the other hand are related when we aim to obtain a good estimation of all aforementioned measures. Looking at it from a reverse perspective, the question we answer in this paper is what is our confidence in evaluating the rules of specific form for a specific problem (that has a particular unbalance ratio of classes) using a given sampling? Our analysis in this paper addresses this question. We show that when the prior of the classes changes, the prior in sampling should change with a rate proportional to the unbalance ratio of the classes. This finding is very different from recent work in the active learning area by [1] that advocates the approach in which the examples from the two classes are balanced.

The contributions of this work are:

• We derive bounds on the estimation error of computing precision, sensitivity, and specificity when a small sample size is used to compute these evaluation measures.

• Using these bounds, we show that the optimum sampling strategy is dependent on the skewness rate of the data and positive rate of the rule. One result of our analysis is that when the data is unbalanced, it is better to sample more from the minority class.

• The bounds also suggest that there is a tradeoff between accurate estimate of precision and sensitivity on one side and specificity on the other side. We show how different samplings from the two classes influence this tradeoff by studying the interaction between these bounds.

• We discuss how the guidelines induced by our analysis can be generalized to the case of evaluating rules by the area under the ROC curve (AUC).

• We discuss how sampling from minority class helps to increase the sample size by introducing blind labeling of examples to the majority class. Our discussion assumes a fixed and limited labeling budget.

• Since our analysis suggests we should sample from the minority class, an open question is how to accomplish this task. We propose practical ways to follow the guideline induced by the analysis. In particular, we suggests four different approaches one might utilize to sample from the minority class.

• We verify the efficacy of the proposed method on two UCI data sets by comparing the evaluation results of random sampling and sampling strategy suggested by the analysis.

This paper is organized as follows: We start with the related work in Section 2. Section 3 analyzes how the number of positive and negative examples in the labeled set influences the estimates of the three common evaluation measures: the sensitivity, the specificity and the precision. In Section 3.2 we derive bounds on the estimation errors for these measures. Then (in Section 3.3) we show that a good sampling procedure must trade-off the estimation accuracies of all these statistics and how this translates to controlling the rate of positive examples in the labeled set. Section 3.4 considers the case when some of the statistics and the quality of their estimates are more important than the estimates of other statistics and in Section 3.5 we describe how the current analysis can be adapted in order to obtain a good estimation of area under the ROC curve (AUC). In Section 4, we describe the practical approaches to implement the guidelines suggested by the analysis in Section 3. Section 5 studies how the methodology works in practice on two different data sets. We conclude the work in Section 6.

2 Related Work

The objective of this work is to select a set of unlabeled examples from a large data set such that when they are labeled by an expert they can be used to assess accurately multiple classification statistics for many (apriori unknown) classification models. To the best of our knowledge, there is no prior work on this problem. In the following we briefly review prior work in active learning, guided learning, and active risk estimation, three research topics most relevant to our problem.

2.1 Active learning

The objective of active learning is to improve the process of learning a model while restricting the training sample size [14, 11]. The methods are motivated by the fact that example labeling is a costly and time-consuming task and that the number of examples we need to label to learn the model can be significantly decreased by choosing the most informative examples. To select the most informative examples, active learning is usually reduced to optimization of a certain criterion. Examples of such criteria include but are not restricted to: minimizing the size of version space for SVM [14], minimizing the variance of the estimated generalization error [3], minimizing the generalization error[10, 4] and minimization of empirical one-step look ahead classification risk [17]. The difference from our problem is that active learning methods optimize the model, while we want to find and optimize the sample itself.

One of our objectives is to analyze highly unbalanced data sets. The problem of active learning in presence of extremely unbalanced data set was recently considered by [1, 2, 13]. To address the problem the authors in [1] suggested to consider equal number of examples from two classes to help the learning classes. Our analyses in this paper show that examples in the minority class are more important. Hence this is a very different conclusion than the one proposed by [1] for the learning problem.

Another research work relevant to this paper is pool-based active learning [15] where the objective is to label all the examples in the pool as accurately as possible by constructing a model that classifies all unlabeled examples in the pool with a high confidence. This is unlike the regular active learning where the objective is to construct an accurate model able to classify unseen examples. Although pool-based active learning has some similarities to our work, our objective and tools are different; first we are looking for sampling guidelines effective for the purpose of evaluation, and second, we have a limited budget and cannot make a confident model to classify accurately all the examples in the pool. Notice that the finite-pool active learning is basically designed to simplify the task of reviewers screening a huge corpus of reports to find the relevant documents and it is assumed that enough budget (yet small when compared to label all examples) is available to label as many examples as needed to construct a good classifier [15].

2.2 Guided Learning

The second research direction relevant to our problem is Guided Learning [1, 16]. The guided learning framework works by asking an expert (or an algorithm) to provide an example with certain characteristics [9]. It then constructs a model using those examples. Note that this is different from active learning: active learning presents samples to the expert to review and label, while guided learning only provides the expert with a guidance (or criteria to be applied) to select an example or a set of examples, and it is the duty of the expert (or a program) to find these examples. In the simplest form, guided learning is interested in finding the examples that belong to a specific class. When applying guided learning to highly imbalanced problems, the main open questions are how to identify the minority class(es) and how to find examples that belong to them.

Our sample selection framework is similar to guided learning in that it provides recommendations of what type (class) of examples to include in the data. The difference is that we do not attempt to learn (optimize) any specific model with a better sample of labeled examples, instead we want to find the sample itself and use it for evaluation purposes. To address the problem of how to select examples from the minority class, we can utilize the solutions introduced in the guided learning literature. Particularly, we rely either on the human expert feedback and his/her ability to identify the examples in the data set or a collection of surrogate classifiers capable of identifying with a better accuracy examples in the minority class that are then reviewed and assessed by a human.

2.3 Active Risk Estimation

Active Risk Estimation recently introduced by Sawade et. al. [12] is probably the most relevant work to our study, where the authors study the problem of evaluating the risk of a given model accurately for a given evaluation measure at a given labeling budget. Unlike active risk estimation that selects examples to label in order to reduce the risk of evaluating one known model, our work is much more general in the sense that it does not assume there is only one apriori-known model to evaluate. The generality of our setting makes the task of sample selection much more difficult and does not allow one to have a detailed sampling strategies of what individual examples are beneficial to be selected. Instead, we can only find some hindsight or guidelines on what general sampling strategies are good.

3 Sampling for Evaluation

Suppose we have a large sample S of unlabeled examples from two classes. We would like to choose a subset L ⊂ S of representative examples from S to be labeled by an expert, such that the labeled set would let us evaluate a set of (apriori unknown) classification rules or models (given to us later either by an expert or an algorithm) as accurately as possible in terms of several evaluation measures. The evaluation measures of interest in our work are the precision, the sensitivity, and the specificity of the classification model, or more generally measures obtained from the contingency table.

A good evaluation set should estimate all aforementioned evaluation measures equally well and with similar accuracy guarantees. But how to select examples in set L to assure this is the case? If classes in S are balanced, we expect a random sample from S will also preserve the balance in L, so random sampling is likely to work well. However, a balanced sample is harder to achieve if the classes in S are unbalanced. Interestingly, if the two classes are extremely unbalanced, the accuracy guarantees can be (relatively) easily satisfied for statistics related to the majority class even without seeing labeled examples from this class. What seems like a contradiction can be easily explained as follows: assuming all unlabeled examples take on the majority class label, the overall error from mislabeling the minority class examples is small because their prevalence (prior) is small. In such a case we may prefer L to be purely from the minority class or at least heavily biased towards this class.

In this section, we provide a careful analysis of the relation of the skewness rate (the ratio of positive class to the whole sample size), the size of the labeled data set, and the quality of different evaluation measure estimates.

3.1 Preliminary

Let S denotes the set of all examples in the data set. We define the rule R : S ↦ {+, −} as a labeling function which maps the members of S to either the positive or the negative class. The set of all possible rules is denoted by ℛ. Let O ∈ ℛ be a special rule which returns the true labelings of the examples in S (“O” stands for the Oracle). Throughout the paper, L ⊆ S and U ⊆ S refer to the set of examples in S for which the true labeling are, respectively, known and unknown; thus, L ∪ U = S, L ∩ U = ϕ. Furthermore, and without loss of generality, we assume that the positive class is the minority class and we denote by B ∈ U the set of examples that are blindly labeled with the majority class (negative class). For A ⊆ S, R ∈ ℛ and c ∈ {+, −}, we define:

• |A| as the cardinality of set A,

• $A_R^c\equiv \{x\in A|R(x)=c\}$,

• ${\epsilon }_R^c(A)\equiv \frac{|A_R^c|}{|A|}$

For instance, $S_O^{+}$ means the set of all true positive examples in S while ${\epsilon }_O^{+}(S)$ is the rate of true positives in S. It is trivial to see that for any given A ⊆ S and R ∈ ℛ, we have $A=A_R^{+}\cup A_R^{-}\text{ and }{\epsilon }_R^{-}(A)=1-{\epsilon }_R^{+}(A)$.

For oracle O and the rule R ∈ ℛ (R ≠ O), the quantities ${\epsilon }_O^{+}(S)\text{ and }{\epsilon }_R^{+}(S)$ are of special interest in this work. The former is the rate of true positives in the data set while the latter is called the positive rate of rule R. Both of these quantities are dictated by the domain and do not change due to any specific sampling strategy. Notice that ${\epsilon }_R^{+}(S)$ is unknown at the time of sampling.

In the following analyses, we first assume the partitioning of S into L and U is known. We then use these results to determine what partitioning yields better estimates of evaluation measures. Table 1 shows the elements of contingency table for a rule R and oracle O.

Table 1.

Contingency table for rule R and oracle O.

	$S_O^{+}$	$S_O^{-}$
$S_R^{+}$	$|S_O^{+}\cap S_R^{+}|$	$|S_O^{-}\cap S_R^{+}|$
$S_R^{-}$	$|S_O^{+}\cap S_R^{-}|$	$|S_O^{-}\cap S_R^{-}|$

Using this contingency table, precision, sensitivity and specificity of rule R over set S = U ∪ L are defined as follows:

$$\mathit{\text{Pr}}(R)=\frac{|S_O^{+}\cap S_R^{+}|}{|S_R^{+}|}=\frac{|U_O^{+}\cap U_R^{+}|+|L_O^{+}\cap L_R^{+}|}{|S_R^{+}|}$$ (3.1)

$$Se(R)=\frac{|S_O^{+}\cap S_R^{+}|}{|S_O^{+}|}=\frac{|U_O^{+}\cap U_R^{+}|+|L_O^{+}\cap L_R^{+}|}{|S_O^{+}|}$$ (3.2)

$$Sp(R)=\frac{|S_O^{-}\cap S_R^{-}|}{|S_O^{-}|}=\frac{|U_O^{-}\cap U_R^{-}|+|L_O^{-}\cap L_R^{-}|}{|S_O^{-}|}$$ (3.3)

where Pr, Se, and Sp stand for the precision, the sensitivity and the specificity, respectively. We would like to identify characteristics of set L or U (one determines the other) that lead to a good estimation of the desired evaluation measures over the whole set S.

3.2 Estimation Bounds

The exact evaluation of precision, sensitivity, and specificity on S is dependent on both U and L; for example, the precision is calculated from $|U_O^{+}\cap U_R^{+}|\text{ and }|L_O^{+}\cap L_R^{+}|$. For a given rule R, the dependency on set L is known and we would like to choose U such that the uncertainty of estimating these evaluation measures for different rules is small. Although the labels in set U are not known, we know that $|U_O^{+}\cap U_R^{+}|~B(n,p)$ follows a binomial distribution with parameters $n=|U_O^{+}|\text{ and }p={\epsilon }_O^{+}(U)$. Using the properties of binomial distribution, we can compute the expected value $E(|U_O^{+}\cap U_R^{+}|)=|U_O^{+}|{\epsilon }_O^{+}(U)$ and variance ${\sigma }^2(|U_O^{+}\cap U_R^{+}|)=|U_R^{+}|{\epsilon }_O^{+}(U)(1-{\epsilon }_O^{+}(U))$. Given that the labels of examples in L are known, the expected value and variance of precision for different labelings on U for a specific but unknown rule R of size $|S_R^{+}|$ is defined as follows:

$$E(\mathit{\text{Pr}})=\frac{E(|U_O^{+}\cap U_R^{+}|)}{|S_R^{+}|}+\frac{|L_O^{+}\cap L_R^{+}|}{|S_R^{+}|}=\frac{|U_R^{+}|{\epsilon }_O^{+}|(U)}{|S_R^{+}|}+\frac{|L_O^{+}\cap L_R^{+}|}{|S_R^{+}|}$$ (3.4)

$${\sigma }^2(\mathit{\text{Pr}})=\frac{{\sigma }^2(|U_O^{+}\cap U_R^{+}|)}{|S_R^{+}{|}^2}=\frac{|U_R^{+}|{\epsilon }_O^{+}(U)(1-{\epsilon }_O^{+}(U))}{|S_R^{+}{|}^2}$$ (3.5)

Given these statistics, we can obtain the concentration bounds for the values of precision and study the variation of precision when the selection of samples in U changes. Using Bernstein bound¹[5], we can bound the deviation of the expected value of precision for unknown labeling of U from the true precision as follows:

$$P(|\mathit{\text{Pr}}-E(\mathit{\text{Pr}})|>{\xi }_{\mathit{\text{Pr}}})\le 2\text{exp}(-\frac{{\xi }_{\mathit{\text{Pr}}}^2}{4{\sigma }^2(\mathit{\text{Pr}})})=2\text{exp}(-\frac{{\xi }_{\mathit{\text{Pr}}}^2|S_R^{+}{|}^2}{4|U_R^{+}|{\epsilon }_O^{+}(U){\epsilon }_O^{-}(U)})$$ (3.6)

where ξ_pr is a positive value. The above equation simply explains that the value of precision is concentrated around its mean with a density dependent on the properties of oracle O (the uncertainty of labeling on U) and the rule R (e.g. the positive examples returned by the rule). We can rewrite the above bound in the probably approximately correct (PAC) form as given in the following proposition.

Proposition 3.1. For any δ ∈ [0, 1], the difference between the true precision and the expected value of precision defined by Equation 3.4 satisfies:

$$|\mathit{\text{Pr}}-E(\mathit{\text{Pr}})|\le 2\frac{\sqrt{|U_R^{+}|{\epsilon }_O^{+}(U){\epsilon }_O^{-}(U)\text{log}\left(\frac{2}{\delta }\right)}}{|S_R^{+}|}$$ (3.7)

with probability at least 1 − δ.

Proof. The proof is standard and as follows. By defining $\delta =2\text{exp}(-\frac{{\xi }_{\mathit{\text{Pr}}}^2|S_R^{+}{|}^2}{4|U_R^{+}|{\epsilon }_O^{+}(U){\epsilon }_O^{-}(U)})$, solving it for ξ_Pr, and replacing it in Equation 3.6, we get:

$$P(|\mathit{\text{Pr}}-E(\mathit{\text{Pr}})|>2\frac{\sqrt{|U_R^{+}|{\epsilon }_O^{+}(U){\epsilon }_O^{-}(U)\text{log}\left(\frac{2}{\delta }\right)}}{|S_R^{+}|})\le \delta$$

or

$$P(|\mathit{\text{Pr}}-E(\mathit{\text{Pr}})|\le 2\frac{\sqrt{|U_R^{+}|{\epsilon }_O^{+}(U){\epsilon }_O^{-}(U)\text{log}\left(\frac{2}{\delta }\right)}}{|S_R^{+}|})>1-\delta$$

which is equivalent to the claim of the proposition.

Remark I: Notice that in order to get a better estimation of precision, we need to have small values on the right hand side of Equation 3.7. The right hand side of Equation 3.7 is inversely related to $|S_R^{+}|$ that implies we have a better approximation of precision for the rules with large $|S_R^{+}|$. Moreover, the numerator shows how the selection of a particular labeled set L affects this uncertainty: the direct relation of numerator to $|U_R^{+}|\text{ and }{\epsilon }_O^{+}(U)(1-{\epsilon }_O^{+}(U))$ implies that smaller values of $|U_R^{+}|\text{ and }{\epsilon }_O^{+}(U)(1-{\epsilon }_O^{+}(U))$ are preferable. To get smaller value for ${\epsilon }_O^{+}(U)(1-{\epsilon }_O^{+}(U))$, U should become very unbalanced because smaller value for ${\epsilon }_O^{+}(U)\text{ or }1-{\epsilon }_O^{+}(U)$ leads to smaller value in ${\epsilon }_O^{+}(U)(1-{\epsilon }_O^{+}(U))$. Since the uncertainty is also inversely related to the value of $|U_R^{+}|$ (look at the numerator on the right hand side), more positive examples in L are required to reduce the right hand side of Equation 3.7 and obtain a tighter bound. As a summary, by labeling more positive examples, we reduce the number of positive examples left in U and obtain smaller uncertainty when estimating the precision.

Similarly, we can compute the mean and the variance for sensitivity and specificity as follows:

$$E(\mathit{\text{Se}})=\frac{|U_R^{+}|{\epsilon }_O^{+}(U)}{|S_O^{+}|}+\frac{|L_O^{+}\cap L_R^{+}|}{|S_O^{+}|}$$ (3.8)

$${\sigma }^2(\mathit{\text{Se}})=\frac{|U_R^{+}|{\epsilon }_O^{+}(U)(1-{\epsilon }_O^{+}(U))}{|S_O^{+}{|}^2}$$ (3.9)

$$E(\mathit{\text{Sp}})=\frac{|U_R^{-}|(1-{\epsilon }_O^{+}(U))}{|S_O^{-}|}+\frac{|L_O^{+}\cap L_R^{-}|}{|S_O^{-}|}$$ (3.10)

$${\sigma }^2(\mathit{\text{Pr}})=\frac{|U_R^{-}|{\epsilon }_O^{+}(U)(1-{\epsilon }_O^{+}(U))}{|S_O^{-}{|}^2}$$ (3.11)

Consequently, we can obtain the bounds for sensitivity and specificity:

$$P(|\mathit{\text{Se}}-E(\mathit{\text{Se}})|>{\xi }_{\mathit{\text{Se}}})\le 2\text{exp}(-\frac{{\xi }_{\mathit{\text{Se}}}^2|S_O^{+}{|}^2}{4|U_R^{+}|{\epsilon }_O^{+}(U){\epsilon }_O^{-}(U)})$$ (3.12)

$$P(|\mathit{\text{Sp}}-E(\mathit{\text{Sp}})|>{\xi }_{\mathit{\text{Sp}}})\le 2\text{exp}(-\frac{{\xi }_{\mathit{\text{Sp}}}^2|S_O^{-}{|}^2}{4|U_R^{-}|{\epsilon }_O^{+}(U){\epsilon }_O^{-}(U)})$$ (3.13)

The following propositions show how L affects the accuracy of sensitivity and specificity estimates.

Proposition 3.2. For any δ ∈ [0, 1], the difference between the true sensitivity and the expected value of sensitivity defined by Equation 3.8 satisfies:

$$|\mathit{\text{Se}}-E(\mathit{\text{Se}})|\le 2\frac{\sqrt{|U_R^{+}|{\epsilon }_O^{+}(U){\epsilon }_O^{-}(U)\text{log}\left(\frac{2}{\delta }\right)}}{|S_O^{+}|}$$ (3.14)

with probability at least 1 − δ.

Proposition 3.3. For any δ ∈ [0, 1], the difference between the true specificity and the expected value of specificity defined by Equation 3.10 satisfies:

$$|\mathit{\text{Sp}}-E(\mathit{\text{Sp}})|\le 2\frac{\sqrt{|U_R^{-}|{\epsilon }_O^{+}(U){\epsilon }_O^{-}(U)\text{log}\left(\frac{2}{\delta }\right)}}{|S_O^{-}|}$$ (3.15)

with probability at least 1 − δ.

The proofs of Propositions 3.2 and 3.3 are similar to the proof of Proposition 3.1.

Remark II: The interpretation of the bound for sensitivity is similar to the bound on the precision; to improve the sensitivity estimate we need more positive examples in L. The interpretation of the specificity bound is different: in order to minimize the right hand side of the bound for specificity given in Equation 3.15, more negative examples need to be collected in L. This is because smaller values of $|U_O^{-}|\text{ and }{\epsilon }_O^{+}(U)(1-{\epsilon }_O^{+}(U)$ ask for sampling more negative examples in L. Thus the goals for improving the estimates of the precision and sensitivity on one side and specificity on the other are opposite. In general, decreasing one increases the other side.

Proposition 3.4. When the budget size |L| is very small compared to the sample size |S| (i.e. |L| ≪ |S|), we have the following approximations for almost all rules²:

$$|U_R^{+}|\approx \frac{|U|{\epsilon }_O^{+}(U)|S_R^{+}|}{|S|{\epsilon }_O^{+}(S)}$$ (3.16)

$$|U_R^{-}|\approx \frac{|U||S_R^{-}|(1-{\epsilon }_O^{+}(U)))}{|S|(1-{\epsilon }_O^{+}(S))}$$ (3.17)

Proof. First notice that when |L| ≪ |S|, we have ${\epsilon }_O^{+}(U)\approx {\epsilon }_O^{+}(S)$. We also have ${\epsilon }_R^{+}(U)\approx {\epsilon }_R^{+}(S)\text{ if }{\epsilon }_O^{+}(S)\ll \frac{|L|}{|S|}\text{ and }{\epsilon }_R^{+}(S)\ll \frac{|L|}{|S|}$. Therefore:

$$|U_R^{+}|=|U|{\epsilon }_R^{+}(U)\approx |U|{\epsilon }_R^{+}(S)=\frac{|U|}{|S|}|S_R^{+}|=\frac{|U|{\epsilon }_O^{+}(S)}{|S|{\epsilon }_O^{+}(S)}|S_R^{+}|\approx \frac{|U|{\epsilon }_O^{+}(U)}{|S|{\epsilon }_O^{+}(S)}|S_R^{+}|$$ (3.18)

The proof for the second approximation is similar and more intuitive considering that the negative class is majority.

Replacing Equations 3.16 and 3.17 in Equations 3.7, 3.14, and 3.15, we have the following bounds when we use ${\epsilon }_R^{+}(S)=\frac{|S_R^{+}|}{|S|}$:

$$|\mathit{\text{Pr}}-E(\mathit{\text{Pr}})|\le 2\sqrt{\frac{|U|{\epsilon }_O^{+}{(U)}^2{\epsilon }_O^{-}(U)\text{log}\left(\frac{2}{\delta }\right)}{|S{|}^2{\epsilon }_R^{+}(S){\epsilon }_O^{+}(S)}}$$ (3.19)

$$|\mathit{\text{Se}}-E(\mathit{\text{Se}})|\le 2\sqrt{\frac{|U|{\epsilon }_R^{+}(S){\epsilon }_O^{+}{(U)}^2{\epsilon }_O^{-}(U)\text{log}\left(\frac{2}{\delta }\right)}{|S{|}^2{\epsilon }_O^{+}{(S)}^3}}$$ (3.20)

$$|\mathit{\text{Sp}}-E(\mathit{\text{Sp}})|\le 2\sqrt{\frac{|U|{\epsilon }_R^{-}(S){\epsilon }_O^{+}(U){\epsilon }_O^{-}{(U)}^2\text{log}\left(\frac{2}{\delta }\right)}{|S{|}^2{\epsilon }_O^{-}{(S)}^3}}$$ (3.21)

The above bounds depend on two types of parameters. One group includes ${\epsilon }_O^{+}(S)\text{ and }{\epsilon }_R^{+}(S)$ which are the characteristics of the underlying data set and the rule and are not dependent on a particular approach of sampling. We have no control on this group of parameters. ${\epsilon }_O^{+}(U)$ is the second type of parameter that depends on the sampling strategy (how we partition S into L and U). Thus, any optimization of these bounds involves finding the optimal value of ${\epsilon }_O^{+}(U)$.

3.3 Sampling Strategy

As mentioned in the previous subsection, the accuracy of estimates of the three evaluation measures depends on ${\epsilon }_O^{+}(U)$, as a variable that is dependent on our sampling strategy. As explained by Remark I and Remark II, we need small values of ${\epsilon }_O^{+}(U)$ to have a good estimation of precision and sensitivity and large values of ${\epsilon }_O^{+}(U)$ to have a good estimation on specificity. Therefore, getting a good estimation for precision and sensitivity is in contrary to getting a good estimation for specificity. We would like to quantitatively measure how the estimation accuracy of different evaluation measures changes with different number of positive examples in L or U (or equivalently ${\epsilon }_O^{+}(L)\text{ or }{\epsilon }_O^{+}(U)$)³. To understand the interaction between the estimation accuracy of the three evaluation measures, we study how the changes in the value of ${\epsilon }_O^{+}(U)$ trades off between the estimation accuracy of precision, sensitivity, and specificity.

The bounds provided in Equations 3.19, 3.20, and 3.21 depend on several rule and problem specific parameters (i.e. ${\epsilon }_R^{+}(S),|S|,{\epsilon }_O^{+}(S)$, L or U, and δ) that makes the task of visualizing the values of these bounds difficult. To address this problem, we study only the values of ${\epsilon }_O^{+}(U)$ at which similar upper bounds for different evaluation measures are obtained. By the knowledge of these boundary values, we can study at what values we trade the accuracy estimation of one evaluation measures with another. Since we cannot study the trade-off values of ${\epsilon }_O^{+}(U)$ for all three evaluation measures at once, we study the change in the value of ${\epsilon }_O^{+}(U)$ that trades off precision vs. sensitivity and sensitivity vs. specificity separately, in the following subsections.

3.3.1 Precision vs. Specificity

To obtain the boundary values of ${\epsilon }_O^{+}(U)$ that trades off precision vs. specificity, we need to have similar right hand side for the bounds of these evaluation measures. By making the right hand side of bounds in Equation 3.19 and 3.21 equal, we obtain:

$$\frac{{\epsilon }_R^{+}(S){\epsilon }_O^{+}(S)}{{\epsilon }_O^{+}(U)}=\frac{{(1-{\epsilon }_O^{+}(S))}^3}{(1-{\epsilon }_R^{+}(S))(1-{\epsilon }_O^{+}(U))}\Rightarrow \frac{(1-{\epsilon }_O^{+}(U)}{{\epsilon }_O^{+}(U)}=\frac{{(1-{\epsilon }_O^{+}(S))}^3}{(1-{\epsilon }_R^{+}(S)){\epsilon }_R^{+}(S){\epsilon }_O^{+}(S)}\Rightarrow {\epsilon }_O^{+}(U)=\frac{(1-{\epsilon }_R^{+}(S)){\epsilon }_R^{+}(S){\epsilon }_O^{+}(S)}{{(1-{\epsilon }_O^{+}(S))}^3+(1-{\epsilon }_R^{+}(S)){\epsilon }_R^{+}(S){\epsilon }_O^{+}(S)}$$ (3.22)

The value of ${\epsilon }_O^{+}(U)$ determines the rate of positive examples in set U (and equivalently in set L) at which the same estimation accuracy are obtained for precision and specificity. We can also find the exact required number of positive examples with the knowledge of ${\epsilon }_O^{+}(S),{\epsilon }_R^{+}(S),{\epsilon }_O^{+}(U)$, and |L| as follows:

$$|L_O^{+}|=\text{min}(|L|,{[|S|{\epsilon }_O^{+}(S)-|U|{\epsilon }_O^{+}(U)]}_{+})$$ (3.23)

where [a]₊ returns a if a > 0; otherwise it returns zero. Although the above equation provides the required number of positive examples, we need a more qualitative criteria, independent of the budget size |L|, to study the sampling strategy for different values of ${\epsilon }_O^{+}(S)\text{ and }{\epsilon }_R^{+}(S)$. It is easy to see that ${\epsilon }_O^{+}(U)<{\epsilon }_O^{+}(S)$ is an indicator to get more positive examples in L, and ${\epsilon }_O^{+}(U)>{\epsilon }_O^{+}(S)$ is an indicator to get more negative examples in L. Therefore, we define quantity α as a variable determining which class of examples is preferable in L.

$$\alpha =\frac{{\epsilon }_O^{+}(U)}{{\epsilon }_O^{+}(S)}$$ (3.24)

The magnitude of α is inversely related to the required number of positive examples in L; i.e. a small value for α asks for more positive examples while a large value for α asks for more negative examples in L. Figure 1 shows the value α as a function of ${\epsilon }_O^{+}(S)\text{ and }{\epsilon }_R^{+}(S)$, suggested by Equation 3.22. This figure suggests the following results: 1) We expect to reduce the rate of positive examples in set U compared to that in set S for small values of ${\epsilon }_O^{+}(S)$. This is equivalent to say that more positive examples in L are required. 2) We expect to get more positive examples in L for rules with very small or large rate ${\epsilon }_R^{+}(S)$.

Figure 1.

${\epsilon }_O^{+}(U)/{\epsilon }_O^{+}(S)$ for precision vs. specificity as a function of ${\epsilon }_O^{+}(S)$ (the x axis) and ${\epsilon }_R^{+}(S)$ (the y axis).

3.3.2 Sensitivity vs. Specificity

Similarly, the boundary values to trade off sensitivity vs. specificity can be obtained:

$$\frac{{\epsilon }_O^{+}{(S)}^3}{{\epsilon }_R^{+}(S){\epsilon }_O^{+}(U)}=\frac{{(1-{\epsilon }_O^{+}(S))}^3}{(1-{\epsilon }_R^{+}(S))(1-{\epsilon }_O^{+}(U)}\Rightarrow \frac{(1-{\epsilon }_O^{+}(U)}{{\epsilon }_O^{+}(U)}=\frac{{(1-{\epsilon }_O^{+}(S))}^3{\epsilon }_R^{+}(S)}{{\epsilon }_O^{+}{(S)}^3(1-{\epsilon }_R^{+}(S))}\Rightarrow {\epsilon }_O^{+}(U)=\frac{{\epsilon }_O^{+}{(S)}^3(1-{\epsilon }_R^{+}(S))}{{\epsilon }_O^{+}{(S)}^3(1-{\epsilon }_R^{+}(S))+{(1-{\epsilon }_O^{+}(S))}^3{\epsilon }_R^{+}(S)}$$ (3.25)

Figure 2 shows the value α as a function of ${\epsilon }_O^{+}(S)\text{ and }{\epsilon }_R^{+}(S)$ for sensitivity vs. specificity, suggested by Equation 3.25. Notice that in order to guarantee good bounds on both sensitivity and specificity, we need more positive examples in L if ${\epsilon }_O^{+}(S)$ is small compared to ${\epsilon }_R^{+}(S)$. Moreover, compared to the discussion in the previous subsection, here the small value for ${\epsilon }_O^{+}(S)$ is relative and the concept covers a wider domain of situations.

Figure 2.

α for sensitivity vs. specificity as a function of ${\epsilon }_O^{+}(S)$ (the x axis) and ${\epsilon }_R^{+}(S)$ (the y axis).

3.3.3 Special case of ${\epsilon }_R^{+}(S)\approx {\epsilon }_O^{+}(S)$

In this section, we give a comparison of precision, sensitivity, and specificity for rules that have the specific form of ${\epsilon }_R^{+}(S)\approx {\epsilon }_O^{+}(S)$ i.e. rules that have the same rate in returning positive examples as oracle. This set of rules are particularly interesting because ${\epsilon }_R^{+}(S)$ does not provide any information about the quality of the rule R. To see this, notice that if ${\epsilon }_R^{+}(S)\gg {\epsilon }_O^{+}(S)$, we can make the general statement that R has a lot of false positive alarms and a small number of false negative alarms in average. On the other hand, if ${\epsilon }_R^{+}(S)\ll {\epsilon }_O^{+}(S)$, there should be a lot of false negative alarms and in average a small number of false positive alarms. So the case ${\epsilon }_R^{+}(S)\approx {\epsilon }_O^{+}(S)$ provides minimums information in terms of estimating the three evaluation measures. Replacing ${\epsilon }_R^{+}(S)\approx {\epsilon }_O^{+}(S)$ in Equations 3.19, 3.20, and 3.21, we have:

$$|\mathit{\text{Pr}}-E(\mathit{\text{Pr}})|\le 2\sqrt{\frac{|U|{\epsilon }_O^{+}{(U)}^2{\epsilon }_O^{-}(U)\text{log}\left(\frac{2}{\delta }\right)}{|S{|}^2{\epsilon }_O^{+}{(S)}^2}}$$ (3.26)

$$|\mathit{\text{Se}}-E(\mathit{\text{Se}})|\le 2\sqrt{\frac{|U|{\epsilon }_O^{+}{(U)}^2{\epsilon }_O^{-}(U)\text{log}\left(\frac{2}{\delta }\right)}{|S{|}^2{\epsilon }_O^{+}{(S)}^2}}$$ (3.27)

$$|\mathit{\text{Sp}}-E(\mathit{\text{Sp}})|\le 2\sqrt{\frac{|U|{\epsilon }_O^{+}(U){\epsilon }_O^{-}{(U)}^2\text{log}\left(\frac{2}{\delta }\right)}{|S{|}^2{\epsilon }_O^{-}{(S)}^2}}$$ (3.28)

Interestingly, the first two bounds become equivalent and we only need to compare precision (sensitivity) vs. specificity. Similar to the previous section, by making the right hand side of these two bounds equal, we get the following boundary value for ${\epsilon }_O^{+}(U)$.

$${\epsilon }_O^{+}(U)=\frac{{\epsilon }_O^{+}{(S)}^2}{{\epsilon }_O^{+}{(S)}^2+{(1-{\epsilon }_O^{+}(S))}^2}$$ (3.29)

Figure 3 shows α as a function of ${\epsilon }_O^{+}(S)$, suggested by the above equation. As can be seen, for small values of ${\epsilon }_O^{+}(S)$ we would like to reduce the rate of positive examples in U compared to S, i.e. ${\epsilon }_O^{+}(S)\ge {\epsilon }_O^{+}(U)$, and for large values of ${\epsilon }_O^{+}(S)$ we need ${\epsilon }_O^{+}(S)\le {\epsilon }_O^{+}(U)$. In other words, we need to get more positive in L for small values of ${\epsilon }_O^{+}(S)$ and more negative examples in L for large values of ${\epsilon }_O^{+}(S)$. This suggests sampling from the minority class.

Figure 3.

α for precision (sensitivity) vs. specificity for good rules

3.4 Cost Analysis of Different Evaluation Measures

If a cost is associated with the estimation of each evaluation measure, one can utilize such costs directly in the analysis, in a similar approach to what we performed in the previous subsections. To see this, suppose C_pr, C_se, and C_sp are the costs respectively associated with the estimation of precision, sensitivity and specificity. In order to consider these costs in the analysis of precision vs. specificity, for example, we need to have:

$$\frac{{\epsilon }_R^{+}(S){\epsilon }_O^{+}(S)}{{\epsilon }_O^{+}(U)}=\frac{C_{\mathit{\text{sp}}}}{C_{\mathit{\text{pr}}}}\times \frac{{(1-{\epsilon }_O^{+}(S))}^3}{(1-{\epsilon }_R^{+}(S))(1-{\epsilon }_O^{+}(U)}$$

It is easy to see that the costs will be multiplied as a constant coefficient to the previous boundary values for ${\epsilon }_O^{+}(U)$.

3.5 Sampling to Evaluate Area under the ROC curve (AUC)

A receiver operating characteristic (ROC) [7] is the plot of the sensitivity vs. 1-specificity for a binary classifier when the discrimination threshold of the classifier is varied. The area under the ROC curve or AUC is one standard measure of evaluating classification models particularly when the problem is skewed. One might be interested in finding sampling strategies that results a sample of examples for a good approximation of AUC. In the setting of this paper, where the sample is being used to evaluate unknown rules, obtaining a sample to accurately estimate AUC of unknown rules is a tricky problem, yet very related to approximating precision and specificity. To see this, notice that estimating AUC of a given classifier can be summarized in estimating precision and specificity of all the rules obtained from that classifier with varying threshold. Hence, an accurate estimate of AUC for multiple unknown classifiers can be obtained by a sampling strategy that produces an accurate estimation of precision and specificity of all the rules obtained from such classifiers. In other words, the discussion in the previous section is valid for sampling to evaluate unknown rules using AUC.

4 Sampling in Practice

The previous discussion provides a guideline to the sampling strategy based on the parameters of the problem such as the nature of ${\epsilon }_O^{+}(S)$, the total number of examples |S|, the budget size |L|, and some preliminary knowledge about the characteristics of the rules we are interested to evaluate (e.g. ${\epsilon }_R^{+}(S)$ is small). Once this guideline for sampling is available (based on the analysis), the next interesting question is how to follow the strategy dictated by the guideline. For example, if the guideline asks for more positive examples, how should we retrieve positive examples? We call this problem finite-pool sampling. Notice that this problem is different from 1) the problem of regular active learning [11] and guided learning [16] where the objective is to construct a good predictive model; 2) the problem of finite-pool active learning [15] where the objective is to label all the examples in the pool. Unlike finite-pool active learning, the budget in finite-pool sampling is limited and we cannot afford to label as many examples as required to construct a classifier with a good confidence on labeling all the examples in the pool [15]. Nonetheless, the same procedures utilized for finite-pool active learning [15] and guided learning [16] to follow their suggested guidelines can be used for finite-pool sampling.

Here, we summarize four different schemes one can use to implement the task of finite-pool sampling. We note that while some of these schemes do not guarantee the examples from the target class are always selected, they at least try to follow the analysis (i.e. they make every effort to obtain more examples from the minority class).

• The simplest approach is to ask an expert to provide an example from the class the sampling guideline dictates. This example is then included in set L with the corresponding label. The limitation of this approach is that all the burden of finding the example among all possible examples in the data set S is on the expert. This is similar to the strategy utilized in biomedical citation screening [15], where the reviewers manually screen the reports to retrieve the most relevant studies to a research question. Notice that this approach is also similar to guided learning approach (discussed in the related work) where the reviewers are provided with certain characteristics of the data and then the reviewers find such examples and label them [1, 16].

• The second approach still requires expert’s input, but eliminates expert’s responsibility to search for individual examples. The idea is to start from a small initial set of labeled (positive and negative) examples and use them to learn a classification model. The model is then used to label all remaining unlabeled examples. One of the examples the model classifies to the minority class is presented to the expert to provide the true label. The example with its true label is then included in L. As more labeled examples are collected, the model is gradually improved. Active learning approaches can be also utilized to help this process, like in [15].

• The third approach is similar to the second approach and differs in how the model is initialized. The idea here is to use expert’s input to define conditions that are more predictive of the minority class than the baseline population. The examples are then drawn either from examples that satisfy these conditions, or alternatively, from the model trained on the labeling induced by these conditions. The model can be further refined if examples with true labels become available, as was handled in the second approach.

• Finally, yet another approach may rely on the implicit domain information. For example, in getting labeled examples for information retrieval or recommendation systems, the possible relevant items could be detected implicitly by monitoring the user behavior; e.g. the items that get clicked or checked out are relevant. This is the click-through feedback widely utilized in information retrieval [8].

4.1 Blind Labeling

In the previous subsections, we showed that by sampling from the minority class, we reduce the estimation uncertainty for the evaluation measures. An intuitive justification of sampling from minority class is that obtaining examples from the majority class is cheap if the prevalence of the two classes is highly biased toward one of the classes. We say it is cheap because if we randomly sample examples and assign them the label of majority class, we make a small error as we will see in this section. Without loss of generality, let us assume that $|S_O^{+}|\le |S_O^{-}|$; i.e. the negative class is the majority one. If the rate of positive examples is very small (i.e. ${\epsilon }_O^{+}(S)=\frac{|S_O^{+}|}{|S|}\ll \frac{1}{2}$), we propose to blindly assign negative label to a subset B of examples from set U (B ∈ S). By blind labeling, we not only increase the number of labeled examples in L with a small error but also we keep almost the same rate of positive examples in set L as original set S. This is particularly important because if the rate of positive examples in L is very different than that in set S, we might over/under-estimate the values of the evaluation measures. To perform the blind labeling, we propose to bring $\frac{|L_O^{+}|-|L|{\epsilon }_O^{+}(S)}{{\epsilon }_O^{+}(S)}$ random examples from S to L and blindly label them as the majority class (negative). Let us call the new sampled set L̂ that contains examples in L and the extra blindly labeled negative examples. L̂ has the same rate of examples from two classes as S because

$$\frac{|{\widehat{L}}_O^{+}|}{|\widehat{L}|}=\frac{|L_O^{+}|}{|L|+\frac{|L_O^{+}|-|L|{\epsilon }_O^{+}(S)}{{\epsilon }_O^{+}(S)}}={\epsilon }_O^{+}(S)$$ (4.30)

The error caused by the blind sampling will be small if the rate of examples from the minority class is small enough. To see this, notice that if we sample |B| examples from U for blind labeling, the average number of positive examples in B will be $|B|{\epsilon }_O^{+}(U)$, a small number if |L| and ${\epsilon }_O^{+}(S)$ are small.

One practical problem with this approach is that it needs the knowledge of ${\epsilon }_O^{+}(S)$. In many domains, there is a domain knowledge about approximate value of ${\epsilon }_O^{+}(S)$. In case that there is not such knowledge, one approach to obtain an approximation is to get an initial set of randomly selected labeled examples and estimate ${\epsilon }_O^{+}(S)$ using this set. This set can further be used to learn an initial model to select positive examples. The following proposition shows that the approximation can be reasonably good for very small or large values of ${\epsilon }_O^{+}(S)$.

Proposition 4.1. For any δ ∈ [0, 1], with probability at least 1 − δ, we have the following bound on the difference between ${\epsilon }_O^{+}$ and the approximation made using a random sample M:

$$|{\epsilon }_O^{+}(M)-{\epsilon }_O^{+}(S)|\le 2\sqrt{\frac{{\epsilon }_O^{+}(S){\epsilon }_O^{-}(S)\text{log}\left(\frac{2}{\delta }\right)}{|M|}}$$ (4.31)

Proof. Notice that the mean and variance of ${\epsilon }_O^{+}(M)$ is:

$$E({\epsilon }_O^{+}(M))=E(\frac{|M_O^{+}|}{|M|})=\frac{E(|M_O^{+}|)}{|M|}=\frac{|M|{\epsilon }_O^{+}(S)}{|M|}={\epsilon }_O^{+}(S)$$

$${\delta }^2({\epsilon }_O^{+}(M))=\frac{{\delta }^2(|M_O^{+}|)}{|M{|}^2}=\frac{|M|{\epsilon }_O^{+}(S){\epsilon }_O^{-}(S)}{|M{|}^2}=\frac{{\epsilon }_O^{+}(S){\epsilon }_O^{-}(S)}{|M|}$$

Using Bernstein inequality, we have

$$P(|{\epsilon }_O^{+}(M)-{\epsilon }_O^{+}(S)||>\xi )\le 2\text{exp}(-\frac{{\xi }^2|M|}{4{\epsilon }_O^{+}(S){\epsilon }_O^{-}(S)})$$ (4.32)

Similar to the proof of Proposition 3.1, we can conclude the result in this proposition.

5 Experiments

In this section, we verify the efficacy of the guidelines proposed by the analysis in this paper on covtype and connect-4 data sets from UCI data repository [6], as described here. Covtype has about 580, 000 records, each represented by 54 attributes and one of the 7 classes. We preprocessed this data and constructed a binary problem by considering classes 4 and 7 as positives and other classes as negatives⁴. This results in 23257 positive and 557755 negative examples, a positive rate of 0.04. Connect-4 has 67557 records, with each record represented by 126 features and one of the three classes (−1,0,1). We construct a binary problem from this data by considering class 0 as the positive class, which results a positive rate of 0.1.

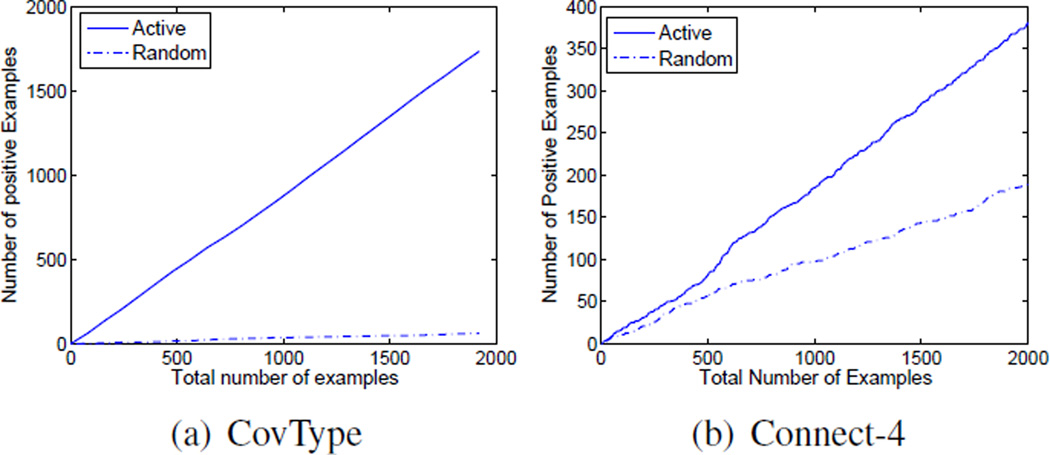
To retrieve positive examples in the active mode, we utilize 100 randomly selected examples and construct an initial decision tree classifier. Using the recommendation of this decision tree, we randomly choose 5 positive examples⁵, and add them to the labeled set. We then construct a new classifier and repeat the same procedure until we collect a total number of 2000 examples. Note that not all 5 selected examples in each round are positive. Figure 4 shows the retrieved number of positive examples over the trials for both the active and random sampling for two data sets.

Figure 4.

The retrieved number of positive examples over the trials.

As the baseline, we randomly sample from the data set until we obtain 2000 examples. To compare the results, we create rules with different rate of positive examples, i.e. $|S_R^{+}|$ ∈ {10000, 20000, 30000, 40000, 50000}. For each $S_R^{+}$, we create 100 random rules and report the average performance and the confidence interval of both active sampling and random sampling. We report the absolute value of the difference between the true value of each evaluation measure (the gold standard computed using the whole data set) and the value computed on the subsets created by active/random sampling.

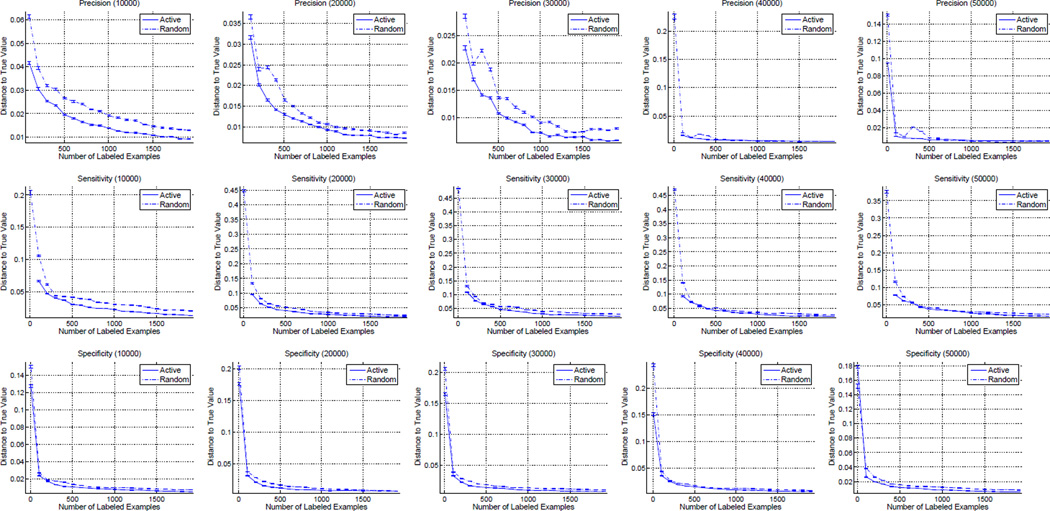
Figures 5 and 6 shows the result for rules with varying value of ${\epsilon }_R^{+}(S)$ on two data sets. Column i^th in these features is the average result in estimating three evaluation measures on 100 rules with positive rate of ${\epsilon }_R^{+}(S)=i\times 10000$. As can be seen, the active sampling approach results in a better approximation of the evaluation measures. The results confirms that with only a small labeled set of examples, we obtain much better estimation accuracy than random sampling. Consider the computation of precision on CovType data set for rules with ${\epsilon }_R^{+}(S)=10000$, as an example. With only about 80 labeled examples, we can obtain an accuracy of 0.025 using active sampling while to obtain the same estimation accuracy using random sampling, more than 2000 examples are required. Overall in all the figures for CovType, a reduction rate of 95% in the number of labeled examples is achieved when compared to the random sampling of examples. The reduction rate for connect-4 data set is smaller than that for the CovType data sets. This is because CovType data set is very unbalanced in which random sampling performs very poor as shown by the analysis. Also notice that the smaller is the ${\epsilon }_R^{+}(S)$, the more effective is sampling from minority class, as predicted by the analysis. As we go from unbalanced data set and unbalanced rules (rules with small ${\epsilon }_O^{+}(S)$) to balanced data set and balanced rules, the advantage of sampling from one class disappears and it becomes more beneficial to perform random sampling.

Figure 5.

The difference between the true value of evaluation measure (computed over S) and the estimated ones on CovType data set. The dot line is the estimation using random sampling and the solid line is the estimation using active sampling. Column i in the figure shows the average of 100 random generation of rules of size i * 10000.

Figure 6.

The difference between the true value of evaluation measure (computed over S) and the estimated ones on Connect-4 data set. The dot line is the estimation using random sampling and the solid line is the estimation using active sampling. Column i in the figure shows the average of 100 random generation of rules of size i * 10000.

6 Conclusion

We provided a theoretical analysis of the sampling strategy for evaluating classification rules of unknown nature. In particular, we showed that for unbalanced data sets, it is much more beneficial to sample from the rare class. We discuss how the proposed framework can be generalized to the case where a cost associated with estimating each evaluation measure. We also verified and confirmed our theoretical analyses experimentally using two data sets from the UCI data repository.