Non-negative Matrix Factorization of Multimodal MRI, fMRI and Phenotypic Data reveals Differential Changes in Default Mode Subnetworks in ADHD

Abstract

In the multimodal neuroimaging framework, data on a single subject are collected from inherently different sources such as functional MRI, structural MRI, behavioral and/or phenotypic information. The information each source provides is not independent; a subset of features from each modality maps to one or more common latent dimensions, which can be interpreted using generative models. These latent dimensions, or “topics,” provide a sparse summary of the generative process behind the features for each individual. Topic modeling, an unsupervised generative model, has been used to map seemingly disparate features to a common domain. We use Non-Negative Matrix Factorization (NMF) to infer the latent structure of multimodal ADHD data containing fMRI, MRI, phenotypic and behavioral measurements. We compare four different NMF algorithms and find the sparsest decomposition is also the most differentiating between ADHD and healthy patients. We identify dimensions that map to interpretable, recognizable dimensions such as motion, default mode network activity, and other such features of the input data. For example, structural and functional graph theory features related to default mode subnetworks clustered with the ADHD inattentive diagnosis. Structural measurements of the default mode network (DMN) regions such as the posterior cingulate, precuneus, and parahippocampal regions were all related to the ADHD-Inattentive diagnosis. Ventral DMN subnetworks may have more functional connections in ADHD-I, while dorsal DMN may have less. We also find that ADHD topics may be dependent upon diagnostic site, raising the possibility of the diagnostic differences across geographic locations. We assess our findings in light of the ADHD-200 classification competition, and contrast our unsupervised, nominated topics with previously published supervised learning methods. Finally, we demonstrate the validity of these latent variables as biomarkers by using them for classification of ADHD in 730 patients. Cumulatively, this manuscript addresses how multi-modal data in ADHD can be interpreted by latent dimensions.

1. Introduction

Structural MRI, functional MRI (fMRI), phenotypic and behavioral information all are examples of multimodal data that can be used to measure different aspects of a patient. A challenging problem in multimodal imaging is the integration of EEG and fMRI data, both measures of neuronal activation. Finding a mapping between the observed and latent feature spaces is not a trivial process. These features are on very different spatial and temporal domains, and are subject to different sources of artifacts. Despite this, advances have been made in this mapping with methods such as multiway partial least squares [42], ICA-based methods [16][6][37][41], canonical correlation analysis [60], and Bayesian-ICA hybrid approaches [35].

When combining other data sources that are not measures of neuronal activity, such as structural imaging, phenotypic information, or behavioral data, this problem becomes even more difficult. Although these information sources are distinct in the general case, they likely all share some common information. Because of this, investigating the latent dimensions of multimodal data allows observations from different modalities to be linked together. When contrasting healthy and diseased patient groups, identifying the latent dimensions could suggest a generative model of the disease itself.

Generative models such as Hidden Markov Models [52], Restricted Boltzmann Machines [58], and Latent Dirichlet Allocation [3] (LDA) can be used to infer the underlying joint probability distribution by which the observations are generated. Non-negative matrix factorization (NMF) is a related technique that can be mapped directly to LDA when applying non-informative priors with maximum-likelihood estimation [25] [24]. NMF can also be viewed as a positively-constrained version of independent component analysis (ICA) [29] [30].

NMF and ICA are both matrix decomposition methods; NMF is a parts-based representation where the basis images, W, are constrained to be positive, while ICA is a holistic decomposition that instead constrains each basis to be statistically independent, thus permitting negative basis values and encoding values. When applying these tools to imaging data, the results are drastically different. For example, running ICA on images of faces produces ghostly-appearing faces for the basis functions, while performing NMF on the same sets of images would yield identifiable body parts, such as a pair of eyes or a mustache [34].

In the NMF framework a matrix, V, is broken down into a product using multiplicative updates, given by V ≈ WH [34]. This technique has been applied widely elsewhere to genetics [14] [32] [49], document retrieval [46], document clustering [68] and image classification [27] [39]. We apply it here to our multimodal data, including the demographic variables in our model.

In this paper we use NMF to identify latent dimensions in multimodal data, finding “topics” across phenotypic, behavioral, structural and functional MRI onto which all the multimodal data map. Each dimension would contain a subset of the original features, providing both a sparse summary of a subject's information, as well as a mapping across modalities. We apply this technique to the ADHD-200 dataset [44] containing MRI, fMRI, behavioral and phenotypic information from Attention Deficit Hyperactivity Disorder (ADHD) youth and typically developing (TD) patients. We identify the latent dimensions behind this multimodal dataset, and demonstrate how these latent features additionally can be used for classification of ADHD. Although our results are specific to ADHD, the methods are applicable to multimodal data in general. These topics are directly interpretable, relating to specific domains such as the default mode network (DMN) which has been implicated previously in ADHD.

As opposed to supervised discriminative models where the features predict a diagnosis (ADHD vs. healthy controls), we use an unsupervised generative model to map multimodal features to a common space. We do not limit this mapping to exclusively imaging features, but include in our latent variable model the behavioral and demographic features. We hypothesize that topics which link the diagnosis to imaging and phenotypic variables may nominate biomarkers related specifically to the disease state, while topics not containing the diagnosis variable can still illuminate the relationship of features across modalities.

1.1. Default Mode Network

The default mode network (DMN), represents a collection of distributed brain regions that oscillate coherently at low frequency during passive resting state when an individual is not focusing on external stimuli [53]. The brain regions that comprise the DMN nodes are intrinsically functionally correlated with one another [2], and are connected via direct and indirect anatomic projections [26]. DMN low frequency oscillations are typically attenuated during goal-oriented tasks, and activity strength in task related brain regions (e.g. dorsal anterior cingulate cortex (dACC)) tend to be anticorrelated with DMN. Changes in the DMN have become hallmark indicators of pathogenesis in a number of conditions including Alzheimer's disease [26], depression [55], and autism spectrum disorder (for review see [5]).

Recently, a number of studies have demonstrated both structural and functional changes in the DMN associated with ADHD (e.g. [69]). It has been speculated that ADHD individuals may have diminished ability to continuously sustain attention on a task due to interference by the DMN ([59]) ([20]). Fair et al. (2010) suggested that this may be due to different rates of maturation of the DMN [19].

1.2. ADHD

ADHD is a highly complex disorder marked behaviorally by problems with sustained attention and task prioritization. Its spectrum of clinical features typically is expressed along the domains of persistent inattention (ADHD-I), hyperactivity-impulsivity (ADHD-H) or a combination of both (ADHD-C) [1], often a ecting cognitive, emotional, and motor processes [10]. The clinical diagnosis in children is made after gathering information from parent and teacher surveys and ratings on ADHD-specific behavioral rating scales. In order for the diagnostic criteria to be met, the clinical features must be present in at least two settings and the core symptoms must actually interfere with daily life at school, home, and/or work [1].

Despite its high prevalence in children (~ 5%) [62], the precise neural, genetic and cognitive underpinnings of ADHD remain unclear. While the heritability of ADHD also is well established, a clear link between genes and the heterogeneous clinical features of ADHD remains elusive, and it is likely that multiple neural pathways and factors lead to the phenotypic expression of ADHD and its three subtypes. It is possible that identification of quantitative neuroimaging biomarkers would improve detection and diagnosis, thus providing the impetus for the machine learning (ML) contest. Further, an improved understanding of the interactions of both the neuroimaging and other biomarkers may offer clues of the physiological basis of the disease.

1.3. ADHD-200 Competition

Towards this aim, the ADHD 200 global ML competition (http://fcon_1000.projects.nitrc.org/indi/adhd200/index.html) challenged the neuroimaging and data mining communities to develop a pattern classification method to predict ADHD diagnosis based on a combination of structural MRI, resting state functional MRI (rs-fMRI), and demographic metrics. To provide data for this competition, one of the largest multisite data consortiums was initiated to provide open access to data from nearly a thousand children and adolescents with ADHD as well as age-matched controls. This dataset has been much published on in a short time [64] [45] [65] [8] [12] [48], allowing a direct comparison of the methodology and the common problems they all faced.

This competition was remarkable for many reasons, including the large sample size for the training set (491 TD, 285 ADHD), the number of contributing data centers (8), and the number of international teams competing (21). Even more remarkable, however, were the results of the competition. In general, it was much easier to classify TD than ADHD, with high specificity and low sensitivity from all the teams. The scoring system used within the competition was biased toward this, as it gave more ”points” for diagnosing correctly TD than ADHD-subtype. However, even when equal weightings were used, diagnostic accuracy was still much greater for TD children.

Surprisingly, the top placing team from University of Alberta was disqualified on the grounds of not using any neuroimaging data in a neuroimaging competition, predicting their results on the phenotypic variables alone [4]. After testing various fMRI measures (temporally-meaned fMRI Signal per voxel, voxel-projected timecourses into PCA space, low-frequency voxel Fourier components, voxel weightings on functional connectivity maps derived from ICA) in competition with phenotypic information (site, age, gender, handedness, IQ measures) with multiple machine-learning algorithms (linear SVM, cubic SVM, quadratic SVM, and Radial Basis Function(RBF) SVM classifiers, the Alberta team selected a logistic classifier that used only the diagnostic information to classify on the test-set. This classifier obtained the highest prediction-accuracy within the competition of 62.5%.

Following the disqualification, the official top-scoring team from Johns Hopkins University predicted using a voting scheme across four different algorithms [18]. They used as features functional connectivity data from the motor cortex, as well as seed-voxel correlation analysis. Structural features were not used. The most accurate of their four algorithms used a CUR matrix decomposition of the functional scans [40] along with gradient boosting method, which they suspected of capturing the residual motion that was not removed by the motion correction during preprocessing. Another of their algorithms used Latent Dirichlet Allocation to identify subsets of imaging features which were then used for classification. This team created in total four different algorithms which they combined to vote on the diagnosis for each subject. The most accurate algorithm in a hold-out set was used as a the tie-breaking vote.

Our group from UCLA/Yale used structural, functional, and phenotypic information within each site to predict ADHD, yielding a 55% accuracy with 33% sensitivity and 80% specificity [9]. We generated nearly 200,000 neuroimaging features from each subject's data - ranging from structural attributes such as cortical thickness, to functional connectivity and graph theoretic measures. In this analysis we ranked features, and found that caudate volume was one of the highest-ranked structural features. We used SVM based recursive feature elimination (SVM-RFE) as a wrapper method based on the multiple SVM-RFE (mSVM-RFE) extension described by [15], which imposes a resampling layer on each recursion pass such that the weights used for feature ranking/dropping are stabilized by averaging across results for multiple subsamples. We generated accuracy curves that related the number of features and error using a 10 fold cross validation approach. Features that together resulted in minimum error were selected for our feature set. Further details can be found in Colby et al. 2012. Diagnostic functional features included graph theoretic measures related to changes in default mode network (DMN) activity, consistent with the hypothesis that ADHD subjects are impaired in their ability to inhibit the DMN consistently for task execution [19]. Because of intra-site variability we selected features and trained classifiers within each site, instead of pooling observations together across sites.

In published studies of ADHD classification using imaging data not obtained from the ADHD-200 competition, the classification accuracies were an astonishing 85% [70], which made the classification results of the ADHD-200 competition seem rather lackluster by comparison. Brown et al. [4] posited that the ADHD-200 competition had produced inferior results compared to other neuroimaging studies for three possible reasons. 1.) Most neuroimaging classification studies focused on Binary classification, which is a computationally simpler task than trinary competition as in this study (TD, ADHD-Combined, ADHD Inattentive). Because there is likely to be similarities between the two subtypes of ADHD, training a classifier to distinguish among such subtle conditions is likely to result in higher error rates than when distinguishing between a diseased population and healthy controls. In addition, the scoring system used in ADHD-200 placed a higher priority on classifying TD children than ADHD, which meant that the best ”classifier” might not have the greatest overall classification accuracy. 2.) The ADHD-200 competition used a hold-out dataset which was entirely independent and separate from the testing set. Although in most publications 10-fold cross-validation is used to separate the training and testing sets of data, these usually are not kept in a “lock-box during the model selection procedure. Models can still be trained, features can be selected, and parameters can be optimized across the cross-validation error, leading to the testing set being biased [31]. This means that a true, lock-box validation set is likely to produce lower classification accuracy than a hold-out set from a cross-validation set that likely has played a role in the model selection and training. 3.) The ADHD-200 dataset was likely much more difficult to classify upon because of the heterogeneity and large sample size. For example, there were 8 sites used for the classification training and testing, each with different scanners used to acquire the data. In addition, two sites contributed only healthy controls and one site did not submit any training data (Brown), which undoubtedly a ected the way the algorithms treated Site during classification.

While the task of optimal feature subset selection is difficult for any dataset, it becomes even more complex when classification is performed on multimodal data, where the features themselves are represented in different subspaces and may vary in number over many orders of magnitude. In particular, it is highly likely that a better selection of features could lead to improved methods for isolating and excluding noise, which could have improved the overall predictive capability of classifiers that used neuroimaging features in addition to demographic data.

1.4. Generative vs. Discriminative Methods

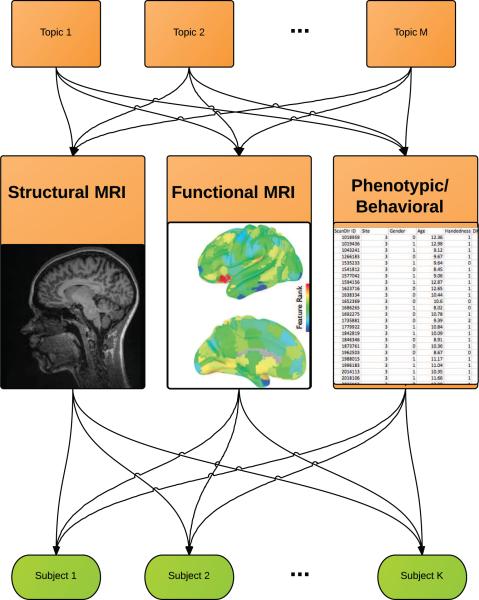
As opposed to supervised classification algorithms where features are used to discriminate between certain states (ADHD vs. healthy controls) and redundant features are e ectively eliminated, generative models of multimodal data map features to each other even when they are unrelated to the diagnosis. These groupings are the latent dimensions onto which a subset of the multi-modal features all map. This is shown in Figure 1. This is similar to saying that the observed features from all modalities are all created by common set of latent topics, where each topic is a subset of features from across modalities. In comparison, discriminative algorithms identify and combine the strongest information sources to predict a single outcome. Because their primary objective is to map features to a diagnosis, they are mute on the relationship of features to each other when the features themselves are unrelated to the disease.

Figure 1.

Topic Modeling of Multimodal Features in ADHD: a conceptual illustration. The structural MRI, functional MRI, and phenotypic observations are all generated by latent topics, which in turn generate each subject's multimodal dataset. By learning the topics, we get a mapping across multimodal features and a generative model behind the observed data. The data matrix V has n feature rows and m observation columns. If V contained a collection of multimodal features (total features by patients), then NMF would decompose the data into a set of “basis images” and encodings, such that $V_{i\mu }\approx {\left(WH\right)}_{i\mu }={\sum }_{k=1}^K{W}_{ik}{H}_{k\mu }$ where the W matrix contains the basis set of multimodal features (topics) and is of dimension n × k, and the “encoding matrix” H is of dimensions k × m, for row i and column μ.

Using the ADHD-200 competition dataset, we present our results from un-supervised topic-modeling and discuss how they relate to previously-published supervised classification models. Although this application uses a generative model, we validate this construct by using latent features within a discriminative model to predict ADHD. If these topics were merely random subjective constructs, using them to summarize the raw multimodal observations would prove futile to “diagnose” ADHD. If, however, they were meaningful constructs, then patients’ latent feature scores would be a sparse summary of all observed multimodal features, which could then be used for classification. This would be analogous to the feature selection or dimension reductions step undertaken in most machine learning models.

2. Methods

2.1. Subject Demographic Profiles

We limited this study to the original training dataset, to allow direct comparison to the published studies. This left 7 total Sites. We use 748 subjects, of whom 472 had been diagnosed as healthy controls. The subjects ranged in age from 7.1 years of age to 21.8 years, with a mean age of 12.4 years. The full demographic summary tables within Site are shown in Table 1. The diagnosis rate of ADHD varied across the 7 sites, of which 2 had only healthy controls. The diagnostic subtypes for ADHD and the medication status for the patients are shown in Table 2. The IQ information within each site is shown in Table 3. The ADHD information is shown in Table 4. Finally, we break down the demographic and behavioral information within diagnosis in Tables 6 and 7, which are listed supplementally in the Appendix.

Table 1.

Summary Statistics by Site

Site	Site ID	N	ADHD (%)	RightHanded (%)	Male (%)	Age (SD)
Kennedy Krieger Institute	Site 3	83	0.27	0.9	0.55	10.24 (1.35)
NeuroImage Sample	Site 4	48	0.52	0.88	0.65	16.99 (2.74)
New York University Child Study Center	Site 5	216	0.55	0.99	0.65	11.67 (2.92)
Oregon Health & Science University	Site 6	79	0.47	1	0.54	8.84 (1.12)
Beijing University	Site 1	194	0.4	0.98	0.74	11.98 (1.86)
University of Pittsburgh	Site 7	89	-	0.96	0.52	15.11 (2.9)
Washington University in St. Louis	Site 8	50	-	1	0.54	11.33 (3.57)

Table 2.

ADHD Statistics by Site

	Typically Developing	ADHD Combined	ADHD Hyperactive	ADHD Inattentive	% Medicated Patients
Kennedy Krieger Institute	0.73	0.19	0.01	0.06	0.27
NeuroImage Sample	0.48	0.38	0.12	0.02	-
New York University Child Study Center	0.45	0.34	0.01	0.20	0.47
Oregon Health & Science University	0.53	0.29	0.03	0.15	0.29
Beijing University	0.60	0.15	-	0.25	0.33
University of Pittsburgh	1.00	-	-	-	-
Washington University in St. Louis	1.00	-	-	-	-

Table 3.

IQ Information within Site

	Instrument	Verbal (SD)	Performance (SD)	Full2 (SD)	Full4 (SD)
Kennedy Krieger Institute	WISC-IV	112.76 (14.52)	108.54 (11.99)	-	109.89 (11.96)
NeuroImage Sample	-	-	-	-	-
New York University Child Study Center	WASI	108.57 (15.96)	105.44 (14.64)	-	108.30 (14.36)
Oregon Health & Science University	WASI	-	-	-	113.76 (14.02)
Beijing University	WISCC-R	116.03 (15.12)	106.66 (15.69)	-	113.02 (14.66)
University of Pittsburgh	WASI	108.68 (10.89)	112.47 (11.30)	111.83 (9.68)	109.81 (11.53)
Washington University in St. Louis	WASI-2 subtest	-	-	-	115.86 (14.30)

Table 4.

ADHD Information within Site

	Instrument	ADHD (SD)	Inattentive (SD)	Hyper Impulsive (SD)
Kennedy Krieger Institute	CPRS-LV	52.99 (14.17)	53.30 (14.24)	53.79 (13.52)
NeuroImage Sample	-	-	-	-
New York University Child Study Center	CPRS-LV	59.29 (5.49)	59.02 (14.79)	58.16 (14.45)
Oregon Health & Science University	CRS-3E	-	59.14 (14.76)	57.38 (15.87)
Beijing University	ADHD-RS	37.60 (13.46)	20.52 (7.46)	17.08 (6.89)
University of Pittsburgh	-	-	-	-
Washington University in St. Louis	-	-	-	-

Table 6.

Summary Statistics by Site for Typically Developing Children

Site	N	RH (%)	Male (%)	Age (SD)
Kennedy Krieger Institute	61	0.9	0.56	10.25 (1.27)
NeuroImage Sample	23	0.91	0.48	17.33 (2.57)
New York University Child Study Center	98	0.98	0.47	12.22 (3.12)
Oregon Health & Science University	42	1	0.4	8.9 (1.2)
Beijing University	116	0.99	0.61	11.71 (1.74)
University of Pittsburgh	89	0.96	0.52	15.11 (2.9)
Washington University in St. Louis	50	1	0.54	11.33 (3.57)

Table 7.

IQ Information within Site for Typically Developing Children

	Instrument	Verbal (SD)	Performance (SD)	Full2 (SD)	Full4 (SD)
Kennedy Krieger Institute	WISC-IV	114.02 (13.21)	108.03 (12.64)	-	110.55 (11.22)
NeuroImage Sample	-	-	-	-	-
New York University Child Study Center	WASI	111.61 (13.61)	107.22 (15.01)	-	110.62 (14.34)
Oregon Health & Science University	WASI	-	-	-	118.40 (12.55)
Beijing University	WISCC-R	119.74 (13.33)	112.40 (14.21)	-	118.18 (13.34)
University of Pittsburgh	WASI	108.68 (10.89)	112.47 (11.30)	111.83 (9.68)	109.81 (11.53)
Washington University in St. Louis	WASI-2 subtest	-	-	-	115.86 (14.30)

2.2. Features

We used fMRI data that was preprocessed and made publicly available by the Neurobureau using tools from FSL (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/) and AFNI (http://afni.nimh.nih.gov/afni). The full details of the preprocessing pipleline are available at http://www.nitrc.org/plugins/mwiki/index.php/neurobureau:AthenaPipeline. Briefly, fMRI data were slice time corrected (AFNI 3dTshift), motion corrected (AFNI 3dvolreg), registered to MNI-152 space with 4mm³ resolution (FSL FLIRT), denoised to statistically control for nuisance signals from the ventricles and white matter (AFNI 3dDeconvolve), and bandpass temporal filtered between .008-.09Hz (AFNI 3dFourier). For the functional data, we used the 12-dimensional motion parameters, the number of independent components intrinsically estimated for each subject by FSL Melodic, and a measure of functional connectivity based upon pairwise regional time-series correlation of 90 regions of interest defined by Grecius and colleagues [56]. We derived 90x90 functional connectivity matrices and analyzed them with the Brain Connectivity Toolbox (https://sites.google.com/site/bctnet/), calculating four graph theory properties for each node: positive/negative strength and the positive/negative participation coefficient [54].

For the structural analysis Freesurfer [21] was used to parcellate and segment each subject's T1 MP-RAGE anatomical scan into 68 cortical regions (34 per hemisphere, based on the Desikan-Killiany atlas) and 40 subcortical regions. For each of the cortical regions, the curvature index, folding index, Gaussian curvature, gray matter volume, mean curvature, surface area, thickness average, and thickness standard deviation were used to describe the behavior and form of each region. For each of the subcortical regions, we characterized the volume, normalized mean intensity, and the normalized standard deviation of the intensity.

The phenotypic data contained: the diagnosis (TD, ADHD-Combined, ADHDHyperactive/ Impulsive, ADHD-Impulsive), handedness (left /right/ ambidextrous), gender, IQ scores and Instrument used to assess intelligence, ADHD Behavioral measures and the instrument, and the patients’ medication status. All categorical observations were coded as factors. For example, each site variable was coded as a binary variable where ‘1’ indicated a member of that site, and ‘0’ otherwise. Subjects with more than 12 missing structural measurements were excluded from the analysis. We variance-normalized all variables and removed those variables with excessive missing values. All remaining missing values were imputed using median imputation. This left 730 total patients with 1068 total features, detailed in Table 5.

Table 5.

Multimodal Features Description

Modality	n	Description
Phenotypic	26	Demographic, Diagnostic, medication status.
Independent Components	1	Number of independent components found within subject
Motion	12	12-dimensional motion parameters from functional scans
Structural	667	Freesurfer cortical and subcortical measurements
Functional	362	Functional connectivity matrices based upon Grecius atlas

2.3. Non-Negative Matrix Factorization

We applied the Non-Negative Matrix Factorization [34] (NMF) algorithm to this dataset instead of more commonly used methods such as ICA, because the NMF constraints yield qualitatively different, and arguably more meaningful, dimensions of the data. As its name suggests, NMF requires all values in the decomposition to be exclusively positive. This is similar to imposing a sparsity constraint on both the encodings and basis “images”; because the superposition of basis images must be linear, and because no values are allowed to be negative, many values are shrunk towards zero. This sparsity offers an additional interpretative benefit since, as there are no “negative” loadings. For categorical features where someone is either female or not (but not negatively female), this positive encoding offers a more intuitive explanation of the underlying structure being evaluated.

Furthermore, ICA is usually applied as a within-modality means of dimension reduction. For example, ICA is frequently applied either across a group of fMRI scans or within a single scan to extract plausible networks, which themselves form a within-modality basis set. These networks can be used to obtain estimates of functional connectivity. Instead of applying NMF within modality, we are applying it across modality where we provide normalized features and let the algorithm nominate a multimodal basis set.

The data matrix V has n feature rows and m observation columns. If V contained a collection of multimodal features (total features by patients), then NMF would decompose the data into a set of “basis images” and encodings, such that

$$V_{i\mu }\approx {\left(WH\right)}_{i\mu }=\sum _{k=1}^K{W}_{ik}{H}_{k\mu }$$

where the W matrix contains the basis set of multimodal features and is of dimension n × K, and the “encoding matrix” H is of dimensions K × m, for row i and column μ.

The topics are the individual basis images, which have been thresholded to remove those features with weightings ≈ 0. Because NMF indirectly encourages sparsity by its positive constraints, roughly 75% of all weights within the basis images are nearly null. This allows a clear distinction between multimodal features that contribute to a topic and features that drop out.

2.4. Implementation

We implemented NMF using the statistical programming environment R [51] using the package NMFN [38], and by a separate implementation within Matlab [36]. Because our goal was to maximize the sparsity of the latent features, we compared four different NMF algorithms and ultimately selected the algorithm providing the sparsest basis set. This was equivalent to selecting the NMF algorithm that produced the maximal amount of null (zero) values in the basis set. We compared the decompositions of four different NMF algorithms: NMF can be formulated as a minimization problem with linear constraints, which can be solved by alternating least squares (ALS), multinomial, multiplicative-update. These represent different functions measuring the distance between V and WH. We additionally implemented the projected-gradient to solve the alternating non-negative least squares problems to obtain NMF; this has faster convergence and stronger optimization properties than the multiplicative update approach. We implemented NMF by projected gradient using the Matlab code in [36].

We selected our final algorithm based upon the sparsity of the encodings within the 20 estimated basis images. This is similar to making the assumption that only a subset of the entire set of multimodal features will be related to each other: by looking at each basis vector, we can effectively zero-out the features with weights that are close to zero, and interpret the rest as contributing to a given topic. This is shown in Figure 2. Based upon this, without knowledge of the actual features, we selected the ALS results for further analysis. We thresholded basis images, where each “dimension” corresponded to a multimodal feature, at the 25^th percentile. This threshold was selected to eliminate all null-weight features of the W matrix, and left roughly 263 features (n) per topic k ∈ K.

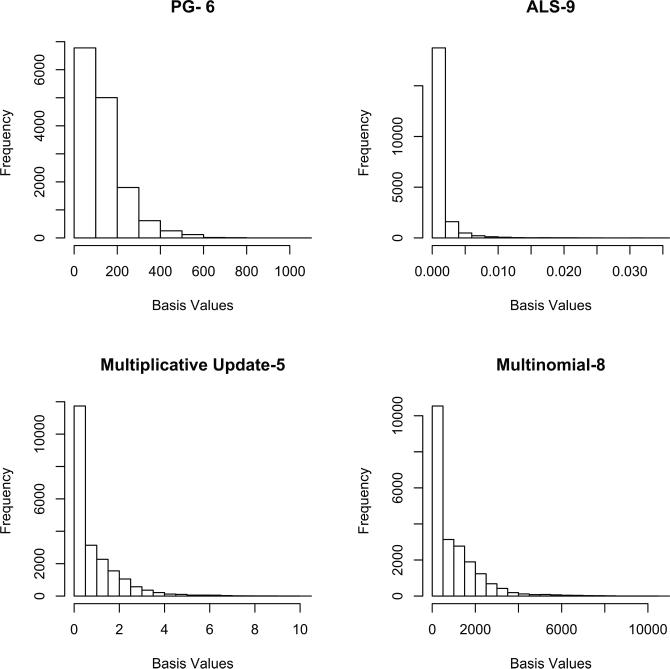
Figure 2.

Basis Values resulting from NMF factorization of Feature Matrix using four different NMF algorithms: PG (Projected Gradiant), ALS (Alternating Least Squares), Multiplicative Update, and Multinomial Estimation. The number represents the total number of encoding dimensions which were different (statistically significant) between ADHD and TD, based upon a 2-sample t-test. There were 20 total dimensions extracted using NMF.

We additionally tested how each algorithms’ encoding matrix differed between ADHD and TD patients using a 2-sample t-test on the associated encoding variable for each topic. This is answering the question of whether any topics were more likely to be expressed in the patients than the controls, and vise versa. This also was done to assess whether a sparse feature set was truly a more efficient representation of the disease. All algorithms gave encoding values with more than chance difference between patients and controls, but the selected ALS algorithm, which was the sparsest, also had the maximal differentiation between ADHD and TD patients with 9 of the Topics showing statistically significant (uncorrected) encoding levels between groups.

2.5. Validation using Machine Learning

We next validated the latent features by rerunning NMF on a dataset that had been stripped of all diagnostic information and ADHD scale scores, leaving behind only the functional, structural, demographic, and IQ testing information. We set the number of topics to 20 according to [57], although this is a parameter which could be investigated in future work. After running NMF with 20 dimensions, we extracted the encoding matrix, H, of dimension (20 × 730), or number of basis values by subjects. Each of the 20 values per subject represent the subject's score within that latent dimension. These were used as features to predict diagnosis (ADHD vs. TD).

Using leave-one-out cross-validation, we used Weka [28] to train a C4.5 decision tree using data from all but one patient to diagnose the left-out patient [50]. The identity of the validation patient was then permuted so that each patient was the validation patient once and only once. At each node, the tree was trained to split the training data into two daughter populations based on a threshold value for one of the 20 encoding bases vectors, such that the Kullbeck-Leibler divergence, or information gain, between the two daughter populations was maximized. The tree was pruned such that this information gain and number of training instances per daughter population was greater than 0.25 and 2, respectively. Due to the fact that only one of 730 patients was left out in each of the 730 trees trained on each training set, we expect this to closely resemble the actual decision tree used for each validation case.

The topics learned from the data not containing diagnostic information are subtly different than those learned on the full dataset. To illustrate the learned decision tree with respect to the topics discussed in this paper, we create a mapping from the “unbiased” features (learned without diagnostic information), to the biased features (learned with biased information) using the correlation of the basis vectors. This is shown in Figure 7. Between the “biased” dataset and the “unbiased” dataset, the mapping across topics learned was fairly consistent with a correlation of roughly 90% between pairs of Topics from each dataset's NMF. This was established by using the encoding matrix, and identifying topics from the different analyses which had highly correlated encoding values across patients. This shows a consistency of the NMF algorithm itself, where Topics across slightly changed datasets can be matched up.

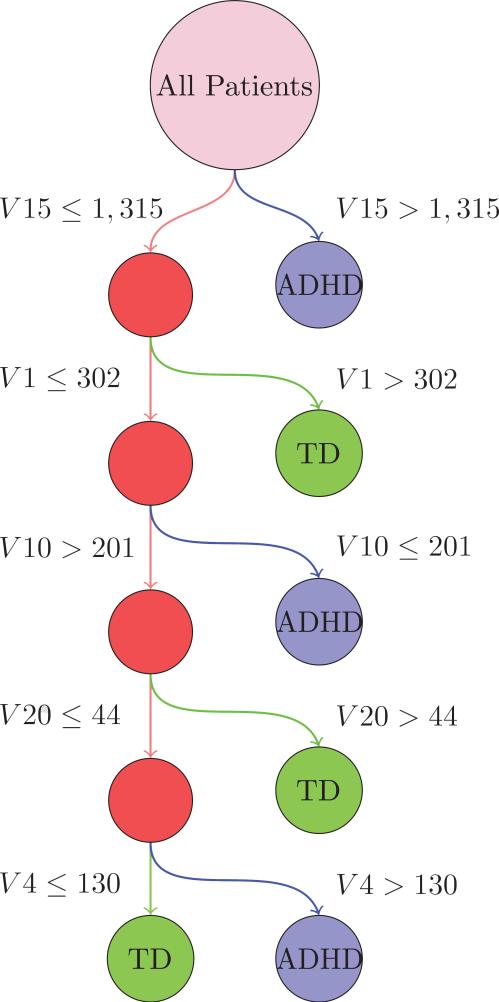
Figure 7.

Decision tree for discriminating between ADHD patients and healthy controls. The primary tree split (Topic 15) contained a marker for the Site Pittsburg, which contained only healthy controls. The second split, Topic 1, contained IQ phenotypic variables. The third split, Topic 10, contained many motion parameters.

3. Results

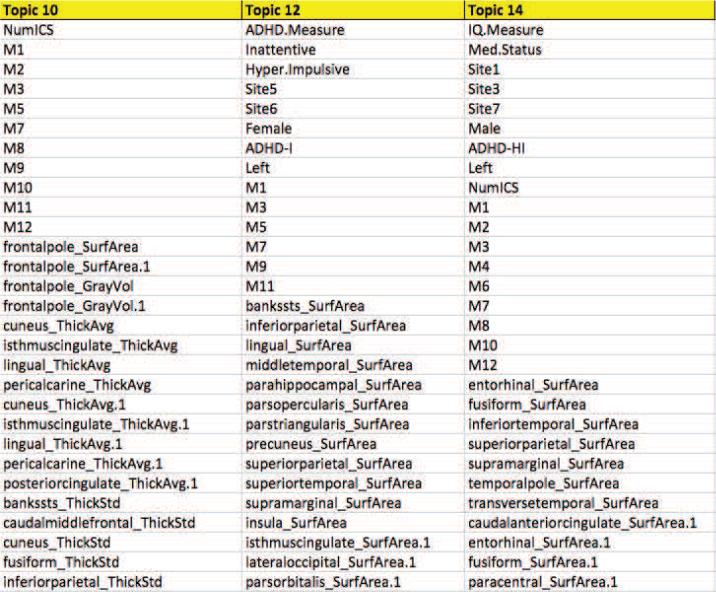
Among the 20 topics, 9 had statistically significant differences between ADHD and TD patients within the encoding values (uncorrected p-values) as shown in Figure 2. This significance was established across all Sites, even though some topics were site-specific; many topics contained “Site Y” variables indicating that being a member of that site was associated with that particular topic. If we had performed testing only within the sites identified within the topics, we likely would have seen more significant tests but, as this was not the primary objective of the paper, we didn't pursue this testing further. We use this Site-wide significance level to help us identify topics that may be associated uniquely with the disease, but also interpret non-significant topics as well. The full list of topics is available at http://ariana82.bol.ucla.edu/downloads-2/files/ALSNMFTopics.xlsx as well as a supplement to this article, showing the decomposition with NMF using ALS. We show 3 partial topics in Figure 3.

Figure 3.

Sample of features selected within topics 10, 12 and 14 . For each topic, there were 236 features selected. All 20 topics, each containing 236 features, are available at http://ariana82.bol.ucla.edu/downloads-2/files/ALSNMFTopics.xlsx for download.

3.1. Topic Distributions

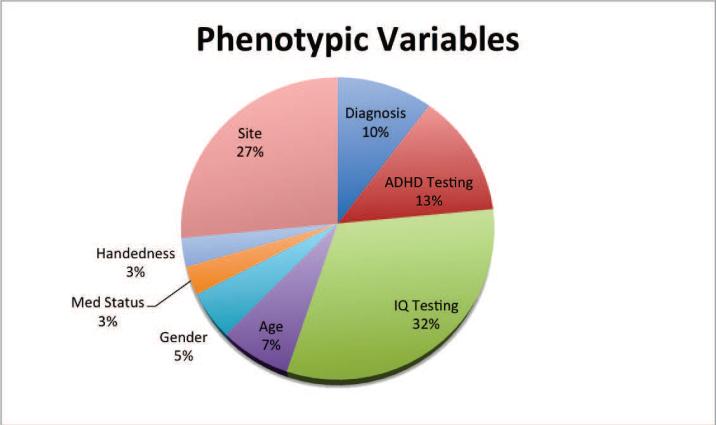
The most frequently selected phenotypic variables across topic was IQ (32%) followed by Site (27%), as shown in Figure 4. This was followed by diagnostic information, with 10% of the phenotypic variables selected being diagnosis related (TD, ADHD-HI, ADHD-I) as well as ADHD testing-related (13%).

Figure 4.

Phenotypic features selected by topics, across 20 topics. The most common phenotypic variables nominated across topics were IQ-related, describing either the IQ scores on a given test or the IQ test given.

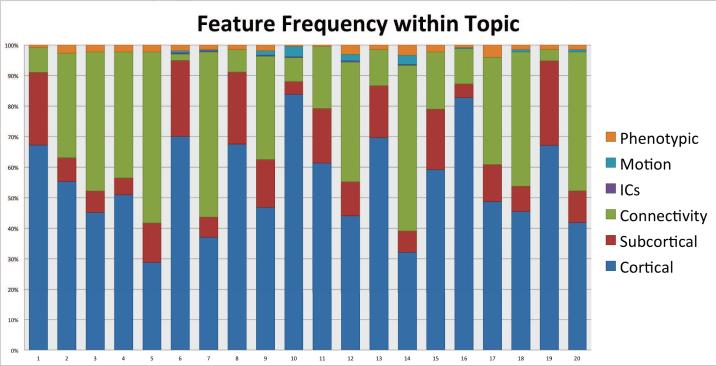
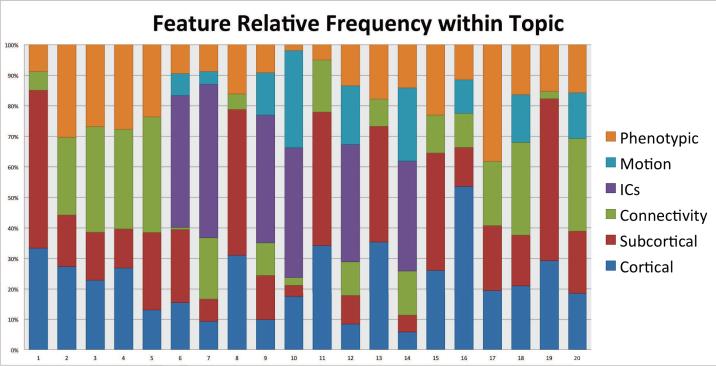
The most commonly selected features were cortical structural information as shown in Figure 5, but this may have been because the largest feature set was cortical; the total number of features in each modality were: Cortical (545), Sub-cortical (124), Connectivity (363), Number of Independent Components (ICs) (1), Motion (12), and Phenotypic (23). When we normalized by the number of features in each modality, we were able to identity more striking patterns in the distributions where phenotypic observations, motion parameters, ICs and subcortical measurements were over-represented in their selection for topics, as shown in Figure 6.

Figure 5.

Total feature modality selected within topic. Cortical features were more likely to be present in the topics than others, due to them having a greater representation in the original dataset.

Figure 6.

Relative feature modality selected within topic, relative to the total number of features within that modality. After correcting for features which were over-represented in the dataset, we see that phenotypic observations, motion parameters, ICs, and subcortical were selected heavily within topics.

3.2. Interpreting Topics in the DMN Context

In the context of the current work, we found a number of structural, functional connectivity, and graph theoretic metrics occurring with ADHD test score that are consistent with the DMN in Topic 12. Morphologic metrics related to the rostral ACC, for example, clustered with ADHD index score and ADHDI, perhaps related to decreased anticorrelation between posterior DMN nodes and rostral ACC that has been noted in both ADHD adults ([7]) and children ([61]). ADHD score also clustered with changes in caudate and putamen volume. Recent meta-analyses of structural differences have reported decreased volume in basal ganglia regions including the caudate, putamen, and globus pallidus [17], possibly related to observations that ADHD subjects have altered levels of dopamine (DA) transporter densities in striatal regions [43].

3.3. Motion: Topics 10 and 14

Topics 10 and 14 contained 10/12 and 9/12 possible motion parameters. These topics also identified a larger number of cortical than subcortical features identified, indicating that cortical measurements may be more susceptible to motion than subcortical. Topic 10 was statistically different between patients and controls, and did not have any Site markers. The encoding values for each topic indicate how strongly that topic is implicated in that subject; the ADHD patients had higher encoding values than the TD patients, indicating that ADHD patients were more likely to contain motion-related features from this topic (p-value = 1.0 e-04). Topic 14 was not significant between patient groups, yet included the Site variables 1,3, and 7, indicating that this was a unique pattern found in those locations. For both of these features, the number of ICs from the fMRI analysis was a selected feature.

3.4. Validation

The cross-validation accuracy using our C4.5 decision tree was 66.8% (63.4-70.2%) with a specificity of 50.6% (44.6-56.6%) and sensitivity of 76.2% (72.3-80.1%). All intervals reflect 95% confidence intervals and were compared to a naïve classifier that classifies everything as the most common class (TD).

4. Discussion

4.1. Default Mode Network in ADHD

Topic 12 was statistically different between TD and ADHD and clustered with the ADHD-I diagnosis. A number of structural metrics related to DMN nodes were present in the topic including posterior cingulate, precuneus, and parahippocampal regions. Increasing evidence and meta-analysis suggests that the DMN actually consists of a series of subnetworks that communicate and coactivate through overlapping nodes [33]. For example, the medial temporal lobe is thought to provide episodic memory associations that are used while generating self-referential thought patterns. Although the exact number of subsystems is still debated, the pCC and precuneus are thought to be key DMN integration nodes. This clustering is interesting given that an overall decreased network homogeneity, particularly with respect to precuneus functional connectivity, has been reported in resting state data from ADHD children [66].

Nearly half the features in this topic were related to graph theoretic metrics. Negative strength in the dorsal DMN nodes including pCC and medial PFC and negative strength (number of connections) related to the precuneus network clustered with ADHD-I. Despite the low strength related to the precuneus network, a high participation coefficient also clustered in Topic 12 with ADHD-I. While this may be some form of compensation mechanism, the reason for this remains unclear. Positive strength in ventral DMN nodes, including the retrosplenial cortex and medial temporal lobe were also part of this cluster. In interpreting this topic, it appears as though ventral DMN subnetworks may have more connections in ADHD-I, while dorsal DMN may have less. Overall, this may be related to the fact that the latency of recovery of the DMN appears different across the DMN subnetworks [67]. Fair et al. (2010) also applied graph measures to DMN data in ADHD adolescents and found that DMN was a more strongly connected network in TD patients, though these results were below the threshold of significance [19].

4.2. Motion Topics

The identification of motion artifacts and the presence of higher motion topics in ADHD was an expected finding given the known relationship between ADHD and motion. In a study using infrared motion analysis, boys with ADHD were found to have 2.3 times greater head motion than healthy boys [63]. Motion is a known contaminant in fMRI and MRI [23], and many methods exist to mitigate this artifact [47]. Motion correction algorithms in fMRI may, however, induce artifacts of their own when high levels of motion aren't present [22]. This could be problematic in studies where one patient group is expected to move more than others. Uncorrected data would naturally have higher levels of noise in the ADHD group, while motion-corrected data may have artifacts introduced in the TD group. The motion topics also contain both contain as a feature the NumberofICs. This is consistent with the finding that ICA can frequently identify and nominate motion artifacts, and has been used as a method of motion artifact correction [13]. Finally, the high presence of motion artifacts in two topics echoes the earlier findings of [18] who found that motion parameters were quite powerful for classification of ADHD in their winning algorithm.

4.3. Machine learning validation

Using latent features as variables for classification proved to be a valid means of dimension-reduction prior to classification. The observed cross-validation accuracy within this (training) dataset is comparable to the testing accuracy in the ADHD-200 competition using individual neuroimaging features, but is still less than the accuracy of classifiers that used only the demographic information. Our objective in identifying topics was to map multimodal features to each other; their ability to map observational data to a diagnosis is a fringe benefit, and indicates the flexibility of generative models.

The tree split first on Topic 15, which was also the Topic with the most different p-values between ADHD and TD (p < 4e − 16). This Topic contained the variable Site 7, which contained only TD patients. It also contained several IQ measures. The second split, Topic 1, contained only IQ-related phenotypic features, and was significant between patients and controls (p < 2.5e − 07). The third topic, Topic 10, contained many motion parameters and was statistically different between patients and controls.

5. Conclusion

We see several factors which may have contributed to the dismal classification accuracy of this ADHD-200 dataset relative to other studies. For this dataset, the demographics within each subpopulation were different, with OHSU females having substantially higher IQs than the rest of the population. Because many prior studies were on small samples with a median of 39 participants obtained from a single site, the samples were likely homogenous and thus easier to discriminate amongst. The classification accuracy accuracy was maximized when training each model within site, and that even pooling the data and adjusting for Site did not outperform training within each Site alone.

Pittsburg/Site 7, and Washington University/Site 8, contributed only normal controls. Site 8 loaded on Topics 3 and 18; for neither of these topics did the model distinguish between ADHD and control subjects. Interestingly, Site 4 (NeuroImage) is implicated in these same topics and Site 5 (NYU) in Topic 3 and Site 6 (OHSU) in Topic 18. Site 4 ( NeuroImage) subjects were substantially older than the subjects in other sites as the mean age was almost 17 years. Sites 5 and 6 had the highest proportion of Inattentive subtype patients. As people with ADHD age, hyperactive symptoms become more internalized and inattention becomes the more dominant expression of the disorder. Note that of all topics where the Inattentive subtype was included, Topics 5, 7, 12, and 17, Site 6 was also included. As Topic 12 distinguished between ADHD and control subjects and included loadings for the Inattention scale and Site 5 and Site 6, this topic might be of special interest in characterizing subjects with primarily inattentive subtype of ADHD. According to Cortese [11], patterns of FMRI activation di er between adults and children. Therefore, it may be advantageous to repeat the analysis in future work with this dataset only among younger participants who are not of inattentive subtype.

This frequent nomination of Site within NMF-derived topics raises important questions about diagnostic homogeneity and the possibility that either ADHD is not a distinct diagnosisf. There may be different diagnostic practices within each site. For example, in the Beijing site, females with low IQs were exclusively diagnosed with ADHD. This may indicate a subjectivity in the diagnosis, where two identically matched people may receive a different diagnosis depending on where they are evaluated.

There are certain limitations to this work; we set the number of topics based on previous imaging work [57], but did not investigate this parameter. We selected our NMF algorithm based upon our hypothesis that sparsity in the basis set would improve classification accuracy. Although we demonstrated that sparsity did coincide with the ability to separate patients and controls in a t-test, a set of thorough machine learning models was never constructed to validate this hypothesis. Although we had information on who was being medicated for most Sites, there was no information on dosages, specific medications, and compliance. This necessarily implies that topics on an unmedicated group, or on a homogeneously medicated group, could be quite different, as it is impossible to disentangle the disease from the medication status. Finally, our hypothesis of sparsity producing better topics was never fully tested, but could be in future work by seeing how the sparsity of topics a ected the classification accuracy of ADHD. Future research is needed in more homogeneous samples with respect to medication status, disease, behavioral measures as well as with more extensive behavioral and demographic measures to explore the utility of this model in classifying subjects.

This analysis began initially with modeling the features using traditional topic modeling, or Latent Dirichlet Allocation. This model produced null results, where neither Site nor ADHD Diagnosis were identified within any of the topics. We believe this finding to be an artifact of the model used possibly relating to the priors; since LDA learned the entire distribution uniformly even though the data originated from different Sites, it was unable to perceive hierarchical structures where the diagnosis of ADHD was contingent upon Site. Because of this, the model failed to identify site-specific e ects such as diagnosis. It is possible that extensions of LDA such as Author-Topic modeling would be able to correct for the diagnostic and patient inhomogeneity.

We believe that generative models offer a strong alternative to discriminative models in the analysis of multimodal data. Because generative models do not focus exclusively on a single feature or diagnosis, they are able to propose a more complete picture of how the modalities relate to each other. This framework allows an unconstrained mapping across features. Although we have investigated only two models for this dataset (LDA and NMF), both methods proposed plausible latent dimensions with the DMN topics present in both. Because of this, we expect future work on generative models to prove a promising approach for analysis of multimodal data.

Highlights.

We identify latent dimensions (topics) in multimodal ADHD (fMRI, MRI, phenotypic).

We compare four different Non-negative Matrix Factoriation (NMF) algorithms.

The sparsest NMF algorithms discriminates best between ADHD and healthy subjects.

“Site” nominated within “topics” suggests ADHD diagnosis may differ by location.

One topic suggests differential changes in the default-mode subnetwork for ADHD.

Table 8.

ADHD Diagnostic Information within Site for Typically Developing Children

	Instrument	ADHD (SD)	Inattentive (SD)	Hyper Impulsive (SD)
Kennedy Krieger Institute	CPRS-LV	45.19 (4.27)	45.67 (4.95)	46.62 (4.52)
NeuroImage Sample	-	-	-	-
New York University Child Study Center	CPRS-LV	45.28 (6.04)	45.32 (5.87)	46.31 (5.53)
Oregon Health & Science University	CRS-3E	-	47.02 (6.24)	45.93 (6.64)
Beijing University	ADHD-RS	28.15 (5.98)	15.08 (3.66)	13.07 (3.46)
University of Pittsburgh	-	-	-	-
Washington University in St. Louis	-	-		-

Table 9.

Summary Statistics by Site for ADHD Children

Site	N	RH (%)	Male (%)	Age (SD)
Kennedy Krieger Institute	22	0.91	0.55	10.22 (1.56)
NeuroImage Sample	25	0.84	0.8	16.69 (2.91)
New York University Child Study Center	119	0.99	0.79	11.26 (2.67)
Oregon Health & Science University	37	1	0.7	8.77 (1.04)
Beijing University	78	0.97	0.94	12.38 (1.98)
University of Pittsburgh	-	-	-	-
Washington University in St. Louis	-	-	-	-

Table 10.

IQ Information within Site for ADHD Children

	Instrument	Verbal (SD)	Performance (SD)	Full2 (SD)	Full4 (SD)
Kennedy Krieger Institute	WISC-IV	109.32 (17.48)	109.91 (10.16)	-	108.09 (13.90)
NeuroImage Sample	-	-	-	-	-
New York University Child Study Center	WASI	107.12 (14.30)	103.99 (14.31)	-	106.48 (14.18)
Oregon Health & Science University	WASI	-	-	-	108.49 (13.88)
Beijing University	WISCC-R	110.56 (16.01)	98.21 (13.90)	-	105.40 (13.17)
University of Pittsburgh	-	-	-	-	-
Washington University in St. Louis	-	-	-	-	-

Table 11.

ADHD Diagnostic Information within Site for ADHD Children

	Instrument	ADHD (SD)	Inattentive (SD)	Hyper Impulsive (SD)
Kennedy Krieger Institute	CPRS-LV	73.55 (9.78)	73.41 (10.56)	72.68 (10.77)
NeuroImage Sample	-	-	-	-
New York University Child Study Center	CPRS-LV	71.25 (8.69)	70.41 (9.17)	68.02 (11.89)
Oregon Health & Science University	CRS-3E	-	72.89 (7.86)	70.38 (12.99)
Beijing University	ADHD-RS	51.04 (8.92)	28.27 (3.64)	22.77 (6.54)
University of Pittsburgh	-	-	-	-
Washington University in St. Louis	-	-	-	-