Effects of Overlapping Generations on Linkage Disequilibrium Estimates of Effective Population Size

Abstract

Use of single-sample genetic methods to estimate effective population size has skyrocketed in recent years. Although the underlying models assume discrete generations, they are widely applied to age-structured species. We simulated genetic data for 21 iteroparous animal and plant species to evaluate two untested hypotheses regarding performance of the single-sample method based on linkage disequilibrium (LD): (1) estimates based on single-cohort samples reflect the effective number of breeders in one reproductive cycle (N_b), and (2) mixed-age samples reflect the effective size per generation (N_e). We calculated true N_e and N_b, using the model species’ vital rates, and verified these with individual-based simulations. We show that single-cohort samples should be equally influenced by N_b and N_e and confirm this with simulated results: ${\widehat{N}}_{\text{b}}$ was a linear (r² = 0.98) function of the harmonic mean of N_e and N_b. We provide a quantitative bias correction for raw ${\widehat{N}}_{\text{b}}$ based on the ratio N_b/N_e, which can be estimated from two or three simple life history traits. Bias-adjusted estimates were within 5% of true N_b for all 21 study species and proved robust when challenged with new data. Mixed-age adult samples produced downwardly biased estimates in all species, which we attribute to a two-locus Wahlund effect (mixture LD) caused by combining parents from different cohorts in a single sample. Results from this study will facilitate interpretation of rapidly accumulating genetic estimates in terms of both N_e (which influences long-term evolutionary processes) and N_b (which is more important for understanding eco-evolutionary dynamics and mating systems).

THE recent explosion of population genetic information for nonmodel species has been driven by the confluence of several developments: nonlethal methods for sampling DNA in natural populations, rapid increases in availability of a large number of molecular markers, increases in computational power, and more sophisticated data analysis software (Beaumont and Rannala 2004; Excoffier and Heckel 2006; Allendorf et al. 2010). One result of this information explosion has been a surge in the use of genetic methods to estimate effective population size (Wang 2005; Leberg 2005; Luikart et al. 2010), fueled largely by a 10-fold increase over the last 3–5 years in estimates based on single-sample methods [as opposed to the two-sample temporal method] (Palstra and Fraser 2012). Effective population size is the evolutionary analog of census size (N). Whereas N governs ecological processes such as competition, predation, and population growth rate, evolutionary processes (including the rates of genetic drift and loss of genetic variability and the effectiveness of selection and gene flow) depend primarily on the effective size of the population, which is generally lower than the census size because of disparities among individuals in their genetic contribution to the next generation (Frankham 1995).

Although most genetic methods for estimating effective size use models that assume discrete generations, they are widely applied to iteroparous species with overlapping generations. For such species, two related quantities are of interest: effective size per generation (N_e) and the effective number of breeders in one reproductive cycle (N_b). N_e is more important in shaping long-term evolutionary processes, and almost all population genetic theory is based on the concept of N_e per generation (Crow and Kimura 1970; Charlesworth 2009). However, many eco-evolutionary processes in age-structured species (such as sexual selection) play out in a theater defined by seasonal bouts of reproduction, for which N_b is a more relevant parameter than N_e (see Waples and Antao 2014). Furthermore, N_b is easier to estimate and monitor for long-lived species, because it requires data only for one breeding season rather than the species’ entire life span (Schwartz et al. 2007). A few of the many recent articles that use genetic methods to estimate N_b in natural populations include Côté et al. (2013), Duong et al. (2013), and Whiteley et al. (2014). The relationship between N_b and N_e for semelparous, age-structured species (e.g., Pacific salmon and monocarpic plants) was worked out by Nunney (2002), Vitalis et al. (2004), and Waples (2002, 2006), but those analyses did not consider effects of iteroparity.

As a result of these developments, researchers faced with the task of trying to interpret the rapidly accumulating body of estimates of effective size in iteroparous species have faced two major difficulties: (1) How does one know whether a particular genetic estimate is more applicable to N_e or to N_b—or is not a reasonable proxy for either one? (2) What is the relationship between N_e and N_b in iteroparous species? A recent study (Waples et al. 2013) that calculated both N_e and N_b from published demographic data for 63 species of animals and plants provides new insights into the second question. The ratio N_b/N_e varied a surprising sixfold across species and, unexpectedly, N_b per season was larger than N_e per generation in over half the species. However, up to two-thirds of the variance in N_b/N_e was explained by just two life history traits (age at maturity and adult life span). Factors that produce high N_b/N_e ratios include early maturity combined with a long life span, constant fecundity with age, and Poisson variance in reproductive success of same-age, same-sex (SASS) individuals; factors that produce low N_b/N_e ratios include delayed maturity combined with a short adult life span, large variations in fecundity with age, and overdispersed variance of SASS individuals (Waples et al. 2013). These results suggest that, for the first time, it should be possible to translate estimates of N_b in iterporarous species into estimates of N_e per generation, as long as one can estimate some basic life history traits for the target species. That study, however, was based entirely on the species’ vital rates and did not consider population genetics data.

Here we tackle the first major information gap identified above: What biases associated with age structure are involved in estimating N_e or N_b from genetic data for iteroparous species, and how do the patterns of bias depend on the life history of the target species and the experimental design? Robinson and Moyer (2013) made a start at addressing these issues by simulating age-structured data for three species and applying the single-sample genetic estimator based on linkage disequilibrium (LD) (Hill 1981; Waples and Do 2008). We considerably expand this approach, using simulated data for 21 iteroparous species, selected for taxonomic and life history diversity from the larger set examined by Waples et al. (2013). We used the simulated data to evaluate two published but untested hypotheses regarding performance of the LD method: (1) estimates based on samples from a single cohort primarily reflect N_b (Waples 2005), and (2) mixed-age samples drawn from a number of cohorts equal to a generation length (e.g., 3 cohorts for a sparrow or ∼10 for a grizzly bear) provide a reasonable estimate of N_e (Waples and Do 2010).

We show that the pattern of bias in estimates of effective size (${\widehat{N}}_{\text{e}}$ or ${\widehat{N}}_{\text{b}}$) from the LD method is determined primarily by the actual ratio N_b/N_e for the target species. Because the N_b/N_e ratio can be predicted from simple life history traits (Waples et al. 2013), this provides a generally applicable, quantitative means of adjusting LD estimates of effective size to produce largely unbiased estimates of N_b or N_e in iteroparous species. We also quantify the effects of variation in some important life history features (intermittent breeding by females, constraints on litter size, overdispersed variance in reproductive success, and skewed primary sex ratio) that are not accounted for in most models but are important for many real species.

Methods

Model species

Notation and definitions are provided in Table 1. Our analyses focused on 21 of the 63 species analyzed by Waples et al. (2013), including three plants, three invertebrates, two amphibians, two reptiles, three fish, three birds, and six mammals; see Supporting Information, Table S1. For some analyses we also evaluated a synthetic “species” based on generic vital rates (age-specific survival and fecundity) used in figure 1A of Waples et al. (2011). The vital rates for each model species (which are provided in Appendix S2 in Waples et al. 2013) were used in two major ways: (1) to calculate N_e and N_b using a hybrid Felsenstein–Hill method [AgeNe (Waples et al. 2011)], and (2) to parameterize simulations of age-structured genetic data. We then estimated effective size from the simulated genetic data, using the LD method, and assessed bias by comparing the estimates with the true N_e and N_b. These processes are described in more detail below.

Table 1. Definitions and notation used in this study.

Ne	Effective population size per generation
Nb	Effective number of breeders in one time period
${\widehat{N}}_{\text{b}},{\widehat{N}}_{\text{e}}$	An estimate of Nb or Ne based on genetic data
${\widehat{N}}_{\text{b(Adj)}}$	An estimate of Nb adjusted to account for bias due to age structure
NT	Total number of individuals age 1 and older alive at any given time
NA	Total number of adults (individuals with age ≥α) alive at any given time
N1	Total number of offspring produced per time period that survive to age 1
x	Age (units can be days, weeks, months, or years)
sx	Probability of surviving from age x to age x + 1
lx	Cumulative probability of surviving to age x ($l_x={\displaystyle {\prod }_{i=1}^x{s}_{i-1}},$ with s0 = l1 = 1)
bx	Mean number of offspring in one time period produced by a parent of age x
ω	Maximum age
α	Age at maturity (first age with bx > 0)a
AL	Adult life span = ω – α + 1
Gen	Generation length (mean age of parents of a newborn cohort)
CVf	Coefficient of variation of bx for adult life span (using only ages with bx > 0)b
HMean	Harmonic mean
SASS	Individuals of the same age and sex

^aThis follows the definition used by Waples et al. (2013), who adopted a simple rule to deal with a large number of diverse data sets. When sufficient data are available, a more precise estimate would be age at which 50% are mature or weighted age at first maturity.

^bWhen b_x varied between sexes, CVf was computed over data for both sexes, after standardizing b_x to values that produce a population of constant size.

Analysis of vital rates

AgeNe uses a discrete-time, age-structured, and deterministic model. Individuals of age x produce an average of b_x offspring and then survive to age x + 1 with probability s_x. Both b_x and s_x can differ between males and females. We track only individuals that survive to their first birthday, so fecundities are scaled to result in a stable population that produces a fixed number (N₁) of individuals per cohort that survive to age 1. Given a specified value for N₁ and a life table of vital rates, AgeNe calculates the total population size (N_T), the adult population size (N_A), and numbers in each age class (N_x), as well as N_e and N_b. N_T, N_A, N_e, and N_b all scale linearly with N₁, but ratios of these key variables are independent of N₁.

AgeNe uses a species’ vital rates to calculate mean (${\overline{k}}_{•}$) and variance ($V_k{}_{•}$) of lifetime reproductive success for the N₁ individuals in a cohort. The modeled populations are constant in size, so $E({\overline{k}}_{•})$ = 2, in which case the generational effective size for the population is given by

$$N_{\text{e}}\approx \frac{4N_1\text{Gen}}{V_{k•}+2}$$ (1)

(Hill 1972, equation 16), where Gen = generation length = mean age of parents of a newborn cohort. From the vital rates, AgeNe also calculates the mean and variance ($\overline{k}$ and $V_k$) in the number of offspring produced in one reproductive cycle by all N_A adults in the population. These data are then used to calculate inbreeding N_b for each cycle as (Crow and Denniston 1988; Caballero 1994)

$$N_{\text{b}}=\frac{\overline{k}{N}_{\text{A}}-2}{\overline{k}-1+V_k/\overline{k}}.$$ (2)

The following assumptions of AgeNe follow those of Felsenstein (1971) and Hill (1972): (1) all reproduction occurs at intervals of exactly one time unit (on an individual’s birthday), (2) survival and fecundity are independent of events in previous time periods, and (3) there is no upper bound to the number of offspring an individual can produce in one breeding cycle. In addition, we adopted the following assumptions for what we refer to as the standard model: each newborn had an equal probability of being male or female, and SASS individuals had Poisson variance in reproductive success (so $V_k$ = $\overline{k}$).

We also considered the following variations of the standard model, using subsets of the model species: skewed primary sex ratio, overdispersed variance in reproductive success of SASS individuals, intermittent breeding by females, and small litter/clutch size. The first two variations were evaluated using AgeNe; for intermittent breeding and small litter size, we used results developed by Waples and Antao (2014).

Computer simulations

We used the forward-time, individual-based program simuPOP (Peng and Kimmel 2005; Peng and Amos 2008) to simulate realistic, age-structured genetic data for each of the study species. Each simulation tracked both demographic and genetic processes for 100 time periods, with each period representing one reproductive cycle (measured in days, months, or years, depending on the species; Table S1). Demographics were governed by the same vital rates used in the AgeNe analyses described above.

In time period 0, the age of each of the N_T individuals was drawn randomly from the stable age distribution. Because survival and reproduction were random and independent, total population size, and the number of each sex in each age class, varied randomly around the mean values expected in a stable population. Furthermore, although the primary sex ratio varied randomly around 0.5, the adult sex ratio could differ from this due to sex-specific survival rates and ages at maturity. Each newborn individual “picked” its two parents by drawing one male and one female randomly from the pool of potential parents, with the probability of choosing a parent of age x proportional to b_x for that sex. Thus, all potential parents of the same sex and age had an equal opportunity to be the parent of each newborn, but that was not necessarily true for individuals of different ages or sex. After a burn-in period of 50 cycles (more than enough to allow approximate demographic and genetic equilibrium; Figure S1), we tracked demographic and genetic parameters for another 50 cycles before starting another replicate. Twenty replicates were run for each scenario, which provided 20 × 50 = 1000 time periods for sampling. Multiple temporal samples within each simulation are not entirely independent, but (as shown in Results) overall replication was more than sufficient to produce robust measures of central tendency.

Analysis of simulated data

Beginning in time period 51, we tracked lifetime production of offspring by each of the N₁ newborns in a single cohort, and from these data we calculated lifetime ${\overline{k}}_{•},$ $V_k{}_{•},$ and N_e from Equation 1. We also calculated seasonal $\overline{k},$ $V_k,$ and N_b for each reproductive cycle. Arithmetic means of these means and variances, and harmonic means of N_e and N_b, were calculated across replicates and compared with values predicted by analysis of the vital rates, using AgeNe. Negative and infinite estimates of effective size were converted to 10⁶ (see Waples and Do 2010 for a discussion of how to interpret negative estimates of effective size).

For the genetic analyses, because we are interested in evaluating potential biases related to age structure rather than precision, we used large samples (S = 100 individuals) and a large number (100) of “microsatellite-like” markers, each having 10 possible allelic states. Allele frequencies for each locus in each replicate were separately initialized using a Dirichlet distribution with equal prior for each allele. The simulations covered only relatively few generations, so mutation was ignored. Multilocus genotypes in offspring were generated randomly, assuming simple Mendelian inheritance from the two randomly chosen parents. During the period of sampling, heterozygosities were generally in the range 0.7–0.85, comparable to what is found for microsatellite data in many natural populations. For model validation, we conducted longer runs (50 cycles burn-in + 550 cycles = 600 cycles total) for selected species to track the loss of heterozygosity over time and compare that with the rate expected given the values calculated by AgeNe for N_e and generation length.

Following Waples and Yokota (2007), in each of the 1000 replicate time periods we used three sampling strategies for the genetic data: (a) only newborns (i.e., a single cohort), (b) only adults, and (c) all individuals in the population. We also considered samples from two or three consecutive cohorts. In each case, individuals were sampled randomly without replacement from these targeted groups; for the population and adult samples, this meant that samples were skewed toward younger individuals. For each sample, we used the genetic data to estimate effective size, using the LD method implemented in LDNe (Waples and Do 2008). The LD method is based on the following relationship for unlinked loci, as assumed here (Hill 1981),

$$\begin{array}{c}E\left(r^{2^{\prime }}\right)\mathrm{\approx }\frac{1}{\left(3N_{\text{e}}\right)},\mathrm{so}\\ {\widehat{N}}_{\text{b}}=\frac{1}{\left(3r^{2^{\prime }}\right)},\end{array}$$ (3)

where r^2′ is the squared correlation of alleles at different loci and is an index of the amount of disequilibrium due to drift, after accounting for effects of sampling. We screened out alleles at frequencies <0.05 because Waples and Do (2010) found this minimized bias for samples sizes of ≥50.

Performance of bias adjustments was evaluated by calculating the percent root mean-squared bias (RMSB), which is analogous to the root mean-squared error except that our analysis focuses on bias and does not include a term for precision. We calculated the percent RMSB as $100\overline{)\sqrt{[{\displaystyle \sum {(1-{\widehat{N}}_{\text{b}}/N_{\text{b}})}^2}]/21}},$ where the summation is across all 21 model species, or the equivalent for N_e.

Results

Model validation

We first verified that demographic data generated by simuPOP were consistent with analytical expectations from AgeNe based on each species’ vital rates. As expected for dynamically stable populations, lifetime ${\overline{k}}_{•}$ from the simulations was almost exactly 2.0 in every species. Similarly, mean lifetime $V_k{}_{•},$ N_e per generation, and N_b per cycle calculated from the demographic data were within 1% of the expected (AgeNe) values for most species and within 4% for all species (Table 2). Simulated N_b was slightly higher than expected in a few species, a result that can be attributed to small numbers of individuals in older age classes. For example, N_b/E(N_b) for bison, bottlenose dolphin, and grizzly bear was 1.015–1.024 for small (100–200) values of N₁, but this slight disparity largely disappeared for N₁ = 1000 [N_b/E(N_b) = 1.001–1.004; Table 2].

Table 2. Demographic data for the modeled species.

			Per generation						Per cycle
Species	N1	Gen	$V_k{}_{•}$	$E(V_k{}_{•})$	$V_k{}_{•}/E(V_k{}_{•})$	Ne	E(Ne)	Ne/E(Ne)	Nb	E(Nb)	Nb/E(Nb)	${\widehat{N}}_{\text{b}}/E(N_{\text{b}})$
Mole crab	1000	12.8	187.72	190.41	0.986	270.4	266.1	1.016	133.7	131	1.021	1.137
Mosquito	50	22.5	3.75	3.83	0.979	781.9	771.2	1.014	214.3	206	1.040	1.136
Sea urchin	500	1.5	3.92	3.92	1.000	517.2	517.8	0.999	655.5	656	0.999	0.864
Primrose	500	8.4	42.34	41.96	1.009	380.1	382.8	0.993	456.9	457	1.000	0.862
Sagebrush	200	7.8	17.54	17.35	1.011	318.7	322.8	0.987	514.3	518	0.993	0.739
Seaweed	500	8.3	27.37	27.35	1.001	565.9	566.9	0.998	714.4	715	0.999	0.838
Cascade frog	1000	3.3	25.45	25.36	1.003	484.3	485.4	0.998	243.4	244	0.998	1.078
Wood frog	2000	2.1	28.26	28.10	1.006	556.4	559.4	0.995	332.9	335	0.994	1.057
Great tit	500	1.9	4.31	4.30	1.002	590.5	591.9	0.998	856.0	854	1.002	0.801
Sage grouse	200	3.9	5.23	5.25	0.996	426.8	425.3	1.004	733.1	720	1.018	0.739
Sparrow	1000	3.0	30.48	30.41	1.002	369.5	370.0	0.999	363.3	365	0.995	0.934
Atlantic cod	2000	12.9	443.60	443.90	0.999	231.4	230.8	1.003	161.1	161	1.001	1.043
Brown trout	5000	8.0	494.77	491.97	1.006	320.8	321.8	0.997	154.2	155	0.995	1.116
Sardine	1000	5.9	28.94	28.94	1.000	756.8	757.7	0.999	800.4	801	0.999	0.903
Bison	200	7.4	12.40	12.44	0.997	408.9	409.0	1.000	401.0	395	1.015	0.947
Bison	1000	7.4	12.46	12.44	1.002	2039.8	2043.1	0.998	1985.0	1978	1.004	0.947
Bighorn sheep	200	5.7	6.80	6.80	1.000	520.4	521.5	0.998	641.5	640	1.002	0.858
Bottlenose dolphin	100	14.7	8.91	9.04	0.986	538.8	533.2	1.011	526.5	514	1.024	0.944
Bottlenose dolphin	1000	14.7	9.03	9.04	0.999	5334.5	5331.6	1.001	5163.0	5158	1.001	0.944
Elephant seal	500	7.9	31.38	30.99	1.013	471.0	477.2	0.987	211.3	211	1.001	1.156
Grizzly bear	100	10.5	8.88	8.92	0.996	386.0	385.2	1.002	455.2	444	1.025	0.854
Grizzly bear	1000	10.5	8.90	8.92	0.998	3861.2	3852.0	1.002	4473.5	4461	1.003	0.854
Red deer	100	8.4	2.57	2.58	0.995	734.8	732.2	1.004	625.4	607	1.030	1.008
Green snake	400	2.5	6.93	6.93	1.000	447.4	447.5	1.000	607.9	608	1.000	0.827
Synthetic	250	2.6	4.07	4.08	0.997	430.6	429.6	1.002	503.3	501	1.005	0.886

Observed values from simulations are compared to expected values from AgeNe based on age-specific survival and fecundity for each model species. See Table S1 for the model species’ life history information and Table 1 for notation. Not shown are empirical values for ${\overline{k}}_{•}$ (mean lifetime number of offspring), which were all within 0.25% of the expected value of 2.0. The last column shows how raw (unadjusted) genetic estimates from single cohorts compare to true Nb.

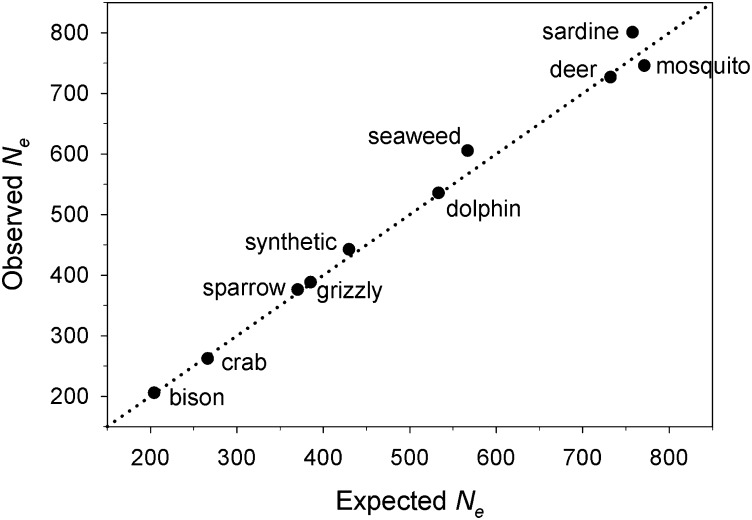
For 10 species we also verified that modeled populations lost heterozygosity at the rate expected based on the nominal N_e value obtained from AgeNe. Results (Figure 1) show that, despite the random demographic variability generated in the simulations, actual rates of genetic drift in the modeled populations agreed closely with theoretical expectations. These results supported the use of effective sizes calculated by AgeNe to represent the true N_e and N_b for each scenario. We then assessed bias in the genetically based estimates by comparing these AgeNe values with LDNe estimates for each sample of genotypes simulated with simuPOP.

Figure 1.

Comparison of observed N_e (based on rate of loss of heterozygosity in simulated populations) and the expected value (calculated from AgeNe based on published vital rates). Results are shown for nine modeled species, in addition to the synthetic life table used in Waples et al. (2011).

Genetic estimates of N_b

Samples from single cohorts:

Waples (2005) suggested that when the LD method is used based on such samples, the estimate primarily reflects N_b in the parents that produced the cohort. However, those results were for a model involving semelparity with variable age at maturity, as occurs in Pacific salmon and some other species, and its applicability to iteroparous species remains untested. We can refine the expectation for ${\widehat{N}}_{\text{b}}$ for iteroparous species as follows. Assuming selective neutrality, the amount of LD in a closed population with discrete generations is the sum of two quantities: (1) residual or “background” LD from previous generations that has not broken down by recombination between loci and (2) new LD generated by reproduction of a finite number of individuals (Hill and Robertson 1968). If the population is stable in size, overall LD reaches an equilibrium value characteristic of N_e and the recombination rates of the loci involved (Sved 1971). At that point, creation of new LD each generation must exactly compensate for the LD lost through recombination. When loci are unlinked, half of the existing LD decays each generation, so (from Equation 3) the expected amount of residual LD left after recombination is E(r^2′) ≈ 1/(6N_e). At equilibrium, therefore, the same amount must be newly generated by mating of N_e effective individuals each generation.

If population size changes, the residual disequilibria and the newly generated disequilibria reflect different effective sizes, and an estimate of N_e based on r^2′ can be biased upward or downward for a few generations (Waples 2005). Something like this occurs within age-structured populations. LD generated by breeders in a single time period is a function of N_b, while residual LD in the population as a whole is a function of N_e. In general, therefore, we expect that in the progeny of parents that reproduce in a single time period, the total amount of drift LD can be approximated by

$$E\left(r^{2^{\prime }}\right)\mathrm{\approx }\frac{1}{\left(6N_{\text{e}}\right)}+\frac{1}{\left(6N_{\text{b}}\right)}=\frac{1/N_{\text{e}}+1/N_{\text{b}}}{6}.$$ (4)

If N_e = N_b, this simplifies to Hill’s relationship E(r^2′) ≈ 1/(3N_e). More generally, if we note that the harmonic mean of N_e and N_b is HMean(N_e, N_b) = 2/(1/N_e + 1/N_b), then (1/N_e + 1/N_b) = 2/HMean(N_e, N_b), and making this substitution in Equation 4 produces

$$E\left(r^{2^{\prime }}\right)\approx \left(\frac{1}{6}\right)\times \frac{2}{\text{HMean}\left(N_{\text{e}},N_{\text{b}}\right)}=\frac{1}{3\times \text{HMean}\left(N_{\text{e}},N_{\text{b}}\right)}.$$ (5)

That is, when N_e and N_b differ, the amount of LD in a sample from a single cohort should be a function of the harmonic mean of N_e and N_b. It follows that if N_e is larger than N_b, the amount of residual LD will be smaller than would typically occur in a population with N_e = N_b, and ${\widehat{N}}_{\text{b}}$ should be upwardly biased. The reverse should occur when N_e < N_b, while there should be little bias for species for which N_e and N_b are about the same magnitude (e.g., sparrow, sardine, and bison; Table S1).

The 21 species modeled here exhibit the full range of values for the ratio of N_b to N_e considered in the larger study by Waples et al. (2013) (from N_b/N_e = 0.267 in the mosquito to N_b/N_e = 1.694 in the sage grouse; Table S1). When analyzing samples from a single cohort, the ratio of estimated N_b (${\widehat{N}}_{\text{b}}$) to true N_b in these species clustered around 1.0 (Table S1). However, for 10 species ${\widehat{N}}_{\text{b}}$ was >10% lower than true N_b, and for 4 species the estimate was >10% too high. The species with the strongest downward bias were the sage grouse and the sagebrush (both with ${\widehat{N}}_{\text{b}}/N_{\text{b}}$ = 0.74), while the strongest upward bias (${\widehat{N}}_{\text{b}}/N_{\text{b}}$ = 1.14) occurred in the mole crab and the elephant seal.

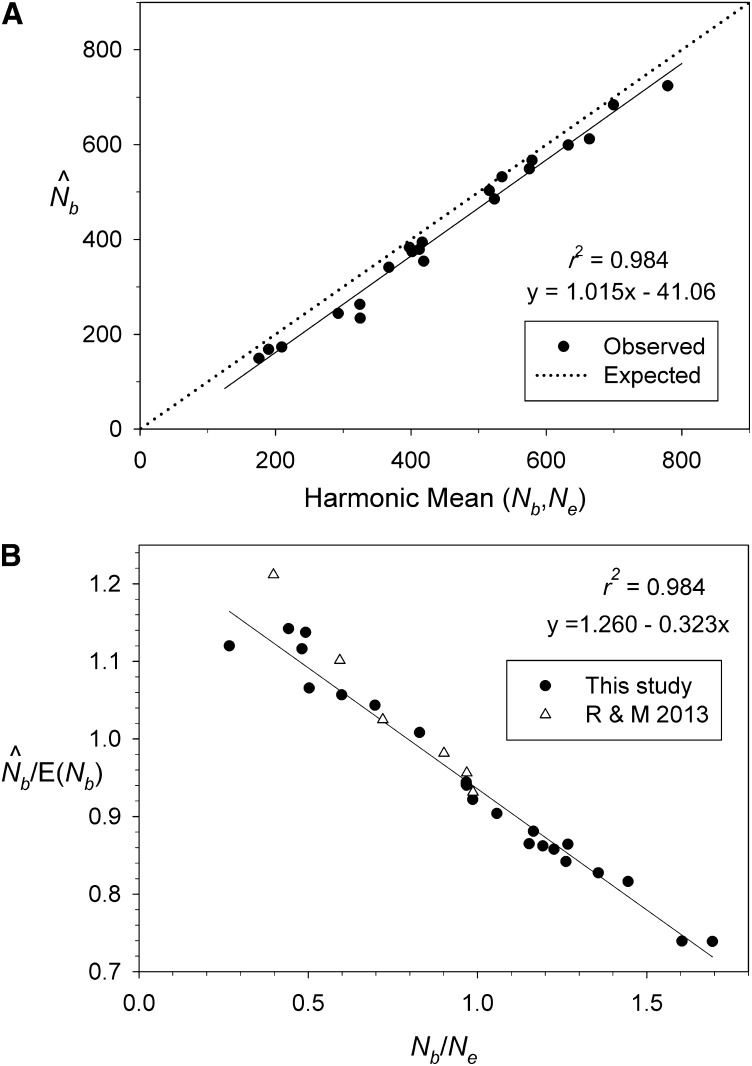
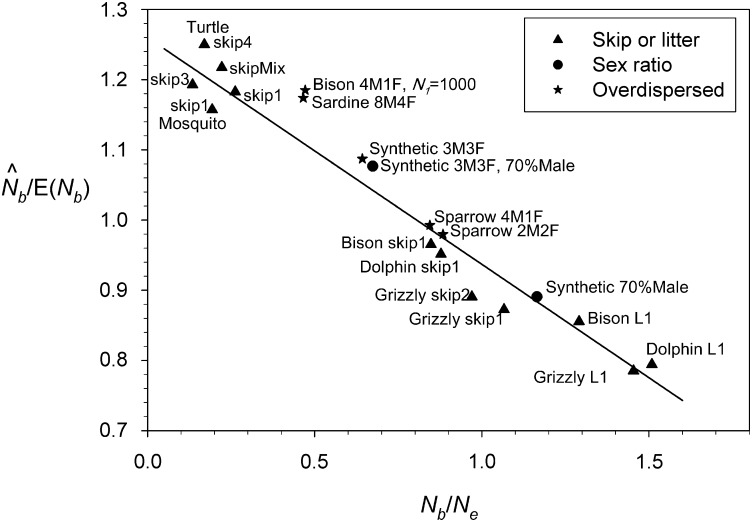
The relationship between ${\widehat{N}}_{\text{b}}$ and HMean(N_e, N_b) was almost perfectly linear (r = 0.992), with slope that did not differ significantly from 1 (b = 1.015 ± 0.029) (Figure 2A). Consistently, however, ${\widehat{N}}_{\text{b}}$ was slightly lower (median = 7% lower) than HMean(N_e, N_b). We believe this reflects a factor not accounted for in Equation 5 above: in each cycle the newborn cohort is produced by matings among parents of a variety of ages, who themselves were progeny of different groups of parents with slightly different allele frequencies. This produces a type of mixture LD [a two-locus Wahlund effect (Nei and Li 1973; Sinnock 1975)] in the parents every cycle, and (for unlinked loci) half of this is passed on to their offspring.

Figure 2.

Bias associated with genetic estimates of N_b when using samples from a single cohort. (A) Relationship between ${\widehat{N}}_{\text{b}}$ and the harmonic mean of true N_e and N_b for 21 model species and one synthetic life table. Dotted line is the expectation based on Equation 3 in the text; solid line is regression for empirical data. (B) Pattern of bias in ${\widehat{N}}_{\text{b}}$ as a function of the ratio N_b/N_e. Solid circles are results for model species from this study; open triangles are from Robinson and Moyer (2013) for comparable analyses (single-cohort samples of 100 individuals; ${\widehat{N}}_{\text{b}}$ calculated from LDNe, using P_crit = 0.05 criterion for screening out rare alleles). The regression line is plotted using only data from this study.

Although the relationship in Figure 2A is striking, it does not provide a practical method for accounting for effects of both true N_e and true N_b on ${\widehat{N}}_{\text{b}}$. Fortunately, this can be accomplished with a simple rearrangement of the variables. Combining Equations 3 and 4 produces the following when considering use of single-cohort samples to estimate N_b:

$$\mathrm{E}\left({\widehat{N}}_{\text{b}}\right)\mathrm{\approx }\frac{1}{\left(3r^{2^{\prime }}\right)}=\frac{6/3}{1/N_{\text{e}}+1/N_{\text{b}}}=\frac{2}{\left(N_{\text{e}}+N_{\text{b}}\right)/\left(N_{\text{e}}\times N_{\text{b}}\right)}.$$ (6)

We wish to find an expression for the relative bias in ${\widehat{N}}_{\text{b}}$ (measured by ${\widehat{N}}_{\text{b}}$/N_b = the ratio of estimated and true N_b) as a function of the ratio N_b/N_e, because we know the latter can be estimated from life history data independent of the absolute magnitude of N_e or N_b (Waples et al. 2013). Dividing each side of Equation 6 by N_b gives

$$\frac{E\left({\widehat{N}}_{\text{b}}\right)}{N_{\text{b}}}\mathrm{\approx }\frac{\mathrm{2}/N_{\text{b}}}{\left(N_{\text{e}}+N_{\text{b}}\right)/\left(N_{\text{e}}\times N_{\text{b}}\right)}=\frac{2}{1+N_{\text{b}}/N_{\text{e}}}.$$ (7)

Equation 7 predicts a curvilinear relationship between the index of bias (${\widehat{N}}_{\text{b}}$/N_b) and the ratio of seasonal and generational effective size (N_b/N_e). However, this is not a good fit to the empirical data for the model species, even when Equation 7 is adjusted to account for the Wahlund effect (Figure S2). Instead, the relationship between ${\widehat{N}}_{\text{b}}$/N_b and N_b/N_e was almost perfectly linear in the model species (r² = 0.984; Figure 2B). As expected from Equation 5, ${\widehat{N}}_{\text{b}}$ consistently overestimates N_b in species for which true N_e is larger than true N_b, consistently underestimates N_b in species for which N_e < N_b, and is relatively unbiased in species for which N_b and N_e are approximately equal. Actually, the “no bias in ${\widehat{N}}_{\text{b}}$” point occurs with N_b slightly larger than N_e (Figure 2B), which reflects the fact that ${\widehat{N}}_{\text{b}}$ in Figure 2A is slightly lower than HMean(N_e, N_b), due presumably to the mixture LD from age structure mentioned above.

A bias adjustment for ${\widehat{N}}_{\text{b}}$:

A simple adjustment to raw ${\widehat{N}}_{\text{b}}$ can remove most of the bias. Rearrangement of the regression in Figure 2B leads to the following:

$${\widehat{N}}_{\text{b}\left(\text{Adj}\right)}=\frac{{\widehat{N}}_{\text{b}}}{1.26-0.323\times \left(N_{\text{b}}/N_{\text{e}}\right)}.$$ (8)

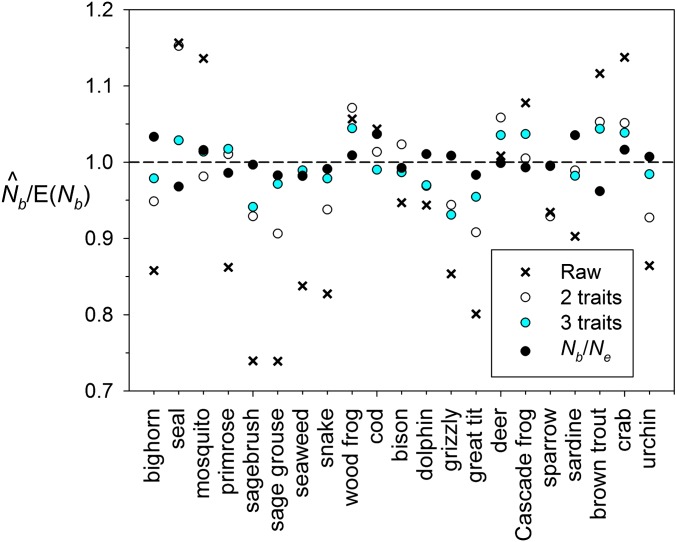
Figure 3 shows that after applying this correction, adjusted ${\widehat{N}}_{\text{b(Adj)}}$ was within 5% of the true value for all 21 study species.

Figure 3.

Effects of adjusting bias in raw ${\widehat{N}}_{\text{b}}$ for each model species, based on information for two life history traits (AL and α), three life history traits (AL, α, and CVf), or the true ratio N_b/N_e. Samples were taken from single cohorts.

Unless they have detailed demographic information for their target species, researchers will not know the true ratio N_b/N_e, but this can be predicted from just two or three simple life history traits (Waples et al. 2013). Using the ratio of two traits [adult life span (AL) and age at maturity (α)], this relationship holds: N_b/N_e = 0.485 + 0.758 log × (AL/α); adjusted r² = 0.67. With the addition of CVf (an index of variation in fecundity with age), the relationship becomes N_b/N_e = 0.833 + 0.637 log × (AL) – 0.793 × log(α) – 0.423 × CVf; adjusted r² = 0.84. Inserting these results into Equation 8 produces the bias adjustments shown in Table 3, based on life history traits of the study species. Figure 3 also shows how the pattern of bias in the 21 species is reduced by adjusting ${\widehat{N}}_{\text{b}}$ based on two or three life history traits.

Table 3. Formulas to adjust genetic estimates of effective size to correct biases due to age structure.

Method	Formula
To estimate Nb
Using true Nb/Ne	${\widehat{N}}_{\text{b(Adj)}}=\frac{\text{raw}\hspace{0.17em}{\widehat{N}}_{\text{b}}}{1.26-0.323\times \text{(}{N}_{\text{b}}/N_{\text{e}}\text{)}}$
Using two traits	${\widehat{N}}_{\text{b(Adj2)}}=\frac{\text{raw}\hspace{0.17em}{\widehat{N}}_{\text{b}}}{1.103-0.245\times \text{log(AL/}\alpha \text{)}}$
Using three traits	${\widehat{N}}_{\text{b(Adj3)}}=\frac{\text{raw}\hspace{0.17em}{\widehat{N}}_{\text{b}}}{0.991-0.206\times \text{log(AL)}+0.256\times \text{log(}\alpha \text{)}+0.137\hspace{0.17em}\text{CVf}}$
To estimate Ne
Using true Nb/Ne	${\widehat{N}}_{\text{e(Adj)}}=\frac{{\widehat{N}}_{\text{b(Adj)}}}{N_{\text{b}}/N_{\text{e}}}$
Using two traits	${\widehat{N}}_{\text{e(Adj2)}}=\frac{{\widehat{N}}_{\text{b(Adj2)}}}{0.485+0.758\times \text{log(AL/}\alpha \text{)}}$
Using three traits	${\widehat{N}}_{\text{e(Adj3)}}=\frac{{\widehat{N}}_{\text{b(Adj3)}}}{0.833+0.637\times \text{log(AL)}-0.793\times \text{log(}\alpha \text{)}-0.423\times \text{CVf}}$

Raw ${\widehat{N}}_{\text{b}}$ is the unadjusted estimate obtained using the LD method from a sample from a single cohort. AL, adult life span; α, age at maturity; CVf, an index of variation in age-specific fecundity (see Table 1 for definitions and notation). Different adjustments are provided, depending on whether the goal is to estimate N_b or N_e and on the type of information available for the species of interest (data for two or three life history traits or an estimate of true N_b/N_e). Adjustments based on N_b/N_e use results from AgeNe and the regression shown in Figure 2B; adjustments based on two or three life history traits use the relationships described in Waples et al. (2013).

We illustrate these adjustments using data for the great tit, Parus major. From Table S1 we see that α = 1, AL = 8, AL/α = 8, CVf = 0.249, and true N_b/N_e = 1.443. For the simulated data and sampling from a single cohort, ${\widehat{N}}_{\text{b}}$ = 684, 20% lower than the true value of 854. If all one knew was that the ratio AL/α was ∼8, the two-variable formula in Table 3 could be used to adjust the raw estimate: ${\widehat{N}}_{\text{b(Adj2)}}$ = 684/[1.103 – 0.245 × log(8)] = 684/0.882 = 776. This would cut the bias by about half. If one also could estimate the variation in age-specific fecundity, a (generally) more accurate adjustment could be made using the three-variable formula from Table 3: ${\widehat{N}}_{\text{b(Adj3)}}$ = 684/[0.991 − 0.206 × log(8) + 0.256 × log(1) + 0.137 × 0.249]= 684/0.839 = 815, which is closer but still ∼5% too low. Finally, if one knew the true N_b/N_e ratio, the optimal adjustment would be ${\widehat{N}}_{\text{b(Adj)}}$ = 684/[1.26 – 0.323 × 1.443] = 684/0.794 = 862, which is just under 1% too large.

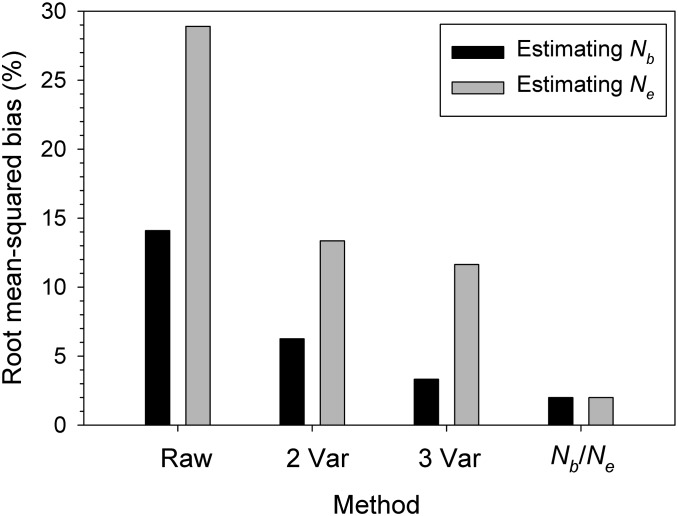
Figure 4 shows how adjustments to ${\widehat{N}}_{\text{b}}$ in Table 3 reduced the percent RMSB in the 21 model species. The raw (naive) estimate of N_b has a typical bias of ±14%, and this can be reduced sevenfold (to 2%) if one knows the N_b/N_e ratio. If N_b/N_e is estimated from two life history traits, the RMSB can be reduced by more than half (to 6.3%) compared to the naive ${\widehat{N}}_{\text{b}}$, and with information for three traits the RMSB can be nearly halved again (to 3.3%).

Figure 4.

Percent root mean-squared bias in ${\widehat{N}}_{\text{b}}$ and ${\widehat{N}}_{\text{e}}$ and how it changes when raw estimates are adjusted per formulas in Table 3, using true N_b/N_e or information for two or three life history traits. Results apply to samples from single cohorts and are averaged across the 21 model species.

Samples from multiple consecutive cohorts:

Often it is easier to sample mixed-age individuals than it is to collect individuals from a single cohort. Furthermore, even when sampling individual cohorts is feasible, sample sizes can be so small that it is necessary to combine individuals from several cohorts (e.g., Skrbinšek et al. 2012). To examine these scenarios, for 16 of the modeled species we evaluated how the pattern of bias in ${\widehat{N}}_{\text{b}}$ changes when samples are taken randomly and in equal proportions from either two or three consecutive cohorts.

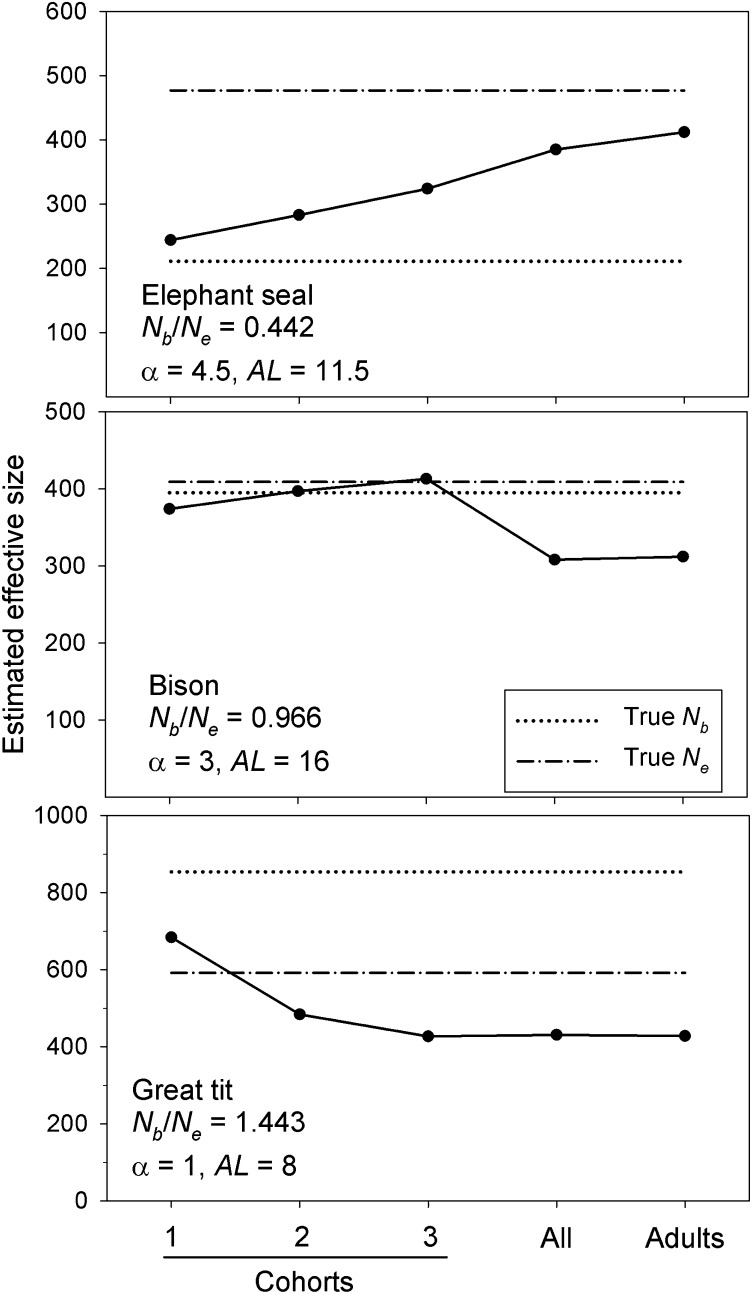
Again, the general pattern of bias depends on the ratio N_b/N_e (Figure 5; see also Figure S4, Figure S5, Figure S6, Figure S7, Figure S8, and Figure S9). When N_b << N_e (as in the elephant seal), ${\widehat{N}}_{\text{b}}$ from a single cohort is higher than true N_b and increases when the sample combines two or three cohorts; when N_b >> N_e (as in the great tit), ${\widehat{N}}_{\text{b}}$ from a single cohort underestimates true N_b and the downward bias increases when the sample combines two or three cohorts; when N_b ≈ N_e (as in the bison), there is little bias for any of these sampling schemes. Results for all species are plotted in Figure S3A, which includes the regression line from Figure 2B based on single-cohort samples; Figure S3A shows that multiple-cohort samples follow the same general pattern, but with stronger overall bias. The ratio N_b/N_e is a good quantitative predictor of bias in ${\widehat{N}}_{\text{b}}$ for samples from two or three cohorts; the relationship is strong for N_b/N_e > 0.6, but higher variability for species with low N_b/N_e ratios reduces the overall fit (r² = 0.79 and 0.77 for samples from two or three cohorts, respectively).

Figure 5.

Effects of different sampling strategies (sampling from one to three consecutive cohorts or randomly from all adults or the population as a whole) on genetic estimates of effective size, using the LD method. Results are shown for three model species with low (elephant seal), medium (bison), and high (great tit) N_b/N_e ratios. The empirical estimates (solid circles and solid lines) are compared to true N_e (dashed-dotted line) and true N_b (dotted line). See Figure S4, Figure S5, Figure S6, Figure S7, Figure S8, and Figure S9 for similar results for all model species.

Genetic estimates of N_e

Samples from single cohorts:

In the case of single-cohort samples, we saw above that it is possible to make quantitative adjustments for bias in ${\widehat{N}}_{\text{b}}$, provided one knows the ratio N_b/N_e or can estimate it from life history traits. If so, then it is also possible to obtain an estimate of N_e via a simple two-step process, using the equations in the bottom half of Table 3: (1) calculate the bias-adjusted ${\widehat{N}}_{\text{b}}$ based on known or estimated N_b/N_e, and (2) divide adjusted ${\widehat{N}}_{\text{b}}$ by N_b/N_e or by the estimators of N_b/N_e developed by Waples et al. (2013) based on two or three life history traits. If the raw ${\widehat{N}}_{\text{b}}$ is used naively as an estimate of N_e, the RMSB is twice as large as for an estimate of N_b (Figure 4). If N_b/N_e can be estimated from two life history traits, this bias can be cut in half, and if true N_b/N_e is known, ${\widehat{N}}_{\text{e}}$ and ${\widehat{N}}_{\text{b}}$ both have the same low bias (2%).

Population samples:

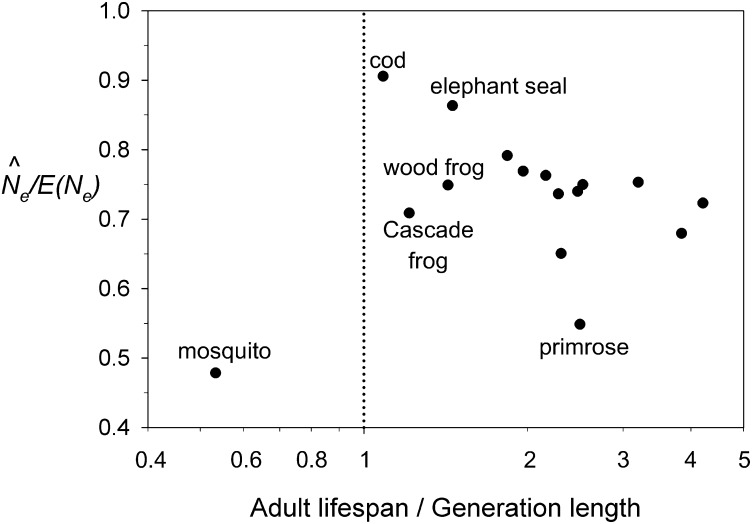
Another potential strategy to estimate N_e is to sample only mature adults or from the population as a whole; for many species this will be the only feasible option. Waples and Do (2010) speculated that if such samples included enough cohorts to approximately represent a generation, the resulting estimate from the LD method might be close to N_e per generation. We tested this conjecture in two ways. First, we drew samples randomly from all adults; these samples included a number of cohorts equal to the AL for each species. If the conjecture were correct, we would expect that estimates based on these adult samples should converge on true N_e as AL approaches the generation length (Gen) (Table S1 lists AL, Gen, and other life history information for each model species). In every species, estimates based on random samples of adults were lower than true N_e (Figure 5, Figure 6, Figure S4, Figure S5, Figure S6, Figure S7, Figure S8, and Figure S9). However, the least amount of downward bias in ${\widehat{N}}_{\text{e}}$ occurred in the cod (Figure 6), which is the species for which the number of cohorts in an adult sample is closest to the generation length (AL/Gen = 14/12.9 = 1.09 generations of cohorts; ${\widehat{N}}_{\text{e}}$ = 91% of true N_e). AL/Gen is also relatively close to 1 for the species with the second-smallest bias (elephant seal; ${\widehat{N}}_{\text{e}}/N_{\text{e}}$= 0.86, AL/Gen = 1.46). As AL/Gen increased across species, estimates of N_e based on adult samples generally declined.

Figure 6.

Pattern of bias in estimates of N_e based on random samples of all adults. The number of cohorts represented in a sample of adults is the adult life span (AL). Values on the x-axis (note the log scaling) therefore indicate how many generations of cohorts are included in a sample of adults. The four species for which AL is closest to Gen, as well as some outliers, are indicated.

These results are generally consistent with predictions of the above hypothesis. On the other hand, the results showed considerable variability, and for two other species with 1 < AL/Gen < 1.5 (wood frog and Cascade frog), ${\widehat{N}}_{\text{e}}$ based on adult sampling was 25–30% lower than true N_e. The only species for which adult samples represented less than one generation of cohorts was the mosquito, for which ${\widehat{N}}_{\text{e}}$ based on just over one-half of a generation of cohorts showed the strongest downward bias (${\widehat{N}}_{\text{e}}$ less than half of true N_e; Figure 6).

A second test of the hypothesis is possible for the four species for which Gen ≤ 3, in which case we can compare estimates based on combined samples from two or three cohorts with true N_e. For the great tit (Gen = 1.9) and wood frog (Gen = 2.1), estimates based on two cohorts were 82% and 101% of true N_e, respectively, and for the Cascade frog (Gen = 3.3) the estimate based on three cohorts was 102% of true N_e. Generation length for the green snake is 2.5, and estimates based on samples from two or three cohorts were 98% and 82% of true N_e, respectively.

Life history variations

By relaxing some of the assumptions of the standard model for AgeNe, we evaluated whether variant life histories change N_b and N_e in ways that would cause a deviation in the pattern of bias depicted in Figure 2B. Analytical methods were used to develop expectations for true N_b and N_e, and we compared these results with demographic estimates of effective size from the age-structured simulations. Results of these analyses are summarized in Table S2, which shows generally excellent agreement between expected (analytical) and observed (simulated) effective sizes. Analytical expectations for effects of intermittent breeding and small litter size on N_e per generation are not available, so we used simulated demographic values for these scenarios to represent true N_e.

Consequences of these life history variations for N_b and N_e can be summarized as follows. Skewed primary sex ratio reduces both N_b and N_e in a predictable way, but the proportional reductions are identical so this does not affect the ratio N_b/N_e (Waples et al. 2013). Overdispersed variance of SASS individuals generally reduces N_b more than N_e and hence reduces the N_b/N_e ratio, but the magnitude of this effect varies considerably across species (Waples et al. 2013). N_b is increased sharply if females can produce only one offspring per litter or clutch; conversely, N_b is reduced if some females are excluded from breeding each season, and the effect is more pronounced for high-fecundity species with type III survival (mosquito and loggerhead turtle) than it is for low-fecundity species with type I survival (bison, dolphin, and grizzly bear) (Waples and Antao 2014). Neither skip breeding nor small litter size had much effect on N_e per generation in these scenarios (Waples and Antao 2014).

Next, we calculated ${\widehat{N}}_{\text{b}}$ based on single-cohort genetic samples and plotted the pattern of bias as a function of the updated N_b/N_e ratios (Figure 7). It is apparent from these results that bias in ${\widehat{N}}_{\text{b}}$ for simulated populations with variant life history features is very similar to the pattern found for scenarios that used the standard model. All of the intermittent-breeding and litter-size scenarios produced results that fall closely on the regression line developed for the standard model. A slight (<5%) additional upward bias in ${\widehat{N}}_{\text{b}}$ was found for some species (sardine and bison) modeled with overdispersed variance in reproductive success.

Figure 7.

Pattern of bias in estimates of N_b for single-cohort samples from simulated populations under life history variations that deviate from the standard model. Solid triangles, maximum litter size is 1 (L1) or females are forced to skip up to four breeding cycles after reproducing; solid circles, skewed (70% male) primary sex ratio; stars, overdispersed variance among same-age, same-sex individuals. For example, “sardine 8M4F” denotes results for simulations using the sardine life table with V_k for males of each age being eight times the mean and V_k for females of each age being four times the mean. The solid line is the regression of ${\widehat{N}}_{\text{b}}/N_{\text{b}}$ with N_b/N_e under the standard model (from Figure 2B). Data for life history variants for the model species are taken from Table S2.

Discussion

Many natural populations have overlapping generations, whereas most population genetics theory assumes discrete generations and ignores age structure. This disconnect introduces a number of potential biases that have received limited quantitative evaluation. Here, we use verbal arguments and numerical methods to conduct the first comprehensive evaluation of how genetic estimates of effective size based on the single-sample LD method are related to true N_b and true N_e and how this relationship is affected by the species’ life history and the experimental design.

Estimating N_b

We showed using an extension of standard population genetics theory that single-cohort samples for iteroparous species using the LD method should be equally affected by N_b and N_e (Equation 5). Empirical results for simulated age-structured populations confirmed this, although we found that the estimates were consistently slightly lower than HMean(N_e, N_b) (Figure 2A). We attribute this latter result to a type of two-locus Wahlund effect that creates mixture LD when parents of different ages (and with slightly different allele frequencies) mate.

The strongly linear relationship (r² > 0.98) shown in Figure 2B makes it possible to develop a simple linear adjustment to raw ${\widehat{N}}_{\text{b}}$ to produce an adjusted estimate that is nearly unbiased, provided the true ratio N_b/N_e is known (RMSB = 2%; Table 3, Figure 3, and Figure 4). If this ratio is not known but can be estimated from two or three simple life history traits (Waples et al. 2013), modified adjustments to ${\widehat{N}}_{\text{b}}$ are possible (Table 3). The effect of these adjustments in reducing bias can be substantial (Figure 3 and Figure 4).

We used two cross-validation methods to evaluate robustness of the relationship shown in Figure 2B. First, we compared our results to those reported by Robinson and Moyer (2013), who used AgeNe to calculate true N_e and N_b for three age-structured species (mussel, sturgeon, and white-crowned sparrow) and three additional variants of the sparrow fecundity schedule; they then used SPIP (Anderson and Dunham 2005) to simulate age-structured genetic data for these species and used LDNe to estimate effective size. Results for the six Robinson and Moyer “species” are plotted as open triangles in Figure 2B. It is evident that the key relationship derived for our 21 model species also holds for these independently derived estimates of N_b. Second, for a subset of our model species we considered life history variations that can change both N_b and N_e (and hence the N_b/N_e ratio) in ways not accounted for in most standard models. These evaluations created 19 new datapoints not used in deriving the regression between ${\widehat{N}}_{\text{b}}/N_{\text{b}}$ and N_b/N_e, and these new results clearly reflect the same underlying pattern of bias in ${\widehat{N}}_{\text{b}}$ (Figure 7). Therefore, we believe the adjustments to raw ${\widehat{N}}_{\text{b}}$ proposed in Table 3 should be widely applicable to populations in nature. Our simulation results also indicate that mixed samples from two or three cohorts can provide reasonably reliable adjusted estimates of N_b, although the pattern of bias is not quite as predictable as it is for single-cohort samples, particularly for species with N_b/N_e < ∼0.6 (Figure S2 and Table 3).

Estimating N_e

Our empirical results provide some qualified support for the hypothesis (Waples and Do 2010) that a sample that includes as many cohorts as there are in a generation should produce an estimate approximately equal to N_e. For four short-lived species with Gen ≤ 3, estimates based on combined samples from two or three cohorts produced estimates that averaged 93% of true N_e. All estimates based on random samples of adults were smaller than true N_e (Figure 6, Figure S4, Figure S5, Figure S6, Figure S7, Figure S8, and Figure S9), but there was a tendency for the bias to be less when the number of cohorts included in the adult sample corresponded more closely to the generation length (Figure 6).

Fortunately, a more robust approach is possible. Although single-cohort samples have traditionally been thought of as providing information primarily about N_b [based on a model involving semelparous, age-structured species (Waples 2005)], Equation 5 and Figure 2 indicate that both N_b and N_e strongly influence effective size estimates in iteroparous species. This means that samples from single cohorts can also be used to estimate N_e directly, using the bias-adjusted ${\widehat{N}}_{\text{b}}$ and an estimate of N_b/N_e, as shown in Table 3. The raw estimate from a single-cohort sample is not a reliable indicator of true N_e (RMSB ≈ 28%; Figure 4), but the bias can be cut in half if N_b/N_e can be estimated from two key life history traits, and if enough information about vital rates is available to accurately calculate N_b/N_e, then N_e can be estimated with as much accuracy as N_b (Figure 4). If samples can be obtained from individual cohorts, therefore, this appears to provide the most reliable means for estimating N_e using the LD method.

Caveats

The 21 model species used here to develop the bias adjustments span the full range of true N_b/N_e ratios (0.267–1.694) reported by Waples et al. (2013) in their 63-species study. Nevertheless, care should be taken in extrapolating outside this range. The relationship between ${\widehat{N}}_{\text{b}}/N_{\text{b}}$ and N_b/N_e becomes more variable for N_b/N_e < 0.5 (Figure 2B); all estimates are upwardly biased, but it is difficult to predict the exact amount of bias. Nevertheless, even accounting for these uncertainties, residual bias after applying the proposed corrections should be no larger than ∼5–10%, which is relatively small considering the other sources of uncertainty typically associated with estimating effective size in natural populations (Wang 2005; Luikart et al. 2010; Palstra and Fraser 2012). It should be noted that because we wanted to focus on effects of age structure, in computing the bias adjustments for ${\widehat{N}}_{\text{b}}$ (Table 3) we screened out alleles with frequencies <0.05 for the LDNe estimates, as Waples and Do (2010) found that this minimized bias due to rare alleles. Using a more lenient criterion (e.g., 0.02 or 0.01) increases precision but at the cost of some upward bias in the estimates that is not modeled here.

So far our discussion has focused on samples drawn from one or a few cohorts or randomly from all adults. We also present results for random samples from the entire population (Figure 6, Figure S4, Figure S5, Figure S6, Figure S7, Figure S8, and Figure S9), which for some species might be the easiest to obtain. Estimates based on these samples generally produce results that are qualitatively similar to those for adult samples; however, interpretation of whole-population samples is complicated because they can be strongly affected by assumptions about juvenile survival rates, which are poorly known for many species. Mortality before age at maturity does not affect any of the ratios N_b/N_e, N_b/N_A, and N_e/N_A, but it has a large effect on the proportional representation of different age classes in a sample drawn randomly from the population as a whole. Caution should therefore be used in interpreting results for such samples when estimating effective size in iteroparous species.

Some life history variations can affect N_b more strongly than N_e, which means that it is important to account for these factors in estimating the N_b/N_e ratio. This is particularly true for species with highly overdispersed variance in reproductive success of SASS individuals (Waples et al. 2013), species for which intermittent breeding of females is common, and species for which females can produce only a single offspring per reproductive cycle (Waples and Antao 2014). AgeNe can explicitly account for any user-specified magnitude of overdispersion in V_k, and the analytical methods described by Waples and Antao (2014) can account for effects of intermittent breeding and litter-size constraints. Once these adjustments to the N_b/N_e ratio are made, the pattern of bias follows that developed for standard model scenarios (Figure 7). One life history variant we did not consider is when individuals consistently (across multiple breeding cycles) have higher or lower reproductive success than others in their cohort. Persistent differences like this can reduce N_e (Lee et al. 2011) and perhaps increase the N_b/N_e ratio in ways not accounted for here.

Because of the complexity of the issues involved in evaluating effective size in iteroparous species, our evaluations have focused entirely on bias. Precision also can be a limiting factor for genetic estimates of effective size and is important to consider in any practical application. Fortunately, a number of previous studies have evaluated precision of the LD method under realistic experimental designs with known N_e (England et al. 2010; Tallmon et al. 2010; Waples and Do 2010; Antao et al. 2011; Robinson and Moyer 2013; Holleley et al. 2014), and these should be consulted for general guidelines. Figure S10 depicts the range of variation among replicate ${\widehat{N}}_{\text{b}}$ estimates among the model species under standard model conditions.

Relationship to previous work

In an evaluation of bias that can result if the standard temporal method (Nei and Tajima 1981) is applied to iteroparous species with overlapping generations, Waples and Yokota (2007) used three model species—one each with type I, type II, and type III survivorship. Subsequently, it has become clear that other life history traits, especially age at maturity and adult life span, have a greater influence on N_e and N_b than does juvenile survivorship (Waples et al. 2013). Accordingly, in this article we used a much larger and taxonomically diverse array of model species.

Wang et al. (2010) proposed a single-sample method based on parentage assignments to estimate N_e and other genetic parameters in species with overlapping generations. This approach uses a modification of Wang’s (2009) sibship method, as implemented in the computer program Colony (Wang 2004); it appears to have considerable potential but requires the user to know the age and sex of each individual in the sample and perhaps as a consequence has not been widely used or evaluated.

Robinson and Moyer (2013) concluded that single-cohort samples generally provide an adequate estimate of N_b; they did not propose a quantitative bias adjustment, but Figure 2B shows that their results fit nicely into the relationship we found between ${\widehat{N}}_{\text{b}}/N_{\text{b}}$ and N_b/N_e. Robinson and Moyer (2013) also found that random samples of adults produced estimates that were no more than 15% downwardly biased compared to true N_e; in contrast, we found downward bias >15% in 14 of the 16 species we evaluated and ≥30% in 5 species (Figure 6). We believe this difference can be explained by the much wider range of life histories considered in this study: N_b/N_e = (0.267–1.69) in our model species vs. (0.4–0.99) in the species Robinson and Moyer considered and the number of generations of cohorts included in an adult sample = (0.53–4.2) in the present study vs. (1.06–1.72) in Robinson and Moyer’s study.

Conclusions

Genetic estimates of effective size of age-structured populations using the LD method are strongly affected by both N_e per generation and N_b per season or reproductive cycle. This complicates interpretation but also provides a means for correcting bias. Samples from single cohorts are the most amenable to quantitative bias adjustment. If the ratio N_b/N_e is known or can be estimated from two or three simple life history traits, N_b can be estimated with little (≤5–10%) bias. Single-cohort samples also can be used to estimate N_e, albeit with slightly more potential bias. Random samples of adults consistently underestimated true N_e, but the downward bias tended to be less when the number of cohorts in the sample more closely approximated the generation length. Results from this study will facilitate interpretation of rapidly accumulating genetic estimates in terms of both N_e (which influences long-term evolutionary processes) and N_b (which is more important for understanding eco-evolutionary dynamics and mating systems).