Abstract
Background
High-frequency electricity is used in a majority of surgical interventions. However, modern computer-based training and simulation systems rely on physically unrealistic models that fail to capture the interplay of the electrical, mechanical and thermal properties of biological tissue.
Methods
We present a real-time and physically realistic simulation of electrosurgery, by modeling the electrical, thermal and mechanical properties as three iteratively solved finite element models. To provide sub-finite-element graphical rendering of vaporized tissue, a dual mesh dynamic triangulation algorithm based on isotherms is proposed. The block compressed row storage (BCRS) structure is shown to be critical in allowing computationally efficient changes in the tissue topology due to vaporization.
Results
We have demonstrated our physics based electrosurgery cutting algorithm through various examples. Our matrix manipulation algorithms designed for topology changes have shown low computational cost.
Conclusions
Our simulator offers substantially greater physical fidelity compared to previous simulators that use simple geometry-based heat characterization.
Keywords: Physics-based simulation, electrosurgery, minimally invasive surgery, virtual reality, surgical simulation, cutting simulation
1. Introduction
Electrosurgical devices are used in the majority of surgical procedures today [1]. These devices generate a high-frequency (300 kHz – 700 kHz) and high power density electric current through the tissue, heating the tissue directly [2]. An expert surgeon can precisely control the heating effect to burn tissue locally while minimizing inadvertent thermal damage and blood loss. Limiting the thermal spread is a key surgical skill, yet current hands-on approaches to teaching electrosurgery have severe drawbacks. In vivo animal models provide the highest fidelity, but are expensive for basic skills training. Ex vivo tissue models are unable to model blood flow effects and generate carcinogenic smoke [3]. Computer simulation of electrosurgery promises low cost, safe and flexible training [4]. However, previously proposed systems have limited physical fidelity, relying on geometric and graphical means of estimating and communicating tissue effects. A barrier to improved physical realism is that the thermal, electrical and viscoelastic states of the simulated tissue are interdependent, greatly increasing the implementation and computational complexity.
In this paper, we propose a novel approach to simulating the effects of external forces and electrical current on tissue. We focus on tissue cutting through vaporization, an important skill for safe and effective practice [1]. Our approach is based on a finite-element electro-thermo-elastic analysis of the biological tissue. A volumetric tetrahedral mesh simulates the elastic deformation with a linear, co-rotational finite element model [5]. The electrical current and temperature are similarly modeled using linear finite element models. Deformation can be decoupled from the thermal and electrical models because vaporization takes place at time scales that are much faster compared to the timescales on which the tissue parameters change due to thermal or electrical effects. However, the thermal and electrical models have similar time-scales and therefore must be coupled for accurate results.
We introduce a novel dual mesh algorithm, with a coarse tetrahedral volumetric mesh for physics computation and a detailed surface mesh for isotherm-based visual rendering, for rendering partially vaporized tissue at spatial resolutions much finer than the underlying tetrahedral mesh. An isothermal surface that represents the extent of vaporization is interpolated from the thermal model. The isothermal surface is dynamically calculated each time-step and forms the visible tissue geometry. This approach provides greatly increased visual resolution of the thermal effects, yet remains physically accurate.
A difficult problem for finite-element models of surgery is topological changes such as from cutting [6]. Our approach relies on online manipulation of the matrix data structure to achieve cutting through vaporization in real-time.
To achieve high-quality, physically realistic electrosurgical simulation capable of real-time rates on modest hardware, this work introduces: (a) a method for coupled thermo-electrical FEM combined with an elastic deformation FEM, (b) an electrosurgical cutting model based on tissue vaporization, (c) a novel method for rendering sub-tetrahedron tissue surfaces using the isothermal surface, and (d) the online manipulation of the matrix data structures.
In spite of its importance in surgery, the literature on modeling of electrosurgery procedures is surprisingly limited. Dodde et al [7] use a coupled thermal-electric FEM formulation to analyze temperature-dependent electrical and thermal properties for the tissue. Though the physics of electrosurgical procedures is analyzed in this paper, the simulations are performed off-line and real-time interaction and rendering is not considered. Maciel et al [8] simulates an electrosurgery process on a three-dimensional domain using a mass-spring model in real-time. However, mass-spring systems can be unstable and require many sensitive parameters. Furthermore, even arbitrarily dense mass-spring meshes may not converge to the solution of the underlying partial differential equation. In Lu et al [9], a commercial physics engine, PhysX (TM) is used for physics-based deformation and the electrical heat source is modeled as a simple spherical distribution. In [10] Lu et al modeled the heat conduction and deformation combined with the cutting model to achieve real-time interactive electrocautery simulation. We have extended this method to include modeling of electric potential using finite elements.
Developing computational models for electrosurgery procedures requires investigation of tissue properties. Tissue deformation and force feedback during monopolar electrosurgery procedures have been measured. Jacob et al. estimated the critical temperatures for cutting tissues of various organs [11]. A physics-driven neural networks-based simulation system was shown to be capable of simulating the response of nonlinear deformable objects in real time [12], however this approach cannot be easily extended to changing topology, e.g. cutting, or to dynamic interactions.
While models of electrosurgical cutting are rare, surgical cutting in general has been extensively investigated. Cutting algorithms can be broadly classified into two categories. In the first category of algorithms, the existing geometry is manipulated by either splitting the shared vertices [9] or removing them [13]. In the second category, new geometry is created by remeshing along the cut. Remeshing involves either connecting new vertices or subdividing existing elements. After multiple cuts, the number of newly generated elements might be prohibitively high using this method. In [14], a cutting simulation using tetrahedral elements is proposed which uses a hybrid approach that combines both the above methods.
All previous cutting algorithms targeting surgery simulation use a scalpel. However, during electrosurgery procedures, the cut is initiated by the high-frequency current, which heats the tissue, ultimately vaporizing tissue. This phenomenon is predominantly a heat transfer process taking place in the vicinity of the tool tip causing the temperature to rise locally to about 400°C to 600°C [15]. To the best of our knowledge, no previous work has accounted for this temperature rise as the determinant of the cutting process in electrosurgery procedures.
2. Materials and Methods
2.1. Numerical modeling of the electrosurgery process
The interaction of the electrosurgical tool with soft tissue results in the deformation of the tissue, localized heating and corresponding force feedback to the tool. In section 2.1.1, we present the relevant equations of linear elastodynamics and their finite element discretization followed by the thermo-electric FEM formulation in section 2.1.2. A co-rotational formulation is used to account for large nonlinear rotations of the organs due to manipulation by the surgical tools. Time integration schemes are presented in section 2.1.3.
2.1.1. Linear elastodynamics
The elasticity model is based on linear continuum elasticity theory [27]. We use the finite element method with linear displacement tetrahedral to solve the governing equation [21].
Then the displacement field is discretized as
| (1) |
where Ne(x) is a 3×12 matrix that contains the shape functions of the tetrahedral element and Ue(t) =[u1, v1, w1,…, u4, v4, w4]T is nodal point displacement vector [16].
Hence, the discretized problem corresponding to equation (6) is
| (2) |
subject to
| (3) |
| (4) |
| (5) |
where M is the global mass matrix assembled using element consistent mass matrices , C is the viscous Rayleigh damping matrix with C =αM + βK α and β being the damping constants [17] and K is the global stiffness matrix assembled using element stiffness matrices where E is a 6 × 6 elasticity matrix which, for isotropic materials, depends on two scalars - the Young’s modulus and the Poisson’s ratio - and the strain- displacement matrix Be = ∇Ne can be pre-computed for every tetrahedron, Fe = ∫Ve f · Ne dV +∫Γe h · NedΓ is the vector of external nodal point forces where f is the vector of body forces and h is the vector of natural boundary conditions.
To account for large rotations, the stiffness matrix and force vector are corrected using the co-rotational framework [5], [18].
| (6) |
| (7) |
where Re is the element rotation matrix with respect to the element’s barycenter, is the nodal coordinate vector of the element in initial configuration (t=0), Fe is the elemental internal force vector. These elemental force vectors are assembled at each time step. The element wise rotations are computed using polar decomposition.
2.1.2. Thermo-electric FEM formulation
During electrosurgery, alternating current is used to directly heat the tissue, while the probe tip remains relatively cool. The temperature distribution T (x, t) in the tissue is governed by the following bio-heat differential equation [19]:
| (8) |
where is the Laplace operator, k is the thermal conductivity of the tissue, wb is the effective blood perfusion parameter, cb is the blood heat capacity, Ta is the blood inlet temperature or steady state temperature of the tissue, qm is the metabolic heat generation rate of the tissue and qg is the externally induced heat generation rate due to electrosurgical heating. In this work, qm and wb are both assumed to be negligible as the energy input into the tissue is much greater than that produced during metabolism and compression of the tissue from the electrode inhibits local blood flow. Hence, equation (8) can be written as
| (9) |
At the frequencies employed and within the area of interest, the tissues can be considered purely resistive, because the displacement currents are negligible. For this reason, a quasi-static approach is usually employed to resolve the electrical problem. The distributed heat source qg is given by
| (10) |
where J is the current density (A/m2), and E is the electric field intensity (V/m). These two vectors are evaluated using Laplace’s equation [20]:
| (11) |
where V is the potential (V) and σ is the electrical conductivity (S/m). Assuming the electrical conductivity is constant, Laplace’s equation can be solved independently. The electric potential can be solved efficiently over the entire volume and the solution can be implemented into the source term of the heat conduction equation.
As the effect of heat radiation is considered insignificant, the major boundary conditions are convective heat loss from the surface Γh of the organ given by
| (12) |
where h is convection heat transfer coefficient, Ta is the ambient temperature and n is the unit outward normal on the boundary. Then, the discretized problem corresponding to equation (9) is
| (13) |
where CT is the heat capacity matrix, KT is the heat conductivity matrix, Q is the heat supply vector, T is vector of nodal point temperatures, and Ṫ is the time derivative of T with the following expressions:
| (14) |
| (15) |
| (16) |
where N is the matrix of shape functions. Then, the electrical boundary conditions are insulating conditions ((σ∇V)·n = 0), electric ground condition (V =0), and energy input condition at the contacting area between the electrode and tissue (V ≠ 0). Therefore, the discretized problem corresponding to equation (11) is
| (17) |
where Ke = ∫Ve σ(∇N)T·(∇N)dV, S = ∫Γh (σN·∇V)·ndΓ.
Then, we can use the equation qg = J·E = σ(∇V)2 to get the source term of the heat conduction equation.
2.1.3. Time integration
Time integration in equation (2) is performed using the Newmark-beta method [21]. The resulting set of discretized equations is of the following form
| (18) |
where Keff = K +a0M +a1C is the effective stiffness matrix and Feff(t + Δt) = F(t) + M[a0U(t) + a2U̇(t) + a3Ü(t)] + C[a1U(t) + a4U̇(t) + a5Ü(t)] is the effective force vector (a0 ~ a5 are Newmark constants).
For heat transfer equation (9), we use the following central difference scheme:
| (19) |
where T1 = T(t + (Δt/2)), T0 = T(t − (Δt/2)) and Δt is the time step. The resulting set of equations to be solved at a given time step is
| (20) |
2.2. Isotherm-based dual mesh algorithm
An electrosurgical tool works by vaporizing nearby tissue. As the instrument tip moves through tissue, the model must be updated at each time step. This amounts to locally remeshing and regenerating the global stiffness matrix at every time step, which is prohibitively expensive and would not allow real-time interactive simulation. Also, remeshing at every time step may result in irregular element shapes which result in poor solution accuracy. The dual mesh algorithm developed in this paper overcomes this problem by dynamically computing a surface mesh for graphical output. This visual surface is derived from the simulation’s tetrahedral mesh and the temperature distribution. Portions of the finite element mesh that exceed a critical vaporization temperature (Tv) are visually removed from the visual surface. However, for physics-based computations, a finite element is not removed until all its nodes have temperatures in excess of Tv. The algorithm is first summarized below and then explained in detail.
2.2.1. Isotherm definition
The first step is to define the Tv isotherms. Assuming T1 and T2 are the nodal temperatures on an element edge, if T1 < Tv and T2 > Tv then the isotherm intersects the edge at
| (21) |
where X1, X2 and Xc are the coordinates of the two end nodes and the intersecting node on the edge, a = (Tv − T1)/(T2 − T1).
For a tetrahedral finite element, the following four cases may occur:
Case 1: Temperatures of all four nodes are ≤ Tv. In this case the element remains intact and is considered for both deformation and temperature computations.
Case 2: Temperatures of all four nodes are ≥ Tv. In this case the element is removed from the mesh and not considered for deformation and temperature computations.
Case 3: Temperatures of one or three nodes exceed Tv. In this case the isotherm is represented by a plane defined by three points. Portion of the tetrahedron with temperature exceeding Tv is removed for visual rendering only. The tetrahedron is, however, considered for both deformation and temperature computations. As shown in Figure 1, plane EFG represents the isotherm, and the tetrahedron AEFG is removed from the mesh for visual rendering purpose only.
Case 4: Temperatures of two nodes exceed Tv. In this case the isotherm is represented by a plane defined by four points. Portion of the tetrahedron with temperature exceeding Tv is removed for visual rendering only. The tetrahedron is, however, considered for both deformation and temperature computations. As shown in Figure 2, plane EFGH represents the isotherm and the polyhedron ABEFGH is removed from the mesh for visual rendering purpose only.
Figure 1.

Case 3. (a) with the temperature of node A of the tetrahedral element exceeding the threshold temperature. (b) resulting in the visual surface EFG.
Figure 2.
Case 4. (a) with temperature of two nodes A, B exceeding the threshold temperature (b) resulting in the visual surface EFGH.
As the electrosurgery tip moves away, due to conductive heat loss, some of the nodes will cool down to temperatures below Tv. However, the cutting procedure is irreversible. This is implemented by recording the highest temperature of every node in the electrosurgery process and using that temperature to define the final isotherm.
2.2.2. Visual rendering
In our simulation, only the surface of the model is visually rendered. During initialization, each face of each tetrahedron is labeled as either a surface face or an interior face. If a tetrahedron is cut by the Tv isotherm (shown as the purple contour in Figure 3a), new element faces are created and portions of existing elements are removed based on the algorithm described above. The new faces are added to the rendering buffer.
Figure 3.
A two-dimensional illustration of splitting of nodes with temperatures greater than the threshold temperature (red) in (a) into two nodes each shown in (b). The direction of split is chosen based on the temperatures of neighboring nodes as shown in (c), (d).
As mentioned above, a tetrahedron is not removed from the mesh until all its nodes have temperatures exceeding Tv. This may cause visual artifacts in rendering the deformation as the mesh for deformation computation remains unchanged. To overcome this problem, we split the nodes along the normal to the plane defined by three nodes with the highest temperatures, as shown in Figure 3.
The dual mesh algorithm enables us to consider the visual rendering and physical computation separately, and also the two procedures are conducted in different threads. Hence, although the mesh complexity dynamics during the rendering procedure will lead to a slight increase in time due to the increase in the number of elements involved in the cuts (0.4~15 miliseconds), it will not affect the subsequent physical computation. The mesh for physical simulation changes only when the temperatures at all nodes of a tetrahedron exceed the isotherm. Therefore, the accuracy and computational cost of physical simulation are determined by the size of physical mesh itself.
2.3. Fast matrix updates
During the electrosurgery process new nodes are created by node splitting and nodes are removed when the temperature of all nodes of a single tetrahedron exceed the threshold. When a new node is added during splitting, some of the old connections must be deleted and connections to the new nodes created. Since each edge corresponds to a 3×3 block in the global stiffness matrix, the sparse structures have to be modified based on the nodal addition or deletion. Hence, a block-based storage structure is suitable for dealing with the nodal addition and deletion. Additionally, the block compressed row storage (BCRS) scheme exploits non-zero elements in contiguous locations by packing. If we know the column index of the first nonzero element in a block, then we also know the column indices of all the other nonzero elements. In other words, only one memory indirection is required for each block [22].
The FEM deformation matrices are block-sparse and we apply the block compressed row format storage as shown in Figure 4. To store a sparse matrix K, we encode the non-zero entries and their respective column indices in two separate arrays in a row-wise fashion. Additionally, an index is stored for every row, which references the first non-zero entry in that row.
Figure 4.

Block compressed row storage scheme.
If the node is split and if one edge linking nodes i and j (i < j) is deleted then 3×3 blocks Aij and Aji need to be removed in the BCRS structure. So the size of data block is minus 2, the same as the size of column index. As shown in Figure 5, the data block and column index move 1 unit between Aij and Aji, 2 units after Aji. Similarly if a new edge is added, one has to expand the arrays to add an additional 3×3 block. As shown in Figure 6, in case a new node is created, the size of the global stiffness matrix is increased by 3 and the new row is filled according to the nodal connections [23].
Figure 5.
Scheme for deleting one edge.
Figure 6.

Matrix manipulations to add a new node.
Node splitting also creates a new node and its corresponding edges have to be established. First a new row is appended in the BCRS structure and all the deleted connections of its parent node are established. The edges that the split nodes have are governed by the cutting plane as shown in Figure 3.
In the thermo-electric coupled model, each node is associated with a single scalar variable; hence a compressed row storage structure (CRS) is used. Only one non-zero value is added or deleted according to procedure described above.
3. Results
As our target is a low-cost simulator, performance is measured on modest hardware: an Intel Core 2 Quad Q9550 CPU and NVIDIA GTX 280 graphics processor. Two PHANToM Omni haptic interface devices are used for input and force feedback and OpenGL is used as the graphic rendering environments. During the simulation, physics updates (including deformation, heat transfer, current density flow and node splitting) average around 50 Hz; graphics and haptics rendering are around 60 Hz and 1000 Hz, respectively. The electrosurgical tools are modeled based on real surgical tools in Autodesk 3DS Max software. Four execution threads are used, one each for isothermal rendering, collision detection, physics update and force rendering. Figure 7 shows an overview of the simulation.
Figure 7.

Overview of the components of the overall simulation system.
In the present simulation we use the material properties as listed in table 1. These properties are based on the study conducted by Carter and Doddle [7], [24].
Table 1.
The physical properties of tissue used in the simulation
| Parameter | Simulation value |
|---|---|
| Young’s Modulus (N/m2) | 2.7×105 |
| Poisson’s Ratio | 0.4 |
| Thermal conductivity (W/m·K) | 0.512 |
| Density (kg/m3) | 1060 |
| Specific heat (J/kg·K) | 3600 |
| Electric conductivity (S/m) | 0.33 |
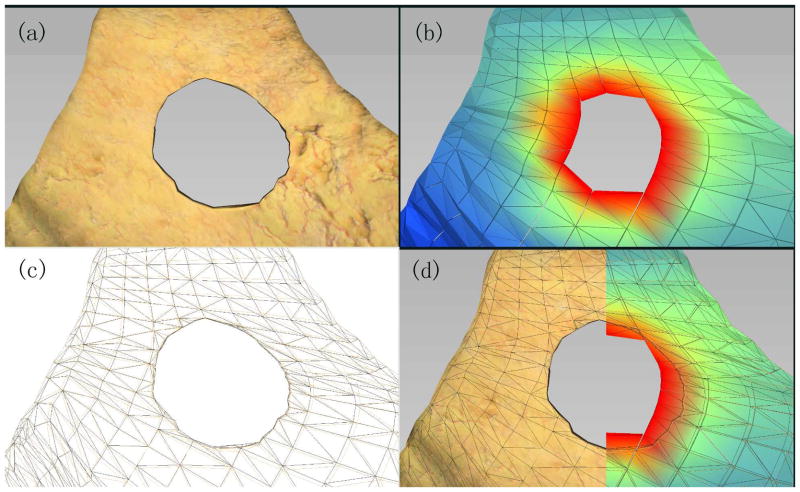
The effects of dual mesh algorithm based on isotherm rendering are shown in Figure 8. Note that the computationally expensive remeshing process is avoided, yet the displayed geometry shows fine details around the region of vaporization. This improved visual accuracy is physically correct, as it is derived from the temperature model. During training surgical procedures, the physical fidelity of our simulator can enable trainees to obtain near realistic response by adjusting energy input parameters. This is not possible with simulators that use simple geometry-based heat characterization. In addition, the mesh as shown in Figure 8(c) is used only for rendering purpose while the mesh in Figure 8(b) is used for multi-physics computation. Thus the very small elements or badly shaped elements (i.e. slivers) appearing in the vicinity of cuts of Figure 8(c) will not cause simulation slowdown or ill-conditioning and the element count will not dramatically increase, which is essential for real-time simulation.
Figure 8.
(a) Geometric rendering of the cut part of the tissue based on isotherm (b) corresponding mesh for the underlying physics simulation (c) mesh used for rendering based on isotherm and (d) comparison between the simulation mesh and the rendering mesh.
Figure 9 shows the simulation results of multi-physics computation: deformation, electric potential distribution and temperature distribution, respectively.
Figure 9.
An example of progressive vaporization (from left to right) due to a stationary electrosurgical instrument (not shown) on a thin tissue. The three finite element models (a) deformation, (b) electric potential and (c) temperature are shown.
Figure 10 shows an example tetrahedral mesh with 1022 nodes representing a human liver. Table 2 provides the computational time required for each stage of simulation. The execution time for deformation, heat transfer and current flow are stable while the time consumed in isotherm rendering ranges between 0.4 and 15 milliseconds. This large variation in computational load is due to the varying number of tetrahedral intersecting the isotherm. The isotherm rendering is conducted in a different thread.
Figure 10.

(a) The visual rendering of cauterized portion of the liver (b) the underlying tetrahedral model color-mapped based on the temperature.
Table 2.
Computational time of simulation components (liver mesh in Figure 10)
| Process | Time (milliseconds) |
|---|---|
| Deformation | 18~19 |
| Heat transfer | 1.5~1.6 |
| Current flow | 1.5~1.6 |
| Isotherm rendering | 0.4~15 |
Figure 11 shows the computation time in updating the deformation, nodal temperature and current density within each iteration. A preconditioned conjugate gradient iterative solver is used with a tolerance of 10−6 for the deformation, temperature and current density updates. As expected, the deformation update required more computation, as the degrees of freedom of the deformation model is three times that of the temperature or electrical models. Additionally, the co-rotational method is used in the deformation simulation in order to solve large nonlinear rotations. This requires additional computation cost.
Figure 11.
Comparison of the execution time for updating the nodal displacement, temperature and current density.
Cutting through vaporization is implemented using the algorithm described in section 2.2. The main cost in cutting is associated with isotherm definition, nodal splitting and the resulting modification of the sparse structures. A comparison of the costs of rebuilding the sparse matrix directly versus using the BCRS method is shown in Figure 12. The comparison is made with respect to the mesh sizes which are proportional to the array sizes in the BCRS. A speed up of at least 270% is observed. In order to reach an update rate of 30 Hz for real time graphics, the corresponding numbers of tetrahedral of the two methods are about 1500 and 3450. Hence, more realistic and detailed cutting can be conducted using our method.
Figure 12.
Comparison of the time for node splitting and corresponding sparse matrix manipulation using direct method and using BCRS structure for various size of cuts.
Figure 13 shows screenshots of a real time simulation scenario for a virtual laparoscopic adjustable gastric banding (LAGB) surgical procedure. This is the mostly widely used procedure in the United States for achieving weight loss in a reversible manner [25].
Figure 13.

Snapshot of an interactive electrosurgery simulation. Note the increased graphical detail (a) due to the isotherm rendering approach (b) compared to the tetrahedral temperature model.
4. Discussion
In this paper we have presented an algorithm for real-time multi-physics-based interactive electrosurgical simulations, with a coarse tetrahedral volumetric mesh for computing deformations, current flow and temperature fields and a detailed surface mesh for isotherm-based visual rendering. To account for large rotations, a co-rotational deformation method is used. A block compressed row storage structure is used to solve the sparse matrices, which is shown to greatly reduce the computational expense of tetrahedron removal. The algorithm has been successfully incorporated into an existing surgical simulator [25].
At this point, the only tissue effect is vaporization. Other temperature-dependent tissue effects, particularly desiccation, denaturation and charring, are important [26] and will be incorporated as part of future work. In addition, we plan to incorporate other visible tissue changes, such as in color, subsurface scattering and transparency, due to changes in temperature and deformation. Such changes would further enhance the visual fidelity of the simulator. Further, the simulator requires physical contact between the tissue and the instrument to conduct electricity, ignoring the possibility of electrical arcs through the intervening air.
As described above, our dual mesh algorithm separates physics computations with the visual rendering procedure. The algorithm avoids the complexity of simulating the underlying physics on the locally tessellated mesh near the tool tip during electrosurgery. This of course comes at the cost of sacrificing accuracy of physics computation near the tool tip. We will leave the accurate computation of physics near the tool tip over the tessellated mesh as a future work.
Finally, in this work we have performed elastodynamic computations which are decoupled from the thermo-electrical simulations. Performing a fully coupled mechanical-thermal-electrical simulation may improve physical realism and simulation accuracy, but will be more expensive. Hence novel algorithms may need to be developed. This is thus left as future work. Experimental techniques are being developed to measure more accurate tissue properties for a variety of tissue types and states.
Given the current widespread use of electrosurgery and the limitations of existing electrosurgery training systems, an inexpensive and physically accurate simulator has the potential to greatly improve physician skills training. This work provides the first physically accurate electrical heating model in a real time surgery simulator. The novel isotherm surface algorithm provides greatly improved visual detail while bypassing the computational complexity of standard remeshing approaches. These contributions combine to produce a detailed physical simulation of electrosurgery in real time.
Acknowledgments
Grant
Support of this work through the NIH/NIBIB grant # 1R01EB014305-01A1.
The authors gratefully acknowledge the support of this study by NIH/NIBIB (Grant No. 1R01EB014305-01A1).
Contributor Information
Zhonghua Lu, Intelligent Manufacture and Control Institution at Wuhan University of Technology, Wuhan, China.
Venkata S Arikatla, Department of Mechanical, Aerospace and Nuclear Engineering, at Rensselaer Polytechnic Institute, Troy, USA.
Zhongqing Han, Department of Mechanical, Aerospace and Nuclear Engineering, at Rensselaer Polytechnic Institute, Troy, USA.
Brian F. Allen, Department of Mechanical, Aerospace and Nuclear Engineering, at Rensselaer Polytechnic Institute, Troy, USA.
Suvranu De, Department of Mechanical, Aerospace and Nuclear Engineering, at Rensselaer Polytechnic Institute, Troy, NY, USA.
References
- 1.Liane F, Pascal F, Daniel JB. The SAGES Manual on the Fundamental Use of Surgical Energy (FUSE) Springer; [Google Scholar]
- 2.Pearce JA. Electrosurgery. Wiley; [Google Scholar]
- 3.Fitzgerald JEF, Malik M, Ahmed I. A single-blind controlled study of electrocautery and ultrasonic scalpel smoke plumes in laparoscopic surgery. Surg Endosc. 2012 Feb;26(2):337–342. doi: 10.1007/s00464-011-1872-1. [DOI] [PubMed] [Google Scholar]
- 4.Lim YJ, Jin W, De S. On Some Recent Advances in Multimodal Surgery Simulation: A Hybrid Approach to Surgical Cutting and the Use of Video Images for Enhanced Realism. Presence: Teleoperators and Virtual Environments. 2007 Nov;16(6):563–583. [Google Scholar]
- 5.Müller M, Dorsey J, McMillan L, Jagnow R, Cutler B. Stable real-time deformations. Proceedings of the 2002 ACM SIGGRAPH/Eurographics symposium on Computer animation; New York, NY, USA. 2002. pp. 49–54. [Google Scholar]
- 6.Bro-Nielsen M, Cotin S. Real-time Volumetric Deformable Models for Surgery Simulation using Finite Elements and Condensation. Computer Graphics Forum. 1996;15(3):57–66. [Google Scholar]
- 7.Dodde RE, Miller SF, Geiger JD, Shih AJ. Thermal-Electric Finite Element Analysis and Experimental Validation of Bipolar Electrosurgical Cautery. J Manuf Sci Eng. 2008 Apr;130(2):021015–021015. [Google Scholar]
- 8.Maciel A, De S. Physics-based real time laparoscopic electrosurgery simulation. Stud Health Technol Inform. 2008;132:272–274. [PubMed] [Google Scholar]
- 9.Lu Z, Sankaranarayanan G, Deo D, Chen D, De S. Towards physics-based interactive simulation of electrocautery procedures using PhysX; 2010 IEEE Haptics Symposium; 2010. pp. 515–518. [Google Scholar]
- 10.Lu Z, Arikatla VS, Chen D, De S. Real-time electrocautery simulation for laparoscopic surgical environments. Stud Health Technol Inform. 2011;163:311–316. [PubMed] [Google Scholar]
- 11.Paz Jacob D. Electrocautery health and safety handbook of modern hospital safety. CRC Press; 1999. pp. 383–388. [Google Scholar]
- 12.De S, Deo D, Sankaranarayanan G, Arikatla VS. A Physics-driven Neural Networks-based Simulation System (PhyNNeSS) for multimodal interactive virtual environments involving nonlinear deformable objects. Presence (Camb) 2011 Aug;20(4):289–308. doi: 10.1162/pres_a_00054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Delingette H, Cotin S, Ayache N. A hybrid elastic model allowing real-time cutting, deformations and force-feedback for surgery training and simulation. Computer Animation, 1999. Proceedings. 1999:70–81. [Google Scholar]
- 14.Steinemann D, Harders M, Gross M, Szekely G. Hybrid Cutting of Deformable Solids. Virtual Reality Conference, 2006. 2006:35–42. [Google Scholar]
- 15.Kaplan L, Uribe JW. The acute effects of radiofrequency energy in articular cartilage: an in vitro study. Arthroscopy. 2000 Feb;16(1):2–5. doi: 10.1016/s0749-8063(00)90119-1. [DOI] [PubMed] [Google Scholar]
- 16.Müller M, Gross M. Interactive virtual materials. Proceedings of Graphics Interface 2004, School of Computer Science, University of Waterloo; Waterloo, Ontario, Canada. 2004. pp. 239–246. [Google Scholar]
- 17.Liu M, Gorman DG. Formulation of Rayleigh damping and its extensions. Computers & Structures. 1995 Oct;57(2):277–285. [Google Scholar]
- 18.Cakir O, Yazici R, Cakir O. Real-time cutting simulation based on stiffness-warped FEM. 24th International Symposium on Computer and Information Sciences, 2009. ISCIS 2009; 2009. pp. 721–724. [Google Scholar]
- 19.Pennes HH. Analysis of Tissue and Arterial Blood Temperatures in the Resting Human Forearm. J Appl Physiol. 1948 Aug;1(2):93–122. doi: 10.1152/jappl.1948.1.2.93. [DOI] [PubMed] [Google Scholar]
- 20.Berjano EJ. Theoretical modeling for radiofrequency ablation: state-of-the-art and challenges for the future. Biomed Eng Online. 2006 Apr;5:24. doi: 10.1186/1475-925X-5-24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bathe K-J. Finite Element Procedures. Prentice Hall; 2006. [Google Scholar]
- 22.Pinar A, Heath TM. Improving performance of sparse matrix-vector multiplication. Proceedings of the 1999 ACM/IEEE conference on Supercomputing (CDROM); New York, NY, USA. 1999. [Google Scholar]
- 23.Shahnaz R, Usman A, Chughtai IR. Review of Storage Techniques for Sparse Matrices. 9th International Multitopic Conference, IEEE INMIC 2005; 2005. pp. 1–7. [Google Scholar]
- 24.Carter FJ, Frank TG, Davies PJ, McLean D, Cuschieri A. Measurements and modelling of the compliance of human and porcine organs. Med Image Anal. 2001 Dec;5(4):231–236. doi: 10.1016/s1361-8415(01)00048-2. [DOI] [PubMed] [Google Scholar]
- 25.Sankaranarayanan G, Adair JD, Halic T, Gromski MA, Lu Z, Ahn W, Jones DB, De S. Validation of a novel laparoscopic adjustable gastric band simulator. Surg Endosc. 2011 Apr;25(4):1012–1018. doi: 10.1007/s00464-010-1306-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sankaranarayanan G, Resapu RR, Jones DB, Schwaitzberg S, De S. Common uses and cited complications of energy in surgery. Surg Endosc. 2013 Apr; doi: 10.1007/s00464-013-2823-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bower BF. Applied Mechanics of Solids. CRC press; 2010. [Google Scholar]