Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Jun 20;4:5376. doi: 10.1038/srep05376

Wetting failure of hydrophilic surfaces promoted by surface roughness

Meng-Hua Zhao 1, Xiao-Peng Chen 1,a, Qing Wang 2
PMCID: PMC4064338  PMID: 24948390

Abstract

Wetting failure is of vital importance to many physical phenomena, such as industrial coating and drop emission. Here we show when and how the surface roughness promotes the destabilization of a moving contact line on a hydrophilic surface. Beyond the balance of the driving force and viscous resistance where a stable wetting interface is sustained, wetting failure occurs and is modified by the roughness of the surface. The promoting effect arises only when the wetting velocity is high enough to create a gas-liquid-solid composite interface in the vicinity of the moving contact line, and it is a function of the intrinsic contact angle and proportion of solid tops. We propose a model to explain splashes of rough solid spheres impacting into liquids. It reveals a novel concept that dynamic wetting on hydrophilic rough surfaces can be similar to that on hydrophobic surfaces, and brings a new way to design surfaces with specific wetting properties.

Wetting phenomena are ubiquitous in biological activities1, liquid coating2,3,4,5,6, microfluidics7, etc. As a limiting case, wetting failure gives rise to abundant physical problems such as solid-liquid impact splashes8,9, drop emission10, and air entrainment in industrial coating2,3,4,5,6. Wetting dynamics on rough surfaces dates back to the experimental work by Cazabat11,12. He observed the spreading of the silicone oil on both smooth and rough glass surfaces, and revealed complex spreading regimes in addition to the traditional regimes of spreading driven by capillarity and gravity. With further experimental and theoretical studies of the contact line dynamics on ideally smooth surfaces13,14,15,16,17,18,19, the influences of roughness on dynamic wetting have been explored recently, e.g., hemi-wicking of superhydrophilic spreading20,21, coating limits on rough surfaces5,6, pinning potential by defects22, and topographically driven spreading23,24,25. However, most present studies only consider one certain aspect such as superwetting limit20,22,23,24,25, superhydrophobic limit26, and low capillary number limit20,22,23,24,25. Clarke5 and Benkreira6 carried on experiments to determine how the roughness modifies the wetting failure systematically outside of those limits; however, no explanation was provided to describe when and how the roughness effects occur on an arbitrary hydrophilic surface.

The impact of a solid sphere onto a liquid pool provides a very ingenious and economical way for the study8 on the effect of surface roughness on dynamic wetting. The promotion of the wetting failure is observed in our experiments and there are currently no convincing explanations available. In fact, the enhancement of dynamic wetting has been observed in previous studies23,24,25, which showed dynamic influences of roughness on the superhydrophilic drop spreading and discovered a simple modified power law relationship between the edge speed and dynamic contact angle. The experimental and theoretical work, albeit falling into the limits of low spreading speed and superwetting regimes, indicates that the wetting dynamics is strongly dependent on the surface roughness. However, when the static contact angle is finite or the wetting velocity is high (corresponding to a relatively high capillary number), what will happen? Will the wetting process be enhanced or inhibited by the surface roughness?

In this paper, by observing the spreading film generated by the solid-water impact experimentally, similar to what has been performed by other groups before8,9,27, we are going to explore when the promoting effect on wetting failure will occur by providing a criterion to predict the appearance of a liquid-gas-solid composite interface in the vicinity of the moving contact line (MCL). We will also show how the promoting effect works based on the contact-line instability induced by the imbalance between the capillary driving force and viscous friction force8,10,17,19,24.

Results

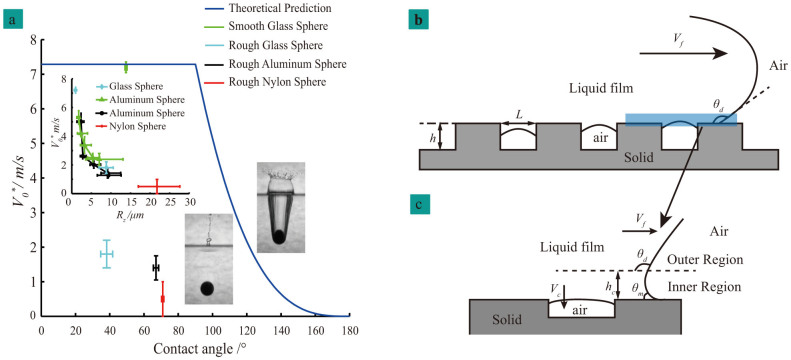
The stability of the thin liquid film climbing on an impact body, which is relevant to surface roughness, determines whether an air cavity will be created or not5,6,19(as illustrated in Fig. 1). On impacting into a water pool, a smooth sphere partly roughened by the abrasive sanding process shows complex splash patterns: a distinct air cavity is created along the sanding patch where a typical sawtooth-shaped MCL is always observed, while a well-developed MCL in the smooth portion moves smoothly up along the sphere periphery. Since the physical and chemical parameters in and out of the patch are identical, except for the static contact angle and surface roughness, it can be sure that these two parameters make the difference. Detailed results on the wetting failure of statically hydrophilic spheres with various roughness and materials are depicted in Fig. 2 (see Tables S1–4 for more details), which indicates a strong dependence of wetting failure on the surface roughness.

Figure 1. Splashes generated by a partly roughened glass sphere impacting into water pool with velocity 3.6 ms−1.

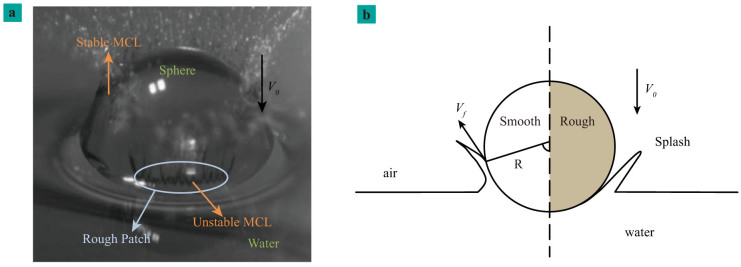
Figure 1

Open in a new tab

When a glass sphere partly roughened with sandpapers impacts into the initially quiescent water pool (a), a water film generated by the impact propagates in different manners. On the roughened patch, the film detaches from the sphere surface and induces a big cavity, as illustrated by the right half of the sphere in (b); however, on the smooth periphery, the film moves well up conforming to the sphere surface, as illustrated by the left half of the sphere in (b). The behavior of the water film is a dynamic wetting phenomenon and the static wetting property of the surface is a key factor in determining the stability of MCL8,10,18 marked in (a). Static contact angles of the smooth and rough part of the sphere are about 49.5° and 38.2°, respectively; thus, the roughness promotes wetting failure significantly in comparison with previous predictions and experiments8,10,19. (b) is the schematic of splashes on a half roughened surface. V0 and Vf are the impact velocity of sphere and wetting velocity of the water film, respectively. Vf ≈ ζV08,34,35. The thickness of splash, δfilm, is on the scale of a millimeter35.

Figure 2. Wetting failure velocity versus static contact angle and surface roughness (a) and schematic of a water film moving on the surface topography (b), (c).

Figure 2

Open in a new tab

The blue curve in (a) is extracted from the experimental data and theory8,10. Inset images are experimental snapshots of 30 ms after impact for two identical aluminum spheres, with diameter 25.4 mm and impact velocity 2.9 ms−1, except for their surface roughness (Left, Rz = 2.37 μm; Right, Rz = 9.35 μm). Above the blue curve in (a)8,10,19, a big cavity is always observed for a smooth surface (the cavity forming entry), while below the curve, no cavity is created (the silent entry). In sharp contrast to this prediction, the surface roughness on a statically hydrophilic surface decreases the wetting failure velocity, Vf*, significantly, as depicted in the inset of (a). Further, a rough surface is artificially approximated as a smooth surface patterned by capillaries (b), and the characteristic depth h and diameter L of capillaries are determined experimentally and statistically. Near the moving contact line (b), two regions10,19 are defined (c) according to the transition length hc. In the outer region, the profile of the film is dominated by external forces and capillarity, and the dynamic contact angle θd is observed10,16,17,18,19. In the inner region, the interface is mainly portrayed by the capillarity and viscous friction force, and it meets the solid at a truncated length scale hm with a microscopic contact angle θm10,16,17,18,19. When the water film moves on the topography, not only will the liquid front advance in the direction parallel to the surface with velocity Vf, but also it will fill up the valleys of the topography in the vertical direction with a speed Vc.

Discussion

Figure 2a demonstrates that the surface roughness plays more evident roles than the static contact angle. A crucial question is evoked: how could the surface roughness decrease the wetting failure velocity in such a generic manner? Multi-scale forces are involved in propagating the water film8,10,19,24: external force, capillarity, and viscous stresses. In the inner region as depicted in Fig. 2c, the viscous friction force and capillarity dominate the bending of the interface. While in the outer region out of a characteristic length hc from the surface wall, capillarity and the external forces, such as inertia and gravity, are dominant ones to sustain the balance. The characteristic length, hc, dividing the inner and outer region, is on the scale of the capillary length 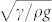Inline graphic, where γ is the surface tension between the liquid and air, ρ is the density, and g is the gravitational acceleration. A global stability of the advancing water film is achieved by an intimate matching of the boundary restrictions and outer interface through the inner region. The outer interface can always bend its profile to hold the outer balance, but there is a limitation for the inner region to achieve the matching17. Therefore the wetting failure always starts from the inner one. Consequently, to characterize the dynamic wetting failure, we cast our attention on the inner region.

In the inner region8,10,19,24, the capillary driving force could be considered as the rate of change of surface free energy. Based on that, we will show how the dynamic wetting behavior is modified by the topography into two regimes.

  • When a liquid film creeps on a rough surface at a low velocity, it advances conforming to the surface topography5. Thus, the change of surface free energy, when the contact line propagates by a distance dz, is modified as dE = r(γSL − γSV)dz + γcosθddz. In this equation, r, γSL, and γSV are the ratio of the actual surface to the projective area, the surface tension between the solid and the liquid, and the surface tension between the solid and the air, respectively. By employing the Wenzel equation21, we deduce the driving force dE/dz = γ(cosθW − cosθd). On a smooth surface with a static contact angle θY, this driving force is simply γ(cosθY − cosθd). As θW is smaller than θY, the driving force is enhanced by the surface roughness. More importantly, if the variation of the viscous dissipation due to the surface roughness is ignored, the dynamic wetting behavior is driven by the topography24.

  • However, when the liquid film skips from peak to peak on rough surfaces, composite liquid-air-solid interfaces will be induced by the MCL5. As the MCL moves by dz, the surface free energy changes by dE = fs(γSL − γSV)dz + (1 − fs)γ dz + γcosθddz, where fs is the fraction of solid tops. Consequently, the capillary driving force in this case is γ(cosθCB − cosθd), where θCB is calculated by the Cassie-Baxter equation21. If the viscous dissipation change is ignored, the dynamic wetting process is inhibited because the driving force is decreased.

Since the driving force in the inner region can always be written as γ (cosθm − cosθd), here we provide a tentative explanation for the ubiquitous microscopic contact angle θm in regard to the surface roughness. θm depends on the instantaneous state of the MCL: if the MCL propagates clinging to the topography, θm can be obtained by Wenzel equation; if the MCL propagates on tops of the topography, θm is calculated by Cassie-Baxter equation. The understanding is crucial to filling the full scope of wetting dynamics, and brings out a subtle mechanism in which the surface heterogeneity may hinder or facilitate the wetting motion. Before going further, another two significant questions arise: when will the effect of promoting and postponing the wetting failure occur, and what is the effect of surface roughness on the viscous friction force?

To obtain a reasonable driving force on rough surfaces, we approximate the rough surface as a smooth surface sculptured with arrays of vertical capillaries (as shown in Fig. 2b and c) and analyze the criterion at which the Wenzel to Cassie-Baxter state transition appears. Therefore, it is worth considering the case that a liquid film passes over one single capillary and comparing two time scales: τc which is the time scale of filling up the gap with the liquid and τf which is the time scale of the MCL moving over the opening of the capillary with the advancing velocity of Vf. The ratio, Σ = τc/τf > 1, is therefore proposed as the criterion for establishing the forced Cassie-Baxter state, in which case air is sealed in topography valleys and thus the wetting film front moves on a liquid-air-solid composite surface. The invading of the liquid into the valley is considered as a spontaneous wetting process in a capillary, which is shown in Fig. 3. Since τc is calculated based on a free capillary rise28, it is rather under-estimated due to the neglect of the impedance of the contact area, inlet sharp edge, air pressure, etc. As to the viscous friction force, the influence of topography is expected to be marginal8,29,31,32,33. By taking the two aspects, i.e. capillary driving force and viscous resistance, into consideration, the dynamic contact angle on the rough surface is larger than that on the smooth one at the same wetting velocity if the two surfaces (smooth and rough) have the same static contact angle θe, when the Wenzel to Cassie-Baxter transition occurs. As a result, the dynamic wetting is inhibited.

Figure 3. Capillary tube rise of low viscosity liquid27.

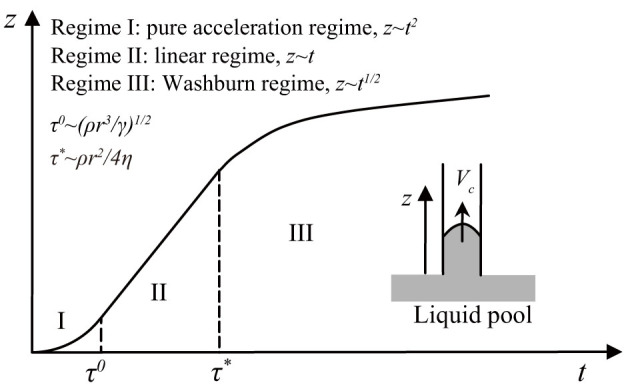
Figure 3

Open in a new tab

r, z, ρ, γ, η, and Vcare the radius of a capillary tube, height of meniscus, liquid density, surface tension, viscosity, and meniscus rising velocity, respectively. The liquid-air interface of the liquid pool is located at z = 0 and the liquid starts to intrude into the capillary at t = 0. If the liquid is more viscous than gρ3/2r5/2γ−1/2, the capillary tube imbibition process can be divided into three stages28: acceleration, linear, and Washburn regimes (see Supplementary Information for the description of the capillary rise). Accordingly, Σ for a given system can be calculated (Table S5).

Now let us go back to the results summarized in Fig. 2a. First of all, for spheres with almost ideally smooth surfaces (the smooth glass sphere), the critical velocity agrees well with the theoretical prediction8,10, where the driving force is derived based on the deviation of the dynamic contact angle from static one and the viscous resistance including the contributions of the liquid (FL ≈ CμLvf) and the air (Fair ≈ (3μairl/[π − θd])vf)8,29,30. However, as to rough hydrophilic spheres, the critical velocity decreases drastically with the increasing of roughness plotted in Fig. 2(a), implying that effective driving force is reduced or the overall viscous friction force is increased in the diagram of hydrodynamic model. To find out the reasons, we detected sphere surfaces with roughmeter and SEM, and reconstructed their 3-D topography with the Laser Scanning Confocal Microscope. Results show that Σ > 1 (See Supplementary Information and Table S5 for more details) when the wetting velocity approaches the critical velocity. This implies that the MCL moves on an air-liquid-solid composite surface depicted in Fig. 2b. In this situation, the capillary driving force is decreased from γ (cosθe − cosθd) to γ(cosθCB − cosθd), as aforementioned. On the other hand, following Ybert's procedure32, the slip length induced by the surface roughness is no more than 5 μm, indicating that overall viscous resistance will not be altered more than 5%29,30,31,32,33. Thus the viscous dissipation is treated similar to that on a smooth surface or a hydrophobic surface with micro-roughness8,29. An obvious drop of the critical velocity is then expected. For rough surfaces, Duez and Ybert's threshold of impact velocity8,10,19 is explicitly modified as

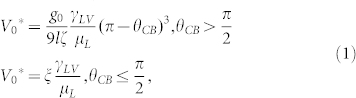graphic file with name srep05376-m1.jpg

where C, l, g0 are numerical pre-factors introduced to account for the liquid, air, and overall viscous dissipations8,29,30. These factors can be roughly determined through other more fundamental experiments. The value of l falls in the range of about 15 ~ 208,29,30, depending on details of interactions of the liquid and the solid substrate. g0 and C can be determined by balancing the viscous friction force and the capillary driving force when l is fixed. The dependence of g0 and C on l is numerically presented in supplementary information; their experimental values fall in the expected range8,15,29,30, verifying the validity of the model. ς is the ratio of the splash film velocity and impact velocity (~28,9,34,35). ξ is an experimentally and theoretically determined constant in that the increase of the capillary driving force with the surface hydrophilicity is almost neutralized by a simultaneously enhanced viscous resistance8,19,29 for hydrophilic surfaces. From equation (1), the critical capillary number remains the same for the revised contact angle θCB for an arbitrary rough hydrophilic surface. It agrees with the previous theoretical and experimental conclusions8,10,19. As is shown in Fig. 4 (Calculation parameters can be found in Tables S5 and Supplementary Information), the modified theoretical prediction agrees well with experimental results, which validates the feasibility of our model.

Figure 4. Air entrainment velocity after revising the driving force vs. theoretical predition.

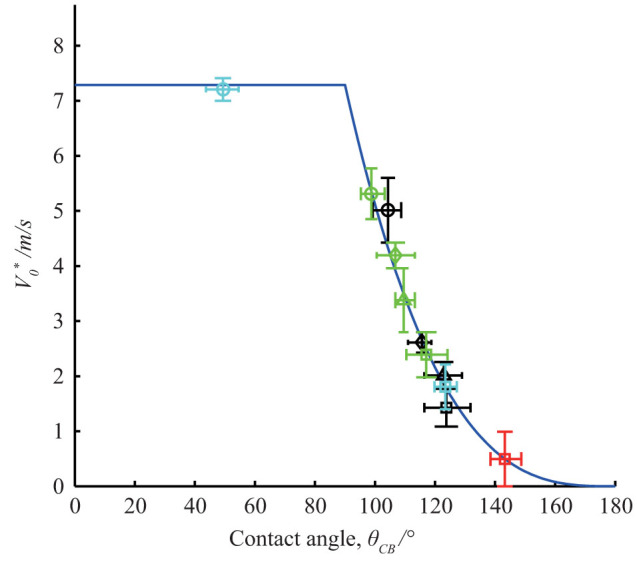
Figure 4

Open in a new tab

The x-axis coresponds to the Cassie-Baxter contact angle; the y-axis coresponds to the range of air entraiment velocities. Blue line is the theoretical prediction8,10. Different symbols stand for differet surfaces: smooth glass sphere(diameter = 48 mm, Rz = 0.96 μm; cyan circle), rough glass sphere(diameter = 48 mm, Rz = 8.83 μm; cyan square), aluminum sphere I (diameter = 25.4 mm, Rz = 2.37 μm; black circle), aluminum sphere II (diameter = 25.4 mm, Rz = 2.83 μm; black diamond), aluminum sphere III (diameter = 25.4 mm, Rz = 5.61 μm; black triangle), aluminum sphere IV (diameter = 25.4 mm, Rz = 9.16 μm; black square), aluminum sphere V (diameter = 30 mm, Rz = 1.76 μm; green circle), aluminum sphere VI(diameter = 30 mm, Rz = 2.3 μm; green diamond), aluminum sphere VII(diameter = 30 mm, Rz = 3.25 μm; green triangle), aluminum sphere VIII (diameter = 30 mm, Rz = 7.02 μm; green square), rough nylon sphere(diameter = 50 mm, Rz = 21.77 μm; red square). Intrintic contact angle θY are experimentally extracted as 37.4°, 76.5°, 59.2°and 71.2° for glass sphere, aluminum sphere I–IV (diameter = 25.4 mm), aluminum sphere V–VII (diameter = 30 mm) and nylon sphere, respectively.

In conclusion, we have demonstrated a hidden mechanism for the wetting failure promoted by surface roughness. The surface roughness can modify wetting dynamics by changing the capillary driving force in the inner region. At a low wetting velocity, the roughness of a hydrophilic surface enhances the wetting process. As the wetting velocity increases to a critical value, the Wenzel to Cassie-Baxter transition occurs and the surface roughness starts to inhibit wetting. This mechanism is different from the conventional theory on roughness-induced wettability, and it provides a new prospective to understanding the ubiquitous micro-contact angle and opens a novel way to design specific rough surfaces.

Methods

Experimental setup

The apparatus used for determining the critical velocity of the water impact is detailed in our previous work27. High speed camera was set at the frequency of 2000 frames per second, and the shot images were used to identify wetting failure transition and calculate the impacting velocity. The critical velocity for each sphere was obtained by averaging high speed camera data from at least 3 runs to ensure the repeatability of results. Before each run, spheres were cleaned in the deionised water and dried naturally in lab conditions. Experimental temperature was stabilized at 20 ± 2°C.

Surface treatment and measurement

Spheres used were aluminum (diameter, 25.4 mm and 30 mm), nylon (diameter, 50 mm) and glass spheres (diameter, 48 mm). Different addictive materials were added to aluminum spheres with different diameters. The surface roughness was acquired by an abrasive sanding process with the grit size in the range of 150 ~ 2000-grit and quantitatively measured by a roughmeter. Measurement parameters of the roughmeter were set as Lt = 1.75 mm, Lc = 0.25 mm, and n = 5. Static contact angles of different surfaces were measured by a contact angle meter, OCA15EC of DataPhysics Instruments, using the standard sessile drop method. Surfaces were detected further by SEM and Laser Scanning Confocal Microscope, Olympus LEXT OLS4000, and their 3-D patterns were reconstructed according to the data obtained. The material ratio rate with regard to the altitude of the 3-D surface was used to determine the ideal smooth surface (the reference plane), and then the surface characteristic length and the ratio of solid tops were calculated based on the reference plane. The length scale of the detection area was at least five times of the surface characteristic length.

Author Contributions

M.H.Z. conducted experiments, analyzed the data, performed the study on theories of moving contact lines; X.P.C. supervised the program, performed the study on theories of moving contact lines; Q.W. conducted parts of the data and image analyses. All authors discussed the results and models, and commented on the manuscript.

Supplementary Material

Supplementary Information

Table 1

srep05376-s1.xls (32KB, xls)
Supplementary Information

Table 2

srep05376-s2.xls (25KB, xls)
Supplementary Information

Table 3

srep05376-s3.xls (21.5KB, xls)
Supplementary Information

Table 4

srep05376-s4.xls (24KB, xls)
Supplementary Information

Table 5

srep05376-s5.xls (29KB, xls)
Supplementary Information

Supplymentary Information

srep05376-s6.doc (40KB, doc)

Acknowledgments

We thank Doctor T.D. Blake, Professor P. –T. Yue for serious discussions and reading of the manuscript, F. -C. Yang, Y. Yu, L. Lu and C.-L. Zhang for conducting part of experiments. This work is funded by the National Natural Science Foundation of China (Grant No. 11172241) and the National High Technology Research and Development Programs of China (Grant No. 2012AA011803).

References

  1. Parker A. R. & Lawrence C. R. Water capture by a desert beetle. Nature 414, 33–34 (2001). [DOI] [PubMed] [Google Scholar]
  2. Burley R. & Kennedy B. S. An experimental study of air entrainment at a solid/liquid/gas interface. Chem. Eng. Sci. 31, 901–911 (1976). [Google Scholar]
  3. Buonopane R. A., Gutoff E. B. & Rimore M. M. T. Effect of plunging tape surface properties on air entrainment velocity. AlChE J. 32, 682–683 (1986). [Google Scholar]
  4. Ghannam M. T. & Esmail M. N. Effect of substrate entry angle on air entrainment in liquid coating. AlChE J. 36, 1283–1286 (1990). [Google Scholar]
  5. Clarke A. Coating on a rough surface. AlChE J. 48, 2149–2156 (2002). [Google Scholar]
  6. Benkreira H. The effect of substrate roughness on air entrainment in dip coating. Chem. Eng. Sci. 59, 2745–2751 (2004). [Google Scholar]
  7. Atencia J. & Beebe D. J. Controlled microfluidic interfaces. Nature. 437, 648–655 (2004). [DOI] [PubMed] [Google Scholar]
  8. Duez C., Ybert C., Clanet C. & Bocquet L. Making a splash with water repellency. Nat. Phys. 3, 180–183 (2007). [Google Scholar]
  9. Aristoff J. M. & Bush J. W. Water entry of small hydrophobic spheres. J. Fluid Mech. 619, 45–78 (2009). [Google Scholar]
  10. Ledesma-Aguilar R., Nistal R., Hernández-Machado A. & Pagonabarraga I. Controlled drop emission by wetting properties in driven liquid filaments. Nat. Mater. 10, 367–371 (2011). [DOI] [PubMed] [Google Scholar]
  11. Cazabat A. M. & Stuart M. C. Dynamics of wetting: effects of surface roughness. J. Phys. Chem. 90, 5845–5849 (1986). [Google Scholar]
  12. Cazabat A. M. & Stuart M. C. Dynamics of wetting on smooth and rough surfaces. Prog. Colloid Polym. Sci. 74, 69–75 (1987). [Google Scholar]
  13. Huh C. & Scriven L. E. Hydrodynamic model of steady movement of a solid/liquid/fluid contact line. J. Colloid Interface Sci. 35, 85–101 (1971). [Google Scholar]
  14. Blake T. D. & Ruschak K. J. A maximum speed of wetting. Nature 282, 489–491 (1979). [Google Scholar]
  15. De Gennes P. G. Wetting: statics and dynamics. Rev. Mod. Phys. 57, 827–863 (1985). [Google Scholar]
  16. Voinov O. V. Hydrodynamics of wetting. Fluid Dynamics. 11, 714–721 (1976). [Google Scholar]
  17. Eggers J. Hydrodynamic theory of forced dewetting. Phys. Rev. Lett. 93, 094502 (2004). [DOI] [PubMed] [Google Scholar]
  18. Bonn D., Eggers J., Indekeu J., Meunier J., & Rolley E. Wetting and spreading. Rev. Mod. Phys. 81, 739–805 (2009). [Google Scholar]
  19. Ledesma-Aguilar R., Pagonabarraga I. & Hernández-Machado A. Theory of wetting-induced fluid entrainment by advancing contact lines on dry surfaces. Phys. Rev. Lett. 110, 264502 (2013). [DOI] [PubMed] [Google Scholar]
  20. Ishino C., Reyssat M., Reyssat E., Okumura K. & Quéré D. Wicking within forests of micropillars. Europhys. Lett. 79, 56005 (2007). [Google Scholar]
  21. Quéré D. Wetting and roughness. Annu. Rev. Mater. Res. 38, 71–99 (2008). [Google Scholar]
  22. Semal S., Blake T. D., Geskin V., De Ruijter M. J., Castelein G. & De Coninck J. Influence of surface roughness on wetting dynamics. Langmuir. 15, 8765–8770 (1999). [Google Scholar]
  23. McHale G. & Newton M. I. Frenkel's method and the dynamic wetting of heterogeneous planar surfaces. Colloids Surf., A. 206, 193–201 (2002). [Google Scholar]
  24. McHale G., Shirtcliffe N. J., Aqil S., Perry C. C. & Newton M. I. Topography driven spreading. Phys. Rev. Lett. 93, 036102 (2004). [DOI] [PubMed] [Google Scholar]
  25. McHale G., Newton M. I. & Shirtcliffe N. J. Dynamic wetting and spreading and the role of topography. J. Phys.: Condens. Matter. 21, 464122 (2009). [DOI] [PubMed] [Google Scholar]
  26. Richard D. & Quéré D. Viscous drops rolling on a tilted non-wettable solid. Europhys. Lett. 48, 286(1999). [Google Scholar]
  27. Zhao M. -H., & Chen X. -P. A combined data processing method on water impact force measurement. J. Hydrodyn. Ser. B. 24, 692–701 (2012). [Google Scholar]
  28. Quéré D. Inertial capillarity. Europhys. Lett. 39, 533 (1997). [Google Scholar]
  29. Duez C. Effets du mouillage en hydrodynamique macroscopique: traînée, impacts et ruissellement. Thesis, Université Claude Bernard - Lyon I. (2008).
  30. De Gennes P. G., Brochard-Wyart F. & Quéré D. Gouttes, Bulles, Perles et Ondes. Belin, Paris. 2005. [Google Scholar]
  31. Duez C., Ybert C., Barentin C., Cottin-Bizonne C. & Bocquet L. Dynamics of fakir liquids: from slip to splash. J. Adhes. Sci. Technol. 22, 335–351 (2008). [Google Scholar]
  32. Ybert C., Barentin C., Cottin-Bizonne C., Josep P. & Bocquet L. Achieving large slip with superhydrophobic surfaces: Scaling laws for generic geometries. Phys. Fluids. 19, 123601 (2007). [Google Scholar]
  33. Hyväluoma J, Harting J. Slip flow over structured surfaces with entrapped microbubbles. Phys. Rev. Lett. 100, 246001 (2008). [DOI] [PubMed] [Google Scholar]
  34. Oliver J. Water Entry and Related Problems. Thesis, Oxford Univ. (2002).
  35. Kubota Y. & Mochizuki O. Splash formation by a spherical body plunging into water. J. Visual-Japan. 12, 339–346 (2009). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Table 1

srep05376-s1.xls (32KB, xls)
Supplementary Information

Table 2

srep05376-s2.xls (25KB, xls)
Supplementary Information

Table 3

srep05376-s3.xls (21.5KB, xls)
Supplementary Information

Table 4

srep05376-s4.xls (24KB, xls)
Supplementary Information

Table 5

srep05376-s5.xls (29KB, xls)
Supplementary Information

Supplymentary Information

srep05376-s6.doc (40KB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES