Abstract
Electrophysiological recordings show intense neuronal firing during epileptic seizures leading to enhanced energy consumption. However, the relationship between oxygen metabolism and seizure patterns has not been well studied. Recent studies have developed fast and quantitative techniques to measure oxygen microdomain concentration during seizure events. In this article, we develop a biophysical model that accounts for these experimental observations. The model is an extension of the Hodgkin-Huxley formalism and includes the neuronal microenvironment dynamics of sodium, potassium, and oxygen concentrations. Our model accounts for metabolic energy consumption during and following seizure events. We can further account for the experimental observation that hypoxia can induce seizures, with seizures occurring only within a narrow range of tissue oxygen pressure. We also reproduce the interplay between excitatory and inhibitory neurons seen in experiments, accounting for the different oxygen levels observed during seizures in excitatory vs. inhibitory cell layers. Our findings offer a more comprehensive understanding of the complex interrelationship among seizures, ion dynamics, and energy metabolism.
Keywords: hippocampus, hypoxia, bifurcation, epilepsy, potassium
the brain consumes 20% of the body's metabolic energy with muscles and digestive system at rest, despite being only 2% of the human body mass (Attwell and Laughlin 2001). The majority of the brain's metabolic energy is dedicated to supporting neural spiking activity, most of which is used by Na+-K+-ATP pumps that transport 3Na+ outwards with 2K+ inwards against their concentration gradients (Erecińska and Dagani 1990; Attwell and Laughlin 2001; Lennie 2003). Oxygen is an essential element for brain activity due to its central role in producing adenosine triphosphate (ATP). A complete lack of oxygen will result in the death of brain cells within tens of minutes (Hochachka and Guppy 1987).
The delicate balance between energy supply and expenditure becomes critically strained in pathological brain activity such as seizures and spreading depression, during which excessive O2 demands transiently exceeded O2 supply (Bahar et al. 2006; Galeffi et al. 2011). Although such oxygen changes with high levels of neural activity are well known, and patterns of damage to selectively vulnerable areas of the brain well characterized (such as Sommer's sector in the hippocampus, see Aitken and Schiff 1986), the methodology to examine rapid oxygen changes at small spatiotemporal scales has only become recently available (Koo et al. 2004; Bahar et al. 2006). To improve the spatiotemporal limitations of O2 sensing, we designed a ratiometric nano quantum dot (NQD) fluorescence resonance energy transfer (FRET) excited optical sensor to rapidly measure interstitial oxygen quantitatively from single cell microdomains to an entire hippocampal slice with high spatiotemporal resolution (Ingram et al. 2013). In a companion article (Ingram et al. 2014), we used this and related technologies to perform experiments relating seizure activity at the cellular level with simultaneous real-time oxygen microdomain measurements.
To better understand the relationship between seizures and oxygen dynamics, we here construct a biophysical model to account for experimental observations. We extend the Hodgkin-Huxley formalism by including the dynamics of Na+ and K+ ion concentrations as well as oxygen homeostasis. These ion concentrations are coupled to Na+-K+-ATP pump activity, a simplified glia-endothelium system, and diffusive transport from either the bath solution in a slice preparation, or the vasculature in the intact brain (Cressman et al. 2009; Ullah et al. 2009; Ullah and Schiff 2009 2010). We focus on energy consumed by Na+-K+-ATP pump activity, because most of the energy expenditure in active neurons is due to restoring ion gradients (Lennie 2003). We here demonstrate that a computational model incorporating basic features of oxygen metabolism can account for the broader spectrum of experimental observations including differential oxygen consumption between layers in the hippocampus, the delays to restore the O2 deficit after intense activity, the mechanisms contributing to excitatory-inhibitory cell interplay, and how seizures can be supported only within a narrow range of tissue oxygen concentration (companion article, Ingram et al. 2014). Our work suggests the critical importance of modeling extracellular ion concentration and oxygen dynamics to properly understand the underlying mechanisms behind seizures and related phenomena.
MATERIALS AND METHODS
Our mathematical model builds on previous work (for review, see Schiff 2012). Instead of using constant ion concentrations, we modified the Hodgkin-Huxley formalism incorporating dynamics of sodium and potassium ion concentrations to account for the spontaneous periodic seizure events (Cressman et al. 2009; Ullah et al. 2009) observed in vitro following exposure to high extracellular [K+] (Traynelis and Dingledine 1988) or partial K+ channel blockade through 4-aminopyridine (4-AP) (Žiburkus et al. 2006, 2013). To investigate the relationship between seizures and available oxygen, we here add oxygen dynamics to the model.
Membrane potential dynamics.
We used a single compartment model to represent neurons in this study to focus on the fundamentals of how oxygen and energy availability alters the fundamental dynamics of the neuronal membrane. Nevertheless, we find that such simplistic modeling accounts for several of the important features of our experiments. Our model contains transient sodium currents, delayed rectifier potassium currents, and specific leak currents for sodium, potassium, and chloride ions. The dynamics of the membrane potential, V, are described with Hodgkin-Huxley equations:
| (1) |
where Iext is the external applied current or synaptic current from other neurons and INa and IK are the sodium and potassium currents passing through the voltage-gated ion channels including the sodium and potassium leak current, respectively. ICl is the chloride leak current. These currents can be expressed as:
| (2) |
where G represents conductance and the subscript L indicates the nonvoltage-sensitive leak. The activation and inactivation variables m, h, and n vary between 0 and 1 and represent the fraction of channels in the closed and open states. The parameters αm, βm, αh, βh, αn, and βn are opening and closing rate constants of the ion channel state transitions that are dependent on V. The equations of these rate constants are from a pyramidal cell model (Gloveli et al. 2005), originally derived from a model of hippocampal neurons (Traub et al. 1991), shown as follows:
| (3) |
The reversal potentials of Na+ (ENa), K+ (EK), and Cl− (ECl) are given by Nernst equations
| (4) |
where [·]i and [·]o represent concentrations inside and outside the cell, respectively. Unlike the Hodgkin-Huxley equations where various ion concentrations are fixed, our model adds potassium and sodium ion concentration dynamics. We do, however, assume that the chloride ion concentration is constant, with [Cl−]o = 130.0 mM and [Cl−]i = 6.0 mM (Cressman et al. 2009; Ullah et al. 2009). The units and description of all parameters used in this article are summarized in Table 1.
Table 1.
Overview of the parameters in the model
| Parameters | Units | Description |
|---|---|---|
| C | 1 μF/cm2 | Membrane capacitance |
| GNa | 30 mS/cm2 | Maximal conductance of sodium current |
| GK | 25 mS/cm2 | Maximal conductance of potassium current |
| GNaL | 0.0175 mS/cm2 | Conductance of leak sodium current |
| GKL | 0.05 mS/cm2 | Conductance of leak potassium current |
| GClL | 0.05 mS/cm2 | Conductance of leak chloride current |
| [Cl−]i | 6 mM | Intracellular chloride concentration |
| [Cl−]o | 130 mM | Extracellular chloride concentration |
| γ | 0.0445 (mM/s)/(μA/cm2) | Conversion factor current to concentration |
| β | 7 | Ratio of intra-/extracellular volume |
| ρmax | 1.25 mM/s | Maximal Na-K pump rate |
| Gglia | 8 mM/s | Glial uptake strength of potassium |
| εk | 0.33 s−1 | Potassium diffusion rate |
| [K+]bath | 4.0 mM | Normal bath potassium concentration |
| εo | 0.17 s−1 | Oxygen diffusion rate |
| α | 5.3 g/mol | Conversion factor from pump current to oxygen concentration change |
| λ | 1 | Relative cell density |
| [O2]bath | 32 mg/l | Normal bath oxygen concentration |
Ion concentration dynamics.
Each specific ion concentration is continuously updated by integrating the relevant ion currents. The extracellular potassium ion concentration, [K+]o, is a function of membrane potassium current (IK), the neuronal Na+-K+ pump current (Ipump), lateral diffusion of potassium (Idiff) from bath solution in vitro or blood vessel in vivo, glial uptake surrounding the neurons (Iglia) (Cressman et al. 2009), and glial Na+-K+ pump current (Igliapump) (Grisar 1984; Øyehaug et al. 2011)
| (5) |
where the dimensionless factor β = 7 accounts for the ratio of the intracellular volume to the extracellular volume and γ = A/(F × Vol) is a unit conversion factor that converts current from μA/cm2 into mM/s (Cressman et al. 2009). A and Vol are the surface area and the volume of the cell with a radius of 7 μm. F is the Faraday constant.
The intracellular sodium ion concentration, [Na+]i, is modeled based on the membrane sodium current (INa) and the Na+-K+ pump current (Ipump)
| (6) |
We suppose that the flow of Na+ into the cell is compensated by the flow of K+ out of the cell and the total amount of sodium is conserved (Cressman et al. 2009). Thus the intracellular potassium, [K+]i, and extracellular sodium, [Na+]o, concentration dynamics are
| (7) |
The activity of Na+-K+-ATP pump, largely independent of membrane potential, is modulated by [Na+]i, [K+]o, and ATP (Erecińska and Dagani 1990). The Na+-K+-ATP pump current can be expressed as (Cressman et al. 2009)
| (8) |
where ρ = ρmax is a maximal Na+-K+-ATP pump rate for the fully oxygenated state. The extracellular potassium is not only actively regulated by neurons but also by glial cells. Several mechanisms in the glial membrane contribute to the regulation of [K+]o, such as a glial Na+-K+-ATP pump (Grisar 1984; Øyehaug et al. 2011), the inwardly rectifying K+ channels (Øyehaug et al. 2011), and the Na-K-Cl cotransporter (Øyehaug et al. 2011). The Na-K pump strength is modified by one-third for glia in our model because the relative resting energy consumption in neurons vs. glia is ∼3:1 (Attwell and Laughlin 2001)
| (9) |
Here, we assume a fixed intracellular sodium concentration [Na+]gi = 18 mM in the glial compartment. The inward rectified K+ current and Na-K-Cl cotransporter are modeled as a simple glial buffer system for [K+]o
| (10) |
where Gglia is the maximal glial buffering rate of [K+]o. The diffusion of potassium from the distant perfusion bath potassium concentration ([K+]bath) to the extracellular space in a slice preparation is modeled by
| (11) |
where εk is the potassium diffusion constant (Cressman et al. 2009).
Oxygen concentration dynamics.
Oxygen is in such high demand in the brain in large part to support neural spiking activity. Oxygen metabolism in the neuron is used for restoring and maintaining ionic balances in soma, axon, dendrite, and synaptic sites. In our single compartment model, the oxygen consumption can be estimated by the activity of Na+-K+-ATP pumps that transport 3Na+ outwards with 2K+ inward against their concentration gradients for each ATP hydrolyzed (Attwell and Laughlin 2001; Erecińska and Dagani 1990; Lennie 2003). Typically, in the aftermath of a spike 2.4 × 109 molecules of ATP may be consumed, 91% of which is consumed on Na+-K+-ATP pumps (Lennie 2003). As neural activity increases so does oxygen and ATP utilization.
The extracellular oxygen concentration, [O2]o, around a single neuron is supplied diffusively by the bath solution in in vitro experiments. Therefore, [O2]o can be modeled as:
| (12) |
where [O2]bath is the bath oxygen concentration in the perfusion solution, with a normal value at ∼32 mg/l, when aerated with 95% O2-5% CO2 at 32–34°C. The diffusion rate εo, obtained from Fick's law, is εo = D/Δx2. We used a diffusion coefficient D = 1.7 × 10−5 cm2/s for oxygen in brain tissue (Homer 1983) and Δx = 100 μm for the average distance from electrode tip to the surface of the slice. λ Is a relative cell density, usually set to be 1. α Is a conversion factor that converts charge carrier utilization (mM/s) to the rate of oxygen concentration change (mg·l−1·s−1).
The detailed calculation of α is shown as follows. When the Na+-K+-ATP pump current is 1 mM/s, it transports 3 mM/s Na+ outward and 2 mM/s K+ inward. The amount of ATP required to be hydrolyzed for this process is 1 mM/s. The pump is fueled primarily by oxidative phosphorylation, which yields up to 36 molecules of ATP from the complete oxidation of 1 glucose with 6 oxygen molecules:
The amount of oxygen needed to generate 1 mM/s ATP is 1/6 mM/s. Since the molar mass of O2 is 32 g/mol, the concentration of oxygen expended on 1 mM/s pump current is 5.3 mg·l−1·O2−1. Therefore, the conversion factor α between pump current (mM/s) and oxygen concentration change (mg·l−1·s−1) was set to 5.3 g/mol.
With oxygen dynamics in the model, we have modified the Na+-K+-ATP pump rate (ρ) in Eqs. 8 and 9 according to a sigmoid function of [O2]o (Petrushanko et al. 2007)
| (13) |
Both the neuronal and glial Na+-K+-ATP pump are modified so that they depend on the available oxygen concentration in the extracellular space. This dynamic microenvironment will be found essential to account for our experimental findings.
Two-neuron model.
To account for the temporal interplay between excitatory pyramidal cells and inhibitory oriens lacunosum moleculare (OLM) cells seen in experiments (Žiburkus et al. 2006, 2013), as well as metabolism dynamics observed in the their cell body layers stratum (st.) pyramidale and st. oriens (Ingram et al. 2014) in the hippocampus, we used the same neuron model for both cells and coupled them through synaptic interactions and potassium diffusion. Each cell has its own extracellular microenvironment, such as potassium diffusion from bath solution (εk), glial uptake of extracellular potassium (Gglia), and relative cell densities (λ). The membrane potentials of pyramidal cell (Ve) and OLM interneuron (Vi) are modeled as
| (14) |
where the equations modeling inhibitory (Isyn,e) and excitatory (Isyn,i) synaptic inputs are adopted from Ullah and Schiff (2010) and are given as follows:
| (15) |
where η is 0.4 when V is in the range of −30 to −10 mV. Otherwise, η is 0. The variable Sei gives the temporal evolution of the synaptic input from the pyramidal cell to the interneuron, and Sie is the synaptic input from the interneuron to the pyramidal cell. The variables χie and χei take into account the firing interplay between pyramidal cells and interneurons (Ullah et al. 2009). The excitatory and inhibitory synaptic conductances are Gei = 0.22 mS/cm2 and Gie = 0.12 mS/cm2. The reversal potentials of inhibitory (Ein) and excitatory (Eex) synapses are −80 and 0 mV, respectively. The time constants for the excitatory and inhibitory synapses are τei = 4 and τie = 8.
Pyramidal cell and OLM interneurons are also coupled with potassium diffusion. The potassium Eq. 5 for each neuron is updated by adding the following lateral diffusion terms (Ilateral).
| (16) |
where the subscript o in [K+]oe and [K+]oi represents extracellular space, and the superscript e and i represent excitatory and inhibitory cells, respectively. The distance Δxei between two neurons is usually 30–200 μm (Žiburkus et al. 2006), and the potassium diffusion coefficient is DK = 2.5 × 10−5 cm2/s (Tuckwell and Miura 1978).
To mimic 4-AP and decreased magnesium in in vitro experimental seizures (Žiburkus et al. 2006) in the normal bath potassium solution, we reduced the voltage-gated potassium conductances GK of both cells to be 7.25 mS/cm2. We also increased the leak sodium conductance GNaL of pyramidal and OLM cells to be 0.0275 mS/cm2 to help represent the increased excitatory network activity under the influence of 4-AP. The different oxygen level in two layers is related to cell densities, since cells are more highly packed in the st. pyramidale layer than in the st. oriens layer, and we set the relative cell density λ for pyramidal and OLM cells at 1 and 0.5, respectively.
Bifurcations.
The bifurcation analysis of the neuronal model ordinary differential equations were performed using XPPAUT (Ermentrout 2002) and MATLAB (Mathworks, Natick, MA) software. We used the fourth-order Runge-Kutta method for integrating the differential equations.
Code archive.
To facilitate dissemination of these results, the Matlab code required to reproduce the fundamental model, shown in Fig. 2 of this article, and the XPPAUT code required to reproduce the bifurcation diagram in Fig. 5 of this article are available in Supplemental Material archived with this article available online at the J Neurophysiol website.
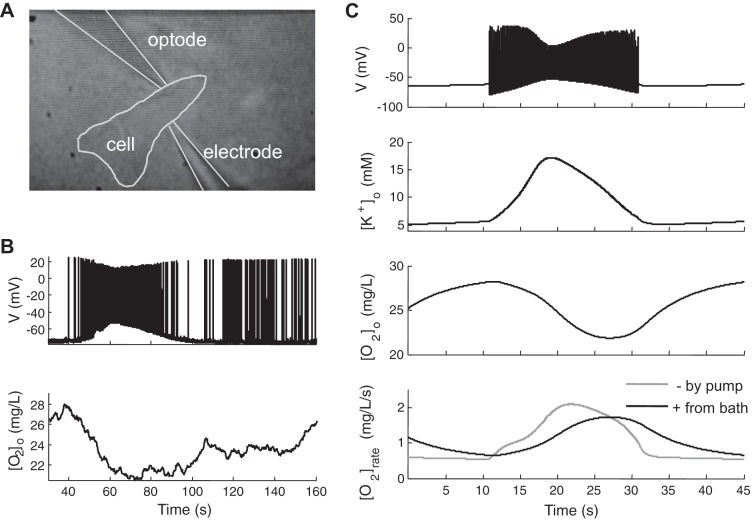
Fig. 2.
Oxygen dynamics during a seizure event. Experimental dual-recording (A) of membrane potential and oxygen concentrations at 100-μm depth within hippocampal brain slices [reproduced with permission from Ingram et al. 2013], showing that, the oxygen deficit outlasts the seizure (B), indicating an increased oxygen requirement after high neuronal activity. C: model data show membrane potentials, extracellular K+ and O2 concentration ([K+]o and [O2]o), and oxygen consumption rate ([O2]rate) based on consumption by pump activity and replenished by diffusion from bath solution during and after a seizure event. The time course of O2 deficit is similar to that observed experimentally.
Fig. 5.
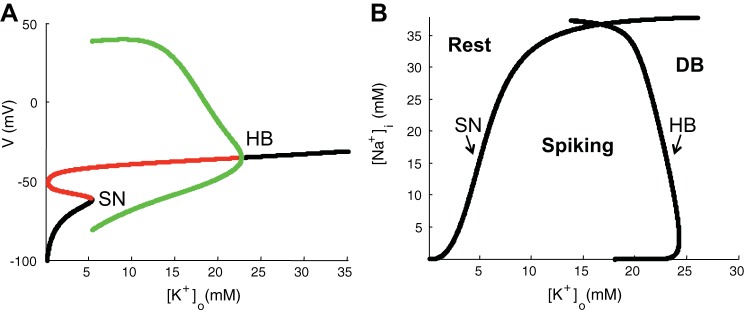
Bifurcation analysis with fixed ion concentrations. A: bifurcation diagrams of membrane potential V with [K+]o as a parameter for fixed intracellular Na+ concentration ([Na+]i) = 18 mM. Stable and unstable steady states are depicted as black and red lines, respectively. Stable limit cycles are depicted as green lines. Transition between stable and unstable attractors occurred at saddle-node bifurcation (SN) and Hopf bifurcation (HB) points. B: 2-parameter bifurcation diagram describes neuronal asymptotic behaviors to different fixed values of [K+]o and [Na+]i. SN and HB lines indicate bifurcation curves corresponding to transitions between resting state and spiking state and between spiking state and depolarization block (DB) state, respectively.
RESULTS
Oxygen dynamics during seizure-like events.
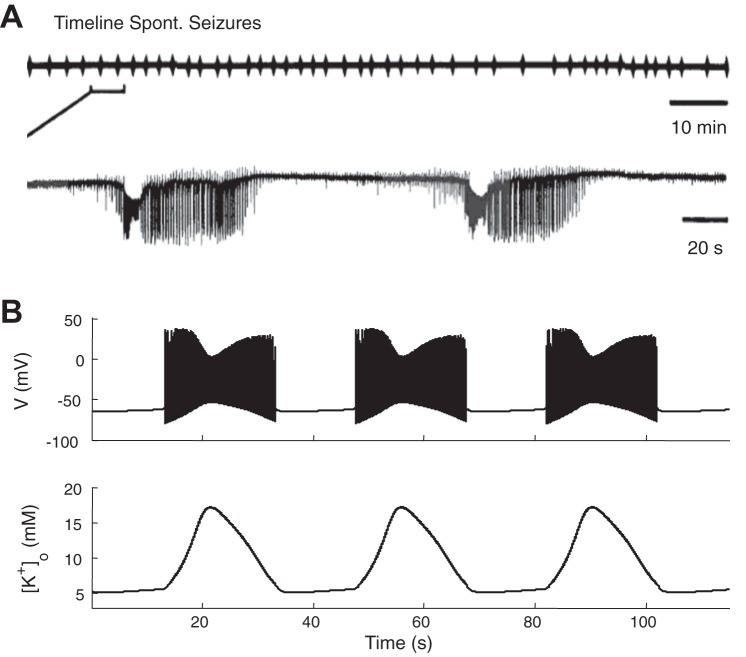
In slice preparations, network activity is typically quiescent in the absence of external input at normal [K+]bath (∼4 mM), while burst firing (Rutecki et al. 1985) and seizure-like events (Traynelis and Dingledine 1988) occur spontaneously and periodically at higher [K+]bath concentrations (∼8.5 mM) in the CA1 region (Fig. 1A, from Traynelis and Dingledine 1988). In our model, we set [K+]bath at 8.5 mM to generate periodic and spontaneous seizures (Fig. 1B) similar to experimental seizures in the slices (Traynelis and Dingledine 1988). Seizure events are accompanied by large amplitude oscillations of [K+]o (Fig. 1B, bottom trace).
Fig. 1.
Periodic and spontaneous seizures. A: experimentally observed spontaneous periodic seizures in the CA1 region at 8.5 mM potassium in the perfusate [reproduced with permission from Traynelis and Dingledine 1988]. B: in the model, membrane potential and local extracellular potassium concentration, [K+]o, shows periodic seizures occur with similarly elevated 8.5 mM bath potassium.
During seizures, a variety of voltage gated channels are activated resulting in substantial ion flux across the neuronal membrane. Energy (ATP) and O2 are required to restore ionic gradients (as well as neurotransmitter release and recycling, not modeled here). We show experimental voltage and oxygen data from a seizure event of a typical single cell (Fig. 2, A and B, and data from Ingram et al. 2013) and the model (Fig. 2C) for comparison. The membrane potential and oxygen concentration (Fig. 2B) were simultaneously recorded from an intracellular electrode and extracellular optode at a single cell (Fig. 2A). At the begin of a seizure, a sudden burst of neuronal firing increases the extracellular [K+]o and intracellular [Na+]i, which further increases the Na+-K+-ATP pump activity, resulting in an increased O2/ATP demand. The [O2]o profile given by the model (Fig. 2C) compares qualitatively well with the experimental measured values. In Fig. 2C, bottom trace, the gray line shows the rate of oxygen consumed by the sodium/potassium pump from the model neuron and glia, while the black line shows the rate of oxygen supplied from bath solution. These traces suggest that 1) oxygen utilization increases during and following seizures when the pumps work harder to restore ion gradients; 2) it takes significant time for oxygen to diffuse from bath solution to the extracellular space; and 3) pump activity becomes limited when local available oxygen decreases. All of these factors contribute to account for a substantial decrease in extracellular local [O2]o during seizure events and a prolonged period of oxygen deficit following the electrical event as shown in Fig. 2C, consistent with our experimental data recorded juxtaceullarly near a single neuron in Fig. 2B, and reflected in the layer specific measurements in Ingram et al. (2014) (companion article).
Seizure-like events driven by hypoxia.
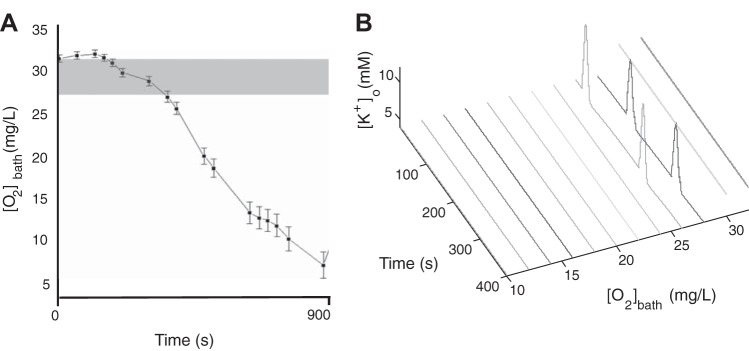
With hypoxia occurring during seizure events, we investigated whether brief hypoxic periods can increase cell firing and push an excitable cell into a seizure state with a normal bath potassium concentration (see companion article, Ingram et al. 2014). In experiments, the slices are in a slightly hyperexcitable state by partially lowering Mg2+ and Ca2+ in the recording chamber perfused with normal oxygen (∼32 mg/l). Lowering divalent cation concentrations tends to make neurons more excitable by changing intrinsic electrical properties through decreased charge screening (Frankenhaeuser and Hodgkin 1957) and decreasing the Mg2+ blockade of NMDA channels (Dingledine et al. 1999). The chamber oxygen concentration was then decreased by switching from perfusate aerated with 95% O2-5% CO2 to one aerated with 95% N2-5% CO2 and then increased back to 95% O2-5% CO2. Seizure events were observed to occur experimentally only during a narrow range of bath oxygen pressure (Fig. 3A, gray region, and data from companion article, Ingram et al. 2014).
Fig. 3.
Seizure events occurred within a narrow range of [O2]bath in normal bath potassium concentration. A: gray region shows the range of [O2]bath permissive of seizures in the experiments described in detail in Fig. 3 of the companion article (Ingram et al. 2014). B: large oscillations of [K+]o in the model occur in an almost identical range of [O2]bath hypoxia where seizure events occur experimentally.
In our model, we injected a small amount of external positive current (Iext = 0.5 μA/cm2) into the neuron to mimic a slightly cellular excitable state with a normal bath potassium concentration (no divalent cation effects are in this model). The neuron was tonically firing but not in a seizure state with normal bath oxygen pressure (32 mg/l in experiments) as shown in Figs. 3B and Fig. 4B, which slightly elevated [K+]o outside the seizure oscillation region. As we decreased [O2]bath, local available [O2]o decreased, which decreased the maximal neuronal and glial Na+-K+-ATP pump strength, leading to higher extracellular [K+]o thus initiating seizures. In the model, we observed that hypoxia can induce large slow [K+]o oscillations with a concentration range seen in periodic seizure-like events, which occurred within a narrow range of bath oxygen pressure as shown in Fig. 3B. The seizure-permissive [O2]bath band was generally 24–29 mg/l in the model and slightly higher at 27–31 mg/l in experiments.
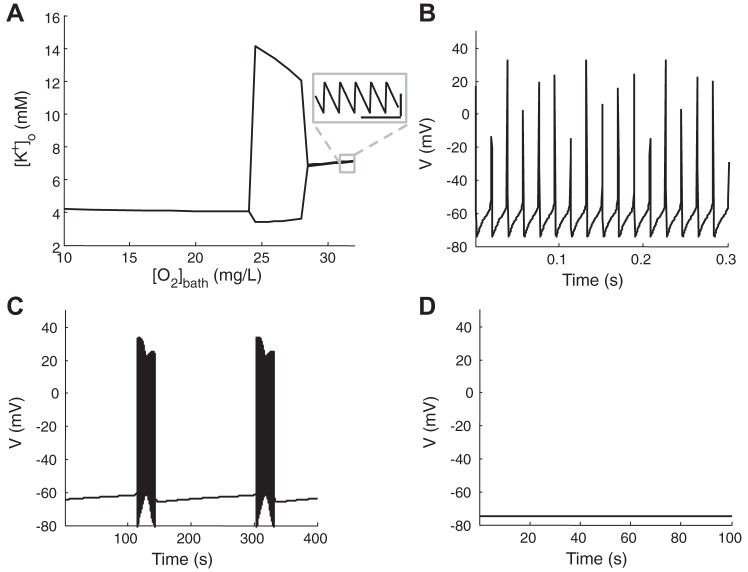
Fig. 4.
A: maximum and minimum of [K+]o as a function of [O2]bath in a hyperexcitable neuron (Iext = 0.5 μA/cm2) with [K+]bath = 4.0 mM. Inset: small fast local [K+]o oscillation during tonic firings. The calibration bars are 0.05 s (horizontal) and 0.05 mM (vertical). Membrane potential traces for the 3 regions of bifurcation diagram when [O2]bath is 32 mg/l (B), 27 mg/l (C), and 10 mg/l (D), respectively.
Under conditions of mild hypoxia, singlet spiking can become multistable, a dynamical bifurcation. Figure 4A shows the minimum and maximum of local potassium [K+]o plotted with bath oxygen concentration [O2]bath as a parameter. Membrane potential traces for three values of [O2]bath = 32, 27, and 10 mg/l are shown in Fig. 4, B–D, respectively. The neuron fires tonically producing small fast local potassium [K+]o oscillations in normal oxygen bath solution (see Fig. 4A, inset), similar to results of Frankenhaeuser and Hodgkin (1956) for singlet spiking. As [O2]bath is reduced, oxidative metabolism becomes limited, resulting in a significant decline in ATP generation and a reduction of pump strength. When the pump cannot work fast enough to restore ion gradients, a region of large slow potassium [K+]o oscillations appear forming a foundation for spontaneous seizures (Fig. 4C). When [O2]bath decreases further, the neuron goes to a quiescent resting steady state as shown in Fig. 4D. In this hypoxic region, the pump is too weak to restore the sodium gradient, resulting in the inactivation of the neuron seen in anoxia. A further decrease in available [O2]bath leads to a terminal “wave of death” (Zandt et al. 2011).
Bifurcation analysis.
To further understand the relationship between oxygen and seizures, we performed a formal analysis of these dynamical bifurcations as a function of [K+]o and [Na+]i.
We set [K+]o and [Na+]i to fixed values for the following analysis. Figure 5A shows a bifurcation diagram of membrane potential V by varying [K+]o while holding [Na+]i at 18 mM. We observed two of the common bifurcation mechanisms known to occur in such a neuronal model: the Hopf bifurcation (HB) and the saddle-node bifurcation (SN) (Barreto and Cressman 2011; Krishnan and Bazhenov 2011; Øyehaug et al. 2011). The HB appears around [K+]o = 22.7 mM, when a stable limit cycle (Fig. 5A, green) and the coexisting unstable equilibrium (Fig. 5A, red) merge to a stable equilibrium (Fig. 5A, black, [K+]o >22.7 mM). This stable equilibrium at high [K+]o represents the state of depolarization block. The SN on invariant cycle bifurcation occurs around [K+]o = 5.4 mM, when a SN appears simultaneously with an invariant closed circle or limit cycle (Izhikevich 2007). For the values of [K+]o between 5.4 and 22.7 mM, a stable limit cycle represents regular spiking in the neuron. This is depicted as green lines in Fig. 5A that reflect maximum and minimum values of the membrane voltage during a spiking cycle. For [K+]o <5.4 mM, a stable equilibrium exists representing the resting state.
Figure 5B is a two-parameter bifurcation diagram showing the location of the SN and HB points as functions of [K+]o and [Na+]i. The SN and HB curves divide the parameter space into different regions of behavior. The neuron approaches a stable equilibrium resting state when the region of the ([K+]o and [Na+]i) plane is to the left of the SN curve. The neuron spikes regularly between SN and HB curves. To the right of HB curve, the cell is attracted to a stable equilibrium depolarization block state. This is the dynamical foundation that determines the neuron behavior as a function of [K+]o and [Na+]i (Barreto and Cressman 2011).
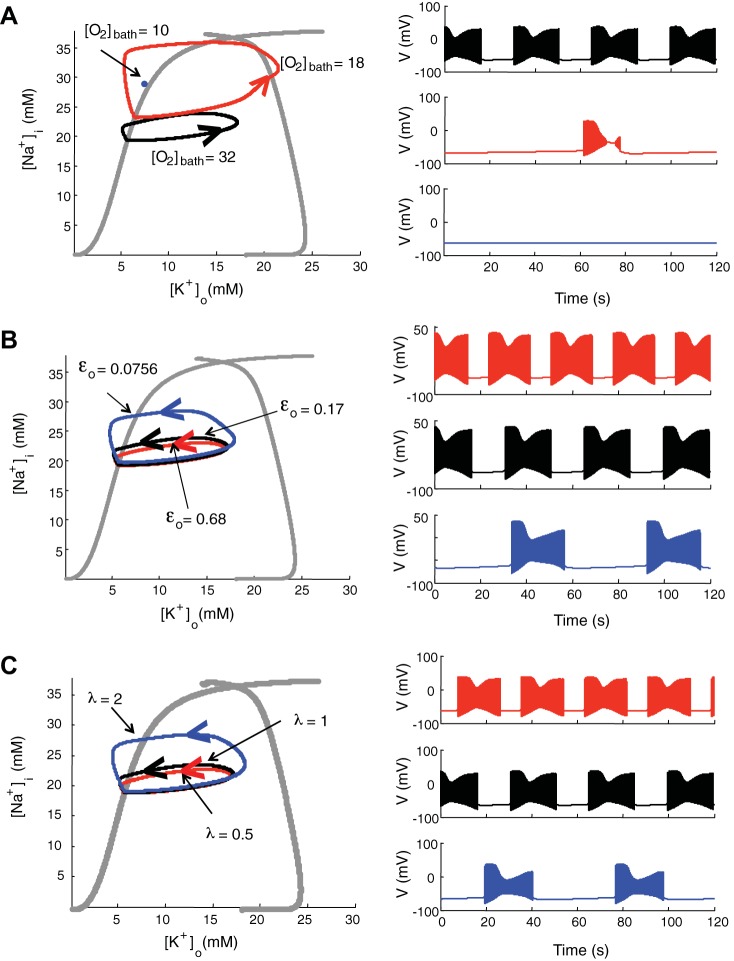
The dynamics of [K+]o and [Na+]i is coupled to glial uptake, diffusion, and pump activity. The Na+-K+-ATP pump strength depends on available local oxygen, which is associated with bath oxygen concentration [O2]bath, oxygen diffusion constant εo and relative cell density λ. To study the effect of oxygen parameters on the neuron behavior, we overlaid on the bifurcation diagram of fixed [K+]o and [Na+]i (Fig. 6, grey traces) the trajectories of ion dynamics (when not fixed) as oxygen parameters vary (Fig. 6). The loops represent the periodic orbits of neuron behavior that traverse among resting, spiking, or depolarization block in a counterclockwise manner. The corresponding membrane time traces with the same color scheme are shown in the right column. With normal bath oxygen concentration ([O2]bath = 32 mg/l; Fig. 6, black traces), the cell exhibits spontaneous periodic seizures alternating with a resting state at bath potassium concentration of 8.5 mM as in Fig. 1. As we reduce bath oxygen concentration ([O2]bath = 18 mg/l), the neuron behavior traverses from rest, to spiking, to depolarization block, and to rest directly in a cyclic fashion, which has feature of seizures and spreading depression (Fig. 6, red trace). Our result is consistent with previous findings that seizures are related to mild hypoxia, while spreading depression is related to more severe hypoxia (Aitken et al. 1991; Bahar et al. 2000) and the mixture state of seizure and spreading depression seen in hypoxia (Czéh et al. 1993). The pattern from the red trace is also seen experimentally in OLM cells and occasionally pyramidal cells during seizures when they go into transient depolarization block (Žiburkus et al. 2006, 2013). Decreasing [O2]bath further ([O2]bath = 10 mg/l), the blue dot in Fig. 6A is a quiescent steady-state point following a single spreading depression event. At a low oxygen concentration, the pump activity to restore ion gradients is limited, and the neuron remains inactivated.
Fig. 6.
Bifurcation analysis with ion concentration dynamics when oxygen parameters vary. A: asymptotic behavior of the ion concentration as [O2]bath is varied. The loops are traversed in a counterclockwise manner, with [O2]bath = 32 (black), 18 (red), and 10 (blue) mg/l, respectively. B: asymptotic behavior of the ion concentration as oxygen diffusion constant εo is varied. The loops represent limit cycles with εo = 0.68 (red), 0.17 (black), and 0.0756 (blue) Hz, respectively. C: asymptotic behavior of the ion concentration as relative cell density λ is varied, for λ = 0.5 (red), 1 (black), and 2 (blue), respectively. The corresponding membrane potential traces with same color are shown at right. All behaviors are calculated with the same bath potassium concentration, potassium diffusion coefficient, maximal pump strength, and maximal glial uptake strength.
We also studied the effect of oxygen diffusion constant εo and relative cell density λ on neuron behavior, with normal oxygen bath concentration ([O2]bath = 32 mg/l). When the depth from the surface of the slice increases, the effective diffusion constant εo decreases (see Oxygen concentration dynamics). We chose εo = 0.68, 0.17, and 0.0756 Hz, corresponding to the depth from the surface of the slice at Δx = 50, 100, and 150 μm, respectively (Fig. 6B). As the depth from the surface increases, the interseizure intervals increase, because it takes more time to recover oxygen in deeper layer after seizures. Since the cell density is different in pyramidal cell body and oriens layers, we can change the value of relative cell density λ in the model. The highly packed pyramidal cell layer consumes more oxygen than the lower cell density in the oriens layer for comparable spiking rates and more easily induces seizure-like events (Fig. 6C). The interseizure interval gets longer as we lower εo or increase λ, because it takes more time to restore ion gradients with less available oxygen. Therefore, although neuron behavior (resting, spiking, bursting/seizure, spreading depression, or depolarization block) is mainly dependent on bath potassium concentration, oxygen, and tissue architecture substantially modify the resulting neuronal dynamics.
Interplay between pyramidal cell and inhibitory interneuron.
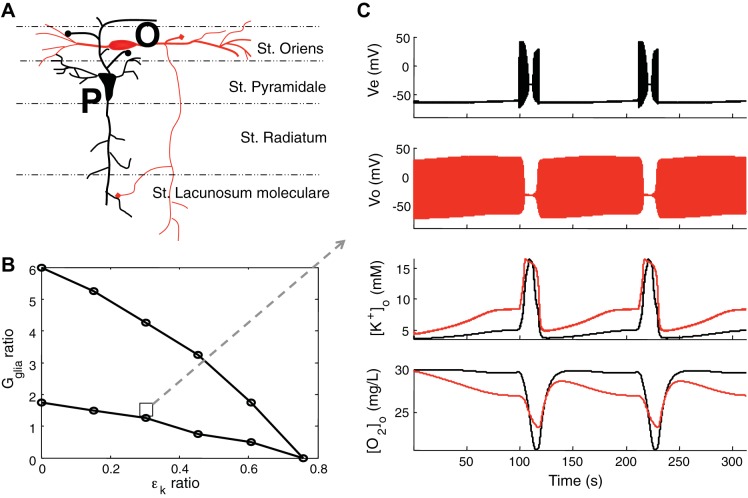
Previous experiments reported a strongly interdependent pattern between excitatory pyramidal cells and OLM interneurons during spontaneously seizures in the hippocampus (Žiburkus et al. 2006, 2013). We probed oxygen dynamics around individual cell types in both st. pyramidale and st. oriens layers to see the metabolic energy demands during seizure events. Experimentally, we found that although OLM interneurons typically fire at higher rates than pyramidal cells, the maximal oxygen reduction was observed in the densely packed cell body layer of CA1 st. pyramidale as shown in the companion article (Ingram et al. 2014).
In the model, pyramidal cells and OLM interneurons (Fig. 7A) share the same potassium bath concentration but have different local architecture and independent microenvironments, such as glial buffering of potassium and potassium diffusion rate. To study the parameter space of the ratio of Gglia and εk (calculated as OLM/pyramidal) where the model exhibits firing interplay, we fixed the parameters of the pyramidal cell as in Table 1 and varied the parameters surrounding the OLM interneuron. The region between two lines shows that the region for alternating interplay within the parameter space is robust (Fig. 7B). Figure 7C shows a typical two neuron interplay example. OLM interneurons are more active at ictal onset, followed by a period of depolarization block when pyramidal cells exhibited runaway excitation as in Žiburkus et al. (2006, 2013). Our model also reproduces the different [O2]o levels that we have observed in st. pyramidale and st. oriens layers during seizures (companion article, Ingram et al. 2014) by reflecting in the model that cells in the pyramidal layer, and therefore their Na-K-ATP pumps, are more densely packed than in oriens layer. This leads to more intense hypoxia in the pyramidal layer but preserves a higher level of [O2]o and thus a higher energy charge (Atkinson 1968) in the oriens layer that is needed to recover inhibitory control (Fig. 7C). Although the interplay between pyramidal cell and inhibitory OLM interneuron shows they fire alternatively, local available oxygen increases and decreases simultaneously. This is a manifestation that oxygen consumption is not directly coupled to firing rates, which dissipate stored energy, but rather is directly related to restoring ion gradients. Because ion gradients reach their maximum collapse during depolarization block, energy requirements are highest at the peak of excitatory runaway excitation when inhibitory neurons may be in depolarization block. The model illustrates and offers an explanation for this experimental set of measures from current clamp, voltage clamp, and oxygen measures at several spatial scales (Žiburkus et al. 2006, 2013; Ingram et al. 2013; and companion article, Ingram et al. 2014).
Fig. 7.
Interplay between pyramidal cell and inhibitory interneuron. A: structure of the hippocampal CA1 2-neuron model. The cell body of pyramidal cell (P, black) in stratum (st.) pyramidal layer and the cell body of oriens lacunosum moleculare (OLM; O, red) interneuron in the st. oriens layer. B: region for the alternating interplay in firing between 2-neuron model. When the ratio of Gglia and oriens OLM, calculated as OLM/pyramidal, are in the region bounded by the 2 lines, the 2 cells exhibit firing interplay. The ratios are calculated when the parameters of the pyramidal cell are fixed as in Table 1. An example of the interplay in the region of the square is shown in C. In C, the dual-layer model shows a nearly identical electrical and [O2]o interplay as seen experimentally (Žiburkus et al. 2006, 2013, Ingram et al. 2014, companion article). When the OLM cell (Vo, red) goes into depolarization block the pyramidal cell (Ve, black) is released and exhibits runaway excitation behavior until the OLM cell resumes firing. Extracellular potassium concentrations of pyramidal cell (black) and OLM cell (red) are elevated during seizure events. Even though the OLM cell fires more than the pyramidal cell, local oxygen concentration around cell body in st. pyramidale (black) is lower than in st. oriens layer (red), which is due to the higher packing density of pyramidal cells. Note, importantly, that the maximal O2 consumption occurs during depolarization block in the model, consistent with experimental observations, reflecting maximal stimulation of Na-K pump under conditions of maximal gradient collapse.
DISCUSSION
In this study, we constructed a computational model that incorporates sodium and potassium ion concentration dynamics as well as oxygen homeostasis to account for experimental observations. Our findings help elucidate the mechanisms of seizure development and termination as well as the interaction between seizure and energy metabolism. During neural activities, the greatest energy requirement is consumed in restoring ion gradients following action and synaptic potential activity, while neurotransmitter release and recycling are also demanding (Lennie 2003). Although we mainly consider the energy consumed by Na+-K+-ATP activity, the model reflects sufficient dynamics of oxygen metabolism to account for several experimental observations of the interrelationship between oxygen and seizures.
First, we observe prolonged oxygen depletion during and after high rates of neural activity such as seizure events. High levels of neural activity initiate extracellular K+ and intracellular Na+ accumulation, which increases the activation of the Na+-K+-ATP pump. The pump consumes ATP, leading to increased oxygen consumption, which decreases local tissue [O2] and impairs the ability of a cell to reestablish its ionic gradients in a positive feedback loop that leads cells first to increased excitability and then to reduced activity and potentially depolarization block. This basic finding is consistent with experimental oxygen measurements during high neural activities in vivo (Thompson et al. 2003; Bahar et al. 2006). The postactivity oxygen deficit reflects the increased energy needed to restore membrane ion gradients and the finite diffusion time of oxygen in tissues. Neuronal firing activity dissipates but does not directly utilize energy. Energy requirements are highest when ion gradients are most collapsed, such as in the depolarization block. This is consistent with previous studies linking an increase in oxygen consumption with a concomitant rise in the extracellular potassium concentration (Erecińska and Dagani 1990). Our model further demonstrates the relatively long time scale of restoring cellular ionic gradients following intense seizure activity, which introduces an effective refractory period on such events seen in model, experiments, and clinical seizures.
Second, we have shown that hypoxia can drive a neuron into seizure states with a normal bath potassium concentration. This behavior occurs within a narrow range of oxygen concentration, which is consistent with experimental observations (companion article, Ingram et al. 2014). Our findings show that neurons are more likely to go into periodic seizures when the Na+-K+ pump rate is reduced as overall oxygen availability to the neurons is reduced, consistent with the observations in Grisar (1984) that the activity of the Na+-K+ pump may be reduced in human epilepsy patients. Our findings are also consistent with the early work of Foerster and Penfield (1930), who described how seizures could be reliably produced in scarred posttraumatic brain by gently pulling on the attached dura producing mild transient vascular compromise.
Third, we performed a detailed dynamical bifurcation analysis of the model. Since our model consists of a fast (neuron model) and a slow (ion concentration) subsystem, it is difficult to pinpoint the exact mechanism underling the complex oscillatory behavior using the full model. Cressman et al. (2009) performed a bifurcation analysis with a simplified reduced model and showed that pump rate strength can be a bifurcation parameter that changes the model from steady state to oscillatory burst firing and seizures. Here we extended these results to oxygen driven bifurcations (Barreto and Cressman 2011; Krishnan and Bazhenov 2011; Øyehaug et al. 2011). By characterizing the trajectories of ion concentration from the full model in a phase plane where each point reflects dynamics solved from fixed ion concentrations, we can gain insight into the transition of rest, spiking and depolarization block state. We studied how oxygen parameters, such as bath oxygen concentration [O2]bath, oxygen diffusion constant εo, and relative cell density λ, change the seizure behavior of oscillatory ion concentrations. As [O2]bath decreases, the neuron can cycle from seizure to hypoxic spreading depression-like events and lastly into quiescence. Less oxygen pressure in the tissue increases extracellular potassium concentration in vitro (Schiff and Somjen 1987). Although the local oxygen concentration is asymptotically dominated by oxygen bath concentration, the depth from the surface of slices in vitro or distance from the vasculature in vivo, and relative cell density, also change network behavior. When the distance from tissue surface is increased, or when cell density is higher, the cells have longer interseizure intervals because it takes longer to restore ion gradients with less oxygen available. Similarly, the cells would more readily transition into spreading depression in deeper layers since less oxygen is available. At the lowest levels of oxygen availability, cell ionic gradients will not be maintained and quiescence ensues.
Lastly, our model can accurately describe the cellular interplay as well as differential oxygen levels between pyramidal cells and OLM interneurons during seizure-like events in the same manner as seen in experiments (Žiburkus et al. 2006, 2013; companion article, Ingram et al. 2014). The most robust alternating firing interplay can be seen when εk surrounding OLM interneurons is lower than around pyramidal cells. This may be physically manifest by perineuronal nets of extracellular matrix ensheathing interneurons (Morris and Henderson 2000). Regarding differential oxygen levels, the simplest explanation is that the more densely packed CA1 pyramidal neurons contribute to the greatest change in ionic distribution and subsequently the greatest reduction in [O2]o.
In this article, we demonstrated three biophysical routes to induce seizure-like events: high potassium, low oxygen, and 4-AP. By making the Na+-K+-ATP pump O2 dependent, our model accounts for several prominent features of experimental seizures. Oxygen concentration does not merely decrease as a result of intense neuronal activity during seizures, but differential [O2]o changes within layers and about specific neuronal types can help sculpt and orchestrate the neuronal spatiotemporal interplay seen in seizure patterns. Seizure foci in epileptic patients can be complex in structure, and oxygen availability is likely an important factor that can contribute to seizure initiation and dynamics. Our work also demonstrates that the complex relationship between seizure and spreading depression may be considerably simplified using a framework in which oxygen dynamics are taken into account.
In future work, it is important to include the cell volume in the model. Cell swelling during seizure or spreading depression would restrict the extracellular space and further restrict the diffusion of ions or oxygen. For simplicity, we did not model full dynamics of intracellular and extracellular Na+, K+, and Cl−, but more complete accounting for these analytes is required when volume is introduced. When modeling oxygen dynamics in vivo, we should take blood flow and pressure into consideration. We used deterministic models to seek an underlying bifurcation structure to account for experimental observations. Nevertheless, incorporating stochastic dynamics into such models to better reflect such effects in vivo will complicate this simple dynamical picture we have presented. To achieve simplicity, we also incorporated single compartment neuronal models. Although such simple models were successful in capturing some of the fundamental dynamics seen in a variety of experimental findings, a more accurate representation of the spatial structure of neurons with multicompartment models, and with larger ensembles of neurons embedded within more realistic tissue, will be important to better characterize the influence of oxygen on neuronal network dynamics. Such dynamics will, of course, be applicable to a broader range of phenomena than seizures.
Our findings confirm the critical need for including oxygen dynamics in our efforts to better understand the fundamental biophysical mechanisms that underlie patterns of normal or pathological neuronal activity.
GRANTS
This work is supported by National Institutes of Health US-German Collaborative Research in Computational Neuroscience (CRCNS) Grant 1R01-EB-014641-01 (to S. J. Schiff) and Long Term Visitor (to S. J. Schiff) and Early Career Award (to G. Ullah) from the Mathematical Bioscience Institute.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
AUTHOR CONTRIBUTIONS
Author contributions: Y.W., G.U., J.I., and S.J.S conception and design of research; Y.W., G.U., J.I., and S.J.S performed experiments; Y.W., G.U., J.I., and S.J.S analyzed data; Y.W., G.U., J.I., and S.J.S interpreted results of experiments; Y.W., G.U., J.I., and S.J.S prepared figures; Y.W., G.U., J.I., and S.J.S drafted manuscript; Y.W., G.U., J.I., and S.J.S edited and revised manuscript; Y.W., G.U., J.I., and S.J.S approved final version of manuscript.
Supplementary Material
ACKNOWLEDGMENTS
Present address of J. Ingram: Dept. of Biology, Pennsylvania College of Technology, Williamsport, PA (e-mail: jmi2@pct.edu).
REFERENCES
- Aitken P, Schiff SJ. Selective neuronal vulnerability to hypoxia in vitro. Neurosci Lett 67: 92–96, 1986. [DOI] [PubMed] [Google Scholar]
- Aitken PG, Jing J, Young J, Somjen GG. Ion channel involvement in hypoxia-induced spreading depression in hippocampal slices. Brain Res 541: 711, 1991. [DOI] [PubMed] [Google Scholar]
- Atkinson DE. The energy charge of the adenylate pool as a regulatory parameter interaction with feedback modifiers. Biochemistry 7: 4030–4034, 1968. [DOI] [PubMed] [Google Scholar]
- Attwell D, Laughlin SB. An energy budget for signaling in the grey matter of the brain. J Cereb Blood Flow Metab 21: 1133–1145, 2001. [DOI] [PubMed] [Google Scholar]
- Bahar S, Fayuk D, Somjen GG, Aitken PG, Turner DA. Mitochondrial and intrinsic optical signals imaged during hypoxia and spreading depression in rat hippocampal slices. J Neurophysiol 84: 311–324, 2000. [DOI] [PubMed] [Google Scholar]
- Bahar S, Suh M, Zhao M, Schwartz TH. Intrinsic optical signal imaging of neocortical seizures: the “epileptic dip”. Neuroreport 17: 499–503, 2006. [DOI] [PubMed] [Google Scholar]
- Barreto E, Cressman JR. Ion concentration dynamics as a mechanism for neuronal bursting. J Biol Phys 37: 361–373, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cressman JR, Ullah G, Žiburkus J, Schiff SJ, Barreto E. The influence of sodium and potassium dynamics on excitability, seizures, and the stability of persistent states: I. Single neuron dynamics. J Comput Neurosci 26: 159–170, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Czéh G, Aitken PG, Somjen GG. Membrane currents in CA1 pyramidal cells during spreading depression (SD) and SD-like hypoxic depolarization. Brain Res 632: 195–208, 1993. [DOI] [PubMed] [Google Scholar]
- Dingledine R, Borges K, Bowie D, Traynelis SF. The glutamate receptor ion channels. Pharmacol Rev 51: 761, 1999. [PubMed] [Google Scholar]
- Erecińska M, Dagani F. Relationships between the neuronal sodium/potassium pump and energy metabolism. J Gen Physiol 95: 591–616, 1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ermentrout B. Simulating, Analyzing, and Animating Dynamical Systems: a Guide to XPPAUT for Researchers and Students. Philadelphia, PA: Society for Industrial & Applied Mathematics, 2002. [Google Scholar]
- Foerster O, Penfield W. The structural basis of traumatic epilepsy and results of radical operation. Brain 53: 99–119, 1930. [Google Scholar]
- Frankenhaeuser B, Hodgkin A. The after-effects of impulses in the giant nerve fibres of Loligo. J Physiol 131: 341–376, 1956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frankenhaeuser B, Hodgkin A. The action of calcium on the electrical properties of squid axons. J Physiol 137: 218–244, 1957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galeffi F, Somjen GG, Foster KA, Turner DA. Simultaneous monitoring of tissue PO2 and NADH fluorescence during synaptic stimulation and spreading depression reveals a transient dissociation between oxygen utilization and mitochondrial redox state in rat hippocampal slices. J Cereb Blood Flow Metab 31: 626–639, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gloveli T, Dugladze T, Saha S, Monyer H, Heinemann U, Traub RD, Whittington MA, Buhl EH. Differential involvement of oriens/pyramidale interneurones in hippocampal network oscillations in vitro. J Physiol 562: 131–147, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grisar T. Glial and neuronal Na+-K+ pump in epilepsy. Ann Neurol 16, Suppl: S128–134, 1984. [DOI] [PubMed] [Google Scholar]
- Hochachka PW, Guppy M. Metabolic Arrest and the Control of Biological Time. Cambridge, MA: Harvard Univ. Press, 1987. [Google Scholar]
- Homer L. Diffusion of oxygen in slices of rat brain. Am J Physiol Regul Integr Comp Physiol 244: R15–R22, 1983. [DOI] [PubMed] [Google Scholar]
- Ingram JM, Zhang C, Xu J, Schiff SJ. FRET excited ratiometric oxygen sensing in living tissue. J Neurosci Methods 214: 45–51, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ingram J, Zhang C, Cressman JR, Hazra A, Wei Y, Koo YE, Žiburkus J, Kopelman R, Xu J, Schiff SJ. Oxygen and seizure dynamics: I. Experiments. J Neurophysiol (March 5, 2014). 10.1152/jn.00540.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izhikevich EM. Dynamical Systems in Neuroscience. Cambridge, MA: MIT Press, 2007. [Google Scholar]
- Koo YL, Cao Y, Kopelman R, Koo SM, Brasuel M, Philbert MA. Real-time measurements of dissolved oxygen inside live cells by organically modified silicate fluorescent nanosensors. Anal Chem 76: 2498–2505, 2004. [DOI] [PubMed] [Google Scholar]
- Krishnan GP, Bazhenov M. Ionic dynamics mediate spontaneous termination of seizures and postictal depression state. J Neurosci 31: 8870–8882, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lennie P. The cost of cortical computation. Curr Biol 13: 493–497, 2003. [DOI] [PubMed] [Google Scholar]
- Morris NP, Henderson Z. Perineuronal nets ensheath fast spiking, parvalbumin-immunoreactive neurons in the medial septum/diagonal band complex. Eur J Neurosci 12: 828–838, 2000. [DOI] [PubMed] [Google Scholar]
- Øyehaug L, Østby I, Lloyd CM, Omholt SW, Einevoll GT. Dependence of spontaneous neuronal firing and depolarisation block on astroglial membrane transport mechanisms. J Comput Neurosci 32: 147–165, 2011. [DOI] [PubMed] [Google Scholar]
- Petrushanko IY, Bogdanov NB, Lapina N, Boldyrev AA, Gassmann M, Bogdanova AY. Oxygen-induced regulation of Na/K ATPase in cerebellar granule cells. J Gen Physiol 130: 389–398, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rutecki PA, Lebeda FJ, Johnston D. Epileptiform activity induced by changes in extracellular potassium in hippocampus. J Neurophysiol 54: 1363–1374, 1985. [DOI] [PubMed] [Google Scholar]
- Schiff SJ. Neural Control Engineering. Cambridge, MA: MIT Press, 2012. [Google Scholar]
- Schiff SJ, Somjen GG. The effect of graded hypoxia on the hippocampal slice: an in vitro model of the ischemic penumbra. Stroke 18: 30–37, 1987. [DOI] [PubMed] [Google Scholar]
- Thompson JK, Peterson MR, Freeman RD. Single-neuron activity and tissue oxygenation in the cerebral cortex. Science 299: 1070–1072, 2003. [DOI] [PubMed] [Google Scholar]
- Traub RD, Wong RK, Miles R, Michelson H. A model of a CA3 hippocampal pyramidal neuron incorporating voltage-clamp data on intrinsic conductances. J Neurophysiol 66: 635–650, 1991. [DOI] [PubMed] [Google Scholar]
- Traynelis SF, Dingledine R. Potassium-induced spontaneous electrographic seizures in the rat hippocampal slice. J Neurophysiol 59: 259–276, 1988. [DOI] [PubMed] [Google Scholar]
- Tuckwell HC, Miura RM. A mathematical model for spreading cortical depression. Biophys J 23: 257–276, 1978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ullah G, Cressman JR, Barreto E, Schiff SJ. The influence of sodium and potassium dynamics on excitability, seizures, and the stability of persistent states. II. Network and glial dynamics. J Comput Neurosci 26: 171–183, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ullah G, Schiff SJ. Tracking and control of neuronal Hodgkin-Huxley dynamics. Phys Rev E Stat Nonlin Soft Matter Phys 79: 040901, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ullah G, Schiff SJ. Assimilating seizure dynamics. PLoS Comput Biol 6: e1000776, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zandt BJ, ten Haken B, van Dijk J, van Putten MJ. Neural dynamics during anoxia and the “wave of death”. PLoS One 6: e22127, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Žiburkus J, Cressman JR, Barreto E, Schiff SJ. Interneuron and pyramidal cell interplay during in vitro seizure-like events. J Neurophysiol 95: 3948–3954, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Žiburkus J, Cressman JR, Schiff SJ. Seizures as imbalanced up states: excitatory and inhibitory conductances during seizure-like events. J Neurophysiol 109: 1296–306, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.