Competitive interactions in sensorimotor cortex: oscillations express separation between alternative movement targets

Abstract

Choice behavior is influenced by factors such as reward and number of alternatives but also by physical context, for instance, the relative position of alternative movement targets. At small separation, speeded eye or hand movements are more likely to land between targets (spatial averaging) than at larger separation. Neurocomputational models explain such behavior in terms of cortical activity being preshaped by the movement environment. Here, we manipulate target separation, as a determinant of motor cortical activity in choice behavior, to address neural mechanisms of response selection. Specifically, we investigate whether context-induced changes in the balance of cooperative and competitive interactions between competing groups of neurons are expressed in the power spectrum of sensorimotor rhythms. We recorded magnetoencephalography while participants were precued to two possible movement target locations at different angles of separation (30, 60, or 90°). After a delay, one of the locations was cued as the target for a joystick pointing movement. We found that late delay-period movement-preparatory activity increased more strongly for alternative targets at 30 than at 60 or 90° of separation. This nonlinear pattern was evident in slow event-related fields as well as in beta- and low-gamma-band suppression. A comparable pattern was found within an earlier window for theta-band synchronization. We interpret the late delay effects in terms of increased movement-preparatory activity when there is greater overlap and hence less competition between groups of neurons encoding two response alternatives. Early delay-period theta-band synchronization may reflect covert response activation relevant to behavioral spatial averaging effects.

seminal work by georgopoulos and colleagues (1982) showed that individual neurons in the nonhuman primate motor cortex are only broadly tuned to a particular direction and that the actual direction of a movement is coded by a population of neurons through a mechanism of vector averaging (Georgopoulos et al. 1986). Although current knowledge of directional tuning of motor cortex neurons and population coding of movement direction still largely derives from single-unit recordings in monkeys, these phenomena are not intractable to noninvasive study in humans (e.g., Fabbri et al. 2010). Eisenberg et al. (2010) used functional MRI to demonstrate that motor cortex neurons with similar directional preference tend to cluster in groups. Furthermore, spatial patterns of active voxels became less correlated with increasing separation of movement directions. These findings indicate a comparable structural organization of movement-direction encoding in humans compared with nonhuman primates, established by noninvasive means, but do not yet address how such an anatomic organization functionally shapes response selection and movement generation. Here, we address this functional question, using magnetoencephalography (MEG) to investigate the competitive and cooperative interactions between cell groups coding for alternative movement directions.

Behavioral work on eye- and hand-movement trajectories expressing a choice between alternative targets has distinguished between continuous and discrete modes of movement-direction specification. At angular separations smaller than ∼35°, speeded hand and eye movements directed to one target frequently land between the targets (Ghez et al. 1997; Ottes et al. 1984; Van der Stigchel and Nijboer 2013). At wider separation, such responses to a central default value are rare. Computational models of (pre)motor cortex function (Cisek 2006; Erlhagen and Schöner 2002) explain such behavior in terms of motor cortical activity being preshaped by the movement environment. Movement targets at close proximity will preactivate overlapping populations of neurons, thus explaining coactivation and an averaging tendency, resulting in a unimodal response distribution. At larger separation, the preactivated populations share fewer cooperative interactions while there are more mutually inhibitory connections, ensuring a bimodal response pattern. Data and models thus suggest that target proximity is an important determinant of motor cortical activity in choice behavior, providing a window on neural mechanisms of response selection.

In the present study, we investigate whether varying spatial separation of two alternative movement targets is expressed in the power spectrum of MEG-recorded sensorimotor cortex rhythms, using angular distances of 30, 60, and 90°, as originally used in related behavioral studies (Ghez et al. 1997; Ottes et al. 1984). Relevant previous neurophysiological work in humans was restricted to effects of target number or did not manipulate target proximity in isolation (Praamstra et al. 2009; Rawle et al. 2012; Tzagarakis et al. 2010). Based on the distinction between continuous and discrete modes of direction specification, we conjecture a nonlinear attenuation of preparatory activity with increasing separation, most likely expressed in the motor cortex beta-rhythm. In addition to this modulation in strength of preparatory activity (cf. Pastor-Bernier and Cisek 2011), we hypothesized that lateral interactions between competing cell groups, “producing” this modulation, might be expressed in power and spectral properties of higher-frequency gamma-rhythms, analogous to effects on visual cortex gamma-oscillations dependent on the dispersion of horizontal connections (Pinotsis et al. 2012; Schwarzkopf et al. 2012). Although gamma-oscillatory activity in the motor cortex is most pronounced during motor execution, there is a buildup of gamma-activity during preparation (Donner et al. 2009). The results confirm the predictions in part and provide new information on oscillatory signatures of motor cortical activity involved in the preparation for and decision between alternative movement options.

METHODS

Participants.

Twenty healthy participants, all right-handed (by self-report), took part in the experiment. Data from 18 of them (mean age 26.4 ± 9.8 yr; 11 women) were included in the final analyses. Two participants were excluded because of technical problems or poor data quality. Participants either were paid (€8/h) or received student credit points for their participation. The study and experimental procedures were approved by the local Committee on Research Involving Human Subjects, region Arnhem-Nijmegen, The Netherlands. Subjects provided written, informed consent after explanation of the task and experimental procedures, in accordance with the guidelines of the local Research Committee.

Experimental setup.

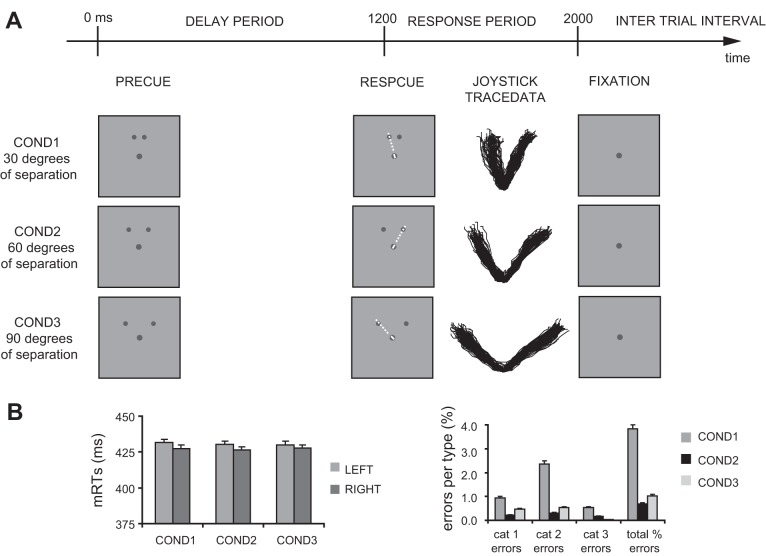
The task was a cued center-out movement task with visually presented stimuli and pointing responses made with a Logitech Attack 3 joystick (custom-modified to ensure MEG compatibility) to one of two precued target locations (Fig. 1A). A dark gray fixation dot (RGB 64-64-64, diameter 0.79° visual angle) was presented continuously, placed at the center of a slightly lighter gray screen (RGB 96-96-96) at 80-cm distance from the participants' eyes. Two dark gray target location dots (RGB 64-64-64, diameter 0.64° visual angle) were presented at precue onset and remained on screen during a delay period (1,200 ms) and a subsequent response period (800 ms). The targets were displayed at locations above the central fixation dot on an imaginary circle extending 4.3° of visual angle (center-to-center distance). The two target locations were placed symmetrically around the vertical meridian, separated by 30° (COND1), 60° (COND2), or 90° (COND3). These target separations were chosen on the basis of previous behavioral studies (Ghez et al. 1997; Ottes et al. 1984). The smallest separation is just in the range where spatial averaging is most frequent. The wider separations are both well into the range where it is rare. Intertrial interval varied randomly between 1,500 and 2,000 ms. The choice between alternative targets was cued by the response cue consisting of a small, thin, white line on top of the central fixation dot, with the line pointing in the direction of the designated target (Fig. 1A, 2nd column). Stimuli and joystick position feedback (presented as a small, moving, white cursor box across the screen; 0.43 × 0.43° visual angle) were presented with Presentation 16.2 software (Neurobehavioral Systems), using a liquid crystal display video projector, back-projected onto a translucent screen with two front-silvered mirrors.

Fig. 1.

Behavioral data. A: at the top, the timeline of a single trial, independent of conditions. Below, an example of stimuli shown in each of the 3 conditions (COND1–3). The dashed white lines between the central cue and 1 of the 2 peripheral target locations in the response cue (RESPCUE) indicate joystick trajectories. Following the onset of the response cue, example joystick traces are shown of 1 participant's correct trials in each condition. B: left histogram shows mean reaction times (mRTs) for all conditions, separately for left and right targets. Right histogram shows corresponding error rates, broken down into the 3 main categories (cat 1: timing and choice errors, cat 2: online corrections, and cat 3: inaccurately targeted responses). Error bars represent SE of the mean.

The experiment consisted of 10 blocks of 60 trials each (20 trials for each condition; 50% probability of left/right targets; duration ∼4 min) preceded by 2 comparable practice blocks. The order of presentation of trials from the 3 conditions was randomized within each block of trials and for each participant. Participants were instructed to move as little as possible, to keep their eyes fixed at the fixation dot at all times, and to hold the joystick with their right hand in a relaxed grip. They were instructed to prepare for responding during the precue period and then respond as fast and accurately as possible with a ballistic joystick-guided pointing movement to the cued target after the onset of the response cue. They were also asked to make swift, ballistic responses instead of slow visually guided movements. Hence, they were allowed to overshoot the target location. Maximum hand displacement was 4–5 cm, corresponding to a displacement of the joystick cursor position on the screen of maximally ∼10 cm (∼2 cm exceeding the target location). Participants were instructed to relax arm and hand as much as possible during the intertrial and delay periods without releasing the joystick grip.

Recordings.

MEG data were recorded continuously using a whole-head system with 275 axial gradiometers (VSM/CTF Systems). Head position with respect to the sensor array was measured and monitored during the course of the experiment (Stolk et al. 2013), using localization coils attached to anatomic landmarks (the nasion and, using earplugs, the left and right ear canal). Furthermore, horizontal and vertical electrooculogram (EOG) were recorded in a bipolar montage using electrodes placed below and above the left eye and at the outer canthi. Joystick position was sampled continuously on the stimulus presentation computer to enable updated joystick cursor positions at screen refresh rate (60 Hz) during task performance. In addition, the joystick x–y coordinates were continuously recorded together with the MEG data. All MEG, EOG, and joystick x–y streaming data were low-pass filtered at 300 Hz, sampled at 1,200 Hz, and saved to disk.

Structural T1 MRI scans were obtained for all subjects on a Siemens 1.5T Avanto (TR/TE 2,250/2,950 ms) MRI scanner. During MR acquisition, identical earplugs (now with vitamin E capsules in place of the MEG localization coils) were used to allow for offline coregistration of the MRI and MEG data.

Behavioral analysis.

Task performance was analyzed on the basis of the joystick position data. Reaction time was calculated from movement onset, defined as the time when the joystick displacement was first exceeding a threshold of 2.5 SD above the mean amplitude during a 200-ms baseline before the response cue, determined separately for each condition. Error analyses were based on an offline trial-by-trial visual inspection of movement trajectories. Errors were classified into three categories: 1) choice and timing errors, 2) corrections, and 3) inaccurately targeted responses. Choice and timing errors included: 1) trials in which the movement trajectory ended or passed the incorrect target (wrong location), 2) trials in which a response occurred during the delay period (premature response), and 3) trials in which a response was too fast (<200 ms), too slow (>800 ms), or missing altogether. Corrections were trials in which the joystick trajectories revealed online corrections from the incorrect to the correct location, estimated by comparing the cursor position at 50 and 75% of maximum velocity. In more detail, when the two positions were not on a single line through the center cue and one of the targets, the trial was classified as incorrect due to online correction. Finally, trials were classified as inaccurately targeted if the target location was missed by >10° (on either side) in the 30° separation condition or >15° in the other two conditions.

Differences in mean reaction times and error rates (averaged across error types) between conditions were assessed using repeated-measures ANOVAs including the within-subject factors CONDITION (30, 60, or 90°) and DIRECTION (left or right movements). Differences between conditions in terms of error types were tested separately, averaged across movement direction, using ANOVAs and the within-subjects factors CONDITION (30, 60, or 90°) and ERRORTYPE (choice and timing error, correction, or inaccurately targeted response).

MEG sensor-data analysis.

MEG data were analyzed with MATLAB (The MathWorks) using the open-source FieldTrip toolbox (Oostenveld et al. 2011). Nonoverlapping epochs of 3,400 ms (800-ms baseline), centered around precue onset, were extracted separately per condition and for correct response trials only, combining the data from left and right target trials within each condition (as those were not behaviorally different between conditions). Preprocessing included the following steps. First, line noise contamination was removed by applying a digital 50-Hz discrete Fourier transform filter (including the 1st 2 harmonics: 100 and 150 Hz) on the continuous data. Second, artifact cleaning was performed, including semiautomatic removal of trials contaminated by muscle activity, slow drift, or SQUID jump artifacts, followed by independent component analysis (ICA)-based removal of eyeblink, eye movement, and ECG contamination, using downsampled (300 Hz) data. This resulted in remaining data sets for further analyses consisting of on average 169 trials for COND1 (15.5 ± 6.8% rejected), 173 trials for COND2 (13.5 ± 8.9% rejected), and 172 trials for COND3 (14 ± 8.9% rejected).

Further analyses included time-frequency analysis, time-domain analysis, beamformer source estimation, and statistical analysis. Time-frequency decompositions were performed for horizontal and vertical planar-transformed MEG data that were subsequently combined to obtain the power at each virtual planar gradiometer location regardless of the orientation of the gradient (Bastiaansen and Knösche 2000). This procedure simplifies the interpretation of the sensor-level data, as with planar gradients the maximal signal is located above the source (Hämäläinen et al. 1993). A comparable transformation was applied to time-domain event-related field (ERF) averages.

Time-frequency power representations were computed based on a sliding-window Fourier approach, with a step size of 50 ms. Power of lower frequencies (range 1–60 Hz) were estimated based on 4 s of padded data (original length 3.4 s), using an adaptive sliding window of three cycles per frequency bin (step size 1 Hz), multiplying the data with a Hanning taper before power estimation. From these data, beta (17–29 Hz)- and theta (4–6 Hz)-power estimates were extracted for further analysis. For the higher-frequency range, a multitapering approach was used with orthogonal Slepian tapers (Mitra and Pesaran 1999), which allows better capture of the broad-band oscillatory activity in the higher range while reducing spectral leakage. For this frequency range (30–120 Hz; step size 5 Hz), power was estimated using sliding windows of 30 cycles per frequency bin and applying a spectral smoothing of 10 Hz by adapting the number of orthogonal Slepian tapers (2–9 tapers: higher number used for lower frequencies and vice versa). From these data, low-gamma (30–50 Hz)- and high-gamma (60–80 Hz)-band power estimates were extracted for further analysis.

MEG source reconstruction.

Source estimation of oscillatory activity was performed using the dynamic imaging of coherent sources (DICS) beamforming approach (Gross et al. 2001; Liljeström et al. 2005). Participant-specific anatomic MRIs were used to transform linearly a three-dimensional template grid (8-mm spacing) in Montreal Neurological Institute (MNI) coordinates to the coregistered MEG coordinates system specific to the participant's head. Subsequently, the inverse of this transformation was applied to obtain grid points at matched brain locations across participants. Spatial filters were constructed for each of the grid positions, passing the activity from the location of interest with unit gain while maximally suppressing activity from all other possible sources of neural and nonneural activity. The beamformer spatial filter is constructed from the lead field and the cross-spectral-density matrix of the data. The lead field is the physical forward model of the field distribution calculated from an assumed source at a given location and the participant-specific volume-conduction model of the head. Here, we used a single-shell volume-conduction model of the brain based on the brain boundaries determined by the segmented anatomic MRI to compute the lead field (Nolte 2003).

Source estimation procedures included DICS across conditions of 1) delay-period event-related desynchronization (ERD) in the beta- and low-gamma-range, using data from a window between 600 and 1,100 ms following precue onset against a 500-ms precue baseline, and 2) response-period event-related synchronization in the theta- and high-gamma-range, using data from a window of 1,400–1,900 and 1,450–1,750 ms following precue onset against a 500- or 300-ms precue baseline, respectively. In all cases, a common spatial filter was estimated first, based on the pooled data from both time intervals (active and baseline), using all single trials. Subsequently, this filter was used to obtain power estimates within each interval by projecting the single-trial data of each time interval through the common spatial filter. Finally, source activity across conditions was estimated by computing the difference between active and baseline source activity as a relative power change from baseline (i.e., by dividing the difference between active and baseline source activity by the baseline source activity).

MEG statistical analysis.

For sensor-level analyses, significance of left sensorimotor cortex (LMtctx)-related oscillatory activity and slow-wave ERF changes among conditions were assessed with ANOVAs, using the within-subject factor CONDITION (COND1, COND2, COND3). Reported P values were Greenhouse-Geisser-corrected to deal with violations of sphericity. In case of a significant main effect of CONDITION, subsequent pairwise comparisons were used to delineate further significant differences between pairs of conditions. The reported P values of these analyses were Bonferroni-corrected to deal with the multiple-comparison problem. For all of these analyses, sensor-level LMtctx region of interest (ROI) data (for ROI location, see Fig. 2C) was used, averaged across ROI sensors, frequency bins, and time points of interest. The LMtctx ROI contained a selection of 14 sensors covering the area of maximum grand-average preresponse (−200 to 0 ms; response-locked) beta-ERD activity measured against a 500-ms baseline (1,000 to 500 ms before response onset). Time windows of interest were a priori-selected for beta-, low-gamma-, and high-gamma-band activity, covering the late delay period, thus avoiding stimulus-related effects early in the delay period. The time window for analysis of early theta-activity was defined on the basis of visual inspection of the grand average. For the delay-period oscillatory activity, the selected windows were 600–1,100 ms for beta-, low-gamma-, and high-gamma-band activity and 150–450 ms for early theta-band activity, all against a 500-ms precue baseline. For the ERF activity, however, delay-period activity included the last 500 ms of the delay period (700–1,200 ms), as no backward shift of 100 ms was needed to avoid (frequency) bleeding of response-cue triggered activity into the delay period.

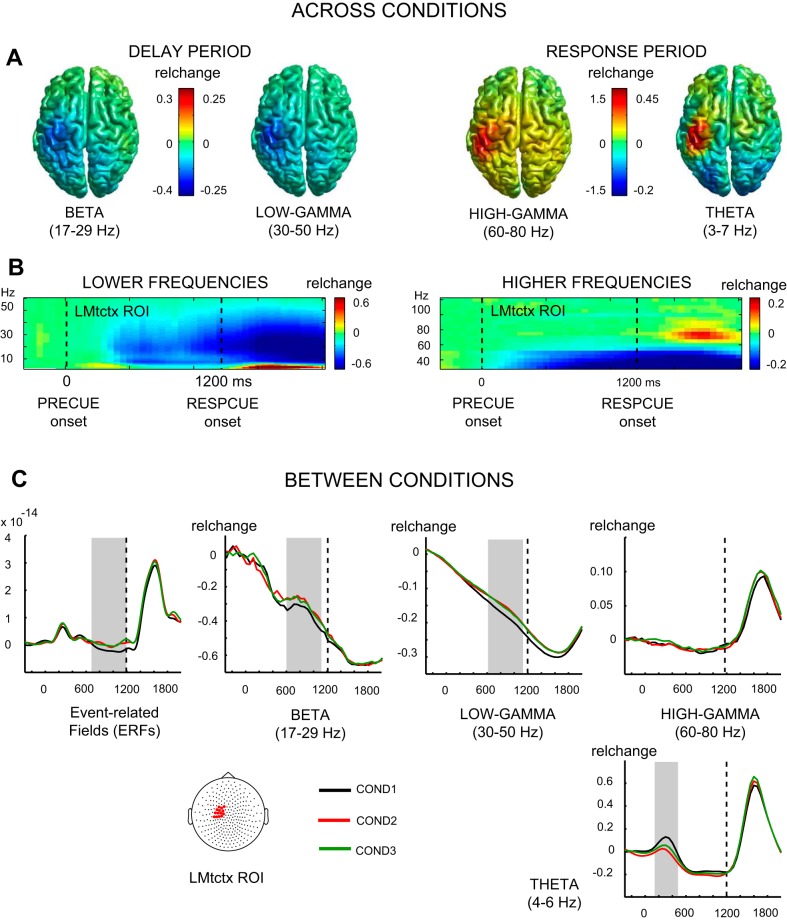
Fig. 2.

Magnetoencephalography activity. A, left: beamformer source reconstructions of baseline-normalized, late delay (600–1,100 ms) beta (17–29 Hz)- and low-gamma (30–50 Hz)-band activity, averaged across trials from all 3 conditions, projected onto the surface of a Montreal Neurological Institute (MNI) template brain. Right shows the same for response period activity in the high-gamma (60–80 Hz; 1,450–1,750 ms)- and theta-range (3–7 Hz: 1,400–1,800 ms). All 4 frequency bands show left sensorimotor cortex (LMtctx) activity of comparable location. B: grand-average (n = 18) time-frequency representations of lower-frequency range (1–60 Hz: left) and higher-frequency range (30–120 Hz: right) LMtctx region of interest (ROI) activity across conditions. The LMtctx ROI sensors, indicated with red dots on cartoon head, were selected on the basis of maximum grand-average beta-power suppression before responding. C: LMtctx ROI derived grand-average (precue-locked) traces of baseline-normalized relative changes (relchange) in event-related field and beta-, low-gamma-, high-gamma-, and theta-band activity, separately per condition (black lines representing COND1, red lines COND2, and green lines COND3). Gray boxes indicate statistical windows of significant differences between conditions.

RESULTS

Behavioral performance.

Figure 1 shows example trajectories of joystick responses from a single participant (A) and an overview of the behavioral response profiles across all participants and all conditions (B). Despite the emphasis on speed, movement endpoints and trajectories were generally highly accurate, even in the condition of smallest target separation (COND1: 30°). Response onset times were not affected by the manipulation of target separation. The average left and right response times (and corresponding SD of the mean) were 432 ± 44 and 428 ± 41 ms for the 30° separation condition (COND1), 430 ± 45 and 427 ± 39 ms for the 60° separation condition (COND2), and 430 ± 42 and 428 ± 40 ms for the 90° separation condition (COND3), respectively. Statistical analysis confirmed that participants responded equally fast in each condition and to each of the two targets. Error rates, however, although generally low, showed a significant main effect of CONDITION [F(2,34) = 18.9, P < 0.0001] independent of movement direction. Mean error rates were higher for COND1 (1.1 ± 1.1%, left; 2.7 ± 3.0%, right) than for COND2 (0.2 ± 0.2%, left; 0.5 ± 0.6%, right) and COND3 (0.4 ± 0.7%, left; 0.6 ± 0.7%, right), a pattern confirmed by pairwise comparisons between conditions (COND1vs2 contrast P < 0.0001, and COND1vs3 contrast P = 0.004, whereas COND2vs3 contrast was not significantly different).

The condition of smallest spatial separation between movement targets also induced a different pattern of error types, as apparent from the right histogram of Fig. 1B. Although percentage of inaccurately targeted responses averaged across movement directions (COND1: 0.5 ± 0.9%, COND2: 0.2 ± 0.3%, and COND3: 0.03 ± 0.1%) and percentage of choice and timing errors (COND1: 0.9 ± 1.0%, COND2: 0.2 ± 0.4%, and COND3: 0.5 ± 0.6%) were comparable across conditions, participants were more likely to correct their response in COND1 (2.4 ± 2.4%) than in the other two conditions (COND2: 0.3 ± 0.5%, COND3: 0.5 ± 0.8%). This was statistically confirmed by significant main effects of CONDITION [F(2,34) = 18.9, P < 0.001] and ERRORTYPE [F(1.2,20.1) = 9.0, P = 0.005] and an additional CONDITION × ERRORTYPE interaction effect [F(1.5,25.0) = 5.1, P = 0.021].

To summarize, reaction times were identical across conditions, and movement trajectories showed clear bimodal response distributions for all separation conditions. The absence of spatial averaging effects in movement trajectories, even in COND1 with 30° separation between targets, is attributed to the instructed delay before the response. The increased error rate for this condition (although still low in number and removed from the MEG analyses) may nonetheless be due to a residual averaging tendency. Since there were no effects of response direction, for further analyses, MEG data were pooled across movement directions.

Delay period effects reflecting strength of motor preparation.

Neural field models of motor cortical activity involved in the representation and decision between alternative responses conceive this activity as sensitive to the layout of the movement environment. Specifically, the strength of competition between movement alternatives depends on the degree of overlap of the relevant neural representations. Empirically, at the cell level, monkey (pre)motor cortex neural activity during a delay period gets indeed weaker with increasing angular distance between two alternative movement targets (Pastor-Bernier and Cisek 2011). The present results comprise a similar effect of movement-related fields in humans but also predicted oscillatory effects indicative of differential movement preparation dependent on target separation.

Time-frequency decomposition across conditions showed that, following the onset of the precue, preparatory sensorimotor-cortex activity (LMtctx ROI; for sensor locations, see Fig. 2C) was evident at the sensor level as a general pattern of power suppression in the alpha-, beta-, and lower-gamma-range during the later part of the delay period and during most of the response period (Fig. 2B). Furthermore, within the lower theta-range (Fig. 2B, left; approximately 3–7 Hz), a weak and more transient power increase was present early in the delay period (approximately 200–500 ms) and during a later response selection and execution period (approximately 1,400–1,900 ms). In addition, a clear transient power increase was evident within the high-gamma-range (Fig. 2B, right; approximately 60–80 Hz) around response onset (approximately 1,500–1,800 ms) and during movement. Source modeling localized the delay-period beta- and low-gamma-activity and the response-related high-gamma- and theta-activity most clearly to the sensorimotor cortex (Fig. 2A). In addition to ERF activity, these frequency bands were analyzed further for signs of differential preparatory activity between conditions.

Movement-related fields.

The leftmost panel of Fig. 2C shows sensor-level ERF activity, for each of the three conditions separately, plotted across time and averaged across LMtctx ROI sensors. The delay period shows the magnetic counterpart of the contingent negative variation (mCNV; Elbert et al. 1994), typically of lower amplitude in MEG than in EEG. Visual inspection of the mCNV nevertheless suggests that the condition of smallest spatial separation (COND1: 30°), compared with the other two conditions, induced increased negative slow-wave activity. The difference in amplitude corresponded to a significant main effect of CONDITION [F(1.7,29.2) = 5.5, P < 0.02]. Subsequent pairwise comparisons revealed that COND1 differed significantly from COND2 (P = 0.01), whereas the difference between COND1 and COND3 reached a trend toward significance (P = 0.08).

Beta-band oscillatory power.

The second panel of Fig. 2C represents sensor-level time courses of beta-power for each of the three conditions, averaged across LMtctx ROI sensors. These traces demonstrate the preparatory reduction in beta-power typically seen in an instructed delay before movement. Similar to the behavior of the mCNV, visual inspection suggests a difference between the condition of smallest spatial separation on the one hand and the two conditions with wider separation on the other hand. Repeated-measures ANOVAs confirmed these observations partially. A main effect of CONDITION was found for beta-power [F(2.0,33.5) = 3.4, P < 0.05]. Subsequent pairwise comparisons revealed that COND1 yield significantly more suppression of beta-power than COND2 (P = 0.046). The difference between COND1 and COND3 did not reach significance.

Low gamma-band power.

The third panel of Fig. 2C shows the time course of low gamma-power. Although the depth of the modulation is smaller than in the beta-band, there is a similar pattern of a gradual reduction in power during the delay period. This contrasts with the commonly observed movement-related augmentation of gamma-power most consistently seen in the higher gamma-range (Crone et al. 2011). The low-gamma-ERD may, therefore, be functionally related more to beta-ERD. Importantly, the low-gamma-ERD displays the same pattern of differences between conditions as beta-ERD and the mCNV. That is, there is a stronger ERD for COND1 compared with the other two conditions. The visual evaluation was confirmed by a main effect of CONDITION [F(1.9,31.5) = 5.9, P < 0.01], whereas pairwise comparisons confirmed that COND1 differed significantly from COND2 as well as from COND3 (P = 0.036 and 0.042, respectively).

Together, the mCNV, beta-ERD, and low-gamma-ERD show a convergent nonlinear pattern of stronger movement-preparatory activity for alternative movement targets at 30° compared with targets at 60 or 90°.

Gamma-band signatures of lateral interactions.

Based on previous work associating spectral characteristics of gamma-activity with lateral interactions in the visual cortex (Pinotsis et al. 2012), gamma-band activity is also a candidate rhythm to reveal interactions between cell groups in the motor cortex. Of particular relevance is the relation between peak frequency of MEG-recorded gamma-activity and the dispersion of horizontal connections (Pinotsis et al. 2012). As the width of interneuronal axon arbors is reflected in the firing rate of the interneuron in frontal cortex (Krimer and Goldman-Rakic 2001), such a relation may exist in the motor cortex as well and provide a basis for spectral changes in gamma-activity dependent on target separation. Previous work by our group has also found gamma-activity serving the maintenance of an action goal, providing further support to possible sensitivity of delay-period gamma-activity to target separation (van der Werf et al. 2008, 2010). As is evident from the top, most right panel of Fig. 2C, however, although there was a clear peak in high-gamma (60–80 Hz)-band power around responding, this activity was not preceded by an increase (or decrease) of power in this frequency band during the delay period. Tested within the same window (600–1,100 ms) as the beta-ERD and low-gamma-ERD, high-gamma-band activity was not different between conditions. Therefore, unlike high-gamma-activity in the visual cortex, the current data on motor cortex gamma-activity do not support an association of high-gamma-activity with lateral interactions.

Theta-synchronization effects.

Although we did not entertain an explicit hypothesis concerning the behavior of theta-activity, we found a conspicuous modulation of theta-power, with a brief phase of synchronization approximately 200–500 ms after precue onset and a second phase of theta-ERS concomitant with the motor response (Fig. 2C, bottom, right). As shown in Fig. 2A, right, this theta-activity was clearly localized to the sensorimotor cortex and displayed differences between conditions (Fig. 2C, bottom, right traces). Specifically, the early phase of theta-ERS was of higher amplitude for COND1 than for the conditions with wider target separations. Repeated-measures ANOVAs revealed a main effect of CONDITION for theta (4–6 Hz)-power between 150 and 450 ms following precue onset [F(1.8,31.1) = 6.7, P < 0.01]. Subsequent pairwise comparisons revealed that COND1 differed significantly from COND2 in theta-power (P = 0.005). The difference between COND1 and COND3 did not reach significance.

DISCUSSION

This study explored whether preparatory oscillatory activity in the motor cortex is influenced by the spatial separation between two alternative movement targets. The results show effects on slow ERFs, beta-ERD, low-gamma-ERD, and theta-ERS during the delay period. These neurophysiological effects tend to distinguish the small separation condition (30°) from the wider separation condition (60 and 90°), consistent with behavioral effects of target separation (i.e., spatial averaging). In the sections below, we discuss how the oscillatory changes may be associated with the interactions between competing cell groups encoding alternative movements.

Behavioral effects of target separation.

Both for saccades and reaching movements, direction specification is such that, with small separation between alternative targets, responses tend to land at a central default or averaged value. Beyond a certain separation, the distribution of endpoints is bimodal (Chapman et al. 2010; Ghez et al. 1997; Ottes et al. 1984; Van der Stigchel and Nijboer 2013). Very strong averaging tendencies are found for separations up to 30° for reaching movements (Ghez et al. 1997) and 35° for saccades (Van der Stigchel and Nijboer 2013).

Whereas these previous behavioral experiments strongly emphasized response speed, the present study used a delayed-response task and neural measures obtained during the delay to investigate motor cortical correlates of target separation. Based on a theoretical framework assuming simultaneous encoding of alternative movement targets (Cisek and Kalaska 2010), such an approach may detect delay-period effects related to competitive interactions between the neural populations encoding the targets. However, the experimental approach cannot be expected to induce behavioral averaging effects, dependent as they are on speeded responses immediately on a temporally and spatially unpredictable target display (Edelman and Keller 1998; Ghez et al. 1997; Meeter et al. 2010). Accordingly, none was obtained, unless the slightly higher error rate for the smallest separation condition results from a residual averaging tendency.

As to reaction times, there is, likewise, no meaningful comparison with studies reporting averaging behavior. A few previous studies have also used a delay between target exposition and response signal. Similar to the present study, Pellizzer and Hedges (2003) found, for their two-target condition, no effect of target separation. Praamstra et al. (2009) reported extremely small (<10 ms) effects. The absence of reaction time effects in the present study is therefore in agreement with previous work, albeit surprising in the light of differential delay-period motor preparation between conditions. We have previously suggested that this apparent contradiction is probably explained by the fact that close target proximity is a disadvantage for visual selection (Bahcall and Kowler 1999; Hilimire et al. 2009), canceling out any motoric advantage.

Oscillatory brain activity and competitive interactions between neural populations.

Several reasons predict that the geometric relations between groups of neurons encoding the cued directions will translate into delay-period effects on oscillatory activity. First, neural oscillations play a fundamental role in shaping cortical circuit activity, for example, by providing precise timing of action potentials of pyramidal cells and by controlling local network interactions (Bartos et al. 2007; Buzsaki and Chrobak 1995). Second, given the orderly structure of the motor cortex, with a clustering of cells that share directional preference (Eisenberg et al. 2010; Georgopoulos et al. 2007), interactions between groups of neurons coding for widely separated targets requires interneurons with wide horizontal arbor spans, whereas cell groups coding for more closely spaced targets interact through interneurons with a narrower span. In the prefrontal cortex, different horizontal arbor spans are associated with different interneuron firing rates, with rates going up with increasingly narrower arbor span (Krimer and Goldman-Rakic 2001). If the same applies for the motor cortex, oscillatory activity may be modulated by different spatial arrangements of alternative movement targets. Especially gamma-oscillations have been suggested to play a role in cell-tuning and associated mechanisms of lateral inhibition (Bartos et al. 2007; Merchant et al. 2012). In line with this reasoning, MEG-recorded visual cortex gamma-activity was reported to reflect columnar size, and hence range of horizontal connections, in the gamma-peak frequency (Pinotsis et al. 2012).

The present results do not contain similar effects for the most prevalent sensorimotor gamma-activity in the higher frequency range >50 Hz. Although there was robust gamma-synchronization concomitant with the response, gamma-power in this range was low during the delay period and unaffected by target proximity. In the lower gamma-range of 30–50 Hz, by contrast, there was task-related desynchronization, the amplitude of which was modulated by target proximity. The desynchronization is similar to the well-known movement-preparatory desynchronization of beta-activity, biasing the interpretation toward a movement-preparatory function. To our knowledge, however, this behavior of lower-range gamma-activity is unusual. Hence, it is possible that these effects express changes in lateral interactions as a function of target proximity, the more so since relevant visual gamma-effects occur in this frequency range (Pinotsis et al. 2012).

Nonlinear effects of target separation on movement-preparatory activity.

We tentatively distinguish between oscillatory changes expressing the regulatory action of horizontal connections (see previous section) and the resulting net effect on known indices of movement preparation, such as the mCNV and beta-ERD. Modulation of the strength of preparatory activity by target separation is suggested by single-unit recordings in monkey premotor cortex (Cisek and Kalaska 2005; Pastor-Bernier and Cisek 2011). A similar modulation occurs with variation of target number in various cortical and subcortical structures (Churchland and Ditterich 2012). The present results show a convergent pattern of stronger delay-period motor preparatory activity in the 30° separation condition compared with the 60 and 90° separation conditions, expressed in mCNV, beta-ERD, and low-gamma-ERD. The mCNV modulation replicates CNV effects previously found in an EEG study (Praamstra et al. 2009).

This nonlinear effect of target separation on neural indices associated with movement preparation is presumably related to microstructural properties of the motor cortex underlying the interaction between competing movement representations, resulting in spatial averaging for angular separations up to approximately 30–40° in direct- instead of delayed-response paradigms. As Pastor-Bernier and Cisek (2011) put it succinctly, the competition between potential actions is determined “by simple facts of geometry: when choosing between two nearby targets, the nervous system can mix their neural representations and start moving between the targets. However, choosing between two targets in opposite directions implies that the choice has to be all-or-none.”

An important remaining question is whether the modulation in strength of movement-preparatory activity directly reflects the representation of alternative movement targets at different separation in the sensorimotor system and the changed interaction between the involved cell groups or whether it just signals that close proximity of movement targets elicits in subjects a stronger inclination to prepare for responding. The latter explanation has been put forward for the observation of stronger beta-ERD with a smaller number of response alternatives, expressed in the proposal that response (un)certainty is an important determinant of beta-power (Tzagarakis et al. 2010). Although there is no reason to favor such an explanation of the present effects as endogenously driven over an explanation as exogenously induced, that is, shaped by the task space, the former cannot be ruled out without dissociating visual input and motor requirements. We are currently exploring this approach.

Theta-synchronization and spatial averaging.

Theta-activity was characterized by an early synchronization phase following the precue and a later, higher amplitude synchronization concomitant with the response, well-localized to the sensorimotor cortex. Theta-activity is observed in parietofrontal regions in reaching and pointing tasks (Perfetti et al. 2011; Rawle et al. 2012; Tombini et al. 2009) as well as with simple finger movements (Yamanaka and Yamamoto 2010). Rawle et al. (2012) found a time course as in the present study, with the amplitude of the early phase modulated by the number of possible pointing targets. They proposed that the common factor in reported work on theta-synchronization in motor tasks is that they require spatial attentional selection of a target to capture it with a movement. On this interpretation, the theta-synchronization can be regarded as a precursor to movement (Cisek and Kalaska 2010). Furthermore, the stronger the early theta-ERS is, the more easy attentional capture will evolve in an exogenously elicited response tendency.

The modulation of the early theta-synchronization may be relevant to spatial averaging behavior. Although the neural basis of spatial averaging in reaching is uncertain, it is more extensively investigated in eye movements (Edelman and Keller 1998; McPeek et al. 2003; van Opstal and Van Gisbergen 1990). Based on recordings in the superior colliculus, there is no evidence for loss of spatial segregation of targets for express saccades exhibiting spatial averaging. Instead, spatial averaging of saccade targets is seen as the result of a premature launch of the saccade before the process of saccade target selection, and computation of the saccade vector, is completed. A premature launch of saccades is facilitated by the greater salience of targets at close proximity, exerting a pull on the saccade system likened to the visual grasp reflex (Edelman and Keller 1998). The covert response activation represented by the early theta-synchronization in our data may thus represent a cortical correlate of a premature response tendency when alternative targets are close.

Conclusion.

The results of this study show that motor cortical activity preceding a choice between two alternative pointing targets is not immune to the layout of the workspace, here the spatial separation of targets. The well-characterized neural population coding of movement direction makes spatial separation of alternative movement targets a suitable testing ground for the question whether cooperative and competitive interactions between involved cell groups is expressed in modulations of ongoing oscillatory activity. The results do not show the modulation in the higher frequency range where we expected such effects. The effects that we found in lower frequency bands have a prima facie interpretation as a modulation of movement-preparatory activity, suggesting the downstream effect of altered interactions between the relevant cell groups.

GRANTS

This work was supported by the Netherlands Organization for Scientific Research (NWO) Maatschappij- en Gedragswetenschappen (MaGW) Grant no. 404-10-414 to P. Praamstra and W. P. Medendorp. W. P. Medendorp is also supported by the European Research Council (EU-ERC 283567) and NWO-VICI (453-11-001).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

T.G.-t.J., R.O., O.J., W.P.M., and P.P. conception and design of research; T.G.-t.J. performed experiments; T.G.-t.J. analyzed data; T.G.-t.J., O.J., W.P.M., and P.P. interpreted results of experiments; T.G.-t.J. prepared figures; T.G.-t.J. and P.P. drafted manuscript; T.G.-t.J., O.J., W.P.M., and P.P. edited and revised manuscript; T.G.-t.J., R.O., O.J., W.P.M., and P.P. approved final version of manuscript.