Scaling and coordination deficits during dynamic object manipulation in Parkinson's disease

Abstract

The ability to reach for and dynamically manipulate objects in a dexterous fashion requires scaling and coordination of arm, hand, and fingertip forces during reach and grasp components of this behavior. The neural substrates underlying dynamic object manipulation are not well understood. Insight into the role of basal ganglia-thalamocortical circuits in object manipulation can come from the study of patients with Parkinson's disease (PD). We hypothesized that scaling and coordination aspects of motor control are differentially affected by this disorder. We asked 20 PD patients and 23 age-matched control subjects to reach for, grasp, and lift virtual objects along prescribed paths. The movements were subdivided into two types, intensive (scaling) and coordinative, by detecting their underlying self-similarity. PD patients off medication were significantly impaired relative to control subjects for both aspects of movement. Intensive deficits, reduced peak speed and aperture, were seen during the reach. Coordinative deficits were observed during the reach, namely, the relative position along the trajectory at which peak speed and aperture were achieved, and during the lift, when objects tilted with respect to the gravitational axis. These results suggest that basal ganglia-thalamocortical circuits may play an important role in fine motor coordination. Dopaminergic therapy significantly improved intensive but not coordinative aspects of movements. These findings are consistent with a framework in which tonic levels of dopamine in the dorsal striatum encode the energetic cost of a movement, thereby improving intensive or scaling aspects of movement. However, repletion of brain dopamine levels does not restore finely coordinated movement.

reaching for and dynamically manipulating an object in a dexterous fashion is a complex action critical to interactions with the environment. This ability requires coordination of the arm and hand during the reach (Jeannerod 1984) and coordination of fingertip force vectors with arm posture and arm transport (Johansson and Cole 1992). While there is an extensive literature in monkeys and humans demonstrating the key roles of frontal-parietal networks in reaching for and in grasping static objects (Archambault et al. 2011; Castiello 2005; Cavina-Pratesi et al. 2010; Filimon 2010; Gallivan et al. 2013; Grafton 2010; Sakata et al. 1995), there are relatively few studies examining the neural substrates of reaching for and dynamically manipulating an object in a dexterous fashion. Dexterous manipulation requires both generating fingertip forces of sufficient magnitude to stabilize an object and dynamically modulating the fingertip forces to match environmental demands. Such demands could be imposed by changes in object properties during the manipulation or by varying torsional loads, due, for example, to lifting the object at a tilt relative to gravity. A notable exception to the dearth of neural studies on dynamic dexterous manipulation is a functional imaging study in which activation of a frontal-parietal-cerebellar network was found, irrespective of the level of dynamic dexterity required (Mosier et al. 2011), consistent with previous literature. However, increases in dexterity requirements were associated with selective increases in basal ganglia activity. This finding was surprising, as the cerebellum, rather than the basal ganglia, is traditionally associated with fine motor coordination (Grimaldi and Manto 2012; Thach et al. 1992).

An important perspective on the role of basal ganglia-cortical circuits in dynamic object manipulation can come from the study of patients with Parkinson's disease (PD), in which reduced tonic levels of dopamine in midbrain neurons result in dysfunction of basal ganglia-thalamocortical circuits, which produces motor deficits. Reductions in tonic levels of dopamine in turn result in dysfunctional basal ganglia-thalamocortical circuits, taking the form of abnormal neuronal firing patterns and pathologically synchronized oscillatory activity at multiple levels within these circuits (Hammond et al. 2007; Oswal et al. 2013). The pioneering work of Castiello and colleagues (Castiello et al. 1993; Scarpa and Castiello 1994) demonstrated that PD patients show deficits in the integration/coordination of multiple movement components during a reach-to-grasp movement, and that dopaminergic therapy improves the speed of the reach more than coordination of the reach and grasp (Castiello et al. 2000). Consistent with these findings, we previously suggested that motor deficits in PD across a range of tasks can be decomposed into at least two major aspects, namely, intensive such as amplitude and speed, relating to how energetically forceful a movement is, and coordinative, relating to the integration and/or coordination of multiple movement components (Lukos et al. 2013; Schettino et al. 2006). We further suggested that dopaminergic medications can remediate intensive functions to a much greater degree than coordinative functions (Levy-Tzedek et al. 2011; Lukos et al. 2013; Schettino et al. 2006). However, all of the grasping studies mentioned above examined reaching for and grasping static objects, without dynamic manipulation. Dexterous manipulation of dynamic objects, as opposed to static objects, is a more natural functional task and introduces greater challenges for motor coordination, which appears to specifically depend on the basal ganglia (Mosier et al. 2011).

In the present study, PD patients on and off medication reached for, grasped, and transported dynamic virtual objects having either symmetric or asymmetric centers of mass. The lifts were performed in different spatial directions, either aligned with or tilted off of the vertical (gravitational) axis, the latter of which accentuates precise coordination of fingertip force vectors with arm posture and transport, thereby permitting a more rigorous test of motor coordination in PD and the effect of dopamine therapy. We also introduced a novel quantitative metric for determining whether a given movement parameter can be classified as intensive or coordinative. If intensive aspects of movements are obtained by scaling a single parameter, such as speed or aperture, and small changes in the parameter lead to small changes in movement, then the underlying motion must be strictly stereotyped (Barenblatt 1996) and produce a smoothly related family of speed profiles that are self-similar. In contrast, self-similarity is unlikely to be observed for motions requiring coordination of multiple movement components, such as tilt away from the instructed transport direction. Thus changes in speed and aperture of motion were expected to exhibit self-similarity, whereas tilt of the object during transport was not. We further hypothesized that PD patients would show both intensive (speed and aperture) and coordinative (increase object tilt during transport) deficits and that dopamine therapy would only alleviate intensive deficits.

MATERIALS AND METHODS

Subjects

Study protocols were reviewed and approved by the Human Research Protections Program Institutional Review Board at the University of California San Diego, and written informed consent was obtained from all participants. Study participants included 20 individuals with idiopathic PD (10 men, 10 women) and 23 age-matched control subjects (12 men, 11 women). Two additional PD subjects who performed the reach-to-grasp aspect of the task, but did not successfully lift the object off medication, were excluded from the lift analysis (leaving 18 PD subjects) but included in the reach analysis (20 PD subjects). In addition, one PD subject was unable to perform the task at all, and one PD subject could only perform the task on medication; both were excluded. Volunteers were also excluded if they exhibited signs of dementia on the Mini-Mental Status Exam (MMSE; score < 25) or had a neurological disturbance other than PD, a major psychiatric disorder (DSM-IV), or alcohol/substance abuse. All subjects had normal or corrected to normal vision, and all but two were right handed (1 control and 1 PD). Age, educational level, Edinburgh handedness scores, and MMSE scores were balanced between the groups (Table 1).

Table 1.

Characteristics of control and PD groups

Variable	Control Group	PD Group	P Level
Age, yr	64.6 (8.9)	65.9 (6.7)	0.60
Education, yr	17.2 (3.1)	17.0 (3.2)	0.86
Edinburgh Handedness Inventory*	66.1 (30.3)	66.2 (47.5)	0.99
Mini-Mental Status Exam†	29.3 (0.9)	29.2 (1.1)	0.73

Means (SD) are reported for each variable. The P level is reported for independent-sample t-tests of group differences in the variables.

^*Positive values designate greater dominance of the right hand (Oldfield 1971).

^†The total score is reported (maximum score = 30) (Folstein et al. 1975). PD, Parkinson's disease.

Control subjects completed one test session. PD participants completed two test sessions on separate days, one when they took their normal medication dosage ∼1 h before testing (on) and the other after refraining from taking medication for 16–24 h or at least 2 half-lives of the longest-acting medication (off). The order of on/off test sessions was counterbalanced across subjects. Three PD participants were taking levodopa/carbidopa, 11 were taking levodopa/carbidopa plus one or more dopamine agonists, and 8 were taking only dopamine agonists. Symptoms on the motor examination section of the United Parkinson's Disease Rating Scale (UPDRS) were significantly worse off [mean (SD) = 41.9 (11.4)] than on [mean (SD) = 37.4 (10.1)] medication [F(1,19) = 7.43, P = 0.013, η² = 0.04]. On the Hoehn and Yahr staging scale, 7 PD participants were stage 2 and 13 were stage 3, both off and on medication. Table 2 presents the clinical characteristics of the individual PD patients.

Table 2.

Characteristics of PD patients

Subject	Age, yr	Sex	Handedness	Disease duration, yr	UPDRS (on meds)	H & Y Stage (on meds)	UPDRSr(off meds)	H & Y Stage (off meds)	Medications
1	63	M	R	2	34	3	41	3	Lev, LevR, Pr
2	56	M	R	8	24	3	29	3	Lev, Rop
3	52	M	R	10	59	3	67	3	Lev; Sel; Am
4	74	F	R	6	31	3	27	2	Lev; Ras
5	69	M	R	16	47	3	52	3	Lev; Sel; Am
6	68	F	R	7	44	3	57	3	Pr; Sel; Am
7	76	F	R	8	41	3	39	2	Sel
8	68	F	R	15	49	2	64	3	Lev; LevR; Pr; Am; Ras
9	66	M	R	3	41	3	42	3	Ras
10	56	M	R	8	37	2	41	3	St; Ras
11	61	M	R	4	37	2	43	2	Lev; Pr; Ent
12	64	F	R	7	20	2	39	2	Lev; Pr
13	54	F	L	11	32	3	41	3	LevR; Ras; Tol
14	70	F	R	3	40	3	39	3	RopXL; Ras
15	69	M	R	7	31	2	32	3	St
16	60	M	Ambi	2	51	3	46	2	Rop
17	62	F	R	7	26	2	28	2	Lev; Rop; Ras; Am
18	71	M	R	7	40	2	49	2	Lev; LevR; Pr; Am; Ras
19	72	F	R	10	42	3	30	3	LevR
20	61	F	R	5	23	3	32	3	Rop

UPDRS, United Parkinson's Disease Rating Scale, Motor section (range from 0 to 108; higher scores indicate greater impairments; H & Y, Hoehn and Yahr staging scale; Duration, years since first remembered parkinsonian symptom. Medication codes: LevR, carbidopa/levodopa sustained release; Lev, carbidopa/levodopa (regular formulation); Pr, pramipexole; Sel, selegiline; Ent, entacapone; Tol, tolcapone; Rop, ropinirole; RopXL, ropinirole extended release; St, Stalevo (carbidopa/levodopa/entacapone); Ras, rasagiline; Am, amantadine.

Stimuli

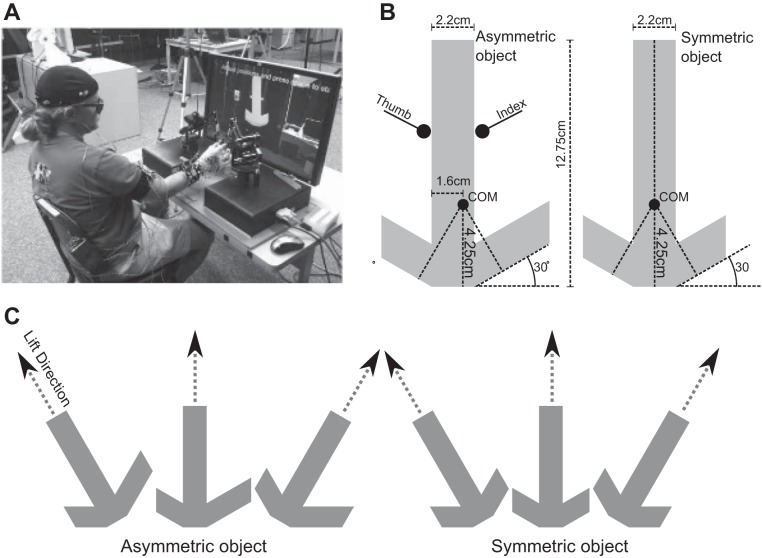
Stimuli for the task were two virtual objects, one symmetric about its center of mass and one asymmetric. The objects looked like a hammer, with a long handle and a head on one end, and were presented resting on their heads with the handle either vertical or tilted 30° to the left or right (Fig. 1). For both the asymmetric and symmetric objects, the handle was 12.75 cm tall, 2.2 cm wide, and 2.5 cm in depth. When grasped on the side, the asymmetric object tended to hang at about a 10° angle from vertical because of a 0.519-cm offset center of mass (rightward with respect to the subject). The apparent weight of the objects was a consistent 200 g. The weight was a point mass 4.25 cm above the bottom of the object and felt like a heavy weight stuck into a light, stiff object. Objects were presented with Vizard 3D software (WorldViz, Santa Barbara, CA) on a 30-in. LCD monitor ∼1 m in front of seated subjects (Fig. 1).

Fig. 1.

Experimental setup and stimuli. A: the subject was seated facing the screen with the hand reaching between the 2 robots, which were held in a custom, calibrated scaffold. The initial hand position was at the front (closest to the subject), and the object was toward the back. B: the 2 stimuli, asymmetric (left) and symmetric (right), had the same height, width of the handle, and total weight, and subjects were instructed to grip them at the center of the handle. The center of mass (COM) of the asymmetric object was shifted 0.5 cm to the right of the midline, indicated as an extended right arm. C: the 2 stimuli were presented on each of their flat edges, and the subjects were instructed to lift upward ∼10 cm along a guideline while maintaining the initial tilt.^…

Two Sensable Phantom 1.0 three degree of freedom (DoF) robots (Geomagic, Rock Hill, SC) were placed facing each other, and the subjects placed the thumb and index finger of their dominant hand into thimbles attached with a two DoF gimbal to allow free motion of the hand. The initial forearm orientation was midway between pronation and supination, with the heel of the palm resting on a 5 × 2 × 2-in. Styrofoam pad. The thumb and the index finger were contacting each other, and the remaining fingers of the hand were fully flexed. Subjects began each trial in this initial position. Custom software built on top of the open-source Chai3D haptic library (version 2.0, http://www.chai3d.org) rendered the haptic object with the open dynamics real-time physics engine (ODE version 0.11, http://www.ode.org) updating the force applied to the object with ODE's dWorldQuickStep method to keep up with the 1,000-Hz robot update time. The net effect was realistic, real-time haptic interaction with the thumb and index finger that was totally immersive even for naive performers. Simulated gravitational forces (10 m/s² downward) were included in the environment.

The stimuli were viewed through red-cyan glasses. There was a translucent virtual table with a checkerboard pattern to aid depth perception. The fingers were represented by two white 0.4-cm-radius spheres, which cast a virtual shadow straight down onto the checkerboard table, again to aid depth perception. The haptic interaction with the virtual object occurred along the entire surface of the cursor sphere. Since the robots only had three DoF (Euclidean x,y,z), the cursor spheres did not rotate, and the physics engine treated them as having infinite inertial mass. Lack of cursor rotation did not interfere with the motion studied here. An invisible haptic shield was placed between the resting point of the hand and the position of the objects to provide a safety zone. To increase immersion, a picture of the room behind the screen was added to the background of the stimuli (Fig. 1A).

Procedure

At the beginning of each trial, a virtual object was placed in front of the subject in one of three orientations (vertical or tilted 30° to the left or right) (Fig. 1). Visual guidelines extended from the object to indicate lift direction. The task was to reach, grasp, and lift the virtual object along the indicated direction. Thus there were six conditions (Fig. 1C): two objects (symmetric, asymmetric) × three orientations (tilted 30° to left, vertical, tilted 30° to right). The task was first explained and demonstrated with real aluminum objects approximating the perceived size of the virtual objects but not the weight. The subjects were then seated in front of the monitor and introduced to the use of the haptic robots by interacting with the two virtual objects until they felt comfortable with the interactions, which usually took ∼5–10 min. The interaction was very intuitive in almost every case. During the main task, an auditory cue coincided with the presentation of an object presented near the end of the available reach (away from the subject). The subjects were instructed to start with their thumb and finger together and their hand as far back as possible given the constraints of the robot. They then reached at a comfortable speed, grasped the object, and lifted it along a guideline. Any time after the object passed an instructed height (∼8 cm vertical) the subjects could drop the object and return to the start position. There was no requirement to lift the object to an exact height and then stop. Rather, subjects continued lifting the object a short distance beyond the minimum required height and then dropped the object. Thus there was no added planning constraint of lifting the object to an exact height. The next object was presented by the experimenter pressing a key.

The session began with two practice blocks of trials to acclimate subjects to the environment and task: 1) 20 reaches with 10 symmetric and 10 asymmetric objects presented at a vertical orientation and 2) 20 reaches with 10 symmetric and 10 asymmetric objects presented at vertical orientation. There was an ∼10-min break between blocks 1 and 2. This allowed some consolidation time for the task, and subject performance stabilized by block 2. Two further practice blocks were presented with the objects taking on their tilted orientations: 1) 45 reaches with the symmetric object presented at all three orientations (15 trials of each condition) and 2) 45 reaches with the asymmetric object at all three orientations (15 trials of each condition). Finally, an experimental block with all conditions mixed was presented, with 60 reaches with both objects and all three orientations (10 trials of each condition). In each block, conditions were presented in a random order. The final mixed block of trials was analyzed here.

Data Processing

Temporally aligned finger and arm data were processed by custom software developed with MATLAB (The MathWorks, Natick, MA) and C++ codes. The position of the fingers was measured from the data recorded with the haptic robot. Movement onset was defined as the midpoint of the thumb and index finger speed exceeding 5% of its peak value. Movement offset was defined as the time when either thumb or index finger touched the object as indicated by a nonzero haptic force.

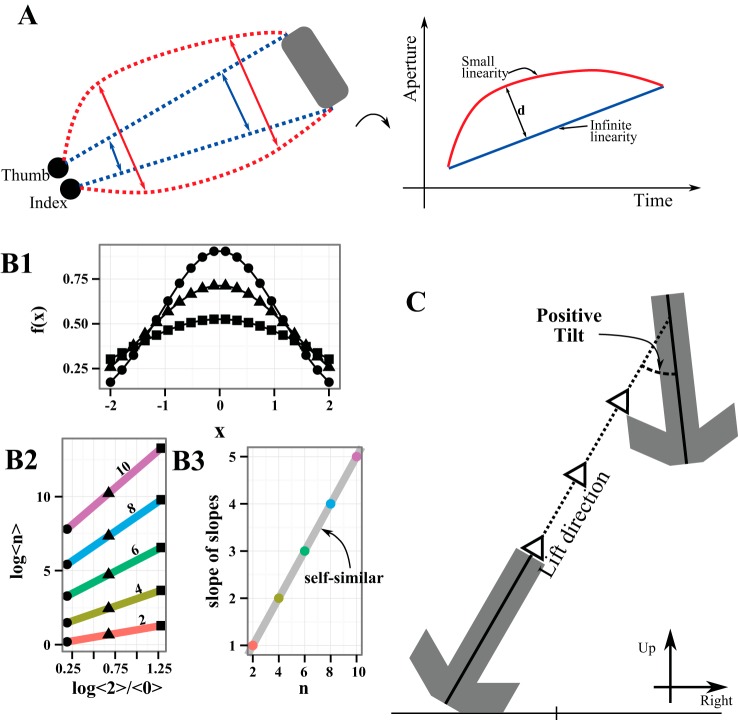
Two intensive measures, peak speed and peak aperture, and two coordinative measures, preshape coordination and object tilt error, were calculated (Fig. 2C). We previously have referred to peak speed and peak aperture as intensive aspects of movement as they can be modulated by the gain of a signal (Lukos et al. 2013). Likewise, preshape coordination was selected as a coordinative measure as it previously has been used as such, since it reflects the coordination of the hand and arm during the reach (Lukos et al. 2013). Object tilt error also was selected as a coordinative measure since maintaining the instructed tilt of the object during the lift requires coordination of fingertip force vectors with arm posture and arm transport, while taking into account effects of gravity.

Fig. 2.

Experimental measures. A: sketch of trajectories of the thumb and index finger for a single trial. Subjects start with their thumb and index finger pinched together and open their hand while translating to the object (gray box). The blue line indicates a perfectly linear path over which the aperture opens exactly enough to encompass the object, and the corresponding evolution of the aperture over time (right) is a straight line with infinite linearity. Contrarily, the red line indicates a path with finite linearity (left) and a curved evolution over time (right). The inverse of the maximum distance to the infinite linearity line (1 over d, as indicated) quantifies the decreased linearity. B: example of the self-similarity calculation. B1 shows 3 representatives of a family of functions, indicated by circles, triangles, and squares. B2 shows the nth moments (for n = 2, 4, 6, 8, 10) plotted vs. the 2nd moment normalized by the 0th. The markers match B1, so that each colored line is determined by contributions from each of the functions. The slope of the colored lines is then plotted in B3 and is seen to increase proportionally to the moment number, n, divided by 2. This indicates perfect self-similarity, as it is by construction. For real data bootstrapped errors are propagated through the calculation and used to determine significance. C: the object during the lift. The tilt is measured as the signed angle from the guideline (dashed line with arrows) in the coronal plane. By convention, counterclockwise tilts are positive (as shown) and clockwise tilts are negative.

Intensive measures.

Hand tangential velocity (speed) was calculated from the mean position of the thumb and forefinger using a linear fit on a 10-ms sliding window. Peak speed was computed.

Hand aperture was calculated as the distance between the thumb and index finger. Peak aperture was computed.

Coordinative measures.

PRESHAPE COORDINATION.

To grasp an object, healthy subjects do not mold their hand to the object at the end of a reach but rather gradually open their grip to achieve an aperture wider than the object to be grasped and then gradually close their grip so that it conforms to the size of the object to be grasped (Jeannerod 1984). This facet of hand and arm coordination is measured by the separation along the trajectory between peak aperture of the hand and peak speed of the arm. In more highly coordinated movements, the hand achieves peak aperture close to when the arm achieves peak speed, reflecting an integration of these two components in mapping the motor action to the object.

OBJECT TILT ERROR.

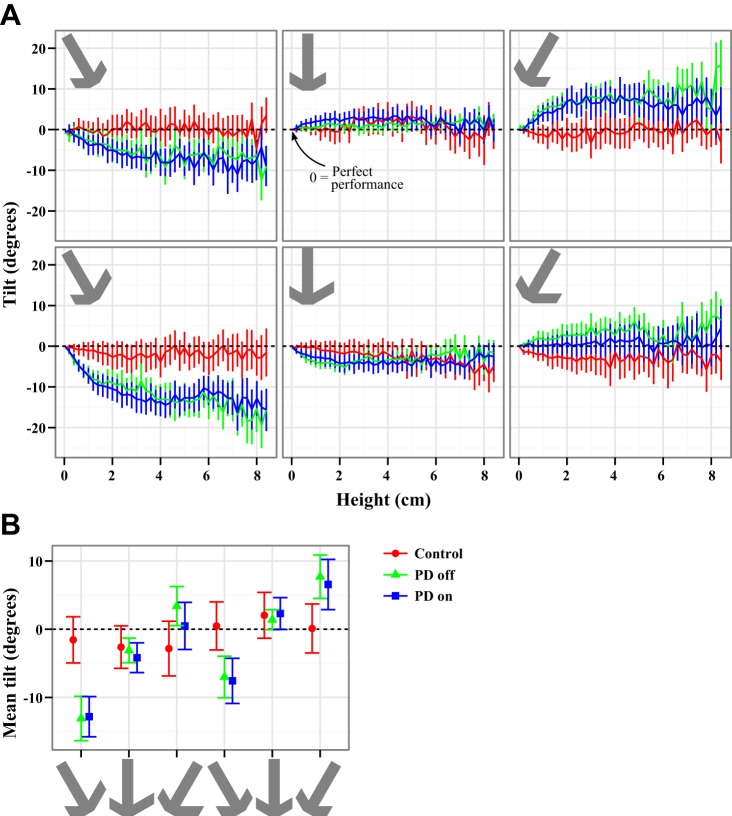
The lift time was defined by the first time the object was lifted above its initial height and then continued upward. The tilt during the lift was calculated as the signed angular deviation from the guideline in the coronal plane: arcsin(h_xd_z − h_zd_x) where h is the vector direction of the handle, d is the direction of the guideline, x is the lateral direction (positive right), and z is the superior-inferior direction (superior positive). This produced a signed deviation in angle to the left and right from the desired angle. Since the virtual object started out in the correct direction and had realistic physics, it took some time for it to equilibrate. Figure 6 shows that 4–6 cm of height was approximately where the tilt stabilized. Thus statistical tests were done on the average tilt over 4–6 cm in height. In these postprocess analyses, trials were rejected if the object never reached the instructed height (i.e., it fell over) or if its upward velocity was negative during the lift (i.e., the subject dropped the object too early). Deviations of object tilt during the lift from the instructed direction provided a measure of how well subjects met the task requirement.

Fig. 6.

Tilt during lift. A: mean and SE of the tilt with respect to the instructed tilt vs. the height of the object. In all cases a tilt of 0 indicates perfect performance, negative tilt indicates a rightward error with respect to the subject, and positive tilt indicates a leftward error. Control subjects were successfully able to lift the object in the instructed direction in all cases. PD subjects could only maintain the instructed tilt when the object was lifted vertically. For the tilted objects, PD subjects allowed the objects to tilt toward vertical, as they would by the gravitational force. To capture the tilt, B shows the tilt averaged over 4–6 cm in height (indicated by gray shading in A, top left) with SE. In all cases, control subjects were within error bars of 0, although they had a consistent tendency to allow the asymmetric object to tilt rightward and overcompensated on the symmetric object, tilting it leftward. Off medication, PD subjects show significant tilts for the left and right objects and do not correctly compensate for the weight distribution of the asymmetric object, allowing it to tilt farther rightward (down on the plot) in all cases. This effect was not alleviated by medication.

Visual guidance of movement.

APERTURE LINEARITY.

We observed that PD patients often opened their hand in a linear fashion rather than modulating hand aperture, as if they were visually aligning the finger cursors with the left and right sides of the object and maintaining that visual alignment throughout the reach. Aperture linearity quantified this behavior by comparing the actual aperture of the hand to a purely linear opening of the hand throughout the reach (Fig. 2A). For convenience, we took the inverse of the maximum perpendicular distance of the actual aperture to the reference line (defined by the initial and final apertures), so that higher values of the measure reflect more linear opening of the hand during the reach. Aperture linearity was log transformed for statistical testing because of a large peak near zero.

Statistical Analyses

For each measure, the mean value across trials for each of the six object × orientation conditions was calculated for each subject. Two repeated-measures analyses of variance (ANOVAs) were performed to directly test the following two hypotheses: 1) PD patients would show both intensive (speed and aperture) and coordinative (increase object tilt during transport) deficits, and 2) dopaminergic therapy would only alleviate intensive deficits. To test hypothesis 1, we compared control subjects and PD patients off medication. A mixed-model repeated-measures ANOVA was performed on each variable with group (PD-off medication, control) as an independent (between) factor and object symmetry (symmetric, asymmetric) and object orientation (tilted left, vertical, tilted right) as repeated (within) factors. To test hypothesis 2 examining the effects of dopaminergic therapy, a repeated-measures ANOVA was performed on each dependent variable with group (PD-on, PD-off medication), object symmetry (symmetric, asymmetric), and object orientation (tilted left, vertical, tilted right) as repeated (within) factors. For significant effects with more than two levels, t-tests were performed and corrected for multiple comparisons (Holm 1979). The t-tests were paired when making within-group comparisons (i.e., on and off medication). Normality was checked graphically. In one case, hand linearity, a log transform was applied to make the data more Gaussian. F values were calculated using type II sums of squares with the ez package in R version 1.15.2 (http://cran.us.r-project.org/). Sphericity corrections were calculated (Greenhouse-Geisser and Huynh-Feldt) but had no effect on significance in any case, and raw P values were reported. A significance level of 0.05 was used for all statistical testing.

Self-Similarity

We previously introduced the concept of scaling or “intensive” aspects of movement as those that primarily modulate gain of movement, such as peak speed or peak aperture, whereas coordinative aspects involve joint coordination or coordination of multiple independent movement attributes (Levy-Tzedek et al. 2011; Schettino et al. 2006). Here we extend these concepts to the relation between a control signal and the behavioral measure and formalize their distinction in the framework of self-similarity. We hypothesized that a consequence of single-parameter control of a movement would be self-similarity of the resulting trajectories. For example, some trajectories might be faster or slower than others, but if they were generated by a single control parameter they should have exhibited self-similarity. Assuming self-similarity, strict relations between moments of the trajectory follow. However, if multiple control parameters were needed to produce an aspect of movement, then the functions should not be self-similar.

To provide a quantitative measure of whether or not a given movement parameter, such as hand speed or object tilt during the lift, conforms to a scaling relation, we utilized a test of self-similarity. Self-similarity was assessed with a moment test (Snider et al. 2010). Self-similar functions have the form f(x) = λ^αf(x/λ) where λ is a scaling parameter. In the case of movement control, λ corresponds to some neuronal control signal with the assumption of continuity: a small change in the control signal leads to a small change in the movement. Along with existence of a single parameter, continuity is the main assumption of self-similarity. The moments of the function f(x) are defined as the average value of powers of x over the function, e.g., the zeroth moment is the average of f(x) and the second moment is the variance. Because the functions in question tend to be nearly symmetric, only even moments are considered since odd moments result in small magnitudes and thus small signal-to-noise qualities (Stevens 2009). From these relatively weak assumptions, it can be shown that the moments of the function can be written as <n> ∼ λ^n+α+1, where α is a constant exponent. In addition, the moments can be written entirely in terms of measurable quantities as

$$\text{log}\langle n\rangle \sim \frac{n+\alpha +1}{2}\log \frac{\langle 2\rangle }{\langle 0\rangle }$$

Thus the test for self-similarity is to measure the moments and verify (or not) that the log of the higher moments increases as a linear function of log<2>/<0> with slope increasing like n/2. An example of this procedure is illustrated in Fig. 2B, starting with three sample functions from a self-similar family (Gaussians with standard deviation 1.1, 1.4, and 1.9). Each of the moments of these functions is calculated, and <2> is plotted versus <2>/<0> for the lowest line (Fig. 2B2), continuing upward with <4> versus <2>/<0>, etc. . . . Given the relation constructed above, the slope of each of the lines formed from the moments is measured to generate a final plot, the so-called “slope of the slopes” (Fig. 2B3). Finally, we test (statistics below) that the slopes for the moments increase like n/2 marked by the solid gray line in Fig. 2B3.

For statistical analysis of self-similarity, we used a bootstrapping algorithm to fit the moments from individual subject/condition data. For each subject/condition, the moments were measured for every trial. The trials were then resampled with replacement, and the slope of the log-log plot was measured with least squares for 100 repeated resamplings. The error in the slope was then estimated as the standard deviation of the resampled slopes. This resulted in a slope plus error estimate for the moments, and that was used to estimate the slope of the slopes as a function of n/2, i.e., the main test quantity (see Snider et al. 2010). To test the probability that the data satisfied scaling, the test quantity was averaged across subjects and conditions with propagated error estimates to calculate a t value. This was then tested with a t-test and corrected for familywise error rates (Holm 1979). The result was a probability that the data satisfied scaling. In cases where scaling was satisfied, we also estimated the scaling exponent as α = 2(β − n/2)−1, where β was the intercept of the slope-slope test (as opposed to the slope used to verify scaling) with error propagated from the bootstrapping.

RESULTS

Reach Trajectories Varied Between PD Patients and Control Subjects

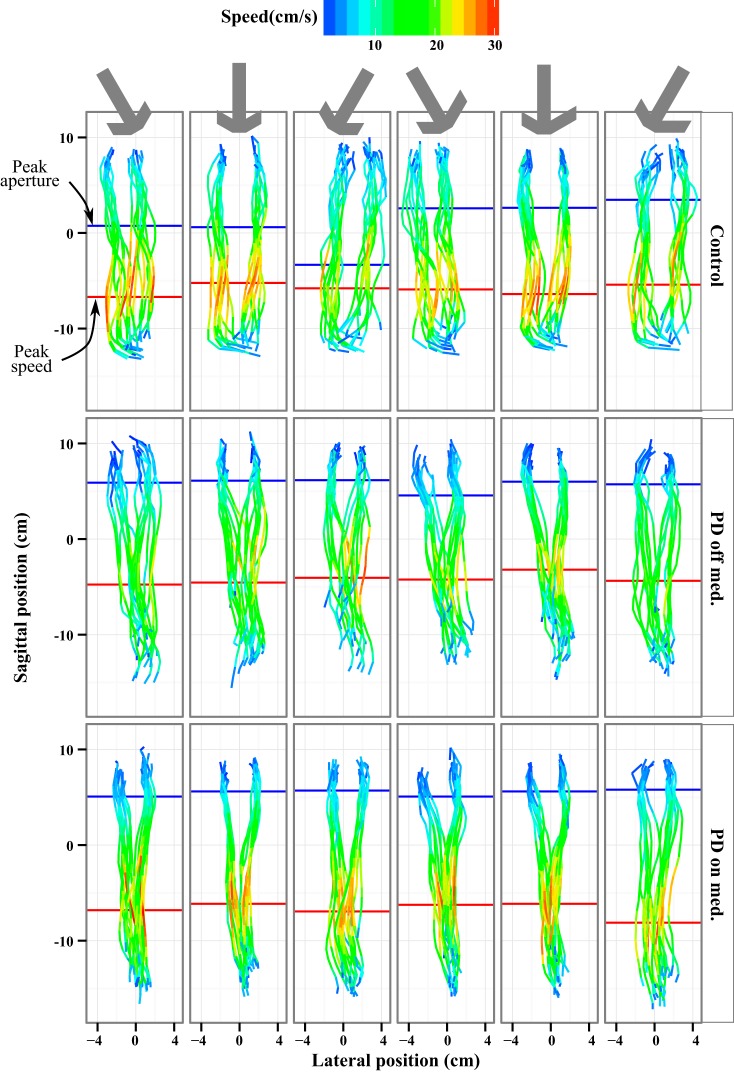
Figure 3 shows trajectories for all trials for a control subject and a PD patient on and off medication while reaching toward the objects. Reach speed is projected onto the finger paths, with hotter colors reflecting higher speeds. The red line indicates the position along the path at which peak speed was achieved and the blue line the position along the path of peak aperture. Qualitatively, Fig. 3 shows, first of all, that the PD patient off medication (Fig. 3, middle) moved at slower speeds than the control subject (Fig. 3, top) throughout most of the reach, reflecting the bradykinesia typical of PD. Second, the control subject achieved peak speed approximately one-third of the way to the object, smoothly accelerating and decelerating the hand. In contrast, the PD patient off medication achieved peak speed also at approximately one-third of the way to the object but had a less smooth speed profile. Third, the finger trajectories of the control subject and the PD patient also differed markedly. The control subject modulated hand aperture, opening the hand wide during the reach and then closing the hand as it neared the object. In contrast, the PD patient off medication maintained the two fingers in close proximity, opening the hand only very gradually during the reach. Thus the PD patient reached peak aperture farther along the reach, closer to the object, than the control subject. From the PD patient's perspective, the linear opening of the hand markers on the screen during the approach of the hand to the object is consistent with the patient visually aligning the finger cursors with the left and right sides of the object and maintaining that visual alignment throughout the reach. This pattern was seen repeatedly in the PD patients.

Fig. 3.

Speed and trajectory during the reach. An overhead view of the finger positions during the reach is plotted for the 3 groups. The start points were constrained by instruction, and the end positions were at the object (see materials and methods for details). Note that the objects were sometimes tilted and the finger placement was unconstrained, so the aperture at the end varied. The color represents the reaching speed of each thumb (left) and index finger (right) position. The mean peak reaching speed is marked with a red line. The mean peak aperture, distance between the fingers, is marked with a blue line. The subjects showed very little positional dependence of the peak speed, but Parkinson's disease (PD) subjects opened their hands the widest just before contacting the object. The control subject (top) quickly opened the hand and translated to the object, maintaining a wide aperture for most of the reach. The PD patient off medication slowly opened the hand on a V-shaped trajectory and moved much slower than the control subject. On medication, the PD subject sped up, but while the trajectories widened, their V shape remained unchanged.

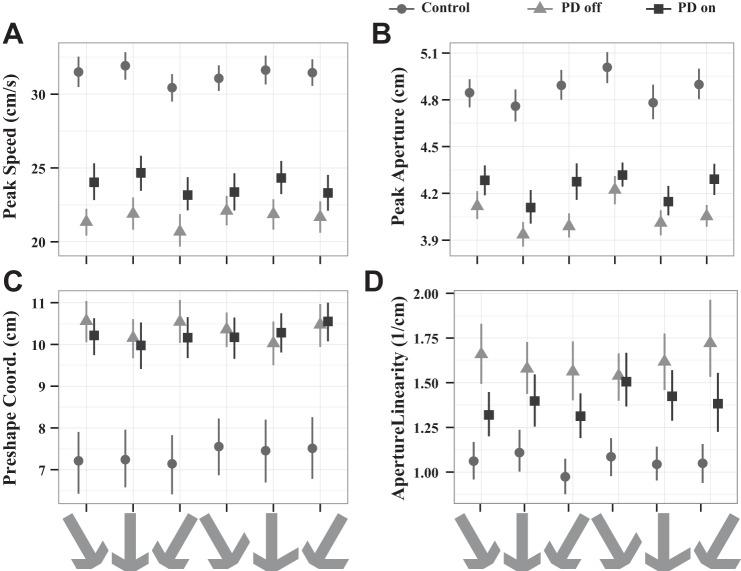
We quantified aperture linearity (Fig. 2A) as the inverse maximum distance of the aperture from its straight line path (see Fig. 5D). More linear paths correspond to larger inverse distances. An ANOVA comparing log linearity between control subjects and PD patients off medication showed that PD patients off medication had an aperture linearity (15.3 ± 0.4 cm⁻¹) that was 53% larger than that of control subjects (10.0 ± 0.4 cm⁻¹), a difference that was highly significant [F(1,40) = 10.56, P = 0.002] (Table 3).^… This very gradual increase in aperture is consistent with PD patients operating under visual control of the movement during the reach. An ANOVA comparing PD patients on and off medication did not identify any significant differences in aperture linearity (Table 4). Thus, unlike control subjects, PD patients on or off medication exhibited linear aperture trajectories consistent with visual control of the movement during reach.

Fig. 5.

Peak speed and aperture of the hand during reach (mean and 95% confidence interval). A: average peak speed. Control subjects are always faster than PD patients, and medication increased the speed of PD patients toward that of control subjects. B: peak aperture: control subjects tended to open their hand wider than PD patients on or off medication. However, dopaminergic therapy significantly increased peak aperture in the PD patients. All subject groups increased their aperture for the tilted objects. C: distance between hand position at peak aperture and peak speed (preshape coordination). PD patients on and off medication did not achieve peak aperture until the hand was nearer the object than control subjects. Medication did not affect this difference. D: linearity of the hand opening on the reach (aperture linearity; larger is more linear). PD patients opened their hand on a more linear trajectory than control subjects, and medication had no significant effect. See also Fig. 3.

Table 3.

Control vs. PD off medication ANOVA tables for significant effects only

Measure	Effect	DFn	DFd	F	P	η2
Peak speed	Group	1	40	32.429	1.26 × 10−6	0.435
	Orientation	2	80	5.608	0.00526	0.003
	Symmetry × orientation	2	80	3.602	0.0317	0.002
Peak aperture	Group	1	40	34.02	8.12 × 10−7	0.408
	Orientation	2	80	8.966	3.06 × 10−4	0.022
Preshape coordination	Group	1	40	11.752	0.00142	0.185
Aperture linearity	Group	1	40	10.563	0.00234	0.190
Tilt	Symmetry	1	39	24.830	1.32 × 10−5	0.053
	Orientation	2	78	7.395	0.00115	0.078
	Group × orientation	2	78	10.922	6.58 × 10−5	0.111

Table 4.

PD on medication vs. PD off medication ANOVA tables for significant effects only

Measure	Effect	DFn	DFd	F	P	η2
Peak speed	Medication	1	18	4.770	0.0424	0.050
	Orientation	2	36	5.942	0.00589	0.003
	Symmetry × orientation	2	36	3.740	0.0334	0.001
	Symmetry × medication	1	18	11.831	0.00292	0.001
Peak aperture	Medication	1	18	4.534	0.0473	0.038
	Orientation	2	36	7.695	0.00165	0.021
Preshape coordination	None
Aperture linearity	None
Tilt	Symmetry	1	17	33.750	2.09 × 10−5	0.074
	Orientation	2	34	19.831	1.96 × 10−6	0.261

Self-Similarity Distinguished Intensive from Coordinative Measures

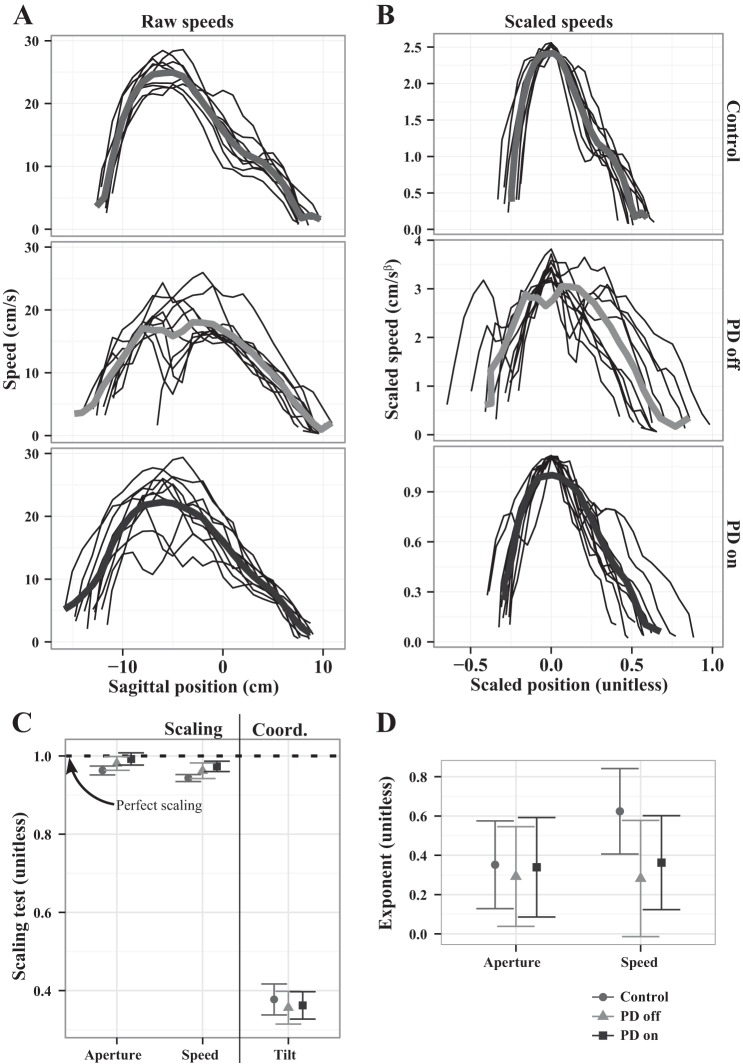
Figure 4A shows an example of the self-similarity transform applied to speed data for a control subject and a PD patient (off and on medication). The raw data were scaled with the self-similarity transform and shrinking the x-axis by a factor of 1 over the peak speed and multiplying the y-axis by the peak speed raised to the power of the individualized scaling exponent (measured below). The resulting scaled versions (Fig. 4B) showed less trial-to-trial variability, especially near the peak, which is the hallmark of self-similar functions. To scale the data explicitly, as in Fig. 4A, a scaling parameter (λ in the self-similarity transform) had to be chosen. Such a choice is constrained only by our knowledge and intuition about the system. Here, for visualization purposes, we assumed that the scaling parameter influenced the peak speed linearly; however, without direct measures of the underlying system, for example, firing rates of all neurons, there is no guarantee that the scaling parameter was chosen correctly. Fortunately, we can avoid this identification problem by assuming only that the scaling parameter exists without having to measure it directly (Snider et al. 2010).

Fig. 4.

Self-similarity. A: raw speed traces for a control subject and PD patients off and on medication (symmetric, upward object for clarity). These were scaled to the shapes shown in B with the derived scaling exponent and approximating the peak speed as the scaling parameter. The scaled representations have less variability, especially near their peaks. C: result of the scaling test (means and SE) for 3 aspects of the motion: aperture, speed, and tilt. These are calculated over the entire range of motion, not just the peaks. The dashed line indicates perfect self-similarity. The parameters that were previously qualitatively identified as scaling (speed and aperture) show self-similarity. Tilt, which was identified as coordinative, does not. D shows the exponents from self-similarity for the scaling of mean aperture and speed vs. distance. They indicate sublinear scaling so that, for example, doubling the distance traveled increases the speed by ∼50%.

Self-similarity of speed was assessed by aligning the speed for each trial on its peak and calculating moments over time. Alignment with the peak factored out any position dependence. The bootstrap-based statistical test for self-similarity, which included all participants (both PD and control), was satisfied [t(39) = −1.23, P = 0.89] (Fig. 4C). Similarly, aperture was also aligned on its peak to factor out position dependence, tested, and satisfied self-similarity [t(39) = −0.456, P = 0.90]. Satisfying self-similarity is consistent with a single, continuous control of the motion. Thus the two scaling kinematic measures identified above, peak speed and aperture, were also controlled by single, continuous parameters.

The scaling of tilt was assessed by aligning it on the peak, and, as seen in Fig. 4C, self-similarity is not observed [t(39) = −4.92, P = 0.013]. Thus there was no way to break down the intricately coordinated motion required to lift the dynamic objects over a prescribed path with a single continuous parameter.

Figure 4D shows the exponent of the self-similar functions for speed and aperture by group (tilt did not scale, so there was no scaling exponent). The exponents are completely agnostic toward the shape of the trajectories, but they indicate how the average of the measures depended on the control signal. Exponents were measured per subject and were thus amenable to ANOVA analysis for group and medication effects. The exponents describing aperture were 0.36 ± 0.22 for control, 0.29 ± 0.25 for PD off medication, and 0.34 ± 0.25 for PD on medication and did not differ significantly across groups. These nearly equal values indicated a similarity in the response of all subjects to task demands on the opening of the hand. In contrast, the speed profiles, as represented by the self-similarity exponents, were different between control, with an exponent of 0.62 ± 0.22, and PD off medication, with an exponent of 0.28 ± 0.30 [F(1,38) = 6.57, P = 0.014], but did not differ between PD on (exponent of 0.36 ± 0.24) and off medication [F(1,16) = 0.939, P = 0.35; Fig. 4B]. These exponent values are describing movements such that a doubling of the control signal would imply an ∼50% increase in response (e.g., peak speed) for control subjects, but that same doubling would only imply an ∼25% increase in response for PD patients. Thus, while both groups satisfied scaling, PD patients may have altered their underlying behavior so that their average speed was less sensitive to the control signal than that of the control subjects.

PD Patients Off Medication Showed Reduced Intensive Parameters of Movement (Peak Speed and Aperture)

Peak speed.

Figure 5A plots the mean peak speed to each object-orientation condition for each group. Across all conditions, the peak speeds had similar magnitudes and were consistently slowest for PD patients off medication with normalization toward control on medication. PD patients off medication had an overall 21 ± 2 cm/s mean peak speed, which was 34% slower than control subjects at 31 ± 1 cm/s [F(1,40) = 32.4, P = 1.27 × 10⁻⁶]. In addition to the expected bradykinesia in PD patients, there were also effects of the task conditions. There was a main effect of orientation on peak speed [F(2,80) = 5.61, P = 0.005] as well as a symmetry × orientation interaction [F(2,80) = 3.60, P = 0.032]. Post hoc tests did not indicate any significant differences in speed × orientation or symmetry × orientation.

Peak aperture.

Figure 5B shows the mean peak aperture for the each subject group × task condition. Consistent with the qualitative observation of differing opening of the hand for PD off medication and control, peak aperture was significantly smaller in PD patients off medication (4.0 ± 0.1 cm) than in control subjects (4.9 ± 0.1 cm) [F(1,40) = 34.0, P = 8.1 × 10⁻⁷]. The aperture at contact with the object was 3 cm, so control subjects padded their peak aperture by 1.9 ± 0.1 cm, or nearly twice the 1.0 ± 0.1 cm of padding PD patients exhibited. In addition, there was an orientation effect on the peak aperture [F(2,80) = 8.97, P = 3.1 × 10⁻⁴]. Figure 5B also shows a distinctive “V” shape for the orientation within each symmetry type [F(2,80) = 9.04, P = 2.9 × 10⁻⁴], signifying the differing preshaping required to perform the task in each orientation. Post hoc tests indicated that no individual pairs were different. The average aperture was 4.6 ± 0.6 cm for the leftward orientation, 4.4 ± 0.7 cm for upward, and 4.5 ± 0.6 cm for rightward. Thus, as with peak speed, PD patients off medication showed significantly reduced peak aperture.

PD Patients Off Medication Showed Impaired Motor Coordination

Preshape coordination.

A measure of the coordination between the hand achieving the proper shape to grasp an object and the arm movement during a reach is the distance along the trajectory between the peak aperture position and the peak speed position (Fig. 3), or preshape coordination (Fig. 5C). As in previous work (Lukos et al. 2013), PD patients off medication separated their peak aperture and speed by a significantly greater distance than control subjects [PD: 10.3 ± 0.4 cm, control: 7.3 ± 0.7, F(1,40) = 11.8, P = 0.001]. The wider separation is consistent with poorer coordination.

Tilt.

Figure 6A presents the mean tilt averaged across all subjects in each group during the lift. A 0° tilt from the guideline direction reflects a lift perfectly aligned with the instructed lift direction. Negative tilts reflect clockwise errors and positive tilts counterclockwise errors (Fig. 2B). Maintaining the instructed tilt of the object required dynamic coordination between the fingers and arm, especially when the effects of gravity and inertia were factored in. During the lift, PD patients off medication showed tilt errors significantly increased from control subjects. Figure 6A shows that PD patients off medication allowed the object to tilt so that the heavy end pointed too far down when they were asked to lift it at an angle but were able to lift the object nearly as well as control subjects vertically. This pattern reflects an undercompensation for the effect of gravity. This was highlighted by a significant group × orientation interaction for the PD off versus control contrast [F(2,78) = 10.9, P = 6.7 × 10⁻⁵]. In addition to the interaction, there was also a main effect of orientation [F(2,78) = 7.4, P = 0.0011]. Post hoc tests agreed with the observed pattern in Fig. 6: PD patients off medication were significantly different from control subjects for both the left orientation (P < 1e-15) and the right (P < 1e-15) but did not differ from control subjects in the vertical orientation. Only PD patients showed orientation differences in the post hoc tests, indicating that performance of control subjects was similar at all orientations whereas PD patients showed specific difficulty maintaining tilt of the objects in the off-vertical orientations.

Neither subject group fully compensated for the symmetry of the object [F(1,39) = 24.8, P = 1.3 × 10⁻⁵]. As seen in Table 5, control subjects undercompensated slightly for the asymmetric object and overcompensated for the symmetric object, but only by ∼2°. PD patients off medication showed much larger deviations, as much as 13°, or almost 10 times greater than control subjects, for the most difficult asymmetric, leftward-oriented case. Interestingly, the unsigned tilt (i.e., just the magnitude of the deviation) did not show any symmetry effect. Thus the magnitude of the error in tilt to the right or left was the same for both objects, but the sign of the error was different.

Table 5.

Deviation of lift direction with respect to guideline

Group	Symmetry	Leftward Orientation, °	Upward Orientation, °	Rightward Orientation, °
Control	Symmetric	0.47 ± 3.5	2 ± 3.4	0.1 ± 3.6
	Asymmetric	−1.6 ± 3.4	−2.6 ± 3.1	−2.8 ± 4
PD off med	Symmetric	−7 ± 3	2.3 ± 2.3	6.6 ± 3.7
	Asymmetric	−13 ± 3.3	−3.1 ± 1.8	3.4 ± 2.9
PD on med	Symmetric	−7.6 ± 3.3	2.3 ± 2.3	6.6 ± 3.7
	Asymmetric	−13 ± 2.9	−4.2 ± 2.2	0.47 ± 3.4

Values are averages ± SE over 4–6 cm in height.

Dopaminergic Therapy Increased Peak Speed and Aperture but Did Not Improve Coordination

Dopaminergic therapy had multidimensional rather than unidimensional effects on task performance. First of all, medication significantly increased peak speed overall [by 16% to 24 ± 2 cm/s, F(1,18) = 4.77, P = 0.042; Fig. 5A]. There were also significant task-related effects. There was a symmetry × medication interaction, reflecting differences in medication effect for the two symmetries, and an orientation main effect along with a symmetry × orientation effect (Table 4). Post hoc tests revealed that all the orientations were different from each other (P < 2.7e-4), but singularly for the asymmetric object, the left and right orientations were not different. Medication also significantly increased peak aperture [by 5% to 4.2 ± 0.1 cm, F(1,18) = 4.53, P = 0.047; Fig. 5B]. Interestingly, the orientation effect on peak aperture was only significant in the post hoc tests for left versus up and left versus right, while the right versus up comparison was not significantly different from zero. This may reflect the right-handedness of the subjects.

On the other hand, medication did not significantly improve the coordinative measures, preshape coordination [F(1,18) = 1.53, P = 0.23] and tilt error [F(1,17) = 0.24, P = 0.63]. These measures involve coordination of multiple components: timing of hand opening relative to position on the path for preshape coordination and precise coordination of the hand and arm to maintain the required tilt over the lift interval (Fig. 6). For the tilt, there were significant effects of both object symmetry [F(1,17) = 33.8, P = 2.1 × 10⁻⁵] and orientation [F(2,34) = 19.8, P = 2 × 10⁻⁶], but neither factor interacted with medication state (Table 4). Finally, medication did not significantly alter visual control over the movement, as reflected in aperture linearity [F(1,18) = 2.71, P = 0.12; Fig. 5D].

Thus the main effects of antiparkinsonian medication were to significantly increase peak speed and peak aperture; however, medication did not significantly improve preshape coordination, tile error, or aperture linearity. Overall, we observed that the trajectories that were consistent with self-similarity in scaling measures (speed and aperture) were significantly improved by medication but the main coordinative measure (tilt), which did not show self-similarity, was not.

DISCUSSION

In the present study, trajectories of the finger and thumb were measured while PD patients reached for, grasped, and lifted dynamic objects along prescribed paths that were oriented vertically or tilted. We demonstrated that the movements could be broken up into two types, intensive and coordinative, by detecting the self-similarity of the underlying movements. PD patients and control subjects showed the same self-similarity pattern, indicating that intensive and coordinative facets of movement are fundamental to the dynamic control of movement. As predicted, we also found that PD patients off medication exhibited deficits in both intensive and coordinative aspects of movement. During the reach, patients showed reduced peak speed and peak aperture (intensive) and reduced coordination of aperture and speed. During the lift, PD patients were unable to compensate for gravity when instructed to transport objects along a tilted trajectory, which required precise coordination of finger force vectors with arm posture and arm transport. Dopaminergic therapy improved the intensive, but not the coordinative, aspects of movement. We now turn to a detailed discussion of these findings.

Visual Feedback Control of Movement in PD

We also observed that PD patients, especially off medication, tended to open their hands on a linear path (Fig. 2, Fig. 5D), consistent with using visual feedback to control their movement (Conte et al. 2013; Flash et al. 1992; Poizner et al. 2000).^… PD patients opened the aperture between their thumb and index fingers just enough to encompass the object, whereas control subjects modulated the aperture by opening their hand wider than the object and then closing it on the object. The reduced hand opening of the PD patients confirms that the patients exhibited hypometria, consistent with the literature (Rand et al. 2006). This modulation of aperture may have allowed for a larger margin of error in grasping the object by the control subjects. The behavior of the PD patients, in contrast, is associated with loss of alignment between the aperture and the hand motion as indicated by the splitting of the peak aperture and velocity positions. Thus it appears that the PD patients are adapting a motor plan with separate control of the aperture and translation, while control subjects scaled the two together. While this behavior is successful in that the hand arrives at the object with the correct aperture, it is somewhat risky because any motor or sensory miss-estimation would likely result in knocking the object over. From a computational standpoint, there would be a significant cost increase of tracking the fingertips for the entire reach over that of opening the hand wide and then ignoring aperture for much of the reach phase. However, visual feedback control of the movement would be beneficial if proprioceptive signals or proprioceptive-motor integration was abnormal, as appears to be the case in PD (Adamovich et al. 2001; Conte et al. 2013; Konczak et al. 2009).

Movement Scaling, Coordination, and Basal Ganglia-Thalamocortical Loops

Intensive movement deficits.

The rich studies of pointing, reach, grasp, and lift movements indicate that PD patients show deficits in some but not all aspects of movement (Adamovich et al. 2001; Albert et al. 2010; Ansuini et al. 2010; Ingvarsson et al. 1997; Lukos et al. 2013; Park et al. 2012; Poizner et al. 1998, 2000; Schettino et al. 2006). We previously suggested that the movement deficits consisted of two distinct types, namely, intensive (scaling) and coordinative deficits (Schettino et al. 2006). Intensive deficits involve a loss of motor power or gain, resulting in small, slow movements, whereas coordinative deficits involve deficits in the integration and/or coordination of a number of movement components and result in poorly coordinated or clumsy movements. Both types of deficits were observed in the present study (Fig. 5, Fig. 6), which also provided a quantitative measure of whether or not a given movement parameter could be classified as intensive or coordinative (self-similarity; Fig. 4). Movement attributes that are self-similar form families of function that are smoothly deformable onto each other by tuning a single parameter, or control variable, which in turn corresponds to varying an overall gain (Snider et al. 2010). This is exactly analogous to intensive movements, and thus we proposed that intensive movement attributes satisfy self-similarity whereas coordinative aspects should not, which was what we found in the present study. Thus designation of a movement parameter as intensive versus coordinative no longer needs to be determined qualitatively or intuitively but can be rigorously characterized in computational terms.

The adverse effects of PD on the distinct movement types implicate basal ganglia networks as playing a prominent role in their modulation. Neuroimaging studies and direct recordings from the basal ganglia show strong correlations between basal ganglia activity and scale of movement or gain (Brücke et al. 2012; Desmurget et al. 2004; Joundi et al. 2012; Turner et al. 2003a, 2003b; Turner and Desmurget 2010). Adaptation to a gain modulation also activates basal ganglia structures (Krakauer et al. 2004). Thus the scaling movements identified here are consistent with basal ganglia networks controlling an overall gain, which can be chosen independently from the motor plan itself (Vindras et al. 2005). The basal ganglia are in a strategic position to modulate motor cortex activity through projection to motor cortex via the thalamus (Alexander et al. 1986) and through the direct dopamine projection to motor cortex from midbrain dopamine-containing neurons (Gaspar et al. 1992). Motor cortex activity, in turn, is associated with the speed of the hand during reaching movements (Moran and Schwartz 1999; Reina et al. 2001). In PD, there may be a maladaptive braking influence on motor systems exerted by tonic inhibitory projections from basal ganglia on motor thalamus, combined with a failure to achieve substantial desynchronization of pathologically enhanced beta band oscillations within the basal ganglia-thalamocortical motor circuit (Rodriguez-Oroz et al. 2009). Such pathologically enhanced synchronization “locks in” the motor systems, preventing appropriate recruitment of motor neurons for voluntary actions (Jenkinson and Brown 2011; Rodriguez-Oroz et al. 2009).

Recently it has been shown that tonic dopamine levels in the dorsal striatum, which are reduced in PD, may encode sensitivity to the energy cost of a movement, providing an implicit “motor motivational” signal for movement (Mazzoni et al. 2007). PD patients may physically be able to reach as rapidly as healthy individuals but place more emphasis on minimizing their effort, and thus reach more slowly (Mazzoni et al. 2007). Direct measurements of the trade-off between movement cost and reward for reaching to a target are amenable to analysis by optimal control (Shadmehr and Krakauer 2008; Todorov and Jordan 2002), and such analyses have shown that motor cost is a more important factor for PD patients than for control subjects (Baraduc et al. 2013; Gepshtein et al. 2014). The 50% drop in the speed exponent of the self-similarity analysis from control to PD found in the present study is in line with the idea of impaired motor vigor, especially decreased motor range: the same increase in movement difficulty leads to a smaller range of observed speeds in patients than in control subjects. Thus the data presented here add to the evidence of impaired motor vigor as a major component of intensive, or scaling, deficits in PD.

Coordinative movement deficits.

PD patients showed coordination deficits, failing to appropriately link and time hand opening (aperture) with speed of arm transport (preshape coordination; Fig. 5). Normally, subjects gradually open their grip to achieve an aperture wider than the object to be grasped and then gradually close their grip so that it conforms to the size of the object to be grasped (Jeannerod 1984). Consistent with previous studies (Castiello et al. 1993; Scarpa and Castiello 1994), we found that PD patients showed impaired preshape coordination (Fig. 5C). Moreover, as in previous studies (Rand et al. 2006; Schettino et al. 2004, 2006), patients did not achieve peak aperture until the hand approached the object where hand and object could be simultaneously visualized.

PD patients also were unable to compensate for gravity when instructed to transport objects along a tilted trajectory, which required precise coordination of finger force vectors with arm posture and arm transport, that is, with forearm pronation/supination and shoulder-elbow rotations (Fig. 6). Patients allowed the object to tilt considerably off of the visible guideline so that the heavy end pointed too far down when they were asked to lift it at an angle and had almost 10 times larger deviations than control subjects for the most difficult asymmetric, leftward oriented object. However, they were able to lift the object nearly as well as control subjects vertically. This pattern of results reflects an undercompensation for the effect of gravity.

Although traditionally the cerebellum is most closely associated with multisegmental coordination (Thach et al. 1992), coordination deficits in PD patients have been widely reported (Alberts et al. 1998; Benice et al. 2007; Levy-Tzedek et al. 2011; Lukos et al. 2013; Park et al. 2012; Poizner et al. 1998; Rand et al. 2014). Our results build upon these findings, providing strong support for the importance of basal ganglia-thalamocortical circuits in motor coordination. As noted by Costa et al. (2006), “PD may not stem from changes in the overall levels of cortical activity, but from dysfunctional activity coordination in corticostriatal circuits.” Precise, differentiated functioning of partially segregated corticostriatal circuits may facilitate the integration of different brain regions needed for coordinated motor output.

Major cortical targets of basal ganglia projections in primates include the supplementary motor area (SMA) and lateral premotor cortices (as well as motor cortex) (Akkal et al. 2007; Alexander et al. 1986; Hoover and Strick 1993). Activity in these motor areas is disrupted in PD (Berardelli et al. 2001; Niethammer and Eidelberg 2012; Yu et al. 2007). Since SMA and dorsal premotor cortex are known to be important for the coordination for reach-and-grasp motions (Cavina-Pratesi et al. 2010), aberrant basal ganglia outflow may produce coordination deficits in PD patients. Another consideration is that cells in basal ganglia nuclei, basal ganglia receiving areas in the thalamus, and the SMA show a lack of specificity in responding to limb proprioception in primate models of PD (Boraud et al. 2000; Escola et al. 2002; Pessiglione et al. 2005), consistent with proprioceptive processing deficits in PD (Conte et al. 2013; Konczak et al. 2009). Since proprioception is a key sensory requirement for the coordination of motor acts (Messier et al. 2003; Sainburg et al. 1993, 1995), loss of precision of proprioceptive signals in motor circuits linking cortex and basal ganglia is another possible mechanism for impaired motor coordination in PD. Precision in processing proprioceptive signals would have been amplified in the present study, since subjects had to precisely manipulate dynamic objects aligned at various orientations with respect to gravity.

A third possible mechanism for impaired motor coordination in PD may involve defective cerebellar activity. Animal studies have revealed reciprocal disynaptic projections between the basal ganglia and the cerebellum (Bostan et al. 2010, 2013). In PD, cerebellar activity is increased, which may be compensatory or pathological (Rascol et al. 1997; Wu and Hallett 2013; Yu et al. 2007). Although the cerebellum also exhibits morphological changes in PD (Borghammer et al. 2010), more research is need to understand its functional significance in PD. However, it has been suggested that in mild to moderate PD patients, altered cerebellar activity may help maintain relatively normal motor function (Wu and Hallett 2013). Since the patients in the present study were in the mild to moderate stages of the disease, it is likely that the observed coordination deficits were not due to pathological changes in the cerebellum. However, to examine the specificity of the deficits to dysfunctional basal ganglia-thalamic-cortical circuits, it would be important in future studies to contrast the performance of PD patients with patients having damage in other brain regions. A contrast with cerebellar patients or with deafferented patients would be particularly interesting. Such studies are currently under way in our laboratory. It should be noted that the three possible mechanisms for impaired motor coordination in PD described above are not mutually exclusive, and multiple mechanisms could be contributing.

The traditional view of grasping is that grasping movements can be decomposed into two independent visuomotor channels, one controlling the arm transport and the other controlling the size of the grip (Jeannerod 1981, 1984). An alternative description was proposed by Smeets and Brenner (1999) in which grasping was considered to be two-finger pointing. In this framework, a subject determines suitable contact points on the object to be grasped and then moves his/her thumb and index finger more or less independently to those points. Since in the present experiment visual feedback of finger positions was given as two spheres in the virtual environment, subjects might have planned and executed a double pointing movement. However, no matter which framework is used to describe the grasping movement, our intensive and coordinative measures still apply. The arm needs to be transported to the object, reaching a peak speed, and the distance between the thumb and index finger needs to increase from its initial closed position to eventually conform to the size of the object. Both speed and aperture were considered to be intensive components, and both were found to show self-similarity in their trajectories. That is, both of these measures were found to conform to a scaling relation, namely, that a small change in a single control signal leads to a small change in the movement parameter. The fact that aperture was found to be self-similar indicates that under the present experimental conditions subjects were not controlling multiple control signals to widen the grip, as would be the case with independent planning and coordination of thumb and finger opening during the reach. Rather, they seemed to be controlling a single parameter of aperture.

Dopaminergic Therapy Improves Intensive but Not Coordinative Aspects Of Movement

Dopaminergic therapy significantly improved clinical scores on the UPDRS and the intensive aspects of the movements (speed and aperture). Dopaminergic therapy increases tonic levels of dopamine in the brain and, in particular, in the dorsal striatum, which is thought to encode an implicit motivational signal for the motor system (Mazzoni et al. 2007) analogous to the role of tonic levels of ventral striatum dopamine in reward-seeking. In this framework, PD patients move slowly because of their heightened sensitivity to the energetic cost of movement. The fact that dopaminergic therapy significantly increased peak speed and peak aperture in the present study is consistent with the role of tonic dopamine levels in the dorsal striatum encoding the energetic cost of a movement.

However, dopaminergic therapy did not improve the coordinative aspects of movement (preshape coordination and tilt), just as it does not improve adaptation of movements to a mechanical (Tunik et al. 2007) or visual (Lukos et al. 2013) perturbation, hand-arm coordination of reach-to-grasp movements (Schettino et al. 2006), coordination of grip aperture and arm transport (Castiello et al. 2000), or coordination of speed and amplitude of single-joint rhythmic movements of the elbow (Levy-Tzedek et al. 2011). Unlike the improvement of intensive aspects of movement with medication, coordinative aspects depend upon something other than increasing tonic levels of dopamine in the dorsal striatum. One possibility is that neurotransmitters other than dopamine help mediate motor coordination, since patients with PD are known to have deficits in multiple nondopaminergic neurotransmitter systems (Fox et al. 2008; Pifl et al. 2013). Pifl et al. (2012), for example, have shown that there is profound loss of norepinephrine in thalamic motor areas in the brains of patients dying with PD. Pifl et al. (2013) have extended these results to show that in the 1-methyl-4-phenyl-1,2,3,6-tetrahydropyridine (MPTP) primate model of PD there is loss of norepinephrine in the motor thalamus and that this loss may contribute to the parkinsonian motor disorder. Moreover, there are marked neurotransmitter interactions in the striatum that also may be relevant to parkinsonian symptoms (Morales et al. 2012). Deficits in nondopaminergic neurotransmitter systems may be contributing to PD motor symptoms such as motor coordination.

A second possibility is that finely coordinated movements depend upon precise processing of proprioceptive signals. The effects of dopaminergic therapy on proprioception have not yet been fully elucidated, but studies indicate that dopaminergic therapy has either no effect (Maschke et al. 2003) or deleterious effects (Bronte-Stewart et al. 2002; O'Suilleabhain et al. 2001) on proprioception (but see Li et al. 2010). The available data suggest that noisier, less differentiated proprioceptive signals are transmitted to cortical areas in both off- and on-medication states. Such signaling may produce deficits in fine motor coordination. In future studies, it would be informative to contrast the effects of different dopaminergic and nondopaminergic therapies on PD performance in this task, as well as to examine the effects of chronic deep brain stimulation to the subthalamic nucleus, which may improve proprioception and coordination in PD patients (Maschke et al. 2003; Schettino et al. 2009; Shukla et al. 2013).

Conclusions

We demonstrated that reach-to-grasp and lift movements could be broken up into intensive and coordinative components by detecting the self-similarity of the underlying movements. PD patients off medication were significantly impaired in both aspects of movement, suggesting that basal ganglia-thalamocortical circuits may play an important role in fine motor coordination. Dopaminergic therapy, which increases tonic dopamine levels, significantly improved the intensive aspects of movements. This improvement is consistent with a framework in which tonic levels of dopamine in the dorsal striatum encode the energetic cost of a movement. Dopaminergic therapy did not improve the coordinative aspects of the movements, indicating that increasing tonic levels of dopamine is not sufficient to restore the precise, differentiated activity of corticostriatal circuits needed for finely coordinated movement.

GRANTS

This work was supported by Department of Veterans Affairs Grants B5015R and CX000146, National Science Foundation (NSF) Grant SMA-1041755, National Institute of Neurological Disorders and Stroke Grant 2 R01 NS-036449, and NSF Grant ENG-1137279 (EFRI M3C).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).^…

AUTHOR CONTRIBUTIONS

Author contributions: J.S., D.L., D.L.H., and H.P. conception and design of research; J.S. and D.L. performed experiments; J.S. analyzed data; J.S., D.L., D.L.H., and H.P. interpreted results of experiments; J.S. prepared figures; J.S., D.L., D.L.H., and H.P. drafted manuscript; J.S., D.L., D.L.H., and H.P. edited and revised manuscript; J.S., D.L., D.L.H., and H.P. approved final version of manuscript.