Abstract
The signaling properties of thalamocortical (TC) neurons depend on the diversity of ion conductance mechanisms that underlie their rich membrane behavior at subthreshold potentials. Using patch-clamp recordings of TC neurons in brain slices from mice and a realistic conductance-based computational model, we characterized seven subthreshold ion currents of TC neurons and quantified their individual contributions to the total steady-state conductance at levels below tonic firing threshold. We then used the TC neuron model to show that the resting membrane potential results from the interplay of several inward and outward currents over a background provided by the potassium and sodium leak currents. The steady-state conductances of depolarizing Ih (hyperpolarization-activated cationic current), IT (low-threshold calcium current), and INaP (persistent sodium current) move the membrane potential away from the reversal potential of the leak conductances. This depolarization is counteracted in turn by the hyperpolarizing steady-state current of IA (fast transient A-type potassium current) and IKir (inwardly rectifying potassium current). Using the computational model, we have shown that single parameter variations compatible with physiological or pathological modulation promote burst firing periodicity. The balance between three amplifying variables (activation of IT, activation of INaP, and activation of IKir) and three recovering variables (inactivation of IT, activation of IA, and activation of Ih) determines the propensity, or lack thereof, of repetitive burst firing of TC neurons. We also have determined the specific roles that each of these variables have during the intrinsic oscillation.
Keywords: thalamocortical neuron, subthreshold conductances, resting membrane potential, repetitive burst firing
the resting membrane permeability of neurons defines the resting membrane potential (RMP) and determines neuronal excitability. This resting membrane permeability is determined by ion channels that are active at levels below the threshold for action potential firing. The molecular identification and biophysical characterization of ion channels in vertebrates has revealed a large diversity of molecular mechanisms potentially involved in controlling the membrane behavior at subthreshold potentials (Hille 2001; Yu and Catterall 2004). Members of many different families of potassium channels display biophysical properties consistent with activation at subthreshold potentials (Coetzee et al. 1999; Rudy et al. 2009). Similarly, hyperpolarization-activated cationic channels (HCN) (Biel et al. 2009), low-threshold calcium channels (Perez-Reyes 2003), persistent sodium currents (Waxman et al. 2002), and leak sodium channels (Ren 2011) also operate at subthreshold potentials. Most neurons express combinations of several of these ion channels, indicating that the RMP results from the complex interaction of several subthreshold operating conductances. Yet, the detailed ionic mechanisms that establish and control the resting membrane permeability of any neuron have not been described.
The subthreshold ionic mechanisms of thalamocortical (TC) neurons have been studied extensively due to the physiological relevance of these neurons and the richness of their membrane behavior at subthreshold potentials. These cells display two modes of firing (tonic and bursting) that originate at two different “resting” potentials and also subthreshold oscillations. Three different conductances have been shown to affect the subthreshold membrane behavior of these neurons: the potassium leak current (McCormick 1992), the hyperpolarization-activated cationic current (Ih; McCormick and Pape 1990), and the low-threshold calcium current (IT; Jahnsen and Llinas 1984). The first two currents control RMP directly, whereas IT underlies the transient depolarization (low-threshold calcium spike) over which rides a high-frequency burst of Na+ action potentials elicited when the membrane potential is released from hyperpolarization (rebound burst; Jahnsen and Llinas 1984). In addition, the reciprocal activation of Ih and IT at hyperpolarized potentials is believed to be the core mechanism of intrinsic repetitive burst firing (McCormick and Bal 1997). Other subthreshold operating conductances in TC neurons that might also contribute to controlling their excitability include an inwardly rectifying potassium current (IKir; Williams et al. 1997), a persistent sodium current (INaP; Jahnsen and Llinas 1984), and a fast transient A-type potassium current (IA; Huguenard et al. 1991). However, the contribution of these conductances to the regulation of the membrane behavior at subthreshold potentials has not been studied.
With the aim of reconstructing the steady-state conductance of TC neurons at subthreshold potentials, we combined electrophysiological recordings in brain slices from mice with computational modeling. We first characterized a strong inwardly rectifying potassium conductance. We then built a biophysically accurate conductance-based model of TC neurons that reproduces the experimental findings, using results from our recordings and the large amount of information available on the electrophysiological properties of TC neurons in rodents. Hodgkin and Huxley (HH)-like models of the different conductances active at subthreshold potentials for tonic firing were adjusted and incorporated into the model cell. By matching our steady-state recordings to simulations performed with the model cell, we determined the maximum conductance values for each component of the steady-state conductance and their individual contributions to the TC neuron RMP. To study the role of the subthreshold operating conductances in the intrinsic oscillatory behavior of TC neurons, we determined the minimal requirements for generation and maintenance of oscillations compatible with physiological (or pathological) intrinsic repetitive burst firing. Finally, we determined the relative contribution of each subthreshold conductance to simulated repetitive bursts by examining their time course on the subthreshold model. Some of these results have been presented in abstract form (Amarillo 2007; Amarillo and Nadal 2011; Amarillo et al. 2005).
METHODS
Slice Preparation and Animals
All experiments were carried out in accordance with the NIH Guide for the Care and Use of Laboratory Animals and were approved by the New York University School of Medicine Animal Care and Use Committee. Brain slices were prepared from 2- to 4-wk-old ICR mice. Following induction of deep anesthesia with pentobarbital sodium (50–75 mg/kg ip), mice were decapitated and the brains removed into an ice-cold oxygenated artificial cerebrospinal fluid (ACSF) that contained (in mM) 126 NaCl, 2.5 KCl, 1.25 Na2PO4, 26 NaHCO3, 2 CaCl2, 2 MgCl2, and 10 dextrose. The brain was blocked at a coronal plane, and 350-μm-thick slices were cut using a manual vibroslicer (WPI, Sarasota, FL). Slices including the ventrobasal thalamic nuclei were maintained at room temperature in oxygenated ACSF (95% CO2-5% O2) until they were transferred to the recording chamber continuously perfused with oxygenated ACSF.
Kir2.2 knockout (KO) mice where obtained from the laboratory of Dr. Thomas Schwarz (Zaritsky et al. 2001). The original FVB background was re-derivated and subsequently back-crossed to ICR background in the animal facility of New York University School of Medicine (Skirball Institute).
Electrophysiology
Neurons from ventrobasal thalamic nuclei (ventral posterolateral and ventral posteromedial nucleus) were visualized using a Dage-MTI camera mounted on a fixed-stage microscope (Olympus BX50WI) equipped with infrared-differential interference contrast optics. Localization and identity of some cells were confirmed by including biocytin in the recording pipette, followed by histological processing. Patch pipettes were made from borosilicate glass in a Sutter P-97 horizontal puller (Sutter Instrument, Novato, CA) with resistances between 2 and 5 MΩ and were filled with an intracellular solution containing (in mM) 119 CH3KO3S, 12 KCl, 1 MgCl2, 0.1 CaCl2, 1 EGTA, 10 HEPES, 0.4 Na-GTP, and 2 Mg-ATP, pH 7.4. Neurons were recorded using an Axopatch 200B amplifier (Molecular Devices, Sunnyvale, CA) after stabilization of holding current while in voltage-clamp mode (∼5 min after whole cell was achieved) and/or after 15 min of stable RMP while in fast current-clamp mode. Voltage-clamp recordings were low-pass filtered at 2 kHz, pipette capacitance was canceled, and series resistance (lower than 10 MΩ) was compensated to the extent possible (typically 60%). To determine RMP, the amplifier was switched between voltage-clamp and fast current-clamp (with zero current injection) modes before and after drug treatments. A junction potential of 4 mV was directly measured and corrected off-line from all command potentials. All recordings were performed at room temperature unless otherwise stipulated. Drugs were applied by bath superfusion. The results obtained in the presence of synaptic activity blockers [in μM: 10 CNQX (6-cyano-7-nitroquinoxaline-2,3-dione), 20 APV, and 10 bicuculline] were not significantly different (data not shown). Recordings were sampled at 20 kHz, acquired on a personal computer using the pCLAMP8 software (Molecular Devices), and stored for further analysis.
In most of the voltage-clamp recordings performed in this study, we used a command protocol consisting of a slow voltage ramp at 7.5 mV/s between −114 and −54 mV (after junction potential correction). This protocol allowed us to achieve nearly steady-state conditions at every point during the ramp. However, time-dependent mechanisms were still present in recordings in which Ih was not eliminated pharmacologically (see results). Slower ramp protocols resulted in recording instability.
Data Analysis and Computer Simulations
Continuous current-voltage (I-V) plots were obtained from voltage-clamp recordings by replacing time with a linear incremental function of voltage between the initial and final voltage values of the ramp protocols used. When data from several cells were pooled together, data points every 3.75 mV were selected from these continuous I-V plots for illustration purposes.
IKir characterization and modeling.
The barium-sensitive component was obtained by subtracting the ramp current traces before from those after application of 50 μM Ba2+ to TC neurons from wild-type mice (Fig. 1B). Application of higher concentrations of Ba2+ did not produce any additional response in the voltage range analyzed in this study. Conductance values obtained by dividing the current by the driving force were plotted against voltage for each cell and fitted to a single Boltzmann function of the form
| (1) |
where gKir(V) is the conductance of the barium-sensitive component at a given voltage value; gmax and gmin are the maximum and minimum conductances, respectively; V is the voltage value at every point during the ramp protocol; V1/2 is the half-activation voltage; and k is the slope factor. After normalization to the predicted gmax, the mean conductances were Boltzmann fitted, and the obtained parameter values were then used to model the Kir current with the following equation (Fig. 1C):
| (2) |
where ḡKir is the maximum Kir conductance and EK is the equilibrium potential for potassium (−99 mV).
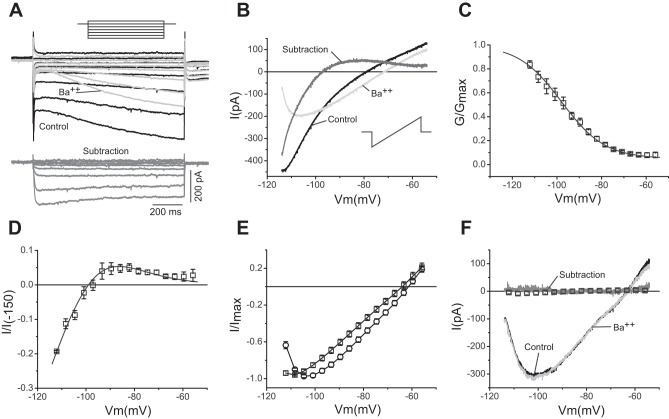
Fig. 1.
Characterization of a strong inward rectifier potassium current (IKir) in thalamocortical (TC) neurons. A: voltage-clamp recordings before (black traces) and after (light gray traces) application of 50 μM Ba2+ (top). Bottom traces (dark gray) show the barium-sensitive component obtained by subtraction. The recordings were obtained using a protocol of square pulses from −124 to −64 mV in increments of 10 mV (inset) from a holding potential of −74 mV. B: barium experiment similar to that in A using a slow ramp from −114 to −54 mV (inset). Conventions as in A; Vm, membrane potential. C: normalized barium-sensitive conductance (G/Gmax) from 8 cells (average ± SE) obtained using the ramp protocol in B, with superimposed average Boltzmann fit (solid line). D: barium-sensitive current obtained with the ramp protocol from 8 cells (average ± SE) normalized to the extrapolated current at −150 mV (I/I−150; see methods). Superimposed (solid line) is the simulated current-voltage (I-V) curve obtained with a model using the parameters of the Boltzmann fit from C and ḡKir (average maximum conductance) = 2.0 × 10−5 S/cm2. E: normalized current (I/Imax; average ± SE) from wild-type (□; n = 24) and Kir2.2 knockout (KO) mouse TC neurons (○; n = 19) obtained with the ramp protocol in the absence of pharmacological agents. F: voltage-clamp recordings before and after application of 50 μM Ba2+ and barium-sensitive component obtained by subtraction from a Kir2.2 KO TC neuron. Conventions as in A and B. Superimposed (□) is the average ± SE (error bars are not visible) barium-sensitive component from 8 cells.
The cell was modeled as a single-compartment cylinder with a length and diameter of 69 μm for an approximated total area of 2.0 × 104 μm2, assuming a membrane capacitance of 0.88 μF/cm2 (Destexhe et al. 1998). The total membrane area was obtained by dividing the measured input capacitance (168 ± 8.2 pF; range 99–239 pF; n = 23) by this per-unit-area value. Input membrane capacitance was measured online in TC neurons from wild-type mice (before application of any pharmacological agent) using the membrane test tool of the pCLAMP software. Voltage-clamp simulations were performed using a single-point electrode with an access resistance of 10 MΩ to mimic the recording conditions. Model simulations were performed using the NEURON environment (Hines and Carnevale 1997) with a time resolution of 0.025 ms.
Normalized Kir currents were obtained by dividing the measured currents on each cell by the current calculated at −150 mV, using their corresponding maximum conductances obtained with Eq. 1 (Fig. 1D). An ohmic behavior at this potential was assumed due to the complete unblock of Kir channels (Panama and Lopatin 2006) and the complete saturation of the Boltzmann fits at these voltages. ḡKir was then adjusted in the model to match the average value of the normalized currents (Fig. 1D).
Ih modeling.
Pharmacological isolation of Ih was obtained by subtracting ramp current traces before and after application of 10 μM of the specific Ih blocker ZD-7288 (Tocris, Minneapolis, MN). Because of the slow kinetics of activation of Ih, current traces obtained with the ramp protocol show time dependence as well as voltage dependence. To model Ih, we adapted the mathematical formulation of Ih from guinea pig TC neurons as used by McCormick and Huguenard (1992) with activation parameters previously obtained in mice (Santoro et al. 2000). Subsequently, we used voltage-clamp simulations in NEURON of this modeled Ih, adjusting its maximum conductance to match our experimental recordings. The steady-state activation and time constant of activation equations used for modeling Ih were
| (3) |
| (4) |
Equations 3 and 4 correspond to data obtained at a temperature of 34°C. A Q10 of 4 (Santoro et al. 2000) was used for simulations at different temperatures.
The HH-style equations used to model the voltage and time variation of Ih were
| (5) |
| (6) |
where ḡh is the maximum conductance and Eh is the reversal potential for Ih (−43 mV).
INaP modeling.
The persistent sodium current was defined as the component obtained by subtraction of the ramp current traces before and after application of 300 nM TTX. Since kinetics of INaP have not been characterized in TC neurons, we used the model developed by Wu et al. (2005), which is based on experimental data from mesencephalic trigeminal sensory neurons from rat. This model considers instantaneous activation and slow inactivation kinetics, and thus
| (7) |
| (8) |
| (9) |
and
| (10) |
| (11) |
where mNaP and hNaP are the activation and inactivation gates, respectively; τhNaP(V) is the time constant of inactivation at a given voltage value; and ENa is the equilibrium potential for sodium (45 mV). Since there are no biophysical data available on the dependency of temperature for INaP, a Q10 of 3 was assumed.
IT modeling.
We used the previously published mathematical model of IT (Huguenard and McCormick 1992), as implemented by Destexhe et al. (1998; https://senselab.med.yale.edu/modeldb/, accession no. 279), with modifications introduced to match our ramp current recordings. An overall depolarizing shift of +6 mV was applied to match the threshold of activation of the window T current. An additional hyperpolarizing shift of −2 mV in the voltage dependence of activation and activation kinetics was necessary to reproduce the shape of the deflection induced by the window T current on the ramp traces. The final equations used were
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
and
| (17) |
| (18) |
| (19) |
with
| (20) |
where Cao and Cai are the extracellular and the intracellular concentrations of Ca2+; Z is impedance; and R, F, and T have their usual meanings. A Q10 of 2.5 for both activation and inactivation of IT was assumed as described previously (Destexhe et al. 1998).
IA and leak currents modeling.
The mathematical formulations of IA and the leak currents from the study of McCormick and Huguenard were used without modifications (Huguenard and McCormick 1992; McCormick and Huguenard 1992). The experimentally determined Q10 of 2.8 (Huguenard et al. 1991) was used for the gating variables of IA. The reversal potential for the sodium leak current (INaleak) was set at 0 mV in agreement with the lack of cation selectivity of the channel subunits that carry this current (Lu et al. 2007; Swayne et al. 2009).
Modeling the conductances generating and controlling spiking.
To model spiking and high-threshold phenomena such as afterhyperpolarizations, the following conductances with biophysical parameters taken from previous studies were included in the final model. The fast transient sodium current INa and the delayed rectifier potassium current IK were modeled as in the study of Destexhe et al. (1998; https://senselab.med.yale.edu/modeldb/, accession no. 279). A global depolarizing shift of 10–15 mV was used for these currents to better match the spiking threshold of our current-clamp recordings. These kinds of corrections have been used previously to model spiking of TC neurons (Rhodes and Llinas 2005). Maximum conductances of 1.0 × 10−2 and 2.0 × 10−3 S/cm2 were used for INa and IK, respectively. The high-threshold calcium current IL was implemented as in the model of McCormick and Huguenard (1992) with the corrections included in the erratum of that publication (http://huguenard-lab.stanford.edu/pubs.php) using a maximum permeability of 1.0 × 10−4 cm/s. Finally, the calcium-activated potassium conductances IKCa and IKAHP were incorporated into the model by using parameters from Traub et al. (2003) as implemented by Lazarewicz and Traub in ModelDB (https://senselab.med.yale.edu/modeldb/, accession no. 20756) with a correction factor of 10−6 to convert their arbitrary units of calcium concentration to millimoles per liter. Maximum conductances of 1.0 × 10−4 and 1.5 × 10−5 S/cm2 were used for IKCa and IKAHP, respectively. These calcium-sensitive currents were made dependent on calcium concentration changes resulting from activation of the high-threshold calcium current IL, but not from IT. Calcium dynamics were modeled as described previously (McCormick and Huguenard 1992).
Stacked area plots showing the relative contribution of ionic conductances (see Fig. 5) or currents (see Figs. 9 and 10) to the total conductance (current) were obtained by normalizing the absolute values for each particular conductance (current) at every voltage (time) point by the total conductance (current) at that point.
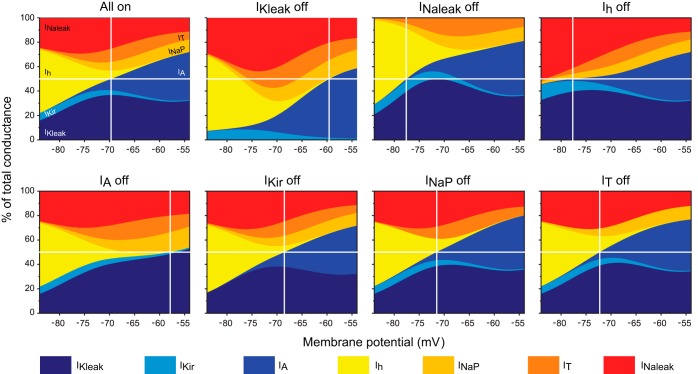
Fig. 5.
Contribution of subthreshold conductances to the steady-state total conductance of TC neurons and establishment of RMP. Stacked area representations show the voltage-dependent contribution of the subthreshold conductances as nonoverlapping percentages of total conductance (sum of absolute current values at every voltage point is 100%). RMP (vertical lines; see Table 1) occurs at the membrane potential at which inward conductances (tones of red and yellow) equal outward conductances (tones of blue) at 50% (horizontal lines). Top right panel (All on) shows the contribution of all 7 conductances, whereas the other panels show the reconfiguration of the contributions after each of the subthreshold conductance is turned off one by one (as indicated above each panel).
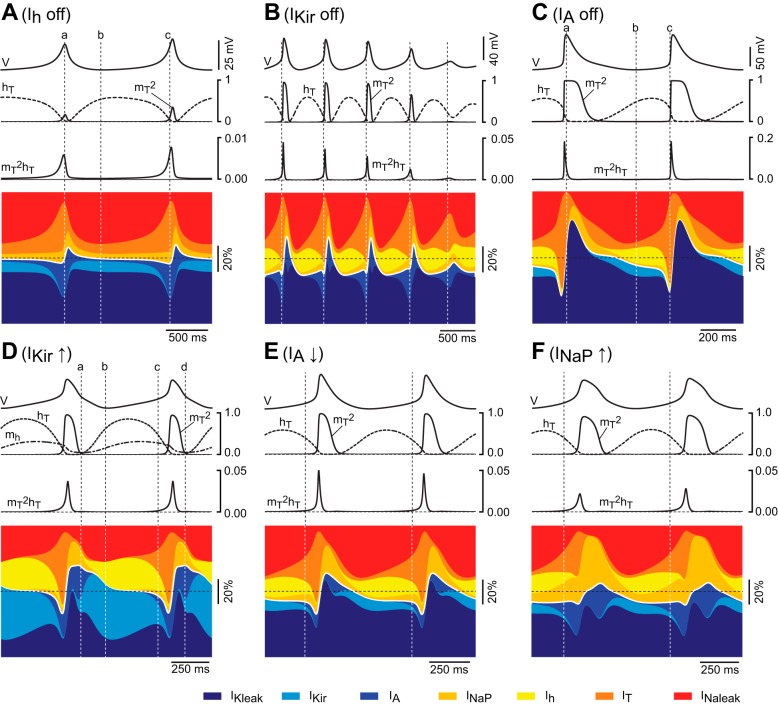
Fig. 9.
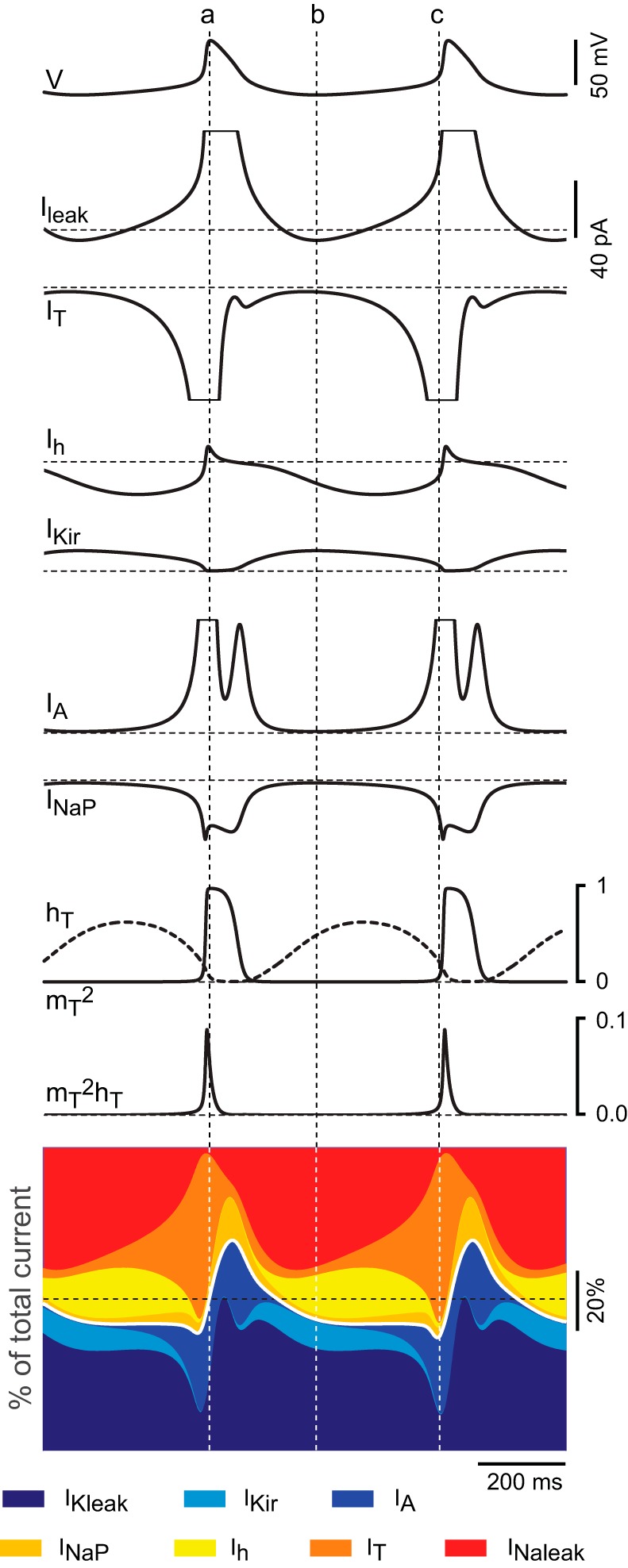
Time course and relative contribution of subthreshold conductances during oscillations in the TC neuron model. A: time course of the currents and gating variables of IT during 2 cycles of oscillation of the TC neuron containing all 7 subthreshold conductances, induced by injection of hyperpolarizing current. The ḡ values were set to default for all conductances except IT (pT = 8.0 × 10−5 cm/s). The Ileak trace is the sum of IKleak and INaleak. For illustration purposes, the scale is the same for all currents and large deflections are truncated. The diagram at bottom represents the time course of the relative contribution of each current during oscillations. Horizontal dotted lines represent zero values for currents and gating variables and 50% of the total current in diagrams of relative contribution. Vertical dotted lines are positioned at the peak of the oscillation (a), the valley of the oscillation (b), and the time point of maximum contribution of IT (c).
Fig. 10.
Effects of simulated modulation of subthreshold conductances (other than IT) on the oscillatory behavior of the TC neuron model. Under the same conditions as in Fig. 9, data in A–C show the time course of the gating variables of IT and the relative contribution of the currents during spontaneous oscillations of the TC neuron model (colored stacked area plots) in the absence of Ih (A), during dampening oscillations of the TC model in the absence of IKir (B), and during oscillations induced by injection of hyperpolarizing current in the absence of IA (C). Vertical dotted lines in A and C are positioned similarly to those in Fig. 9; vertical dotted lines in B indicate the time points of maximum contribution of IT on each cycle. D: time course of the gating variables of IT (mT and hT) and Ih (mh) and the relative contribution of the currents during 2 cycles of oscillation induced by injection of depolarizing current after an increase of ḡKir to 1.2 × 10−4 S/cm2 while all other parameters are maintained at default (including IT at 5.0 × 10−5 cm/s). The interval between lines a and c illustrates the transient hyperpolarization generated by the interaction IKir-Ih, and the interval between lines c and d illustrates the transient depolarization (low-threshold spike, LTS) generated by the activation and inactivation of IT (see text). E: time course of the gating variables of IT and the relative contribution of the currents during oscillations induced by hyperpolarization after a decrease of ḡA to 1.5 × 10−3 S/cm2. All other parameters are set to default. F: time course of the gating variables of IT and the relative contribution of the currents during oscillations induced by hyperpolarization after an increase of ḡNaP to 1.8 × 10−5 S/cm2. Vertical lines in F and G are placed on the initial phase of depolarization to indicate the competing activation of IA and INaP. Note that during this phase the absolute current amplitude and the relative contribution are larger for INaP than for IA in both F and G.
RESULTS
A Strong Inward Rectifying Potassium Current Contributes to the Steady-State Conductance of TC Neurons
The ionic currents of TC neurons recorded under voltage clamp display inward rectification at negative potentials. As previously shown, this rectification can be separated into at least two components with the use of pharmacology: a fast component sensitive to barium and a slow component sensitive to the drug ZD-7288 (Williams et al. 1997). The slow component is mediated by the hyperpolarization-activated cationic current Ih (see below), whereas an inwardly rectifying potassium current (IKir) has been assumed to underlie the fast component (Williams et al. 1997). Yet, Ikir has not been fully characterized in these cells, and its role is unknown. To isolate IKir, we initially used a protocol of hyperpolarizing pulses in whole cell voltage clamp and application of 50 μM Ba2+ (see methods) (Fig. 1A). The barium-sensitive component quickly reached steady state (τ = 5.7 ± 0.6 ms at −114 mV; n = 9), whereas the remaining barium-insensitive component rose very slowly and did not reach steady state during the duration of the 1-s-long pulse protocol. The fast kinetics of the barium-sensitive component (IKir) allowed us to use a slow ramp protocol (see methods) to eliminate the fast inactivating currents and thus obtain continuous I-V plots of IKir at steady state. Figure 1B shows recordings from one TC neuron obtained using the ramp protocol before and after application of 50 μM Ba2+, and the barium-sensitive component obtained by off-line subtraction. The I-V relationship of this barium-sensitive component is characterized by strong inward rectification, a reversal potential at the predicted Nernst reversal potential for K+ (−99 mV), and a region of negative slope conductance at potentials positive to about −85 mV. By fitting the normalized conductance-voltage (G-V) plot to a Boltzmann function, we obtained a V1/2 of activation of −97.9 ± 1.17 mV and a slope factor (k) of 9.7 ± 0.6 mV−1 (Fig. 1C). These parameters were then used to create a mathematical model of IKir that was incorporated into a blank model cell (without any other conductances) with dimensions and capacitance resembling those of TC neurons (see methods). Figure 1D shows a simulation of the modeled Kir current superimposed on the normalized currents recorded with the ramp protocol. The maximum conductance of the model was set to 2.0 × 10−5 S/cm2 to match the normalized currents. This value is within the range of maximum conductance values obtained by extrapolating values from individual cells (gmax between 3.4 and 25.3 nS), assuming a membrane area of 2.0 × 104 μm2.
The I-V relationship, the high sensitivity to Ba2+, and the values used to fit the barium-sensitive component are reminiscent of the properties of inward rectifier potassium channels of the Kir2 family (Anumonwo and Lopatin 2010). In addition, previous in situ hybridization studies in rodent brain have indicated that the only Kir2 channel mRNA expressed in the thalamus corresponds to Kir2.2 (Karschin et al. 1996). We tested the hypothesis that Kir2.2 potassium channels underlie the Kir current in these neurons by recording TC neurons from Kir2.2 KO mice. We found that recordings from Kir2.2 KO neurons under control conditions (without any pharmacological treatment) differ in their rectification properties from those recorded in wild-type mice (Fig. 1E). Furthermore, application of 50 μM Ba2+ to TC neurons from Kir2.2 KO mice had no effect on the currents recorded at these potentials, and the I-V curve obtained by subtraction is flat at zero current (Fig. 1F). The I-V plots that result after pharmacological elimination of other current components in TC neurons from wild-type and Kir2.2 KO mice (see below) further indicate that Kir2.2 channels are the predominant, if not the only, molecular constituents of IKir in TC neurons from mice.
Other Components of the Steady-State Conductance of TC Neurons
At least six additional currents active at subthreshold potentials can contribute to the subthreshold current recorded in TC neurons. These are the persistent sodium current INaP, the hyperpolarization-activated cationic current Ih, the low-threshold activated calcium current IT, the low-threshold transient potassium current IA, the potassium leak current IKleak, and the sodium leak current INaleak. We used the selective drugs TTX and ZD-7288, in combination with computer modeling, to obtain quantitative measurements of the contribution of INaP and Ih, respectively. To unveil the contribution of IT, IA, and leak currents to the steady-state conductance of TC neurons, we used modeling to match simulations of combined currents to ramp recordings obtained after elimination of IKir, Ih, and INaP.
INaP.
Application of 300 nM TTX increased the outward rectification of the I-V curve obtained with the ramp protocol at potentials positive to −78 mV (Fig. 2A). The TTX-sensitive component obtained by subtraction corresponds to INaP, the persistent sodium current (Fig. 2A), which is not inactivated during the slow ramp. Subsequently, an HH-like model of INaP with parameters taken from Wu et al. (2005; see methods) was incorporated into a blank model cell and compared with the experimental TTX-sensitive component obtained by subtraction. Figure 2C shows the match between the recorded data from five cells (squares) and the model simulation using a ramp protocol similar to that used during the experiments (7.5 mV/s). A ḡNaP value of 5.5 × 10−6 S/cm2 was used for the simulation to match the amplitude of the recorded currents.
Fig. 2.
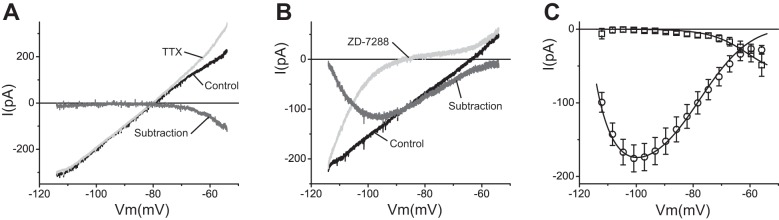
Pharmacological isolation of persistent sodium current (INaP) and hyperpolarization-activated cationic current (Ih) in TC neurons. A: voltage-clamp recordings obtained using the ramp protocol before (black trace) and after (light gray trace) application of 300 nM TTX. Dark gray trace is the TTX-sensitive component (INaP) obtained by subtraction. B: recordings before (black trace) and after (light gray trace) application of 10 μM ZD-7288. Dark gray trace is the ZD-7288-sensitive component (Ih) obtained by subtraction. C: TTX-sensitive component (□; average ± SE) and ZD-7288-sensitive component (○; average ± SE) from 5 and 9 cells, respectively. Superimposed (solid lines) are voltage-clamp ramp simulations obtained with the corresponding models using ḡNaP = 5.5 × 10−6 S/cm2 and ḡh = 2.2 × 10−5 S/cm2.
Ih.
Application of 10 μM of the Ih blocker ZD-7288 eliminated most of the inward current, especially at potentials positive to EK (Fig. 2B). The remaining current after blocking of Ih shows strong inward rectification consistent with the unmasking of IKir (Fig. 2B). In agreement with the slow kinetics of Ih, the ZD-7288-sensitive component obtained by subtraction was unable to follow the slow ramp protocol and displays complex time dependence (Fig. 2B). However, by using the data from the study of Santoro et al. (2000) to recreate a model of Ih from mice (see methods), we were able to reproduce the response of TC neurons to the slow ramp protocol (Fig. 2C). The ḡh value used for the simulation (2.2 × 10−5 S/cm2) is consistent with previous reports (McCormick and Huguenard 1992; Santoro et al. 2000). This model realistically captures the biophysical behavior of the ZD-7288-sensitive current, reproducing both the time course and the voltage dependence of Ih during the ramp.
The resulting I-V relationship after elimination of IKir, Ih, and INaP is not linear.
Elimination of IKir, Ih, and INaP results in an incomplete linearization of the I-V relationship obtained with the ramp protocol, indicating that other players besides linear leaks also contribute to the steady-state conductance of TC neurons, especially at potentials positive to about −80 mV. Concomitant application of TTX, ZD-7288, and Ba2+ to wild-type TC neurons (Fig. 3A), or application of TTX and ZD-7288 to Kir2.2 KO TC neurons (Fig. 3B), resulted in an I-V relationship that is linear at potentials negative to −82 mV. The slope of these plots decreases between −82 and −70 mV, where the reversal potential lies, and then increases again at more positive values.
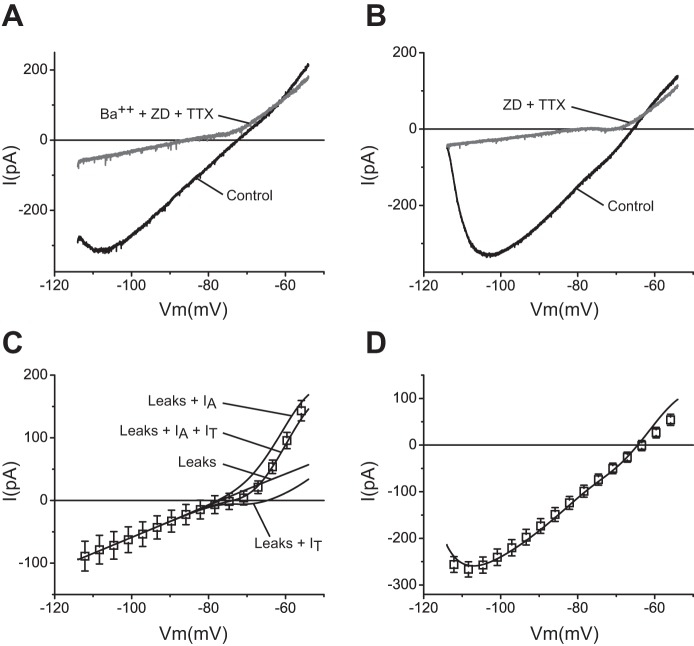
Fig. 3.
The simulated leak conductances and window current components of low-threshold calcium current (IT) and fast transient A-type potassium current (IA) recapitulate the remaining component after elimination of IKir, Ih, and INaP. A: voltage-clamp ramp recordings before (black trace) and after (gray trace) application of 50 μM Ba2+, 300 nM TTX, and 10 μM ZD-7288 to a wild-type TC neuron. B: voltage-clamp ramp recordings before (black trace) and after (gray trace) application of 300 nM TTX and 10 μM ZD-7288 to a Kir2.2 KO TC neuron. C: average values (symbols ± SE) from 10 Kir2.2 KO cells after application of TTX and ZD-7288 (remaining component). Solid lines are simulated I-V plots of the leaks (sodium and potassium), the leaks plus IT, the leaks plus IA, and the leaks plus IT and IA as indicated. Simulations were obtained with the corresponding models (see methods) using ḡKleak = 1.0 × 10−5 S/cm2, ḡNaleak = 3.0 × 10−6 S/cm2, ḡA = 5.5 × 10−3 S/cm2, and pT (maximum permeability) = 5.0 × 10−5 cm/s. D: average voltage-clamp ramp data (±SE) from 24 wild-type TC neurons in the absence of pharmacological agents. Solid line is a voltage-clamp ramp simulation using the model cell with all 7 subthreshold conductances turned on, using the same maximum conductances as in Figs. 1D, 2C, and 3C (default maximum conductances).
Leak currents.
To reconstruct the nonlinear I-V relationship that remains after elimination of IKir, Ih, and INaP, we first incorporated potassium and sodium leak currents (IKleak and INaleak) into a blank model cell (see methods). The ḡ values of IKleak (1.0 × 10−5 S/cm2) and INaleak (3.0 × 10−6 S/cm2) were adjusted to match the slope and the extrapolated reversal potential of a linear fit to the average ramp recordings of 10 cells from Kir2.2 KO mice after application of TTX and ZD-7288. The fit was performed on the linear region negative to −84 mV (slope between −114 and −84 mV = 2.53 ± 0.05 pA/mV, corresponding to a membrane resistance of 395.3 MΩ, and with an extrapolated reversal potential of −76.6 mV) (Fig. 3C).
Window current components of IT and IA.
Consistent with a contribution of a window current component of IT to the steady-state conductance of TC neurons (Crunelli et al. 2005; Dreyfus et al. 2010; Perez-Reyes 2003), introduction of this current into the model cell together with the leaks induces an N-like deflection of the I-V curve characterized by a region of decreased slope between −80 and −68 mV, followed by an increase in the slope at potentials positive to −68 mV (Fig. 3C). On the other hand, incorporation of the transient potassium current IA together with the leaks into the model cell induces a prominent outward rectification of the I-V plot at potentials positive to −77 mV (Fig. 3C). Simulating the combined steady-state activation of these two currents with the leaks accurately reproduces the complex I-V relationship that was observed after elimination of IKir, Ih, and INaP (Fig. 3C). The maximum conductance for IA (ḡA = 5.5 × 10−3 S/cm2) and maximum permeability for IT (pT = 5.0 × 10−5 cm/s) are within the range of values found experimentally (Destexhe et al. 1998; Huguenard et al. 1991). The nonlinear behavior that persists after removal of Ih, INaP, and IKir is reproduced by the fraction of window currents of modeled IA and IT, indicating that these two window currents contribute to the steady-state conductance of TC neurons at potentials positive to −80 mV.
Finally, we performed a simulation including all the identified components, using the maximum conductance values established in the preceding sections, and compared it to the experimentally recorded I-V plots in the absence of pharmacological agents (Fig. 3D); this figure shows a rather precise correspondence between the simulation and the experimental data. This computational reconstruction indicates that the subthreshold conductance of TC neurons is composed by at least seven different ion currents: IKleak, INaleak, Ih, IKir, IT, INaP, and IA, and that the modeled biophysical properties of these currents can account for the complex nonlinearity observed experimentally.
Computational Reconstruction of the Steady-State Conductance of TC Neurons
To determine the contribution of each individual component to the steady-state conductance, we performed simulations of the I-V relationship at steady-state (i.e., with all the gates set at infinite time values), with all the seven currents switched on and in the presence of each one of them at a time. Figure 4A shows a comparison of the steady-state I-V relationships of the seven subthreshold conductances at physiologically relevant subthreshold potentials, highlighting their differential voltage-dependent contributions to the total steady-state current (black). The main determinants of the RMP (the reversal potential of the total I-V curve) in these neurons, determined as fractions of the total current, are the leak conductances gKleak and gNaleak (36.7% and 24.5% of the total conductance, respectively). The other contributing conductances (in decreasing order) are gT (11.2%), gA (10.7%), gNaP (7.5%), gh (5.8%), and gKir (3.5%) (Fig. 4B). It is worth noting that these percent contributions do not reflect the importance of each current. As we show below, each of these conductances plays a key role at specific times during the oscillatory behavior of TC neurons. For example, even gKir, which makes the smallest contribution, becomes the most important conductance during interburst periods.
Fig. 4.
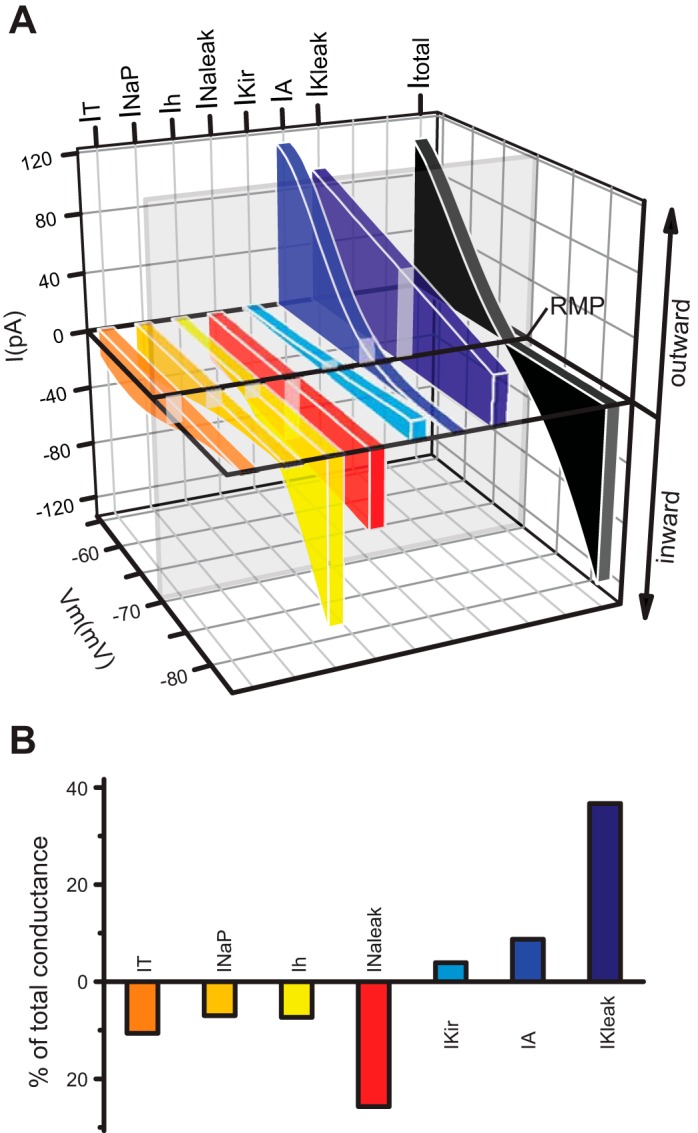
Subthreshold steady-state conductance of TC neurons. A: comparison of simulated steady-state I-V (Y and Z axes) plots of the subthreshold conductances obtained using the default maximum conductances at physiologically relevant potentials (−84 to −54 mV). The total steady-state I-V curve (black) corresponds to the algebraic sum of all 7 subthreshold conductances. The transecting vertical plane (glass) represents the resting membrane potential (RMP), at which the algebraic sum of inward (tones of red and yellow) and outward currents (tones of blue) is 0. B: contribution of the subthreshold conductances at RMP (see transecting plane in A) as a percentage of the total conductance (100%, of which 50% is the sum of inward current and the other 50% is the sum of outward current). Color conventions as in A.
Contribution of the Steady-State Conductance Components to the RMP of TC Neurons
To verify the individual contribution of each conductance component to the RMP of TC cells, we switched each of these conductances on and off in the model TC neuron (Fig. 5) and contrasted these results with values of RMP obtained before and after pharmacological elimination of those currents in TC cells (Table 1). Simulations with and without spiking mechanisms produced similar values of RMP (see discussion).
Table 1.
Effect of manipulating, experimentally and computationally, subthreshold conductances on resting membrane potential of TC neurons
| Experiment |
Model |
||||||
|---|---|---|---|---|---|---|---|
| RMP |
RMP |
||||||
| Current | Treatment | Before | Aftera | Reference | Treatment | Before | After |
| IKleak | 1 mM MCh (300 nM TTX) | −68.6 ± 2.5 | −55.0 ± 2.5b | Present study | Turn off IKleak | −69.7 | −59.3 |
| 250 μM MCh | 12 ± 6 mV depolarization | Varela and Sherman 2007 | Turn off IKleakc | −71.5 | −62.3 | ||
| INaleak | Turn off INaleak | −69.7 | −77.6 | ||||
| Ih | 10 μM ZD-7288 | −71.1 ± 2.4 | −78.3 ± 1.7d | Present study | Turn off Ih | −69.7 | −77.9 |
| 100 μM ZD-7288 | −71.0 ± 1.0 | −79.0 ± 2.0 | Meuth et al. 2006 | ||||
| HCN2 KO | −69.0 ± 1.0 | −81.0 ± 1.0 | Meuth et al. 2006 | ||||
| −68.0 ± 1.0 | −80.0 ± 1.0 | Ludwig et al. 2003 | |||||
| INaP | 300 nM TTX | −71.0 ± 1.5 | −71.9 ± 1.6e | Present study | Turn off INaPf | −69.7 | −71.5 |
| IKir | 50 μM Ba2+ | −69.0 ± 1.1 | −66.5 ± 0.9g | Present study | |||
| Kir2.2 KO | −69.3 ± 0.7 | −66.8 ± 0.8h | Present study | Turn off IKir | −69.7 | −68.6 | |
| IT | 1-3 μM TTA-P2 | 3.1 ± 0.5 mV hyperpolarization | Dreyfus et al. 2010 | Turn off IT | −69.7 | −72.3 | |
| IA | Turn off IA | −69.7 | −57.2 | ||||
Values are resting membrane potential (RMP; ±SE) in experimental or model-simulated thalamocortical (TC) neurons.
Comparison between wild type and knockout (KO) genotypes in the case of genetic elimination of HCN2 or Kir2.2.
Comparison of RMP before and after application of 1 mM β-methylcholine (MCh) in the presence of 300 nM TTX (n = 7; paired t-test, P = 0.00003).
Comparison of RMP before and after IKleak is turned off, with the sodium conductances previously switched off.
Comparison of RMP before and after application of 10 μM ZD-7288 (n = 10; paired t-test, P = 0.0004).
Comparison of RMP before and after application of 300 nM TTX (n = 18; paired t-test, P = 0.003).
Concomitantly turning off INaP and INa produces similar results.
Comparison of RMP before and after application of 50 μM Ba2+ (n = 17; paired t-test, P = 0.001).
Comparison between wild type (n = 66) and Kir2.2 KO (n = 19; 2-sample t-test, P = 0.02). TTA-P2, 3,5-dichloro-N-[1-(2,2-dimethyl-tetrahydropyran-4-ylmethyl)-4-fluoro-piperidin-4-ylmethyl]-benzamide. See text for current definitions.
We tested the effect of blocking IKleak on RMP of TC neurons by applying the muscarinic receptor agonist β-methylcholine (MCh). Application of 1 mM MCh in the absence of any other drug induced a strong depolarization that was sufficient to generate spontaneous firing in three cells tested (not shown). After elimination of sodium spiking with 300 nM TTX, MCh induced a significantly large change in RMP: from −68.6 ± 2.5 to −55 ± 2.5 mV (n = 7; paired t-test, P = 0.00003) (Table 1). In contrast, elimination of IKleak in the model after INa and INaP were turned off produced a smaller depolarization to −62.3 mV. In the presence of active sodium conductances, elimination of IKleak depolarized the model cell to −56.8 mV without reaching firing threshold. This discrepancy could be explained by the lack of selectivity of MCh at blocking IKleak. In addition to blocking potassium leak channels, MCh is a nonselective muscarinic agent that produces a broad spectrum of cellular effects. For example, Zhu and Uhlrich (1998) observed that application of MCh to rat TC neurons not only blocked a potassium leak conductance but also increased an inward current that was suspected to be Ih. Recent investigations have demonstrated that channels that carry sodium leak are also activated by second messenger-dependent mechanisms, including signaling cascades activated by muscarinic receptors (Lu et al. 2009; Swayne et al. 2009). Thus MCh could be acting on both IKleak (blocking) and INaleak (activating) to produce a synergistic depolarizing effect on RMP. We were able to simulate this effect in the model cell: an amount of depolarization sufficient to reach firing threshold was obtained after IKleak was turned off and ḡNaleak was increased by 30%, an effect consistent with previous observations (Lu et al. 2009; Swayne et al. 2009).
We then performed a similar analysis with the other conductances. There is a consistent agreement between the effect that changing the maximum conductance of the different components of the steady-state conductance has on the RMP of the TC neuron model and the effect that selective pharmacological agents have on the RMP of real TC neurons (Table 1). Table 1 also shows the agreement between RMP values of TC neurons from KO mice of Kir2.2 and HCN2 channel subunits, with the RMP values obtained after the simulated elimination of IKir and Ih, respectively. Figure 5 summarizes the simulated effect of eliminating each subthreshold conductance on RMP and the consequent reconfiguration of the remaining conductances.
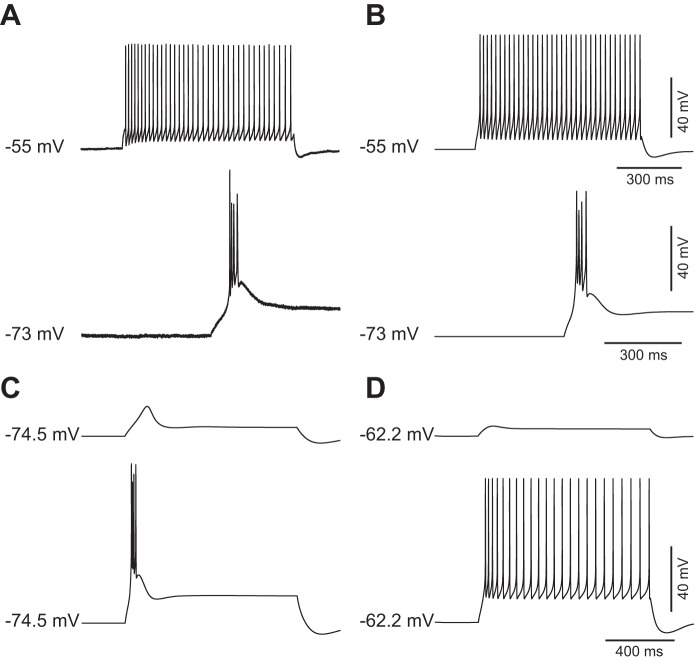
The Model Reproduces the Firing Behavior of Rodent TC Neurons
One of the most prominent features of TC neurons is the ability to fire action potentials in two different modes depending on the level of the membrane potential at which the depolarizing stimulus occurs (Llinas and Jahnsen 1982). To assess whether the modeled steady-state conductance would uphold the complex firing behavior of TC neurons, we fed the model with mechanisms that enable fast sodium-mediated action potential firing (see methods). Both the model and the TC neurons recorded under current clamp displayed the typical tonic firing and rebound burst responses when stimulated with a square pulse of current from a depolarized holding potential and when released from a hyperpolarized holding potential, respectively (Fig. 6, A and B). In addition, decreasing (or increasing) the maximum conductance of IKleak in the model TC neuron was sufficient to disable (or enable) the mechanism of low-threshold spike (LTS) generation. This is in agreement with the proposed role of this current in mediating the neuromodulator-dependent switch between bursting and tonic firing modes in TC neurons (McCormick and Bal 1997; McCormick and Prince 1987). Thus a depolarizing current applied after ḡKleak is increased (which causes hyperpolarization and deinactivation of IT) results in the generation of an LTS and burst firing, whereas a similar depolarizing step after ḡKleak is decreased (which causes depolarization and inactivation of IT) elicits a tonic train of action potentials (Fig. 6, C and D; compare with Fig. 9 of McCormick and Prince 1987).
Fig. 6.
The model reproduces the physiological behavior of TC neurons. A: current-clamp response of a TC neuron to injection of a depolarizing square pulse from a depolarized holding potential (top trace) and rebound response after release from a hyperpolarized holding potential (bottom trace). B: current-clamp responses of the model cell to protocols similar to that in A. The current-clamp responses of the model cell were obtained after incorporation of suprathreshold conductances (see text). Holding potentials and scales are the same for both TC neuron and model cell. Experimental recordings and simulations were performed at 32°C. C: current-clamp responses of the model cell to application of depolarizing subthreshold (top trace) and suprathreshold (bottom trace) square pulses after ḡKleak was increased to 150% of the default value (1.5 × 10−5 S/cm2). D: current-clamp responses of the model cell to application of current pulses of the same magnitude as in C after ḡKleak was decreased to 30% of the default value (3.0 × 10−6 S/cm2).
Inducing Intrinsic Periodic Burst Firing in the Rodent TC Neuron Model
Repetitive burst firing of TC neurons has been linked to the expression of the rhythms that characterize slow-wave sleep (particularly oscillations in the delta frequency band) (Dossi et al. 1992; Steriade and Deschenes 1984) and the pathological spike and wave discharges of absence epilepsy (Paz et al. 2007; Steriade and Contreras 1995). Although the synchronized expression of repetitive burst firing of TC neurons in the behaving animal is the result of the interaction between their intrinsic properties with the synaptic activity of all the cellular elements of the thalamo-reticulo-cortical network (Destexhe and Sejnowski 2003; Lytton et al. 1996), experimental evidence indicates a prominent role of intrinsic ionic mechanisms in the generation and maintenance of the oscillations at the cellular level (McCormick and Pape 1990).
Most rodent TC neurons recorded in brain slices are unable to sustain repetitive burst firing in isolation (McCormick and Pape 1990; McCormick and Prince 1988). In agreement with these experimental observations, our TC neuron model is unable to sustain repetitive burst firing with the default set of parameters used in the reconstruction of the steady-state conductance (Fig. 7A). It is possible to induce the appearance of rhythmic burst firing in rodent brain slices by manipulating the concentration of extracellular divalent cations (Jacobsen et al. 2001; Leresche et al. 1991). The underlying cause of the dependence of the oscillatory activity on the ionic environment is unknown. It was shown using dynamic clamp that the conductance of IT must exceed a certain threshold in order for TC neurons to exhibit spontaneous rhythmic activity (Hughes et al. 2009). Previous modeling studies (McCormick and Huguenard 1992; Wang et al. 1991) showed that the ability of TC neuron models to fire bursts of action potentials periodically could be achieved by increasing the availability of the low-threshold calcium current IT. We investigated which specific adjustments in the parameters of IT and the other subthreshold conductances enable repetitive burst firing in TC neurons.
Fig. 7.
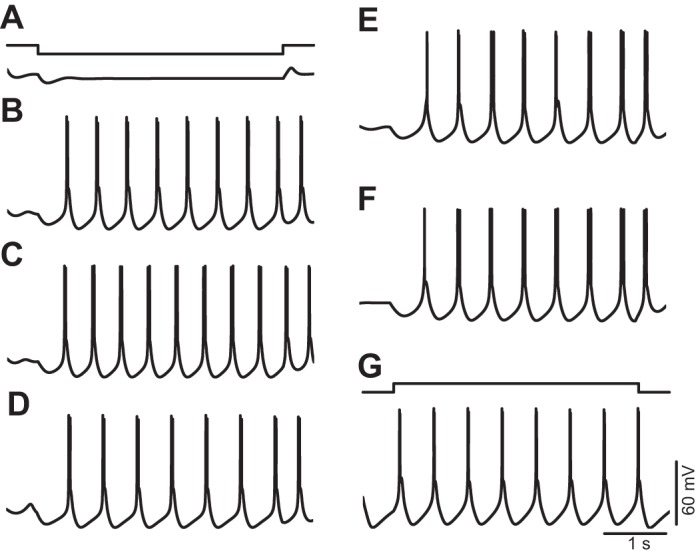
Single-parameter modifications enable repetitive burst firing in the murine TC neuron model. A: hyperpolarizing current injection (top trace) fails to elicit repetitive bursts (bottom voltage trace) when the model is set to the default parameters that reproduce the steady-state conductance of murine TC neurons. B–F: repetitive burst firing elicited by hyperpolarization after increase of pT from 5 × 10−5 to 8 × 10−5 cm/s (B), after a global negative shift of the mT gate of −2 mV (C), after a global positive shift of the hT gate of +3 mV (D), after a decrease of ḡA from 5.5 × 10−3 to 2.0 × 10−3 S/cm2 (E), and after an increase of ḡNaP from 5.5 × 10−6 to 1.5 × 10−5 S/cm2 (F). G: repetitive burst firing elicited by depolarization after an increase of ḡKir from 2.0 × 10−5 to 1.0 × 10−4 S/cm2. Voltage traces in A–F were obtained by simulating negative current injection of −15 pA. Voltage trace in G was obtained by simulating positive current injection of +10 pA.
We found that all of the following parameter modifications introduced independently (one at a time) enabled the model to continuously discharge LTSs at low frequencies (below 3 Hz), which are crowned by high-frequency bursts of action potentials: 1) increasing the maximum permeability of IT from 5.0 × 10−5 cm/s to values higher than 8.0 × 10−5 cm/s (Fig. 7B), 2) applying a global negative shift to the activation variable of IT larger than −2 mV (Fig. 7C), 3) applying a global positive shift to the inactivation variable of IT larger than +3 mV (Fig. 7D), 4) decreasing the maximum conductance of IA below 2.1 × 10−3 S/cm2 (Fig. 7E), 5) increasing the maximum conductance of INaP above 1.5 × 10−5 S/cm2 (Fig. 7F), and 6) increasing the maximum conductance of IKir above 1.0 × 10−4 S/cm2 (Fig. 7G). Modification of the maximum conductance of Ih alone did not support periodic burst firing. After each one of these modifications was introduced, the level of depolarization or hyperpolarization required to induce oscillations was obtained by injecting DC current or, alternatively, by modifying the leak conductances within certain values (see below).
These findings prompted us to investigate the role of each different subthreshold operating channels in the generation of TC oscillations, using the parameter values that reproduce the steady-state conductance of murine TC neurons (named default values) as a starting point. In the following sections, oscillations in the model were initiated by current injection unless otherwise indicated.
Minimal Requirements for Generating Periodic Burst Firing
From a theoretical perspective, the only requirement for generating neuronal oscillations (repetitive action potential firing, subthreshold oscillations, or resonance phenomena) is the appropriated combination of an amplifying variable and a resonant (or recovering) variable in the presence of an ohmic leak (Hutcheon and Yarom 2000; Izhikevich 2005). To determine the minimal requirements that enable sustained low-threshold oscillations in TC neurons compatible with physiological repetitive burst firing in the delta band (or pathological spike and wave discharges of absence epilepsy), we systematically performed simulations with the model cell containing only pairs of amplifying and resonant variables (or currents) together with the leaks. We started by investigating the ability of the low-threshold calcium current IT to sustain periodic low-threshold oscillations by itself. In the absence of all currents except IT and the leak currents, and with the use of the default parameters (pT = 5.0 × 10−5 cm/s; ḡKleak = 1.0 × 10−5 S/cm2; ḡNaleak = 3.0 × 10−6 S/cm2; and leak reversal potential = −76.6 mV) and the temperature set to 36°C, the membrane potential of the model TC neuron stabilized at −71.4 mV and injection of sustained current failed to induce oscillations (Fig. 8A, first 3 traces). Increasing pT to 7.0 × 10−5 cm/s induced spontaneous oscillations of 32 mV of amplitude (negative and positive peaks at −68 and −36 mV, respectively) at 2.3 Hz (Fig. 8A, 4th trace). Similarly, introducing a hyperpolarizing shift in the activation gate of IT larger than −2 mV or a depolarizing shift in the inactivation gate larger than +2 mV enabled oscillations (Fig. 8A, 5th and 6th traces, respectively). These simulations indicate that the amplifying variable mT and the resonant variable hT are sufficient to generate low-threshold oscillations in the delta band. Notably, the adjustments required to enable the oscillatory behavior are small and physiologically plausible (see discussion).
Fig. 8.
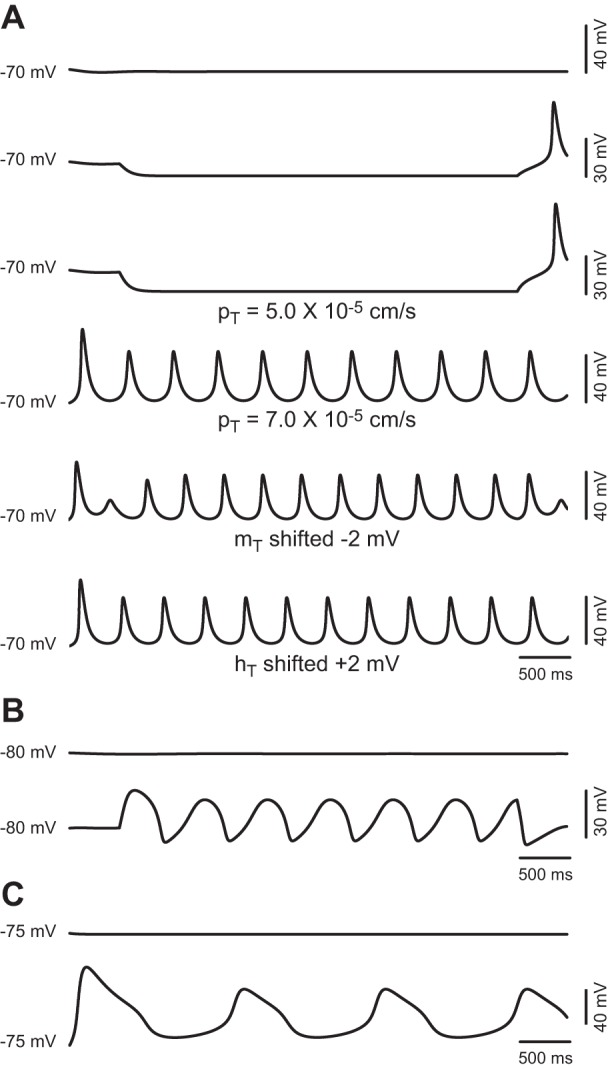
Minimal models capable of sustaining oscillations compatible with repetitive burst firing of TC neurons. A: top 3 traces show the effect of increasing magnitudes of hyperpolarizing current injection on the model cell containing IT and the sodium and potassium leak conductances with parameters set to default. Bottom 3 traces show spontaneous oscillations after an increase of pT to 7.0 × 10−5 cm/s (4th trace), oscillations induced by hyperpolarizing current injection of −3 pA after a shift of mT by −2 mV (5th trace), and spontaneous oscillations after a shift of hT by +2 mV (6th trace). B: voltage traces before (top trace) and after (bottom trace) depolarizing current injection on the model cell containing only Ih (ḡh = 4.4 × 10−5), IKir (ḡKir = 3.0 × 10−4 S/cm2), and the leak conductances (default values of ḡ). C: voltage traces from the model cell containing only IA, INaP, and the leak conductances with the maximum conductances set to default (top trace) and after ḡA is changed to 3.0 × 10−3 S/cm2 and ḡNaP to 3.0 × 10−5 S/cm2 (bottom trace).
Next, we explored whether there is a minimal TC model for generating sustained low-threshold oscillations compatible with repetitive bursting that does not require the low threshold calcium current IT. Charles Wilson proposed a model to explain the spontaneous burst firing of cholinergic interneurons in the striatum based on the interaction between Ih and IKir (Wilson 2005). In agreement with that model, turning on Ih and IKir in the presence of the leak currents bestows the TC model cell with periodic oscillatory activity. For example, we obtained sustained oscillations (26.5 mV of amplitude at a frequency of 1.6 Hz, Fig. 8B) with ḡh increased to 4.4 × 10−5 and ḡKir increased to 3.0 × 10−4 S/cm2 (while keeping the maximum conductance for the leaks at the default values). In contrast to the oscillations based on IT (Fig. 8A), the oscillations generated by the interaction of IKir and Ih are elicited by injecting depolarizing current and occur in a more negative voltage regime.
We also tested other combinations of subthreshold currents that could sustain periodic oscillations in the model without modifying parameters other than maximum conductance. Interestingly, turning on IA and INaP, in the presence of only the leak currents enables the model cell to oscillate. Figure 8C shows oscillations at 0.7 Hz obtained (without injecting current) with ḡA set to 3.0 × 10−3 S/cm2, ḡNaP set to 3.0 × 10−5 S/cm2, and the leak currents set to default.
Role of Subthreshold Conductances in Periodic Burst Firing
To study the contribution to repetitive burst firing of each of the seven subthreshold conductances described for TC neurons, we analyzed systematically the time course of the currents and the gating variables during periodic LTSs. First, we analyzed the time course of the currents during oscillations enabled by increasing the availability of IT (we used the minimum pT value that sustains periodic LTSs: 8.0 × 10−5 cm/s) while maintaining the ḡ values of the other conductances at their default values (Fig. 9). Under these conditions, we then analyzed the effect of eliminating (turning off) each of the conductances on the oscillatory behavior of the model (Fig. 10, A–C). Finally, we analyzed the behavior of the currents during oscillations enabled by modifying the ḡ values of all the other conductances but IT (pT = 5.0 × 10−5 cm/s; Fig. 10, D–F). Since we did not find qualitative differences when including spiking mechanisms [albeit the values of maximum conductance required to induce periodic oscillations are slightly lower in their presence (Fig. 7) than in their absence (Fig. 10, D–F)], the following simulations were performed in the absence of suprathreshold conductances (see discussion).
After pT is increased to 8.0 × 10−5 cm/s and in the absence of current injection, the membrane potential of the model cell is stable at −67.7 mV. All simulations in this section started at this RMP of −67.7 mV to provide similar initial conditions for all voltage-dependent variables of the model. Under these initial conditions, injection of hyperpolarizing current elicits repetitive LTSs (Fig. 9, 1st trace) at a frequency that changes little with the magnitude of the current injected (from 1.6 to 1.9 Hz). The traces in Fig. 9 (2nd to 9th) show the time course of the different currents and of the gating variables of IT during two cycles elicited by injecting the minimum current required to induce the oscillation (−12 pA). Figure 9 shows the sequence of events underlying the oscillations: at the most hyperpolarized point during the cycle (dotted vertical line b in Fig. 9), there is a net inward current contributed mostly by Ih and the leaks (note that at this point the total leak current is inward since INaleak is larger than IKleak) and opposed by IKir (9% of the total current). The contribution of Ih increases from 13% (line b) to a maximum of 16.5% of the total current as the cycle progresses. After this point, the contribution of Ih decreases rapidly at the same time that IT becomes the dominant inward component. The regenerative activation of IT then slowly depolarizes the membrane toward the LTS threshold (dotted vertical line c in Fig. 9), at which the sudden upstroke of the LTS occurs. During this time, the simultaneous activation of IA and INaP has opposing effects on the depolarizing drive of IT: IA negative and INaP positive. At the peak of the LTS (vertical dotted line a in Fig. 9), the total inward current is completely counterbalanced by the large contribution of IA (28% of the total current) and the large driving force of the potassium leak current. During the repolarizing phase of the LTS, IT decreases to a minimum due to its almost complete inactivation. At this time, the contribution of INaP is maximal but is nonetheless outweighed by the potassium leak and IA. At the end of the repolarizing phase, the membrane potential hyperpolarizes toward the most negative point of the oscillation assisted by the unblock of IKir, which becomes the dominant outward current during most of the inter-LTS interval, despite its small magnitude (Fig. 9, 5th trace). This hyperpolarization, in turn, initiates the next cycle by activating Ih and removing the inactivation of IT.
Ih.
Surprisingly, after Ih is switched off (with pT increased to 8.0 × 10−5 cm/s), the model is still capable of sustaining periodic LTSs (36-mV amplitude at 1.2 Hz) in the absence of current injection (Fig. 10A). Under these conditions, the net total current at the most hyperpolarized point of the oscillation is zero (vertical dotted line b) due to the complete balance of inward (mostly IT) and outward (mostly IKir) currents. Beyond this point, the inward current becomes dominant by the regenerative increase of IT, which produces the upstroke of the LTS on its own accord. During the peak and the repolarization of the LTS, the trajectory (albeit not the scale) of the other currents is similar to the condition where Ih is present, because this current is nonetheless deactivated at this point (Fig. 9).
IKir.
With the model set to the conditions that enable oscillations (pT increased to 8.0 × 10−5 cm/s and all other parameters set to their default values), switching off IKir prevents the maintenance of repetitive LTS. By using the optimum current injection (−20 pA), the model is capable of generating a maximum of seven cycles before declining to a stable potential (−71 mV). Slightly lower, or higher, current magnitudes generate a lower number of cycles. Inspection of the time course of the gates of IT as the oscillation progresses reveals a gradual decline in the availability of IT (mT2hT product) due to a progressive drop in the deinactivation during the inter-LTS intervals (Fig. 10B). This suggests that the additional hyperpolarizing drive, timely provided by IKir during inter-LTS intervals, optimizes the fine balance of inactivation-activation of IT that underlies sustained oscillations.
IA.
Switching off IA under similar conditions of increased availability of IT (pT = 8.0 × 10−5 cm/s) induces a large depolarization (RMP stabilizes at −54.8 mV without current injection). Injection of hyperpolarizing current induces the appearance of sustained repetitive LTSs characterized by larger amplitudes (Fig. 10C, top trace). Comparison of current magnitudes before and after IA is switched off shows about 50% increase of peak T current for any given current injection. Furthermore, the maximum contribution of IT to the total current increases from 59% to 80% during LTSs after IA is switched off (compare the stacked area plots of Figs. 9 and 10C, vertical lines c), indicating that IA counteracts the surge of IT and hence controls the amplitude of the LTS.
INaP.
Similar to the effect of eliminating IKir, turning off INaP prevents repetitive LTS generation at all values of current injection (not shown). The negatively shifted activation of INaP (with respect to transient sodium current) boosts depolarization during the initial phase of the LTS, when the membrane potential rushes toward the threshold of rapid regenerative activation of IT (see Fig. 8). The minimum ḡNaP value that allows repetitive LTSs while maintaining the other conductances at their default value (pT = 8.0 × 10−5 cm/s) is 2.8 × 10−6 S/cm2.
Leak currents.
As expected, turning off IKleak produces a large depolarization. This can be overcome by injecting enough hyperpolarizing current to bring the membrane potential to the level of activation of IT, inducing repetitive LTSs. Reciprocally, oscillations are induced by injecting depolarizing current to the level of activation of IT after INaleak is turned off, which hyperpolarizes the model cell to −77.1 mV. The model is able to sustain repetitive LTSs by using ḡKleak values between 0 and 1.2 × 10−5 S/cm2 while maintaining ḡNaleak at the default value (after adjusting the level of current injection). Similarly, ḡNaleak values between 0 and 5.0 × 10−6 S/cm2 also support periodic LTSs while maintaining ḡKleak at default. In fact, any ḡleak combination (ḡKleak + ḡNaleak) below 1.5 × 10−5 S/cm2 supports sustained oscillations. In contrast, above this value, it is not possible to induce oscillations even if the hyperpolarizing drive of a large ḡKleak (or the depolarizing drive of a large ḡNaleak) is compensated by current injection. This highlights the importance of the electrotonic compactness of TC neurons. Indeed, we observed a direct relationship between ḡleak and the minimum pT value required to induce oscillations. For example, elimination of both leak currents allows oscillations with pT values as low as 4.0 × 10−5 cm/s; conversely, oscillations are rescued by increasing pT when using large values of ḡleak.
Oscillations induced using the default maximum permeability of IT.
As mentioned earlier, when the maximum permeability of IT is maintained at the default value (5.0 × 10−5 cm/s), increasing the maximum conductance of IKir above 1.0 × 10−4 S/cm2, decreasing the maximum conductance of IA below 2.1 × 10−3 S/cm2, or increasing the maximum conductance of INaP above 1.5 × 10−5 S/cm2 enables sustained repetitive burst firing. In this section we examine the mechanisms of repetitive LTS induced by these manipulations of ḡ on the reduced model (without spiking mechanisms) while keeping pT at the default value.
IKir.
Under these default conditions, increasing ḡKir to values equal to, or above, 1.2 × 10−4 S/cm2 enables the generation of sustained repetitive LTSs. This increase in the availability of IKir hyperpolarizes the membrane potential to −78 mV. Oscillations are then induced by application of compensatory depolarizing current (Fig. 10D). In this case, the hyperpolarizing drive of a large IKir pulls down the membrane potential to a level at which Ih becomes strongly activated at the same time that the inactivation of IT is largely removed (vertical dotted line b in Fig. 10D). Activation of Ih, in turn, depolarizes the membrane toward the voltage range at which IT becomes activated. Thus, under these conditions of low availability of IT, oscillations do not result from the interaction of the amplifying and resonant gates of IT alone. Instead, the interaction of the amplifying activation of IKir with the recovering activation of Ih results in a negative transient deflection of the membrane potential between LTSs, thereby removing the inactivation of IT. Hence, the complete cycle is composed of a transient hyperpolarization (mediated by IKir-Ih, between vertical lines a and c in Fig. 10D), followed by a depolarizing LTS (mediated by IT, between vertical lines c and d).
IA and INaP.
Despite their different kinetics, these two opposing currents increase with similar time courses during the initial phase of depolarization, before the upstroke of the LTS. In the model with all subthreshold conductances set to default, it is not possible to elicit sustained repetitive LTSs, which are otherwise enabled by increasing pT to values higher than 8.0 × 10−5 s/cm. Under these conditions, the magnitude of the A current in the initial phase is larger than that of INaP (see Fig. 8), and the net combined influence of this pair of currents timely opposes depolarization. When pT is decreased back to default (pT = 5.0 × 10−5 s/cm), the counteracting influence of IA effectively thwarts the oscillatory behavior. In this case, repetitive LTSs can be generated by either decreasing ḡA below 1.8 × 10−3 S/cm2 (Fig. 10E) or increasing ḡNaP above 1.7 × 10−5 S/cm2 (Fig. 10F). Hence, a small change in the balance of these two currents favoring the amplifying activation of INaP promotes periodicity by boosting the activation of IT, whereas an excess of IA current suppresses the oscillation.
DISCUSSION
In this study we present a comprehensive analysis of the interaction among seven different conductances operating at membrane potentials below the threshold for tonic action potential firing in somatosensory TC neurons (ventroposteromedial and ventroposterolateral nuclei) of mice. Our computational analysis shows how this interaction dynamically controls the RMP of these cells, and hence their excitability. We also explore the mechanisms of generation and maintenance of low-threshold oscillations compatible with the intrinsic oscillatory activity in the delta band that has been linked to physiological and pathological EEG rhythms.
We modeled the subthreshold behavior of TC neurons using a single-compartment model cell that does not include information about the complex geometry of these neurons or the subcellular distribution of ion channels. Although the subcellular compartmentalization of the conductances analyzed in this study could have an unforeseen impact on the conclusions reached in our study (for example, see Wei et al. 2011; Zomorrodi et al. 2008), the fact that the model cell reproduces the electrophysiological behavior of TC neurons indicates that either the high electrotonic compactness of TC cells allows for an effective space-clamp control of a large membrane area or, alternatively, the modeled parameters capture most of the inaccuracies of recording in the soma. In any case, the simplification is validated from a phenomenological perspective, whereas further investigation is required to clarify the functional effect of subcellular localization, which is largely unknown. In that regard, ongoing research in our group is being carried out to computationally explore the consequences of compartmentalization of the conductances analyzed in this article.
The agreement between simulations and experimental traces indicates that most of the key players of the steady-state conductance of TC neurons are included in our analysis. This conclusion is also supported by data on ion channel mRNA expression in TC neurons. Based on these data and on functional studies, other ion channels expressed by TC neurons that could contribute, albeit minimally, to the steady-state conductance in the voltage range considered in this study include the negatively activated slow potassium channels of the KCNQ and ether-à-go-go (EAG) families and the calcium-activated potassium channels. All KCNQ and EAG channels are weakly expressed in thalamic ventrobasal nuclei with the exception of Kcnq3 channels (Saganich et al. 2001). However, in agreement with previous studies (Kasten et al. 2007; McCormick 1992), our results suggest that their contribution in the subthreshold voltage range is negligible.
On the basis of pharmacological experiments, calcium-activated potassium channels are known to account for AHP potentials and to be involved in controlling tonic firing frequency in TC neurons (Jahnsen and Llinas 1984; Kasten et al. 2007). Consequently, most computational models of TC neurons include one or two calcium-activated potassium currents (McCormick and Huguenard 1992; Rhodes and Llinas 2005). In contrast to the established role of channels of the small-conductance calcium-activated potassium (SK) channel family in controlling the oscillatory behavior of thalamic reticular neurons (Cueni et al. 2008), indirect experimental evidence indicates that these channels do not contribute to either RMP or rhythmic bursting of TC neurons. For instance, application of neither SK channel blockers nor large-conductance calcium-activated potassium (BK) channel blockers modified the resting membrane conductance of TC neurons (Kasten et al. 2007). In addition, these same blockers only modify slightly the number of action potentials within a burst, without modifying the bursting propensity of TC neurons from tree shrew (Wei et al. 2011). We performed simulations in the presence or absence of spiking mechanisms that included two calcium-activated potassium currents, and we did not observe any qualitative difference in the conductance control of the RMP or propensity to fire bursts rhythmically.
The Complex Interplay of Subthreshold Conductances Controls Both the RMP and the Intrinsic Oscillatory Behavior of TC Neurons
On the basis of the time course and voltage range of operation of the seven subthreshold conductances, and how modifications of single parameters of these currents shift the propensity of the TC neuron model to either oscillate or get stabilized at RMP, we propose a model to explain the electrophysiological behavior of TC neurons at subthreshold potentials for tonic firing (Fig. 11). The model includes three resonant (recovering) variables: hT and the activation of IA recover the membrane potential from depolarization, whereas activation of Ih recovers the membrane potential from hyperpolarization; and three amplifying variables: mT and the activation of INaP amplify depolarization, whereas unblocking of IKir amplifies hyperpolarization. All these currents interact over the background provided by the leak conductances. In TC neurons, the densities of these leak conductances are small, which is important for their control of the RMP. A small leak (large input resistance) enhances the physiological effects of the voltage-dependent conductances, which are also small. Likewise, small variations in leak produced by the modulation of the leak channels also have a great functional impact, like the one observed during the neuromodulator-induced transition from burst to tonic firing in these cells. Under these electrotonically compact conditions, the RMP of TC cells is about 10 mV depolarized from the reversal potential of the leak (Eleak). This deviation from Eleak is due to the steady activation of the depolarizing variables (Ih, INaP, and mT; left quadrants in Fig. 11). In turn, the steady activation of the repolarizing variables (IA, IKir, and hT; right quadrants in Fig. 11) prevents this depolarization from becoming regenerative. It is the balance between these counteracting influences that establishes the RMP. This balance is dynamic, and small modifications can set in motion the oscillatory behavior of TC neurons.
Fig. 11.
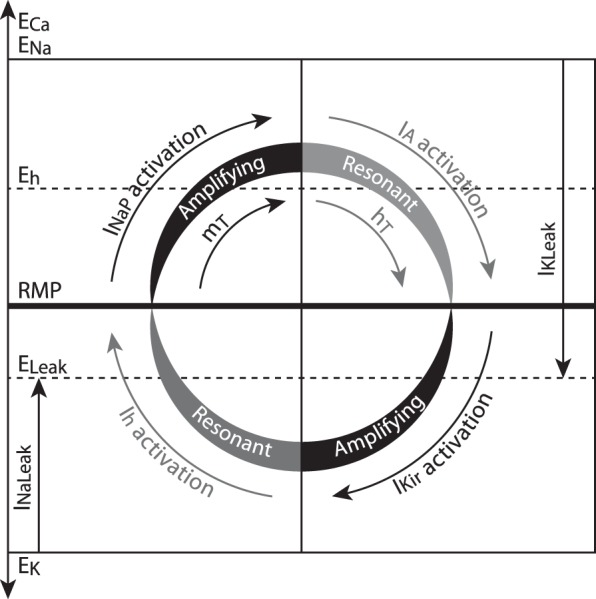
Schematic representation of the interaction between the 7 subthreshold conductances and their roles in controlling the RMP and the oscillatory behavior of TC neurons. The leak conductances establish a background on which the other 5 voltage-dependent conductances interact: steadily active depolarizing variables (left quadrants) displace the membrane potential from the reversal potential (E) of the leak at the same time that steadily active hyperpolarizing variables (right quadrants) counteract depolarization. The RMP is a stable equilibrium (horizontal bar) reached by the balance achieved among all these forces. Periodicity is promoted by changes in certain parameter values that allow the destabilization of this equilibrium and the cyclic behavior of the membrane potential (curved arrows). Changes that favor the regenerative activation of the amplifying variables (black) increase the propensity to oscillate. These changes include either increasing the magnitude of amplifying variables themselves or decreasing the magnitude of resonant variables (gray). Conversely, an increase in the magnitude of resonant variables (and/or a decrease in the magnitude of amplifying variables) renders the model unable to oscillate periodically.
Indeed, the dynamic balance between amplifying and resonant variables is responsible for the TC neurons' ability, or lack thereof, to oscillate intrinsically. Intrinsic oscillations (spontaneous or induced by injection of constant current) are enabled if the amplifying variables are allowed to become regenerative by opposing resonant variables of the right magnitude (i.e., strong enough to fulfill their recovering function of pulling the membrane potential back toward RMP). Conversely, oscillations are impeded if the resonant variables are so large that the regenerative activation of amplifying variables is thwarted (Fig. 11). Consistent with this model, our simulations show that 1) increasing the amplifying variable mT (either by increasing pT or by displacing its voltage dependence opposite to that of hT), increases the propensity to oscillate, whereas decreasing mT hampers oscillations; 2) increasing amplifying INaP augments the propensity to oscillate, whereas decreasing INaP opposes oscillations; 3) a large amplifying IKir increases the propensity to oscillate, whereas a small one decreases it; 4) decreasing resonant IA increases the propensity to oscillate, whereas increasing IA prevents oscillations; and 5) under conditions of increased IT and in the absence of current injection, decreasing resonant Ih induces oscillations, whereas increasing Ih promotes stabilization. Except for the first one, the other model predictions are novel and reveal a far more complex modulation of the subthreshold behavior of the TC neuron membrane potential. The specific roles of these currents in establishing RMP and enabling oscillations in TC neurons are discussed in detail below.
IT: The Amplifying Variable mT and the Resonant Variable hT
Repetitive burst firing is enabled in the TC neuron model (tuned to reproduce the murine steady-state conductance) by increasing the availability of IT, which is consistent with previous observations (Hughes et al. 2009; Noebels 2012; Wei et al. 2011). We show that a minimal model containing only IT and the leaks is capable of sustaining periodic oscillations (Fig. 7A). This model predicts that IT alone, with physiologically plausible parameter values, could originate the oscillatory behavior of TC neurons. This tendency to oscillate is inherent to the dynamic interplay between the amplifying variable mT and the resonant variable hT. Preliminary results in our group indicate that the bifurcation structure of the minimal IT-leaks model is similar to the structure of the HH model and that the two gating variables of IT are perfectly fitted for the pacemaker function of TC cells (Amarillo Y, Mato G, and Nadal MS, personal communication; see also Rush and Rinzel 1994). Nonetheless, as discussed below, in real TC neurons this intrinsic oscillatory property of IT is modulated by the other subthreshold operating ionic conductances.
In addition to the contribution of low-threshold calcium currents to the generation of rhythmic oscillations and LTSs, their biophysical properties predict the expression of window currents at low membrane potentials (Crunelli et al. 2005; Perez-Reyes 2003). Consequently, these window currents could contribute to the establishment and control of RMP. Indeed, the expression of a window T current and its contribution to the steady-state conductance of TC neurons have been demonstrated using a novel selective blocker of calcium channels of the Cav3 subfamily (Dreyfus et al. 2010). In agreement with that study, we report in this article a moderate contribution of the T window current to the RMP of TC neurons (Fig. 4B and Fig. 5, “IT off”).
Amplifying INaP
Pharmacological blockade of sodium channels produces a small but significant hyperpolarization of TC neurons (Table 1), indicating a contribution of a persistent sodium current (or sodium current that is active at steady state) to the RMP of these cells. Consisting with this finding, persistent sodium currents from different neuronal types, including TC neurons (Parri and Crunelli 1998), start to activate at potentials as negative as −80 mV and have a V1/2 of activation about 20 mV more negative than that of transient sodium currents (Wu et al. 2005 and references therein).
The study by Parri and Crunelli (1998) also shows a contribution of INaP to the amplification of rebound LTSs in TC neurons from rat. In our simulations, the time course and the relative contribution of INaP during oscillations (Figs. 9 and 10) indicate that INaP activates during the ascending phase of repetitive LTSs and adds to the depolarizing drive of the regenerative activation of IT. In line with this amplifying effect, increasing INaP is sufficient to enable periodic bursting (while the other subthreshold conductances are kept at their default values, Figs. 7E and 10F). Moreover, switching off INaP abolishes the oscillatory behavior when the default parameter values are used for all conductances except IT (availability increased). To recover the oscillation under the latter conditions, the maximum permeability of IT needs to be increased further (above 9 × 10−5 cm/s) or the maximum conductance of IA should be decreased about 20% (below 4 × 10−3 S/cm2).
This indicates that INaP is not essential for the oscillation; however, it could have a strong effect depending on the availability of other subthreshold conductances. In particular, the balance between INaP and IA seems to play a role on the expression (or suppression) of rhythmic burst firing (Fig. 10, E and F) and could explain the propensity or failure to sustain repetitive burst firing of individual TC neurons (see also Resonant IA below).
Amplifying IKir
Strong inward rectifier potassium channels of the Kir2 family (which underlie IKir in TC neurons) show a distinctive negative slope conductance region in the I-V relationship (Dhamoon et al. 2004; Lopatin and Nichols 2001; see also Fig. 1, A and D). It has been suggested that this biophysical feature could generate bistability and oscillations (Tourneur 1986). In fact, it has been proposed that the interaction between the amplifying unblock of IKir and the resonant activation of Ih is responsible for the rhythmic bursting behavior of cholinergic interneurons in the striatum (Wilson 2005). Early investigations on the mechanisms of repetitive burst firing in TC neurons showed that deactivation of Ih during the burst produces an afterhyperpolarization that follows each burst and that is crucial for the maintenance of the oscillation (McCormick and Pape 1990). We show in the present work that this afterhyperpolarization results not only from the deactivation of Ih but also from the activation (unblock) of IKir during the repolarizing phase of the LTS. This mechanism differs from the repolarizing effect of the leaks in that the conductance of IKir increases as the membrane repolarizes due to the negative slope conductance. The repolarizing effect of the leaks is nonetheless minimal at the valleys because at these points the membrane potential is very close to the reversal potential of the total leak. Taking all this together, the “undershoot” between LTSs, below the reversal potential for the leaks, is produced by the timely activation of IKir. This extra hyperpolarization in turn contributes to the maintenance of the oscillation by allowing a larger removal of inactivation of IT and also by activating Ih.
Resonant IA
The expression of large A-type currents that activate at negative potentials in TC neurons predicts a contribution of this current to RMP and burst firing (Huguenard et al. 1991). In this report we show that IA is active at rest (window current) and during repetitive burst firing. IA exerts an opposing effect to LTS generation by counteracting the development of the T current. In addition, when IT is large enough to overcome this opposition, IA curtails the amplitude of the LTSs. These findings agree with those of previous investigations (Gutierrez et al. 2001; Rush and Rinzel 1994). Interestingly, IA develops during the initial phase of depolarization of each cycle of the oscillation with similar time course and reaches magnitudes roughly similar to those of INaP such that these two currents counterbalance each other. Although the relative contribution of these currents during this phase is small (see the relative contribution plot in Fig. 9), changes in their balance favoring amplifying INaP over resonant IA enable oscillations, whereas changes in the opposite direction prevent periodicity (Fig. 10, E and F). This balance between INaP and IA could provide yet another control mechanism for the oscillatory behavior of TC neurons, which could also have an impact on the expression of physiological or pathological thalamocortical rhythms.
On the other hand, our reconstruction of the steady-state conductance of TC neurons indicates that Ih and IA have roughly similar contributions to the steady-state conductance at equilibrium (rest) and that these contributions increase symmetrically around RMP (for example, at −10 mV from rest, Ih contributes 34.8% of the total conductance, whereas at +10 mV from rest, IA contributes 33.9% of the total conductance; Fig. 5, “all on”). Thus any hyperpolarizing perturbation of the membrane potential is opposed by activation of Ih, whereas any depolarizing perturbation is counteracted by IA. This arrangement suggests that these two resonant conductances act as a functional stabilization unit that maintains RMP within certain bounded values in TC neurons. Interestingly, there is experimental and computational evidence of the concerted expression of Ih and IA in other neurons, indicating that they indeed balance each other at the molecular level to control excitability (Burdakov 2005; Hoffman et al. 1997; MacLean et al. 2005; O'Leary et al. 2013).
Resonant Ih
According to the model in Fig. 11, it is expected that increasing Ih would have a hampering effect on the oscillations, whereas decreasing Ih would promote oscillations. Indeed, these effects are reproduced by the TC neuron model under conditions of increased IT and without injection of constant current. Under these specific conditions, increasing Ih induces depolarization and further stabilization of the membrane potential, and decreasing Ih induces hyperpolarization with the consequent deinactivation and regenerative activation of IT leading to spontaneous oscillations (Fig. 10A). However, oscillations can be elicited under conditions of increased Ih by injection of constant hyperpolarizing current under conditions of increased IT. This is due to the overlap between the voltage range of the initial phase of activation of IT and the final stages of deactivation of Ih (not depicted in Fig. 11). The induced hyperpolarization activates Ih and deinactivates IT, whose availability becomes transiently increased. Activation of Ih, in turn, recovers the membrane potential toward RMP, as mentioned before. Yet, as the membrane depolarizes, and before Ih is completely deactivated, IT starts to activate and eventually becomes regenerative, initiating the oscillations. Thus, although Ih is a recovering conductance that tends to stabilize the membrane potential, it may promote oscillations under conditions of imposed hyperpolarization, such as those produced by synaptic inhibition.
Repetitive Burst Firing and EEG Rhythms
The occurrence of rhythmic burst firing of TC neurons is more frequent during the phases of sleep characterized electroencephalographically by slow waves at a frequency of 1–4 Hz (delta oscillations; see review, McCormick and Bal 1997). In addition, rhythmic burst firing is also timely correlated with electroencephalographic spike and wave discharges (2–4 Hz) during episodes of absence seizures (Steriade and Contreras 1995). A third type of thalamocortical EEG rhythm associated with repetitive burst firing is characterized by spindle waves occurring during the early stages of non-rapid eye movement sleep. During these transient oscillations (every 1–3 s at 7–14 Hz), TC neurons also discharge repetitive bursts at 2–4 Hz (see review, McCormick and Bal 1997). Whether the periodicity of TC neuron burst firing associated with these EEG rhythms is intrinsically generated or is dependent on the synaptic connectivity in the thalamo-reticular-cortical network is still an unresolved matter. Our computational analysis shows that repetitive burst firing of TC cells can be enabled/disabled with small modifications of the intrinsic subthreshold conductances. This implies that physiological (or pathological) modulation of ion channel availability could easily modify the propensity of TC neurons to fire bursts repetitively. This hypothesis is supported by studies of KO mice of the ion channel subunits underlying IT and Ih in TC neurons (Lee et al. 2004; Ludwig et al. 2003) and the study of animal models of absence epilepsy (see review, Noebels 2012). It is also known that most of the subthreshold channels are susceptible to modulation by neurotransmitters and neuropeptides acting via multiple signaling pathways. Except for INaP, the molecular identity of these subthreshold ion channels expressed in TC neurons is known today, including IKir (this study). This paves the way to assess how the modulation of these channels affects the propensity of TC neurons to fire repetitively, and what consequences this might have in the generation of the associated EEG rhythms.
The functional role of slow wave sleep is still conjectural. The proposed functions include halting the flow of sensory information to the cerebral cortex (McCormick and Feeser 1990) and some aspects of memory consolidation (Stickgold 2005). The occurrence of burst firing of TC neurons during wakeful states is also controversial, albeit it has been proposed that bursting increases feature detectability (see review and discussion, Llinas and Steriade 2006). In a more general context, an increasing amount of data now indicates that the thalamus not only functions as a relay station in the flow of information but that it also plays a central role in modulating and integrating signals across the brain (Sherman 2007). The qualitative analysis presented in this article shows that the dynamic interaction among subthreshold conductances determines both the excitability and the oscillatory properties of TC neurons. It remains to be established how changes in this dynamic interaction affect the neurocomputational properties of these cells. Studies are under way in our group, using both theoretical and experimental approaches, to determine how changes in these conductances impact the input-output transformation of TC neurons.
GRANTS
This work was subsidized in part by Consejo Nacional de Investigaciones Científicas y Técnicas-Argentina Grant PIP 112 200901 00738 and National Institute of Neurological Disorders and Stroke Grant NS30989 (to B. Rudy).
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
Y.A., B.R., and M.S.N. conception and design of research; Y.A. performed experiments; Y.A., E.Z., G.M., and M.S.N. analyzed data; Y.A., E.Z., G.M., B.R., and M.S.N. interpreted results of experiments; Y.A. prepared figures; Y.A. and M.S.N. drafted manuscript; Y.A., B.R., and M.S.N. edited and revised manuscript; Y.A., E.Z., G.M., B.R., and M.S.N. approved final version of manuscript.
ACKNOWLEDGMENTS
We thank Dr. Thomas L. Schwarz (Children's Hospital, Boston, MA) for gently providing the Kir2.2 KO mouse line.
Present address of E. Zagha: Department of Neurobiology, Yale School of Medicine, New Haven, CT.
REFERENCES
- Amarillo Y. Control of Neuronal Excitability by Subthreshold Operating Potassium Channels (PhD thesis). New York: New York University, 2007 [Google Scholar]
- Amarillo Y, Nadal MS. On the repetitive burst firing of thalamic relay neurons. Program No. 46.08. 2011 Neuroscience Meeting Planner. Washington, DC: Society for Neuroscience, 2011 [Google Scholar]
- Amarillo Y, Nadal MS, Rudy B. The inward rectifying potassium channel Kir2.2 regulates the excitability of thalamic relay neurons. Program No. 174.3 2005 Neuroscience Meeting Planner Washington, DC: Society for Neuroscience, 2005 [Google Scholar]
- Anumonwo JM, Lopatin AN. Cardiac strong inward rectifier potassium channels. J Mol Cell Cardiol 48: 45–54, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biel M, Wahl-Schott C, Michalakis S, Zong X. Hyperpolarization-activated cation channels: from genes to function. Physiol Rev 89: 847–885, 2009 [DOI] [PubMed] [Google Scholar]
- Burdakov D. Gain control by concerted changes in IA and IH conductances. Neural Comput 17: 991–995, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coetzee WA, Amarillo Y, Chiu J, Chow A, Lau D, McCormack T, Moreno H, Nadal MS, Ozaita A, Pountney D, Saganich M, Vega-Saenz de Miera E, Rudy B. Molecular diversity of K+ channels. Ann NY Acad Sci 868: 233–285, 1999 [DOI] [PubMed] [Google Scholar]
- Crunelli V, Toth TI, Cope DW, Blethyn K, Hughes SW. The ‘window’ T-type calcium current in brain dynamics of different behavioural states. J Physiol 562: 121–129, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cueni L, Canepari M, Lujan R, Emmenegger Y, Watanabe M, Bond CT, Franken P, Adelman JP, Luthi A. T-type Ca2+ channels, SK2 channels and SERCAs gate sleep-related oscillations in thalamic dendrites. Nat Neurosci 11: 683–692, 2008 [DOI] [PubMed] [Google Scholar]
- Destexhe A, Neubig M, Ulrich D, Huguenard J. Dendritic low-threshold calcium currents in thalamic relay cells. J Neurosci 18: 3574–3588, 1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Destexhe A, Sejnowski TJ. Interactions between membrane conductances underlying thalamocortical slow-wave oscillations. Physiol Rev 83: 1401–1453, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dhamoon AS, Pandit SV, Sarmast F, Parisian KR, Guha P, Li Y, Bagwe S, Taffet SM, Anumonwo JM. Unique Kir2.x properties determine regional and species differences in the cardiac inward rectifier K+ current. Circ Res 94: 1332–1339, 2004 [DOI] [PubMed] [Google Scholar]
- Dossi RC, Nunez A, Steriade M. Electrophysiology of a slow (0.5–4 Hz) intrinsic oscillation of cat thalamocortical neurones in vivo. J Physiol 447: 215–234, 1992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dreyfus FM, Tscherter A, Errington AC, Renger JJ, Shin HS, Uebele VN, Crunelli V, Lambert RC, Leresche N. Selective T-type calcium channel block in thalamic neurons reveals channel redundancy and physiological impact of IT window. J Neurosci 30: 99–109, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutierrez C, Cox CL, Rinzel J, Sherman SM. Dynamics of low-threshold spike activation in relay neurons of the cat lateral geniculate nucleus. J Neurosci 21: 1022–1032, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hille B. Ion Channels of Excitable Membranes. Sunderland, MA: Sinauer Associates, 2001 [Google Scholar]
- Hines ML, Carnevale NT. The NEURON simulation environment. Neural Comput 9: 1179–1209, 1997 [DOI] [PubMed] [Google Scholar]
- Hoffman DA, Magee JC, Colbert CM, Johnston D. K+ channel regulation of signal propagation in dendrites of hippocampal pyramidal neurons. Nature 387: 869–875, 1997 [DOI] [PubMed] [Google Scholar]
- Hughes SW, Lorincz M, Cope DW, Crunelli V. Using the dynamic clamp to dissect the properties and mechanisms of intrinsic thalamic oscillations. In: Dynamic-Clamp: From Principles to Applications, edited by Destexhe A, Bal T. New York: Springer, 2009, p. 321–346 [Google Scholar]
- Huguenard JR, Coulter DA, Prince DA. A fast transient potassium current in thalamic relay neurons: kinetics of activation and inactivation. J Neurophysiol 66: 1304–1315, 1991 [DOI] [PubMed] [Google Scholar]
- Huguenard JR, McCormick DA. Simulation of the currents involved in rhythmic oscillations in thalamic relay neurons. J Neurophysiol 68: 1373–1383, 1992 [DOI] [PubMed] [Google Scholar]
- Hutcheon B, Yarom Y. Resonance, oscillation and the intrinsic frequency preferences of neurons. Trends Neurosci 23: 216–222, 2000 [DOI] [PubMed] [Google Scholar]
- Izhikevich E. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting. Cambridge, MA: MIT Press, 2005 [Google Scholar]
- Jacobsen RB, Ulrich D, Huguenard JR. GABAB and NMDA receptors contribute to spindle-like oscillations in rat thalamus in vitro. J Neurophysiol 86: 1365–1375, 2001 [DOI] [PubMed] [Google Scholar]
- Jahnsen H, Llinas R. Ionic basis for the electro-responsiveness and oscillatory properties of guinea-pig thalamic neurones in vitro. J Physiol 349: 227–247, 1984 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karschin C, Dissmann E, Stuhmer W, Karschin A. IRK(1–3) and GIRK(1–4) inwardly rectifying K+ channel mRNAs are differentially expressed in the adult rat brain. J Neurosci 16: 3559–3570, 1996 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kasten MR, Rudy B, Anderson MP. Differential regulation of action potential firing in adult murine thalamocortical neurons by Kv3.2, Kv1, and SK potassium and N-type calcium channels. J Physiol 584: 565–582, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee J, Kim D, Shin HS. Lack of delta waves and sleep disturbances during non-rapid eye movement sleep in mice lacking alpha1G-subunit of T-type calcium channels. Proc Natl Acad Sci USA 101: 18195–18199, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leresche N, Lightowler S, Soltesz I, Jassik-Gerschenfeld D, Crunelli V. Low-frequency oscillatory activities intrinsic to rat and cat thalamocortical cells. J Physiol 441: 155–174, 1991 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Llinas R, Jahnsen H. Electrophysiology of mammalian thalamic neurones in vitro. Nature 297: 406–408, 1982 [DOI] [PubMed] [Google Scholar]
- Llinas RR, Steriade M. Bursting of thalamic neurons and states of vigilance. J Neurophysiol 95: 3297–3308, 2006 [DOI] [PubMed] [Google Scholar]
- Lopatin AN, Nichols CG. Inward rectifiers in the heart: an update on IK1. J Mol Cell Cardiol 33: 625–638, 2001 [DOI] [PubMed] [Google Scholar]
- Lu B, Su Y, Das S, Liu J, Xia J, Ren D. The neuronal channel NALCN contributes resting sodium permeability and is required for normal respiratory rhythm. Cell 129: 371–383, 2007 [DOI] [PubMed] [Google Scholar]
- Lu B, Su Y, Das S, Wang H, Wang Y, Liu J, Ren D. Peptide neurotransmitters activate a cation channel complex of NALCN and UNC-80. Nature 457: 741–744, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ludwig A, Budde T, Stieber J, Moosmang S, Wahl C, Holthoff K, Langebartels A, Wotjak C, Munsch T, Zong X, Feil S, Feil R, Lancel M, Chien KR, Konnerth A, Pape HC, Biel M, Hofmann F. Absence epilepsy and sinus dysrhythmia in mice lacking the pacemaker channel HCN2. EMBO J 22: 216–224, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lytton WW, Destexhe A, Sejnowski TJ. Control of slow oscillations in the thalamocortical neuron: a computer model. Neuroscience 70: 673–684, 1996 [DOI] [PubMed] [Google Scholar]
- MacLean JN, Zhang Y, Goeritz ML, Casey R, Oliva R, Guckenheimer J, Harris-Warrick RM. Activity-independent coregulation of IA and Ih in rhythmically active neurons. J Neurophysiol 94: 3601–3617, 2005 [DOI] [PubMed] [Google Scholar]
- McCormick DA. Cellular mechanisms underlying cholinergic and noradrenergic modulation of neuronal firing mode in the cat and guinea pig dorsal lateral geniculate nucleus. J Neurosci 12: 278–289, 1992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormick DA, Bal T. Sleep and arousal: thalamocortical mechanisms. Annu Rev Neurosci 20: 185–215, 1997 [DOI] [PubMed] [Google Scholar]
- McCormick DA, Feeser HR. Functional implications of burst firing and single spike activity in lateral geniculate relay neurons. Neuroscience 39: 103–113, 1990 [DOI] [PubMed] [Google Scholar]
- McCormick DA, Huguenard JR. A model of the electrophysiological properties of thalamocortical relay neurons. J Neurophysiol 68: 1384–1400, 1992 [DOI] [PubMed] [Google Scholar]
- McCormick DA, Pape HC. Properties of a hyperpolarization-activated cation current and its role in rhythmic oscillation in thalamic relay neurones. J Physiol 431: 291–318, 1990 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormick DA, Prince DA. Actions of acetylcholine in the guinea-pig and cat medial and lateral geniculate nuclei, in vitro. J Physiol 392: 147–165, 1987 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormick DA, Prince DA. Noradrenergic modulation of firing pattern in guinea pig and cat thalamic neurons, in vitro. J Neurophysiol 59: 978–996, 1988 [DOI] [PubMed] [Google Scholar]
- Meuth SG, Kanyshkova T, Meuth P, Landgraf P, Munsch T, Ludwig A, Hofmann F, Pape HC, Budde T. Membrane resting potential of thalamocortical relay neurons is shaped by the interaction among TASK3 and HCN2 channels. J Neurophysiol 96: 1517–1529, 2006 [DOI] [PubMed] [Google Scholar]
- Noebels JL. The voltage-gated calcium channel and absence epilepsy. In: Jasper's Basic Mechanisms of the Epilepsies, edited by Noebels JL, Avoli M, Rogawski MA, Olsen RW, Delgado-Escueta AV. New York: Oxford University Press, 2012 [Google Scholar]
- O'Leary T, Williams AH, Caplan JS, Marder E. Correlations in ion channel expression emerge from homeostatic tuning rules. Proc Natl Acad Sci USA 110: E2645–E2654, 2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panama BK, Lopatin AN. Differential polyamine sensitivity in inwardly rectifying Kir2 potassium channels. J Physiol 571: 287–302, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parri HR, Crunelli V. Sodium current in rat and cat thalamocortical neurons: role of a non-inactivating component in tonic and burst firing. J Neurosci 18: 854–867, 1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paz JT, Chavez M, Saillet S, Deniau JM, Charpier S. Activity of ventral medial thalamic neurons during absence seizures and modulation of cortical paroxysms by the nigrothalamic pathway. J Neurosci 27: 929–941, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perez-Reyes E. Molecular physiology of low-voltage-activated t-type calcium channels. Physiol Rev 83: 117–161, 2003 [DOI] [PubMed] [Google Scholar]
- Ren D. Sodium leak channels in neuronal excitability and rhythmic behaviors. Neuron 72: 899–911, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rhodes PA, Llinas R. A model of thalamocortical relay cells. J Physiol 565: 765–781, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudy B, Maffie J, Amarillo Y, Clark B, Goldberg EM, Jeong HY, Kruglikov I, Kwon E, Nadal MS, Zagha E. Voltage-gated potassium channels: structure and function of Kv1 to Kv9 subfamilies. In: Encyclopedia of Neuroscience, edited by Squire LR. New York: Academic, 2009, p. 397–425 [Google Scholar]
- Rush ME, Rinzel J. Analysis of bursting in a thalamic neuron model. Biol Cybern 71: 281–291, 1994 [DOI] [PubMed] [Google Scholar]
- Saganich MJ, Machado E, Rudy B. Differential expression of genes encoding subthreshold-operating voltage-gated K+ channels in brain. J Neurosci 21: 4609–4624, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santoro B, Chen S, Luthi A, Pavlidis P, Shumyatsky GP, Tibbs GR, Siegelbaum SA. Molecular and functional heterogeneity of hyperpolarization-activated pacemaker channels in the mouse CNS. J Neurosci 20: 5264–5275, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sherman SM. The thalamus is more than just a relay. Curr Opin Neurobiol 17: 417–422, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steriade M, Contreras D. Relations between cortical and thalamic cellular events during transition from sleep patterns to paroxysmal activity. J Neurosci 15: 623–642, 1995 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steriade M, Deschenes M. The thalamus as a neuronal oscillator. Brain Res 320: 1–63, 1984 [DOI] [PubMed] [Google Scholar]
- Stickgold R. Sleep-dependent memory consolidation. Nature 437: 1272–1278, 2005 [DOI] [PubMed] [Google Scholar]
- Swayne LA, Mezghrani A, Varrault A, Chemin J, Bertrand G, Dalle S, Bourinet E, Lory P, Miller RJ, Nargeot J, Monteil A. The NALCN ion channel is activated by M3 muscarinic receptors in a pancreatic beta-cell line. EMBO Rep 10: 873–880, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tourneur Y. Action potential-like responses due to the inward rectifying potassium channel. J Membr Biol 90: 115–122, 1986 [DOI] [PubMed] [Google Scholar]
- Traub RD, Buhl EH, Gloveli T, Whittington MA. Fast rhythmic bursting can be induced in layer 2/3 cortical neurons by enhancing persistent Na+ conductance or by blocking BK channels. J Neurophysiol 89: 909–921, 2003 [DOI] [PubMed] [Google Scholar]
- Varela C, Sherman SM. Differences in response to muscarinic activation between first and higher order thalamic relays. J Neurophysiol 98: 3538–3547, 2007 [DOI] [PubMed] [Google Scholar]
- Wang XJ, Rinzel J, Rogawski MA. A model of the T-type calcium current and the low-threshold spike in thalamic neurons. J Neurophysiol 66: 839–850, 1991 [DOI] [PubMed] [Google Scholar]
- Waxman SG, Cummins TR, Black JA, Dib-Hajj S. Diverse functions and dynamic expression of neuronal sodium channels. Novartis Found Symp 241: 34–51; discussion 51–60, 2002 [PubMed] [Google Scholar]
- Wei H, Bonjean M, Petry HM, Sejnowski TJ, Bickford ME. Thalamic burst firing propensity: a comparison of the dorsal lateral geniculate and pulvinar nuclei in the tree shrew. J Neurosci 31: 17287–17299, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson CJ. The mechanism of intrinsic amplification of hyperpolarizations and spontaneous bursting in striatal cholinergic interneurons. Neuron 45: 575–585, 2005 [DOI] [PubMed] [Google Scholar]
- Williams SR, Turner JP, Hughes SW, Crunelli V. On the nature of anomalous rectification in thalamocortical neurones of the cat ventrobasal thalamus in vitro. J Physiol 505: 727–747, 1997 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu N, Enomoto A, Tanaka S, Hsiao CF, Nykamp DQ, Izhikevich E, Chandler SH. Persistent sodium currents in mesencephalic v neurons participate in burst generation and control of membrane excitability. J Neurophysiol 93: 2710–2722, 2005 [DOI] [PubMed] [Google Scholar]
- Yu FH, Catterall WA. The VGL-chanome: a protein superfamily specialized for electrical signaling and ionic homeostasis. Sci STKE 2004: re15, 2004 [DOI] [PubMed] [Google Scholar]
- Zaritsky JJ, Redell JB, Tempel BL, Schwarz TL. The consequences of disrupting cardiac inwardly rectifying K+ current (IK1) as revealed by the targeted deletion of the murine Kir2.1 and Kir2.2 genes. J Physiol 533: 697–710, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu JJ, Uhlrich DJ. Cellular mechanisms underlying two muscarinic receptor-mediated depolarizing responses in relay cells of the rat lateral geniculate nucleus. Neuroscience 87: 767–781, 1998 [DOI] [PubMed] [Google Scholar]
- Zomorrodi R, Kroger H, Timofeev I. Modeling thalamocortical cell: impact of ca channel distribution and cell geometry on firing pattern. Front Comput Neurosci 2: 5, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]