Abstract
Objective
Nonlinear system identification approaches were used to develop a dynamical model of the network level response to patterns of microstimulation in-vivo.
Approach
The thalamocortical circuit of the rodent vibrissa pathway was the model system, with voltage sensitive dye imaging capturing the cortical response to patterns of stimulation delivered from a single electrode in the ventral posteromedial thalamus. The results of simple paired stimulus experiments formed the basis for the development of a phenomenological model explicitly containing nonlinear elements observed experimentally. The phenomenological model was fit using datasets obtained with impulse train inputs, Poisson-distributed in time and uniformly varying in amplitude.
Main Results
The phenomenological model explained 58% of the variance in the cortical response to out of sample patterns of thalamic microstimulation. Furthermore, while fit on trial averaged data, the phenomenological model reproduced single trial response properties when simulated with noise added into the system during stimulus presentation. The simulations indicate that the single trial response properties were dependent on the relative sensitivity of the static nonlinearities in the two stages of the model, and ultimately suggest that electrical stimulation activates local circuitry through linear recruitment, but that this activity propagates in a highly nonlinear fashion to downstream targets.
Significance
The development of nonlinear dynamical models of neural circuitry will guide information delivery for sensory prosthesis applications, and more generally reveal properties of population coding within neural circuits.
1. Introduction
Artificially activating neural cells has a long history, pre-dating even the recording of the electrical activity of neurons. As early as the late 1800’s, electrical stimulation was used to activate neurons in the central nervous system (Fritsch & Hitzig, 1870; Schafer, 1888). The maturity of electrical stimulation as a means for artificially activating neurons is evident in the long history of studies concerning the effects of electric fields on single neurons at the microscopic scale (Stoney et al. 1968; Jankowska and Roberts 1972; Ranck 1975) and as an input in behavioral studies at the macroscopic scale (Salzman et al. 1992; Romo et al. 1998; Pezaris and Reid 2007; O’Doherty et al. 2009). Despite this fact, how electrical stimulation activates and engages the population of neurons within the neural circuit that ultimately gives rise to behavioral percepts is far less well understood, creating an obstacle for the advancement of sensory prostheses.
Sensory prostheses seek to use electrical stimulation to deliver information to the brain about the sensory environment when the native neural pathways have been damaged due to trauma or disease. While peripheral sensory prostheses, like the cochlear or retinal implants, have been successful (Humayun et al. 2003; Wilson and Dorman 2008), attempts at delivering information directly to the central nervous system have proven difficult. Whether the aim is to reproduce natural neural activity or merely to deliver discriminable inputs to the brain, the advancement of sensory prostheses requires a greater understanding of the mapping from electrical stimuli to neural response within complex circuits and the resulting propagation along neural pathways.
Recent work has pushed towards recording population responses downstream of the delivery of patterned microstimulation in-vivo (Castro-Alamancos and Connors 1996; Kara et al. 2002; Butovas and Schwarz 2003; Civillico and Contreras 2005; Histed et al. 2009; Logothetis et al. 2010; Brugger et al. 2011; Weber et al. 2011). In all but the simplest scenarios, the neural response to electrical stimulation is highly nonlinear, ranging from paired stimulus facilitation in the thalamocortical augmenting response (Dempsey and Morison 1943; Castro-Alamancos and Connors 1996) to paired stimulus suppression at the level of the cortex (Kara et al. 2002; Butovas and Schwarz 2003). Furthermore, the nonlinear effects of natural sensory stimuli and electrical stimuli are behaviorally and electrophysiologically different, indicating that electrical stimuli activate neural circuits in a manner distinct from the natural physiological recruitment (Logothetis et al. 2010; Masse and Cook 2010). In order to design patterns of stimulation to faithfully represent ongoing changes in the sensory environment for prosthesis applications, particularly in the central nervous system, we must develop predictive models of these dynamical nonlinear mappings in-vivo. Here we perform nonlinear system identification within the central nervous system, specifically using the thalamocortical circuit, to model the system dynamics in response to patterns of microstimulation.
System identification has a long history of application in sensory neuroscience for creating nonlinear dynamical models (Krausz 1975; Marmarelis and Marmarelis 1978; Hunter and Korenberg 1986; Wu et al. 2006). Typically, system identification takes advantage of nonparametric model structures capable of estimating complicated system dynamics with few assumptions; however, these types of models often require a large amount of data to fit (Marmarelis 2004). In-vivo experimental models are typically limited in the amount of data that can be realistically collected during an experimental session, often precluding the high-order modeling that is necessary to adequately capture the complexity of the system. However, through a combination of non-parametric modeling and empirical observations of the system, it is possible to constrain the model subspace, greatly reducing the number of parameters needed, while only minimally restricting the generality of the model (Morrison et al. 2008; Stern et al. 2009).
Through both nonparametric and parametric system identification techniques, we develop a model of the nonlinear system dynamics in the thalamocortical circuit in-vivo. Specifically, using voltage sensitive dye imaging (VSDI) techniques, we recorded the cortical layer 2/3 response to upstream microstimulation in the ventral postero-medial (VPm) region of the thalamus in the anesthetized rat. The canonical network architecture of the thalamocortical circuit (Sherman and Guillery 1996), along with the extensive literature on the anatomy of the rodent vibrissa system (Woolsey and Van der Loos 1970; Diamond et al. 2008), makes this an ideal model system for studying the network level neural response to electrical stimuli. Systematic probing of the input-output relationship enabled the development of a nonlinear phenomenological model based upon experimental observations that is highly predictive of the cortical response to patterns of thalamic microstimulation. The ultimate structure of the model revealed complex interactions within a multi-stage architecture composed of canonical facilitative and suppressive dynamics, and a sensitivity to noise that mediates trial-by-trial bimodality in the facilitative/suppressive dynamics. Finally, from simulations with the model, we suggest that electrical stimulation activates local circuitry through linear recruitment, but that this activity propagates in a highly nonlinear fashion to downstream targets. More generally, the nonlinear dynamical model developed in this study informs future encoding schemes that map sensory signals to patterns of microstimulation for sensory prosthesis implementation.
2. Methods
2.1 Experimental Preparation
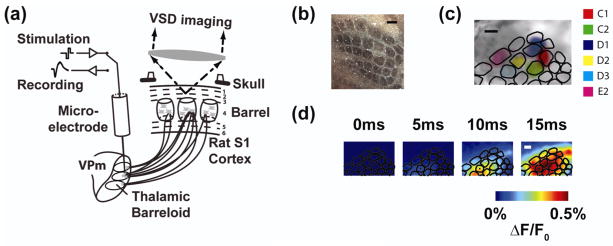
All procedures were approved by the Georgia Institute of Technology Institutional Animal Care and Use Committee and followed guidelines established by the National Institutes of Health. Female sprague-dawley rats (250–300g) were initially anesthetized with 4% isoflurane before intraperitoneal injection of Nembutal (50mg/kg weight) for long term anesthesia. Subsequent doses of Nembutal were used to maintain a surgical level of anesthesia.
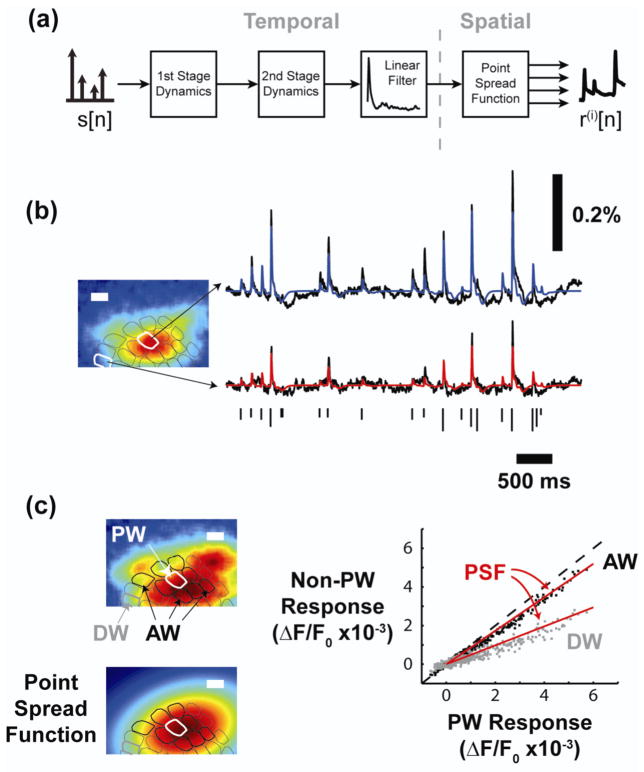
Animals were mounted in a stereotactic device and a craniotomy was performed over the left parietal cortex (coordinates: 1–4mm posterior to bregma, 4–7mm lateral to midline) to expose the barrel representation of the primary somatosensory cortex (Paxinos and Watson 2007). Another craniotomy was performed to allow access to the ventral postero-medial (VPm) region of the thalamus (coordinates: 2–4mm posterior to bregma, 1.5–2.5mm lateral to midline, 4.5–5.5mm depth at a 12 degree angle to brain surface). A diagram of the in-vivo experimental preparation is shown in figure 1(a).
Figure 1. Voltage sensitive dye imaging captures the cortical response with high spatial and temporal resolution.
(a) Diagram of the imaging system. The electrode is positioned in a “barreloid” in the thalamus, a collection of cells that respond most vigorously to a common whisker. Imaging in cortex captures the response of each cortical column. (b) Histological analysis provides an anatomical map of the cortical column structure (see methods). (c) The anatomical map is aligned to the VSDI image through a least squares mapping to functional data. (d) The cortical response to electrical microstimulation of the thalamus begins ~5–10 milliseconds after stimulation, but quickly grows in amplitude and spreads spatially. Scale bars in (b), (c), and (d) are 500 micrometers.
2.2 Voltage Sensitive Dye Imaging
Voltage sensitive dye imaging (VSDI) was used to monitor cortical activation in response to thalamic microstimulation. After the craniotomy was performed, the dura was allowed to dry for 15 minutes according to the protocol of Lippert, et al (Lippert et al. 2007). The cortex was stained with dye RH1691 (1mg/mL; Optical Imaging, Rehovot, Israel) for two hours and subsequently washed for 30 minutes. After washing the cortex, saline was deposited in the cranial window. A 1.0x magnification lens was used in conjunction with a 0.63x condenser lens to provide 1.6x magnification (48 pixels/millimeter). A 150W halogen lamp filtered at 621–634nm wavelength was used for imaging the brain surface and providing excitation of the dye. The VSDI data were acquired at five millisecond interframe intervals beginning 200 milliseconds preceding stimulus presentation. A diagram of the VSDI setup is included in figure 1(a).
Multiple trials of VSDI data were collected for each stimulus. For each trial, the 40 frames (200ms) collected before the presentation of the stimulus were averaged to calculate the background fluorescence, against which the activation was measured. For each frame, the background fluorescence was subtracted to produce a differential signal ΔF. Additionally, each frame was divided by the background image to normalize for uneven illumination and staining to produce the signal ΔF/F0. For presentation purposes only, the individual trials were averaged together and then filtered with a 9×9 pixel (~200μm × ~200μm) spatial averaging filter.
For model development, the VSDI data were functionally registered to the anatomical map of the barrel cortex in order to discretize the spatiotemporal cortical signal with regard to well-defined cortical columns. The outlines of the barrel cortex columns within a cytochrome oxidase stained tangential slice, shown in figure 1(b), were created using the Neurolucida software (MBF Bioscience, Williston, VT) and imported into MATLAB (MathWorks, Natick, MA). The functional cortical columns were determined in the VSDI data by deflecting a single whisker using a piezoelectric actuator and recording the cortical response (for methods, see Wang et al. 2012). The initial frame of cortical activation, which has previously been shown to be restricted to a single cortical column (Petersen et al. 2003), was captured for deflection of 4–6 different whiskers during each experiment. An example of the initial VSDI activation in response to the deflection of six different whiskers is overlaid in figure 1(c).
The anatomical mapping from histology was registered with the functional column mapping from VSDI by solving a linear inverse problem, the details of which are described in Wang, et al (2012). Following the functional image registration, the cortical response was discretized, where each signal corresponds to a single functional cortical column. In so doing, the VSDI signal was averaged spatially within the contour of the cortical column. An example of the spatiotemporal VSDI response to a single electrical stimulation pulse is shown in the top portion of figure 1(d), with the discretized temporal trace shown in figure 2(a). The registration procedure did not produce results qualitatively different from averaging within a contour defined by the VSDI activation in response to a single whisker deflection. However, the added benefit of the registration procedure was to generate an output for each of the 32 whiskers in the anatomical map, using only the functional response to the deflection of a few whiskers. In this way, the model was extended spatially (see sections 2.5 of Methods and 3.4 of Results) to capture the response of all cortical columns within the barrel cortex.
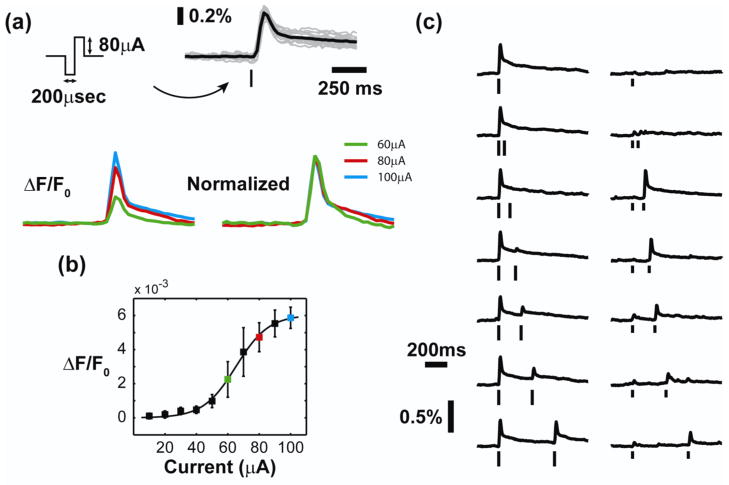
Figure 2. Microstimulation of the thalamus produces a nonlinear cortical response.
(a) Top: By averaging within a single cortical column, we obtain a timecourse of cortical activation with high signal to noise ratio. The “tick” represents the presentation time of the stimulus, which is a symmetric biphasic current waveform. The height of the “ticks” throughout the paper indicates the current amplitude of the stimulus. Microstimulation elicited a characteristic timecourse in the cortical response (single trials in gray, trial-averaged response in black). Bottom: When normalized by the amplitude of the response, the timecourse was consistent across a wide range of stimulus intensities and response amplitudes. (b) The amplitude of the cortical response displayed a nonlinear relationship with the current intensity of the single electrical stimulus. The currents used in (a) are color-coded in (b) for reference. (c) Microstimulation of the thalamus engaged two sets of nonlinear dynamics. A strong electrical stimulus suppressed the response to a second electrical stimulus, with the suppression decreasing for long inter-stimulus intervals. A weak electrical stimulus, however, caused profound facilitation of the response to the second stimulus. This facilitation principally occurs for inter-stimulus intervals of 100–200 milliseconds.
2.3 Electrical Stimulation
A glass coated tungsten microelectrode (impedance = 1–2 MΩ at 1kHz) was advanced to the ventral posterio-medial (VPm) region of the thalamus using a precision microdrive (Knopf Instruments, Tujunga, CA). The principal vibrissa was determined by manually deflecting individual whiskers and confirmed using the latency and spike count of single unit recordings in response to controlled whisker deflection using a piezo-electric actuator (Wang et al. 2010). In the event that single unit recordings could not be achieved, multi-unit activity was used.
Following electrophysiological determination of the electrode position and its associated principal vibrissa, the electrode was used to deliver microstimulation to the surrounding tissue. The stimulus waveforms were designed using a digital stimulus generator (WPI Inc, Sarasota, Florida) and delivered using a current controlled, optically isolated stimulator (WPI Inc, Sarasota, Florida). Individual electrical stimuli were charge-balanced, cathodal-first, biphasic waveforms of 200 microsecond duration per phase. A diagram of the stimulus waveform is displayed in figure 2(a). More complicated stimuli were generated through temporal patterns of this base stimulus unit with varying amplitudes. Although we have recently shown a topographic displacement of the spatial cortical response to symmetric and asymmetric waveforms of thalamic microstimulation (Wang et al. 2012), we observed no difference in the dynamics presented in this study between the two stimulus waveforms (data not shown).
Three different stimulation protocols were used in this study. A series of single electrical stimulation pulses with varying amplitude between 10 and 100 microamperes was used to test the static nonlinearity of the system (shown in Figure 2(b), discussed in the results section). The current range was chosen to elicit the full range of sub-threshold to maximal cortical responses. To sample the nonlinear dynamics of the system, pairs of electrical stimulation pulses were delivered with varying inter-stimulus intervals between 50 and 500 milliseconds. For the system identification procedure, random impulse trains were generated, where the event times were determined by a Poisson distribution and the intensities of the events were drawn randomly from a set of current amplitudes (30, 40, 50, 60, 80, 100 microamperes), all with equal probability. Throughout the remainder of the document, these stimuli will be referred to as random amplitude Poisson (RAP) impulse trains, consistent with previous literature (Wu and Sclabassi 1997). In four experiments, twenty different random instances of RAP impulse trains were used with a Poisson homogeneous rate of 10Hz, while the remaining three experiments used thirty different random instances with a Poisson homogeneous rate of 3Hz. The results were not qualitatively different using the two different stimulus rates. While previous studies have used high frequency pulse trains as the fundamental unit for stimulating the brain (Romo et al. 1998; Pezaris and Reid 2007; Logothetis et al. 2010; O’Doherty et al. 2012), we treated each single stimulus pulse as its own event. Given the inter-event intervals were generated from a Poisson process, the RAP stimulus presented a wide bandwidth (up to 500Hz) to the experimental system.
2.4 System Identification
Two different model structures were used in this study: a second order Volterra series and a custom phenomenological model. Each model was fit using the cortical response, r[n], averaged within the principal cortical column, to the RAP impulse trains, s[n], where n are the discrete timepoints sampled by the VSD imaging for a given trial of length T. A block diagram of the experimental system is shown in figure 3(a). Each electrical stimulus was considered a discrete Dirac delta function with amplitude in units of microamperes. The second order Volterra series was fit according to the cross-correlation based methods of Wu and Sclabassi (1997). The parameters of the phenomenological model were fit simultaneously through a least squares regression algorithm in MATLAB. Confidence intervals on the parameters were estimated by fitting the models with shuffled versions of the stimuli, where each instance of the RAP impulse train was randomly reassigned to a cortical response generated by a different instance of the stimulus.
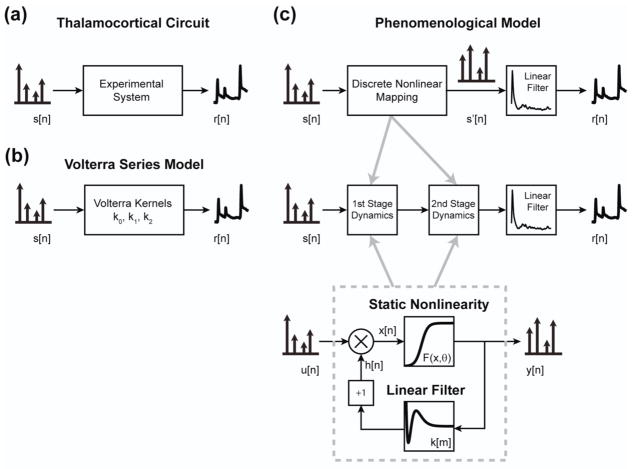
Figure 3. Nonlinear modeling architecture.
(a) The goal of the study was to create a nonlinear dynamical model of the response of the thalamocortical circuit to patterns of thalamic microstimulation. A train of microstimulation pulses was delivered as the input, while a continuously varying signal, generated by averaging within a single cortical column, was used as the output. (b) A second order Volterra series model was developed in an attempt to capture the dynamics of the system. The kernels of the model mapped trains of discrete inputs to continuously varying signals. (c) Top: The phenomenological model was developed according to experimental observations described in Figure 2. The response of the system was similar in shape, regardless of stimulus or response amplitude, allowing separation of the model into a nonlinear mapping of discrete impulses followed by a linear filter. Middle: Further, two distinct sets of dynamics were observed and directly incorporated into the model architecture. Bottom: Each of the two stages within the model was comprised of a canonical unit, in which the static and dynamic nonlinearity were independently modeled and parameterized.
The models were cross-validated using the “leave one out” method (Kearns and Ron 1999). The models were fit using all but one instance of the RAP impulse train and then tested on the remaining instance of the RAP impulse train stimulus. This procedure was then repeated for all instances of the stimulus. Performance was measured as the percent of variance accounted for (VAF) by the model:
| (1) |
where yi is the experimental response and ŷi is the predicted response to the ith stimulus of the RAP impulse train and ȳ is the mean experimental response across all stimuli. The VAF in a given experiment was calculated as the median of the VAF across the set of test stimuli. To compare the Volterra and phenomenological models, the VAF was then averaged across experiments (N=7). The model parameters displayed throughout the paper are the average across all test stimuli for a single experiment and then across all animals (N=7). A VAF of 100% would indicate that the model prediction exactly matches the timeseries of the cortical response. However, due to noise in the biological signal, the variance that the models could realistically be expected to explain was bounded below 100%. For instance, a single trial of the cortical response predicts ~85% of the variance in the mean cortical response, indicating a degree of stochasticity that a deterministic model could not be expected to account for. However, each of the models is affected identically, such that the variance accounted for measure can be used to compare the two models.
Volterra Model
The goal of this study was to identify the nonlinear system dynamics that govern the cortical response to patterns of electrical stimulation delivered to the thalamus. Traditionally, system identification has been performed using nonparametric black box methods, such as Volterra kernel estimation, which have a long history in neuroscience applications (for review see Marmarelis 2004; Wu et al. 2006). A Volterra series model describes the n-th order nonlinear dynamics of a system with input, s[n], and output, r[n], through a series of kernel functions, k0, k1, …, kn, according to the following equation:
| (2) |
where M is the memory of system, indicating how far in the past that previous inputs will still affect the output, and mi represent each time index of the VSDI signal (5ms), such that a memory of 100 timepoints corresponds to 500ms. A diagram of the Volterra series model is shown in figure 3(b). Here we used a second order Volterra series that, with a memory of 100 timepoints, contained 5150 parameters. Many of these parameters were not important descriptors of the system dynamics, but this information was not available a priori. In this study the second order Volterra system was estimated according to the methods of Wu and Sclabassi (1997). Briefly, a set of RAP-kernels were orthogonalized with respect to the RAP stimulus, such that they could be identified through cross-correlation techniques. These RAP kernels were then mapped into the true Volterra kernels of the system.
Extension to a third order Volterra system would require a prohibitively long data record due to the extremely large number of additional parameters it would require. There exist methods for parameterizing the Volterra kernels for more computationally and experimentally efficient estimation of higher order kernels. The most common approach in neuroscience applications uses Laguerre polynomials as basis functions for the kernels, providing support for high frequency content at short time lags and exponentially vanishing support at long time lags (Marmarelis 1993; Song et al. 2009). However, these approximations are only useful if the chosen basis set can adequately represent the structure of the true Volterra kernels, which likely is not known a priori. These methods did not perform better than the cross-correlation based approach for our data set (data not shown), leading to the development of the phenomenological model.
Phenomenological Model
The phenomenological model used many fewer parameters by including specific elements into the model that were derived from experimental observations. First, the temporal structure of the VSDI response to a single electrical stimulus was not affected by the strength of the stimulus or the amplitude of the response, as shown in figure 2(a). In this way, the experimental system in figure 3(a), with input s[n] and output r[n], can be modeled as a nonlinear mapping of the discrete input followed by a linear filter to convert the discrete inputs to the continuously varying VSDI output. This is depicted in the top portion of figure 3(c), where the input, s[n], undergoes a nonlinear mapping to the intermediate variable, s′[n], before passing through the linear filter to produce the output, r[n]. This simplification is common for systems classified as “same response shape” (SRS) systems, where only the amplitude of the response is affected by the discrete inputs and system dynamics (Krausz 1975; Sen et al. 1996; Stern et al. 2009).
The model for the discrete nonlinear mapping was also derived from experimental observations. The system exhibited two different sets of nonlinear dynamics, as illustrated by figure 2(c). For the high current intensity in the left portion of figure 2(c), the response to the second stimulus was suppressed relative to the response to the first, and this suppression relaxed for long inter-stimulus intervals. For the low current intensity in right portion of figure 2(c), the response to the second stimulus was strongly facilitated relative to the response to the first, but only for interstimulus intervals of 100–200 milliseconds.
These two sets of nonlinear dynamics were explicitly included into the structure of the phenomenological model as a cascade, shown in the middle portion of figure 3(c). This was done for two reasons. First, the separate dynamics outlined in figure 2(c) were each second order, indicating that the total order of nonlinearity in the system was at least third order. However, a serial cascade simplified the high order nonlinear system into two second order systems, each with a simpler description of the dynamics. Second, the cascade mirrors the multi-stage biology of the neural circuit between the thalamus and layer 2/3 of cortex.
The architecture of the nonlinear mapping within each cascade was identical and is shown diagrammatically in the bottom portion of figure 3(c) as a canonical unit. The canonical model separated the static and dynamic nonlinearity within each stage. The static nonlinearity was modeled as a sigmoidal function, F, with input argument, x, and parameters, θ, according to (3) below and in line with the experimental observations in figure 2(b):
| (3) |
where θ1, θ2, and θ3 are the amplitude, threshold, and sensitivity of the sigmoid, respectively. The output of the canonical unit, y[n], was equal to the output of the sigmoidal function, F(x; θ). The dynamic nonlinearity was modeled through a history term, h[n], that scaled the input of the canonical unit, u[n], before the static nonlinearity, according to (4) below:
| (4) |
In this way, the history term modified how the static nonlinearity acted on the input, such that when the history term was greater than one, the output was facilitated, and when the history term was less than one, the output was suppressed. The history term in the standard phenomenological model was generated using feedback according to (5):
| (5) |
where y[n−m] gives the previous outputs within the memory, M, of the canonical unit, and k[m] is a linear filter. The convolution between the previous output and the linear filter was zero when there were no previous outputs within the memory of the system. For this reason, a value of one was added to the convolution such that the history term was equal to one when there had been no previous inputs or outputs for the system and thus had no scaling effect on future inputs. In this way, a positive result from the convolution creates a history term greater than one, leading to facilitation, and a negative result from the convolution produces a history term less than one, leading to suppression.
The static and dynamic nonlinearity were separated to allow for a high order description of the static nonlinearity, while restricting the dynamic nonlinearity to second order. The output of the first canonical unit was the input to the second canonical unit. Finally, the output of the second canonical unit was passed through a linear filter to convert the delta functions into a continuously varying signal. The sigmoidal static nonlinearity functions had 3 parameters each, while the dynamical filters were parameterized through a basis set composed of the first five Laguerre polynomials (Marmarelis 1993). The final linear filter that produced the characteristic shape of a VSDI signal had a basis set composed of the first eight Laguerre polynomials. Thus, the phenomenological model contained 24 parameters in total.
The standard phenomenological model described above was compared with a feedforward implementation of the model. Whereas the phenomenological model with feedback used the previous responses to implement the dynamic nonlinearity, the feedforward model used the previous stimuli according to (6) below:
| (6) |
Otherwise, the two implementations of the phenomenological model were identical. The parameters were fit specifically for the feedforward model. A diagram of the canonical unit for the feedforward architecture is shown in figure 7(d).
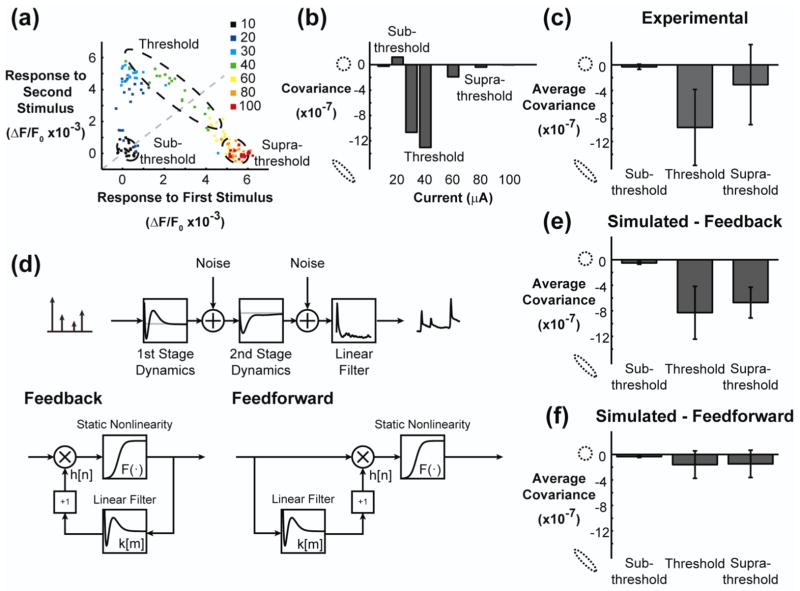
Figure 7. Phenomenological model with feedback reproduced single trial variability in facilitation and suppression.
(a) The response to the second stimulus (ISI = 150ms) is plotted against the response to the first stimulus for experimental data. The color of each point indicates the current intensity in units of microamperes. The unity line is shown in gray. (b) The trial by trial covariance in the response to the two stimuli was calculated for each stimulus intensity. At sub-threshold and supra-threshold currents, the covariance between the first and second response was low. At a threshold current, there was a strong negative covariance between the first and second response. (c) The negative covariance at the threshold current was consistent across animals. (d) The phenomenological model was used to simulate an identical experiment. The simulated data was created by injecting noise into the model at the output of the first and second stages during presentation of stimuli. A feedback model (same as in Figure 5, displayed in bottom-left of the panel) and a feedforward model (fit specifically for this analysis, displayed in the bottom-right of the panel) were used. Both models utilized a two-stage model architecture, where each stage consisted of a canonical unit. The canonical unit for the feedback (left) and feedforward (right) model are shown in this panel. (e) The feedback model reproduced the strong negative covariance at the threshold current and recovers for supra-threshold currents, and was not significantly different from the experimental data in (c) (p = 0.89, N=7, two-sided paired Student’s t-test). (f) The feedforward model did not reproduce the negative covariance for threshold currents, and the difference from the experimental data was statistically significant (p = 0.003, N=7, two-sided paired Student’s t-test).
2.5 Extension of the phenomenological model to include space
The phenomenological model was extended spatially in an effort to model the entire spatiotemporal cortical response measured using VSDI. In this way, the cortical response was described by the set of r(i)[n], where i indicates the ith cortical column. The objective was to minimize the mean squared error between the neural response, r(i)[n], and the predicted neural response, , with model parameters θ and across all i:
| (7) |
With 24 parameters required to fit a single instance of the phenomenological model, a total of 768 parameters would need to be estimated to fit the phenomenological model for each of the individual cortical column outputs. Instead, we employed a point spread function, A(x, y; ϕ), modeled as a two dimensional Gaussian function that mapped the output of the phenomenological model into an image. The Gaussian function was defined by the parameters ϕ, where ϕ1 and ϕ2 determine the center of mass of the Gaussian in the two dimensional image, ϕ3 and ϕ4 give the width of the Gaussian along the major and minor axis, respectively, and ϕ5 represents the angular orientation of the major and minor axes with respect to the x and y axes of the image, and given by the following equation:
| (8) |
where
| (9) |
| (10) |
| (11) |
The point spread function simplified the model in that the phenomenological model only needed to be fit for a single cortical column and then the point spread function determined the relative activation levels for all cortical columns. This reduced the number of required parameters to 29, with 24 corresponding to the phenomenological model of a single cortical column and 5 parameters for the point spread function. Ultimately, the parameters for the model were determined using the following augmentation of the objective function in (7):
| (12) |
where xi and yi are the coordinates for the center of the ith cortical column, and j indicates the principal cortical column. The above optimization was performed for parameters θ and ϕ both serially and simultaneously with identical results.
2.6 Model Simulations
The models were fit on input-output response data that have been averaged across trials and thus would only be expected to predict trial-averaged responses. However, to simulate single trial responses from the deterministic phenomenological model, Gaussian white noise was injected at the output of the first and second stages. The variance of the injected noise for the second stage was tuned to reproduce the variance of the background noise in the VSDI signal. The variance of the injected noise in the first stage was scaled according to the relative amplitudes of the static nonlinearity in the first and second stage, such that the noise inputs in the two stages were equally weighted. The simulations were performed with the standard feedback model presented in figures 3(c) and 4, and also the feedforward implementation of the model.
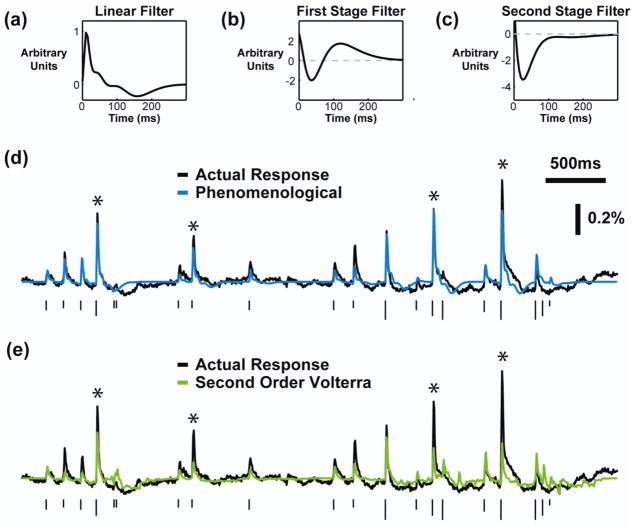
Figure 4. Phenomenological model based on experimental observations accurately predicted the cortical response to patterned microstimulation.
The average (a) linear kernel, (b) first stage feedback kernel, and (c) second stage feedback kernel of the phenomenological model fit on Poisson train stimuli and VSDI response data (N=7). In each case, the first stage kernel implemented the facilitation dynamics and the second stage implemented the suppression dynamics. (d) An example of the performance of the phenomenological model (blue), with the actual response shown in black. (e) An example of the second order Volterra model performance (green), with the actual response shown in black. In (d) and (e), the height of the ticks indicates the current intensity and the asterisks mark stimuli for which the Volterra model severely under-predicted the response. The phenomenological model performed better for these responses.
3. Results
In this study, we created a phenomenological nonlinear dynamical model of the cortical response to patterns of microstimulation in the thalamus. We compared this model to a non-parametric model fit with traditional system identification techniques and derived predictions about the circuit level activation caused by electrical microstimulation. Finally, we extended the phenomenological model to capture the spatial properties of the cortical response.
3.1 The cortical response to thalamic microstimulation is highly nonlinear
All experiments utilized in-vivo voltage sensitive dye imaging (VSDI) of layer 2/3 in the whisker representation of the primary somatosensory cortex with electrical microstimulation delivered to the topologically matched ventral postero-medial (VPm) portion of the thalamus in the anesthetized rodent, as depicted in figure 1(a). For a detailed account of the methods, see Wang, et al (2012). Briefly, post-experiment cytochrome oxidase staining revealed the anatomical structure of the cortical columns, with an example shown in figure 1(b). This anatomical map was registered to the VSDI recordings using functional measurements in response to the deflections of multiple whiskers individually, as in figure 1(c) (see methods). The spatiotemporal VSDI response to electrical stimulation is shown in figure 1(d), where the activation of cortex begins 5–10 milliseconds following thalamic microstimulation, and quickly grows in amplitude and spreads spatially. The electrical stimuli used in this study were symmetric, cathode-leading biphasic waveforms. Each stimulus is indicated by a “tick” throughout the figures, where the height of the “tick” indicates the current amplitude.
For the purposes of this study, we averaged the VSDI response spatially within the area outlined by the cortical column topologically matched to the position of the electrode in thalamus, as verified by electrophysiological recordings. By averaging within the cortical column, we obtained a high signal to noise ratio for single trials, as shown in figure 2(a) where the gray traces are the single trials and the mean across trials is given by the black trace. The response in cortex over time exhibited a consistent trajectory for a wide range of stimulus intensities and response amplitudes. This is illustrated by the example in figure 2(a) by normalizing the response to three different supra-threshold current intensities, such that the temporal profile of activation was qualitatively similar across the stimulus range. While the temporal response shape was consistent, suggesting a simple linear filter as a model, the response amplitude demonstrated a nonlinear relationship with stimulus intensity. Figure 2(b) shows an example of the nonlinear relationship, which was well approximated by a sigmoidal function. This observation, along with previous literature, suggests a nonlinear projection from the thalamus to cortex for thalamic microstimulation.
Pairs of electrical stimuli were then delivered to the thalamus with varying current intensity and varying inter-stimulus interval to sample the dynamics of the system. Figure 2(c) shows the response to pairs of stimuli with high (left) and low (right) current amplitudes. For the high current intensity in the left portion of figure 2(c), the response to the second stimulus was suppressed relative to the response to the first, and this suppression relaxed for long inter-stimulus intervals. For the low current intensity in right portion figure 2(c), the response to the second stimulus was strongly facilitated relative to the response to the first, but only for interstimulus intervals of 100–200 milliseconds. This observation alone points to dynamics higher than second order. For a second order system, the nonlinear contribution between two pairs of stimuli will have the same shape, with only the amplitude scaled by the stimulus intensity. Here two different sets of second order dynamics were observed: suppression for high current intensities and facilitation for low current intensities with an inter-stimulus interval between 100 and 200 milliseconds.
3.2 Development of a phenomenological model based on experimental observations
We devised a phenomenological model using the experimental observations described above. Two stages with identical architecture were used in series, with each stage being a modified version of models used previously to study synaptic physiology (Sen et al. 1996; Stern et al. 2009). The model is shown diagrammatically in figure 3(c) and the details are described in the methods section. Briefly, the model implemented a cascade approach with multiple elements in series. The initial portion of the model was a nonlinear mapping of the discrete stimulus, and the final portion of the model transforms the impulses from the stimulus into a continuous VSD signal. This separation was based on the observation that the VSDI temporal response exhibited a consistent shape for a wide range of current intensities and response amplitudes, as in figure 2(a). The nonlinear dynamical mapping contained two stages because of the two distinct sets of dynamics observed in the figure 2(c). Each stage consisted of a static nonlinearity, modeled as a sigmoid function as in figure 2(b), and a history term that scaled the input to the static nonlinearity (see Methods, section 2.4). The history term was created by feeding back the output from the static nonlinearity through a linear filter and adding one. In this way, the history term only scaled the input when previous stimuli had occurred within the memory of the system. The architecture was the same for the second stage of the model, with the output of the first stage being the input into the second.
Each stage was initialized with the same linear feedback filter and all of the parameters were fit simultaneously. In every case, although not constrained to do so, the first stage filter captured the time course of the facilitative dynamics and the second stage captured the time course of the suppressive dynamics. The average linear filter, first stage dynamical filter, and second stage dynamical filter are shown in figures 4(a), 4(b), and 4(c), respectively. The actual and predicted responses for an example train of stimuli are shown in figure 4(d), with the predicted response of the Volterra model presented in figure 4(e) for comparison purposes. The responses labeled with an asterisk illustrate typical examples of the primary improvement of the phenomenological model over the Volterra model. The Volterra model was not able to capture the facilitative dynamics causing significant under-predictions of the response, whereas these dynamics were explicitly built into the phenomenological model and resulted in fewer under-prediction errors. The variance accounted for by the phenomenological model was 58 ± 12% across animals, whereas the second order Volterra model accounted for 28 ± 18% of the variance in the cortical response. The improvement of the phenomenological model over the Volterra model was statistically significant (p = 0.002, N=7, two-sided paired Student’s t-test).
3.3 Error residuals illustrate the improved performance of the phenomenological model
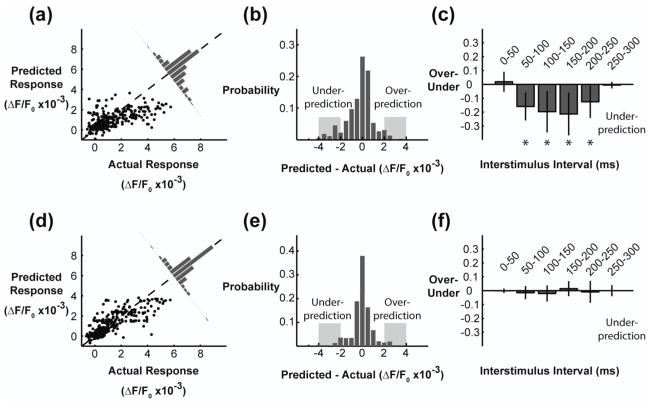
The mechanism for the increased performance of the phenomenological model is illustrated by examining the residuals. In the top portion of figure 5, the error residuals from the Volterra model are presented. In figure 5(a), the actual response was plotted against the predicted response for each stimulus within the Poisson train. At low values of the actual response, the Volterra model consistently over-predicted the response, whereas at high values of actual response, the model under-predicted the response. The probability distribution of the errors was calculated by subtracting the actual from the predicted, as in the figure 5(a) inset and figure 5(b). The distribution has a non-zero median and heavy tails, especially towards under-prediction. By examining the heavy tails we can determine if there was a bias towards the model incorrectly predicting certain features of the stimulus. In comparing the prevalence of over-prediction vs. under-prediction as a function of the interstimulus intervals in the stimulus, we found that the large errors made by the Volterra model were predominantly under-predictions for stimuli that occur within 50–200 milliseconds of a previous stimulus. These particular errors indicate a failure of the Volterra model to account for the facilitation dynamics presented in the right portion of figure 2(c). The skewness of the error distribution was also used to quantify the bias of under-prediction vs. over-prediction. The skewness of the error distribution was −0.77 ± 0.44, indicating a significantly heavy left tail for under-prediction (p = 0.003, N=7, two-sided Student’s t-test).
Figure 5. Phenomenological model improved error residuals compared to the Volterra model.
(a) Error residuals for the second order Volterra model fit via cross-correlation. Each data point is the response to a single stimulus in the RAP stimulus train. (b) The residual distribution had a heavy tail towards under-prediction. (c) The responses were systematically under-predicted for stimuli separated in time by 50–250 milliseconds. (d) Error residuals for the phenomenological model. (e) The residual distribution shows few large errors (indicated by the gray regions) and no bias towards under-prediction or over-prediction. (f) The responses were not systematically under-predicted or over-predicted for any interstimulus intervals.
The error residuals for the phenomenological model are presented in the lower panels of figure 5. In figure 5(d), the residuals were closer to the unity line, but still exhibited trends of over-prediction for weak responses and under-prediction for strong responses. However, the collapsed error distribution showed no systematic bias in the residuals towards over-prediction or under-prediction (figure 5(e)) and fewer large errors overall due to the increased variance accounted for by the model. Furthermore, there was no systematic bias in the residuals as a function of interstimulus interval. The skewness of the error distribution was −0.02 ± 0.79, indicating a symmetric distribution, and was not statistically significant from a lack of skewness (p = 0.94, N=7, two-sided Student’s t-test). Furthermore, the lack of skewness was statistically different from the skewness for the Volterra model (p = 0.05, N=7, two-sided paired Student’s t-test). By including experimental observations explicitly in the phenomenological model, the predictive capabilities were significantly increased while using many fewer parameters. For the remainder of the study, only the phenomenological model was considered.
3.4 Linear point spread function captures spatial spread in cortex
The phenomenological model was extended to capture the spatial properties of the cortical response to patterns of thalamic microstimulation. In the previous sections, the VSDI signal was discretized according to the anatomical map of the cortical columns, and only the signal from the principal cortical column was used to fit the phenomenological model. The phenomenological model performed equally well for the principal cortical column and adjacent cortical columns. However, fitting an instance of the model for each cortical column would require a large number of parameters, while ignoring the correlation structure of the spatial cortical response. As a first order approximation, we appended a point spread function, A(x, y; ϕ), to the output of the phenomenological model, as in figure 6(a), mapping a scaled version of the timeseries response from the principal cortical column to the entire set of cortical columns within the barrel cortex. The details of the point spread function (PSF) are described in the methods. Briefly, the PSF was modeled as a two dimensional Gaussian function, with parameters ϕ describing the center of mass, spread along the major and minor axis, and orientation with respect to the coordinate axis of the VSDI images. The resulting PSF was identical whether fit simultaneously with, or immediately following, the identification of the phenomenological model.
Figure 6. Extension of phenomenological model captures spatial spread.
(a) A linear point spread function, modeled as a two dimensional Gaussian, was used to extend the model spatially across all cortical columns. (b) The spatial extension to the model captured the dynamics for the principal cortical column as well as distant cortical columns. (c) A representative cortical response (top left) and the point spread function (bottom left) were similar. In the scatter plot, the point spread function (red) captures the relative response properties of the principal cortical column and adjacent cortical column for neighboring (black) and distant (gray) cortical columns. Each data point indicates the response to a single impulse within the RAP impulse train. Scale bars in (b) and (c) are 500 micrometers.
Figure 6(b) presents an example of the actual and predicted cortical response to a train of electrical stimuli for the principal cortical column (top, blue) and a distant cortical column (bottom, red). The PSF function accurately maps the output of the phenomenological model to each of the cortical columns. The total variance in the response accounted for by the spatial model, across all cortical columns, was 45 ± 8% (N=7). The PSF linearly maps the output of the phenomenological model to the various cortical columns. To assess the validity of this assumption, we analyzed the relative response of the primary and adjacent cortical column for neighboring cortical columns (AW, black data points) and a distant cortical column (DW, gray data points) in figure 6(c). The relative locations of the cortical columns are shown in the left portion of figure 6(c), with the actual cortical response at the top and the PSF at the bottom. The white contour indicates the primary cortical column, the black contours demarcate the eight nearest neighbor cortical columns, and the gray contour represents the distant cortical column. Each point on the scatterplot in the right portion of figure 6(c) came from the peak cortical response to each stimulus in the RAP impulse train used to the fit the model, while the red lines represent the relative response amplitudes defined by the PSF. For the entire range of cortical responses, and for adjacent cortical columns near and far, the linear approximation of the relative response magnitudes in the primary and adjacent cortical columns effectively captured the experimentally observed relationship for trial averaged responses.
3.5 Trial to trial variability and feedback
While the model described above was highly predictive, it is also purely deterministic, such that it will always predict the same response for the same stimulus. In this way, it cannot strictly reproduce the trial to trial variability in the cortical response. Here we explore the ability of the model to account for single trial response properties when noise is added to the system through simulation. While the model was only designed to accurately predict the mean cortical response to a pattern of electrical stimuli, we will show that small changes in the input can lead to large changes in the output experimentally and that the architecture of the model is ideally suited to capture these dynamics on a trial by trial basis.
Two sets of nonlinear dynamics were observed in the trial averaged responses in figure 2(c), leading to the explicit inclusion of two stages in the model. Although the dynamics tended to be either suppressive or facilitative, there existed a range of currents for which the occurrence of facilitation or suppression varied on a trial by trial basis. Figure 7(a) plots the single trial responses to an initial stimulus against the responses to a second stimulus delivered 150 milliseconds later, with the different colors indicating varying current intensity and the unity line in gray. There are three clear clusters within this plot. At very low current intensities, no response to either stimulus was observed. For intermediate currents, the response to the second stimulus was facilitated relative to the first, creating a cluster in the upper left portion of the axes. At very high current intensities, the response to the second stimulus was suppressed relative to the first, creating a cluster in the lower right portion of the axes. Interestingly, for a select range of current intensities, the occurrence of facilitation and suppression varied on a trial by trial basis. The 60 microampere current intensity in this example spanned the regime connecting the facilitation cluster (upper left) to the suppression cluster (lower right). Plotting the single trial data in this way creates a characteristic pattern, extending vertically from the origin to the facilitation cluster and then traversing across the unity line to the suppression cluster. This characteristic pattern was consistent across animals. Of the ten paired pulse experiments, one data set showed weak facilitation and one showed no facilitation at all, while the remaining eight showed consistent and robust facilitation. For two of the ten paired stimulus experiments there was a systematic shift from suppressive responses to facilitative responses for the threshold current as the experiment went on; however, this trend was not observed in the other data sets. It should be noted that in these examples, sub-threshold and supra-threshold currents consistently produced facilitative and suppressive responses, respectively, throughout the duration of the experiment. This suggests that the threshold current amplitude is likely a function of the underlying brain state, which was not measured systematically in this study (see discussion).
Examining the trial to trial variability of facilitation and suppression, it is clear that the covariance of the response to the first stimulus and the second stimulus changes dramatically depending on the location within the axes. For very small currents, the individual trials cluster around the origin and have little covariance, creating a circular cloud of points. This is also the case for the facilitative cluster in the top left (30 microampere) and the suppressive cluster in the bottom right (80 microampere). However, for the 40 microampere stimulus, exhibiting roughly half facilitation and half suppression, there is a strong negative correlation between the response to the first stimulus and the response to the second stimulus. Figure 7(b) plots the covariance, σ1,2, between the first and second response as a function of current. For sub-threshold and supra-threshold stimulus intensities, σ1,2 was small. For the threshold current, the responses to the first and second stimulus strongly co-varied, such that knowledge of the response to the first stimulus was a strong predictor of the magnitude of the response to the second stimulus. This phenomenon was consistent across animals, with the average data presented in figure 7(c).
The high variability, , of the response to a threshold stimulus and the strong covariance, σ1,2, of the response to a subsequent stimulus indicate the presence of a feedback element within the neural circuit. The phenomenological model presented in this study contains feedback elements to implement the dynamic nonlinearity of the response. Given this, we sought to determine if the phenomenological model, which was built entirely on averaged data, could reproduce single trial response properties. By injecting noise at the output of each stage in the model, the relationship in Figure 7(a) was simulated and the covariance as a function of current was extracted. The average sub-threshold, threshold, and supra-threshold σ1,2 are presented in figure 7(e), demonstrating that the phenomenological model can reproduce the strong negative covariance observed experimentally for the responses to two threshold stimuli. However, when the phenomenological model was re-fit using a feedforward architecture (illustrated in the bottom-right portion of figure 7(d) and described in the methods), the negative covariance at the threshold current intensity was not observed (figure 7(f)). The feedforward model was implemented in a two-stage architecture in the same way as the feedback model described in the previous sections. Only the structure of the canonical units was different, with the feedforward model using the previous inputs to the system to model the dynamics, as opposed to the feedback model that uses previous outputs to model the dynamics.
These simulations indicate that the feedback architecture within the model is important for producing the experimentally observed trial-by-trial variability. However, the result could also be due to the specific parameters fit in the feedback and feedforward cases. As a control, the dynamical filters and static nonlinearities from the feedforward model were implemented in the feedback architecture and the strong covariance, σ1,2, was still not reproduced (data not shown). Vice versa, when the parameters from the feedback model were implemented in the feedforward architecture, half of the covariance was recovered as compared to the feedback model. This indicates that feedback is necessary, but not sufficient, for creating the covariance observed experimentally, pointing towards a role for either the static nonlinearities or the dynamical filters.
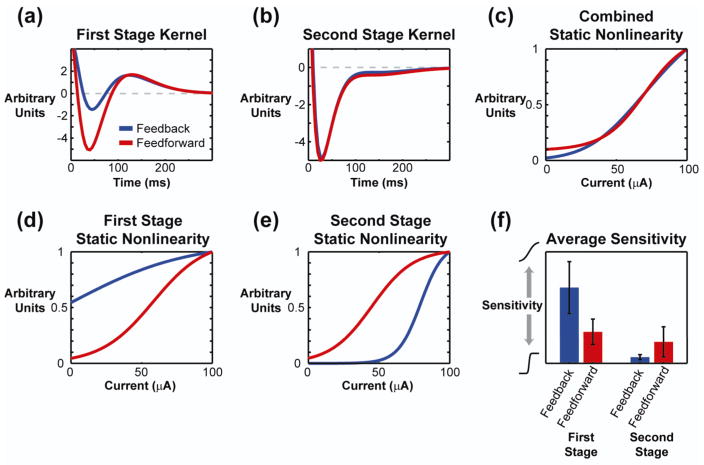
3.6 Activity propagation through electrical microstimulation
The dynamical filters did not vary significantly across the feedforward and feedback models in the first or second stage, as shown in figure 8(a) and 8(b), respectively, nor did the overall static nonlinearity differ in figure 8(c). But, while the overall static nonlinearities were similar, the individual static nonlinearities within each of the two stages were dramatically different. For the first stage, shown in figure 8(d), the feedback model was very insensitive to the current of the input, modeled as a sigmoid function elongated along the horizontal, whereas the feedforward model was moderately sensitive. In the second stage, depicted in figure 8(e), the feedback model was highly sensitive to current intensity, modeled as a sigmoid function compressed along the horizontal, whereas the feedforward model was again moderately sensitive. These model parameters were consistent across animals, as shown in figure 8(f).
Figure 8. Model parameters predict linear local response properties, but nonlinear propagation of activity.
(a) The average first stage kernel from the phenomenological model fit with feedback (red) and feedforward (blue) dynamics. (b) The average second stage kernel. (c) An example of the full static nonlinearity created by combining both stages. (d) and (e) The static nonlinearity at the first and second stages, respectively, for the feedback and feedforward models. (f) The average sensitivity across animals (N=7) is distinctly different for the feedback and feedforward models. The feedback model was weakly sensitive in the first stage and highly sensitive in the second stage. The feedforward model was moderately sensitive in both stages.
Due to the high sensitivity of the second stage in the feedback model, small perturbations from the noise caused large changes in the output of the model near the threshold current leading to a high response variability, . Meanwhile, the highly variable response was fed back into the model and augmented the response to subsequent stimuli resulting in a high σ1,2 value. The moderately sensitive stages of the feedforward model were more robust to noise and thus did not exhibit high at the threshold current, and without feedback the model could not account for σ1,2. In summary, the relative sensitivity in the static nonlinearity of each stage dramatically alters the propagation of activation through a cascade system with feedback. Meanwhile, the similarity of the phenomenological model architecture and the anatomy and physiology of the thalamocortical circuit maps the results of this section to general predictions about information propagation in neural circuits (see discussion).
4. Discussion
Here we have demonstrated a phenomenological model capable of predicting the response of the thalamocortical circuit to temporal patterns of thalamic stimulation in-vivo. By explicitly including nonlinear elements modeled after experimental observations, such as the combination of facilitative and suppressive dynamics, into the model architecture, we significantly increased performance with respect to the Volterra series model architecture while using many fewer parameters. Additionally, although the model was fit using trial-averaged data, it was able to reproduce single trial response properties observed experimentally, lending credence to the physiological significance of the model architecture. Finally, from these single trial simulations, we predict that electrical microstimulation activates neurons in its local environment through linear recruitment, but that this activity propagates to downstream structures in a highly nonlinear manner.
The models in this study were fit using input-output data from the thalamocortical circuit. The input was a train of symmetric biphasic electrical stimuli, Poisson-distributed in time and uniformly varying in amplitude, while the output was the spatially averaged cortical response as measured by voltage sensitive dye imaging. Due to the light scattering of the tissue, voltage sensitive dye imaging principally measures the activity in the superficial layers of cortex (Grinvald et al. 1994). The change in fluorescence of the voltage sensitive dye increases linearly as a function of membrane potential, but the imaging of the signal is too slow to resolve individual action potentials, restricting the interpretation of the signal to sub-threshold activation (Grinvald and Hildesheim 2004). Even though the absolute amplitude of the VSDI response in layer 2/3, and the related probability of action potential generation, is known to be strongly modulated by brain state (Petersen and Crochet 2013), the spatial distribution of sub-threshold activation in layer 2/3 during the onset of activation is likely highly correlated with the supra-threshold activity in layer 4 of cortex (Petersen et al. 2003). All details considered, VSDI provides a high spatial and temporal measure of the cortical response.
Both models were fit using the same input-output data, but the philosophy and architecture of each was very different. The Volterra model is an example of a black box model, which requires little previous information about the system due to its flexibility, making it an ideal starting point for system modeling. The incredible flexibility of a black box model, however, requires a large number of parameters, and it is difficult to determine which will be important a priori. Also, in order to fit a large numbers of parameters, a large amount of data is needed. For these reasons, we explicitly included certain elements into the phenomenological model, increasing the order of nonlinearity in the model to a degree greater than could be estimated with a Volterra series given the data and time limitations. By effectively fitting the model with small amounts of data, we open the possibility of pseudo real time model construction and experimentation and potentially avoid the slow timescale non-stationarities that may exist in an in-vivo anesthetized biological preparation.
The structure of the phenomenological model invites physiological interpretations due to its unique structure. The observation of two distinct second order dynamics motivated the two-stage architecture. Two sets of second order dynamics in series would imply that a fourth order Volterra series may have captured the dynamics of the system. However, the intentional separation of the dynamics into two stages allowed the dynamics to be described in a simpler form. From this, we would hypothesize that the distinct dynamics are carried out by different elements of the neural circuit, and further that these elements may be acting in series. The model parameters consistently show the facilitation dynamics occurring in the first stage, while the second stage employs the suppression dynamics. As the two-stage model mirrors the disynaptic pathway from the thalamus to layer 2/3 of cortex, the model would predict that the facilitation dynamics occur upstream of the suppression dynamics within the neural circuitry. The suppression dynamics can likely be accounted for by recurrent inhibition within the cortex (Kara et al. 2002), and the long timescale of inhibition implicates the involvement of GABA-B receptors (Butovas et al. 2006). With facilitation occurring before suppression in the model, we speculate that the facilitation is sub-cortical in origin. This is in agreement with literature describing the facilitation of successive stimuli termed the thalamocortical augmenting response, which acts through thalamic and cortical structures (Dempsey and Morison 1943; Castro-Alamancos and Connors 1996; Bazhenov et al. 1998). The timescale of facilitation is also consistent with the timescale of calcium T-channel mediated bursts in the thalamus (Lu et al. 1992).
A separate static nonlinearity was included within each stage of the model as well and might be interpreted as the transformation across synapses within the thalamocortical circuit. In this way, the static nonlinearity of the first stage would represent the transformation of electrical current into the number of activated thalamic cells. Similarly, the static nonlinearity of the second stage would represent the transformation of the number of activated thalamic cells to the number of activated cortical cells. While feedback within the model was found to contribute to the single trial response properties, it was the relative sensitivities of the first and second stage static nonlinearities that were most important. Specifically, the first stage was found to be linear with respect to current intensity and exhibit a shallow slope, such that small amounts of noise produced small fluctuations in the output of the first stage. This leads to the prediction that the number of neurons activated in the immediate environment around the electrode are recruited in a nearly linear relationship with the stimulus intensity, and that this recruitment is robust to random fluctuations in membrane potential of the neurons. This interpretation is supported biophysically in that the radius of activation from the electrode tip increases as the square root of the current intensity, while the number of neurons within that sphere increases with the cube of the radius, leading to a weakly nonlinear relationship between the number of neurons activated and the current intensity (Tehovnik et al. 2006). Further, when stimulating a fiber bundle, the relationship between current intensity and the number of axons activated becomes linear (Yeomans 1990). Recent work is also in agreement, as Histed et al, report a linear increase in the number of cells activated by increasing microstimulation intensity as measured by calcium imaging of the cortical population (2009).
Meanwhile, the output of the second stage, or number of cortical cells activated, was found to be quite sensitive to the output of the first stage, which is interpreted as the number of activated thalamic cells. We hypothesize that the cortical activation is highly sensitive to the number of activated thalamic cells due to the high convergence and divergence of the thalamocortical circuit (Sherman and Guillery 1996) and the extreme synchrony with which electrical stimulation recruits the thalamic neurons (Wagenaar et al. 2005; Sekirnjak et al. 2008). This is supported by previous work demonstrating that synchronous activation of thalamic neurons drives downstream neural activation in a highly nonlinear manner (Alonso et al. 1996). The nonlinearity discussed above refers to the static nonlinear relationship between the neural response and the stimulus intensity; however, we believe this phenomenon extends to the dynamic nonlinearity. The extreme synchrony of the activation caused by electrical stimulation may explain how electrical stimulation and natural sensory stimulation could recruit distinct nonlinear responses (Masse and Cook 2010).
This hypothesis applies directly to the implementation of sensory prostheses, the goal of which is to transduce signals from the sensory environment into patterns of stimulation that create surrogate sensory signals in the peripheral or central nervous system. Ideally a sensory neuroprosthesis would generate neural responses similar to those created by natural stimuli; however, this may prove problematic if electrical microstimulation engages circuits in a fundamentally different manner as compared to natural stimuli. Given this, some degree of plasticity, ranging from interpreting unnatural patterns of electrical stimulation (Fitzsimmons et al. 2007) to grasping new coordinate transformations with cross-modal sensory substitution (Bach-y-Rita et al. 1969; Barros et al. 2010), will be required for the successful implementation of a sensory prosthesis. At a minimum, a sensory prosthesis must be capable of producing perceptually distinct neural activations that the patient could learn to interpret functionally. This motivates the mapping of electrical stimuli to downstream neural responses, such that patterns of stimuli can be designed, in real time, with the high spatial resolution and fast timescales that will be needed in the limit of faithfully representing the sensory experience (Gilja et al. 2011). While implementation of this system identification approach may be possible in a human patient, the immediate impact lies in quantitatively describing the neural response generated by patterns of electrical stimulation within sensory pathways of the central nervous system. The development of the cochlear implant followed a similar trajectory, with many early animal studies characterizing the encoding of electrical stimuli into neural activity (Merzenich et al. 1973; Hartmann et al. 1984) to aid in the development of encoding algorithms for early cochlear implants. This work forms an initial step in replicating the cochlear implant development trajectory in the central nervous system.
In addition to the system identification approaches described here, future inclusion of both recording and stimulating electrodes in prosthetic applications will enable control-theoretic approaches to optimize and control the neural activation, and resulting percept, induced by surrogate sensory signals (Liu et al. 2011; Daly et al. 2012). In order to operate in real-time, the model must contain a description of the stochasticity of the system. While the model presented in this study reproduces single trial response properties, it lacks the ability to predict single trial responses. A feedback signal, such as the electroencephalogram or local field potential, would be needed to determine the instantaneous state of the circuit for improving single-trial predictions (Brugger et al. 2011), in so far as the stochasticity in the single trial responses derive from an underlying state variable (Petersen et al. 2003). Additionally, the underlying uncertainty could be built directly into the model parameters in the context of a robust control framework. Importantly, the pathological circuit may function differently from normal (Davis et al. 1998), further emphasizing the importance of closed loop stimulation and recording paradigms.
Precise delivery of information to the brain requires control of the spatial and temporal properties of neural activation. In this study, we modeled the spatial cortical response through a linear point spread function. This simple, linear spatial model performed nearly as well for the entire barrel cortex as the non-spatial phenomenological model did for a single cortical column, indicating the point spread function is a good approximation of the spatial cortical response. This conclusion is consistent with previous studies that coined the term “cortical point spread function”, referring to the region of cortical space activated by a point source stimulus (Grinvald et al. 1994; Das and Gilbert 1995). The point spread function was effective and efficient in our modeling study, yet a significant portion of the variance in the spatial signal remained unexplained. Future work is needed to determine if the spatial and temporal response properties in cortex are separable or co-dependent in order to control the cortical response with high spatial and temporal resolution. There exists some evidence from the literature the patterned stimuli can dynamically shape the spatial properties of the cortical response. Brumberg et al demonstrate a spatial sharpening of the cortical response in the barrel cortex to a single whisker deflection when a noise stimulus is applied to the adjacent whiskers (Brumberg et al. 1996). More generally, adapting stimuli are thought to dynamically shape the cortical response, and have been shown to increase spatial acuity in a two-point discrimination task in humans (Tannan et al. 2006). While space-time separability allows for simpler modeling of the cortical response, co-dependence, if fully understood, could enable complex shaping of the spatiotemporal cortical response and consequent perception.
In this study, through the use of system identification techniques, we have developed a highly predictive phenomenological model of the cortical response to patterns of thalamic microstimulation. Simulations suggest that electrical stimulation may recruit neighboring neurons in a linear manner, but that the resulting activity projects to downstream structures through a highly nonlinear relationship. Future work will extend to a spatiotemporal model of the cortical response and the application of the model as a stimulus design tool for controlling the cortical response. More generally, this framework describes the nonlinear mapping from electrical stimulation to neural response in order to transform environmental cues into surrogate sensory signals at high spatial resolution and fast timescales for the advancement of central nervous system sensory prostheses.
Acknowledgments
This work was supported by the National Institutes of Health (NIH Grant R01NS48285) and D.C.M. and C.A.G. were each supported by National Science Foundation Graduate Research Fellowships.
Contributor Information
Daniel C Millard, Email: dmillard6@mail.gatech.edu.
Garrett B Stanley, Email: garrett.stanley@bme.gatech.edu.
References
- Alonso JM, Usrey WM, Reid RC. Precisely correlated firing in cells of the lateral geniculate nucleus. Nature. 1996;383(6603):815–819. doi: 10.1038/383815a0. [DOI] [PubMed] [Google Scholar]
- Bach-y-Rita P, Collins CC, Saunders FA, White B, Scadden L. Vision substitution by tactile image projection. Nature. 1969;221(5184):963–964. doi: 10.1038/221963a0. [DOI] [PubMed] [Google Scholar]
- Barros CG, Bittar RS, Danilov Y. Effects of electrotactile vestibular substitution on rehabilitation of patients with bilateral vestibular loss. Neurosci Lett. 2010;476(3):123–126. doi: 10.1016/j.neulet.2010.04.012. [DOI] [PubMed] [Google Scholar]
- Bazhenov M, Timofeev I, Steriade M, Sejnowski TJ. Computational Models of Thalamocortical Augmenting Responses. The Journal of Neuroscience. 1998;18(16):6444–6465. doi: 10.1523/JNEUROSCI.18-16-06444.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brugger D, Butovas S, Bogdan M, Schwarz C. Real-Time Adaptive Microstimulation Increases Reliability of Electrically Evoked Cortical Potentials. Biomedical Engineering, IEEE Transactions on. 2011;58(5):1483–1491. doi: 10.1109/TBME.2011.2107512. [DOI] [PubMed] [Google Scholar]
- Brumberg JC, Pinto DJ, Simons DJ. Spatial gradients and inhibitory summation in the rat whisker barrel system. Journal of Neurophysiology. 1996;76(1):130–140. doi: 10.1152/jn.1996.76.1.130. [DOI] [PubMed] [Google Scholar]
- Butovas S, Hormuzdi SG, Monyer H, Schwarz C. Effects of electrically coupled inhibitory networks on local neuronal responses to intracortical microstimulation. Journal of Neurophysiology. 2006;96(3):1227–1236. doi: 10.1152/jn.01170.2005. [DOI] [PubMed] [Google Scholar]
- Butovas S, Schwarz C. Spatiotemporal effects of microstimulation in rat neocortex: A parametric study using multielectrode recordings. Journal of Neurophysiology. 2003;90(5):3024–3039. doi: 10.1152/jn.00245.2003. [DOI] [PubMed] [Google Scholar]
- Castro-Alamancos MA, Connors BW. Short-term plasticity of a thalamocortical pathway dynamically modulated by behavioral state. Science. 1996;272(5259):274. doi: 10.1126/science.272.5259.274. [DOI] [PubMed] [Google Scholar]
- Civillico E, Contreras D. Comparison of responses to electrical stimulation and whisker deflection using two different voltage-sensitive dyes in mouse barrel cortex in vivo. Journal of Membrane Biology. 2005;208(2):171–182. doi: 10.1007/s00232-005-0828-6. [DOI] [PubMed] [Google Scholar]
- Daly J, Liu J, Aghagolzadeh M, Oweiss K. Optimal space-time precoding of artificial sensory feedback through mutichannel microstimulation in bi-directional brain-machine interfaces. J Neural Eng. 2012;9(6):065004. doi: 10.1088/1741-2560/9/6/065004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das A, Gilbert CD. Long-range horizontal connections and their role in cortical reorganization revealed by optical recording of cat primary visual cortex. Nature. 1995;375(6534):780–784. doi: 10.1038/375780a0. [DOI] [PubMed] [Google Scholar]
- Davis KD, Kiss ZH, Luo L, Tasker RR, Lozano AM, Dostrovsky JO. Phantom sensations generated by thalamic microstimulation. Nature. 1998;391(6665):385–387. doi: 10.1038/34905. [DOI] [PubMed] [Google Scholar]
- Dempsey EW, Morison RS. The Electrical Activity of a Thalamocortical Relay System. American Journal of Physiology -- Legacy Content. 1943;138(2):283–296. [Google Scholar]
- Diamond ME, von Heimendahl M, Knutsen PM, Kleinfeld D, Ahissar E. ‘Where’ and ‘what’ in the whisker sensorimotor system. Nature Reviews Neuroscience. 2008;9(8):601–612. doi: 10.1038/nrn2411. [DOI] [PubMed] [Google Scholar]
- Fitzsimmons NA, Drake W, Hanson TL, Lebedev MA, Nicolelis MAL. Primate Reaching Cued by Multichannel Spatiotemporal Cortical Microstimulation. Journal of Neuroscience. 2007;27(21):5593–5602. doi: 10.1523/JNEUROSCI.5297-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fritsch Gustav, Hitzig E. Uber die elektrische Erregbarkeit des Grosshims. Arch Anat Physiol wiss Med. 1870;37:300–332. [Google Scholar]
- Gilja V, Chestek CA, Diester I, Henderson JM, Deisseroth K, Shenoy KV. Challenges and opportunities for next-generation intracortically based neural prostheses. Biomedical Engineering, IEEE Transactions on. 2011;58(7):1891–1899. doi: 10.1109/TBME.2011.2107553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grinvald A, Hildesheim R. VSDI: a new era in functional imaging of cortical dynamics. Nat Rev Neurosci. 2004;5(11):874–885. doi: 10.1038/nrn1536. [DOI] [PubMed] [Google Scholar]
- Grinvald A, Lieke E, Frostig R, Hildesheim R. Cortical point-spread function and long-range lateral interactions revealed by real-time optical imaging of macaque monkey primary visual cortex. The Journal of Neuroscience. 1994;14(5):2545–2568. doi: 10.1523/JNEUROSCI.14-05-02545.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartmann R, Topp G, Klinke R. Discharge patterns of cat primary auditory fibers with electrical stimulation of the cochlea. Hear Res. 1984;13(1):47–62. doi: 10.1016/0378-5955(84)90094-7. [DOI] [PubMed] [Google Scholar]
- Histed MH, Bonin V, Reid RC. Direct Activation of Sparse, Distributed Populations of Cortical Neurons by Electrical Microstimulation. Neuron. 2009;63(4):508–522. doi: 10.1016/j.neuron.2009.07.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humayun MS, Weiland JD, Fujii GY, Greenberg R, Williamson R, Little J, Mech B, Cimmarusti V, Van Boemel G, Dagnelie G, de Juan E. Visual perception in a blind subject with a chronic microelectronic retinal prosthesis. Vision Res. 2003;43(24):2573–2581. doi: 10.1016/s0042-6989(03)00457-7. [DOI] [PubMed] [Google Scholar]
- Hunter IW, Korenberg MJ. The identification of nonlinear biological systems: Wiener and Hammerstein cascade models. Biological Cybernetics. 1986;55(2):135–144. doi: 10.1007/BF00341929. [DOI] [PubMed] [Google Scholar]
- Jankowska E, Roberts WJ. An electrophysiological demonstration of the axonal projections of single spinal interneurones in the cat. J Physiol. 1972;222(3):597–622. doi: 10.1113/jphysiol.1972.sp009817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kara P, Pezaris JS, Yurgenson S, Reid RC. The spatial receptive field of thalamic inputs to single cortical simple cells revealed by the interaction of visual and electrical stimulation. Proc Natl Acad Sci U S A. 2002;99(25):16261–16266. doi: 10.1073/pnas.242625499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kearns M, Ron D. Algorithmic stability and sanity-check bounds for leave-one-out cross-validation. Neural Computation. 1999;11(6):1427–1453. doi: 10.1162/089976699300016304. [DOI] [PubMed] [Google Scholar]
- Krausz HI. Identification of nonlinear systems using random impulse train inputs. Biological Cybernetics. 1975;19(4):217–230. [Google Scholar]
- Lippert MT, Takagaki K, Xu W, Huang X, Wu JY. Methods for Voltage-Sensitive Dye Imaging of Rat Cortical Activity With High Signal-to-Noise Ratio. Journal of Neurophysiology. 2007;98(1):502–512. doi: 10.1152/jn.01169.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, Khalil HK, Oweiss KG. Neural feedback for instantaneous spatiotemporal modulation of afferent pathways in bi-directional brain-machine interfaces. IEEE Trans Neural Syst Rehabil Eng. 2011;19(5):521–533. doi: 10.1109/TNSRE.2011.2162003. [DOI] [PubMed] [Google Scholar]
- Logothetis NK, Augath M, Murayama Y, Rauch A, Sultan F, Goense J, Oeltermann A, Merkle H. The effects of electrical microstimulation on cortical signal propagation. Nat Neurosci. 2010;13(10):1283–1291. doi: 10.1038/nn.2631. [DOI] [PubMed] [Google Scholar]
- Lu SM, Guido W, Sherman SM. Effects of membrane voltage on receptive field properties of lateral geniculate neurons in the cat: contributions of the low-threshold Ca2+ conductance. Journal of Neurophysiology. 1992;68(6):2185–2198. doi: 10.1152/jn.1992.68.6.2185. [DOI] [PubMed] [Google Scholar]
- Marmarelis PZ, Marmarelis VZ. Analysis of physiological systems : the white-noise approach. New York: Plenum Press; 1978. [Google Scholar]
- Marmarelis V. Nonlinear dynamic modeling of physiological systems. Wiley-IEEE Press; 2004. [Google Scholar]
- Marmarelis VZ. Identification of nonlinear biological systems using Laguerre expansions of kernels. Ann Biomed Eng. 1993;21(6):573–589. doi: 10.1007/BF02368639. [DOI] [PubMed] [Google Scholar]
- Masse NY, Cook EP. Behavioral Time Course of Microstimulation in Cortical Area MT. Journal of Neurophysiology. 2010;103(1):334–345. doi: 10.1152/jn.91022.2008. [DOI] [PubMed] [Google Scholar]
- Merzenich MM, Michelson RP, Pettit CR, Schindler RA, Reid M. Neural encoding of sound sensation evoked by electrical stimulation of the acoustic nerve. Ann Otol Rhinol Laryngol. 1973;82(4):486–503. doi: 10.1177/000348947308200407. [DOI] [PubMed] [Google Scholar]
- Morrison A, Diesmann M, Gerstner W. Phenomenological models of synaptic plasticity based on spike timing. Biological Cybernetics. 2008;98(6):459–478. doi: 10.1007/s00422-008-0233-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Doherty JE, Lebedev MA, Hanson TL, Fitzsimmons NA, Nicolelis MAL. A brain-machine interface instructed by direct intracortical microstimulation. Front Integr Neurosci. 2009;3:20. doi: 10.3389/neuro.07.020.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Doherty JE, Lebedev MA, Li Z, Nicolelis MA. Virtual active touch using randomly patterned intracortical microstimulation. IEEE Trans Neural Syst Rehabil Eng. 2012;20(1):85–93. doi: 10.1109/TNSRE.2011.2166807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paxinos G, Watson C. The rat brain in stereotaxic coordinates. Academic Pr; 2007. [DOI] [PubMed] [Google Scholar]
- Petersen CC, Crochet S. Synaptic computation and sensory processing in neocortical layer 2/3. Neuron. 2013;78(1):28–48. doi: 10.1016/j.neuron.2013.03.020. [DOI] [PubMed] [Google Scholar]
- Petersen CCH, Grinvald A, Sakmann B. Spatiotemporal Dynamics of Sensory Responses in Layer 2/3 of Rat Barrel Cortex Measured In Vivo by Voltage-Sensitive Dye Imaging Combined with Whole-Cell Voltage Recordings and Neuron Reconstructions. Journal of Neuroscience. 2003;23(4):1298–1309. doi: 10.1523/JNEUROSCI.23-04-01298.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petersen CCH, Hahn TTG, Mehta M, Grinvald A, Sakmann B. Interaction of sensory responses with spontaneous depolarization in layer 2/3 barrel cortex. Proceedings of the National Academy of Sciences. 2003;100(23):13638–13643. doi: 10.1073/pnas.2235811100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pezaris JS, Reid RC. Demonstration of artificial visual percepts generated through thalamic microstimulation. Proceedings of the National Academy of Sciences. 2007;104(18):7670–7675. doi: 10.1073/pnas.0608563104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranck JB. Which elements are excited in electrical stimulation of mammalian central nervous system: a review. Brain Research. 1975;98(3):417–440. doi: 10.1016/0006-8993(75)90364-9. [DOI] [PubMed] [Google Scholar]
- Romo R, Hernandez A, Zainos A, Salinas E. Somatosensory discrimination based on cortical microstimulation. Nature. 1998;392(6674):387–390. doi: 10.1038/32891. [DOI] [PubMed] [Google Scholar]
- Salzman CD, Murasugi CM, Britten KH, Newsome WT. Microstimulation in visual area MT: effects on direction discrimination performance. J Neurosci. 1992;12(6):2331–2355. doi: 10.1523/JNEUROSCI.12-06-02331.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schafer EA. Experiments on the electrical excitation of the visual area of the cerebral cortex in the monkey. Brain. 1888;11(1):1–6. [Google Scholar]
- Sekirnjak C, Hottowy P, Sher A, Dabrowski W, Litke AM, Chichilnisky E. High-resolution electrical stimulation of primate retina for epiretinal implant design. The Journal of Neuroscience. 2008;28(17):4446. doi: 10.1523/JNEUROSCI.5138-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sen K, Jorge-Rivera JC, Marder E, Abbott LF. Decoding Synapses. The Journal of Neuroscience. 1996;16(19):6307–6318. doi: 10.1523/JNEUROSCI.16-19-06307.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sherman SM, Guillery RW. Functional organization of thalamocortical relays. Journal of Neurophysiology. 1996;76(3):1367–1395. doi: 10.1152/jn.1996.76.3.1367. [DOI] [PubMed] [Google Scholar]
- Song D, Chan RHM, Marmarelis VZ, Hampson RE, Deadwyler SA, Berger TW. Nonlinear modeling of neural population dynamics for hippocampal prostheses. Neural Networks. 2009;22(9):1340–1351. doi: 10.1016/j.neunet.2009.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stern E, García-Crescioni K, Miller MW, Peskin CS, Brezina V. A method for decoding the neurophysiological spike-response transform. Journal of neuroscience methods. 2009;184(2):337–356. doi: 10.1016/j.jneumeth.2009.07.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stoney SD, Jr, Thompson WD, Asanuma H. Excitation of pyramidal tract cells by intracortical microstimulation: effective extent of stimulating current. J Neurophysiol. 1968;31(5):659–669. doi: 10.1152/jn.1968.31.5.659. [DOI] [PubMed] [Google Scholar]
- Tannan V, Whitsel BL, Tommerdahl MA. Vibrotactile adaptation enhances spatial localization. Brain Research. 2006;1102(1):109–116. doi: 10.1016/j.brainres.2006.05.037. [DOI] [PubMed] [Google Scholar]
- Tehovnik EJ, Tolias AS, Sultan F, Slocum WM, Logothetis NK. Direct and indirect activation of cortical neurons by electrical microstimulation. Journal of Neurophysiology. 2006;96(2):512–521. doi: 10.1152/jn.00126.2006. [DOI] [PubMed] [Google Scholar]
- Wagenaar DA, Madhavan R, Pine J, Potter SM. Controlling bursting in cortical cultures with closed-loop multi-electrode stimulation. The Journal of Neuroscience. 2005;25(3):680–688. doi: 10.1523/JNEUROSCI.4209-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Q, Millard DC, Zheng HJV, Stanley GB. Voltage-sensitive dye imaging reveals improved topographic activation of cortex in response to manipulation of thalamic microstimulation parameters. Journal of Neural Engineering. 2012;9(2):026008. doi: 10.1088/1741-2560/9/2/026008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Q, Webber R, Stanley G. Thalamic synchrony and the adaptive gating of information flow to cortex. Nature Neuroscience. 2010;13(12):1534–1541. doi: 10.1038/nn.2670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber DJ, London BM, Hokanson JA, Ayers CA, Gaunt RA, Torres RR, Zaaimi B, Miller LE. Limb-state information encoded by peripheral and central somatosensory neurons: implications for an afferent interface. Neural Systems and Rehabilitation Engineering, IEEE Transactions on. 2011;19(5):501–513. doi: 10.1109/TNSRE.2011.2163145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson BS, Dorman MF. Cochlear implants: A remarkable past and a brilliant future. Hearing Research. 2008;242(1–2):3–21. doi: 10.1016/j.heares.2008.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woolsey TA, Van der Loos H. The structural organization of layer IV in the somatosensory region (SI) of mouse cerebral cortex. The description of a cortical field composed of discrete cytoarchitectonic units. Brain Res. 1970;17(2):205–242. doi: 10.1016/0006-8993(70)90079-x. [DOI] [PubMed] [Google Scholar]
- Wu MC, David SV, Gallant JL. Complete functional characterization of sensory neurons by system identification. Annual Review of Neuroscience. 2006;29:477–505. doi: 10.1146/annurev.neuro.29.051605.113024. [DOI] [PubMed] [Google Scholar]
- Wu YT, Sclabassi RJ. Identification of nonlinear systems using random amplitude Poisson distributed input functions. Systems, Man and Cybernetics, Part A: Systems and Humans, IEEE Transactions on. 1997;27(2):222–234. [Google Scholar]
- Yeomans JS. Principles of brain stimulation. New York: Oxford University Press; 1990. [Google Scholar]