Abstract
Hydrogen bonding is a key contributor to the exquisite specificity of the interactions within and between biological macromolecules, and hence accurate modeling of such interactions requires an accurate description of hydrogen bonding energetics. Here we investigate the orientation and distance dependence of hydrogen bonding energetics by combining two quite disparate but complementary approaches: quantum mechanical electronic structure calculations and protein structural analysis. We find a remarkable agreement between the energy landscapes obtained from the electronic structure calculations and the distributions of hydrogen bond geometries observed in protein structures. In contrast, molecular mechanics force fields commonly used for biomolecular simulations do not consistently exhibit close correspondence to either quantum mechanical calculations or experimentally observed hydrogen bonding geometries. These results suggest a route to improved energy functions for biological macromolecules that combines the generality of quantum mechanical electronic structure calculations with the accurate context dependence implicit in protein structural analysis.
Hydrogen bonds are partially covalent interactions between a hydrogen atom covalently bound to an electronegative atom and an electronegative acceptor atom (1). They play an important role in defining the structure and function of biological macromolecular systems and contribute to the specificity of molecular recognition (2), the formation of secondary structures (3), and the energetics of protein folding (4). Numerous studies of experimentally available protein and small molecule structures have revealed the directional character of hydrogen bonds and in particular the nonlinear geometry at the acceptor atom (5–8). Computational modeling of hydrogen bonding energy landscapes is a challenging problem; current approaches include quantum mechanical calculations on model systems (usually small molecules analogous to either a main-chain peptide unit or an amino acid side chain) (9, 10), molecular mechanics (force field) approaches (11–13), and knowledge-based potentials derived from small molecule structure databases (14) or the Protein Data Bank (PDB) (15, 16).
For application to macromolecular systems, different approaches have complementary strengths and weaknesses. Quantum mechanical electronic structure calculations are clearly the most fundamental and general but can be carried out at a rigorous level of theory only for systems much smaller than biological macromolecules, and the results are not necessarily transferable to the complex macromolecular environment. Empirical molecular mechanics force fields are constructed to apply generally to macromolecules and so are not subject to the size limitations of electronic structure calculations, but their accuracy may be limited by the (necessary) simplification of the quantum mechanical system and the large number of parameters that need to be obtained by fitting against experimental data. Inference of interaction energy landscapes directly from macromolecular structures has the advantage that macromolecular context effects are directly accounted for, and no assumptions about transferability are required, but the physical origin of the resultant potentials of mean force cannot be directly inferred, and the construction of detailed landscapes is limited by the number of observations in high-resolution macromolecular structures. Here we attempt to combine the strengths of the different approaches by comparing quantum mechanics and molecular mechanics energy landscapes for small molecule hydrogen bonded dimers with experimental data on hydrogen bond geometries observed in the Protein Data Bank (PDB) (16). We find a close correspondence between the quantum mechanical energy landscape and the energy landscape inferred from the distribution of side-chain–side-chain hydrogen bonds in protein structures. In contrast, a comparison with several molecular mechanics force fields widely used in molecular dynamics simulations of proteins, nucleic acids, and small molecules reveals systematic deviations from electronic structure calculations and protein structure statistics.
Methods
Choice of Small Molecule Model. It is a nontrivial problem to choose a small hydrogen bonded dimer that accurately represents hydrogen bonds found in protein side chains and main chains. Formamide, acetamide, N-methylacetamide (NMA), formamide–formaldehyde, and water dimers (and combinations thereof) have been explored in the literature, primarily with the purpose of identifying various local and global minima in a given complex (9, 10, 17–23). Although NMA dimers are routinely used to model main-chain hydrogen bonds, the methyl groups on both ends can contribute significantly to the dimerization energy surface (13, 21), and hence formamide is a better model for amino acid side-chain hydrogen bonds. A number of low-energy dimer arrangements (parallel, antiparallel, and out-of-plane) have been described in the literature (17, 18, 21, 22). For comparison with protein side-chain statistics, we used an out-of-plane formamide dimer with a single hydrogen bond (Fig. 1A). Cyclic conformations with two N—H···O C hydrogen bonds occupy global minima for both formamide and NMA dimers (21, 22); however, we wanted to model single hydrogen bonds often occurring in proteins, deferring the issue of multiple hydrogen bonds and cooperativity to a later study. The starting geometry for the formamide dimer optimization was taken from ab initio calculations carried out in ref. 24; it corresponds to one of the out-of-plane conformations identified in ref. 21. We also carried out electronic structure calculations for the out-of-plane acetamide dimer; the conformation of this dimer before optimization was created by adding methylene groups to the out-of-plane formamide dimer. The starting points for the scans of the potential energy surface were generated by unconstrained optimization of these initial conformations (Table 1).
C hydrogen bonds occupy global minima for both formamide and NMA dimers (21, 22); however, we wanted to model single hydrogen bonds often occurring in proteins, deferring the issue of multiple hydrogen bonds and cooperativity to a later study. The starting geometry for the formamide dimer optimization was taken from ab initio calculations carried out in ref. 24; it corresponds to one of the out-of-plane conformations identified in ref. 21. We also carried out electronic structure calculations for the out-of-plane acetamide dimer; the conformation of this dimer before optimization was created by adding methylene groups to the out-of-plane formamide dimer. The starting points for the scans of the potential energy surface were generated by unconstrained optimization of these initial conformations (Table 1).
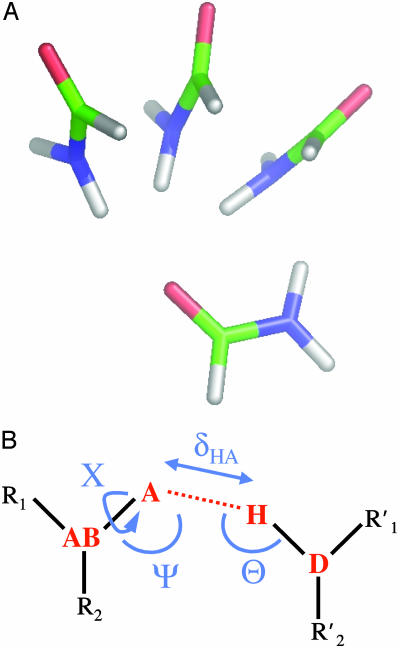
Fig. 1.
(A) Three representative conformations of a formamide dimer. The angle at the acceptor (Ψ) is varied, with all other geometric parameters held fixed at the optimized dimer values. (B) Schematic representation of the hydrogen bond geometry. D, donor atom; H, hydrogen atom; A, acceptor atom; AB, acceptor base; R1,R2, atoms bound to the acceptor base, 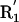 ,
, 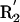 , atoms bound to the donor atom. Hydrogen bond geometric parameters considered here are: δHA, distance between hydrogen and acceptor atoms; Ψ, angle at the acceptor atom; θ, angle at the hydrogen atom; X, torsional angle around the A–AB axis.
, atoms bound to the donor atom. Hydrogen bond geometric parameters considered here are: δHA, distance between hydrogen and acceptor atoms; Ψ, angle at the acceptor atom; θ, angle at the hydrogen atom; X, torsional angle around the A–AB axis.
Table 1. Hydrogen bond geometry parameters for the formamide dimer optimized with quantum chemistry (DFTf, MP2, HF) and molecular mechanics methods (charmm27, opls-aa, mm3-2000), and the acetamide dimer optimized with the DFT method (DFTa).
| Method | δHA, Å | ψ,° | θ,° | X,° |
|---|---|---|---|---|
| DFTa | 1.94 | 112.34 | 159.43 | —177.51 |
| DFTf | 1.94 | 112.91 | 161.57 | 179.78 |
| MP2 | 1.97 | 110.49 | 155.33 | —179.49 |
| HF | 2.10 | 138.16 | 170.94 | —179.54 |
| charmm27 | 1.82 | 170.25 | 170.83 | —106.83 |
| opls-aa | 1.75 | 165.04 | 175.61 | 145.12 |
| mm3-2000 | 1.98 | 121.16 | 161.07 | 149.63 |
| PDB | 1.93 | 115.00 | 175.00 | 175.00 |
Knowledge-based minima (PDB) are based on the most populated frequency bins (see Methods). The geometry parameters are defined in Fig. 1B.
Generation of Dimerization Energy Landscapes. The potential energy surface for the interacting dimers was sampled by systematically varying one of the four parameters describing the hydrogen bond geometry (δHA, Ψ, θ, and X; defined in Fig. 1B) while keeping the other three fixed at their optimal starting values (Table 1). In calculations aimed at comparison with the PDB statistics, the bond lengths and bond angles of the molecules but not the hydrogen bond geometric parameters were allowed to relax for each sample conformation; very similar results are obtained when the three hydrogen bond parameters not being sampled in a given projection of the landscape are allowed to vary during the optimization process as well (data not shown).
Electronic Structure Calculations. nwchem 4.1 quantum chemistry software (25) was used for all electronic structure calculations in this paper. We used the aug-cc-pVDZ basis set for density functional theory (DFT) calculations and took the counterpoise (CP) correction (26) into account when computing dimerization energies to correct for the basis set superposition error resulting from the use of finite basis sets. When dimer geometry optimizations were involved, the CP correction was applied separately to each monomer in a single point calculation. The geometry of the monomers was given by the fully optimized dimer geometry. For DFT calculations, we used the Perdew, Burke, and Ernzerhof correlation-exchange functional (PBE96) (27), which reproduces other ab initio hydrogen bonding calculations with reasonable accuracy (28–30). To test the applicability of this functional, we carried out dimerization and conformational energy calculations on a set of small molecules taken from ref. 24 by using both PBE96 and B3LYP (31) correlation-exchange functionals and found no significant discrepancies between the two (data not shown).
To obtain an independent check of the DFT results, we also carried out second-order Moller–Plesset perturbation theory (MP2) calculations on the same systems. MP2 calculations were counterpoise (CP)-corrected and also used the aug-cc-pVDZ basis set. Previous work on ab initio calculations of small molecules in the gas phase has demonstrated that absolute dimerization energies of hydrogen bonded dimers computed by using CP-corrected MP2 with the aug-cc-pVDZ basis set are within a few tenths of kcal/mol of the experimentally observed values (20). The difference in dimerization energies of two alternative conformations is expected to be even more accurate due to the cancellation of errors related to finite basis sets.
Molecular Mechanics Calculations. Force-field calculations were carried out by using the tinker 4.0 molecular modeling package (32) (http://dasher.wustl.edu/tinker). We considered charmm27 (33), opls-aa (34), and mm3-2000 force fields (35); all atoms were modeled explicitly. All molecular mechanics calculations were set up in the absence of solvent and at zero temperature.
Hydrogen Bond Geometries in Protein Structures. The knowledge-based hydrogen bonding potential is derived as described in ref. 16. Briefly, statistical distributions of the geometric parameters δHA, Ψ, θ, and X (defined in Fig. 1B) describing the geometry of hydrogen bonds were obtained from a data set of 698 proteins with a resolution of 1.6 Å or better and a crystallographic R factor of 0.25 or better, taken from the Dunbrack-culled PDB collection (http://dunbrack.fccc.edu). charmm19 standard bond angles (36) were used to add polar hydrogens in cases where their position was defined by the chemistry of the donor group (His, Asn, Gln, Arg, and Trp). The donor-hydrogen bond length of 1.0 Å, supported by neutron diffraction data (5), was used to define hydrogen positions given by the donor chemistry. Hydrogens attached with rotatable bonds (Ser, Thr, Tyr, and Lys) were not considered in the derivation of hydrogen bonding geometries as their positions would be influenced by the energy function used for rotatable bond optimization. For determination of amino acid protonation states, we used the unperturbed ionization constants of the amino acids and assumed a pH value of 7. Perturbed ionization constants occur mainly in enzyme active sites and are likely not to influence the observed distributions significantly. We preserved the crystal structure conformation of His, Asn, and Gln, without taking into account possible swapping of N, O, and C atoms due to uncertainty in interpreting the crystallographic electron density. We expect an incorrect assignment to result on average in a complete failure to detect a hydrogen bond, rather than in a distortion of the observed hydrogen bonding geometry. For comparison with ab initio calculations on the formamide dimer, in this paper we consider only protein side-chain–side-chain hydrogen bonds involving sp2 hybridized acceptor atoms.
Generation of a Potential of Mean Force from PDB Statistics. The inverting of frequency distributions to obtain potentials of mean force is justified for a set of systems frozen in very low energy states, where the total energy is the sum of many independent contributions that are functions of some parameter p; in such ensembles, the negative logarithm of the frequency of occurrence of a particular value of p is proportional to the interaction energy for that value of p (14). A set of protein crystal structures constitutes such an ensemble to a good approximation, and hence the frequencies fprotein(p), p = (δHA, Ψ, θ, X) with which hydrogen bond parameters δHA, Ψ, θ, or X are observed in protein structures can be related to the hydrogen bond interaction energies according to the Boltzmann-like expression:
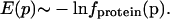 |
[1] |
The energy functions E(p) for the four geometric parameters δHA, Ψ, θ, and X were obtained by using
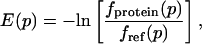 |
[2] |
where fprotein(p) describes the frequency at which a geometric parameter p = δHA, Ψ, θ, X is observed in a certain bin in the protein dataset, and fref(p) is a reference frequency assuming an unbiased distribution over all bins. The angular distributions were computed for all hydrogen-acceptor distances between 1.4 and 2.1 Å; the distance distribution was obtained by using a distance cutoff of 3.0 Å (16). We used 10° bins for all angular distributions and 0.05-Å bins for the distance distribution. For the minima of the knowledge-based potential in Table 1, we report values corresponding to the middle of the most populated bin.
Results and Discussion
Our overall goal is to develop an accurate description of the energetics of side-chain–side-chain hydrogen bonds in proteins. Characterization of the energy landscape by using quantum mechanical calculations requires the choice of a suitable small molecule model for side-chain hydrogen bonds. Truncation of the hydrogen bonding moieties of asparagine and glutamine yields formamide, and the primary model for side-chain hydrogen bonds in this paper consists of two formamide molecules interacting via a single hydrogen bond. We confirm the accuracy of this model with calculations on acetamide (Table 1), which corresponds to the hydrogen bonding groups plus the preceding methylene group on the side chain. NMA, although a reasonable model for the protein backbone is less appropriate for side-chain–side-chain hydrogen bonds because of steric clashes involving the additional methyl groups. We model protein side-chain hydrogen bonds by using the formamide dimer shown in Fig. 1A and the corresponding acetamide dimer (see Methods).
We use DFT for our electronic structure calculations because it has been extensively tested on hydrogen bonded systems and was found to reproduce dimerization energies obtained experimentally or through other theoretical methods with reasonable accuracy (28–30, 37). We also use second-order Moller–Plesset perturbation theory (MP2) applied to the Hartree–Fock (HF) self-consistent field method to ensure that our conclusions are not method dependent.
Description of the hydrogen bonding energy landscape requires the choice of a suitable set of geometric parameters. In general, six parameters are required to describe the relative orientation of two rigid bodies. The parameters we chose to describe hydrogen bond geometry are shown in Fig. 1B: we consider the distance between the hydrogen atom and the acceptor atom (H···A, δHA), the angle at the acceptor atom (AB A···H, Ψ), the angle at the hydrogen atom (D—H···A, θ), and the torsional angle around the acceptor–acceptor base bond (R1—AB
A···H, Ψ), the angle at the hydrogen atom (D—H···A, θ), and the torsional angle around the acceptor–acceptor base bond (R1—AB A···H, X). The dihedral angle X is measured with respect to the hydrogen atom covalently attached to the carbonyl carbon of the acceptor. The relative orientation of the monomers in a dimer with a given hydrogen bond geometry is determined by two additional degrees of freedom, torsional angles around the hydrogen bond and around the hydrogen–donor bond.
A···H, X). The dihedral angle X is measured with respect to the hydrogen atom covalently attached to the carbonyl carbon of the acceptor. The relative orientation of the monomers in a dimer with a given hydrogen bond geometry is determined by two additional degrees of freedom, torsional angles around the hydrogen bond and around the hydrogen–donor bond.
Because the full hydrogen bonding energy surface is four dimensional, it is difficult to visualize and adequately sample by using high-level quantum mechanical methods. Moreover, a full multidimensional dimerization energy landscape cannot be reliably inferred from experimental hydrogen bond distributions due to the limited number of observations. A more practical approach is to examine a 1D projection of the energy surface, where only one parameter (δHA, Ψ, θ, or X) is changed, whereas the others stay equal to those in an optimal hydrogen bond arrangement identified by unconstrained geometry optimization of the initial dimer conformation (see Fig. 1a for three representative dimer conformations with different values of Ψ and Methods for computational details).
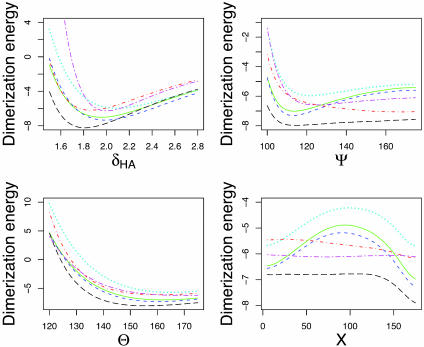
Using DFT, we obtained the dimerization energies as a function of δHA, Ψ, θ, and X, shown as green (solid) curves in Fig. 2. There are pronounced minima in the δHA, Ψ, and X energy dependences (see also Table 1, which shows hydrogen bond geometries resulting from unconstrained optimizations of the formamide dimer via various force field and quantum mechanical approaches) and a shallower minimum in the θ dependence. The results are essentially identical to MP2 calculations performed for the same geometries (blue curves with short dashes in Fig. 2). However, the less accurate HF method, which neglects explicit electron–electron correlations, exhibits substantial differences, especially in the location and the magnitude of the dimerization energy minimum as a function of δHA and Ψ (cyan curves with dots in Fig. 2). HF results are well known to overestimate hydrogen bonding lengths (1); they also appear to favor making the angle at the acceptor atom more linear. When the electron–electron correlation energies are subtracted from the total DFT dimerization energy, the shape of the energy surface becomes closer to that computed by using HF theory, with all minima positions shifted and dimerization energies underestimated as in the case of HF calculations (data not shown).
Fig. 2.
Formamide dimer hydrogen bonding energies (kcal/mol) vs. δHA (Å), Ψ, θ, and X (°). Green (solid), DFT; blue (short dashes), MP2; cyan (dots), HF SCF; red (dots and dashes), charmm27; black (long dashes), opls-aa; magenta (long and short dashes), mm3-2000. All abbreviations are defined in the text.
Current molecular mechanics force fields widely used in biomolecular simulations essentially model hydrogen bonding as a purely electrostatic interaction: positive partial charges are placed on the proton and the acceptor base and negative partial charges, on the acceptor and donor atoms (38, 39). The hydrogen bond modeled in this way is dominated by dipole–dipole interaction and the energy of two dipoles is at a minimum when all four atoms are collinear. Fig. 2 shows a comparison of DFT, mm3-2000 (11, 12, 35), opls-aa (34), and charmm27 (33) energy surfaces, carried out for dimer sets produced from a DFT-minimized hydrogen bonded complex, as described above. We observe significant differences in the opls-aa and charmm27 calculations when compared to the DFT results, in particular for the dependence of the dimerization energy on Ψ. The charmm27 potential function is most favorable for Ψ close to 180°, whereas the opls-aa function does exhibit a shallow minimum at Ψ ≈110°; however, the energy cost of going to larger angles is so small that an opls-aa optimized dimer ends up having an almost linear hydrogen bond (Table 1). Indeed, Fabiola et al. (40) and Lii et al. (11, 12) have argued that hydrogen bond directionality is not correctly reproduced by molecular mechanics force fields unless an explicitly orientation-dependent hydrogen bonding potential is added to the total molecular energy. A purely electrostatic model was also found to be insufficient to model hydrogen bonding in ice (41).
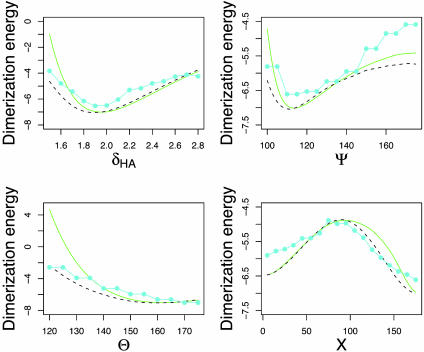
In Fig. 3, we compare the dimerization energy obtained from DFT (both with and without constrained optimization) calculations with the potential of mean force [E(p), Eq. 2] obtained from protein structures. There is a striking correspondence between the electronic structure calculations and the distribution of experimentally observed side-chain–side-chain hydrogen bond geometries. It is especially remarkable because E(p) (Eq. 2) is a potential of mean force, averaged over solvent degrees of freedom and the degrees of freedom of the hydrogen bonded dimer not explicitly taken into account in Eq. 2, such as side-chain bond lengths and bond angles. This similarity between quantum mechanical dimerization energies and hydrogen bond geometry distributions observed in proteins suggests that the DFT and MP2 calculations on the small molecule models capture the essential features of hydrogen bonding interactions between amino acid side chains in protein structures, perhaps because the very short range partially covalent nature of the hydrogen bond makes it relatively insensitive to the large differences in the surrounding environment.
Fig. 3.
Formamide dimer hydrogen bonding energies (kcal/mol) vs. δHA (Å), Ψ, θ, and X (°). Green (solid), DFT (same as in Fig. 2); black (dashes), DFT with constrained optimization; cyan (solid with filled circles), knowledge-based potential (negative logarithm of frequency distributions for side-chain–side-chain interactions in protein structures, binned as described in Methods).
The largest difference between the electronic structure calculations and the PDB statistics on the one hand and the molecular mechanics force fields on the other is in the dependence of the energy on Ψ. The lowest energy value of Ψ in charmm27 and opls-aa molecular mechanics force fields is close to 180° (Table 1 and Fig. 2); in contrast, the most frequently observed value of Ψ for side-chain–side-chain hydrogen bonds in proteins is close to 120°, as is the minimum energy conformation of the formamide dimer in the DFT and MP2 calculations (Table 1; MM3, which has an explicitly orientation-dependent hydrogen bonding potential, has a minimum near 120°). From an elementary chemistry viewpoint, one might expect that the lone pairs of the sp2 hybridized oxygen atom are at positions corresponding to Ψ = 120°, and hence that hydrogen bonds with Ψ = 120° would be most favorable. However, a previous study found only a very small energy difference between the 120° and 180° conformations (42), and this was part of the basis for dropping an explicit hydrogen bonding potential from the charmm force field (33, 36). It is possible, therefore, that both the electronic structure calculations and the PDB statistics are flawed, and their agreement is fortuitous. We consider these possibilities in more detail in the following two paragraphs.
To further check the electronic structure calculations, we carried out optimized MP2 calculations on formamide dimers with Ψ equal to 120° and 175°. In these calculations, all degrees of freedom except the acceptor angle were allowed to relax. The results of these calculations are in very close agreement with the optimized DFT calculations in Fig. 3: the dimerization energies at 120° are -6.90 kcal/mol for MP2 and -6.82 kcal/mol for DFT, whereas the dimerization energies at 175° are -5.99 kcal/mol for MP2 and -5.74 kcal/mol for DFT. Because DFT and MP2 calculations use different treatments of electron correlation and exchange, the similarity in the results strongly suggests that the difference in energy between the two configurations is on the order of 1 kcal/mol, considerably larger than that found in older studies using semiempirical methods (43) or HF calculations over the full Ψ range supplemented with limited Moller–Plesset results for near linear geometries (42), which suggested weak hydrogen bonding energy dependence on the acceptor angle or even preference for more linear hydrogen bonds.
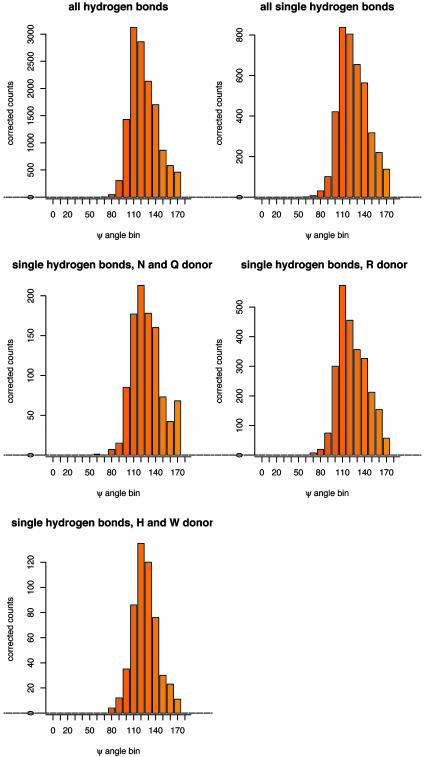
We next considered possible sources of bias in the protein structure analysis (see Methods). There is always a possibility when inferring a potential of mean force from observed distributions that secondary effects introduce considerable bias. In the case of hydrogen bonding, it is possible that the relatively high frequency of hydrogen bonds with Ψ = 120° in proteins does not reflect an intrinsic energetic preference for this orientation but rather that many hydrogen bond acceptor atoms in proteins make two hydrogen bonds, and that to accommodate two hydrogen bonds Ψ must be close to 120°. To avoid possible bias in hydrogen bond geometries involving acceptor atoms making multiple hydrogen bonds, we calculated distributions separately for acceptor atoms making only one hydrogen bond (side chains with multiple hydrogen bonds involving different acceptor atoms were not automatically excluded by this procedure). As is evident from Fig. 4, the distributions for the singly hydrogen bonding acceptor atoms are very similar to those obtained for all acceptor atoms, suggesting that the preference for the acceptor angle of 120° over 180° reflects the energy differences between the two orientations and is not simply a consequence of steric constraints on the formation of multiple hydrogen bonds. Very similar orientation dependencies were also observed for hydrogen bonds involving different types of side-chain donor atoms (Fig. 4).
Fig. 4.
Distributions of the acceptor angle Ψ for hydrogen bonds observed in high-resolution protein crystal structures. Shown are the distributions for all side-chain–side-chain hydrogen bonds with sp2 hybridized acceptor atoms in the data set of 698 protein crystal structures, a subset of those hydrogen bonds where only a single hydrogen bond is made to each acceptor atom, and subsets of the single hydrogen bonds split by the type of the donor amino acid (R, arginine; N, asparagine; Q, glutamine; H, histidine; W, tryptophan). Raw counts were corrected for the different volume elements encompassed by the bins; the angular correction is sin(Ψ).
The calculations in the preceding paragraphs suggest that the agreement between the electronic structure calculations and the protein structure statistics is not fortuitous, and that both reflect the energetics of hydrogen bonding more accurately than the dipole–dipole treatment in molecular mechanics force fields. We emphasize that, whereas the above results suggest that current force fields are inaccurate for side-chain–side-chain hydrogen bonds in proteins, they appear to work reasonably well for main-chain hydrogen bonds, which are usually more linear due to steric constraints in secondary structure elements, and possibly due to the more dipolar nature of main-chain hydrogen bonds (8, 16, 40).
Conclusion
The main observation of this paper is the striking correspondence between the knowledge-based potential derived from side-chain–side-chain hydrogen bond geometries in high-resolution protein structures and the ab initio DFT and MP2 quantum mechanical calculations of the formamide and acetamide dimer hydrogen bonding energies. This close correspondence suggests that the orientation dependence of side-chain–side-chain hydrogen bonds is well modeled by formamide and acetamide dimers, and that the hydrogen bonding distributions in protein structures are surprisingly context independent and close to the Boltzmann-like distribution defined by Eq. 2. This finding suggests that the assumption of additivity and transferability of the properties of the functional groups to proteins is valid for side-chain hydrogen bonds, and implies more generally that short-range recurrent interactions in complex macromolecules can be analyzed by using quantum mechanical calculations on small molecule models (44). Finally, because our quantum mechanical calculations are performed in vacuum, it appears that the electrostatic effects due to solvent polarization around interacting residues do not play a major role in determining short-range hydrogen bonding geometries.
Another observation is the limited degree of accuracy exhibited by molecular mechanics force fields when applied to hydrogen bonded systems (11, 12, 40, 44). To accurately capture the physics of hydrogen bonds, a next generation of molecular mechanics force fields incorporating off atom charges, higher-order multipole interactions and/or electronic polarizability will be necessary (39, 45–47). As it stands now, parameterizations of van der Waals and point charge atom-centered Coulomb interactions used in charmm27 and opls-aa tend to make hydrogen bonds too linear, consistent with a simple dipole–dipole model of a hydrogen bond. This appears to be less of a problem in main-chain hydrogen bonds, where observed hydrogen bonding geometries depend on the secondary structure and are hence constrained to be more linear (5, 8, 16).
The knowledge-based hydrogen bonding potential compared with ab initio electronic structure calculations in this paper has seen considerable success in such diverse applications as protein structure prediction, fixed backbone sequence redesign, protein–protein docking, and prediction of hot spots in protein interfaces (16, 48–50). Based on this observation, we suggest a new approach for creating free energy functions suitable for protein structure prediction and sequence design, in which knowledge-based potentials are augmented by quantum mechanical calculations on small molecule models representative of specific aspects of protein interactions, such as hydrogen bonding, π–π and cation–π interactions. There is considerable synergy between ab initio electronic structure methods and inferring of interaction energies from the distributions observed in protein structures: the former are more general, provide fundamental physical understanding, and are not limited by sparse sampling, whereas the latter require no assumptions about the validity of a small molecule model for biomolecular interactions. The opportunity for synergy is apparent in Fig. 3; the bumpiness of the empirical potential, which stems from the limited number of observations in the PDB, could be replaced by the smoother potential derived from the quantum mechanical calculations. Furthermore, unlike knowledge-based potentials, quantum mechanical calculations can, given sufficient computer time, be used to create more informative multidimensional dimerization energy landscapes. Together, the knowledge-based methods can guide the evaluation of the transferability of the ab initio results, and the quantum mechanical methods can then be used to augment and generalize the observed statistics.
Acknowledgments
We thank Kieron Burke, Jim Havranek, and Carlos Duarte for helpful comments on the manuscript. We are grateful to Eric Bylaska for advice on nwchem capabilities. K.T. also thanks Hannes Jonsson for his support of this work. K.T. was funded by the Division of Materials Science and Engineering, Office of Basic Energy Sciences, U.S. Department of Energy. T.K. was supported by a long-term fellowship from the Human Frontier Science Program Organization. A.V.M. and D.B. were supported by the Howard Hughes Medical Institute. The computational part of this research was performed using a grant from the Pittsburgh Supercomputing Center.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: PDB, Protein Data Bank; DFT, density functional theory; MP2, second order Moller–Plesset perturbation theory; HF, Hartree–Fock.
References
- 1.Scheiner, S. (1997) Hydrogen Bonding: A Theoretical Perspective (Oxford Univ. Press, Oxford).
- 2.Fersht, A. (1985) Enzyme Structure and Function (Freeman, New York).
- 3.Bordo, D. & Argos, P. (1994) J. Mol. Biol. 243, 504-519. [DOI] [PubMed] [Google Scholar]
- 4.Dill, K. A. (1990) Biochemistry 29, 7133-7155. [DOI] [PubMed] [Google Scholar]
- 5.Baker, E. N. & Hubbard, R. E. (1984) Prog. Biophys. Mol. Biol. 44, 97-179. [DOI] [PubMed] [Google Scholar]
- 6.Görbitz, C. H. (1989) Acta Crystallogr. B 45, 390-395. [Google Scholar]
- 7.Ippolito, J. A., Alexander, R. S. & Christianson, D. W. (1990) J. Mol. Biol. 215, 457-471. [DOI] [PubMed] [Google Scholar]
- 8.Stickle, D. F., Presta, L. G., Dill, K. A. & Rose, G. D. (1992) J. Mol. Biol. 226, 1143-1159. [DOI] [PubMed] [Google Scholar]
- 9.Mitchell, J. B. O. & Price, S. L. (1990) J. Comput. Chem. 11, 1217-1233. [Google Scholar]
- 10.No, K. T., Kwon, O. Y., Kim, S. Y., Jhon, M. S. & Scheraga, H. A. (1995) J. Phys. Chem. 99, 3478-3486. [Google Scholar]
- 11.Lii, J. & Allinger, N. L. (1994) J. Phys. Org. Chem. 7, 591-609. [Google Scholar]
- 12.Lii, J. & Allinger, N. L. (1998) J. Comp. Chem. 19, 1001-1016. [Google Scholar]
- 13.Buck, M. & Karplus, M. (2001) J. Phys. Chem. B 105, 11000-11015. [Google Scholar]
- 14.Grzybowski, B. A., Ishchenko, A. V., DeWitte, R. S., Whitesides, G. M. & Shakhnovich, E. I. (2000) J. Phys. Chem. B 104, 7293-7298. [Google Scholar]
- 15.McDonald, I. K. & Thornton, J. M. (1994) J. Mol. Biol. 238, 777-793. [DOI] [PubMed] [Google Scholar]
- 16.Kortemme, T., Morozov, A. V. & Baker, D. (2003) J. Mol. Biol. 326, 1239-1259. [DOI] [PubMed] [Google Scholar]
- 17.Qian, W., Mirkin, N. G. & Krimm, S. (1999) Chem. Phys. Lett. 315, 125-129. [Google Scholar]
- 18.Torii, H., Tatsumi, T., Kanazawa, T. & Tasumi, M. (1998) J. Phys. Chem. B 102, 309-314. [Google Scholar]
- 19.Guo, H. & Karplus, M. (1992) J. Phys. Chem. 96, 7273-7287. [Google Scholar]
- 20.Feller, D. (1992) J. Chem. Phys. 96, 6104-6114. [Google Scholar]
- 21.Vargas, R., Garza, J., Friesner, R. A., Stern, H., Hay, B. P. & Dixon, D. A. (2001) J. Phys. Chem. A 105, 4963-4968. [Google Scholar]
- 22.Watson, T. M. & Hirst, J. D. (2002) J. Phys. Chem. A 106, 7858-7867. [Google Scholar]
- 23.Han, W. & Suhai, S. (1996) J. Phys. Chem. 100, 3942-3949. [Google Scholar]
- 24.Halgren, T. A. (1999) J. Comput. Chem. 20, 730-748. [DOI] [PubMed] [Google Scholar]
- 25.Harrison, R. J., Nichols, J. A., Straatsma, T. P., Dupuis, M., Bylaska, E. J., Fann, G. I., Windus, T. L., Apra, E., de Jong, W., Hirata, S., et al. (2002) nwchem, A Computational Chemistry Package for Parallel Computers (Pacific Northwest National Laboratory, Richland, WA), Version 4.1.
- 26.Boys, S. F. & Bernardi, F. (1970) Mol. Phys. 19, 553-566. [Google Scholar]
- 27.Perdew, J., Burke, K. & Ernzerhof, M. (1996) Phys. Rev. Lett. 77, 3865-3868. [DOI] [PubMed] [Google Scholar]
- 28.Tuma, C., Boese, A. D. & Handy, N. C. (1999) Phys. Chem. Chem. Phys. 1, 3939-3947. [Google Scholar]
- 29.Kaschner, R. & Hohl, D. (1998) J. Phys. Chem. A 102, 5111-5116. [Google Scholar]
- 30.Ireta, J., Neugebauer, J., Scheffler, M., Rojo, A. & Galvan, M. (2003) J. Phys. Chem. B 107, 1432-1437. [Google Scholar]
- 31.Becke, A. D. (1993) J. Chem. Phys. 98, 5648-5652. [Google Scholar]
- 32.Ponder, J. W. & Richards, F. M. (1987) J. Comput. Chem. 8, 1016-1024. [Google Scholar]
- 33.MacKerrell, A. D., Jr., Bashford, D., Bellott, M., Dunbrack, R. L., Jr., Evanseck, J. D., Field, M. J., Fischer, S., Gao, J., Guo, H., Ha, S., et al. (1998) J. Phys. Chem. B 102, 3586-3616. [DOI] [PubMed] [Google Scholar]
- 34.Jorgensen, W. L., Maxwell, D. S. & Tirado-Rives, J. (1996) J. Am. Chem. Soc. 118, 11225-11236. [Google Scholar]
- 35.Allinger, N. L., Yuh, Y. H. & Lii, J. (1989) J. Am. Chem. Soc. 111, 8551-8566. [Google Scholar]
- 36.Neria, E., Fischer, S. & Karplus, M. (1996) J. Chem. Phys. 105, 1902-1921. [Google Scholar]
- 37.Topol, I. A., Burt, S. K. & Rashin, A. A. (1995) Chem. Phys. Lett. 247, 112-119. [Google Scholar]
- 38.Jensen, F. (2002) Introduction to Computational Chemistry (Wiley, New York).
- 39.Ponder, J. W. & Case, D. A. (2003) Adv. Protein Chem. 66, 27-85. [DOI] [PubMed] [Google Scholar]
- 40.Fabiola, F., Bertram, R., Korostelev, A. & Chapman, M. S. (2002) Protein Sci. 11, 1415-1423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Isaacs, E. D., Shukla, A., Platzman, P. M., Hamann, D. R., Barbiellini, B. & Tulk, C. A. (1999) Phys. Rev. Lett. 82, 600-603. [Google Scholar]
- 42.Reiher, W. E. (1985) Ph.D. thesis (Harvard Univ., Boston).
- 43.Adalsteinsson, H., Maulitz, A. H. & Bruice, T. C. (1996) J. Am. Chem. Soc. 118, 7689-7693. [Google Scholar]
- 44.Hu, H., Elstner, M. & Hermans, J. (2003) Proteins Struct. Funct. Genet. 50, 451-463. [DOI] [PubMed] [Google Scholar]
- 45.Beachy, M. D., Chasman, D., Murphy, R. B., Halgren, T. A. & Friesner, R. A. (1997) J. Am. Chem. Soc. 119, 5908-5920. [Google Scholar]
- 46.Cieplak, P., Caldwell, J. & Kollman, P. (2001) J. Comput. Chem. 22, 1048-1057. [Google Scholar]
- 47.Kaminski, G. A., Stern, H. A., Berne, B. J., Friesner, R. A., Cao, Y. X., Murphy, R. B., Zhou, R. & Halgren, T. A. (2002) J. Comput. Chem. 23, 1515-1531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Kortemme, T. & Baker, D. (2002) Proc. Natl. Acad. Sci. USA 99, 14116-14121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Morozov, A. V., Kortemme, T. & Baker, D. (2003) J. Phys. Chem. B 107, 2075-2090. [Google Scholar]
- 50.Gray, J. J., Moughon, S., Kortemme, T., Schueler-Furman, O., Misura, K. M. S., Morozov, A. V. & Baker, D. (2003) Proteins Struct. Funct. Genet. 52, 118-122. [DOI] [PubMed] [Google Scholar]