Additive and Synergistic Membrane Permeabilization by Antimicrobial (Lipo)Peptides and Detergents

Abstract

Certain antibiotic peptides are thought to permeabilize membranes of pathogens by effects that are also observed for simple detergents, such as membrane thinning and disordering, asymmetric bilayer expansion, toroidal pore formation, and micellization. Here we test the hypothesis that such peptides act additively with detergents when applied in parallel. Additivity is defined analogously to a fractional inhibitory concentration index of unity, and the extent and mechanism of leakage is measured by the fluorescence lifetime-based vesicle leakage assay using calcein-loaded vesicles. Good additivity was found for the concerted action of magainin 2, the fungicidal lipopeptide class of surfactins from Bacillus subtilis QST713, and the detergent octyl glucoside, respectively, with the detergent C₁₂EO₈. Synergistic or superadditive action was observed for fengycins from B. subtilis, as well as the detergent CHAPS, when combined with C₁₂EO₈. The results illustrate two mechanisms of synergistic action: First, maximal leakage requires an optimum degree of heterogeneity in the system that may be achieved by mixing a graded with an all-or-none permeabilizer. (The optimal perturbation should be focused to certain defect structures, yet not to the extent that some vesicles are not affected at all.) Second, a cosurfactant may enhance the bioavailability of a poorly soluble peptide. The results are important for understanding the concerted action of membrane-permeabilizing compounds in biology as well as for optimizing formulations of such antimicrobials for medical applications or crop protection.

Introduction

Antimicrobial peptides (AMPs) are an essential part of the host-defense systems of a wide variety of organisms. The failure of many traditional antibiotics and resulting urgent need for alternatives have put these molecules into the focus of interest for medical research. Even more advanced is the use of host-defense lipopeptides as so-called green pesticides for crop protection against, for example, pathogenic fungi (1).

Problems that challenge the understanding and application of antibiotic (lipo)peptides are the extreme diversity of their structures, the multitude of proposed (and probably also of relevant) modes of action, and the fact that organisms typically produce complex mixtures of host-defense molecules that synergize with each other. Virtually all studies agree that typical antibiotic (lipo)peptides act primarily against the structural and functional integrity of the cell membrane of the target cell (for recent reviews, see the literature (2–7)), but some may also bind to intracellular targets (8,9). Somewhat more specific modes of action include models referred to as barrel-stave, toroidal pore, carpet, detergent-like, and electrostatic clustering. However, it is not only that structurally different peptides are likely to act via different mechanisms; these models are not well defined, systematic, or clear-cut alternatives even for one single peptide. They may very well describe different aspects or phenomena of the same mechanism. Here, we study the concerted action of antimicrobial (lipo)peptides and detergents to induce lipid membrane leakage.

The first objective is to improve the understanding and use of synergistic cofactors to tune the activity and selectivity of antibiotic lipopeptides. This may involve one or more additional peptides but also the addition of surfactants or other active molecules to formulations of antibiotic peptides. When Soravia et al. (10) found that Xenopus produces not only magainin but also, e.g., PGLa, they mentioned that the mixture could “provide a more comprehensive spectrum of action” but recognized that overall, the basis of the diversity remained unclear. Matsuzaki et al. (11) showed that the synergistic action of magainin and PGLa against Escherichia coli, which is also reflected in synergistic calcein leakage from liposomes, results from a heterodimer between the two. The dimer combines the advantages of the two constituents when it comes to forming a toroidal pore; these are the fast formation typical of PGLa and the moderate stability of the pore found for magainin. Synergistic effects of different lipopeptides included in the fengycin family, plipastatin (PA1) and agrastatin 1 (AS1), to induce vesicle leakage have been discussed in terms of a solubilization of the more active yet less soluble AS1 in micelles of PA1 (12). This raises the question whether even simple detergents might act synergistically with antimicrobial (lipo)peptides by enhancing their bioavailability. Surfactins alone were inactive against yeast but enhanced the activity of iturin A against yeast (13) and red blood cells (14). Both compounds were found well miscible in monolayers (14). Surfactins inhibited the growth of Candida synergistically with ketoconazole (15), a fungicide inhibiting ergosterol synthesis. AMPs such as magainin and ranalexin showed synergistic activity with echinocandins (16), which inhibit cell-wall synthesis and thus might facilitate the access of the AMPs to the cytoplasmic membrane. In contrast, commercial surfactins were found to reduce the fungicidal activity of fengycins against Rhizopus (17).

The second objective of our work is to improve the conceptual clarity of the modes of action of antibiotic peptides by assessing their concerted action with a detergent. The basic working hypothesis is very simple. The effects of peptides inducing membrane leakage by detergent-like mechanisms should essentially be additive with those of a detergent applied in parallel. Traditionally, the term “detergent-like mechanism” is used for the solubilization of part of the host membrane into mixed micelles (18,19). On the one hand, this is very logical: detergere is Latin for “to wipe off”, pertaining here to greasy stains removed via the formation of mixed micelles. On the other hand, this terminology leads to the confusing paradox that most detergents do not primarily permeabilize membranes by the so-defined detergent-like mechanism. Instead, detergents have been found to induce toroidal pores or transient membrane failure due to asymmetric expansion, chain disordering, and membrane thinning at concentrations well below those needed for the appearance of mixed micelles (20–23). This explains why other authors used the term to describe membrane pores with short lifetime or variable size (24–26). Hence, micelles are not necessary for detergent-like permeabilization, and they might not even be sufficient. The micellar mechanism of membrane solubilization describes a scenario where the detergent is kinetically hindered to disrupt membranes, so that only some lipid from the outer leaflet is solubilized even at high pH 8.5 detergent concentration (27,28). Finally, detergents may also resemble catalysts of peptide action, for example by solubilizing the peptide or by reducing the activation energy for the formation of a detergent-free pore structure.

We define the term “additive action” based on the concept of additivity of fractional activities. This has been found to represent the thermodynamics in ideally mixing systems, such as the critical micelle concentration (CMC) (29,30) and bilayer-micelle phase boundaries (31) as well as the activity of antimicrobial agents (16,32) and drugs. The fractional inhibitory concentration index, also referred to as combination index (CI) in a more general context, is used to quantify synergistic or antagonistic deviations from additive action (16,32). The results illustrate that our simple starting hypothesis (all detergent-like molecules act additively) does not acknowledge the full complexity of the systems but provides a good starting point to tackle the problem.

Materials and Methods

Materials

The lipid, POPC (1-palmitoyl-2-oleoyl-phosphatidylcholine) and POPG (1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-(1′-rac-glycerol) (sodium salt)) were purchased from Avanti Polar Lipids (Alabaster AL). Calcein, TRIS, NaCl, and EDTA were of the highest purity available from Sigma (St. Louis, MO). The nonionic detergents C₁₂EO₈ (octaethyleneglycol mono-dodecylether), OG (n-Octyl-β-D-Glucopyranoside), and the zwitterionic CHAPS (3-[(3-Cholamidopropyl)dimethylammonio]-1-propanesulfonate), were obtained from Anatrace (Maumee, OH) in Anagrade purity (99% HPLC).

Fengycins (JJ372-48 and AQ376-6) and surfactins (JJ297-11-2 and AQ297-11-2), were provided by Bayer CropScience (Davis, CA). We use the plural terms here to indicate that they represent mixtures of closely related lipopeptides as isolated from cultures of B. subtilis QST713. This strain is the basis of the biopesticide Serenade ASO (Bayer CropScience). As detailed by Ongena and Jacques (1), fengycins are a family of lipopeptides with β-hydroxy-fatty acids of 14–18 carbons linked to Glu, Orn, and a lactone ring of eight amino acids. Fengycins include, for example, plipastatin A1 (octapeptide cycle Tyr-Thr-Glu-Val-Pro-Gln-Tyr-Ile) and agrastatin 1 (Tyr-Thr-Glu-Ala-Pro-Gln-Tyr-Val). The native mixture of fengycins forms micelles, but agrastatin 1 was found to crystallize from solution at micromolar concentration (12). Fengycins carry an overall negative charge at neutral pH. Their average molecular mass is 1450 g/mol.

Surfactins consist of a heptapeptide lactone ring interlinked with a β-hydroxy fatty acid; a typical sequence is Glu-X-Leu-X-Asp-Leu-X, with the X’s representing combinations of Val, Leu, or Ile. The effective molecular mass of the fraction is 1036 g/mol. The peptide ring was shown to fold into a saddlelike structure with the two acidic residues localized oppositely from the chain (33). Surfactins form micelles with a CMC of ≈7.5 μM at pH and 110 mM salt (25).

Magainin 2 was purchased from American Peptide (Sunnyvale, CA). It folds into an amphipathic α-helix upon membrane binding.

Two buffers were used for lipopeptides and detergents: standard buffer contained 110 mM NaCl, 10 mM Tris, 0.5 mM EDTA, and was adjusted to pH 8.5. Isotonic calcein buffer used for preparing calcein-loaded vesicles contained 70 mM Calcein, 10 mM Tris, 0.5 mM EDTA, at pH 8.5. Magainin 2 was dissolved in 100 mM NaCl, 10 mM Tris, at pH 7.4.

Vesicles

Vesicles were prepared from POPC-POPG mixtures (1:1 mol/mol) for experiments with magainin and from pure POPC for all other experiments. Large unilamellar vesicles were prepared as described in Heerklotz et al. (34). Briefly, aliquots of a stock solution in chloroform were dried by nitrogen and vacuum and the lipid quantified by weighing. After adding buffer, the samples were vortexed and subjected to 5–7 freeze-thaw cycles. The resulting multilamellar vesicles were extruded 10 times through nucleopore membranes (Whatman Nuclepore, Sigma-Aldrich) with 100-nm pore size in a Lipex pressure extruder (Northern Lipids, Burnaby, BC, Canada) at room temperature. For leakage experiments, calcein-loaded vesicles were prepared in calcein buffer, and the buffer outside the liposomes was exchanged to standard buffer on disposable PD-10 desalting columns (GE Healthcare, Little Chalfont, Buckinghamshire, UK). The lipid concentration then was measured by the phosphate colorimetric assay (BioVision, Milpitas, CA).

Fluorescence

Fluorescence decays were measured using a Fluorolog 3 TCSPC system from Horiba (Edison, NJ). The excitation source was a laser diode at 467 nm pulsed at 1 MHz; gray filters were used to limit the frequency of counts to <20 kHz. The emission was led through a double-grated monochromator (515 nm, 2 nm slit) and recorded by a TBX detector (Horiba), accumulating for 180 s to give rise to ≈10⁴ peak counts. Biexponential fits of the decay were obtained by Horiba’s DAS6 software by deconvolution of the decay with the instrument response function measured with a scattering standard.

Leakage assay

The fluorescence lifetime-based leakage assay was described in detail in Patel et al. (23). Samples for leakage measurements were produced by injecting 10 μL of a 6 mM POPC dispersion of calcein-loaded vesicles into either 190 μL or 1.99 mL of peptide solutions of the desired concentration, c_P, giving rise to a lipid concentration, c_L, of 300 or 30 μM, respectively. The injection of a small volume of lipid suspension into a peptide solution ensures that no lipid is exposed to a higher-than-average peptide concentration before mixing is completed. After mixing, the samples were incubated for 1 h on a gently rocking shaker at room temperature. In some cases, it is desirable to record leakage as a function of time over several hours, but if one needs to select a single, representative parameter we feel that 1 h incubation is appropriate. Note that dye efflux often stops after some 10 min, so that shorter times or starting rates may lead to an overestimation of the leakage effect.

After incubation, the samples incubated at 300 μM lipid were filled up to 2 mL with standard buffer, and those of 30 μM were measured unchanged. Fluorescence decays were measured at 25°C and fitted as described. The signals from free and entrapped dye can be distinguished in a biexponential fit of the fluorescence decay by their different fluorescence lifetimes, with τ_F = 4 ns for the free dye and τ_E = 0.4–4 ns for the entrapped dye, depending on its local concentration remaining within the vesicles (0.4 ns for 70 mM as in nonleaky vesicles). Then, the amounts of free and entrapped dye can directly be quantified in terms of the corresponding preexponential factors, B_F and B_E, yielding the efflux

$$E=\left(B_F-B_{F0}\right)/\left(B_F-B_{F0}+Q_{\text{stat}}{B}_E\right),$$

where B_F0 denotes B_F in the absence of peptide, and Q_stat = 1.2 corrects for static quenching.

Experiments to assess concerted action of two compounds were realized by keeping the C₁₂EO₈ component fixed within a series and varying the concentration of the other component.

Theory

Independent versus additive action

We are considering any parameter quantifying the effect of a compound on the membrane. In our case, this is the dye efflux after a certain incubation time, E, as a function of the concentrations of two components A and B (detergent or peptide), c_A and c_B. The simplest case of what may happen if A and B are combined is the additivity of the E values:

$$E\left(c_A+c_B\right)=E\left(c_B\right)+E\left(c_B\right).$$ (1)

It is important to note that this case does not represent additive, but independent action. Imagine a situation where c_A is just at the threshold of inducing leakage, E = 0, but any small, further addition of A would induce substantial leakage. If another component B is added instead that causes leakage by the same mechanism, one would assume that this makes the system cross the threshold and induce leakage. However, this is not what Eq. 1 predicts. Instead, E(c_A + c_B) = 0 as long as both components are below their individual leakage thresholds.

Independent action may be expected if the two compounds act by mechanisms that are distinct and do not influence each other. For example, a peptide forming barrel-stave channels might act independently of a detergent, but only if the unspecific membrane changes induced by the detergent do not affect the formation of the channel. If, for example, the transmembrane insertion of the peptide or another process involved in the formation of the oligomeric channel is facilitated by global membrane thinning, disordering, or curvature strain, the activity of the two compounds might not be truly independent despite the different mechanisms.

Of course, all values of E > 100% that would mathematically be predicted by Eq. 1 have to be limited to 100% (cutoff).

Additive action and the CI

Activity tests of a combination of antimicrobial compounds, or drugs in general, are routinely interpreted in terms of the fractional inhibitory concentration index or CI (32),

$$CI=\frac{c_A}{c_A^{\ast }}+\frac{c_B}{c_B^{\ast }},$$ (2)

where c_A and c_B represent concentrations of A and B, respectively, that are active if combined with each other, whereas c_A^∗ and c_B^∗ represent the individually active concentrations (e.g., minimum inhibitory concentrations) of A or B only. The case that CI = 1 is referred to as “additive action”. It corresponds to the case that the combined drugs are active when, for example, one is at 40% of its individual active concentration and the other one is at 60%. Additive action suggests that both components act by the same mechanism, so that their effects are essentially exchangeable.

Equation 2 with CI = 1 is a general description of additivity and the behavior of ideal mixtures. It predicts, for example, the CMC of a mixed surfactant system (29,30). In this case, c_A^∗ and c_B^∗ represent the CMC values of the individual components. An analogous equation has also been shown to predict the onset of membrane solubilization by a mixture of two detergents with excellent precision (31).

We can use the same formalism for any other measure of membrane-perturbing activity, such as, in our case, the dye efflux after 1 h of incubation, E. In this study, we keep one concentration, c_A, fixed and seek to compute the concentration c_B (abscissa value of solid fit lines shown below) that is predicted to cause a chosen E^∗ by solving Eq. 2 with CI = 1 to

$$c_B=\left(1-\frac{c_A}{c_A^{\ast }}\right)c_B^{\ast }.$$ (3)

If a pair of c_A, c_B is found to be active that gives rise to CI > 1, A and B act less than additively, and if c_A + c_B are active but c_A > c_A^∗ at c_B > 0, the activity of A is inhibited by B. CI < 1 implies that A and B act superadditively, or synergistically.

We discuss the CI formula in the Appendix, showing that it needs three nontrivial assumptions to derive CI = 1 for additive action:

• 1.The effect or activity (such as leakage, inhibition of microbial growth, etc.) is a function of one parameter quantifying the underlying perturbation (for traditional detergents, this could be membrane curvature stress);
• 2.The perturbation parameters of different molecules applied in parallel are additive; and
• 3.The perturbation parameter is proportional to the concentration of the active molecule.

The last assumption might be a critical approximation, particularly when a very low concentration of one perturbant is combined with a high one of another. We have, therefore, typically challenged the model by studying different ratios of the two perturbants.

Leakage mechanism

The crucial distinction between graded versus all-or-none leakage mechanisms goes back to the pioneering studies of Weinstein et al. (35) and the requenching protocol by Wimley et al. (36). More recently, new approaches have been introduced based on biexponential fits of time-resolved fluorescence decays (23) as well as observations of giant unilamellar vesicles (37–39). For example, E = 50% may mean that half of the vesicles leaked out all of their dye, and the other half leaked out no dye at all (all-or-none). Alternatively, it may mean that all vesicles leaked out half of their entrapped dye, so that their internal dye concentration decreased from 70 to 35 mM (graded).

The fluorescence lifetime-based approach used here is based on the Stern-Volmer equation for collisional quenching,

$$\frac{{\tau }_0}{\tau }=1+K_d{c}_{DE},$$ (4)

with the Stern-Volmer constant K_d (= 0.13/mM for calcein (23)) and the local concentration of the (entrapped) dye, c_DE. In our case, the maximum entrapped dye concentration is c_DE = c_DE⁰ = 70 mM. For all-or-none leakage, c_DE remains constant because whenever a vesicle leaks, none of its former content contributes to the entrapped dye, c_DE, any longer. For homogeneous, graded leakage, the efflux E_HG (subscript here for “homogeneously graded”) is

$$E_{HG}=1-\frac{c_{DE}}{c_{DE}^0}=\frac{{\tau }_0}{K_d{c}_{DE}^0}\times \frac{1}{{\tau }_E}-\frac{1}{K_d{c}_{DE}^0}+1.$$ (5)

The right equality is found by replacing c_DE using Eq. 4. The function E_HG(τ_E) is a hyperbola because K_d, c_DE⁰, and τ₀ are constants. Plotted on a reciprocal scale, E_HG(1/τ_E), it becomes a straight line increasing from 0 at τ_E = τ(c_DE⁰), which is ≈0.4 ns for c_DE = 70 mM, to 1 at τ_E = τ₀ (= 4.0 ns). This ideal behavior is illustrated by the shaded dash-dotted diagonal line in Figs. 1–5 B below, respectively.

Figure 1.

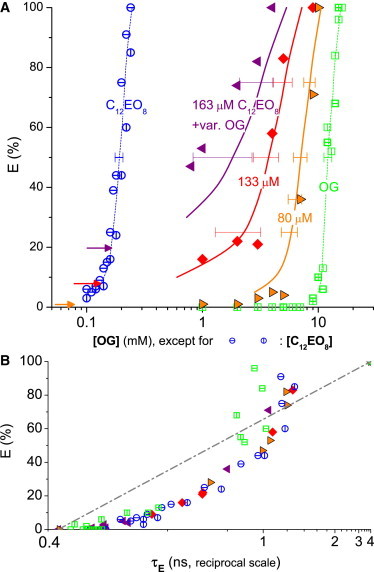
Leakage data for C₁₂EO₈ (open circles; horizontal and vertical bars distinguish independent measurements), octyl glucoside (OG, open squares), and mixtures thereof (solid symbols) acting on 300 μM POPC vesicles. (A) Dye efflux after 1 h, E, as a function of the concentration of OG (for pure OG and mixtures) or C₁₂EO₈. (Solid symbols) Mixtures of three series with constant C₁₂EO₈ of 163 μM (left-pointing triangles), 133 μM (diamonds), and 80 μM (right-pointing triangles), respectively, and variable OG (see abscissa); the leakage values corresponding to these concentrations of C₁₂EO₈ alone are marked (arrows). (Solid lines) Values calculated using Eq. 3 assuming additive action (CI = 1) (dashed lines are to guide the eye only); all mixtures act additively within error. (B) E as a function of the fluorescence lifetime of entrapped dye, τ_E, on a reciprocal scale. To see this figure in color, go online.

Figure 2.

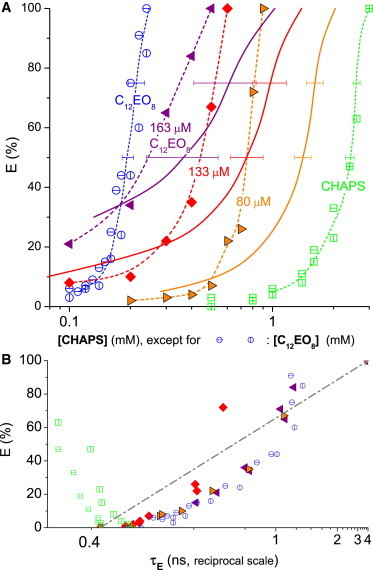
Leakage data for CHAPS (open squares), C₁₂EO₈ (open circles), and mixtures thereof (solid symbols) acting on 300 μM POPC vesicles. (Bars in symbols distinguish independent data sets.) (A) Dye efflux after 1 h, E, as a function of the concentration of CHAPS (for pure CHAPS and mixtures) or C₁₂EO₈. (Solid symbols) Mixtures of three series with constant C₁₂EO₈ of 163 μM (left-pointing triangles), 133 μM (diamonds), and 80 μM (right-pointing triangles), respectively, and variable CHAPS (see abscissa). (Solid lines) Values calculated using Eq. 3 assuming additive action (CI = 1) (dotted lines are to guide the eye only). The fact that the points for mixtures are at lower concentration ( see corresponding solid curves) implies synergistic action. (B) E as a function of the fluorescence lifetime of entrapped dye, τ_E, on a reciprocal scale. To see this figure in color, go online.

Figure 3.

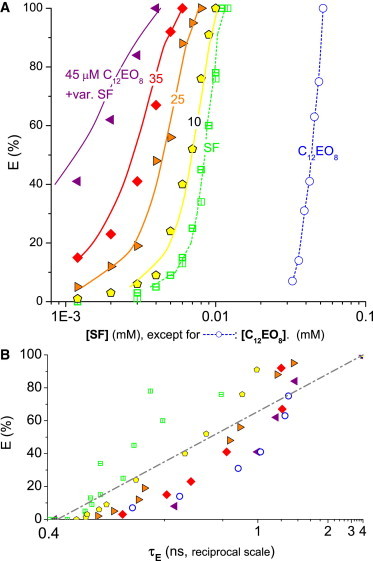
Leakage data for surfactins (SFs, open squares), C₁₂EO₈ (open circles), and mixtures thereof (solid symbols) acting on 30 μM POPC vesicles. (Bars in symbols distinguish independent data sets.) (A) Dye efflux after 1 h, E, as a function of the concentration of SF (for pure SF and mixtures) or C₁₂EO₈. (Solid symbols) Mixtures of four series with constant C₁₂EO₈ of 10 μM (pentagons), 25 μM (right-pointing triangles), 35 μM (diamonds), and 45 μM (left-pointing triangles), respectively, and variable SF (see abscissa). (Solid lines) Values calculated using Eq. 3 assuming additive action (CI = 1) (dashed lines are to guide the eye only). Concerted action is additive, within error. (B) E as a function of the fluorescence lifetime of entrapped dye, τ_E, on a reciprocal scale. To see this figure in color, go online.

Figure 4.

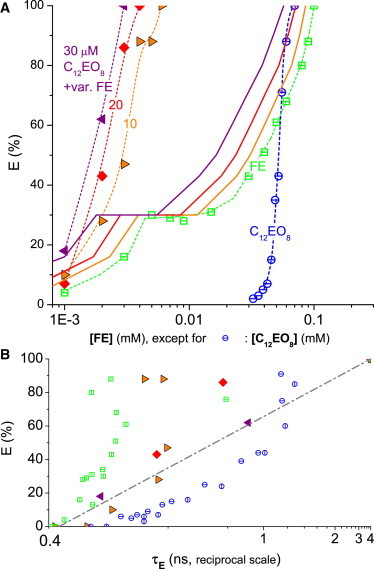
Leakage data for fengycins (FEs, open squares), C₁₂EO₈ (open circles), and mixtures thereof (solid symbols) acting on 30 μM POPC vesicles. (A) Dye efflux after 1 h, E, as a function of the concentration of FE (for pure FE and mixtures) or C₁₂EO₈. (Solid symbols) Mixtures of three series with constant C₁₂EO₈ of 10 μM (right-pointing triangles), 20 μM (diamonds), and 30 μM (left-pointing triangles), respectively, and variable FE (see abscissa). (Solid lines) Values calculated using Eq. 3 assuming additive action (CI = 1) (dotted lines are to guide the eye only). Concerted action is strongly synergistic due to the disappearance of the plateau region seen for FE alone. (B) E as a function of the fluorescence lifetime of entrapped dye, τ_E, on a reciprocal scale. To see this figure in color, go online.

Figure 5.

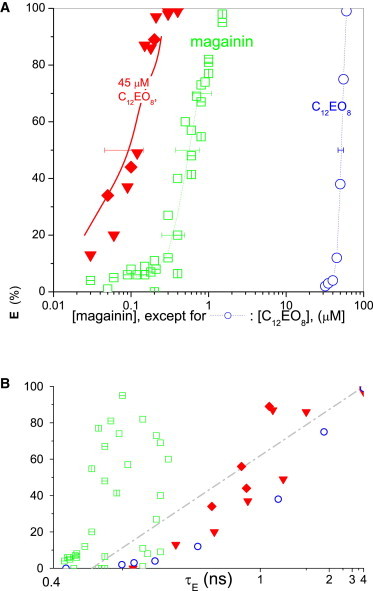
Leakage data for magainin 2 (open squares), C₁₂EO₈ (open circles), and mixtures thereof (solid symbols) acting on 30 μM POPC/POPG (1:1 mol/mol) vesicles. (A) Dye efflux after 1 h, E, as a function of the concentration of magainin (for pure magainin and mixtures) or C₁₂EO₈. (Solid symbols) Mixtures of constant C₁₂EO₈ of 45 μM (diamonds and down-triangles for two independent batches). (Solid line) Value calculated using Eq. 3, assuming additive action (CI = 1) (dotted lines are to guide the eye only). Concerted action is additive, within error. (B) E as a function of the fluorescence lifetime of entrapped dye, τ_E, on a reciprocal scale. To see this figure in color, go online.

In addition to the two ideal cases, all-or-none (τ_E = const) and homogeneously graded (shaded diagonal), the average τ_E values can increase less steeply or more steeply than for homogeneous graded leakage, which gives rise to points below and above the diagonal line, respectively. Such data can be explained by a heterogeneous leakage behavior, where some vesicles show graded leakage whereas others show very low (points below diagonal) or very high (points above diagonal) leakage (23). We will oversimplify and refer to these putative scenarios as some-or-none (below diagonal) and some-or-all (above).

Results

Detergent-detergent mixtures

Fig. 1 A shows the relative dye efflux after 1 h incubation, E, obtained for C₁₂EO₈, OG, and mixtures thereof applied to 300 μM POPC vesicles. C₁₂EO₈ (open circles in Fig. 1, with horizontal and vertical bars labeling two independent data sets) gives rise to a steep increase of leakage, reaching 50% at 190 μM detergent. OG (open squares in Fig. 1) has a weaker spontaneous curvature and a considerably lower partition coefficient than C₁₂EO₈, which contribute to the fact that it needs a much higher concentration of 12.1 mM to induce 50% dye efflux.

The solid symbols represent efflux values obtained for three series with constant C₁₂EO₈, respectively, and increasing concentration of OG (as given in the abscissa). The more C₁₂EO₈ was used, the smaller was the amount of OG necessary to induce leakage and, hence, the curves are shifted to lower concentrations.

Each of the data sets for combinations of the two detergents is accompanied by a solid curve that was simulated for additive action using Eq. 3, i.e., CI = 1. Because these calculations are based on the individual curves for C₁₂EO₈ (open circles) and OG (open squares), estimated errors of these curves (see error bars at E = 50%) will yield errors of the predicted values as illustrated with error bars at E = 25, 50, and 75%. It is important to note that errors are expected to be very substantial at the lowest possible E-values and high C₁₂EO₈ concentrations, a phenomenon resulting simply from the arithmetic of Eq. 3. Overall, we may state that the data are in line with the assumption of additive action of C₁₂EO₈ and OG to induce leakage of POPC membranes.

Fig. 1 B shows that the lifetime of the entrapped dye increases with increasing efflux, indicating graded leakage for C₁₂EO₈, OG, and its mixtures. In the E-versus-1/τ_E-plot explained above, the points are somewhat below the dash-dot diagonal indicating heterogeneously graded or some-or-none leakage. Overall, the graded leakage can be explained by enhanced permeability of thinned and disordered membranes, or many extremely small and short-lived leakage events (12,40).

Fig. 2 shows the results for another pair of detergents, C₁₂EO₈ and CHAPS, analogously to Fig. 1. This system behaves in a fundamentally different manner from the one discussed in Fig. 1. With increasing E and increasing CHAPS concentration (i.e., lower amount of C₁₂EO₈ added), there is a very significant deviation between the data points and the predictions assuming additive action. For example, Eq. 3 predicts for additive action that in the presence of 80 μM C₁₂EO₈, it would need 1.6 ± 0.15 mM CHAPS to induce E = 72% (rightmost solid line). However, the combination experiment yielded 72% leakage already at 0.8 mM CHAPS (right-pointing triangle) and 80 μM C₁₂EO₈. This implies that the combination CHAPS+C₁₂EO₈ acts superadditively or synergistically. For high CHAPS (i.e., low C₁₂EO₈ and high E), CHAPS is ∼30% of its c^∗ while C₁₂EO₈ is at c/c^∗ ≈ 40%, then the CI becomes as small as ≈0.7 (at E = 75%). With increasing contribution of C₁₂EO₈, CI tends toward 1.

The leakage mechanism of CHAPS is all-or-none, as indicated by the virtually vertical traces in the E(1/τ_E) plot (Fig. 2 B). Note that the reciprocal scale expands experimental and fitting errors in the 0.4-ns range. The result indicates that the local concentration of entrapped dye remains largely unchanged; increasing E means that there are fewer vesicles left that still contain the dye. Such behavior is expected if some vesicles establish a distinct pore or leak, and the redistribution of peptide, and reappearance of such pores in other vesicles, is too slow to occur at a large scale within the incubation time of the experiment. The combinations of CHAPS (all-or-none) and C₁₂EO₈ (graded) studied here show graded leakage.

Bacillus Subtilis Lipopeptides

Fig. 3 shows the results for surfactins (SFs) and C₁₂EO₈. Pure SF starts inducing leakage (10%) of 30 μM POPC vesicles at ∼5 μM. Experiments exploring the concerted action of SF and the detergent, C₁₂EO₈, were performed with a series at constant 10, 25, 35, and 45 μM C₁₂EO₈ (solid symbols in Fig. 3). All data are well within estimated error of the prediction obtained with Eq. 3 for CI = 1, i.e., additive action. All samples show graded leakage with some trend from somewhat all-or-some leakage for SF to the well-known some-or-none behavior of C₁₂EO₈.

The data for fengycins (Fig. 4) confirm the results from an earlier batch (12) that it causes all-or-none leakage that starts at a few micromoles but plateaus at E ≈ 25 ± 5% from ∼3–30 μM (values for 30 μM POPC vesicles). Here, the subsequent rise is somewhat steeper, and we measured all the way up to 100 μM, where leakage tends to 100%. This high concentration might be of little direct relevance for fungicidal activity, but it is important for the prediction of additive behavior needed here.

Interestingly, this plateau is not found for fengycins (FE)-detergent mixtures, reflecting a highly synergistic behavior. FE acts via an all-or-none mechanism as reported before and indicated by the vertical trend of the open squares in Fig. 4 B. Increasing contributions of C₁₂EO₈ change this mechanism to heterogeneously graded, via all-or-some to some-or-none.

Magainin 2

In contrast to the other compounds studied here, magainin is virtually inactive against zwitterionic POPC membranes, which contributes to its selectivity of action against bacteria with their anionic lipids in the outer leaflet of the cytoplasmic membrane. Fig. 5 represents leakage data for magainin 2 acting on 30 μM POPC+POPG vesicles (1:1 mol/mol). Three independent batches of vesicles and two batches of peptide yielded a concentration of 0.6 ± 0.2 μM to cause 50% dye efflux, following a clear-cut all-or-none mechanism. The detergent alone causes 50% efflux from 30 μM POPC+POPG at 51 μM, just as from POPC as shown in Fig. 4.

Mixtures of 45 μM C₁₂EO₈ with various concentrations of magainin are illustrated by the solid triangles and diamonds (data for independent batches of lipid and magainin) in Fig. 5. They are in line with a CI of 1, i.e., with additive action as illustrated by the solid line. The all-or-none pattern found for magainin alone (Fig. 5 B) agrees with the mechanism established in Ludtke et al. (41) and Gregory et al. (42). The mixtures of magainin and C₁₂EO₈ studied here show graded leakage.

Discussion

Detergent-like effects and heterogeneity of action

Detergents reduce the barrier function of membranes due to membrane thinning and disordering, bilayer-couple effects, toroidal pore formation, and solubilization of the membranes in mixed micelles (43). All these phenomena have also, among others, been claimed to play a role for the membrane activity of certain antimicrobial peptides (3) and can, therefore, be addressed as detergent-like effects of these peptides in the most general sense (19,24–26,44). At the same time, these antimicrobial peptides are typically more active and selective in their action than ordinary detergents, suggesting that there are principal differences as well. Furthermore, the implication of detergent-like effects of peptides as such is no proof that this activity is sufficient or even essential for their biological activity. Curvature strain, for example, may aid the insertion into and translocation across the membrane, but the activity in vivo might crucially involve a target or cofactor that is not present in the vesicle leakage experiment. An impressive example for this is nisin, which does permeabilize vesicles, but turns out to be far more active in the presence of lipid II (45). The function of an oligomeric barrel-stave channel per se should not benefit from the presence of a detergent, but its formation might be facilitated by membrane thinning and disordering. This would be in line with the finding that unspecific membrane perturbation by magainin promotes the trans-membrane orientation of PGLa, contributing to their well-known synergistic activity (46).

Our results have shown that, indeed, the (lipo)peptides magainin, surfactins, and fengycins as well as the detergents, CHAPS and octyl glucoside, exhibited additive or superadditive membrane permeabilization with C₁₂EO₈. This suggests that their mode of action involves detergent-like effects. However, CHAPS and FE showed a combination index <1 (synergistic action), and surfactins and magainin had a CI ≈ 1 but differed from C₁₂EO₈ in inducing all-or-none leakage.

We postulate that one key to understanding these specifics is the heterogeneity of the distribution and action of the membrane-perturbing agents in the membrane. Rather precise additivity of action of curvature-active molecules is to be expected, if they mix homogeneously with the lipids. This is what typical detergents such as C₁₂EO₈, OG, lauryl maltoside, or sodium dodecyl sulfate seem to do in simple, fluid model membranes such as those of POPC, egg yolk PC, or soybean PC (31,47). Permeabilizers that distribute and act in a homogeneous fashion should typically affect all vesicles similarly and, hence, cause graded leakage.

Other membrane permeabilizers have been shown to distribute unevenly in a membrane and perturb the membrane heterogeneously, even below the thresholds for leakage and lysis. Segregation of the active compound in clusters or domains would then cause a local enhancement of perturbation and promote the formation of oligomolecular complexes or arrangements. Membrane perforation may occur not only within a peptide-enriched domain but also at its boundaries (48).

In the context of this study, it is important to emphasize that there is an optimum, intermediate degree of heterogeneity that causes maximal dye efflux, E. This optimum depends on the size of the vesicle or compartment. Heterogeneity within a vesicle focuses the activity and can thus be expected to enhance efflux. Heterogeneity between the vesicles, however, may limit efflux if it persists over the incubation time of the experiment. It tends to cause all-or-none leakage where some vesicles show enough or more-than-enough leakage to release all entrapped dye whereas others fail to develop an effective leak. As a simple rule of thumb, we may state that graded leakage suggests a less-than-optimal (or close-to-optimal) heterogeneity whereas all-or-none leakage implies too much heterogeneity for maximal dye release.

Consequently, concerted, detergent-like action of two compounds may induce nonadditive leakage effects if the interactions between the two change their heterogeneity of action. The system CHAPS-C₁₂EO₈ seems to be a good example. CHAPS was classified as a heterogeneous perturbant (47) and causes all-or-none leakage (Fig. 2), whereas C₁₂EO₈ acts homogeneously (47) and causes graded leakage. In concerted action, the two synergize significantly, which could be explained by a certain cosegregation of C₁₂EO₈, accumulating in CHAPS-induced domains (i.e., induced heterogeneity of C₁₂EO₈) and/or by a homogenizing effect of C₁₂EO₈ on CHAPS, rendering it active in more vesicles.

The same effects might occur with fengycins (FEs), another heterogeneous perturbant and all-or-none permeabilizer. FEs may tend to oligomerize and small oligomers render them (locally) more active as predicted by a recent molecular dynamics study (49). However, at least for some members of the fengycin family such as agrastatin A, the tendency to aggregate does not always promote membrane-perturbing activity. These molecules can become inactive due to precipitation, forming hexagonal sheet-like crystals if they are not kept in solution or in micelles by other, micelle-preferring, fengycins (12). This phenomenon suggests another obvious mechanism for the particularly strong synergism between fengycins and C₁₂EO₈: the detergent may oppose crystallization of FE components.

Surfactins and magainin are also not ideal detergents, but they showed additive action with C₁₂EO₈. Although SF acts heterogeneously on the molecular level, it causes close to homogeneously graded leakage, indicating a limited degree of heterogeneity. Magainin alone causes all-or-none leakage by forming toroidal pores (41,42). In the presence of detergent, we find additive, graded leakage. This may mean that the pores become smaller and more spread out over the vesicles, with both effects balancing each other in terms of the total efflux measured. We should note that stronger heterogeneity of a toroidal pore system (and, consequently, all-or-none leakage) is expected for high activation energy of pore formation and high stability of the pores; then, peptide might be acquired by a few existing pores rather than forming additional ones (see also related work of Wheaten et al. (39), Ludtke et al. (41), and Gregory et al. (42)). In this sense, the discussion from Matsuzaki et al. (11) of the synergistic action of magainin and PGLa in terms of optimizing rate of formation and stability of pores is related to heterogeneity as well.

Optimal heterogeneity differs between vesicles and cells

Vesicle leakage data have been considered important information on membrane-active peptides for decades, but the specific correlation between dye efflux and antibiotic activity remains to be established in much more detail. The data and concepts discussed here permit discussing one out of many issues governing this vesicle-cell correlation, namely the size of the compartment (see also Patel et al. (12)). The dye efflux from vesicles via all-or-none leakage is not limited by the rate of the efflux but by the compartmentalization of the system into small volumes, not all of which develop a pore or leak. This restriction applies to a far lesser extent to a cell membrane. Because the membrane area of a cell is a hundred or more times larger than that of a 100 nm-vesicle, it appears that a hundred times fewer, large and stable (all-or-none) pores per μm² of membrane are required to make it leak out its contents. Hence, the efflux induced by all-or-none permeabilizers increases with increasing vesicle size and the biologically active concentration of an all-or-none permeabilizer might be orders of magnitude below the critical concentration in an experiment with vesicles of 100 nm size. The opposite might be true for graded permeabilizers that cause a rather homogeneous, slow efflux per membrane area because the area/volume (i.e., efflux/content) decreases with size. This size dependence could also account for the observation of Wheaten et al. (39) that CE-2 switches from graded to all-or-none leakage with increasing vesicle size. This compound might cause all-or-some leakage by both few large pores and many small defects (e.g., membrane thinning and disordering and/or very small and short-lived leaks). With increasing vesicle size, the overall impact of the graded contribution becomes less and that of the all-or-none contribution becomes more, so that the dominant action of the two effects switches to all-or-none.

A similar phenomenon can also account for a switch from all-or-none to graded with increasing incubation time (unpublished results): efflux through large pores is fast but possibly limited to a few vesicles, whereas permeation that is more homogeneous may be slower but unlimited, thus catching up with time.

Improvement of antibiotic products

We have shown that cosurfactants can enhance the membrane permeabilizing activity of antimicrobial peptides in an additive or synergistic fashion. Does this mean that detergents should be considered as part of product formulations of agricultural or medical antimicrobials?

Although this might, indeed, be worth considering, it should be emphasized that antibiotics of biological origin often come as mixtures that appear to exploit such synergisms. Agrastatin, for example, is produced by B. subtilis QST713 along with plipastatins and, in fact, with surfactins that are also likely to fulfill the function of the detergent in the study presented here. Certain aspects discussed here apply also to the synergism between magainin and PGLa. It seems the biological sources have already optimized the formulations of their agents.

Further to lowering the active peptide concentration, detergents can also alter the mechanism and selectivity of action. The active concentration of magainin was reduced by a detergent here, but the addition also changed the mechanism from all-or-none to graded. Given the size dependencies of the optimum mechanism and heterogeneity of action, we cannot exclude detergent to actually inhibit magainin action against cells.

When it comes to the selectivity of action, it should be noted that curvature strain and toroidal pore effects, as such, are quite unspecific. Selective action against bacteria often results from electrostatic interactions between cationic peptides and anionic lipids in bacterial membranes as well as from inhibition by cholesterol in mammalian ones. The concept of membrane heterogeneity to govern the action of peptides explains that a perturbant can also be activated by poor miscibility with a component of the target membrane. One may speculate that the addition of a homogenizing detergent could, by default, decrease the selectivity of a peptide. Such an effect might increase the spectrum of pathogens to be attacked but also decrease the therapeutic window of a compound. However, a cofactor mixing poorly with a membrane component might also enhance or alter the specificity of an active peptide. Triton, for example, has been found poorly miscible with cholesterol (47,50) and might, this way, activate peptides against cholesterol-containing membranes.

Conclusions

The additivity of membrane permeabilizing activities can be modeled analogously to the concept of the fractional inhibitory concentration index.

The antimicrobial (lipo)peptides magainin 2, surfactins, and fengycins exhibited additive or superadditive membrane permeabilization when applied in parallel with a nonionic detergent, C₁₂EO₈. This supports the hypothesis that the antibiotic activity involves detergent-like effects (membrane thinning, bilayer couple, toroidal pore formation, micellization) along with, possibly, more-specific phenomena.

Synergistic action has been found for the two detergents, C₁₂EO₈ (causing homogeneous membrane disordering and graded leakage) and CHAPS (inducing heterogeneous perturbation and all-or-none leakage). This illustrates the importance of the degree of heterogeneity of action for activity and selectivity and suggests ways to improve these parameters by proper formulations or combinations of antimicrobial peptides.

A previous hypothesis of the activity plateau of fengycins to be caused by a lack of micelle-forming components (resulting in precipitation) was supported by the finding that detergent micelles can eliminate the plateau, too.

Appendix

Background of the CI concept

Let us consider the assumptions that are inherent in Eq. 2 in some more detail. We have argued above that for what we refer to as additive action, it is not E but an underlying perturbation that is additive. We will assume that this perturbation can be unequivocally expressed by one parameter, y:

$$E=f\left(y\right).$$ (6)

This function is typically highly nonlinear; no assumptions are made (or needed) with respect to this. The next assumption needed for deriving an expression for additivity is, trivially,

$$y_{AB}=y_A+y_B,$$ (7)

where y_AB denotes the extent of perturbation induced by a combination of A and B, and y_A and y_B the individual perturbations by A or B, respectively. Finally, to obtain Eq. 2, we have to assume that the perturbation y is proportional to the concentration of a perturbant:

$$\begin{array}{c}{y}_A=k_A{c}_A,\\ y_B=k_B{c}_B,\end{array}$$ (8)

where k_A and k_B are constants. Let us now compare three conditions that give rise to the same leakage, E^∗, by inducing the same perturbation, y^∗. This state is reached by adding:

• 1.Only component A at c_A^∗,
• 2.Only B at c_B^∗, or
• 3.Both, so that the sum of their concentrations is (c_A + c_B)^∗:

$$E\left(c_A+c_B\right)=E^{\ast }\Rightarrow y_{AB}=y^{\ast }=k_A{c}_A^{\ast }=k_B{c}_B^{\ast }.$$ (9)

Dividing Eq. 7 by y^∗, we obtain

$$E\left(c_A,c_B\right)=E^{\ast }\text{if}1=\frac{y\left(c_A\right)}{y^{\ast }}+\frac{y\left(c_B\right)}{y^{\ast }}$$ (10)

and inserting Eqs. 8 and 9, the proportionality constants k_A, k_B cancel out and we obtain

$$E=E^{\ast }\Rightarrow 1=\frac{c_A}{c_A^{\ast }}+\frac{c_B}{c_B^{\ast }}.$$ (11)

Summarizing, we have assumed that under the experimental conditions, E is a function of a perturbation parameter y, which is additive and proportional to the concentration of the perturbant. Particularly the latter, proportionality assumption seems far from trivial, implying that the CI concept may be less general and unequivocal than commonly acknowledged.