Abstract
General anesthetics are known to cause depression of the freezing point of transitions in biomembranes. This is a consequence of ideal mixing of the anesthetic drugs in the membrane fluid phase and exclusion from the solid phase. Such a generic law provides physical justification of the famous Meyer-Overton rule. We show here that general anesthetics, barbiturates, and local anesthetics all display the same effect on melting transitions. Their effect is reversed by hydrostatic pressure. Thus, the thermodynamic behavior of local anesthetics is very similar to that of general anesthetics. We present a detailed thermodynamic analysis of heat capacity profiles of membranes in the presence of anesthetics. Using this analysis, we are able to describe experimentally observed calorimetric profiles and predict the anesthetic features of arbitrary molecules. In addition, we discuss the thermodynamic origin of the cutoff effect of long-chain alcohols and the additivity of the effect of general and local anesthetics.
Introduction
General anesthetics (including barbiturates) and local anesthetics were introduced to clinical praxis during the mid-19th century. The first general anesthetic used in surgery was diethyl ether, but many others have since been found. These include nitrous oxide (laughing gas), propofol, halothane, and sevoflurane (1), but also the chemically inert noble gas xenon and barbiturates (2)—molecules that are very different structurally. The first local anesthetic was cocaine, whose analgesic effect was described in the late 1850s. Most known local anesthetics were later developed in an attempt to avoid the addictive effect of cocaine (3). Thus, the distinction between the different classes of anesthetics is partially of historical origin. Today, it is generally believed that general and local anesthetics act by different mechanisms. The effect of local anesthetics has frequently been attributed to their specific interaction with (sodium) channel proteins (4,5). At the same time, there is wide agreement that the action of general anesthetics is not well understood. However, there exists a striking inverse linear correlation between the partitioning of general anesthetics in the lipid membrane and the critical anesthetic dose known as the Meyer-Overton correlation (1,6), and this correlation applies to drugs of quite different chemical structure, such as nitrous oxide (laughing gas), xenon (a noble gas), and sevoflurane (a fluorinated organic solvent). Another way of stating the Meyer-Overton correlation is = const., where is the effective concentration of anesthetics in the alveolar volume or in the blood where 50% of individuals are anesthetized, and P is the partition coefficient between oil and water (or air). At critical dose, the membrane concentration of all general anesthetics obeying the Meyer-Overton correlation is exactly the same (8). The Meyer-Overton correlation leads to the notion that general anesthesia is closely related to the partitioning of the drug in the lipid membrane. Indeed, in his book published in 1901 (6), Overton proposed that the correlation between membrane partitioning and critical dose suggests the existence of a generic physical mechanism for anesthesia. However, Overton did not provide any such mechanism, and his correlation remained a true but unexplained observation.
In the absence of such an explanation, some researchers favor a view involving binding of anesthetics to molecular targets. In particular, Franks and collaborators made this case popular using firefly luciferase as a target protein (9–11). They showed that the equilibrium between two structural forms of the fluorescing luciferase is controlled by most (but not all) general anesthetics. Similar mechanisms have been thought to apply in the case of membrane proteins. This view is probably incompatible with a unique mechanism for anesthesia. As argued above, at critical dose, the membrane concentration of all general anesthetics obeying the Meyer-Overton correlation—including the noble gas xenon—is identical. Thus, if both the Meyer-Overton correlation and binding to a molecular target are true, the equilibrium association constant between membrane-dissolved drug and membrane protein must display the same value for all drugs, including xenon.
Cantor (12,13) proposed combining an unspecific lipid partitioning of the drugs with a protein mechanism by investigating the lateral pressure profile of membranes in the presence of anesthetics. Anesthetics behave like ideal gases that exert forces on interfaces, and this pressure putatively alters protein structure and function. Since lateral pressure profiles would be affected in a very similar manner by different general anesthetics, it is suggested that anesthetics would alter a protein structure in a generic manner. Cantor’s view can only yield quantitative predictions about protein conformations if the precise structures and the equilibrium constants between them are known. However, Cantor and collaborators provide some experimental evidence for currents induced in γ-aminobutyric acid receptors by isoflurane and sevoflurane (14). Cantor's model predicts, in addition, that there is a correlation between lateral pressures in the lipid membrane and the critical dose.
It seems most likely that the influence of anesthetics on the thermodynamics of membranes contains the key for explaining the above correlation. We and other authors (e.g., (8,15–18) and references therein) have observed that general anesthetics induce a lowering of the solid-liquid transition temperature in lipid membranes. The melting point of membranes has exactly the same correlation with the critical anesthetic dose as the partition coefficient for those anesthetics that obey the Meyer-Overton correlation. We showed that this effect can be well explained by the so-called freezing-point depression law that originates from van’t Hoff. When applied to membranes, this law involves a slight modification of the Meyer-Overton relation. Thus, we proposed that these anesthetics are ideally soluble in the liquid phase of the membrane only and are insoluble in the solid phase. The shift of the transition is now due to the difference in the entropy of mixing in the two phases. This explanation of anesthesia has the virtue of explaining several properties of general anesthetics.
-
1.
Excess hydrostatic pressure increases melting temperatures (15,19,20) and opposes the effect of anesthetics on transitions. This can explain quantitatively the effect of the pressure reversal of anesthesia (8,21,22).
-
2.
The freezing-point depression law is based on the notion of ideal solutions in which individual molecules do not interact. The shift is thus linear in the concentration of anesthetics in the liquid membrane. Therefore, freezing-point depression is consistent with the observed additivity of the anesthetic action (6,23,24).
-
3.
Many membrane-soluble molecules do not dissolve ideally in liquid membranes, or they dissolve in the solid phase as well. Such molecules would not act as general anesthetics. For instance, cholesterol does not lower (but rather increases) melting temperatures (25) and therefore does not display anesthetic activity.
-
4.
Molecules that display phase behavior of their own should not behave as ideal anesthetics. This includes most lipids, but also long-chain alcohols (starting from chain lengths of 12, i.e., dodecanol), that display melting points above room temperature and do not act as anesthetics (26). This effect is known as the cutoff effect (see Discussion).
Freezing-point depression by anesthetics is also consistent with a recent theory for nerve pulse propagation that is based on phase transitions in biological membranes (27–29). Close to transitions in membranes, solitary electromechanical waves are possible. Such melting transitions in fact have been found for a number of biomembranes (30). Anesthetics render the excitation of the pulse more difficult, whereas hydrostatic pressure facilitates it (8,31). Freezing-point depression is caused by differences in the concentrations of the anesthetic drugs in gel and fluid lipid membranes. This can be translated into osmotic pressure differences. In this respect, our model displays conceptual similarities to the view of Cantor, described above. Here, the osmotic pressure acts on solid domains rather than on protein conformations (as in the Cantor model).
No law similar to the Meyer-Overton correlation exists for local anesthetics. At high concentrations, these anesthetics are toxic (32). Local anesthetics are typically not administered intravenously, and a critical dose cannot be determined. This has generally led to the notion that local anesthetics work by a different mechanism, e.g., by blocking sodium channels (4,5). However, this is not necessarily inconsistent with local anesthetics having some properties of general anesthetics. The Meyer-Overton correlation implies that the effect of general anesthetics is additive. Two different anesthetics, each with half-critical concentration, yield full anesthesia. Interestingly, it has been reported by various authors that the effects of local and general anesthetics are additive (see, e.g., Hines et al. (33) and Ben-Shlomo et al. (34), and Discussion). This finding is striking, since it is difficult to reconcile with the assumption that local and general anesthesia work by different mechanisms. Rather, one would conclude that local anesthetics display general anesthetic properties. In this context, it is interesting to note that local anesthetics are also membrane-active and have lower melting transitions (35–41). It is therefore plausible to hypothesize that local anesthetics have properties of general anesthetics.
In this publication, we investigate the melting behavior of membranes in the presence of both general and local anesthetics. We provide a thermodynamic formalism to understand the heat capacity profiles of lipid membranes containing both general and local anesthetics. We show that the same theoretical treatment applies to both classes of anesthetics and that their effects on transition temperatures are equally reversed by hydrostatic pressure.
Materials and Methods
Lipids were purchased from Avanti Polar Lipids (Birmingham, AL) and used without further purification. Octanol was purchased from Fluka (Buchs, Switzerland). All other anesthetics were purchased from Sigma-Aldrich (St. Louis, MO). Multilamellar lipid dispersions (10 mM, in buffer consisting of 10 mM Hepes and 1 mM EDTA, pH 7.0, octanol concentration adjusted) were prepared by vortexing the lipid dispersions above the phase-transition temperature of the lipid.
To generate multilamellar vesicles, dry lipids were dissolved in the buffer and vortexed above the main-phase-transition temperature until no visible clumps remained. For the generation of large unilamellar vesicles (LUVs, Ø ∼ 100 nm), multilamellar vesicles were extruded at least 30 times above the phase transition temperature of the respective lipid using an extruder (Avestin Europe, Mannheim, Germany) and filters with a pore size of 100 nm. The resulting LUVs are stable in the refrigerator for at least 2 weeks.
Anesthetics were added to 1,2-dipalmitoyl-sn-glycero-3-phosphatidylcholine (DPPC) in two distinct ways. One way is simply to dissolve the anesthetic in the buffer and then follow the recipe given above. This method has the advantage that the small concentrations needed can be obtained easily by dissolving in large amounts of buffer and then further diluting with the addition of pure buffer. The disadvantage of this method is that many of the anesthetics are so hydrophobic that even small amounts are impossible to dissolve. Under these conditions, we dissolved anesthetics in a 2:1 methanol-dichloromethane mixture and added the solution to the dry lipids in appropriate quantities. The solution was dried under an air stream and subsequently dried further overnight in a high-vacuum desiccator to remove any remaining solvent. The dry lipid films containing anesthetics were then hydrated with buffer and extruded as described above. This method only works for nonvolatile anesthetics.
Heat-capacity profiles were obtained using a VP-scanning calorimeter (MicroCal, Northampton, MA) at scan rates of 5 deg/h. The curves presented in this work are down-scans from high to low temperature. Since anesthetics are soluble in the fluid phase, it seems plausible to assume that the samples equilibrate faster during down-scans. Due to the extrusion process, the total amount of lipid in the dispersion obtained after extrusion may vary slightly. All experimental profiles were renormalized to a constant transition enthalpy of 35 kJ/mol. The shapes of the heat-capacity profiles of extruded vesicles also can vary slightly in time. This may explain some of the minor variations in shape observed with different concentrations of anesthetics. A typical experiment lasted several days. Repeating an experiment with new samples under similar conditions yielded similar but not necessarily identical profiles.
Theory
In the following, we present the thermodynamic analysis of a chemically inert drug ideally soluble in the fluid lipid membrane but insoluble in the gel membrane. This scenario was shown to describe the thermodynamic behavior of general anesthetics in biomembranes (8). Below, we discuss three cases.
-
1.
The absence of an aqueous reservoir, or equivalently, negligible drug partitioning in the buffer (i.e., an infinite partition coefficient in the fluid membrane). All anesthetic drugs reside in the membrane. The melting of the membrane alters the concentration of the anesthetics in the fluid membrane, because the fraction of fluid phase changes.
-
2.
An infinite aqueous reservoir with constant concentration of anesthetics. In this case, the concentration of anesthetics in the fluid membrane is constant. The ratio of the two concentrations is given by the partition coefficient.
-
3.
A finite aqueous reservoir. During melting, the concentrations of anesthetics in both the buffer and in the fluid membrane change.
These cases are schematically depicted in Fig. 1. The goal is to provide a general method for the interpretation of heat-capacity profiles of membranes in an aqueous buffer containing anesthetic drugs.
Figure 1.
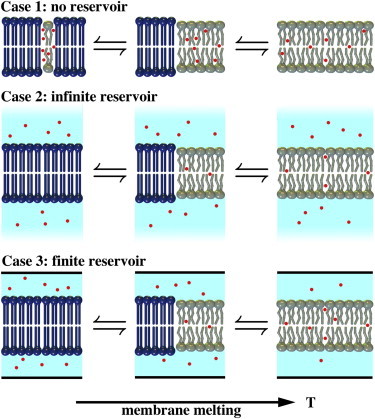
Three different scenarios of a membrane in the presence of anesthetics. (Case 1) The aqueous volume is very small or the partition coefficient of the anesthetic in the fluid membrane is very high. All anesthetic molecules reside in the fluid lipid phase independent of its volume. If the fraction of fluid phase changes as a function of temperature, the concentration of anesthetics in the fluid membrane is also changed. (Case 2) The aqueous volume is infinitely large. The concentration of anesthetics in both the aqueous phase and the fluid membrane is constant and independent of temperature. (Case 3) The aqueous volume is finite. When the amount of fluid phase changes, the concentration of anesthetics changes in both the aqueous phase and the fluid membrane. This is the general case. To see this figure in color, go online.
Highly membrane-soluble anesthetics
Consider the mixture of a lipid membrane with melting temperature and an anesthetic molecule, A, that dissolves ideally in the fluid phase but not in the gel phase of the lipid. We do not consider an aqueous phase, i.e., we assume that practically all drugs dissolve in the membrane and cannot dissociate from the membrane. We considered this case in a previous study (8). The phase diagram of such a mixture is given by ideal solution theory. The chemical potentials of the fluid and the gel membrane are given by and , where is the molar fraction of lipid and is the molar fraction of anesthetics in the fluid phase. If the total membrane is in the fluid state, the total fraction of anesthetics, , is identical to . In equilibrium, , and therefore, . The difference of the standard chemical potentials, , is given by , where is the molar enthalpy of melting and is the molar entropy of melting. The melting temperature in the absence of anesthetics is given by . Thus,
| (1) |
By approximating and , we arrive at
| (2) |
This is the well known freezing-point depression law originating from J. H. van’t Hoff (42).
The laws given in Eqs. 1. and 2 are represented graphically in Fig. 2. We chose the parameters for DPPC membranes, i.e., and . The temperature, T, in Eq. 1 as a function of the concentration of anesthetics in the fluid phase, , is shown as a solid curve in Fig. 2. It is the phase boundary of the gel-fluid coexistence regime, where the concentration of anesthetics in the gel phase is by definition. Here, is the fraction of anesthetics in the total membrane. The dashed line in Fig. 2 represents the freezing-point-depression law of Eq. 2). This approximation is reasonable for molar fractions of anesthetics as high as ∼. It fails at higher concentrations, where shifts of are considerably larger than predicted by the linear approximation. The effective anesthetic dose in the membrane for tadpoles corresponds to 0.026 (8). Thus, the freezing-point-depression law is a good approximation for medically relevant concentrations. The gray-shaded region in Fig. 2 corresponds to the regime where phase separation between the gel and fluid phases takes place.
Figure 2.
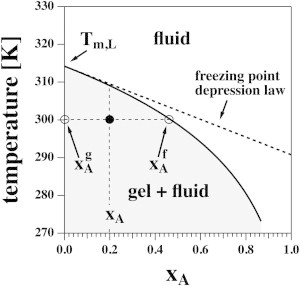
The phase diagram for Case 1 in Fig. 1 for DPPC vesicles in the presence of a general anesthetic. The solid line indicates the concentration of anesthetics in the fluid phase as a function of temperature. The concentration in the gel phase is zero by definition. The solid line also indicates the onset of the lipid melting transition upon cooling at a given anesthetic concentration. The dotted line indicates the freezing-point-depression approximation given by Eq. 2. It is valid up to ∼20 mol % of anesthetics and deviates strongly at higher concentrations. For xA = 0.2 (total membrane fraction of anesthetics) and T = 300 K, the fluid and solid fractions are and .
The fractions of fluid membrane, , and gel membrane, , are given by the lever rule (43):
| (3) |
with . Since by definition, we obtain
| (4) |
The application of the lever rule is demonstrated in Fig. 2 for the example of and K (solid circle), yielding a fluid fraction of . Using Eq. 4, we find that and . Fig. 2 also indicates that the concentration of anesthetics in the fluid membrane is a function of temperature. The lower the temperature, the smaller the fluid fraction and, therefore, the higher the concentration of anesthetics, , in the fluid phase.
This allows us to calculate the melting profile. The enthalpy per mole of lipid is given by
| (5) |
where is the fraction of lipid in the total membrane and is used for normalization to 1 mol of lipid. Both and are temperature-dependent functions. The heat capacity is given by the derivative, . Enthalpy and heat capacity are given for various concentrations of the anesthetics (Fig. 3, left and center). The heat-capacity profiles are asymmetrically broadened toward lower temperatures. This is a consequence of the increase of anesthetic concentration in the remaining fluid regions of the membrane upon cooling.
Figure 3.
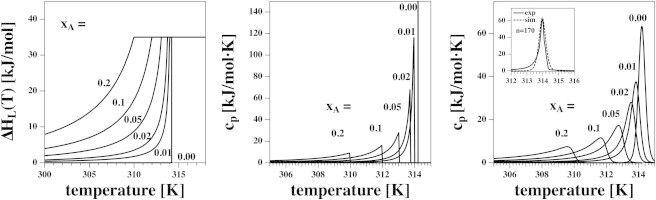
(Left) The enthalpy of DPPC calculated using Eq. 5 for six different mol fractions xA of a general anesthetic. (Center) The derivative of the enthalpies in the left panel yields the corresponding heat capacity profiles. (Right) Broadened cp profiles. Inset shows the experimental heat capacity profile of DMPC LUV (downscan), and a van’t Hoff profile using a cooperative unit size of n = 170 generated using Eq. 6. The latter curve was used to convolute the cp profiles shown at center.
Convolution with the natural width of the transition profile
In the above formalism, the heat capacity of a membrane in the absence of anesthetics is represented by a δ-function. This is a consequence of the assumption of macroscopic phase separation in ideal solution theory. However, experimental profiles typically display a finite transition width. The result for DPPC LUVs is shown in Fig. 3 (right, inset). If phases do not separate macroscopically but rather into domains with a cooperative unit size of n, the temperature-dependent enthalpy of the pure membrane is given as (30)
| (6) |
The temperature derivative is the heat capacity, :
| (7) |
which has an integrated enthalpy of and is shown for unilamellar DPPC vesicles in Fig. 3 (right, inset). A δ-function peak in ideal solution theory at leads to the above peak shape in a calorimetric experiment. The integrated enthalpy of both is . A cooperative unit size of results in the same maximum heat capacity as for DPPC LUVs and yields a satisfactory transition width. This value was used for all convolutions shown in this article.
To be able to compare the theoretical and experimental heat-capacity profiles, we convoluted the theoretical profiles, , with the transition profile of a DPPC LUV, , given by Eq. 7:
| (8) |
In Fig. 3, right, we show the theoretical profiles from Fig. 3 (center) convoluted with the function given in Eq. 7. using the above procedure. (Also see Figs. 4 and 6–8, where we also applied this formalism.)
Figure 4.
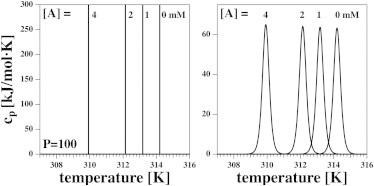
Calorimetric profiles in an infinite reservoir for four different aqueous concentrations of anesthetic, [A], assuming a partition coefficient of P = 100. (Left) In ideal solution theory, the calorimetric peak is a δ-function that is shifted in the presence of anesthetics. (Right) When convoluted with the profile of a DPPC LUV (see Eq. 8), one sees that the peak shape is practically unaffected by the presence of anesthetics.
Figure 6.
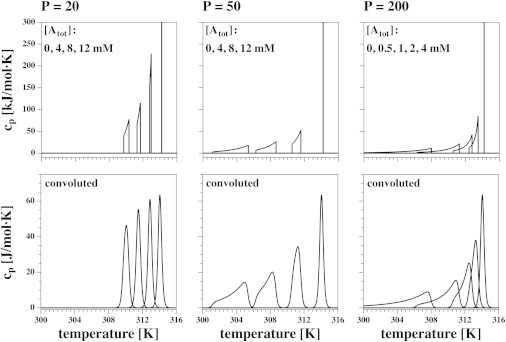
Calculation of heat capacity profiles for Case 3 using Eq. 15 for three different partition coefficients and various anesthetic concentrations. The DPPC lipid concentration was assumed to be 10 mM. The top row contains the theoretical calculations and the bottom row the broadened profiles for DPPC LUVs calculated using the convolution procedure in Eq. 8. (Left) P = 20. (Center) P = 50. (Right) P = 200. The shape of the cp profile depends sensitively on the partition coefficient.
Figure 8.
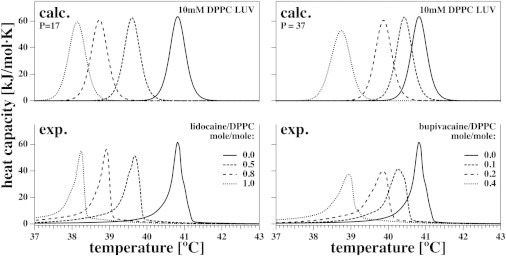
Heat capacity of DPPC LUVs in the presence of two local anesthetics (lidocaine and bupivacaine). Experimental heat-capacity profiles of 10 mM DPPC LUVs in the presence of four concentrations of lidocaine (lower left) and four concentrations of bupivacaine (lower right). Upper graphs show the theoretical results at the same concentrations and at the extracted partition coefficient best suited to describe the experimental results (P = 17 for lidocaine and P = 37 for bupivacaine).
Infinite reservoir size
In the previous section, we assumed that all anesthetics stay in the membrane, i.e., the total number of anesthetic molecules in the membrane is constant. This is the case either if the partition coefficient of the drug is very high or if the amount of aqueous medium is very small.
Let us consider an infinite reservoir and a finite partition coefficient. Now, anesthetic molecules can be exchanged between the aqueous medium and the fluid membrane such that the concentration of anesthetics in the fluid membrane is fixed. This is true because an infinite reservoir displays a constant concentration of anesthetics, and the concentration in the fluid membrane is determined by the partition coefficient alone. The total amount of anesthetics in the membrane is proportional to the fraction of fluid phase. In ideal solution theory, the melting peak is a sharp δ-function. In the presence of anesthetics, the melting profile will not be asymmetrically broadened but will still shift by the value given in Eq. 2. This situation is shown in Fig. 4.
Finite-size reservoir
The most general case is that of a finite aqueous reservoir and a finite partition coefficient. This is the situation in most calorimetric experiments. When the membrane melts, the volume of the fluid phase changes and it can absorb more anesthetic molecules. Since the reservoir is finite, the anesthetic concentration there decreases. Neither the concentration of the anesthetic drug in the fluid membrane nor that in the total membrane stay constant. The considerations of Case 1 remain valid, i.e., the ratio of the sizes of fluid and gel phases of the membrane for a given concentration of anesthetics in the fluid phase is given by the lever rule of Eq. 4. However, the total amount of anesthetics in the membrane and the concentration in the bulk aqueous medium can vary with changes in the amount of fluid phase.
Let us assume a total concentration of anesthetics and a total volume of the sample of . The total molar quantity of anesthetic, , is given by
| (9) |
where is the free anesthetic concentration, P is the partition coefficient, is the volume of aqueous buffer, the volume of the lipid membrane, and . Here, we have assumed that the partial molar volumes of the gel and fluid phases are approximately equal. The volume of fluid membrane, , is given by
| (10) |
where is the fluid membrane fraction. The total amount of anesthetics, , is fixed during an experiment and independent of temperature. We further assume that , , and P are known and fixed. The variables are and . For a given , the fluid membrane fraction, , can be determined using Eqs. 9. and 10:
| (11) |
The molar fraction of anesthetics in the fluid membrane is given by
| (12) |
where is the molar volume of the fluid lipid membrane (∼0.734 L/mol for DPPC assuming a density of 1 g/cm3). For a given , one can calculate the concentration of anesthetics in the fluid membrane (using Eq. 11) and the fluid fraction, (using Eq. 10). When is known, one can calculate the corresponding temperature, T, of the phase boundary using Eq. 1:
| (13) |
According to Eq. 4, the total anesthetic fraction, , in the membrane can be derived from the lever rule:
| (14) |
which is a function of . If we regard the total anesthetic concentration , the total lipid concentration (or total lipid volume, ) and the partition coefficient, P, of the anesthetic in the fluid membrane as fixed input parameters, we can determine phase boundary temperature, the fluid membrane fraction, , the fluid membrane fraction of the anesthetic, , and the anesthetic concentration, , for any given value of [A]. The problem is completely determined. In Fig. 5, we demonstrate the change of both and as a function of temperature for the case of , 10 mM lipids, and a total anesthetic concentration of 4 mM. Upon decreasing temperature, stays constant until the upper phase boundary is reached. Upon further cooling, increases while the total fraction of anesthetics in the bilayer decreases until it becomes zero. This constitutes a lower end of the melting profile.
Figure 5.
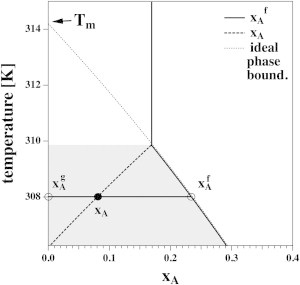
Calculation of xA and for Case 3. In this example we used 10 mM DPPC, P = 100, [Atot] = 4 mM general anesthetic ( mole in 1 ml volume). When the membrane is entirely fluid, i.e., at high temperature, this corresponds to (vertical solid line). Upon cooling, one hits the phase boundary at T = 309.9 K. Below this temperature, increases along the phase boundary while the total anesthetic fraction in the membrane, xA, decreases due to the decrease of the fluid membrane fraction, xf. At T = 306.2 K, xA = 0 and xf = 0.
The melting profile of the membrane can now be determined in analogy to Eq. 5:
| (15) |
where is the fraction of anesthetic in the total membrane, which is a function of temperature. The final term here is needed for normalization to 1 mol of lipid. The heat capacity is the temperature derivative of this function. Fig. 6 shows the heat capacity profiles for three different partition coefficients, P (20, 50, and 200), using various total anesthetic concentrations, . The top panels show the results using the above formalism. One can clearly see the upper and lower limits of the heat capacity anomaly. The lower limit of the melting profile did not exist in Case 1 (Fig. 3). The bottom panels of Fig. 6 display the corresponding convolutions with the profile of unilamellar vesicles.
Experimental Results
Here, we compare calorimetric profiles of DPPC LUVs obtained in the absence and presence of the general anesthetic octanol, the barbiturate pentobarbital, and the two local anesthetics lidocaine and bupivacaine using the theoretical calculations described above. We use experimental differential scanning calorimetry downscans obtained with a scan rate of 5 deg/h.
In the calorimetric experiment, the total aqueous volume, the lipid concentration, and the total anesthetic concentration are fixed. We assumed a lipid membrane density of 1 g/cm3 to calculate the total lipid volume. The molar volume of DPPC is then L/mol (734 g/mol molecular mass). The lipid volume of 1 ml of a 10 mM dispersion is VL = 7.34 μL and the volume of the aqueous buffer is VB = 992.66 μL. For a 1 mM solution, the total molar quantity of anesthetics is mol. The only unknown parameter in Eqs. 9–15 is the partition coefficient, P.
Fig. 7 (lower left) shows experimental heat-capacity profiles for 10 mM DPPC LUV dispersions in the presence of the general anesthetic octanol. The total octanol concentrations, (combined buffer and membrane concentrations), were 0, 0.25, 0.5, 1, and 2 mM (corresponding to molar octanol/lipid ratios of 0, 0.025, 0.05, 0.1 and 0.2). Fig. 7 (upper left) shows the corresponding simulations using a partition coefficient of . This value is similar to the literature value of in erythrocytes (44,45). One sees that the decay of the simulated profiles is somewhat less pronounced than that of the experimental profiles, which may be due in part to the difference between experiment and the theoretical profile of pure DPPC LUVs in the absence of anesthetics, used for the convolution of the theoretical results. Qualitatively similar results have been reported for halothane in DPPC vesicles (19). Fig. 7 (lower right) shows the experimental heat-capacity profiles for 10 mM DPPC LUVs in the presence of the barbiturate pentobarbital. concentrations were 0, 1, 2, 4, and 8 mM (corresponding to molar pentobarbital/lipid ratios of 0, 0.1, 0.2, 0.4, and 0.8). Fig. 7 (upper right) shows simulations using a partition coefficient of .
Figure 7.
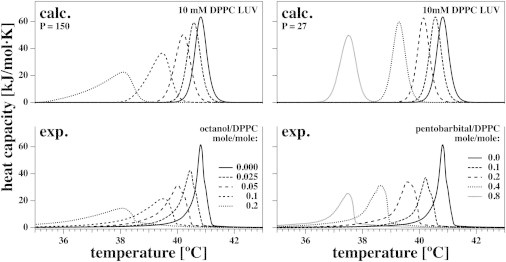
Heat capacity of DPPC LUVs in the presence of two general anesthetics (octanol and pentobarbital). Experimental heat-capacity profiles for 10 mM DPPC LUVs in the presence of five concentrations of octanol (lower left) and five concentrations of the barbiturate pentobarbital (lower right). The theoretical results are shown for octanol (upper left) and pentobarbital (upper right) at the same concentrations and the extracted partition coefficients best suited to describe the experimental results (P = 150 for octanol and P = 27 for pentobarbital).
Fig. 8 shows experimental heat-capacity profiles for 10 mM DPPC LUV dispersions in the presence of the two local anesthetics lidocaine (left) and bupivacaine (right). For lidocaine (Fig. 8, lower left), we used concentrations of 0, 5, 8, and 10 mM (corresponding to molar lidocaine/lipid ratios of 0, 0.5, 0.8, and 1.0). A partition coefficient of 17 yielded the best description of the data (Fig. 8, upper left).
Our calorimetric results for lidocaine agree well with the calculated values and resemble those reported by Ueda et al. (37) for 3 mM DPPC LUVs. For bupivacaine (Fig. 8, lower right), we used concentrations of 0, 1, 2, and 4 mM (corresponding to molar bupivacaine/lipid ratios of 0, 0.1, 0.2, and 0.4). A partition coefficient of 37 yielded a good description of the data (Fig. 8, upper right).
Comparison of octanol/water partition coefficients with calorimetric values
Partition coefficients from the literature and those obtained from our calorimetric experiments are compared in Table 1 and Fig. 9. The partition coefficient, P, is defined as the ratio of the concentration of the dissolved charged or uncharged substances in the organic phase to the concentration in the aqueous phase. Thus, for drugs with a pKA close to experimental conditions, we display partition coefficients for the charged form and for the uncharged form. The distribution coefficient Q corresponds to the partition coefficient for the two forms combined.
Table 1.
Partition coefficients of octanol, pentobarbital, lidocaine, and bupivacaine
| Substance | Q | Pu | Pc | Solvents | pH | T | pKA | Ref. |
|---|---|---|---|---|---|---|---|---|
| Octanol | 1000 | n-oct/water | (47) | |||||
| 1410 | n-oct/water | 25°C | (48) | |||||
| 933 | n-oct/water | 22°C | (49) | |||||
| 691 | n-oct/water | (50) | ||||||
| 1810 | n-oct/water | 45°C | (51) | |||||
| 156.04 | erythr/buffer | 7.0 | RT | (44) | ||||
| 151.8 | erythr/buffer | (45) | ||||||
| 150 (cal) | DPPC/buffer | 7.0 | This work | |||||
| Pentobarbital | 117 | n-oct/water | 25°C | (52) | ||||
| 53.7 | 135 | n-oct/water | 7.4 | (53) | ||||
| 9.6 | erythr/buffer | 7.4 | 23°C | (45) | ||||
| 8.5 | erythr/buffer | 7.4 | 23°C | (54) | ||||
| 25°C | 8.17 | (55) | ||||||
| 37°C | 7.95 | (56) | ||||||
| 27 (cal) | DPPC/buffer | 7.0 | This work | |||||
| Lidocaine | 43.0 | 304 | 0.060 | n-oct/buffer | 7.4 | 25°C | 8.19 | (57) |
| 47.9 | n-oct/buffer | 7.4 | RT | (58) | ||||
| 110.0 | 366 | 0.085 | n-oct/buffer | 7.4 | 36°C | 7.77 | (57) | |
| 245 | n-oct/buffer | 9.86 | 23°C | (59) | ||||
| 25°C | 7.86 | (60) | ||||||
| 17 (cal) | DPPC/buffer | 7.0 | This work | |||||
| Bupivacaine | 346.0 | 2565 | 1.5 | n-oct/buffer | 7.4 | 25°C | 8.21 | (57) |
| 560.0 | 3420 | 2.0 | n-oct/buffer | 7.4 | 36°C | 8.10 | (57) | |
| 37 (cal) | DPPC:buffer | 7.0 | This work |
The distribution coefficient, Q, is the ratio of the concentration of molecules in the organic phase to the concentration of charged and uncharged molecules in the aqueous phase. Pu and Pc are the partition coefficients of the uncharged and charged forms, respectively. Bold values are those used in Fig. 9. Oct, octanol; erythr, erythrocyte; RT, room temperature; cal, calorimetry.
Figure 9.
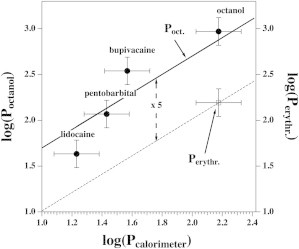
Octanol/water partition coefficients plotted versus the partition coefficient determined by calorimetry (solid circles). The solid line assumes that the two partition coefficients are proportional. The erythrocyte/water partition coefficient for octanol is given for comparison (open square, dashed line). The octanol/water partition coefficients differ by a factor of 5 from the erythrocyte/water coefficients (dashed vertical line). The symbols correspond to bold values in Table 1.
Partition and distribution coefficients vary with temperature. We compared the results from differential scanning calorimetry with octanol/water partition coefficients obtained under similar conditions (i.e., between room temperature and 25°C and at a pH close to the chosen value of 7). These values are shown in bold in Table 1. Assuming a proportional relation between the two quantities, the calorimetric values are smaller by a factor of 5 than the octanol partition coefficients, in very good agreement with the values from Seeman and colleagues (44,45), who found a factor of 5 difference between the octanol and the erythrocyte. The value for the partitioning of octanol in erythrocyte membranes is given in Fig. 9 for comparison. The spread of literature values given in Table 1 is considerable and is of the order of at least a factor of 2. This is tentatively taken into account by the error bars in Fig. 9 that indicate a range of a factor of 2 (end to end of the error bars). Some of the uncertainty may be due to the pH dependence of pentobarbital, lidocaine, and bupivacaine that have pKA values of ∼8.2. The pH in our experiments was 7.0. At this pH, pentobarbital is in its uncharged form (membrane-soluble), whereas lidocaine and bupivacaine are in the charged (water-soluble) form. Thus, the experimental situation is seemingly far away from the pKA. However, if the association constant of the anesthetic is different for the charged and the uncharged forms, due to close thermodynamic cycles, the pKA in the membrane must necessarily be different from that found in solution. This was analyzed and experimentally demonstrated by Kaneshina et al. (46) for the local anesthetic dibucaine. For this reason, it is not trivial to determine the quantity of anesthetic that will associate to the membrane close to the pKA.
Pressure dependence
A theory of anesthesia based on lipid phase transitions has the advantage that it implicitly contains an explanation for the pressure reversal of anesthesia (8,31). Pressure shifts the transitions of lipid membranes because it alters their specific volume upon melting (30):
| (16) |
Here, is the change in hydrostatic pressure and is the excess volume of the lipid transition. The pressure dependence of lipid phase transitions has been studied in detail and is quantitatively understood (20). Since anesthetics lower transition temperatures and hydrostatic pressure increases them, one expects a reversal of the effect of anesthetics. The critical pressure for the reversal of tadpole anesthesia was calculated to be ∼25 bar (8), which is of an order similar to that found in experiments (21,22).
As shown in Fig. 10, we have applied hydrostatic pressure to lipid membranes in the presence of both general and local anesthetics. The average shift of the DPPC transition maximum in the presence of three anesthetics (pentobarbital, lidocaine, and bupivacaine) in Fig. 10 is 0.02441 deg/bar (equivalently, 1 deg/40.95 bar). This is practically identical to the numbers obtained in the absence of anesthetics, as reported in Ebel et al. (20), e.g., 0.02448/bar for DPPC. This implies that the pressure dependence of lipid membranes is unaltered by anesthetics. Thus, the partitioning of the drugs between the liquid and solid phases is unaltered by hydrostatic pressure within experimental accuracy. If this were not true, the shift of the transition would be different in the presence and absence of the anesthetics, which is not the case. Further, the shape of the transition would be influenced by pressure. A minor influence of pressure on the shape of the transition can only be seen at the highest pressure applied (160 bar).
Figure 10.
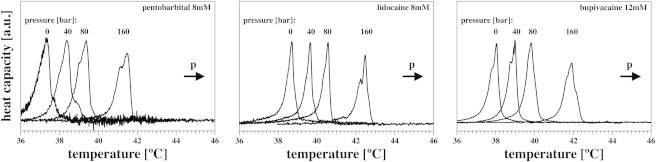
Pressure dependence of membranes in the presence of anesthetics at 0, 40, 80, and 160 bars excess hydrostatic pressure for 10 mM DPPC LUVs in the presence of a total concentration, [Atot], of 8 mM pentobarbital (left), 8 mM lidocaine (center), and 12 mM bupivacaine (right). The shape of the transition profile remains unaltered. The magnitude of the shift is the same as in the absence of anesthetics (20).
Discussion
General and local anesthetics are generally considered to be different classes of drugs. It is further acknowledged that general anesthesia is not well understood. However, it is well known that general anesthetics shift phase transition and generally render membranes more fluid by a mechanism that is independent of the nature of the drug (8,18,28). In contrast, local anesthetics are often assumed to bind specifically to receptors and in particular to sodium channels (4,5). It has been known for a long time that local anesthetics also lower lipid melting transitions (35–41). Kaminoh et al. (16,17) hypothesized that it is not the partitioning in the membrane, but rather the difference in partitioning between the fluid and gel phases, that determines anesthetic effects. That is also the working hypothesis of this article.
Here, we studied the effects of octanol, pentobarbital, lidocaine, and bupivacaine on the melting transition of DPPC LUVs. We demonstrated that general and local anesthetics both lower transition temperature in a qualitatively very similar manner. We provided a formalism to describe the results theoretically. We based our theoretical considerations on ideal solution theory and the assumption that both general and local anesthetics dissolve ideally in the fluid membrane but are insoluble in the gel membrane. We distinguished three cases: 1), all anesthetics dissolve in the membrane due to either a very high partition coefficient or a very small volume of aqueous buffer; 2), an infinite volume of aqueous buffer with constant anesthetic concentration; and 3), the general case, describing a finite amount of buffer and small or medium partition coefficient values. Case 1 leads to large shifts toward lower temperature, with an asymmetric broadening of the profiles that reflects the temperature-dependent change in fluid membrane concentration of the anesthetics. Case 2 leads to a shift in the profile without broadening or change of the peak amplitude. Case 3 displays both a shift and broadening of the profiles, but to a lower extent than in Case 1. Case 3 is the typical situation in a calorimetric experiment, where the aqueous volume is finite. We demonstrated that this description can describe the heat-capacity profiles of both classes of anesthetics in a satisfactory manner. We further showed that for up to 20 mol % of anesthetics in the membrane, the above treatment is consistent with the freezing-point-depression law posited by van’t Hoff (42) that implies a linear dependence of the melting point on the concentration of the solute in the fluid phase. However, the shift in the transition is largely underestimated by the freezing-point-depression law at higher molar fractions of anesthetics. One can extract partition coefficients that reflect the reported partition coefficients in octanol. Freezing-point depression was similarly used to determine concentrations of solutes in aqueous solution in the original publication of van’t Hoff in 1886.
Finally, we demonstrated that hydrostatic pressure leads to a shift of melting peaks toward higher temperatures without a broadening of the profile. This shift is unaffected by the presence of either general or local anesthetics, consistent with findings by Mountcastle et al. (19). From this, it can be concluded that the relative partitioning of anesthetic drugs in the gel and fluid membrane phases is generally not pressure-dependent in the range investigated here (up to 160 bar). A similar finding was reported for the local anesthetic tetracaine (36). In a previous publication (8), we argued that the pressure reversal of general anesthesia (21) can be quantitatively understood by assuming that the shift of the melting transition induced by anesthetics is counteracted by pressure. The results of this study imply that this effect also should be true for local anesthesia. It is interesting to note that Halsey and Wardley-Smith found that general anesthesia induced by the local anesthetic procaine was in fact reversed by hydrostatic pressure in tadpoles (22). Anesthetic inhibition of the protein firefly luciferase, in contrast, does not display pressure reversal in the peak fluorescence intensity (9) but shows pressure reversal at quite high pressures of 100–150 bar in the steady-state fluorescence intensity (61).
One particularly important feature of the above findings is that the thermodynamics of general and local anesthetics is basically the same. Therefore, there is no reason in a thermodynamics theory of membranes to distinguish between the two classes of anesthetic.
Additivity of general and local anesthesia
Both the Meyer-Overton correlation and the law of freezing-point depression are generic linear laws that depend only on the concentration of the drug in question and are entirely independent of its chemical nature. Thus, these laws explicitly predict that the effect of these drugs is additive. This effect is well documented for general anesthetics and was discussed by Overton >100 years ago (6). In this article, we provide strong evidence that the law of freezing-point depression also applies to local anesthetics. This immediately leads to the prediction that the effects of general and local anesthetics are additive, too. From a thermodynamic point of view, the effects of general and local anesthetics on membranes are the same.
There are, in fact, numerous publications providing evidence for the additive effects of general and local anesthesia. Himes et al. (33) reported that the critical anesthetic dose for the general anesthetic halothane in dogs can be lowered by 50% by plasma concentrations of >10 μg/mL of the local anesthetic lidocaine. In a similar way, nitrous oxide anesthesia was enhanced by lidocaine. The intramuscular administration of the local anesthetics lidocaine and bupivacaine increases the hypnotic effect of the general anesthetic midazolam in humans to a degree proportional to the dose of the local anesthetic (34). The effect of bupivacaine is larger than that of lidocaine, in agreement with its larger partition coefficient in membranes. The hypnotic effect of the general anesthetic halothane is enhanced by the local anesthetics lignocaine and bupivacaine (62). In a similar way, Senturk et al. (63) reported that the critical dose of the general anesthetic propofol in humans was significantly lowered by intramuscular administration of both lidocaine and bupivacaine (63). Along the same lines, Altermatt et al. (64) reported a significantly lowered critical dose of propofol in the presence of lidocaine. Additivity of general and local anesthetic effects has also been reported for bupivacaine with the general anesthesia propofol (65). In a similar manner, the critical dose of the general anesthetic cyclopropane is lowered by 40% in the presence of lidocaine (66). Further, the critical dose of the general anesthetic isoflurane was lowered linearly with the administered dose of lidocaine in cats (67), with a reduction of >50% for 10 μg/mL lidocaine (in agreement with Himes et al. (33)). The sedative effect of lidocaine was also discussed by Szmuk et al. (68).
The linear dependence of general anesthesia on the dose of local anesthetic suggests that both classes of drugs can induce general anesthesia, and that they work by similar mechanisms. It should be noted that the generic physical laws are based on ideal solubility (partitioning) of drugs in the membrane and are therefore inconsistent with the idea of specific binding to receptors.
The cutoff effect of long-chain alcohols
In contrast to the Meyer-Overton correlation, the thermodynamic theory presented here relies on the assumption that anesthetics are perfectly miscible in the fluid phase of lipids and perfectly immiscible in the gel phase. This implies that some molecules that are soluble in membranes are not anesthetics. For example, the effect of cholesterol and other membrane-soluble drugs that are not anesthetics was discussed by Cantor and colleagues (12,13). For instance, cholesterol is not an anesthetic, even though it dissolves in membranes. In the framework presented here, this is because it is also soluble in the gel (or liquid-ordered) phases and has the effect of increasing the temperature of the lipid phase transition (69). In a similar way, although other lipids are themselves soluble in a given membrane, they are not generally anesthetics. Many lipids display state transitions close to the experimental temperature where one of the states is soluble in the solid phase and the other in the fluid phase. If the secondary membrane component consists of such a lipid, the phase diagram strongly deviates from the idealized eutectic case shown in Fig. 2 (30). In particular, if the melting point of a secondary lipid component is higher than that of the predominant lipid species, the melting profile is usually shifted toward higher temperatures. Such considerations also apply to lipidlike molecules such as long-chain alcohols. Pringle et al. (26) report that the anesthetic potency of saturated n-alcohols increases up to dodecanol, and that anesthetic action fails at chain lengths >12–14. It is interesting to note that this correlates with the melting temperature of the pure alcohols. The melting temperature of ethanol is −114°C, that of octanol −14.8°C, that of decanol +6.9°C, that of dodecanol 23.9°C, that of tetradecanol 38.2°C, and that of hexadecanol 49.2°C (values taken from Lide (70)). All alcohols with chain length 14 or longer display transitions above body temperature (37°C). All 1-alcohols that do have a general anesthetic effect display transitions well below physiological temperature. Kharakoz (18) showed that all 1-alcohols in lipid membranes up to decanol nicely follow the freezing-point-depression law. Experiments from our lab show that tetradecanol fails to follow this correlation, but instead increases the transition temperature in DPPC vesicles (not shown). In a similar way, Kaminoh et al. (17) showed that 1-tridecanol and 1-tetradecanol increase the melting temperature of DPPC, whereas 1-octanol and 1-decanol decrease it. Thus, we must conclude that the cutoff effect of saturated n-alcohols is in agreement with the theoretical description presented here. An increase of the transition temperature of DPPC in the presence of long-chain alcohols was also reported by Kamaya and Ueda (71,72).
Lipid channels
Papahadjopoulos et al. (73) showed that membranes are more permeable in the vicinity of phase transitions, and Antonov et al. showed the existence of channel-like conduction steps close to these transitions (74). Formation of these channels, consisting of small pores in the lipid membrane, is more likely in the vicinity of transitions where area fluctuations are known to be large. Such channels exist in lipid membranes in the complete absence of proteins and have conduction properties that are virtually indistinguishable from those reported for protein channels, i.e., conductance and channel lifetimes are of the same order and current-voltage relationships display a similar functional form (75,76). Close to transitions, these lipid channels can be blocked by general anesthetics as a simple consequence of their influence on the phase-transition temperature. For instance, we have demonstrated that channels in DOPC/DPPC mixtures can be blocked by the general anesthetic octanol (77) in a manner very similar to the reported blocking of Na+ channels and the acetylcholine receptor by octanol (discussed in Blicher et al. (77)). It is to be expected that local anesthetics have the potential to block lipid channels because they display a comparable influence on the cooperative melting transition.
Nerves
Recently, we proposed that electromechanical solitons (localized pulses) can travel in membranes close to phase transitions (27–29,78). Such transitions exist in biomembranes slightly below physiological temperature (30). Therefore, it was proposed that such pulses are related to the action potential in nerves. The distance of physiological temperature from the transition maximum is closely related to the free energy necessary to excite such a soliton (8). According to the above, both general and local anesthetics change the transition temperature and thus increase the free energy necessary to excite a solitary pulse, resulting in an increase of the stimulation threshold (8,28). This has been found experimentally for both general and local anesthetics (79). Within the soliton concept, pulse shapes and velocities remain basically unaltered, as also found in experiments.
Conclusions
We show here that general and local anesthetics have similar effects on the phase behavior of lipid membranes. This is consistent with a simple freezing-point-depression law based on the ideal solubility (partitioning) of anesthetic drugs in the fluid phase and a low partitioning in the gel phase. Therefore, from a thermodynamic perspective, there is no reason to distinguish between general and local anesthetics. This description is consistent with the cutoff effect of long-chain alcohols. The effects of both general and local anesthetics are subject to pressure reversal.
Acknowledgments
We thank Professor Andrew D. Jackson (Niels Bohr International Academy, Copenhagen) for useful discussions and for a critical reading of this article.
This work was supported by the Villum Foundation (VKR 022130).
Footnotes
Kaare Græsbøll’s present address is DTU Compute, Technical University of Denmark, DK-2800 Kgs. Lyngby, Denmark.
References
- 1.Urban B.W. Die Meyer-Overton-Regel: Was ist geblieben? In: Pasch T., Schmid E.R., Zollinger A., editors. Anästhesie in Zürich: 100 Jahre Entwicklung, 1901–2001. Institut fur Anästhesiologie; Universitäts-Spital Zürich, Zürich: 2002. pp. 15–23. [Google Scholar]
- 2.López-Muñoz F., Ucha-Udabe R., Alamo C. The history of barbiturates a century after their clinical introduction. Neuropsychiatr. Dis. Treat. 2005;1:329–343. [PMC free article] [PubMed] [Google Scholar]
- 3.Ruetsch Y.A., Böni T., Borgeat A. From cocaine to ropivacaine: the history of local anesthetic drugs. Curr. Top. Med. Chem. 2001;1:175–182. doi: 10.2174/1568026013395335. [DOI] [PubMed] [Google Scholar]
- 4.Butterworth J.F., 4th, Strichartz G.R. Molecular mechanisms of local anesthesia: a review. Anesthesiology. 1990;72:711–734. doi: 10.1097/00000542-199004000-00022. [DOI] [PubMed] [Google Scholar]
- 5.Fozzard H.A., Sheets M.F., Hanck D.A. The sodium channel as a target for local anesthetic drugs. Front. Pharmacol. 2011;2:68. doi: 10.3389/fphar.2011.00068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Overton C.E. Springer; New York: 1991. Studies of Narcosis (R. L. Lipnick, trans.) (Original work published 1901.) [Google Scholar]
- 7.Reference deleted in proof.
- 8.Heimburg T., Jackson A.D. The thermodynamics of general anesthesia. Biophys. J. 2007;92:3159–3165. doi: 10.1529/biophysj.106.099754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Moss G.W., Lieb W.R., Franks N.P. Anesthetic inhibition of firefly luciferase, a protein model for general anesthesia, does not exhibit pressure reversal. Biophys. J. 1991;60:1309–1314. doi: 10.1016/S0006-3495(91)82168-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Franks N.P., Lieb W.R. Molecular and cellular mechanisms of general anaesthesia. Nature. 1994;367:607–614. doi: 10.1038/367607a0. [DOI] [PubMed] [Google Scholar]
- 11.Franks N.P. General anaesthesia: from molecular targets to neuronal pathways of sleep and arousal. Nat. Rev. Neurosci. 2008;9:370–386. doi: 10.1038/nrn2372. [DOI] [PubMed] [Google Scholar]
- 12.Cantor R.S. Lateral pressures in cell membranes: a mechanism for modulation of protein function. J. Phys. Chem. B. 1997;101:1723–1725. [Google Scholar]
- 13.Cantor R.S. The lateral pressure profile in membranes: a physical mechanism of general anesthesia. Biochemistry. 1997;36:2339–2344. doi: 10.1021/bi9627323. [DOI] [PubMed] [Google Scholar]
- 14.Cantor R.S., Twyman K.S., Haseneder R. A kinetic model of ion channel electrophysiology: bilayer-mediated effects of agonists and anesthetics on protein conformational transitions. Soft Matter. 2009;5:3266–3278. [Google Scholar]
- 15.Trudell J.R., Payan D.G., Cohen E.N. The antagonistic effect of an inhalation anesthetic and high pressure on the phase diagram of mixed dipalmitoyl-dimyristoylphosphatidylcholine bilayers. Proc. Natl. Acad. Sci. USA. 1975;72:210–213. doi: 10.1073/pnas.72.1.210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kaminoh Y., Tashiro C., Ueda I. Depression of phase-transition temperature by anesthetics: nonzero solid membrane binding. Biochim. Biophys. Acta. 1988;946:215–220. doi: 10.1016/0005-2736(88)90395-1. [DOI] [PubMed] [Google Scholar]
- 17.Kaminoh Y., Nishimura S., Ueda I. Alcohol interaction with high entropy states of macromolecules: critical temperature hypothesis for anesthesia cutoff. Biochim. Biophys. Acta. 1992;1106:335–343. doi: 10.1016/0005-2736(92)90014-d. [DOI] [PubMed] [Google Scholar]
- 18.Kharakoz D.P. Phase-transition-driven synaptic exocytosis: a hypothesis and its physiological and evolutionary implications. Biosci. Rep. 2001;21:801–830. doi: 10.1023/a:1015588825142. [DOI] [PubMed] [Google Scholar]
- 19.Mountcastle D.B., Biltonen R.L., Halsey M.J. Effect of anesthetics and pressure on the thermotropic behavior of multilamellar dipalmitoylphosphatidylcholine liposomes. Proc. Natl. Acad. Sci. USA. 1978;75:4906–4910. doi: 10.1073/pnas.75.10.4906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ebel H., Grabitz P., Heimburg T. Enthalpy and volume changes in lipid membranes. I. The proportionality of heat and volume changes in the lipid melting transition and its implication for the elastic constants. J. Phys. Chem. B. 2001;105:7353–7360. [Google Scholar]
- 21.Johnson F.H., Flagler E.A. Hydrostatic pressure reversal of narcosis in tadpoles. Science. 1950;112:91–92. doi: 10.1126/science.112.2899.91-a. [DOI] [PubMed] [Google Scholar]
- 22.Halsey M.J., Wardley-Smith B. Pressure reversal of narocsis produced by anaesthetics, narcotics and tranquillisers. Nature. 1975;257:811–813. doi: 10.1038/257811a0. [DOI] [PubMed] [Google Scholar]
- 23.DiFazio C.A., Brown R.E., Kennedy S.S. Additive effects of anesthetics and theories of anesthesia. Anesthesiology. 1972;36:57–63. doi: 10.1097/00000542-197201000-00010. [DOI] [PubMed] [Google Scholar]
- 24.Fang Z., Ionescu P., Eger E.I., 2nd Anesthetic potencies of n-alkanols: results of additivity and solubility studies suggest a mechanism of action similar to that for conventional inhaled anesthetics. Anesth. Analg. 1997;84:1042–1048. doi: 10.1097/00000539-199705000-00017. [DOI] [PubMed] [Google Scholar]
- 25.Mabrey S., Sturtevant J.M. High-sensitivity differential scanning calorimetry in the study of biomembranes and related model systems. In: Korn E., editor. Vol. 9. Plenum Press; New York: 1978. pp. 237–274. (Methods in Membrane Biology). [Google Scholar]
- 26.Pringle M.J., Brown K.B., Miller K.W. Can the lipid theories of anesthesia account for the cutoff in anesthetic potency in homologous series of alcohols? Mol. Pharmacol. 1981;19:49–55. [PubMed] [Google Scholar]
- 27.Heimburg T., Jackson A.D. On soliton propagation in biomembranes and nerves. Proc. Natl. Acad. Sci. USA. 2005;102:9790–9795. doi: 10.1073/pnas.0503823102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Heimburg T., Jackson A.D. On the action potential as a propagating density pulse and the role of anesthetics. Biophys. Rev. Lett. 2007;2:57–78. [Google Scholar]
- 29.Andersen S.S.L., Jackson A.D., Heimburg T. Towards a thermodynamic theory of nerve pulse propagation. Prog. Neurobiol. 2009;88:104–113. doi: 10.1016/j.pneurobio.2009.03.002. [DOI] [PubMed] [Google Scholar]
- 30.Heimburg T. Wiley; Berlin: 2007. Thermal Biophysics of Membranes. [Google Scholar]
- 31.Heimburg T., Jackson A.D. Thermodynamics of the nervous impulse. In: Nag K., editor. Structure and Dynamics of Membranous Interfaces. Wiley; Hoboken, NJ: 2008. pp. 317–339. [Google Scholar]
- 32.Cox B., Durieux M.E., Marcus M.A.E. Toxicity of local anaesthetics. Best Pract. Res. Clin. Anaesthesiol. 2003;17:111–136. doi: 10.1053/bean.2003.0275. [DOI] [PubMed] [Google Scholar]
- 33.Himes R.S., Jr., DiFazio C.A., Burney R.G. Effects of lidocaine on the anesthetic requirements for nitrous oxide and halothane. Anesthesiology. 1977;47:437–440. doi: 10.1097/00000542-197711000-00010. [DOI] [PubMed] [Google Scholar]
- 34.Ben-Shlomo I., Tverskoy M., Katz Y. Intramuscular administration of lidocaine or bupivacaine alters the effect of midazolam from sedation to hypnosis in a dose-dependent manner. J. Basic Clin. Physiol. Pharmacol. 2003;14:257–263. doi: 10.1515/jbcpp.2003.14.3.257. [DOI] [PubMed] [Google Scholar]
- 35.Papahadjopoulos D., Jacobson K., Shepherd G. Effects of local anesthetics on membrane properties. I. Changes in the fluidity of phospholipid bilayers. Biochim. Biophys. Acta. 1975;394:504–519. doi: 10.1016/0005-2736(75)90137-6. [DOI] [PubMed] [Google Scholar]
- 36.Winter R., Christmann M.H., Heenan R.K. The influence of the local-anesthetic tetracaine on the temperature and pressure dependent phase-behavior of model biomembranes. Ber. Bunsenges. Phys. Chem. 1991;95:811–820. [Google Scholar]
- 37.Ueda I., Chiou J.S., Kamaya H. Local anesthetics destabilize lipid membranes by breaking hydration shell: infrared and calorimetry studies. Biochim. Biophys. Acta. 1994;1190:421–429. doi: 10.1016/0005-2736(94)90103-1. [DOI] [PubMed] [Google Scholar]
- 38.Matsuki H., Ichikawa R., Ueda I. Differential scanning calorimetric study on the Krafft phenomenon of local anesthetics. J. Colloid Interface Sci. 1996;181:362–369. [Google Scholar]
- 39.Hata T., Matsuki H., Kaneshina S. Effect of local anesthetics on the bilayer membrane of dipalmitoylphosphatidylcholine: interdigitation of lipid bilayer and vesicle-micelle transition. Biophys. Chem. 2000;87:25–36. doi: 10.1016/s0301-4622(00)00175-7. [DOI] [PubMed] [Google Scholar]
- 40.Lygre H., Moe G., Holmsen H. Interaction of articaine hydrochloride with prokaryotic membrane lipids. Acta Odontol. Scand. 2009;67:1–7. doi: 10.1080/00016350802443466. [DOI] [PubMed] [Google Scholar]
- 41.Paiva J.G., Paradiso P., Saramago B. Interaction of local and general anaesthetics with liposomal membrane models: a QCM-D and DSC study. Colloids Surf. B Biointerfaces. 2012;95:65–74. doi: 10.1016/j.colsurfb.2012.02.027. [DOI] [PubMed] [Google Scholar]
- 42.van’t Hoff J.H. University of California; Berkeley, CA: 1900. Die Gesetze des chemischen Gleichgewichtes für den verdünnten, gasförmigen oder gelösten Zustand (G. Bredig, trans.) (Original work published in 1886.) [Google Scholar]
- 43.Lee A.G. Lipid phase transitions and phase diagrams. II. Mixtures involving lipids. Biochim. Biophys. Acta. 1977;472:285–344. doi: 10.1016/0304-4157(77)90001-6. [DOI] [PubMed] [Google Scholar]
- 44.Seeman P., Roth S., Schneider H. The membrane concentrations of alcohol anesthetics. Biochim. Biophys. Acta. 1971;225:171–184. doi: 10.1016/0005-2736(71)90210-0. [DOI] [PubMed] [Google Scholar]
- 45.Seeman P. The membrane actions of anesthetics and tranquilizers. Pharmacol. Rev. 1972;24:583–655. [PubMed] [Google Scholar]
- 46.Kaneshina S., Satake H., Matsuki H. Partitioning of local anesthetic dibucaine into bilayer membranes of dimyristoylphosphatidylcholine. Colloids Surf. B Biointerfaces. 1997;10:51–57. [Google Scholar]
- 47.Hansch C., Leo A., Hoekman D. Vol. 2. American Chemical Society; Washington, DC: 1995. (Exploring QSAR: Hydrophobic, Electronic, and Steric Constants). [Google Scholar]
- 48.Collander R. The partition of organic compounds between higher alcohols and water. Acta Chem. Scand. 1951;5:774–780. [Google Scholar]
- 49.Könemann H., Zelle R., Hammers W.E. Determination of log Poct values of chloro-substituted benzenes, toluenes and anilines by high-performance liquid chromatography on ODS-silica. J. Chromatogr. A. 1979;178:559–565. [Google Scholar]
- 50.Leo A., Hansch C., Church C. Comparison of parameters currently used in the study of structure-activity relationships. J. Med. Chem. 1969;12:766–771. doi: 10.1021/jm00305a010. [DOI] [PubMed] [Google Scholar]
- 51.Rowe E.S., Zhang F., Guy P.T. Thermodynamics of membrane partitioning for a series of n-alcohols determined by titration calorimetry: role of hydrophobic effects. Biochemistry. 1998;37:2430–2440. doi: 10.1021/bi9721602. [DOI] [PubMed] [Google Scholar]
- 52.Wong O., McKeown R.H. Substituent effects on partition coefficients of barbituric acids. J. Pharm. Sci. 1988;77:926–932. doi: 10.1002/jps.2600771105. [DOI] [PubMed] [Google Scholar]
- 53.Yih T.D., van Rossum J.M. Pharmacokinetics of some homologous series of barbiturates in the intact rat and in the isolated perfused rat liver. J. Pharmacol. Exp. Ther. 1977;203:184–192. [PubMed] [Google Scholar]
- 54.Roth S., Seeman P. The membrane concentrations of neutral and positive anesthetics (alcohols, chlorpromazine, morphine) fit the Meyer-Overton rule of anesthesia; negative narcotics do not. Biochim. Biophys. Acta. 1972;255:207–219. doi: 10.1016/0005-2736(72)90023-5. [DOI] [PubMed] [Google Scholar]
- 55.Ishihama Y., Nakamura M., Asakawa N. A rapid method for pKa determination of drugs using pressure-assisted capillary electrophoresis with photodiode array detection in drug discovery. J. Pharm. Sci. 2002;91:933–942. doi: 10.1002/jps.10087. [DOI] [PubMed] [Google Scholar]
- 56.Ballard B.E., Nelson E. Physicochemical properties of drugs that control absorption rate after subcutaneous implantation. J. Pharmacol. Exp. Ther. 1962;135:120–127. [PubMed] [Google Scholar]
- 57.Strichartz G.R., Sanchez V., Martin D. Fundamental properties of local anesthetics. II. Measured octanol:buffer partition coefficients and pKa values of clinically used drugs. Anesth. Analg. 1990;71:158–170. doi: 10.1213/00000539-199008000-00008. [DOI] [PubMed] [Google Scholar]
- 58.Nakazono T., Murakami T., Yata N. Study on brain uptake of local anesthetics in rats. J. Pharmacobiodyn. 1991;14:605–613. doi: 10.1248/bpb1978.14.605. [DOI] [PubMed] [Google Scholar]
- 59.Broughton A., Grant A.O., Strauss H.C. Lipid solubility modulates pH potentiation of local anesthetic block of Vmax reactivation in guinea pig myocardium. Circ. Res. 1984;55:513–523. doi: 10.1161/01.res.55.4.513. [DOI] [PubMed] [Google Scholar]
- 60.Truant A.P., Takman B. Differential physical-chemical and neuropharmacologic properties of local anesthetic agents. Anesth. Analg. 1959;38:478–484. [PubMed] [Google Scholar]
- 61.Ueda I., Minami H., Inoue T. Does pressure antagonize anesthesia? High-pressure stopped-flow study of firefly luciferase and anatomy of initial flash. Biophys. J. 1999;76:478–482. doi: 10.1016/S0006-3495(99)77215-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Ben-Shlomo I., Tverskoy M., Cherniavsky G. Hypnotic effect of i.v. propofol is enhanced by i.m. administration of either lignocaine or bupivacaine. Br. J. Anaesth. 1997;78:375–377. doi: 10.1093/bja/78.4.375. [DOI] [PubMed] [Google Scholar]
- 63.Senturk M., Pembeci K., Akpir K. Effects of intramuscular administration of lidocaine or bupivacaine on induction and maintenance doses of propofol evaluated by bispectral index. Br. J. Anaesth. 2002;89:849–852. doi: 10.1093/bja/aef287. [DOI] [PubMed] [Google Scholar]
- 64.Altermatt F.R., Bugedo D.A., Cortínez L.I. Evaluation of the effect of intravenous lidocaine on propofol requirements during total intravenous anaesthesia as measured by bispectral index. Br. J. Anaesth. 2012;108:979–983. doi: 10.1093/bja/aes097. [DOI] [PubMed] [Google Scholar]
- 65.Agarwal A., Pandey R., Singh U. The effect of epidural bupivacaine on induction and maintenance doses of propofol (evaluated by bispectral index) and maintenance doses of fentanyl and vecuronium. Anesth. Analg. 2004;99:1684–1688. doi: 10.1213/01.ANE.0000136422.70531.5A. [DOI] [PubMed] [Google Scholar]
- 66.DiFazio C.A., Neiderlehner J.R., Burney R.G. The anesthetic potency of lidocaine in the rat. Anesth. Analg. 1976;55:818–821. doi: 10.1213/00000539-197611000-00016. [DOI] [PubMed] [Google Scholar]
- 67.Pypendop B.H., Ilkiw J.E. The effects of intravenous lidocaine administration on the minimum alveolar concentration of isoflurane in cats. Anesth. Analg. 2005;100:97–101. doi: 10.1213/01.ANE.0000139350.88158.38. [DOI] [PubMed] [Google Scholar]
- 68.Szmuk P., Farrow-Gillespie A., Ezri T. The sedative effect of high dose lidocaine. Anesth. Analg. 2007;104:1613. doi: 10.1213/01.ane.0000263287.34826.0d. author reply 1613–1614. [DOI] [PubMed] [Google Scholar]
- 69.Halstenberg S., Heimburg T., Krivanek R. Cholesterol-induced variations in the volume and enthalpy fluctuations of lipid bilayers. Biophys. J. 1998;75:264–271. doi: 10.1016/S0006-3495(98)77513-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Lide D.R. 86th ed. CRC Press; Boca Raton, FL: 2005. Handbook of Chemistry and Physics. [Google Scholar]
- 71.Kamaya H., Matubayasi N., Ueda I. Biphasic effect of long-chain n-alkanols on the main-phase transition of phospholipid vesicle membranes. J. Phys. Chem. 1984;88:797–800. [Google Scholar]
- 72.Kamaya H., Ma S.M., Lin S.H. Dose-dependent nonlinear response of the main phase-transition temperature of phospholipid membranes to alcohols. J. Membr. Biol. 1986;90:157–161. doi: 10.1007/BF01869933. [DOI] [PubMed] [Google Scholar]
- 73.Papahadjopoulos D., Jacobson K., Isac T. Phase transitions in phospholipid vesicles. Fluorescence polarization and permeability measurements concerning the effect of temperature and cholesterol. Biochim. Biophys. Acta. 1973;311:330–348. doi: 10.1016/0005-2736(73)90314-3. [DOI] [PubMed] [Google Scholar]
- 74.Antonov V.F., Petrov V.V., Ivanov A.S. The appearance of single-ion channels in unmodified lipid bilayer membranes at the phase transition temperature. Nature. 1980;283:585–586. doi: 10.1038/283585a0. [DOI] [PubMed] [Google Scholar]
- 75.Laub K.R., Witschas K., Heimburg T. Comparing ion conductance recordings of synthetic lipid bilayers with cell membranes containing TRP channels. Biochim. Biophys. Acta. 2012;1818:1123–1134. doi: 10.1016/j.bbamem.2012.01.014. [DOI] [PubMed] [Google Scholar]
- 76.Blicher A., Heimburg T. Voltage-gated lipid ion channels. PLoS ONE. 2013;8:e65707. doi: 10.1371/journal.pone.0065707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Blicher A., Wodzinska K., Heimburg T. The temperature dependence of lipid membrane permeability, its quantized nature, and the influence of anesthetics. Biophys. J. 2009;96:4581–4591. doi: 10.1016/j.bpj.2009.01.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Lautrup B., Appali R., Heimburg T. The stability of solitons in biomembranes and nerves. Eur Phys J E Soft Matter. 2011;34:1–9. doi: 10.1140/epje/i2011-11057-0. [DOI] [PubMed] [Google Scholar]
- 79.Kassahun B.T., Murashov A.K., Bier M. A thermodynamic mechanism behind an action potential and behind anesthesia. Biophys. Rev. Lett. 2010;5:35–41. [Google Scholar]


