Comparison of Inter-Finger Connection Matrix Computation Techniques

Abstract

A hypothesis was proposed that the central nervous system controls force production by the fingers through hypothetical neural commands (NCs). The NCs are scaled between values of 0 to 1, indicating no intentional force production or maximal voluntary contraction (MVC) force production, respectively. A matrix of finger inter-connections, [IFC], transforms NCs into finger forces. Two methods have been proposed to compute the [IFC]. The first method uses only single finger MVC trials and multiplies the [IFC] by a gain factor. The second method uses a neural network (NN) model based on experimental data. The performance of the two methods was compared on the MVC data and on a data set of sub-maximal forces, collected over a range of total forces and moments of force. The methods were compared in terms of: 1) ability to predict finger forces; 2) accuracy of NC reconstruction; and 3) preserved planarity of force data for sub-maximal force production task. Both methods did a reasonable job of predicting the total force in multi-finger MVC trials; however, the NN model performed better in regards to all other criteria. Overall, the results indicate that for modeling multi-finger interaction the NN method is preferable.

Introduction

Coordinated finger interaction is critical to properly perform numerous everyday tasks. Several characteristic behaviors of finger interaction apparently complicate finger force production. Enslaving is the term that has been used for the documented behavior of fingers producing force unintentionally when other fingers intentionally produce force^1,2. Another phenomenon of finger interaction is referred to as force deficit^3,4. Force deficit refers to lower forces produced by individual fingers in a multi-finger maximal voluntary contraction (MVC) task than in a single-finger MVC task. The force deficit increases with the number of fingers asked to produce maximal force⁴.

The mode control hypothesis was proposed to account for neural commands (NCs) from the central nervous system (CNS) being delivered to muscles and resulting in a pattern of movement or force production by the fingers^1,5,6. The hypothesis accounts for both enslaving and force deficit. The basic assumption of the hypothesis is that the CNS manipulates finger modes (NCs to individual fingers) and that sending a NC to a single finger results in force production by other fingers as well. The NCs are scaled from 0 to 1; 0 corresponding to no intentional force production and 1 being maximal force production. The mathematical relation proposed by Danion et al. (2003) was:

$$\left[F\right]=G\left[IFC\right]\left[NC\right]$$ (1)

where [F] is a (4×1) vector of finger forces, G is gain factor that is inversely proportional to a power function of the number of fingers explicitly involved in the task, [IFC] is a (4×4) inter-finger connection matrix that accounts for enslaving and does not depend on the number of explicitly involved fingers, and [NC] is a (4×1) vector of NCs. This simple model was found to account for finger forces well in the MVC tasks involving different numbers of intentionally active fingers.

Neural network (NN) models have also been used to relate NCs to forces produced by fingers^1,5. Previous NN models have been comprised of three layers: (1) the input layer that models a central neural drive; (2) the hidden layer; and (3) the output layer that models the force output of fingers and receives inputs both from the input and middle layers. The input from the middle layer is scaled by the inverse of the number of the fingers explicitly involved in the task. As shown by Zatsiorsky et al. (1998) the action of the NN can be described by an equation:

$$\left[F\right]=(1∕N)\left[w\right]\left[NC\right]+\left[v\right]\left[NC\right]$$ (2)

where [w] is a (4×4) matrix of connection weights between the fingers, [v] is a (4×4) diagonal matrix and N is the number of explicitly involved fingers. The previous studies based the NN model on all fifteen combinations of single- and multi-finger MVC pressing tasks. It was found that the NN modeling approach fitted finger forces during these tasks relatively well.

A number of previous studies^7,8,9,10 have transformed finger forces to NCs and performed analysis on these values. In these papers the NCs were referred to as finger modes. Finger modes are NCs that have been transformed to force units so that they have a physical meaning when interpreting the data. Several key differences existed in these studies. First the NCs were defined using neither MVC nor NN methods, but one-finger accurate sub-maximal force ramp production that covered the range of typical finger forces that were expected during the main experiment. Secondly, NCs (i.e. finger modes) were expressed in units of N to make comparison with actual performance variables such as total force and total moment of force transparent. A mode of 1 N to a finger corresponded to a command to that finger leading to a force distribution across all fingers such that the total force was 1 N. Note that NCs between 0 and 1 make the same command magnitudes to different fingers corresponding to different force magnitudes.

The purpose of this paper is to compare the techniques purposed by Danion et al. (2003) and the NN modeling approach for estimating finger forces from NCs. The performance of the two techniques has been previously compared only in the MVC tasks⁶. Yet in many applications the NCs are computed for sub-maximal finger forces^11,12. Comparison of the two techniques for sub-maximal finger forces is challenging because in this case the true NCs are unknown (in MVC tasks they are assumed to be either 0 or 1). One way to do this is to compute the percentage of “outliers”, i.e. the cases when the NCs fall out of the 0 to 1 range. Such “outliers” were documented previously in a sub-maximal prehension task¹². A NC less than 0 could theoretically occur if due to the co-activation of the extensors the force due to enslaving was decreased (i.e. flexion moment of the flexor muscles is decreased by extension moment generated by the extensor muscles). A NC greater than 1 could occur if the force produced by a finger was greater than what was measured during a single-finger MVC task involving that finger. This may occur due to an inaccurate single-finger MVC measurement. Another indicator of the better method is the degree to which the transformation from forces to NCs preserves the general tendency of the data distribution. In another study¹³ we have found that the force data are confined to a two-dimensional plane in the four-dimensional space of finger forces. The planarity signifies that the finger force sharing pattern may reflect the minimization of a cost-function^14,15,16,17. If the CNS controls the finger forces through the NCs, then one can expect that the NC values are also confined to a plane.

We chose the following criteria of performance: (1) the precision of finger force prediction in the MVC tasks; (2) the percentage of outliers (i.e. NCs outside of the 0 to 1 range) in sub-maximal tasks; and (3) the preservation of planarity in the NCs.

Methods

Subjects

Eleven right-handed male participants (age: 26.7 ± 4.1 yrs, weight: 80.5 ± 7.8 kg, height: 18.23 ± 7.9 cm, hand length: 19.0 ± 1.2 cm, and hand width: 8.4 ± 0.3 cm; mean ± SD across subjects) volunteered to participate in the current study. None of the subjects had a previous history of illness or injury that would affect the function of their upper arm, hand, or fingers. Hand length was measured from the tip of the middle finger to the distal crease at the wrist. Hand width was measured as the distance across metacarpophalangeal (MCP) joints of fingers 2 to 5, with the fingers in approximately neutral abd/adduction. Prior to performing the experiment subjects signed an informed consent form approved by the Pennsylvania State University.

Equipment

Pressing forces were measured using four uni-directional piezoelectric force transducers (208C02, PCB Piezotronics, Depew, NY). The force transducers were fixed to an aluminum plate that was securely fastened to a table. The aluminum plate had slots cut so that the each of the individual force transducers could be adjusted in the forward-backward direction in order to accommodate for different finger lengths of subjects. Sandpaper covers were placed on the surface of the force transducers to increase friction.

Analog output signals from the force transducers were sent to an AC/DC conditioner (5134B, Kistler, Amherst, NY, USA) then digitized with a 16-bit analog to digital converter (CA-1000, National Instruments, Austin, TX, USA). A LabVIEW program (LabVIEW version 8.0, National Instruments, Austin, TX, USA) was written to provide feedback and control data acquisition during the experiment. The force signals were collected at 100 Hz. Post-processing of the data was performed using custom software written in Matlab (Matlab 7.4.0, Mathworks, Inc, Natick, MA).

Experimental Procedures

During the study subjects were seated in a chair facing a computer screen. The right forearm rested on a padded support and the tip of each finger was positioned in the center of a force transducer. The distal interphalangeal (DIP), proximal interphalangeal (PIP), and MCP joints were all flexed in a posture that subjects felt was comfortable. The upper arm was positioned in approximately 45° shoulder abduction in the frontal plane, 45° shoulder flexion in the sagittal plane, and approximately 45° flexion of the elbow.

The experimental data were collected in two sessions. During the first session subjects were instructed to press with all one-, two-, three- and four-finger combinations (I, M, R, L, IM, IR, IL, MR, ML, RL, IMR, IML, IRL, MRL, and IMRL) to achieve their MVC. Note the following abbreviations were used: I = index; M = middle; R = ring; and L = little. Subjects were asked to increase force in a ramp like manner and to avoid a quick pulse of force production. They were required to maintain the force for at least 1 s before relaxing. Sufficient (at least, 30-s) rest was given between trials to avoid fatigue.

The main purpose of the second experimental session was to collect the data necessary for the inverse optimization (ANIO) analysis performed in another study (Martin et al. in press). The data obtained in this session were also used for the present study. Subjects were asked to produce a specified total force and total moment ({F_TOT; M_TOT}) combination while pressing with all four fingers. F_TOT produced by the fingers was the sum of normal forces of the four fingers. M_TOT produced by the fingers was computed as the moment produced about an axis passing mid-way between the M- and R-fingers. Subjects were required to produce both pronation (PR) and supination (SU) moments. The task set consisted of twenty-five combinations of five levels of F_TOT (20, 30, 40, 50 and 60% of MVC of all four fingers) and five levels of M_TOT (High PR, Low PR, 0, Low SU, and High SU). The high and low moments were scaled to 28% and 14%, respectively, of the moment the index finger could produce in a single finger MVC trial about the neutral axis.

Data Processing

The force signals were filtered using a 4^th order low-pass Butterworth filter at 10 Hz. The force data that was extracted from the MVC trials were the individual finger forces at the point when the peak MVC occurred for the instructed fingers. For the second session the individual finger force data from each trial were averaged over a 2-s time period in the middle of each trial (2- to 4-s windows), where steady-state values of F_TOT and M_TOT were observed. For all trials four data points (average finger forces) were extracted and used in the further analyses.

Enslaving Matrix and Motor Command Computation

The finger forces from the MVC trials were used to construct the IFC matrices describing finger interaction. We compared the performance of two methods for IFC matrix computation. The first method (6), which will be referred to as the MVC method, only uses the forces from single-finger MVC trials. For each single-finger MVC trial the forces produced by the four fingers are placed in a column of the [IFC] matrix. To account for force deficit [IFC] is multiplied by a gain factor G. The value of G depends on the number of fingers (N) involved in a pressing task (6):

$$G=1∕N^{0.712}$$ (3)

The [IFC], with force deficit accounted for, is given by:

$$\left[IF{C}_{MVC}\right]=\left(\frac{1}{N^{0.712}}\right)\left[\begin{array}{cccc}\hfill W_{I,I}\hfill & \hfill W_{I,M}\hfill & \hfill W_{I,R}\hfill & \hfill W_{I,L}\hfill \\ \hfill W_{M,I}\hfill & \hfill W_{M,M}\hfill & \hfill W_{M,R}\hfill & \hfill W_{M,L}\hfill \\ \hfill W_{R,I}\hfill & \hfill W_{R,M}\hfill & \hfill W_{R,R}\hfill & \hfill W_{R,L}\hfill \\ \hfill W_{L,I}\hfill & \hfill W_{L,M}\hfill & \hfill W_{L,R}\hfill & \hfill W_{L,L}\hfill \end{array}\right]$$ (4)

The finger connection weights (w_i,j) represent the force produced by finger i when finger j is instructed to press.

The NCs for the trials with sub-maximal force production, i.e. for the second experimental session, were computed by rearranging equation 1:

$$\left[NC\right]={\left[IFC\right]}^{-1}\left[F\right]$$ (5)

Neural Network Modeling

The second method of the [IFC] computation uses a three-layer NN model (1; 5). The mathematical description of the NN is provided in Zatsiorsky et al. (1998) and Li et al. (2002). The input pattern vector was of the form:

$$\left[NC\right]={\left[N{C}_{I}N{C}_{M}N{C}_{R}N{C}_L\right]}^{\mathrm{T}}$$ (6)

where NC_j is the NC to the jth finger; NC_j equals 1 if the finger was instructed to produce the force and 0 otherwise. The desired output pattern vector, which is the force collected in the corresponding MVC trial, was of the form:

$$\left[F^d\right]={[F_I^d,F_M^d,F_R^d,F_L^d]}^T$$ (7)

where $F_j^d$ is the desired force output of the jth finger from the MVC experimental trials. The NN was trained using all fifteen MVC combinations. The NN returned the vector of model finger forces

$$\left[F\right]={[F_I,F_M,F_R,F_L]}^T.$$ (8)

The weight coefficients of the NN, w_jk and v_k, were chosen to minimize the discrepancy between the model finger forces and those collected in the MVC trials. The discrepancy was characterized be the error function, E, defined as the sum of squares error over all input MVC conditions:

$$E=\sqrt{\frac{1}{15}\sum _{i=1}^{15}{\Vert {\left[F\right]}_i-{\left[F^d\right]}_i\Vert }^2}$$ (9)

The action of the NN on the NCs can be summarized by the linear matrix equation (2):

$$\left[F\right]=(1∕N)\left[w\right]\left[NC\right]+\left[v\right]\left[NC\right]$$ (10)

where [w] is a (4 × 4) matrix of inter-finger connection weights, [v] is a (4 × 4) diagonal matrix, and N is the number of fingers involved in the task. N = 4, since all fingers produced force during the trials of the second session. The [IFC] that was used to compute the NCs from the session two data was computed as:

$$\left[IF{C}_{NN}\right]=\left(\frac{1}{N}\right)\left[w\right]+\left[v\right]$$ (11)

The NN was trained using a back-propagation algorithm. The number of training epochs was set to 500 epochs. The learning rate was 0.01. The number of epochs was sufficient for the convergence of the algorithm with the selected learning rate. A set of different initial conditions was tested and for all of them the algorithm converged to the same minimum. The average value of the error function (across subjects) was 3.68 ± 1.13 N.

Prediction of Experimental Forces

The IFC_MVC and IFC_NN matrices of each subject were used to predict finger forces in each of the fifteen MVC trials using equation 5. The finger(s) that were instructed to press had the NC value set to 1, the NC value of non-instructed fingers was set to 0. The predicted force was compared to the experimental force for all four fingers. The absolute error was computed for each finger as the absolute value of the difference between the experimental and predicted forces.

Planarity of Data

We evaluated the planarity of the data by performing the principal component analysis (PCA). Since the transformation between forces and NCs is linear it is natural to expect the planarity to be preserved in the NCs. In the presence of unavoidable deviation of the actual force data from a perfect plane, the transformation of forces to NCs could potentially enhance any deviations from planarity of the force data. Thus, we checked which method better produced NCs with a planarity closer to the original force data. This was done by performing PCA on the force data set and the NC data sets computed from each method. The variance explained in the first two PCs was assumed to be indicative of whether or not the data was confined to a 2D plane. Previously, it was assumed that if greater than 90% of the variance was explained in the first two PCs then the data was confined to a 2D plane^14,15,16,17.

Percentage of Outliers

The finger forces from the second experimental session were transformed into NCs. The number of NCs that were: (1) less than 0 and (2) greater than 1 was computed. The entire data set contained 1100 total data points (11 subjects × 5 moments × 5 force levels × 4 fingers). The occurrences of NC values less than 0 and greater than 1 were counted in terms of the entire data set, as well as on a finger-by-finger basis.

Statistical Methods

The mean error of the predicted forces was computed across subjects for the total force and individual finger forces. Mean values of the variance explained by the first two principal components were computed on the Fisher z-transformed values; then the inverse z-transformation was performed on the mean values. A repeated-measure (RM) ANOVA was performed to test the effect of multi-finger pressing COMBINATION (11 levels: IM, IR, IL, MR, ML, RL, IMR, IML, IRL, MRL, and IMRL), NC computation METHOD (2 levels: MVC and NN) and FINGER (4 levels: I, M, R, and L) on the force error of individual fingers in the four-finger MVC task. Note: the RM ANOVA was only performed for multi-finger combinations since all the single-finger combinations of the MVC method had zero error. The PCA variance responses were z-transformed prior to performing the RM ANOVA. Statistical analyses were performed using the SPSS software package (SPSS Inc., Chicago, IL, USA). The significance level was set to α = 0.05.

Results

The results are presented in the following order: (1) inter-finger connection matrices [IFC], (2) accuracy of force prediction and (3) accuracy of neural command (NC) reconstruction.

The mean forces for each of the MVC pressing tasks were computed and for all tasks enslaving forces (force production by non-instructed fingers) were present (Table 1). Mean enslaving forces ranged from 0.80 ± 0.29 N (L-finger in MVC_IM task) to 8.28 ± 1.67 N (M-finger in MVC_R task). Qualitatively both IFC_MVC and IFC_NN are similar (Table 2) with the instructed finger force (diagonal elements) several times higher than the non-instructed finger's forces (off-diagonal elements). For all tasks, the diagonal element values are higher in IFC_NN than in IFC_MVC. In fourteen of sixteen cases the values of the non-instructed fingers forces are lower in IFC_NN than IFC_MVC. The two cases that are the exceptions are the L-finger forces when M-finger was instructed to press and when R-finger was instructed to press.

Table 1.

Mean MVC forces for all finger combinations. Standard errors are in parentheses.

	Forces
Finger Combination	I	M	R	L
I	34.92 (2.26)	4.42 (2.19)	1.99 (0.81)	1.34 (0.39)
M	6.71 (1.57)	29.42 (2.63)	5.50 (1.11)	1.10 (0.54)
R	2.07 (0.63)	8.28 (1.67)	26.85 (3.14)	3.27 (0.70)
L	1.59 (0.71)	3.47 (1.61)	7.37 (1.37)	20.88 (1.90)
IM	24.78 (2.11)	23.97 (2.41)	3.51 (1.44)	0.80 (0.29)
IR	22.27 (1.77)	6.64 (2.88)	16.02 (1.75)	3.17 (1.13)
IL	21.99 (2.56)	3.72 (2.25)	3.26 (1.57)	15.19 (1.20)
MR	3.57 (1.68)	23.87 (2.04)	15.74 (1.71)	2.86 (1.31)
ML	3.23 (1.45)	21.00 (2.50)	4.63 (1.41)	11.61 (1.12)
RL	2.12 (0.72)	5.57 (1.72)	19.25 (1.81)	17.63 (1.82)
IMR	19.31 (1.33)	20.56 (2.38)	13.84 (1.81)	1.63 (0.57)
IML	18.55 (2.14)	16.42 (1.98)	3.45 (1.06)	12.78 (1.39)
IRL	19.12 (2.10)	3.26 (1.64)	14.13 (1.54)	14.84 (1.83)
MRL	2.66 (1.16)	18.03 (1.87)	17.98 (2.27)	13.33 (1.70)
IMRL	20.19 (2.03)	21.70 (2.85)	15.64 (1.33)	13.82 (1.61)

Table 2.

Mean inter-finger connection matrices computed using MVC and neural network modeling methods. Column headings are of the finger instructed to press. Standard error is in parentheses.

MVC Method
	I	M	R	L
I	13.01 (0.84)	2.50 (0.59)	0.77 (0.24)	0.59 (0.26)
M	1.65 (0.82)	10.96 (0.98)	3.09 (0.62)	1.29 (0.60)
R	0.74 (0.30)	2.05 (0.42)	10.01 (1.17)	2.75 (0.51)
L	0.50 (0.15)	0.41 (0.20)	1.22 (0.26)	7.78 (0.71)

NN Method
	I	M	R	L
I	16.16 (1.72)	1.16 (0.61)	0.28 (0.23)	0.41 (0.14)
M	1.44 (0.45)	15.34 (1.30)	1.11 (0.31)	0.00 (0.18)
R	0.47 (0.13)	1.98 (0.42)	11.32 (0.99)	1.09 (0.21)
L	0.31 (0.25)	0.57 (0.41)	1.67 (0.38)	11.36 (1.07)

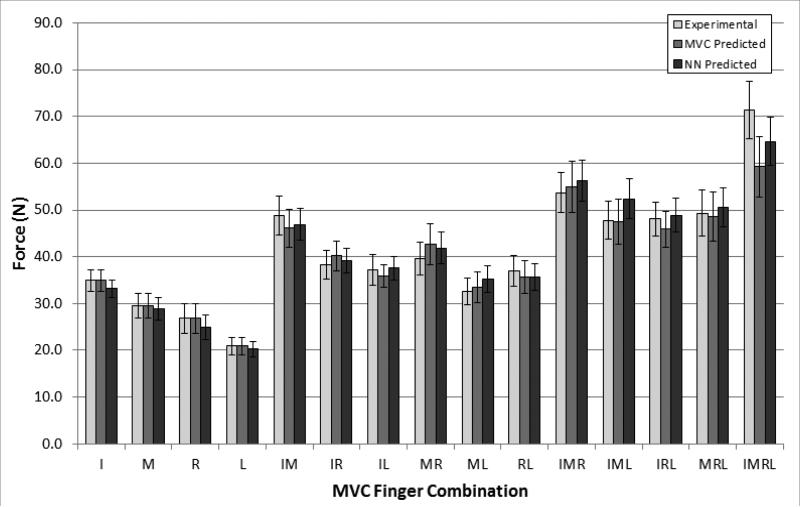
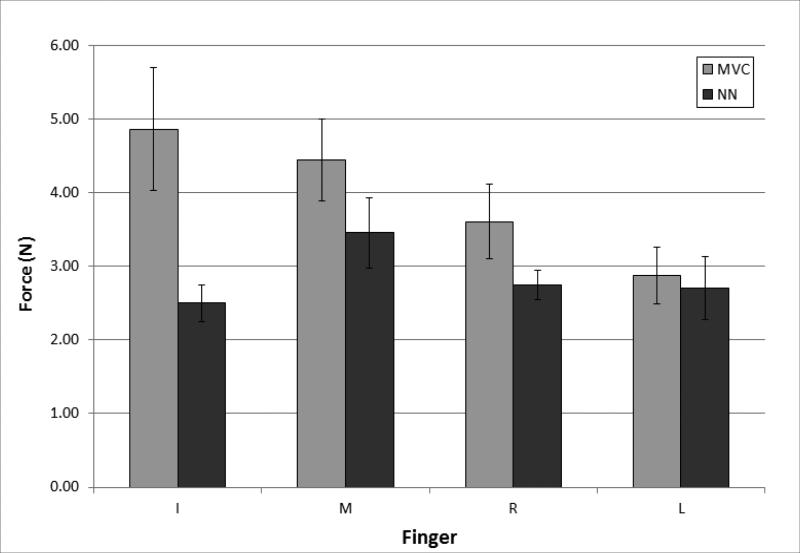
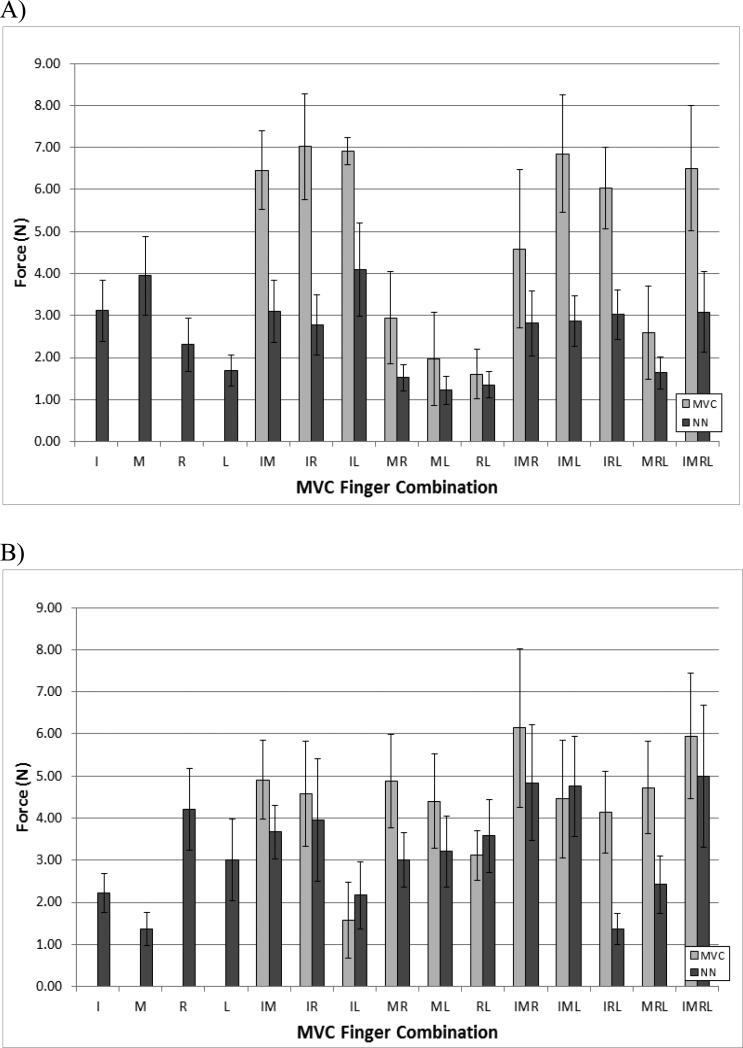
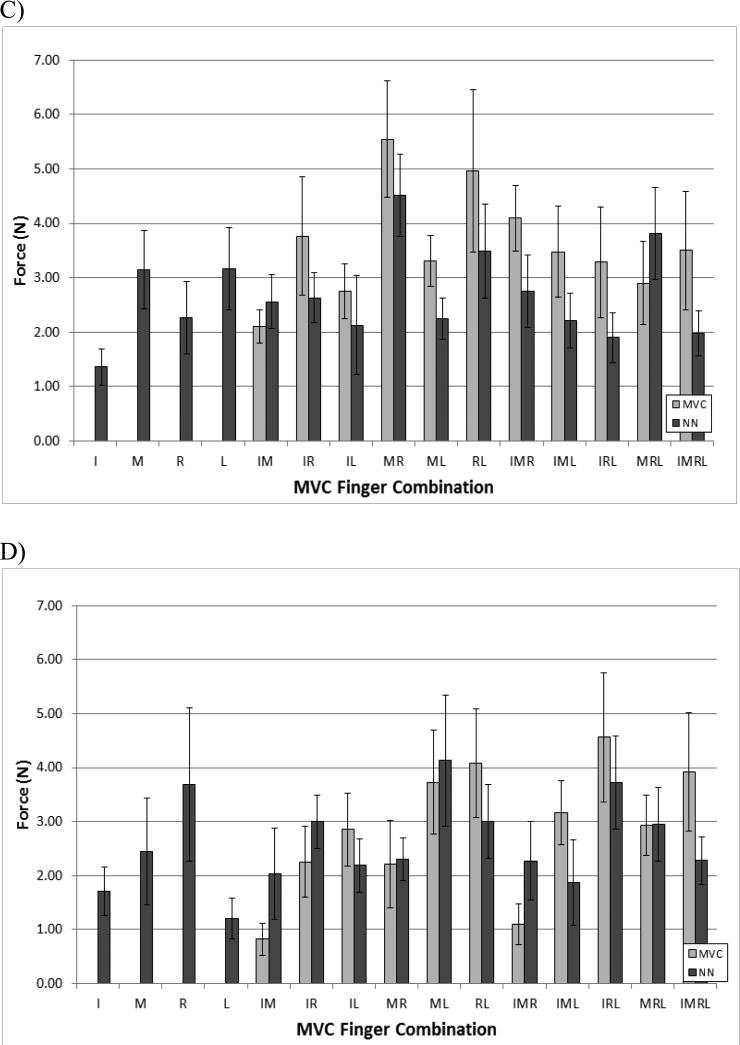
The error between the experimental and predicted forces was quantified (Figures 1-3). Both methods predicted the total forces with a relatively high degree of accuracy. The largest errors were observed in the three- and four-finger tasks. The RMSE error across all combinations is less for the NN method (3.68 ± 0.34 N) than the MVC method (4.43 ± 0.46 N); however, there is no significant difference (p > 0.1) between the METHODs. For the force error of individual fingers the NN method results in smaller absolute errors for the majority of multi-finger tasks (Figures 2 & 3). The RM ANOVA performed on the individual finger force errors in the multi-finger MVC tasks resulted in finding a significant effect of METHOD (F_1,10 = 10.266, p < 0.01); however the effects of FINGER (F_3,30 = 2.324, p > 0.09) and COMBINATION (F_10,100 = 0.994, p > 0.45) were non-significant.

Figure 1.

Comparison of total forces during MVC trials to those predicted by the MVC and neural network based methods. Error bars are standard errors.

Figure 3.

Mean absolute error for multi-finger tasks between experimental forces and forces predicted by the MVC and neural network based methods. Absolute errors were averaged across all finger pressing combinations. Error bars are standard error.

Figure 2.

Comparison of the absolute force error between individual experimental finger forces and forces predicted by the MVC and neural network based methods for: A) index finger, B) middle finger, C) ring finger, and D) little finger. Data for all finger combinations are shown. Error bars are standard errors.

As in indicator of which method produced more accurate reconstructed values of the NCs the percentage of values outside of the range of 0 to 1 was computed for the data from the second experimental session (Table 3). The percentage of values less than 0 was 2.7% and 0.1% for the MVC and NN methods of computing NCs, respectively. The percentage of values greater than 1 was 8.7% and 3.4% for the MVC and NN based NC's, respectively. For the MVC method the most occurrences of NCs less than 0 was for the index finger. The NN method had almost no occurrences of NC values less than 1. For both methods the ring and little fingers displayed the most instances of values greater than 1. None of the subjects produced a NC greater than 1 for the index finger for either method.

Table 3.

Percentage of neural command values less than 0 and greater than 1 observed in the second experimental session. Percentage of values for MVC and NN methods are given. The data set consisted of 275 values per finger.

	% of Values Less Than 0		% of Values Greater Than 1
Finger	MVC	NN	MVC	NN
I	8.0%	0.0%	0.0%	0.0%
M	2.8%	0.0%	8.4%	3.2%
R	0.0%	0.4%	12.4%	6.8%
L	0.0%	0.0%	14.0%	3.6%

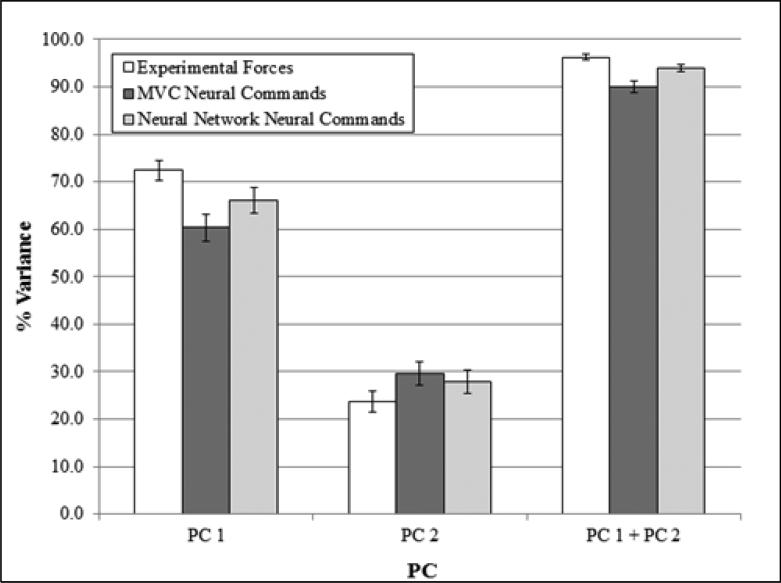
The NN method better preserved the planarity of the original force data (Figure 4). In other words, the variance explained by PC1+PC2 on the NCs computed with the NN method (94.6 ± 7.1%) was closer to the variance explained by the first two PCs on the force data (96.6 ± 7.4%) than that on the NCs computed using the MVC method (90.8 ± 7.2%). The effect of METHOD (F_1,10 = 30.855, p < 0.001) on the variance explained in the first two PCs was significant.

Figure 4.

Variance explained by the principal component (PC) one and two of the principal component analysis. The variance of forces and NC computed using both the single-finger MVC and neural network method is presented. Error bars are standard error.

Discussion

The results indicate that the neural network (NN) method outperforms the MVC method with respect to all three chosen criteria: it provides more accurate predictions of finger forces; the NN method produces a greater percentage of NCs between 0 and 1; and it preserves the planarity of the original force data better than the MVC method.

There are a number of constraints, both in the periphery and centrally, that limit the independence of finger interaction (for review see Schieber and Santello, 2004). The mechanical connections, multi-digit motor unit architecture in the extrinsic muscles, and cortical representation may all differ among people. Architectural properties of a single muscle (first dorsal interosseous) have been shown to display significant variability across healthy persons¹⁸. These differences could be due to practice, training, strength, or age. Although our subjects were all fairly similar in terms of sex, age, strength, and daily use of the fingers the [IFC] were quite unique to individual subjects. Taking this into consideration it is not surprising that the NN method, which provides a broader representation of enslaving and force deficit across finger pressing combinations, outperformed the MVC method in our study.

A previous study investigated differences between [IFC] of twenty subjects¹⁹ computed using the NN method. The subjects were similar to those in our study in that they were all young, healthy males with no reported activities that would abnormally alter their finger independence. The [IFC] were normalized to the MVC values and it was reported that after the normalization the main differences between subjects were in the force sharing patterns and the amount of enslaving.

It appears that the main difference between the MVC and NN methods is their ability to predict force sharing patterns, as well as, model enslaving. Figure 1 shows that both methods predicted the total force of the fingers in the multi-finger MVC trials with similar accuracy. In many cases the absolute error of the MVC method was even less than that of the NN method. The NN method set itself apart from the MVC method in its ability to predict the individual finger forces in the multi-finger MVC trials, which translates to the force sharing pattern. The [IFC] contain sixteen elements, diagonal and off-diagonal. The diagonal elements are several times larger than the off-diagonal elements. The relative magnitude of the off-diagonal elements is an important factor in determining the transformation scaling (singular values) of the [IFC].

In conclusion, finger interaction is a complex behavior due to mechanical connections and central factors. The force sharing patterns of fingers in a given task are affected by both enslaving and force deficit. Subtle, yet significant, physiological differences between subjects lead to differences between finger forces and thus different individual finger inter-connection matrices. It appears better to use the neural network method to model finger interaction as it more accurately predicts individual finger forces. It should be stated that the MVC method, which only requires four trials, did demonstrate an adequate ability to predict the total force of multi-finger MVC trials but was not able to match the NN method in its ability to predict single-finger forces in multi-finger MVC trials.