Directed Progression Brain Networks in Alzheimer's Disease: Properties and Classification

Abstract

This article introduces a new approach in brain connectomics aimed at characterizing the temporal spread in the brain of pathologies like Alzheimer's disease (AD). The main instrument is the development of “directed progression networks” (DPNets), wherein one constructs directed edges between nodes based on (weakly) inferred directions of the temporal spreading of the pathology. This stands in contrast to many previously studied brain networks where edges represent correlations, physical connections, or functional progressions. In addition, this is one of a few studies showing the value of using directed networks in the study of AD. This article focuses on the construction of DPNets for AD using longitudinal cortical thickness measurements from magnetic resonance imaging data. The network properties are then characterized, providing new insights into AD progression, as well as novel markers for differentiating normal cognition (NC) and AD at the group level. It also demonstrates the important role of nodal variations for network classification (i.e., the significance of standard deviations, not just mean values of nodal properties). Finally, the DPNets are utilized to classify subjects based on their global network measures using a variety of data-mining methodologies. In contrast to most brain networks, these DPNets do not show high clustering and small-world properties.

Introduction

The analysis of brain networks derived in vivo from medical imaging technology, often called connectomics (Sporns, 2010; Sporns et al., 2005), has led to new understandings and approaches to the study of the brain and many neurological disorders. In addition to elucidating the global connectivity of the brain, network analysis has also provided a new set of imaging markers of disordered brains' connections that differ significantly from purely structural characteristics (Bullmore and Sporns, 2009). In almost all of these studies, the nodes of the networks correspond to different brain regions, whereas the edges attempt to capture relationships between these regions. For example, in functional networks (constructed from fMRI, EEG, and MEG), edges typically represent a dynamical correlation between two brain regions, whereas in structural networks [constructed from diffusion magnetic resonance imaging (MRI) tractography], the edges capture the physical connections between the regions. Cortical thickness networks are an interesting mix, as they are based on structural data but are akin to functional networks as their edges are typically based on correlations between regions (He et al., 2007).

In this article, we consider a new class of networks, directed progression networks (DPNets), which are closely related to cortical thickness networks, but instead of trying to capture correlations, DPNets attempt to capture temporal progression of a brain disease. The idea of using networks to capture the spreading of a disease through a population is well known from the study of infectious diseases (Anderson et al., 1992), but here, we are considering a network model for the temporal progression of a disease within an individual brain. In addition to providing a new method in connectomics, the DPNets studied here also provide one of the few uses of general directed networks in Alzheimer's disease (AD), that is, where the edges between network nodes have a sense of direction.

Most brain networks studied to date have been predominantly undirected. In structural networks, this arises from technological limitations and the fact that diffusion MRI only detects the orientation of an axon bundle and not the direction of transmission. In functional networks, simple correlations are undirected, but there has been much research devoted to capturing directionality from causation, using tools such as Granger causality (Brovelli et al., 2004), and recent progress is developing this into a viable tool (Deshpande and Hu, 2012). An alternative approach constructs Bayesian networks that capture the dependency structure of the nodes (Huang et al., 2013; Li et al., 2013; Zhou et al., 2013).

The extension to directed networks also requires certain modifications to standard network analysis measures. Some measures, such as characteristic path length (CPL), are easily extended by simply considering directed paths; however, others such as clustering coefficient are more complex in the directed case (Fagiolo, 2007; Rubinov and Sporns, 2010). In addition, the interpretation of CPL is complicated by the lack of directed paths between many pairs of nodes in these directed networks.

Our new approach starts by building upon and combining the ideas behind Granger causality with recent work on the construction of cortical thickness networks (He et al., 2007). We then focus on the ability of DPNets to capture prominent statistical features of abnormal cortical changes in AD. Regional cortical thinning has been a consistent finding in MRI studies of dementias, such as AD and frontotemporal lobar degeneration (Du et al., 2007; Richards, 2009; Rosen et al., 2002). Moreover, the pattern of regional propagation of cortical thinning seems to differ characteristically between different types of dementias (Du et al., 2007), suggesting that the spread of cortical thinning over time follows a systematic course in each disease. We postulate that the relationships between regional changes in cortical thinning—as measured using serial MRI—can be used to establish directed edges in a network that potentially provides a signature of progressive brain damage. This construction is also an attempt to model recent discoveries suggesting “prion-like” propagation of misfolded amyloid-beta proteins in AD, perhaps along axonal tracts (de Calignon et al., 2012; Eisele et al., 2010; Moreno-Gonzalez and Soto, 2011), although our methods are not dependent on any specific theory of disease propagation.

Whereas previous studies have looked at correlations in the rates of cortical thinning between regions to create undirected edges, we focus on the time progression of these correlations from an initial time period to a later time period, thereby creating directed edges for DPNets. In this scenario, an edge from node A to node B implies that node A was initially “infected” and then spread its “infection” to node B in the following period. This is implemented by computing the similarity between the rate of thinning for node A in the initial period with the rate of thinning of node B in the following period, thereby capturing the time progression of thinning rates. In this article, we consider the simplest implementation of this idea, relying only on three sequential thickness measurements. Given the many statistical (and biological) uncertainties in the cortical thickness measurements, we do not claim that individual edges are reliable; however, by using the statistical power of studying entire networks, we are able to obtain statistically significant properties of these networks that can be used for separating the groups, for example, normal cognition (NC) from AD patients, and also prove effective even at the individual level for the classification of AD versus NC. More sophisticated DPNet constructions using longer timeframes or more precise data would likely improve these results significantly, but even the base case studied here with only three temporal thickness measurements yields significant results.

Materials and Methods

Subjects

Data used in the preparation of this article were obtained from the Alzheimer's Disease Neuroimaging Initiative (ADNI).¹ Data from 255 subjects were included, who had (1) 1.5 T MRI scans taken at least every other year for a total of three scans, (2) successful evaluations of their MRIs using Freesurfer software version 4.4 (Fischl, 2012; Reuter et al., 2012), and (3) a diagnosis over 3 years consistent with either AD or stable NC. Subjects were excluded if their diagnosis was stable mild cognitive impairment (MCI), MCI conversion to AD, or if their diagnosis reverted over 3 years, for example, reversion from MCI to NC or AD to MCI. The final sample consisted of 39 AD and 97 NC patients. A summary of the demographic and clinical data of the subjects is listed in Table 1.

Table 1.

Group Demographics and Clinical Summary

	NC	AD	p-Valuea
n	97	39
% Male	48	55	0.12
APOE ɛ4 carriers (%)	33	51	<0.001
Baseline
Age (years)	75.4±5	74.5±6	0.21
ADAS-Cog11b	5.6±2	18.1±6	<0.001
% Annual changec
ADAS-Cog11	−8±80	42±34	<0.001

^ap-Values indicate effects across groups using ANOVA or Fisher exact test (for categorical variables, e.g., male and APOE).

^bAlzheimer's Disease Assessment Scale-cognitive subscale with 11 items (Mohs et al., 1997); total score ranging from 0 to 70; larger scores indicating greater impairment.

^c% Annual change is expressed relative to baseline in percent.

AD, Alzheimer's disease; ANOVA, analysis of variance; APOE, Apoliprotein E; NC, normal cognition.

ADNI standard image acquisition and Freesurfer processing have been described in detail previously (Jack et al., 2008; Reuter et al., 2012). Briefly, the acquisition consisted of T₁-weighted MRI scans, using a sagittal volumetric magnetization-prepared rapid gradient-echo sequence, with an echo time (TE) of 4 msec, repetition time (TR) of 9 msec, flip angle of 8°, and acquisition matrix size of 256×256×166 in the x-, y-, and z-dimensions with a nominal voxel size of 0.94×0.94×1.2 mm. A designated center assessed image quality and corrected the data for system-specific image artifacts (Fischl, 2012). Cortical thickness in Freesurfer is estimated by computing the shortest distance from each point on the gray/white matter surface to the pial surface and vice versa and averaging the results. Furthermore, in Freesurfer version 4.4, the confounding effect of intrasubject morphological variability is reduced by using a longitudinal workflow that estimates brain morphometry measurements unbiased with respect to any time point in each subjects' longitudinal MRI data. This is achieved by building first a template image from all time points as an unbiased prior distribution for each subject before computing morphometric deformations for all time points.

Connectome reconstruction

Previous connectome work in AD has considered thickness correlations between regions, using cross-sectional or longitudinal MRI. For cross-sectional data, previous research constructed a “consensus network” for the group by finding cross-sectional correlation in thicknesses between brain regions (He et al., 2007, 2008, 2009), allowing construction from a single temporal measurement. However, to compare thicknesses among different subjects, this procedure required normalization by personal characteristics, such as age and gender (Barnes et al., 2010; Sowell et al., 2007), as this affects baseline thicknesses, complicating the process. For longitudinal data, personalized (by subject) networks have been constructed using temporal correlations between regions (Li et al., 2012), which we discuss below.

In this project, we considered a modified version of the latter construction, motivated by, but not relying on, emerging data of prion-like propagation of misfolded amyloid-beta proteins in AD, wherein we constructed personalized DPNets for each patient. For simplicity, we consider measurements taken at three timepoints with 2-year intervals between them and then compute the thinning rate for the “early” period (thickness change between timepoint 1 and 2) and the “late” period (thickness change between timepoint 2 and 3). Note that by thinning rate we mean the factor by which the thickness is decreased, for example, a thinning rate of 2 corresponds to a halving of the thickness in one period (2 years); one could also use the inverse of this, but it would not significantly affect our results as we are only considering similarities between rates in the network construction. One could ideally use more timepoints; however, in practice, this would reduce the set of subjects and also introduce complications in comparing subjects with different numbers of timepoints, so three timepoints seemed a good compromise for this initial study. We then compute the similarities between these rates, as opposed to the raw thickness used in earlier articles, thereby mitigating the need to remove individual biases toward initial cortical thickness. To infer spatial propagation we compute the similarity between the thinning rate of the early period of one region and the thinning rate for the late period of a second region, thereby constructing a directed (spatiotemporal) similarity from the first region to the second for all pairs of regions. This procedure captures both the temporal and spatial spread of the “infectious agents” by allowing time for transmission between brain regions. We consider the matrix of these directed similarities over all pairs of nodes to construct directed similarity matrices, one for each subject; however, unless there is thinning during the early period (a thinning rate >1), we set that similarity to 0, capturing the requirement that only “infected” nodes (ones which are thinning) can “transmit” the disease. We denote these “infectious” similarity (ISIM) matrices.

While the lack of thinning over time may be surprising (Hogstrom et al., 2013; Lemaitre et al., 2012), such nodes are common in the data, arising in about 39% of the nodes for NC and 27% of the time for AD. This can be explained by the significant probability that a node which does not appreciably thin will actually appear to thicken in the data due to measurement error and biological variation, for example, inflammation.

It is informative to compare our directed procedure with Li et al.'s (2012) undirected approach. They construct a matrix that is analogous to our ISIM matrices using undirected correlations. Specifically, given a set of thickness measurements for a pair of regions of interests (ROIs) (nodes), Li and colleagues directly compute the (statistical) correlation between the two vectors of thicknesses. The key difference is that their edges capture the degree to which they change thickness in unison, while ours captures the degree to which one ROIs thinning precedes the second ROIs thinning. (Note that there are additional differences between our construction and theirs including the choice of ROIs and the method for computing thicknesses.)

Each node is 1 of the 88 standard Freesurfer ROIs so the ISIM matrices are 88 by 88, with zeros on the diagonals (consistent with the idea of the spread of “infection”). This also leads to networks without self-edges from a node to itself, which is standard practice in most brain network analyses (Bullmore and Sporns, 2009).

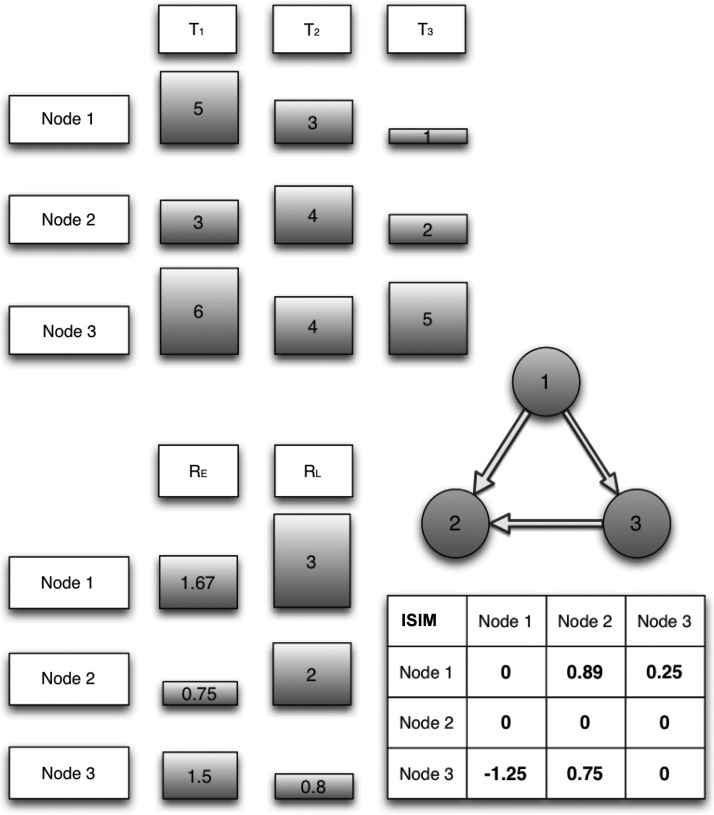
For example, in Figure 1, we consider three ROIs, denoted node 1, node 2, and node 3. Node 1 has thickness=5 at timepoint 1, thickness=3 at timepoint 2, and thickness=1 at timepoint 3, so its thinning rates are R_E=5/3=1.67 in the early period and R_L=3/1=3 in the late period. Note that since node 1 is thinning between timepoint 1 and 2, it is possibly “infected” and may spread its infection to other nodes. A similar calculation shows that node 2 is not thinning in the early period (its rate is 0.75<1) but is thinning in the later period (at rate 2.0>1) and is therefore a candidate “target” of the infection. When we compute the directed similarity between node 1 and node 2, we simply compute the similarity of the thinning in the early period for node 1, 1.67, and the late period of node 2, 2.0, which is given by 1−(1.67−2.0)²=0.89, a relatively high similarity. This will eventually lead to a directed edge from node 1 to node 2 as there is a statistical signal of possible propagation from node 1 to node 2. Clearly, this is not proof of such propagation and no single edge should be taken as more than a potential signal of transmission. However, our results below suggest that all these directed edges do in fact provide statistical significance in the aggregate when fully analyzed.

FIG. 1.

Illustrative directed progression network construction. The top shows cortical thicknesses at times T₁, T₂, and T₃, whereas the bottom left shows the early (year 1–3) and late (year 3–5) thinning rates, R_E and R_L. Bottom right shows the infectious similarity (ISIM) matrix and above it is the induced network with an average outdegree of 1 (edges arise from three highest values in the matrix). Note that the ISIM value for box (2, 3) is 0 since node 2 did not thin in the early period and that element would have been large (0.9975) without the restriction. However, node 2 does thin in the late period and there exists an edge from node 1 to node 2.

Note that the above calculation is not symmetric in the two nodes. If we repeat the calculation for node 2 to node 1, we get 1−(0.75−3)²=−4.06, which is an extremely low similarity. Next consider the calculation from 2 to node 3 for which there is a high similarity, 1−(0.8−0.75)²=0.975, which one might think could lead to an edge. However, if we think of edges as suggesting propagation of an infectious agent, not just a similarity, then the lack of thinning in the early period for node 2 makes this an unlikely path of transmission. To capture this, we construct the ISIM-directed similarities with the requirement that the initial node must be thinning, that is, the thinning rate must be >1 and thus set the directed similarity to zero so as not to create an edge from node 2 to node 3 in the final network.

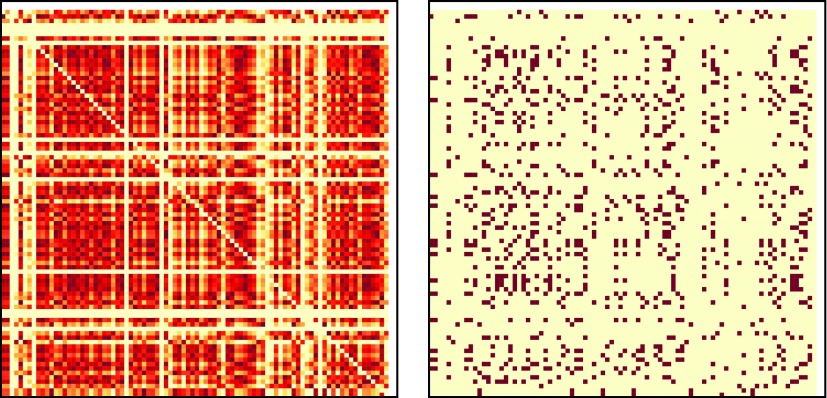
The “similarity matrices” (ISIM) are then thresholded to create DPNets using an individualized threshold for each similarity matrix (i.e., for each subject) to generate a directed network with a fixed average outdegree of 10, that is, on average each node has 10 outgoing edges. (See Fig. 2 for the heatmap of the network before and after thresholding and note the “banded structure” arising from our requirement that the source node be thinning in the early period.) Thus, given an 88×88 ISIM matrix, we generate a network with 88 nodes, with a directed edge from node i to a different node j if the value of the i, j'th element of the matrix exceeds a specific value, where the cutoff value depends on the specific matrix.

FIG. 2.

Heatmap for sample ISIM matrix (left) and its respective network (right) obtained by thresholding with an average degree of 10 as in our analysis. Note the lack of symmetry along the main diagonal, which would arise in undirected networks. Also note the horizontal bands corresponding to nodes that did not thin in the early period. Color images available online at www.liebertpub.com/brain

For comparison purposes, we will also consider the undirected network that we construct by symmetrizing the ISIM matrix (i.e., adding the matrix and its transpose to create a symmetric matrix), which leads to an undirected graph using the binarization method discussed above.

The choice of 10 as the average outdegree was chosen to be consistent with other studies [which have shown that this approximate degree of density is usually the most informative, e.g., Hayasaka, and Laurienti (2010)] and also generates networks that are both sparse (where only about 10% of the potential edges exist) and connected (where there exist paths from any node to any other). As a check for bias using 10 outdegree, we have repeated the analysis with a variety of average outdegrees ranging from 6 to 15 and found substantially similar results.

Network measures

We will consider several standard network measures: nodal degrees (DEG), indegree (INDEG) and outdegree (OUTDEG), the size of the giant component (GIANT), characteristic path length (CPL), global efficiency (GEFF), local clustering coefficient (CLUST), ordinary small-worldness, using CPL (SW-CPL), efficiency based small-worldness (SW-GEFF), and modularity (MOD). We briefly review these below (see Rubinov and Sporns [2010] for a more detailed discussion).

For an undirected network, DEG is simply the number of edges that touch that node, but for a directed network, one typically considers both the OUTDEG, the number of directed edges beginning at a node, and INDEG, the number of edges ending at our node. Given our interpretation of a DPNet as modeling the spread of a disease, a node with high OUTDEG is spreading the infection, while one with high INDEG is being infected from many sources, so it makes sense to consider these two notions of degree separately. Note also that since INDEG and OUTDEG are defined for each node in the network, it is natural to consider the mean values of these quantities. However, in addition to these simple averages, we will find it highly fruitful to also consider the variations in these values, such as their standard deviations (over the nodes in a single network).

We also consider the GIANT measure, which is the size of the largest connected component in the undirected case and the size of the largest strongly connected component in the directed case, which is often significantly smaller. Recall that the strongly connected component is the largest set of nodes so that there is a directed path between every pair of nodes in that set.

In undirected networks, the CPL is the average shortest path length between pairs of nodes, while in the directed case, one only allows directed paths. However, in the directed case, it often arises that there is no directed path between many pairs of nodes, which leads to an infinite (or undefined) CPL. Thus, we only compute the CPL for the giant component. An alternative measure is the GEFF that computes the average of the inverse shortest path lengths. This has the desirable property that infinite paths simply add 0 to the sum of inverse path lengths and do not require restricting to the giant component.

Additionally in the undirected case, CLUST is the fraction of pairs of neighbors of a node that have an edge between them; however, in the directed case, one uses the fraction of possible edges between the neighbors of the node and the formula is more complex than in the undirected case (Fagiolo, 2007). Here again, we will consider not only the average of CLUST but also its standard deviation.

The ratio of CLUST to CPL is known as the “raw” small-worldness (SW) and captures an important structural aspect of a network (Watts and Strogatz, 1998). To gauge the significance of the SW, one typically considers the “normalized” SW, which is the ratio of the raw SW of the networks to the raw SW of matched random degree-distributed (DD) networks, which are discussed below. However, since the CPL is not necessarily a completely satisfactory measure in directed networks when the graph is not strongly connected—the giant component does not contain all of the nodes—we consider an alternative measure small-worldness (SW-GEFF), which uses the inverse of the global efficiency in place of the CPL. Thus, the raw SW-GEFF is the product of the global efficiency and the clustering coefficient and the normalized SW-GEFF is the ratio of the raw SW-GEFFs of the network and its matched random (DD) network.

Finally, we consider the MOD that captures the extent to which the network can be decomposed into smaller well-defined subnetworks.

Statistical methods

To assess the statistical significance of between-group comparisons of the network metrics, a nonparametric permutation testing procedure was used. For each measure, the class labels (NC and AD) were randomly reassigned between group pairs and t-values were computed for each relabeling, for a total of 5000 permutations, to approximate a t-statistic. P-Values were calculated based on this distribution of t-values obtained from the permutations.

We also compared the directed network metrics with those of random networks chosen to match the probabilistic structure of the observed DPNets using DD random networks (Erdős and Rényi, 1960; Newman et al., 2001). This is useful to understand the aspects of the networks that are not arising from degree distribution, such as the relevance of the SW measure. For each subject's network, an associated DD network was constructed by choosing random edges while maintaining the indegree and outdegree of every node. For example, if all nodes in the subject's DPNet had the same degree, then the matched DD network would too, while if outdegrees varied by node, the matched DD would vary exactly in the same manner. To compute the matched DD network, we note that the standard “double edge swap” algorithm in which a pair of edges are chosen at random and then crossed (Newman et al., 2001) is not sufficient to fully randomize. In addition, one must also randomly reverse the orientation of directed triangles (Berger and Müller-Hannemann, 2010), for example, if we have a triangle a→b→c→a, then one randomly reverses the orientation to get c→b→a→c. This procedure, as described in detail in Berger and Müller-Hannemann (2010), was repeated 1000 times to create a randomized DD matched network. (The randomness of this procedure was validated using standard statistical tests.)

For the classification of individual subjects, we considered a variety of algorithms that are available on the Orange data mining system (Demšar et al., 2013), including the Naive Bayes Classifier, Support Vector Machines, Classification Trees, and Neural Network Learner and their Bagging and Boosting variants. We also applied several of the built-in feature selection algorithms as well as a brute force selection algorithm, which we wrote in the Orange scripting language. This algorithm tried all combinations of five or fewer features, using the various classification algorithms. Since the populations were of different sizes, the majority classifier was unfairly effective when using the classification accuracy as the measure of fit. To remove this bias, we optimized the classifiers on the area under the receiver operator characteristics curve (AUC) metric, which was computed using 10-fold cross-validation. We compared these results with those obtained using other classifier scores and obtained very similar results. Below we report both the AUC metric and the classification accuracies (broken out into false positives and false negatives to provide further insight).

Results

Network measures

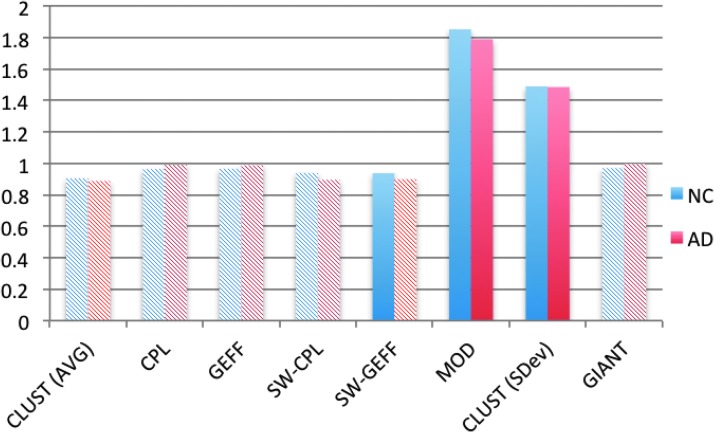
Our first result stands in contrast to most other connectome results: we find no evidence of small-world structure (Fig. 3). In fact both definitions of SW lead to similar results, normalized SW measures that are <1. For the ordinary measure, this result is not statistically significant, but for the perhaps more reliable measure based on global efficiency, it is significant at the 5% level for both NC and AD. While small-world networks typically have slightly larger CPL than their random counterparts, the opposite holds for DPNets, which have a lower CPL than the reference networks. The GEFF is smaller for the DPNets, but these differences are small and not statistically significant at the 5% level. However, the clustering coefficients for the DPNets are smaller than the matched random ones. For the NC subjects, this decrease has a p-value of about 3% and for the AD subjects about 7%.

FIG. 3.

Normalized measures for normal cognition (NC) and Alzheimer's disease (AD). These are the ratios of the measure values for NC and AD to their matched randomized degree-distributed (DD) network. A ratio of 1 implies that the two values are the same. Solid bars indicate statistically significant differences between the AD (or NC) network and its randomized counterpart, that is, a Bonferroni-corrected p-value of<5%. Color images available online at www.liebertpub.com/brain

We also find moderate but statistically significant levels of modularity, an increase of about 80% over the random DD networks. Finally, we note that the giant components are comparable in size to those in the matched random DD networks, containing between 30% and 50% of the nodes.

Group level analysis

For the directed networks at the group level, most network measures have a statistically significant difference between the AD group and the NC group. For SW-CPL, we have an (uncorrected) p<5%, which is not significant when corrected for multiple comparisons (Bonferroni), while for all other measures, we have (Bonferroni-corrected) p<5% (except for p<7% for the standard deviation of indegree). Thus, we see that the directed network measures distinguish well between AD and NC, at the group level (Table 2).

Table 2.

Group Means for Directed Network Measures for ISIM and Uncorrected p-Values of Nonparametric t-Tests

Measure	NC	AD	p-Value
CLUST (AVG)	0.246	0.203	0.005
CPL	1.694	1.944	<0.001
GEFF	0.228	0.295	<0.001
SW-O	0.939	0.895	0.052
SW-E	0.937	0.898	<0.001
MOD	0.227	0.256	0.005
INDEG (SDev)	9.206	8.207	0.007
OUTDEG (SDev)	11.344	9.12	<0.001
CLUGT (SDev)	0.143	0.109	<0.001
GIANT	0.348	0.517	<0.001

Note that all are significant at the 5% level when Bonferroni corrected, except for the standard deviation of indegree, which is only significant at the 7% level when Bonferroni corrected. Note that the average indegree and outdegree is set to 10 for all networks, so these values are not shown. However, their standard deviations are shown, for example, INDEG (SDev).

ISIM, infectious similarity.

The AD subjects have decreased CLUST and increased CPL over the NC subjects. Combining these, one observes a decrease in SW-CPL for the AD subjects. They also have decreased SW-GEFF, due to the decreased clustering even though the GEFF has significantly increased. One also observes increased modularity in the AD subjects and a decreased variability in INDEG and OUTDEG. The AD subjects also have significantly increased giant components.

For comparison, the undirected networks, derived by symmetrizing the ISIM matrices, also do a good job of distinguishing the AD group from the NC group. In fact, all of the undirected measures have (Bonferroni-corrected) p-values of<2% except for the CPL, which is not statistically significant (both corrected and uncorrected).

Classification

The best classification between NC and AD (by AUC) using exhaustive search with at most five features was achieved using Naive Bayes, which was slightly superior to the SVM classifier and significantly better than Classification Trees, Neural Networks, and their Bagging and Boosting variants. It used the features: CPL, MOD, GIANT, and the standard deviation of INDEG. It attained an AUC of 0.87, a false-positive rate of 9% and a false-negative rate of 15%. However, many combinations of features attain approximately the same level of accuracy.

For example, we can replace CPL or MOD with CLUST in the above classifier and suffer <2% loss in AUC. In addition, we found that the SVM classifier produced only slightly worse results than the Naive Bayes, whereas the other classifiers were typically inferior. Interestingly, all of the five best classifiers (Table 3) use the size of the giant component, the top 4 use the standard deviation of the INDEG, and all use at least one out of MOD, CPL, and CLUST.

Table 3.

AUC and Feature Sets for the Five Best Classifiers

Classifier rank	AUC	Features used
1	0.867	GIANT	IDEG (SDev)	MOD	CPL	x
2	0.864	GIANT	IDEG (SDev)	MOD	x	CLUST
3	0.861	GIANT	IDEG (SDev)	MOD	x	x
4	0.860	GIANT	IDEG (SDev)	x	CPL	CLUST
5	0.858	GIANT	x	MOD	CPL	x

AUC, area under the receiver operator characteristics curve.

The use of more sophisticated feature selection techniques, which potentially consider all features, did not produce noticeably better results (below the noise level of the cross-validation procedure). Thus, we believe that the classification results above, in addition to providing insight, are nearly optimal and the addition of more sophisticated techniques would be unlikely to significantly improve our results.

If the directness of the network is ignored and one simply uses an undirected network the classification accuracy substantially declines. In this case, the best classifier simply uses both the standard deviations of INDEG and OUTDEG and attains an AUC of 0.77. In addition, the false-positive rate goes up to 20% and the false negative to 18%. Thus, we see value of directed measures compared to undirected ones in classification.

Discussion

Our primary finding is that a surprisingly simple DPNet construction procedure that uses cortical thickness measurements from just three timepoints has proven capable of producing reliable networks that not only can separate AD patients from NCs but can also classify individual subjects. In contrast, previous work has required either large numbers of subjects to compute average correlations or a larger number of timepoints for each subject. In addition, we see that directed edges can outperform undirected ones, which to our knowledge is the first demonstration of the utility (as opposed to the feasibility) of directed networks in connectomics research.

Network measures

Our first result, the lack of SW in our DPNets, illustrates the inherent differences between DPNets and other connectomic approaches. Small-world networks are ubiquitous in many areas of science and social science (Watts and Strogatz, 1998) and seem to arise in most studies of connectomes (Bassett and Bullmore, 2006; Sporns and Honey, 2006), including those on AD (He et al., 2007; Sanz-Arigata et al., 2010; Stam et al., 2007). However, we find clear evidence that our DPNets are not small-world networks, stemming from the fact that they have lower clustering coefficients than comparable random (DD) networks. Perhaps this is not surprising as DPNets are modeling the spread of a disorder in the brain but are not directly involved with computation, as are standard connectomes. Thus, while SW appears to be important for efficient computation (Sporns and Honey, 2006), there is no a priori reason for high clustering coefficients in networks mapping the spread of a disorder within the brain.

While small-world networks typically have slightly larger CPL than their random counterparts, the DPNets show the opposite tendency, although this is likely driven by the decrease size in their giant components. The GEFF results are consistent with typical small-world networks, but these differences are small and not statistically significant at the 5% level. However, the key factor in understanding the SW is the lack of a significant increase in clustering coefficients for the DPNets compared to the random ones. Whereas these often increase by a factor of 2 or more, for the DPNets, they actually decrease.

Another important property of DPNets is the size of their giant component, which are similar to those of their matched random counterparts and typically contain less than half of the nodes. This affects the analysis and interpretation of the other measures. For example, if a giant component is small, then it is likely that the CPLs, which are only computed over the giant component, will also be small. This contrasts with undirected connectomes in which the giant component typically contains most of the nodes, avoiding these difficulties. For example, in the undirected networks studied in this article, the giant components typically contain more than 90% of the nodes. This appears to arise because the requirement of strong connectedness in directed networks is much more stringent than ordinary connectedness.

Group level analysis

Our initial results supply several insights into the temporal progression of AD in the brain, since unlike most networks previously studied in connectomics, DPNets are based on temporal spread. Our first result is that for most measures that we considered the difference between the AD group and the NC group is statistically significant even after correcting for multiple comparisons.

The AD subjects have lower clustering, suggestive of the spreading of the disease. They also have increased CPL, but this appears to be driven by an increase in the size of the giant component. Since it is likely that the giant component contains much of the range of disease spread, this could be an indication of the greater number of nodes that have been infected in the AD subjects. The GEFF is more reliable and shows an increase in the AD subjects, which is also consistent with the spreading interpretation. One also observes increased modularity in the AD subjects, perhaps indicating an increase in disease structure. The idea of modularity being important in brain disorders has been seen before in studies of AD (Chen et al., 2008).

The observed decreased variability in INDEG and OUTDEG for the AD subjects is consistent with a possible increase in the number of diseased nodes, that is, when there are few diseased nodes (as in the NC subjects) those will have high outdegrees, since the other (uninfected) nodes do not have many outgoing edges.

Classification

Interestingly, all of the best five classifiers (Table 3) use the size of the GIANT, the top four use the standard deviation of the INDEG, and most also use at least one out of MOD, CPL, and CLUST. The importance and interpretation of these as signals of disease spread was discussed in the previous section. We note that the use of the variation by nodes (not merely average values), while discussed qualitatively and analyzed for scientific insights, has not been widely utilized for classification, and our findings that nodal variations in AD are important for classification might suggest the use of nodal variability could have wider applicability in connectomics.

In a sense, our classification results are not competitive with Li et al. (2012), who attained over 95% accuracy; however, they used much more information in their classification. Not only did Li et al. (2012) use five timepoints and over 200 features, but perhaps even more importantly, they used the raw thinning data directly in their discriminant analysis, which allowed their algorithm to use locational information about which specific region was thinning.

Thus, by comparison, our results seem remarkably robust considering that they were based on a minimalist model that used values of only four global measures, and no local or regional information, for a DPNet based on only three temporal MRIs. In addition, by fixing the average degree, we have essentially removed the average thinning rate for the subjects, which is likely the single most valuable feature for classification. (For reference, the average nodal thinning rate in our data is about 0.5%/year for NC and 1.5%/year for AD.) Thus, the demonstrated classification ability of even a noisy feature-limited network like that used here shows the utility and promise of this new DPNet-based approach. In addition, one would expect additional improvements in accuracy with the inclusion of more timepoints, locational information, and basic structural measures, such as the average thinning rate over all nodes.

We also showed that the directed information improves classification accuracy significantly in comparison to using undirected information.

Directions for future work and concluding remarks

As we have shown, directed network measures of DPNets can characterize AD at the group level as well as classify subjects at the individual level; additional tests and extensions of our DPNet constructions would certainly be valuable, such as correlating the edges of the DPNet with the known properties of disease spread in AD or using more timepoints to compute similarities for constructing DPNets.

For example, when there are k>3 timepoints, there are many possible extensions. The simplest would be to consider an r unit time delay model in which we take the vector of the first k−1 rates from the initial node and cross-correlate that with the vector of the last k−1 rates from the final node, comparing time t in the initial to time t+r in the final for t=1…k−r. This could require choosing r from biological considerations based on disease progression or optimizing over r to find the delay that yields the highest cross-correlation. In addition to constructing an interesting DPNet, the resulting value of r would have empirical interest. On could also use more sophisticated Markov Chain thinning model to find the correlation and delay time computationally either individually for pairs of nodes or by optimizing over all nodes simultaneously to find the optimal network that “explains the time-delayed similarities.”

Importantly, we note that our methods can be directly applied to any neurodegenerative disease since DPNets could capture the progression of the neurodegeneration, which varies by disease. For example, progressive supranuclear palsy, corticobasal degeneration, and frontotemporal dementia each has distinct patterns of degeneration (Dickson et al., 2011; Hartikainen et al., 2012; Schofield et al., 2011). In addition, one could apply DPNets to other brain disorders in which it is possible to identify the progression, even those that do not involve cortical thinning but are primarily characterized by changes in white matter, such as multiple sclerosis. At the opposite end of the clinical spectrum, one could also implement these ideas for MRI studies of altered brain development in childhood and adolescence. Although the requirement of at least three serial imaging scans for DPNets construction may seem a high barrier from a practical perspective, it should be judged in the context of information that temporal disease spread can potentially provide for clinical decisions. In particular, DPNets may offer a unique approach for predicting individual trajectories of neurodegenerative progression that could improve individualized clinical planning.

When considering potential directions for future work, it is important to recognize some of the limitations of the present study: Since AD was not confirmed by autopsy, the exact contribution of AD pathology to variations in network measures remains unclear. A limited clinical ability to identify incipient AD in the NC group over the 2-year follow-up may have skewed the network measure distributions of these two groups. One technical limitation of the present study is that by analyzing anatomical regions to keep computations tractable, we implicitly made the assumption of a homogenous propagation of thinning with each region. A finer analysis of cortical thinning, for example, voxel-by-voxel, may modify the results.

In summary, directed connectomics of DPNets based on cortical thickness measurements have shown strong promise in the study of AD, and, as a novel methodology, construction of DPNets may be useful when extended to other neurodegenerative diseases.

Acknowledgments

This work was funded in part by the National Institute of Biomedical Imaging and Bioengineering (NIBIB) (T32 EB001631-05) and the National Institute of Neurological Disorders and Stroke (K25 NS-703689-01).

Data collection and sharing for this project was funded by the Alzheimer's Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: Abbott; Alzheimer's Association; Alzheimer's Drug Discovery Foundation; Amorfix Life Sciences Ltd.; AstraZeneca; Bayer HealthCare; BioClinica, Inc.; Biogen Idec, Inc.; Bristol-Myers Squibb Company; Eisai, Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; GE Healthcare; Innogenetics, N.V.; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Medpace, Inc.; Merck & Co., Inc.; Meso Scale Diagnostics, LLC.; Novartis Pharmaceuticals Corporation; Pfizer, Inc.; Servier; Synarc, Inc.; and Takeda Pharmaceutical Company. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is Rev March 26, 2012, coordinated by the Alzheimer's Disease Cooperative Study at the University of California, San Diego. ADNI data are disseminated by the Laboratory for NeuroImaging at the University of California, Los Angeles. This research was also supported by the NIH grants P30 AG010129 and K01 AG030514. The work was possible by using resources of the Veterans Medical Center, San Francisco, California.

Author Disclosure Statement

Norbert Schuff received consulting honoraria from Eli Lilly as financial interest.