Auto-validation of fluorescent primer extension genotyping assay using signal clustering and neural networks

Abstract

Background

SNP genotyping typically incorporates a review step to ensure that the genotype calls for a particular SNP are correct. For high-throughput genotyping, such as that provided by the GenomeLab SNPstream^® instrument from Beckman Coulter, Inc., the manual review used for low-volume genotyping becomes a major bottleneck. The work reported here describes the application of a neural network to automate the review of results.

Results

We describe an approach to reviewing the quality of primer extension 2-color fluorescent reactions by clustering optical signals obtained from multiple samples and a single reaction set-up. The method evaluates the quality of the signal clusters from the genotyping results. We developed 64 scores to measure the geometry and position of the signal clusters. The expected signal distribution was represented by a distribution of a 64-component parametric vector obtained by training the two-layer neural network onto a set of 10,968 manually reviewed 2D plots containing the signal clusters.

Conclusion

The neural network approach described in this paper may be used with results from the GenomeLab SNPstream instrument for high-throughput SNP genotyping. The overall correlation with manual revision was 0.844. The approach can be applied to a quality review of results from other high-throughput fluorescent-based biochemical assays in a high-throughput mode.

Background

Single nucleotide polymorphisms (SNPs) are the most common type of genetic variation in humans and other species [2]. They commonly occur as alternative alleles (G/A, C/T, G/T, C/A, A/T, or C/G), at intervals averaging 1,000 to 2,000 nucleotides for SNPs currently known in the human genome [3], and occasionally as single nucleotide insertions or deletions. The current human genome database contains about 3,000,000 SNPs [4]. Where efforts to identify associations between SNP genotypes and multi-factorial phenotypes require large numbers of genotypes, ultra-high throughput genotyping methods are necessary. The GenomeLab SNPstream instrument from Beckman Coulter, Inc. allows genotyping of up to 1,000,000 SNP genotypes per day [5]. The instrument uses fluorescent multiplex SNP-IT primer extension assays [5,6] for allele determination of previously discovered SNPs. Following the amplification of the genomic region of interest by the polymerase chain reaction, the instrument determines the allele at a particular SNP site by extending the oligonucleotide primer annealing next to that site with one of two labeled nucleotides. Each nucleotide is complementary to one of the possible alleles and is fluorescing at a different wavelength. The synthesis of each extension primer incorporates a hybridization tag at the 5'-end. After a multiplex extension reaction, the tag affixes an individual SNP primer to the complementary sequence bound to a single spot of a 12-spot grid for fluorescence detection. Two lasers at wavelengths of 488 nm (blue, "B," hereafter) and 532 nm (green, "G," hereafter) detect the fluorescent color of the extended base for every SNP spot. The overview of the image analysis software in the instrument is shown in Figure 1.

Figure 1.

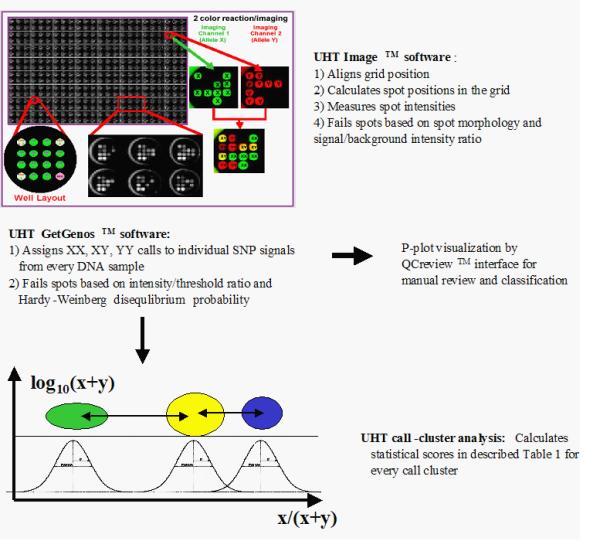
The overview of software flow for image analysis on the UHT instrument. Top – Depiction of 2-color fluorescent readouts analyzed by the UHT Image™ software. Intensities from the two fluorescent channels presented in pseudo-colors are compared to determine genotypes. Three hundred eighty-four replicates of 4 × 4 tag arrays are produced on a single glass plate. Each 4 × 4 tag array has 4 control locations and 12 probe locations for 12 SNPs. The top left location is a positive control for both colors. The top right and bottom left locations are positive controls for the two different alleles, and the bottom right location is a negative control and has a probe that lacks a complementary tag sequence in the reaction. The controls are also used to mark the array boundaries for the image analysis software. Center – The UHT^® GetGenos software assigns genotype calls to individual SNP signal from every DNA sample. The results can be displayed as a P-plot (Figure 1) by QCreview™ software for manual review (arrow to the right) or used to measure clustering parameters for auto-validation by the neural network (arrow down). Bottom – Schematic representation of SNP signal call clusters measured on the P-plot. The neural network uses 64 parameters described in Additional file: 1 to auto-classify P-plot as "Pass" or "Fail".

The imaging software performs the first steps of data analysis: grid alignment and recording of spot images. The software analyzes each spot for morphology; that is, circular shape and uniform pixel intensities across the spot. Spots with low intensity or unsatisfactory morphology are recorded as failed. For spots that pass the morphology test, the values of the fluorescence at the two wavelengths are recorded in a database. The failed spots are recorded as empty (zero intensity) and are carried through the remainder of the analysis.

The GetGenos™ software module performs the next step of the image analysis and assigns the genotype calls to every SNP spot. Three different calls are possible for the SNP site on the two copies of a chromosome in an individual DNA sample: a homozygous genotype (represented by the general XX), indicating that both chromosomes have the same allele of one type; a heterozygous genotype (XY), indicating that the two chromosomes have two different SNP alleles; and the homozygous YY indicating that both chromosomes have the same allele, opposite to the XX type. The software assigns one of these three calls to each point by collecting signals into three clusters, according to the ratio of intensities from two fluorescent colors in the SNP spot and a set of built-in values for cluster geometry and minimum color intensity thresholds. GetGenos may also fail some SNP signal spots if they cannot be included in any cluster or if their intensities are below the default intensity baseline for both allele colors.

The final phase of the signal analysis involves logical groups of samples run on the same SNP and on the same micro-titer plate, which is equivalent to identical experimental conditions. A logical group such as this may represent a particular set of patients in a pharmacogenomic study or a population in an anthropological study. This phase assesses the quality of the genotypes in a group, which makes it possible to detect problems with the assay operation, or with the SNP itself. For low and medium throughput work, the UHT^® software package provides displays of the genotype calls (XX, XY, YY) for a group in a form of P-plot (Figures 2,3,4). As described previously [9], a P-plot represents the data as a fraction of the signal of one allele within the total observed signal (x-axis, B/(B+G)), and the total signal strength (y-axis, log(B+G)). In this view, the rightmost cluster represents the XX genotype (fraction of X allele signal near 1.0), the leftmost cluster is YY (fraction of X signal near 0), and the central cluster represents XY genotypes (Figures 2,3,4). One major advantage of this representation is that the signal call position along a single axis (x-axis) determines the genotype. This linear layout of the data simplifies visual recognition of the data and quantitation of signal clusters. The GetGenos software assigns a suggested grade – "pass" "look" or "fail" – to the plot as a whole by considering the percentage of valid sample points and the Hardy-Weinberg chi-square value [7]. A trained reviewer can study the plot and record P-plot validation by assigning a final grade of "Pass" or "Fail" for a group, which the reviewer may save to a database.

Figure 2.

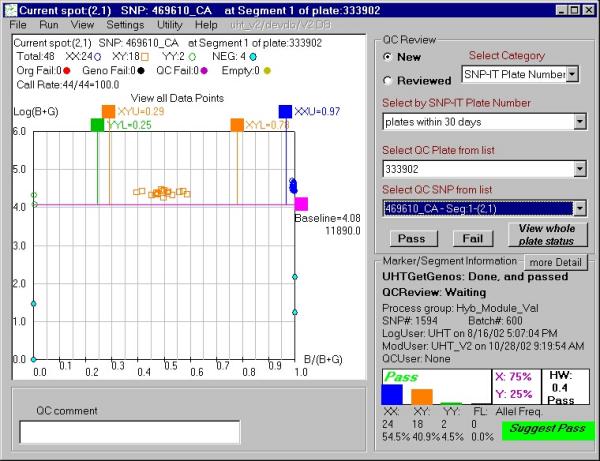
P-plot example displayed by the QCreview interface with a grade "pass" suggested by GetGenos. The QCreview display includes: a) the genotype call values made by UHT^® GetGenos from single SNP but multiple samples; b) the signal values of positive and negative controls; c) basic statistical information about genotype clusters, such as cluster size, d) the chi-square of the Hardy-Weinberg disequilibrium test [7]; e) the plot review status and the suggested GetGenos grade for entire plot. With the QCreview interface, an authorized user can pass or fail individual points and the plot as a whole and record it into an Oracle database.

Figure 3.

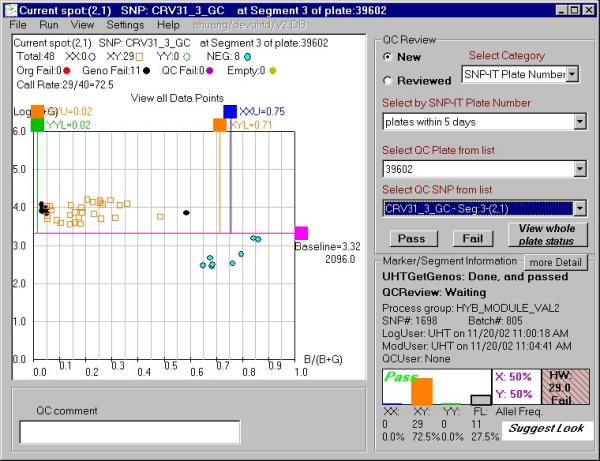
P-plot example displayed by the QCreview interface with a grade "look" suggested by GetGenos. This grade indicates that GetGenos was uncertain about the quality of the plot. The interface components are described in the legend for Figure 2.

Figure 4.

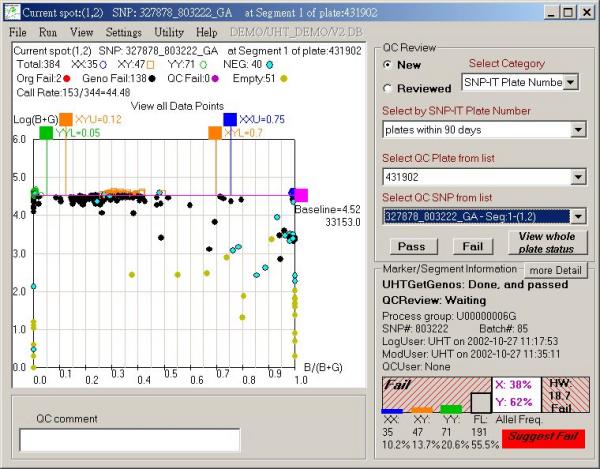
P-plot example displayed by the QCreview interface with a grade "fail" suggested by GetGenos. The interface components are described in the legend for Figure 2.

For ultra-high throughput work, the sheer volume of plots makes manual review for quality impractical. Therefore, we have developed a neural network algorithm to automatically grade plots as "Pass" or "Fail." The algorithm uses 64 statistical measures of plot quality, derived from the genotype calls from the GetGenos phase, for its automatic grading. The goal of the neural network training was to match the "Pass/Fail" grades of the manual grading made by trained reviewers. The present paper describes the training of the network and the analysis of a large test set of manually graded plots by the GetGenos procedure and then by the trained neural network.

Results

GetGenos suggested grade accuracy

The comparison of the suggested grades assigned by GetGenos software to the 26,854 plots used in this study with the grades assigned by trained reviewers is shown in Table 1. Every plot contains data from 384-well micro-titer plate totaling 10,311,936 individual SNP-IT reactions from about 23,000 different SNP markers.

Table 1.

Distributions of the suggested grades of "pass," "look," and "fail" assigned by GetGenos, compared to the P-plot validation made by the trained reviewers.

GetGenos™ suggested grade	Reviewer validation	Number	% from total with this GetGenos grade
Pass	Pass	14924	99.4
Pass	Fail	88	0.6
Look	Pass	2557	99.3
Look	Fail	18	0.7
fail	Pass	1335	14.4
fail	Fail	7932	85.6

Statistical scores measuring signal call clusters quality

The scores are summarized in Additional file: 1. A stored procedure calculates the parameters that provide the input for the neural net. The parameters measure the geometry of the GetGenos signal call clusters and their relative separation, with the exception of a deviation from the Hardy-Weinberg disequilibrium test (score #60), which measures the data reliability from the point of view of statistical genetics (see Additional file: 1).

Review by the neural net

We identified several parameters of the neural network that affected the learning accuracy the most: neuron activation function, number of learning epochs, and frequency of crossovers between different populations in a genetic algorithm. The learning accuracy was estimated as the percentage of the plots classified correctly by the neural net compared with the human validation. These parameters were tested with different values to find the optimal result. The optimal parameters for neural network training are described in the "Methods" section. The size of the training set was also very important. Most failed P-plots in the database did not have any SNP calls from the entire micro-titer plate. Such trivial cases were not included in the training set. We found only 986 P-plots in the database that have SNP calls and were failed by manual review. Therefore, we had to use 10,000 "Passed" P-plot examples to achieve good accuracy. The learning accuracy using training sets with smaller size produced a less accurate neural network. For example, the training with 1,986 P-plots (986 "Failed" and 1,000 "Passed") yielded the net with a 67% prediction accuracy.

The trained neural net graded as "Fail" 97.7% of the plots in the training set that the reviewers had graded as "Fail" and graded as "Pass" 92.4% of the plots the reviewers had graded as "Pass." The weighted average prediction accuracy for the training set was a 95.5% match of the net's calls to the manual calls. We have used a trained neural net to analyze 26,147 additional P-plots that were not included in the training set. As Table 2 indicates, the accuracy of the net is 99.98% for plots the net grades as "Pass" and 79.8% for those the net grades as "Fail." The overall correlation between neural network validation and manual revision was 0.844. The correlation C was computed as C = [(pp*ff)-(pf*fp)]/sqrt((pp+pf)(pp+fp)(ff+pf)(ff+fp)), where pp – number of plots passed by both neural net and human reviewers, ff – number of plots failed by both neural net and human reviewers, pf – number of plots passed by neural net but failed by human reviewers, and fp – number of plots failed by neural net but passed by human reviewers.

Table 2.

Distributions of Pass/Fail grades assigned by the neural net and by reviewers

Net grade	Reviewer grade	Number	% of total for this neural net grade
Pass	Pass	16789	99.98
Pass	Fail	3	.02
Fail	Pass	2027	20.2
Fail	Fail	8035	79.8

To investigate a reason for the less accurate predictions on the failed P-plots, we have manually re-reviewed about 20 plots of the 2,027 manually passed plots that the net graded as "failed." This second manual re-inspection indicated that "Fail" was the correct grade for more than half of them, suggesting that the actual prediction accuracy was higher for plots graded "Fail" by the net. The major sources of the human errors are fatigue, inexperience, and insufficient time to complete the manual review in a high-throughput mode. Because our reviewers had been trained, we concluded that the most likely reason for misjudgment was fatigue due to a large volume of data. All SNPs erroneously labeled as "Passed" had very little successful genotype calls made by GetGenos, and these calls had a low signal intensity on the border of the minimum allowed intensity threshold.

Though training the net required 1.5 days, the processing of the 26,854 test plots by the trained net took only 10 minutes. The trained neurons were recovered from the training program, written in C programming language, and transferred to an Oracle stored procedure written in PL/SQL programming language. The procedure's input is a parameter vector from the procedure calculating 64 statistical scores from Table 1. Every P-plot is classified further as "Pass" or "Fail" in the UHT instrument by applying the neuron net to the parameter vector.

Discussion

It is important to understand that the automated procedure for the validation of the genotype calls described in this paper does not validate the accuracy of the calls themselves. The genotype call is made by the GetGenos software, which has a reported accuracy of 99.5% [5]. Our method validates the reliability of the GetGenos call as applied to a particular SNP measured in a particular sample set on a single micro-titer dish. The neural net algorithm does not modify the GetGenos genotype call; it simply evaluates whether this call is trustworthy or not.

The successful genotyping of a particular SNP depends on the variety of factors. In the case of the SNPstream instrument, they include the following: the quality of the DNA samples; DNA sequence surrounding the SNP [1] site; and the quality of the micro-titer dish preparation. Human and instrumentation errors can also be the source of a failure. These factors are likely to be source of failure for other SNP genotyping technologies as well. We designed our quality control algorithm to detect the failures due to these factors automatically in a high-throughput manner without human manual intervention. The SNPs failed by the algorithm should not affect the results of any statistical analysis because the algorithm does not discriminate SNPs based on their sequence and thus does not favor any particular allele of the SNP. Thus, it does not create any bias towards a particular allele in the discriminated instance of SNP measurement because it fails the entire measurement including both alleles. Thus, the accuracy of the genotype call still remains 99.5%, when calculated for only passed plots, as reported previously [5]. At most, the algorithm may fail a particular SNP variation such as, for example "G/C," more than other variations on average. More investigation is necessary to find such "unfavorable" variations. However, the result of such investigation would only reflect the difficulties to genotype the particular SNP variation by the technology.

With the addition of the neural net for the final review of the GetGenos results, it is possible to automate the entire procedure for assigning genotypes and monitoring the quality of results. The goal of our neural net development was to match the binary output to the Pass/Fail grades assigned to P-plots by trained reviewers. The reviewers agreed with the fully trained net in 99.98% of the cases that the net graded as "pass" but it is more stringent than the reviewers in that it fails 20.2% of the plots passed by the reviewers. The overall agreement is 92.4%.

The SNP genotyping project used for developing the neural net involved a large number of SNPs and a relatively small number of samples. For production work and other cases with a small number of SNPs and a large number of samples, it would be worthwhile to train the neural net on each SNP individually. We have found that, where studies involve samples from related individuals, automated checking of Mendelian Inheritance is an additional useful tool.

The major advantage of the automated approach is that it eliminates the bottleneck that accompanies manual review of the cluster data. In addition, it provides a uniform approach to review that is not attainable with even the most experienced group of reviewers. The neural net method, in particular, should be applicable to other data from high-throughput projects.

Conclusions

We have developed the approach to automatically validate color or fluorescent biochemical reactions. The procedure clusters result from multiple individual assays and require a training set consisting of manually validated signal clusters. The procedure automatically compares new signal measurements from the instrument with the distribution in the training set. The current work demonstrates the success of the approach with high-throughput SNP genotyping reaction, but it is also clearly applicable to other assays involving review of groups of results.

Methods

SNP-IT primer extension reaction

The SNP-IT primer extension reaction has been described previously [5,6]. In brief, the multiplex SNP-IT reaction requires three oligonucleotide primers for each SNP marker and involves the following three steps: 1) multiplex PCR amplification of the sequence surrounding a SNP from the two chromosome copies, 2) multiplex single nucleotide cycling primer extension using the third tagged SNP-IT primer and fluorescent-labeled dideoxynucleoside triphosphates, 3) tag hybridization of SNP-IT primer to complementary tag oligonucleotide spotted on the solid surface (Figure 1).

GetGenos description

The GetGenos procedure converts the blue and green intensities for each point in a sample set to an angle using: Angle = arctan (B/G). The program then finds signal clusters by splitting the angle space into 90 one-degree bins and finding the populated groups of bins. To be in one group, the bins with signals must be closer than a built-in, user-set bin distance threshold (see Appendix). Using the average angle for the group the procedure classifies each group as XX, XY, or YY. Once all the groups have classifications, it sets the boundaries for the XX, XY, and YY genotype clusters. If a calculated boundary is outside a built-in, user-set boundary limit (see Appendix), the boundary is set to the boundary limit. The procedure also determines the threshold for the combined signal strength based on the distribution of all the points.

Manual review of P-plots

About 40,000 manually classified P-plots have accumulated in the database during the development of the instrument. The manual P-plot validation was done by five trained reviewers on three different instruments using the QCreview™ interface for visualization of P-plots from GetGenos results.

Neural network architecture and training

A two-layer neural network was used in the algorithm. The first layer contains six neurons, and the second layer has one. The first and last neurons in the first layer have tangent activation function and the five other neurons from both layers have a "sigma" activation function: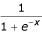

The training was done using 10,986 manually reviewed P-plots from the database. The training set contained 10,000 passed plots and 986 failed plots. The genetic algorithm used for neural net training is described in [8]. The code was optimized substantially to include direct operations on memory for population crossover and mixing functions. The neural activation functions were also changed as described previously in this paper. These optimizations accelerated the learning algorithm more than tenfold. The learning accuracy was also increased by about 10%.

For the genetic algorithm we used 10 populations. Every population contained 60 "peoples" or "individuals". An "individual" in the population contained the vector with the length combined from individual neurons and seven constants added to the vector multiplication product for every neuron. Thus, for an input vector with 64 dimensions, the population matrix for the genetic algorithm had a size of 10 × 60 × 397:

10 - populations, 60 - people in every population, [397 = 64 (size of neuron vector from the first layer) * 6 (number of neurons at first layer) + 6 first layer constants + 6 (second layer neuron size) *1 second layer neuron + 1 second layer constant].

The initial neuron weights were assigned randomly to all 10 populations. The weights for the first half of each population were random value between -1 and 1, the weights from the second half received random values between -100 and 100. Every evolution epoch, or cycle of adjustment of the neuron weights, included the following steps. The five best "people" and the eight "people" selected at random in every population were kept intact. Ten new "people" were added to every population at every epoch. The weights for the new "people" received random values between -10 and 10. Seven "people" were mutated at random by changing the existing weights by no more than twofold. The remaining 35 "individuals" were mutated by crossovers with donors selected randomly from the best five "people" of the same population. The crossover length and site were chosen at random. Every second epoch, the crossover was done with donors from the top five "people" of another randomly selected population. After crossover, the weights in the acceptor vector were also slightly mutated by no more than 1.25 times.

The scoring function evaluating the performance of the single "individual" in the population was calculated as the average of percentage of correctly predicted "passed" vectors plus percentage of correctly predicted "failed" vectors. One thousand learning epochs were executed during training. The training took 1.5 days on an 800 MHz Gateway Pentium PC. The best prediction rate was 65% in the beginning of the training, and the final prediction rate was 95%. The learning rate slowed down exponentially. For example, the prediction rate of 85% was achieved after 150 epochs and 90% after 250 epochs.

Microsoft Visual Studio™ was the development platform for the neural net, which was written in C programming language. It runs as a compiled .EXE file, with a text file exported from an Oracle table as the input.

Authors' contributions

AH developed GenomeLab SNPstream^® Image analysis and GetGenos™ software. JS developed statistical scores for measuring cluster geometry and collected the training set for neural network and statistical analysis. He suggested the use of neural networks for final signal cluster validation. AY developed neural network training and the automatic validation of new measurements by the trained neural net. JH developed the set of statistical scores to measure cluster geometry. JK, SV and KS provided manual validation of P-plots for the training set. SA developed and maintained the database of P-plots used for manual review and for automated validation by the GenomeLab SNPstream instrument. CG developed P-plots for manual signal review and validation. MP managed the software development for the GenomeLab SNPstream instrument. MBJ was a general manager for the GenomeLab SNPstream instrument. All authors read and approved the final manuscript.

Appendix

User-set values for GetGenos

XX_MIN_ANGLE: the lowest angle for a XY cluster center (average). The default value is 7.5.

YY_MAX_ANGLE: the highest angle for a XY cluster center. The default value is 82.5.

XX_ANGLE: a value for used in calculating XX%, below. The default value is 8.

YY_ANGLE: a value for used in calculating YY%, below. The default value is 82.

XX%: The minimum percentage of points in a cluster that must be lower than XX_ANGLE. Otherwise, the cluster will be considered as XY cluster. The default percentage value is 10.

YY%: Set the % of YY cluster to be higher than a certain angle. Otherwise, the cluster will be considered as XY cluster YY_ANGLE. The default % value is 10.

BIG_GROUP: The minimum number of points necessary to form a group or cluster. The default value is 4.

MIN_SPACE: Set the minimum distance, in degrees, between two groups or clusters. The default value is 4.

MIN_BASELINE: The minimum total intensity (Blue + Green) necessary for a point to pass. Points with a total intensity less than this value fail, regardless of angle. The default value is 1000.

PASS_RATE: The percentage of passed sample points must be greater than this value for a plot to receive a provisional grade of "Pass". Default value is 90.

SUGGESTED_PASS_RATE: The percentage of passed sample points must be greater than this value for a plot to receive a provisional grade of "Suggested Pass". The default value is 75.

SUGGESTED_FAIL_RATE: The percentage of passed sample points must be greater than this value for a plot to receive a provisional grade of "Suggested Pass". The default value is 50.

FAIL_RATE: The percentage of passed sample points for a plot that receives a provisional grade of "Fail" is less than this value. The default value is 30.

PASS_HW_SCORE: The maximum Hardy-Weinberg chi-square allowed for a plot that receives a provisional grade of "Pass" or "Suggested Pass". The default value is 5.

SUGGEST_FAIL_HW_SCORE The Hardy-Weinberg chi-square for a plot that receives a provisional grade of Suggested Fail exceeds this value. The default value is 10.