SEDFIT-MSTAR: Molecular weight and molecular weight distribution analysis of polymers by sedimentation equilibrium in the ultracentrifuge

Abstract

Sedimentation equilibrium (analytical ultracentrifugation) is one of the most inherently suitable methods for the determination of average molecular weights and molecular weight distributions of polymers, because of its absolute basis (no conformation assumptions) and inherent fractionation ability (without the need for columns or membranes and associated assumptions over inertness). With modern instrumentation it is also possible to run up to 21 samples simultaneously in a single run. Its application has been severely hampered because of difficulties in terms of baseline determination (incorporating estimation of the concentration at the air/solution meniscus) and complexity of the analysis procedures. We describe a new method for baseline determination based on a smart-smoothing principle and built into the highly popular platform SEDFIT for the analysis of the sedimentation behavior of natural and synthetic polymer materials. The SEDFIT-MSTAR procedure – which takes only a few minutes to perform - is tested with four synthetic data sets (including a significantly non-ideal system) a naturally occurring protein (human IgG1) and two naturally occurring carbohydrate polymers (pullulan and λ–carrageenan) in terms of (i) weight average molecular weight for the whole distribution of species in the sample (ii) the variation in “point” average molecular weight with local concentration in the ultracentrifuge cell and (iii) molecular weight distribution.

Introduction

The molecular weight (Da) or equivalently the ‘molar mass’ (g/mol) is one of the most important parameters defining a polymer, although it is not trivial to measure, particularly for polydisperse systems. Sedimentation equilibrium (SE) in the analytical ultracentrifuge is a well established method for obtaining the molecular weights of polymers^1,2. It has an absolute basis (not requiring calibration standards or markers, or assumptions over conformation) and has an inherent fractionation ability, without the need for columns or membranes and associated assumptions over inertness. It is also not hampered by contamination through large supramolecular particles. With the use of multi-hole rotors and multi-channel cells, it is now possible to run up to 21 samples simultaneously in a single run. One drawback which has held back its wide application is that the procedures for data capture and analysis previously available have not made the method the easiest to apply². For studies on proteins and other molecules with well-defined molecular weights the last two decades has seen the development of powerful software procedures for the analysis of optical records from sedimentation equilibrium, taking advantage of on-line scanning of uv/visible optical records (absorption/ fluorescence) or the on-line capture using a charge-coupled device (CCD) camera of the higher precision data yielded in the form of fringe displacements by the Rayleigh interferometric system. A characteristic feature of the analysis of protein interactions by SE is the direct fit of the measured signal profiles with a few discrete terms of Boltzmann exponentials, each corresponding to a different species of free protein or protein complex, and often linked in their amplitude by mass action law for reversibly interacting system. As recently reviewed³, advanced strategies for SE analysis, such as implemented in the multi-method analysis platform SEDPHAT⁴, include the global fitting of many SE signal profiles acquired at different loading concentrations, different rotor speeds, and different data acquisition with models that create constraints through implicit mass conservation and different interaction models, yielding binding affinities and stoichiometries⁵.

The analysis of polymers with a quasi-continuous distribution of molecular weight – or suspensions of mixtures with a diverse distribution of molecular weight – poses different problems. In contrast to the quasi-discrete problem of protein interactions, where often the buoyant molar mass values and therefore the exponents of the Boltzmann terms for each species are known a priori, here the buoyant molecular weights are unknown and their averages and their entire distribution is estimated from the evaluation of the exponential SE profiles. This problem is further exacerbated by the steep rising of concentration profiles near the cell base, and the shadow of the cell base that leaves a fraction of material undetected and to be extrapolated. Conventional methods of estimating average molecular weights from extrapolation of Rayleigh fringe concentrations or uv/visible absorbancies to the base of the ultracentrifuge cell⁶ can lead to serious error particularly if the position of the bottom of the cell is poorly defined. A different approach was therefore introduced⁷ involving an operational point average molecular weight known as the M* function: this approach offered a significant advantage over conventional methods which involved concentration extrapolation to the cell base, since the M* function is a less sensitive function of radial position, permitting a more accurate evaluation of the (apparent) weight average molecular weight M_w,app for the macromolecular components in the solution. This procedure was initially built into a Wang Desktop calculator, extended into a mainframe FORTRAN algorithm⁸ and then into a QUICKBASIC version for PC⁹. Besides providing a method of obtaining M_w,app the MSTAR programs also provided estimates of the local or point weight average molecular weights M_w,app(r) as a function of radial position (r) in the ultracentrifuge cell^8,9. The “app” signifies that the values obtained are apparent values, which will, at real solute concentration, be affected by thermodynamic non-ideality. Conventionally an “ideal” value is obtained by extrapolation of either M_w,app or M_w,app(r) to zero concentration, although at sufficiently low concentrations M_w,app ~ M_w and M_w,app(r) ~ M_w(r).

A limitation to the accuracy with which M_w (and M_w(r)) could be evaluated was the procedure employed to estimate the meniscus concentration, a long-standing problem with the analysis by fringe optics of sedimentation equilibrium data (see, e.g., ref. 6). Although for absorption optics this involved an extrapolation and an evaluation of the baseline or background absorbance of non-sedimenting species – and does not create too much difficulty, for Rayleigh interference – where the optical records are of the solute concentration relative to a reference position, conventionally taken as the air/solution meniscus¹⁰ – this involved either a rather complex mathematical manipulation of the data followed by an ill-conditioned extrapolation of two functions, based on a method of Teller et al¹¹ – the so-called intercept over slope method⁷ or a separate experiment involving synthetic boundary cells¹². We now present a completely new version of the program which (i) interfaces into the widely used SEDFIT platform for sedimentation analysis of macromolecules (ii) provides a much more rigorous method of obtaining the baseline and meniscus concentration for the Rayleigh interference optical system and (iii) provides an estimate for the distribution of molecular weight. We now describe the relevant theory behind the M* function, followed by a description of the algorithm, correcting for non-ideality where appropriate and then examples are given based on simulated data (single, two solute, data error and a significantly non-ideal system), a monodisperse protein preparation (human IgG1) a fractionated “standard” polysaccharide (pullulan P400) and an unfractionated polysaccharide (λ–carrageenan).

Theory

Average Molecular Weights and M*

Sedimentation equilibrium for a monodisperse ensemble of thermodynamically ideal macromolecules is characterized by the Boltzmann distribution, leading to a recorded signal

$$s(r)=s_1(r)+s_0=c_1(r_0)\epsilon d{e}^{k{M}_{1,app}(r^2-r^2)}+S_0$$ (1)

where s(r) maps the local concentration c(r) at radius r, r₀ denotes an arbitrary reference radius, ε and d denote the macromolecular signal increment and optical path length, respectively, and s₀ denotes a baseline signal offset (often given the symbol ‘E’). In Eq. 1 M_app is an apparent molecular weight on the given partial-specific volume scale, and we use the abbreviation

$$k=(1-\stackrel{‒}{\nu }\rho ){\omega }^2∕2RT$$ (2)

where $\stackrel{‒}{\nu }$ is the partial-specific volume, ρ the solvent density¹³, ω the rotor angular velocity, R the gas constant, and T the absolute temperature¹. The subscript ‘1’ in Eq. 1 indicates that this relationship is for a single species.

For an unknown sample, informed by Eq. 1 one may examine a plot of ln(c) vs r² for an apparent point weight average molecular weight

$$M=\frac{1}{k}\frac{d\ln (s\left(r\right)-s_0)}{d{r}^2}$$ (3)

which would ideally be linear for monodisperse systems and show a positive curvature for heterogeneous mixtures, or negative curvature for systems with thermodynamic non-ideality M_w,app can either be evaluated across the whole radial range of data or as a function of radial position to yield apparent point weight average molecular weights, M_w,app(r). One practical problem arising in this approach is that one will need to know the signal offset s₀, since any incorrect values of s₀ the plot ln(c) versus r² will gain additional positive or negative curvature. Furthermore, information can only be gained over the radial range that is optically accessible between certain radii r_low and r_up, which are at some distance from the meniscus and bottom radii r_m and r_b. Therefore, M_w,app evaluated this way will not necessarily reflect the entire contents of the loaded sample mixture, and, in particular, high molecular weight contributions can be missed.

Addressing this problem, an operational point average molecular weight was defined as⁷

$$M^{\ast }\left(r\right)=\frac{c\left(r\right)-c_m}{k{c}_m(r^2-{r_m}^2)+2k{\int }_{r_m}^r(c\left(r\right)-c_m)rdr}$$ (4)

with the meniscus concentration c_m = c(r=r_m) for sector shaped solution columns. It has the important property that the extrapolation to the bottom of the cell

$$M^{\ast }(r=r_b)=M_{w,app}$$ (5)

yields an apparent weight-average molecular weight of all components present throughout the solution column⁷. The application of Eq. 3 and Eq. 4 to noisy data with unknown baseline offsets presents computational challenges:

First, conventional modes of analysis will require the evaluation of the baseline offset: In the ln(c) vs r² approach s₀ needs to be explicitly known, whereas in the M* approach the macromolecular concentration at the meniscus c_a needs to be distinguished from the total signal at the meniscus that will generally be superimposed by the offset s₀, or c_a = [s(r_a) – s₀](εd)⁻¹ This problem can be posed differently for absorbance or interference optical systems⁸: the absorbance system may allow for an experimental estimate of s₀ to be determined, for example, from the signal close to the meniscus after a final overspeeding phase that leads to meniscus depletion conditions, or from scans performed at a wavelength where solute absorption is absent or minimal. Thus corrected, in absorbance the offset s₀ is usually small. By contrast, the interference optical system fundamentally only allows us to measure fringe increments across the solution column, without an absolute reference.

Second, due to the derivative in Eq. 3, when applied to noisy data it requires the data to be pre-smoothed to allow the determination of the numerical concentration derivative. This can be achieved, for example, with a ‘sliding strip’ procedure^8,9 in the previous software MSTARA with a user-defined width, or with Chebyschev polynomial in the original MSTAR FORTRAN program⁸, or with the Savitzky-Golay smoothing and differentiation method¹⁴ in SEDFIT-MSTAR. By contrast, M* has the virtue of not requiring differentiation. In the calculation of M*, distortion of the signal and noise amplification can occur close to the meniscus, but the fraction in Eq. 4 becomes increasingly more stable at higher radii with the growing integral in the denominator.

Finally, it is necessary for the application of M* to extrapolate the signal to the meniscus r_m and, for the cell average molecular weight, to extrapolate M* to the bottom of the solution column, r_b. In MSTARA the extrapolation of signal to the meniscus is implemented as linear or polynomial extrapolation¹⁴, and similarly is available as an option in SEDFIT-MSTAR for both estimates of c(r=r_m) and M*(r=r_b).

The Molecular Weight Distribution c(M)

In parallel, a method has been developed for the explicit determination of the entire molecular weight distribution, not restricted to its averages^5,15-16. It is based on the idea of direct modeling by least squares the experimental concentration distributions:

$$\stackrel{min}{c\left(M\right),s_0}\sum _{r_{low}}^{r_{up}}{\left\{S_i-{\int }_{M_{lo}}^{M_{up}}c\left(M\right)S_1\left(r_i\right)dM+S_0\right\}}^2$$ (6)

where c(M) is the unknown distribution of species with molecular weight M, each known to sediment in Boltzmann distributions s₁ of the ideal single sedimenting species (Eq. 1), and the minimization is with regard to the sum over all signal data points s_i at the radii r_i across the measureable range from r_low to r_up.

One key difficulty in this approach is the ill-conditioned nature of this Fredholm integral equation, for which it can be shown that many different distributions c’(M) will invariably exist that fit the data indistinguishably well^11,12-14. However, in a Bayesian approach it is straightforward to determine from all distributions that fit the data with statistically indistinguishable quality the simplest distribution, for example, the smoothest distribution with Tikhonov regularization, or the distribution with highest information entropy with the maximum entropy regularization^15-19. This approach is available in the software SEDFIT and SEDPHAT.

A second difficulty is related to the fundamental problem that higher molecular weight species may sediment predominantly between the highest radius r_up that can be optically accessed and the bottom of the solution column. This problem results in the c(M) method in undetermined distributions beyond an upper limit of molecular weight, M_up. It has been shown that this problem can be addressed by the global least squares modeling

$$\stackrel{min}{c\left(M\right),s_0,r_b}\left[\sum _x\sum _{r_{low}x}^{r_{up,x}}{\left\{S_{i,x}-{\int }_{M_{low}}^{M_{up}}c\left(M\right)S_{1,x}\left(r_{i,x}\right)dM+S_{0,x}\right\}}^2\right]$$ (7)

of multiple sedimentation equilibrium profiles at different rotor speeds (with x distinguishing experiments at different rotor speeds) in combination with implicit mass conservation⁵. In Eq. 7, the baseline offset s_0,x may be rotor speed dependent (termed the ‘RI noise option’ in SEDFIT-MSTAR), or, alternatively, Eq. 7 may be solved with the constraint that all s_0,x are equal to s₀. If the data are acquired under conditions that sample both high-molecular weight fractions at low rotor speeds and low-molecular weight fractions at high rotor speed with meniscus depletion conditions, and if total mass of soluble material at the first rotor speed is conserved in all following experiments, then the fit of Eq. 7 can define simultaneously the molecular weight distribution c(M), the baseline s₀, and the bottom position of the solution column r_b ⁵. While this implicit mass conservation method is widely used in the analysis of interacting systems (in SEDPHAT), where it leads to a drastic reduction of unknown parameters and significant improvement of statistical accuracy of binding parameters^5,20,21, a similar benefit arises in the determination of molecular weight distributions of non-interacting macromolecules, as illustrated in ref. 5.

With regard to the computational implementation, SEDFIT-MSTAR solves Eq. 6 and Eq. 7 as a linear least squares problem, which arises after discretization of the distribution c(M) into typically 50 – 100 molecular weight grid points, and from which all unknowns can be determined simultaneously in an algebraic operation employing normal equations²². It should be noted that this includes the simultaneous optimization of both the exponential amplitudes and all baseline terms. This deviates fundamentally from the traditional sequential approach where first baselines are fixed, to be followed by the analysis of the SE gradient. The c(M) distribution at a reference radius r₀ is normalized to units of (uniform) loading signal c₀(M)dM that correspond to the estimated contributions to the SE profile, through analytical integration of Eq. 1 for sector-shaped solution columns. Typically the analysis takes on the order of 1 sec with current personal computers.

Unfortunately, the solution of Eq. 7 strictly as a linear least squares problem prohibits the additional consideration of radial-dependent baseline offsets s(r) (‘TI noise’) from multi-speed global SE analysis. Such radial-dependent baseline offsets are commonly determined as a byproduct of direct boundary modeling of families of concentration profiles in sedimentation velocity²³. While they can never be independently determined from a single concentration profile in SE, their consideration in the analysis of SE at multiple rotor speeds is complicated by the translation Δ_x of the radial-dependent features due to differential rotor stretching (which creates the non-linear constraint s(r + Δ_x,1) = s(r + Δ_x,2) etc.). Although baseline profiles s(r) including rotor stretching can be routinely evaluated in the global SE analysis of interacting systems^5,24. This is due to the description of the macromolecular concentration profiles governed by non-linear concentration parameters, which allows modified algebraic methods for the similar but translated baseline profile s(r + Δ_x) ⁵. Along the same path, a potential future extension of SEDFIT-MSTAR may allow the consideration of radial-dependent baselines through treatment of the distribution as a family of non-linear parameters, although likely incurring significantly higher computational time.

On the other hand, dependent on the range of rotor speeds covered, and other experimental details such as the elasticity of the window cushion material²⁵ the details of the radial-dependent noise may not necessarily remain identical after changing rotor speeds⁵. In any event, for interference optical data acquisition the experimental determination and minimization of radial dependent baseline features, for example, through pre-aging of cell assemblies and recording of water blanks will be the method of choice. These considerations and the magnitude of the residual baseline uncertainty will also pose a limit on the useful concentration range for different types of studies in sedimentation equilibrium.

The removal of TI noise can also be effected experimentally, for interference data, by taking a series of scans immediately at the start of the run, averaging same, and subtracting this averaged set of radial values from the final (usually averaged) data set at equilibrium²⁶. This routine has been followed for all the experimental data reported here.

An executable form of the SEDFIT-MSTAR program can be obtained from the authors on request, or can be downloaded from https://sedfitsedphat.nibib.nih.gov/software/default.aspx or from https://www.nottingham.ac.uk/ncmh/unit/method.html#Software. A brief tutorial with screenshots and further information on its practical application can be obtained from www.analyticalultracentrifugation.com and via the SEDFIT-L forum (https://list.nih.gov/cgi-bin/wa.exe?SUBED1=SEDFIT-L&A=1).

Relationship between c(M) and M* - Exponential Smoothing

Even though the motivation and computational approach of M* is very different from c(M) – the former being a data transformation to derive cell average molecular weights, and the latter attempting a low-resolution explicit representation of the molecular weight distribution in a direct least-squares fit – there is a high degree of synergy from the combined application of both.

First, from the vantage point of M* the c(M) method can be regarded as a highly sophisticated method to smooth and extrapolate the data, and to estimate the baseline signals. To this end, we have implemented in SEDFIT-MSTAR the direct fit of the data with Eq. 6 or Eq. 7. Even disregarding the specific form of c(M), with regard to the extrapolation of the signal to the meniscus for c_a, the exponential superposition represents a special case of polynomial extrapolation (with infinite number of polynomials) that takes advantage of our specific knowledge of the expected functional form of the concentration distribution. As opposed to the polynomial extrapolation based on a trusted region close to the meniscus or cell base, here we use as the basis for extrapolation the entire solution column. Therefore, c(M) is an excellent method for determining baseline offsets, precisely because it takes advantage of data from the entire solution column and provides a best-fit baseline estimate on a least-squares basis.

Second, in addition to extracting these quantities from the c(M) fit, one can apply the M* transformation Eq. 4 to the c(M) fit of the data, i.e. to the integral ${\int }_{M_{low}}^{M_{up}}c\left(M\right)s_1(r,M)dr$, with a result denoted in the following as M*_c(M). These transformations of the c(M) fit to the raw data are shown as red lines in Panels (b) and (c) in Figures 1-3 and 5-7. This not only honors the information on s₀ and c_m, but also produces a model for M*(r) across the entire solution column. Specifically, by design, this M*_c(M) distribution will provide a natural extrapolation of M* to the bottom of the solution column. This extrapolation improves on the standard polynomial fit by taking into account the information from the entire solution column.

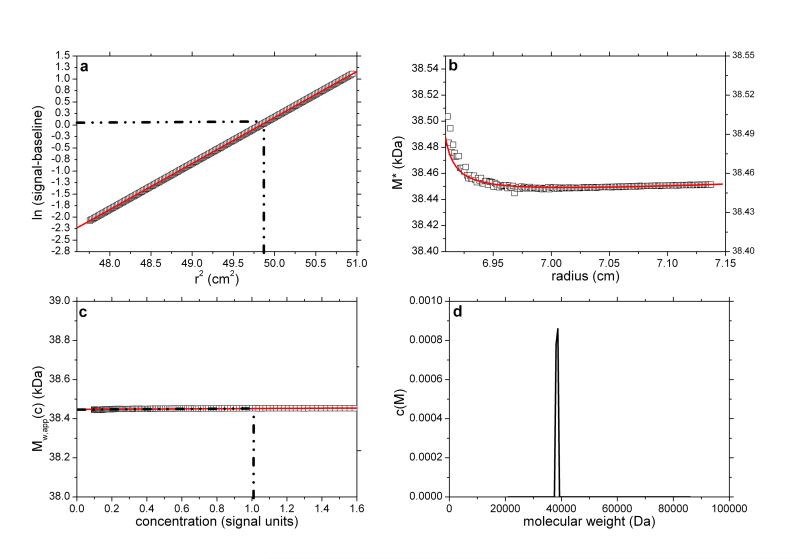
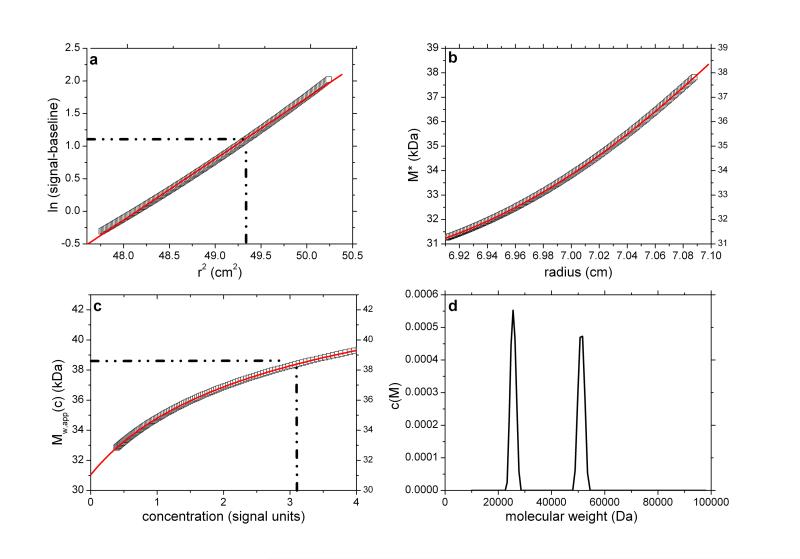
Fig. 1.

SEDFIT-MSTAR output for analysis on a simulation of a sedimentation equilibrium experiment for a single solute of molecular weight 38,450 Da (a) log concentration lnc(r) versus r² plot, where r is the radial distance from the centre of rotation (open squares); and linear regression to highlight deviations from linearity arising from polydispersity and/or non-ideality (red line); (b) M* versus r plot (open squares) and fit based on the M* transformations of the c(M) fit of the raw data (red line): the value of M* extrapolated to the cell base = M_w,app, the apparent weight average molecular weight for the whole distribution. Retrieved value for M_w,app = 38,450 Da; (c) point or local apparent weight average molecular weight at radial position r (open squares) plotted against the local concentration c(r) for different radial positions: red line is the fit based on the equivalent transformation of the c(M) fit of the raw data (d) molecular weight distribution, c(M) vs M plot. The dot-dashed lines show the position of the hinge point (in panel (a)) and the corresponding estimation of M_w,app value (panel (c)), which also retrieves a value for M_w,app = 38,450 Da.

Fig. 3.

As Figure 2 but for concentration (Rayleigh fringe displacement) data with ±0.005 fringe random error with simulated random error. True M_w,app = M_w =38,450 Da. Retrieved M_w,app (from extrapolation of M* to the cell base, and from the hinge point) = 38,500 Da. Fitted lines are as defined in the legend of Figure 1.

Fig. 5.

As Figure 1 but for the analysis of a monodisperse preparation of human/murine IgG1 known as “Erbitux” at a loading concentration = 1 mg/ml. True M_w ~ 150,000 Da. Retrieved M_w (from extrapolation of M* to the cell base) = (148,000±2,000) Da, from c(M), M _w,app ~ 148,000 Da and from the hinge point ~ 147,500 Da. Fitted lines are as defined in the legend to Figure 1.

Fig. 7.

As Figure 1 but for the analysis of λ-carrageenan at a loading concentration of 0.3 mg/ml. M_w,app (from extrapolation of M* to the cell base) = 310,000 Da. Fitted lines are as defined in the legend to Figure 1.

Third, when the best-fit model of c(M) is transformed in the ln(c) vs r² plot, it provides a smooth fit of the noisy raw ln(c) vs r², data from which point averages as a function of signal M_w,app(c), or radius, M_w,app(r) can be easily determined across the entire solution column, provided the c(M) model yields an adequate fit of the data in the raw data space. Even though a fit of a transform will usually distort the statistics of the data errors, because the c(M) fit takes place in the original data space, it will have more appropriate weights than a fit and differentiation in the ln(c) domain.

In the implementation of SEDFIT-MSTAR, it is possible to switch from the M* representation of the data to the c(M) representation showing the raw sedimentation profiles, inspect the quality of fit of c(M) to the raw data and the residuals, and also to study the low-resolution molecular weight distribution c(M) directly. For example, multi-modal distributions may be resolved from suitable data. This can provide more insight in the molecular weight distribution, but in conjunction with information from M* gains robustness. For example, the M* perspective does not depend on regularization, and it may be advantageous when empirically applied to data with thermodynamic non-ideality.

When applied to the analysis of multiple sedimentation equilibrium data sets from the same sample acquired at multiple rotor speeds, the combination of M* with c(M) can be particularly powerful, especially if mass conservation and ideal sedimentation can be assumed. In this case, the global c(M) fit can serve to provide a single consistent interpretation of multiple individual M* transforms, which otherwise may be difficult to mutually reconcile and potentially result in different extrapolations and cell-average molecular weight estimates. An illustration of this with a pauci-disperse protein system has been given in Fig 2 of ref. 5, where a multi-modal distribution was obtained from the global multi-speed analysis, but not in any of the single speed analyses. For the global analysis the question arises whether the baseline can be assumed to be rotor-speed independent or not. In SEDFIT-MSTAR, the data analysis can be carried out with both assumptions and the chi-squares of the c(M) fit can be compared. If a significant improvement in the quality of fit is achieved with rotor-speed dependent offsets s_0,x (Eq. 7, ‘RI noise’ option on) as compared to a fit with a single constant offset s₀ (‘RI noise’ option off), then the analysis with individual offsets is justified. For interference optical data, the baseline cannot be expected to remain the same, as noted above.

Fig. 2.

As Figure 1 but for a simulated ‘perfect data’ 2-solute system, with 50% by weight of a monomer (M₁= 25,630 Da) and 50% by weight of a dimer (M₂ = 51,260 Da). True M_w,app = M_w = 38,450 Da. Retrieved M_w,app (from extrapolation of M* to the cell base, and from the hinge point) = 38,500 Da. Fitted lines are as defined in the legend of Figure 1.

In the implementation of this combined approach in SEDFIT-MSTAR, it is possible to either accept the results from the c(M) fit in the M* transformation, or override specific aspects, for example, to accommodate known baselines or meniscus concentrations. As outlined above, when globally analyzing data from multiple rotor speeds, the user can define whether they have a common baseline offset, or potentially different offsets at the different rotor speeds.

Hinge point-method for evaluation of M_w,app

SEDFIT-MSTAR also evaluates the apparent point weight average molecular weight M_w,app (r) as a function of radial position r using Savitzky-Golay smoothing and differentiation applied to Eq. 3 as noted above. It also allows for the evaluation of the same parameter avoiding transformation of the data with the logarithm⁶:

$$M_{w,app}(r)=\{1∕k\}.\{1∕(r.(s\left(r\right)-S_o))\}.\{d(s\left(r\right)-S_o)∕dr\}$$ (8)

Either Eq 2 or Eq 5 can be used to define the molecular weight at the “hinge point” in the radial distribution – this is the radial position at which the local concentration (s(r) – s_o) is equal to the initial cell loading concentration (in signal units). Hence M_w,app(r) at the hinge point will equal the weight average molecular mass of the whole distribution. Using for example Eq. 8:

$$M_{w,app}=\{1∕k\}.\{1∕\left(r_{hinge.}(s\left(r_{hinge}\right)-s_o)\right)\}.\left\{{(d(s\left(r\right)-s_o)∕dr)}_{hinge}\right\}$$ (9)

SEDFIT-MSTAR provides the facility for obtaining the hinge point by evaluating the initial loading concentration from the conservation of mass equation:

$${(s\left(r\right)-s_0)}_{initial}=\left(2∕({r_b}^2-{r_m}^2)\right).{\int }_{rm}^{rb}(s\left(r\right)-s_0))rdr$$ (10)

For non-sector-shaped channels (as found in the commonly used multi-channel centerpieces (3 pairs of channels) the evaluation of the loading concentration presents difficulties for which there is no solution extant. However, by superimposition of early and late scans an empirical estimate of this parameter can be made, enabling the application of the ‘hinge point method’ described above.

Thermodynamic non-ideality

Thermodynamic non-ideality derives from macromolecular co-exclusion phenomena and, if the macromolecule is a polyelectrolyte, there will also be a contribution from any unsuppressed macro-ion charges, so all estimates for M_w and M_w(r) {and also the distribution c(M) vs M, and M_z values} are apparent values (M_w,app, M_w,app(r), M_z,app(r) etc). The charge contribution can be suppressed by working in a solvent of sufficient ionic strength (see, for example, ref. 27). Although for proteins at loading concentrations ~1mg/ml or less the effects of non-ideality are usually very small, for some polymers – particularly those with a high affinity for the solvent (such as polysaccharides in aqueous solvent), even at the lowest concentrations that can be used in a sedimentation equilibrium experiment (for polymers realistically ~ 0-2-0.3 mg/ml with the longest cell path-length (20mm) that can currently be employed), these effects can still be significant. Table 2 of ref. 28 for example gives a comparison of how M_w,app underestimate the true values for a series of polysaccharides at a loading concentration of 0.2mg/ml. If working at these low loading concentrations the approximations M_w ~ M_w,app or M_z ~ M_z,app are not valid, the conventional way of dealing with this situation is to perform a series of measurements at different loading concentration and extrapolate back to zero concentration where these effects tend to vanish. The form of the extrapolation can be linear or non-linear. For obtaining M_w,app using procedures that do not involve an integration, such as Eq. 8, there is a simple relation relating M_w,app and M_w at dilution solution:

$$M_{w,app}=M_w.\{1∕(1+2B{M}_{w}c)\}$$ 11

where B is the second thermodynamic virial coefficient (ml. mol. g⁻²). M_w,app values evaluated according to Eq. 8 at the hinge point conform to this relation and a simple linear extrapolation of 1/M_w,app plotted versus loading concentration c yields the reciprocal of the true M_w from the intercept at c=0. At higher concentrations the extrapolation may not be linear and an extra virial term in c² may be required. Furthermore, for evaluations involving an integral transformation such as Eq.4 to obtain the whole cell distribution M_w there may also be a speed-dependent enhancement of the non-ideality effects. Fujita^29,30 gave the following approximate relation (see also ref. 6), leading to a larger effective value for B and also departure from a linear form of the extrapolation^28,31:

$$M_{w,app}=M_w-2Bc.{M_w}^2(1+12{\lambda }^2{M_z}^2)+\cdots$$ (12)

where λ = k. (r_b² – r_m²)/2 with k defined by Eq. 2.

So although M_w,app from Eq.4 can generally be obtained to a higher precision than from the point average M_w,app evaluated from Eq. 9 at the hinge point – and without assumptions over conservation of mass - the non-ideality effect will be greater. SEDFIT-MSTAR therefore includes both methods of M_w,app evaluation.

Application to simulated and real data

To illustrate the operation of SEDFIT-MSTAR we consider seven diverse examples, the first four of them based on simulated data (single solute, a mixture of two components, a mixture of two components with data error and a dataset with significant non-ideality. Simulated data was generated and where indicated normal random error added using custom-written plug-ins within the general software and graphical package pro Fit^™ (Quantum Soft, Uitekon am See, Switzerland). Our routine level of normal random error is ±0.005 fringe (see, for example, ref 26). In practice ‘real’ data sets will not, unlike simulated data sets, start from perfectly defined positions for the solution meniscus and the cell base: we therefore also consider the effects of systematic errors in these on the molecular weight evaluation. We also consider a significantly non-ideal system, with and without local random error of ±0.005 fringe. For our practical examples we consider the characterization of a monodisperse protein preparation (immunoglobulin IgG1) and two polysaccharides (a fractionated but still polydisperse preparation of pullulan and an unfractionated preparation of λ-carrageenan) are given.

Simulation 1: single solute (no error)

As a point of reference and test for the correctness of the computations we first simulated noise-free data for a single solute. This is based on a Rinde³² type of simulation for a macromolecule of reduced molecular weight σ = kM = 2.000 (with k defined as in Eq. 2). For a solution density of 1.000 g/ml, partial specific volume of 0.600 ml/g, rotor speed of 17,000 rpm and temperature of 293.15 K this corresponds to a molecular weight of 38,450 Da.

The radial position of the meniscus is at 6.90 cm and the base is at 7.15 cm. The true concentration at the meniscus in Rayleigh fringe units, c_m (traditionally known as the “J_a value”- see ref. 6) is 0.108. The output consists of the signal plot a plot of log concentration versus radial displacement squared (r²) with fit (Figure 1a), the M* versus r plot (with fit and extrapolation to r=r_b) (Figure 1b) a plot of the local or point weight average molecular weight M_w,app(r) vs radial position r, or equivalently a plot of M_w,app(r) vs concentration c(r) (Figure 1c). Values of J_a = 0.108 and M_w,app = 38,450 Da (from M*(cell base) = M_w,app) and from the hinge point method are correctly returned. The point average molecular weight plot (M_w,app(c) versus the corresponding local concentration in the ultracentrifuge cell, c or c(r)) reproduces this value also, and shows perfect monodispersity. Figure 1d shows the estimated molecular weight distribution, again consistent with a monodisperse preparation of M = 38,450Da.

Simulation 2: mixture of two solutes (no error)

The second simulation illustrates the effect of polydispersity, for clarity conducted in the absence of noise. Again based on Rinde, comprising an equal amount (by weight) of monomer, σ₁ = 1.333 (M₁ = 25,630 Da) and dimer, σ₂=2.667 (M₂ = 51,260 Da). Solvent and sedimentation parameters are as in the first simulation, but with a radial position of the meniscus at 6.90 cm and the cell base at 7.10 cm. The true J_a value = 0.639. Figure 2a shows the log concentration versus r² plot, with the best-fit straight line (red) deviating from the data, as expected, due to the polydispersity. This is reflected also in the gradient of M* versus r (Figure 2b), and the M*_c(M) distribution (red line in Figure 2b) that is based on the best-fit least-squares fit of the raw simulated c(r) data with the c(M) model Eq. 5. As can be discerned from Figure 2b, the same M*_c(M) distribution allows the extrapolation to the cell base at r=r_b. Figure 2c shows the M_w,app(c) vs concentration plot together with the c(M)-based best-fit (red line). From the SEDFIT-MSTAR analysis of the raw data, values of J_a = 0.65 and M_w,app = 38,450 are returned, again in excellent (J_a) and exact (M_w) agreement with the true values. The hinge method also yields the same value for M_w, and finally the c(M) vs M plot (Figure 2d) also successfully resolves the two components, returning accurately the molecular weights (25,630 Da and 51,260 Da) and their relative proportions.

Simulation 3: mixture of two solutes with ±0.005 fringe random error

Next, we studied the effect of random errors in the raw data on the different aspects of the analysis. Simulation parameters were identical to simulation 2, and corresponding results are shown in Figures 3a-d. As may be discerned from Figure 3c, the Savitzky-Golay filter sufficiently suppressed the random noise in the derivative of M_w,app. As expected M* is sensitive to the noise mainly close to the meniscus position, with increasing precision towards the base of the cell due to the accumulative effect of the integral in Eq. 3. The biggest impact of the noise in the data is on the c(M) distribution: while it still serves as an excellent fit to both the M* and M_w,app values, the information on the true distribution degrades and the Tikhonov regularization returns a single broad distribution as the simplest distribution consistent with the noisy simulated c(r) data. This is by design, and required to avoid over-intepretation of the data, but, as illustrated here, leads to distributions that do not necessarily reflect the details of the true distribution. Nevertheless, the values of J_a= 0.65, and M_w,app =38,500 are returned, again in excellent agreement with the true values. An identical value for M_w,app is also returned from the hinge point method.

We also explored a ‘worst case’ scenario, in which the meniscus position is in error by ±0.007 cm and the cell base position by ±0.005 cm: this returns J_a = 0.65 and M_w = 38,700 an error of less than 1% from the true value.

Simulation 4: A significantly non-ideal system (with and without random error)

For our final simulation we look at a single solute system which shows significant non-ideality at a level comparable to that found in such a system where the molecular species under study for example is highly extended. The simulation is for a single solute, σ₁ = 3 (M₁ = 40,000 Da, rotor speed = 24721 rpm), J_a value = 0.1276: baseline offset = 0, with 2BM_wc = 0.144. This non-ideality is higher than that for most polysaccharides in dilute solution and greater than that for a bronchial mucin glycoprotein²⁸ (M_w = 6 × 10⁶ Da at c = 0.2mg/ml). It is equivalent to the non-ideality of a typical globular protein (ovalbumin, M= 44,000 Da) at a high concentration (~20mg/ml). The position of the meniscus is at 6.90 cm and the cell base is at 7.10 cm.

Figure 4a shows the log concentration versus r² plot, with the best-fit straight line (red) deviating from the data, as expected, due to the non-ideality. This is reflected also in the strong downward gradient of M* versus r (Figure 4b), and the point average plot (Figure 4c).

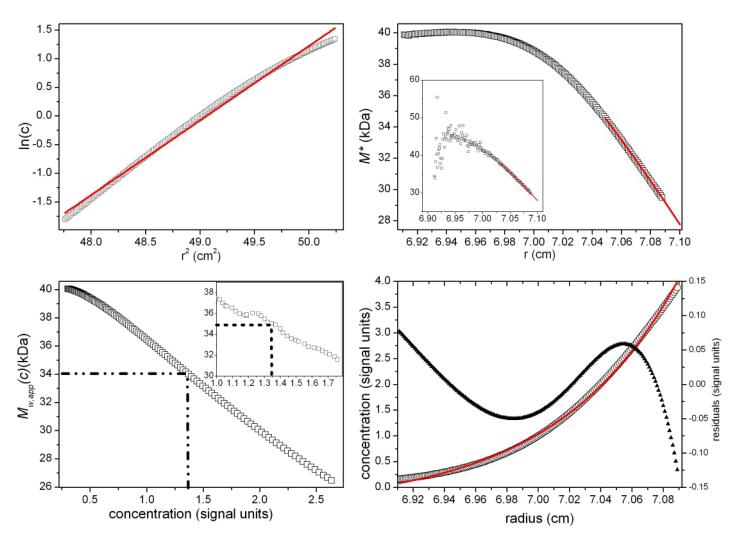
Fig. 4.

As Figure 1 but for a single solute system with significant non-ideality. σ = 3, rotor speed = 24,721 rpm, True M_w = 40,000 Da. Expected M_w,app = 34,950 Da (based on Eq. 11). From Fig 4b, a lower value is obtained ~ 28,000 Da, consistent with Eq. 12. From Fig 4c and the hinge point however (indicated by the dotted lines), the estimate for M_w,app ~ 34,000 Da, close to the expected value. Fitted lines are (a) a linear regression, visually highlighting the characteristic negative curvature of non-ideal data in this transformation; (b) the polynomial extrapolation of M*. Inset Figures (b) and (c): corresponding plots for random data with ± 0.005 fringe error, yielding values for M_w,app ~ 35,000 Da (hinge method) and ~29,000 Da (M* extrapolation). Note the failure of the smart-smooth procedure to obtain a c(M) plot due to the failure of obtaining an adequate fit of the raw c(r) data (d). For systems of low polydispersity this should be used as a diagnostic of the presence of significant non-ideality.

Note the failure of the smart-smooth procedure to obtain a satisfactory fit of c(M) to the raw data (Figure 4d). This can be used as a diagnostic of the presence of significant non-ideality whose effects are unopposed by the presence of polydispersity (which causes upward curvature in a positive exponential way). When this is observed the radial region for the c(M) based baseline analysis is restricted to a narrow data range close to the meniscus (maximal range that still leads to an adequate fit) to solely predict the baseline (Figure 4d)

With this baseline, M* can be calculated, and traditional polynominal extrapolation to the cell base can be used to obtain M_w,app (red line in Figure 4b). The hinge point estimation also successfully reveals M_w,app as before (Figure 4c). The expected M_w,app = 34,950 Da (based on Eq. 11). From Fig 4b, a lower value is obtained ~ (28,000±500) Da, consistent with Eq. 12. From Fig 4c and the hinge point however, the estimate for M_w,app ~ (34,000±500), close to the expected value. For the same simulation with random error of ±0.005 fringe, similar values are returned for M_w,app of (29,000±2,000) from the M* extrapolation method and (35,000±3,000) from the hinge point method respectively (see insets to Figures 4b and 4c).

Application to IgG1

A preparation of the chimeric human/murine IgG. known as “Cetuximab” or “Erbitux”³³ was studied (a gift of Professor R. Jefferis, University of Birmingham). Its amino-acid sequence molecular weight is 145,782 Da. This antibody possesses two N-linked glycosylation sites and with covalently attached carbohydrate its total monomer molecular weight is ~ 150,000 Da. The preparation we studied had been shown to be purely monomeric by sedimentation velocity in the analytical ultracentrifuge. For the sedimentation equilibrium experiment using Rayleigh interference optics, the solvent was 0.1 M phosphate buffered saline at pH 7.0, which had a density of 1.00452 g/ml and a partial specific volume of 0.731 ml/g. A rotor speed of 13,000 rpm was employed at a temperature of 20 °C. The sample had been dialysed against the solvent for 6 h and sample (at a loading concentration of 1.0 mg/ml) and solution and dialysate respectively were placed in the sample and reference sectors of the inner pair of channels in a multi-channel cell with sapphire windows. SEDFIT-MSTAR yields the results shown in Figure 5. Figure 5a shows a ~ linear plot of the log concentration versus r², consistent with a monodisperse species. The M* plot shown in Figure 5b yields a value for the apparent weight average molecular weight M_w,app of (148000 ± 2000) Da. Figure 5c shows the corresponding M_w,app(c) versus c(r) plot, with an estimate for the hinge point M_w,app of ~147,500 Da at a radial position 6.06cm. As is typical for experimental data with more correlated noise and other unavoidable low-level imperfections, smoothing of these data prior to differentiation results in stronger non-random features in the M_w,app(c) data especially at lower radial positions and smaller concentration values.

Even though the resolution of c(M) (Figure 5d) is not very high, it displays a single peak at M_w,app ~ 148,000 Da and is consistent with a single species. Notably, the c(M) method when considered as ‘exponential smoothing’ provides a single consistent ‘best-fit’ interpretation of both M*(r) and M_w,app(c) (red lines in Figures 5b and 5c). All M_w,app values returned are slightly below the “ideal” value of ~150,000 Da, the slight difference due to some thermodynamic non-ideality at c=1.0mg/ml. The slight positive slope in the M_w,app(c) versus concentration plot is suggestive of a weak self-association (although our variously computed values for the whole distribution M_w,app do not directly reflect this fact), and this is currently the subject of further study.

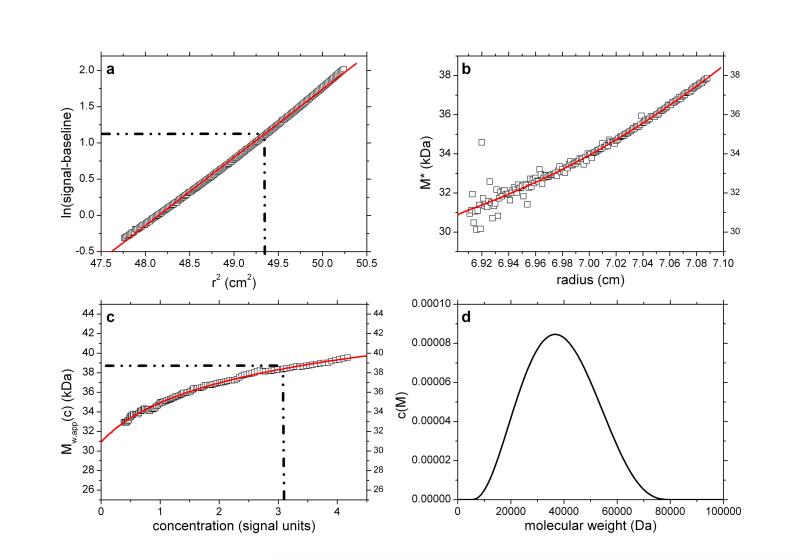
Application to pullulan P400

Pullulan P400 is one of a set of narrowly fractionated polysaccharide standards first prepared and characterized (using sedimentation equilibrium) by Kawahara & coworkers³⁴ and then commercially produced as calibration standards for the size exclusion chromatography of polysaccharides. Pullulan P400 is listed as having a weight average molecular weight M_w ~ 400,000 g/mol and we analysed a commercial sample from Polymer Laboratories (Sample Batch number 20907-2) dialysed against phosphate-chloride buffer (pH=6.8, I=0.1) and loaded into a 12mm path length cell at a concentration of 2 mg/ml, with dialysate in the reference sector. The sample was run at a rotor speed of 5000 rpm, temperature of 20.0°C and equilibrium solute distributions recorded using Rayleigh interference optics. A value for the partial specific volume = 0.602 ml/g ³⁴ was used in the analysis. Figures 6a-d show the results. The value obtained for P400 of from the M* extrapolation of M_w,app of (400,000±5,000) g/mol is in agreement with the commercially stated “standard” value and the findings of Kawahara et al³⁴. The hinge point method also gives a value close to this (395,000±10,000).

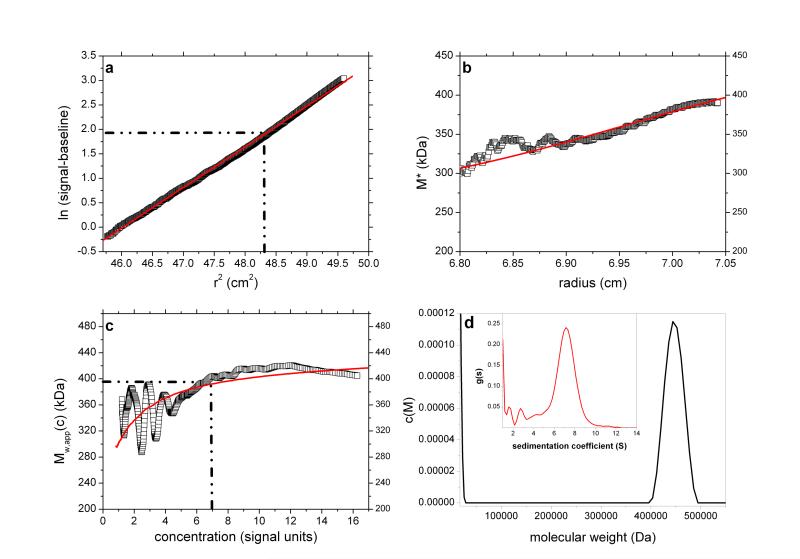
Fig. 6.

As Figure 1 but for the analysis of pullulan P400 at a loading concentration of 2 mg/ml. True M_w ~ 400,000 Da. Retrieved M_w,app (from extrapolation of M* to the cell base – Figure 6b) = 400,000 Da. Figure 6d shows the presence of a trailing edge of a component of molecular weight <20,000Da, a presence comparable to that found from a corresponding experiment using sedimentation velocity analysis (Figure 6d insert). The weighted average of the main + minor components ~ 400,000 Da. Fitted lines are as defined in the legend to Figure 1.

Interestingly, the c(M) vs M plot reveals two peaks. One (main peak) with an estimated weight average molecular weight of ~ 450,000 g/mol and another, partially resolved peak appearing at low molecular weight (<20,000 g/mol) (Figure 6d). When c(M) is integrated across the entire distribution, a weight-average M_w of ~ 400,000 is obtained in exact agreement with the extrapolated M* value, as is the M*_c(M) distribution shown as red line in Figure 6b. Furthermore the bimodal nature of c(M) corresponds well to the profile from sedimentation velocity via application of least squares g*(s) procedure of SEDFIT³⁵ (Figure 6d – inset). Using the extended Fujita approach³⁶ for conversion of the sedimentation coefficient distribution to a molecular weight distribution (assuming a conformation for the polymers – in this case a random coil), the main peak from the SV data is estimated to have an overall weight average molecular weight consistent with the value derived from c(M). Thus whilst information as concerns the presence of a lower weight component is yielded from the c(M) vs M plot, the estimates of the mass and proportion of the individual ‘peaks’ displayed is approximate only.

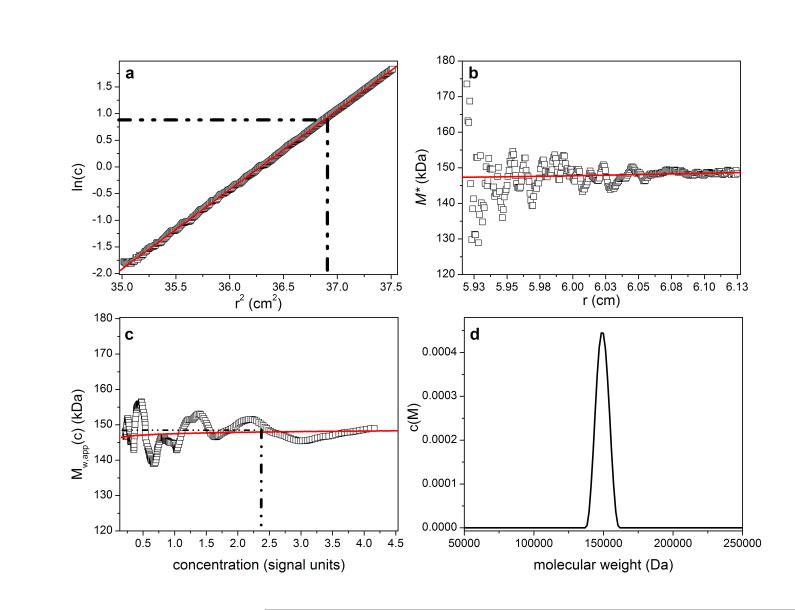
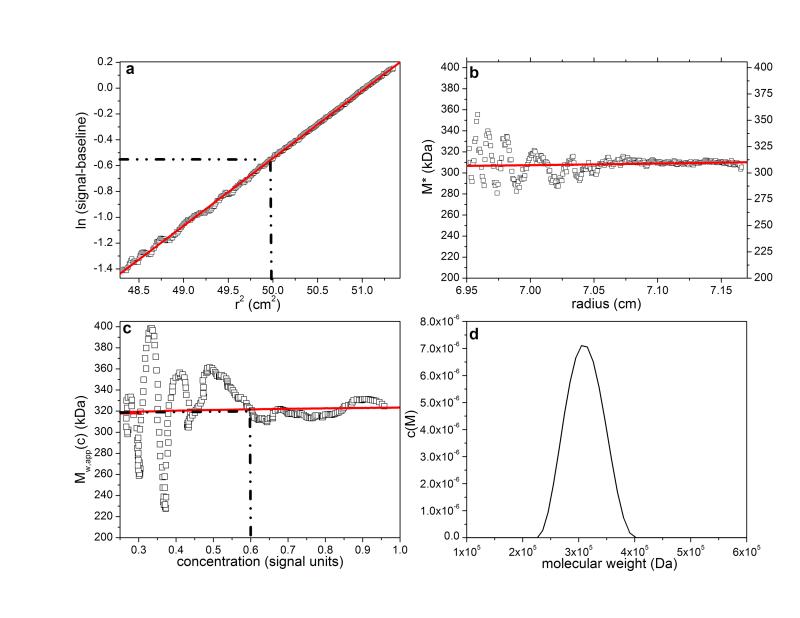
Application to λ-carrageenan

For our final example we have chosen an unfractionated polysaccharide, λ-carrageenan (a gift from Dr. T. Foster, University of Nottingham, School of Biosciences). This was dissolved in deionised distilled water (with the assistance of heating in a microwave for 30 seconds) and then dialysed for ~24 hours against phosphate-chloride buffer (pH=6.8, I=0.1) and loaded into a 12mm path length cell at a concentration of 0.3 mg/ml, with dialysate in the reference sector. The sample was run at a rotor speed of 4000 rpm, temperature of 20.0°C and equilibrium solute distributions recorded using Rayleigh interference optics. A value for the partial specific volume = 0.53 ml/g was used in the analysis. Figures 7a-d show the results, yielding a value for M_w,app of (310,000±10,000) g/mol which after allowance for non-ideality is in excellent agreement with the value obtained using SEC-MALS³⁷. The hinge point method gives a value in good agreement (300,000±20,000) the extra noise/imprecision a consequence of working at very low loading concentration (0.3 mg/ml).

Discussion and perspectives

In the present work, we have developed an efficient and reliable approach for the sedimentation equilibrium analysis of virtually all polymer systems across a wide range of molecular weights – monodisperse, polydisperse and realistically non-ideal, and a high degree of confidence can be placed on the whole distribution weight average molecular weights computed. Our approach integrates the previously separate approaches of derivative-based and integral-based data transforms, which require various smoothing and/or extrapolation produces to determine distribution averages, with direct distribution fitting approaches which is a model-based least-squares fit of the data but is usually ill-conditioned. We found the combination provides a single consistent interpretation that offers information in parallel on different levels of detail. Running of the algorithm takes only a few minutes, in contrast to the time required previously to analyse sedimentation equilibrium data for polymers, and obviating the difficult and inconvenient procedures for obtaining adequate baselines encountered in earlier studies^2,12. A new method (MultiSig) for obtaining accurate values for the baseline offset (E) in fringe optics via multi-exponential fitting has recently been published²⁶. MultiSig returns the mean of 20 estimates using a Monte-Carlo type approach. Our currently described procedure we have found to return a precision very similar indeed to the individual estimates yielded by MultiSig. Thus a high degree of confidence can now be placed upon the whole-cell weight-averaged molecular weight (M_w) values computed. There are some important perspectives deriving from this work:

1. Solvent density. The assumption is made that this is constant throughout the solution column. In the case of the inclusion of dense solutes like caesium salts then a short column is advised (and measurements made at least two rotor speeds to check for possible effects), otherwise the redistribution will need to be taken into account (the extreme case being isopycnic density gradient equilibrium where a density gradient is deliberately set up – see e.g., refs 6 and 28).

2. The non-ideality simulation we quoted was for a strongly non-ideal single solute system: the virtue of having two methods for extracting M_w,_app – one, more precise but more affected by non-ideality, the other (hinge-point) less precise but less affected by non-ideality. When non-ideality is suspected an extrapolation to c=0 is required to obtain M_w: this extrapolation is facilitated by the use of multi-channel cells. In the case of single solute, an extrapolation of the point average M_w,app(r)’s is possible – as shown in Figure 4c: a good practical example is turnip yellow mosaic virus³⁸. For polydisperse systems such a procedure can lead to an underestimate of M_w because of redistribution of the molecular species of different molecular weight in the solution – unless ultra-short columns are used (see ref 39). Although polydisperse non-ideal systems are almost impossible to simulate because of the complex non-linear way the separate virial coefficients B_k (and products B_kM_k) for each affect the fundamental equations of sedimentation equilibrium⁴⁰, it actually helps linearise the extrapolation to c=0 to give M_w, since the effects of polydispersity (upward curvature in the concentration versus radial displacement plots) counteracts either partially or in some cases known as “pseudo-ideal” almost completely the effects of non-ideality (downward curvature). A good example of this behavior is for λ-carrageenan (Figure 7). Although for proteins at loading concentrations ~1mg/ml or less the effects of non-ideality are usually very small (the example of non-ideality given in Fig 4 is equivalent to a globular protein like ovalbumin at a concentration of ~ 20 mg/ml, which is 150x the minimum concentration needed for a sedimentation equilibrium experiment), for some polymers – particularly those with a high affinity for the solvent (such as polysaccharides in aqueous solvent), even at the lowest concentrations that can be used in a sedimentation equilibrium experiment (for polymers realistically ~ 0.3 mg/ml with a long path-length (20mm) cell), these effects can still be significant, and this is the case for λ-carrageenan (Figures 7a-d) – the quasi-linear plot of ln(signal) versus r² and the near flat plot of M_w,app(r) vs c(r) is symptomatic of pseudo-non-ideality where the effects of polydispersity (causing upward curvature in both plots) are counteracted by the downward curvature caused by non-ideality. In such cases a conventional extrapolation of M_w,app (or 1/M_w,app) versus c to c=0 is necessary. Non-ideality will also be apparent from the residuals of the best-fit c(M) model to the raw data, with the raw data showing less curvature than the best-fit model.

3. With broad molecular weight distributions there is still the risk that a proportion of the higher molecular weight material is lost from optical registration at the cell base. If such a problem is suspected then experiments performed at least two different equilibrium speeds should be used and compared. SEDFIT-MSTAR allows the comparison of profiles at different speeds. This comparison can either be conducted in sequential analyses, or a single self-consistent interpretation can be achieved in a global analysis of data at multiple rotor speeds. The success of a global analysis will depend on the localisation of the base of the solution column, which can be treated as an adjustable fitting parameter within reasonable limits. If the self-consistent multi-speed extension of SEDFIT- MSTAR is successful, as can be assessed by the root-mean-square deviations of the global versus the individual single fits, c(M) with higher resolution can potentially achieved. This approach was demonstrated previously for discrete, ideal protein mixtures in ref. 5, and we will further explore this strategy in the context of M* analysis of polymers in future work.

4. The procedure for taking an average of the final scans and subtracting an average of the initial scans, should be followed, and Ang & Rowe²⁶ for example provide a useful protocol for doing this.

5. In recently published work⁴¹ a complementary approach to sedimentation equilibrium analysis of polydisperse systems has been presented, with a focus on point average molecular weights at specific radial positions. The ‘MultiSig’ algorithm – based on a multi-exponential approach – (a) yields profiles of (reduced flotational) molecular weights (i.e. σ values) and returns all three of the principal averages (number-, weight- and z) to a good precision (b) yields profiles of c(σ) vs s - i.e. c(M) vs M if all components have a common partial specific volume – profiles which are shown by simulations using realistic error levels and by experiment to reflect the presence of multiple components or of continuous distributions. MultiSig does at the moment give a somewhat ‘coarse-grained’ (i.e. limited data pair sets) output over a modest range in σ, and is slow to run (~30 minutes for optimal resolution), but these limitations can readily be overcome by the use of greater compute power.

These two approaches (MultiSig and SEDFIT-MSTAR) are thus seen to be complementary: the latter being a specialised technique for characterising whole cell M_w values; the former for defining distributions and interactions, in a range of mono, oligo- and polydisperse systems. We are currently exploring the possibility of providing an easy interface between SEDFIT-MSTAR and MultiSig.

6. Combination with sedimentation velocity data. Sedimentation velocity in the analytical ultracentrifuge – performed in the same instrumentation as sedimentation equilibrium – has a greater resolving power of components, although yields primarily sedimentation coefficient and sedimentation coefficient distributions and to obtain molecular weight distributions of polydisperse systems requires assumptions/ knowledge of conformation or calibration using another technique. In an earlier paper³⁰ we described a procedure for obtaining the distribution of molecular weight for a polymer based on extension of an earlier method by Fujita for transforming a sedimentation coefficient distribution from Sedimentation velocity into a molecular weight distribution. The original Fujita method³⁰ had been based on the assumption that the polymers adopted a random coil conformation. The Extended Fujita method³⁶ covers molecular weight distributions of polymers for any conformation type including spheres and rods and conformations between the extremes of spheres, rods and coils. For its application, knowledge of the weight average sedimentation coefficient s_20,w for at least one value of the weight average molecular weight M_w is required for calibration. Obtaining the weight average s_20,w – and the distribution thereof - has been routine for over a decade now through regular application of SEDFIT to sedimentation velocity data¹⁶. It is now fair to say that estimation of M_w is also routine using the application of SEDFIT-MSTAR to sedimentation equilibrium data for polymer solutions of wide ranging polydispersities and non-idealities.