Calibrating MODIS aerosol optical depth for predicting daily PM_2.5 concentrations via statistical downscaling

Abstract

There has been a growing interest in the use of satellite-retrieved aerosol optical depth (AOD) to estimate ambient concentrations of PM_2.5 (particulate matter <2.5 μm in aerodynamic diameter). With their broad spatial coverage, satellite data can increase the spatial–temporal availability of air quality data beyond ground monitoring measurements and potentially improve exposure assessment for population-based health studies. This paper describes a statistical downscaling approach that brings together (1) recent advances in PM_2.5 land use regression models utilizing AOD and (2) statistical data fusion techniques for combining air quality data sets that have different spatial resolutions. Statistical downscaling assumes the associations between AOD and PM_2.5 concentrations to be spatially and temporally dependent and offers two key advantages. First, it enables us to use gridded AOD data to predict PM_2.5 concentrations at spatial point locations. Second, the unified hierarchical framework provides straightforward uncertainty quantification in the predicted PM_2.5 concentrations. The proposed methodology is applied to a data set of daily AOD values in southeastern United States during the period 2003–2005. Via cross-validation experiments, our model had an out-of-sample prediction R² of 0.78 and a root mean-squared error (RMSE) of 3.61 μg/m³ between observed and predicted daily PM_2.5 concentrations. This corresponds to a 10% decrease in RMSE compared with the same land use regression model without AOD as a predictor. Prediction performances of spatial–temporal interpolations to locations and on days without monitoring PM_2.5 measurements were also examined.

INTRODUCTION

Remotely sensed aerosol optical depth (AOD) is a satellite-retrieved parameter that measures light extinction due to airborne particles in the atmospheric column. AOD retrieved using visible and near IR wavelengths are particularly sensitive to fine particles. Previous studies have found positive associations between AOD and ambient concentration of PM_2.5 (particulate matter <2.5 μm in aerodynamic diameter) at different spatial and temporal scales.^1–7 PM_2.5 represents a complex mixture of solid and liquid particles that mainly arise from anthropogenic sources, such as vehicle emission and power generation. High levels of ambient PM_2.5 have been consistently associated with increased risks of various adverse health outcomes, including premature deaths,^8,9 emergency department visits, hospital admissions due to cardio-pulmonary diseases,^10,11 and adverse birth outcomes.^12,13

Population-based health studies routinely use measurements from ground monitoring stations to characterize short-term and long-term PM_2.5 exposures. However, these monitoring stations are spatially sparse, preferentially located in urban communities, and often without complete daily measurements. Reliance on central monitors not only restricts a study’s geographical region but can also lead to exposure measurement error due to unobserved spatial variations in pollutant concentrations. Consequently, there is a growing interest in supplementing monitor measurements with AOD data to increase the availability of air quality data across space and time. Epidemiological studies that involve geocoded health data can especially benefit from improved exposure assessment.¹⁴ AOD data are also useful for risk assessment on a global scale, particularly in regions where air pollution monitoring networks are not well established.^15–17 Several statistical models that utilize AOD data for predicting PM_2.5 concentrations have been proposed.^1–7 Previous approaches predominantly view AOD as a predictor of PM_2.5 concentration in a linear regression model that also includes meteorology and land use variables. The intercept and the slope coefficient between AOD and PM_2.5 are often assumed to exhibit spatial–temporal trends. For example, penalized cubic spline and thin-plate spline have been used to model, respectively, temporal trends,³ and spatial trends.⁵ Recently, studies have demonstrated that prediction performance for daily PM_2.5 concentrations improves when the regression coefficients are modeled as random effects that vary between days under a linear mixed model framework.^6,7

The main objective of this paper is to develop a new statistical model that utilizes AOD data for predicting daily spatially resolved PM_2.5 concentrations. We bring together recent advances in AOD land use regression models for PM_2.5 and statistical downscaling techniques to address several limitations associated with previous models. The proposed approach is applied to a data set of daily AOD values from the Moderate Resolution Imaging Spectro-radiometer (MODIS) over southeastern United States during the period 2003–2005. Given its high sampling frequency and relative high accuracy over land, MODIS is the major satellite instrument used in air quality studies that require daily to weekly temporal coverage.

The statistical downscaling methodology was first introduced for calibrating daily PM_2.5 and ozone concentration simulations from the Models-3/Community Multiscale Air Quality model (CMAQ).^18,19 It has also been applied to examine discrepancies between climate model outputs and observations.²⁰ Statistical downscaling treats the intercept and the slope between AOD and PM_2.5 as spatially and temporally correlated random effects under a hierarchical modeling framework. This overcomes the challenge of spatial misalignment between the point-referenced monitoring measurements and the gridded areal AOD data. Specifically, by modeling the intercepts and slopes as smooth spatial surfaces, one can predict PM_2.5 concentrations at any point location within a grid cell. Statistical downscaling is also less computationally demanding compared with other statistical approaches that directly model the unobserved PM_2.5 spatio-temporal fields.^21,22

The proposed model extends previous approaches and offers two important advantages. First, our model relaxes the normality assumption associated with independent random effects in a linear mixed model by allowing temporal dependence. This is motivated by the skewness in the estimated AOD random slopes reported by Kloog et al.⁶ Moreover, AOD data exhibit considerable missing values primarily due to cloud cover or high surface reflection caused by snow cover. By borrowing information across neighboring days, temporal dependence enables us to estimate random effects on days without AOD and monitoring observation pairs. Second, previous work often employs a multi-stage regression approach to handle the complex spatial–temporal model structure. Although a multi-stage approach is analytically straightforward, quantifying the uncertainties associated with the resulting predictions remains a challenge. It is well recognized that directly using predicted concentrations in epidemiological studies without considering the associated prediction uncertainties can lead to biased risk estimates and incorrect SEs.^23–26 Our modeling approach is carried out under a unified Bayesian hierarchical framework such that uncertainties in parameter estimation are fully accounted for. Most importantly, Bayesian inference allows uncertainty propagation in the form of prediction intervals and prediction SDs that can be readily used in health effect or health impact analyses.

MATERIALS AND METHODS

Data Collection

MODIS is an aerosol remote sensor launched aboard the National Aeronautics and Space Administration (NASA)’s Terra and Aqua satellites, providing nearly two measurements of AOD per day (at 1030 and 1330 hours local time). The operational MODIS “dark target” aerosol retrieval algorithm uses the consistent spectral relationships between two visible (0.47 and 0.65 μm) and one shortwave IR (2.1 μm) bands that separate aerosol signal from the land surface reflection. AOD is retrieved by minimizing the fitting errors between the observed aerosol reflectance and pre-computed theoretical values. Detailed description of MODIS “dark target” AOD retrieval and validation are provided elsewhere.^27,28

Collection 5 MODIS AOD data were obtained from the Earth Observing System Data Gateway at the Goddard Space Flight Center for the period 2003–2005. MODIS AOD pixels shift in space and pixel size can change as a function of scan angle. We used a nearest neighbor approach to spatially assign each daily MODIS AOD value to a base grid of 12 km × 12 km resolution in order to perform spatio-temporal predictions consistently over a common grid. We chose our base grid to be identical to the 12 km × 12 km CMAQ simulations that have been utilized in previous data fusion applications (http://www.epa.gov/esd/land-sci/lcb/lcb_faqsd.html). This will facilitate future studies that compare the use of AOD versus CMAQ simulations for predicting daily PM_2.5 concentrations.

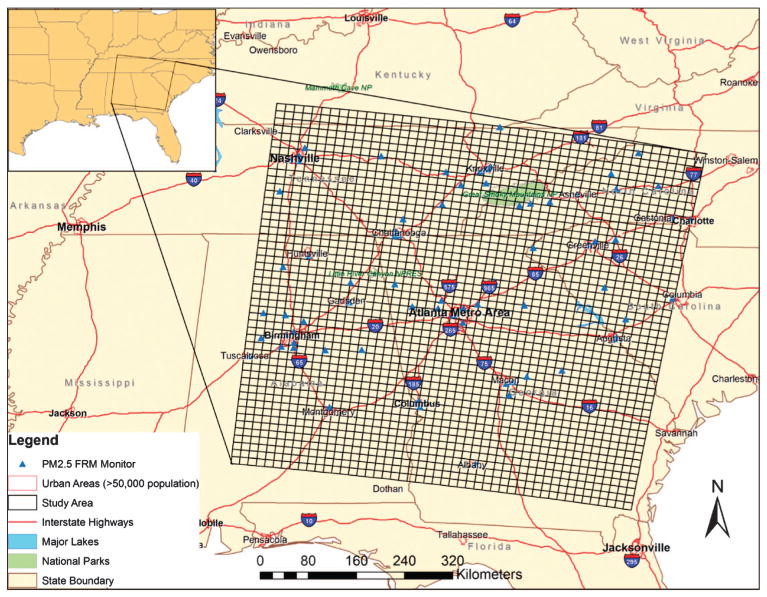
The study domain consisted of 2400 AOD grid cells and is shown in Figure 1. The following land use and meteorological variables were assembled for each MODIS grid cell: elevation (US Geological Survey, http://ned.usgs.gov), meteorology (North American Land Data Assimilation Systems, http://ldas.gsfc.nasa.gov/nldas/), major roadway length and percentage of forest cover (2001 National Land Cover database, http://www.epa.gov/mrlc/nlcd-2001), and PM_2.5 primary emission sources (2002 USEPA National Emissions Inventory Facility Emissions report, http://www.epa.gov/ttnchie1/net/2002inventory.html). Air quality measurements were obtained from 85 monitors in the USEPA Air Quality System (http://www.epa.gov/ttn/airs/airsaqs/). The monitors had three different sampling schemes: daily (13 monitors), every third day (56 monitors), and every sixth day (16 monitors).

Figure 1.

Southeastern US study area with remotely sensed aerosol optical density grid cells and the EPA PM_2.5 monitoring locations.

Spatial–temporal Statistical Downscaler

We linked AOD values and PM_2.5 concentrations in space and time by treating AOD as a predictor of PM_2.5 in a linear regression setting. Let PM(s,t) denote PM_2.5 concentration from an air quality ground monitor at location s and on day t. Here we treat s as a point-referenced geo-location. Each monitor was linked to an AOD measurement denoted by AOD(s,t) at the grid cell containing monitor s. The downscaler is given by the following statistical model:

$$PM(s,t)={\alpha }_0(s,t)+{\alpha }_1(s,t)\text{AOD}(s,t)+\epsilon (\mathrm{s},\mathrm{t})$$ (1)

where α₀(s,t) and α₁(s,t) are the intercept (additive bias) and slope (multiplicative bias) that are assumed to be location-specific and day-specific, respectively. The residual errors ε(s,t) are assumed to be independently normal with mean zero and variance σ². Model (1) can also be viewed as a statistical calibration of AOD data to observed monitoring measurements. We wish to model the additive and multiplicative biases with spatial and temporal dependence structures. This enables us to estimate α₀(s,t) and α₁(s,t) for calibrating AOD values at locations and on days without PM_2.5 monitoring measurements via spatial–temporal interpolation.

The spatial–temporal regression coefficients are specified by two second-level linear regression models given by

$${\alpha }_0(s,t)={\beta }_0(s)+{\beta }_0(t)+{\gamma }_0{Z}_0$$ (2)

$${\alpha }_1(s,t)={\beta }_1(s)+{\beta }_1(t)+{\gamma }_1{Z}_1$$ (3)

where β_i(s) and β_i(t) denote the unobserved correlated random effects that capture, respectively, the purely spatial and purely temporal trends in the intercepts (for i = 0) and the slopes (for i = 1). Parameter vectors γ₀ and γ₁ are fixed-effect regression coefficients associated with land use and meteorological variables Z₀ and Z₁, respectively. By substituting equations (2) and (3) into equation (1), vector γ₁ can be interpreted as the interaction effects between AOD and covariates Z₁ on PM_2.5 concentrations. Based on findings from previous studies and preliminary analyses, Z₀ included elevation, wind speed, average daily temperature, major roadway length, percentage of forest cover, and the presence of PM_2.5 source emissions; and Z₁ included elevation and average daily temperature.

The above model assumes linear relationships between PM(s,t) and the covariates. This assumption was examined and validated using partial regression plots. However, the above model formulation can easily accommodate non-linear relationships using parametric splines. Following Kloog et al.,⁶ we also examined whether random slopes are needed for the effects of temperature but found that it did not improve prediction performance, and none of the random effects for temperature were statistically significant. Logarithmic and square root transformation of the PM_2.5 concentration also did not improve prediction performance.

Spatial Random Effects Specification

Following Berrocal et al.,¹⁸ the spatial random effects’ equations (2) and (3) are correlated and have the form

$$\begin{array}{l}{\beta }_0(s)=c_1{W}_1(s)\\ {\beta }_1(s)=c_2{W}_1(s)+c_3{W}_2(s),\end{array}$$

where W₁(s) and W₂(s) are two spatially varying random effects with zero means and unit-variance; and c₁, c₂, and c₃ are unknown constants. We assume W₁(s) and W₂(s) to be independent but induce correlation between the intercept β₀(s) and slope β₁(s) through a common random effect W₁(s). Specifically, at a given location s, the strength of correlation between the intercept and slope depends on the constant c₂, and independence is achieved if c₂ = 0. Constants c₁ and c₃ control the variability in the spatial random effects.

In our analysis, we assumed W₁(s) and W₂(s) to have a tapered exponential covariance structure, and the strength of spatial dependence depends only on the distance between two locations.²⁹ Let d(s, s′) denote the Euclidean distance between location s and s′. The covariance between W_i(s) and W_i(s′) i = 1,2 is given by an exponential function multiplied by a tapering function:

$$\mathit{Cov}[W_i(s),W_i(s^{\prime })]=exp\{-d(s,s^{\prime })/{\theta }_i\}\times T\{d(s,s^{\prime });{\delta }_i\}.$$

Parameter θ_i controls the rate of exponential decay in correlation, and T{d(s, s′); δ_i } is the Wendland tapering function that forces the spatial correlation between two locations to be zero beyond a threshold distance δ_i.³⁰ Tapered covariance provides significant computational advantage for large spatial data sets, because one can utilize sparse matrix algorithms. In our application, tapered covariance is especially useful for predicting PM(s,t) at a large number of spatial locations simultaneously. The Bayesian spatial kriging process involves inverting a high-dimensional covariance matrix for a large number of iterations. In our analysis, we chose the threshold distance δ₁ = 100 km and δ₂ = 250 km based on an initial analysis using exponential covariance functions without tapering (δ_i = ∞). We then set δ_i to be the approximate distance such that correlations fall <0.01. Fixed effect estimates and spatial random effects were nearly identical between the models fitted with and without tapering.

Temporal Random Effects Specification

The temporal random effects β₀(t) and β₁(t) in equations (2) and (3) are modeled as two independent daily time series using a first-order random walk. This model is often defined through the conditional distribution of a particular day given all other days. Let T be the total number of study days. The conditional distribution of β_i(t),i = 0,1 is normal with mean and variance given by

$$\begin{array}{l}E[{\beta }_i(t)]=\{\begin{array}{cc}{\rho }_i{\beta }_i(t+1)& t=1\\ {\rho }_i\{{\beta }_i(t-1)+{\beta }_i(t+1)\}/2& t=2,\dots ,T-1\\ {\rho }_i{\beta }_i(t-1)& t=T\end{array}\\ \mathit{Var}[{\beta }_i(t)]=\{\begin{array}{rr}\hfill {\tau }_i^2& \hfill t=1\hfill \\ \hfill {\tau }_i^2/2& \hfill t=2,\dots ,T-1\hfill \\ \hfill {\tau }_i^2& \hfill t=T\hfill \end{array}\end{array}$$

where ρ_i is an unknown constant between 0 and 1. Therefore the mean of each β_i(t) on each day is proportional to the average of its neighboring days, and the conditional variance ${\tau }_i^2$ controls the degree of smoothness.

Estimation and Prediction

Statistical inference was carried out under a Bayesian framework by assigning prior distributions to all unknown parameters. The variances of the prior distributions were chosen such that they should contribute negligibly to estimates given the large amount of data. Priors for γ₀ and γ₁ were assumed to be proportional to 1 with infinite variance (improper flat priors). Spatial range parameters log θ_i followed Gamma (5, 0.05) with mean 100 and variance 2000. Variance components σ₂, ${\tau }_1^2,{\tau }_2^2,c_1^2$, and $c_2^2$ followed Inverse-Gamma (0.001, 0.001). Parameter c₂ followed a normal distribution with mean zero and variance 1000². Finally, we discretized the priors of ρ_i to 1000 equally spaced points spanning [0, 1]. Estimation was carried out using Markov Chain Monte Carlo (MCMC) techniques that provide samples from the parameters’ conditional (posterior) distributions given the observed data. We generated 50,000 posterior samples and discarded the first 25,000 samples as pre-convergence burn-in. At each MCMC iteration, each parameter was sampled given the values of all other parameters. Details of the MCMC algorithm are provided in the Online Supplementary Materials. Metropolis–Hastings algorithm³¹ was used to obtain posterior samples of c₂ and θ_i. All other parameters had conditional distributions that are in closed form and were updated using the Gibbs sampler.³² All analyses were carried out in R version 2.15.0.³³ The proposed model cannot be fitted by existing packages for spatio-temporal models, and we developed analytic code that is available upon request from the authors.

Overall prediction performance was evaluated via cross-validation experiments. First, we divided the complete data set into 10 parts of equal sample size. Each part was then treated as a test data set while the other nine parts were used for model fitting. Predicted daily PM_2.5 concentrations were obtained using samples from the posterior predictive distributions of the model parameters. Specifically, for each kth sample of the model parameters, we calculated the corresponding ${\alpha }_0^{(k)}(s,t)$ and ${\alpha }_1^{(k)}(s,t)$ for each AOD(s,t) for location s and day t. A realization of PM(s,t) was then drawn from a normal distribution with mean given by equation (1) and variance σ^2,(k). The above algorithm provides a sample distribution of the predicted concentrations where point estimate and interval estimate (e.g., 95% quantile intervals) can be calculated. The following prediction statistics were examined by comparing the predicted PM_2.5 concentrations to the left-out observed PM_2.5 concentrations: root mean squared error (RMSE), mean absolute error (MAE), 90% posterior interval (PI) length and its empirical coverage probability, and linear coefficient of determination R² value.

We carried out two additional cross-validation experiments to examine the predictive performance: (1) on days without any AOD–PM_2.5 linked observation pair and (2) at locations without PM_2.5 monitors. This allows us to quantify the uncertainties in temporal and spatial extrapolation when the downscaler model is applied to the full AOD data set in practice. This also examines the advantages of spatial–temporal random effect models that borrow information across days and across monitoring locations. To evaluate temporal interpolation performance, 10 cross-validation test data sets were created by randomly dropping all observations for 100 days at each cross-validation iteration. To evaluate spatial interpolation performance, we left out all observations from a particular monitor at each cross-validation iteration and used the remaining monitors for model fitting and prediction.

RESULTS

The study included 85 PM_2.5 monitors linked to 77 unique AOD grid cells in our southeastern US spatial domain. Six grid cells contained more than one monitor. Approximately 11% of the study days had no AOD–PM_2.5 linked pairs. On days with at least one PM_2.5 measurements, the median number of monitor observations was 9 (25th quantile of 5, and 75th quantile of 22). The small number of observations per day was due to two factors. First, among AOD grid cells linked to a PM_2.5 monitor, about 43% of the daily AOD values were missing. Second, PM_2.5 monitoring measurements also contained missing values with a median of 16% (range: 1–90%) across monitors.

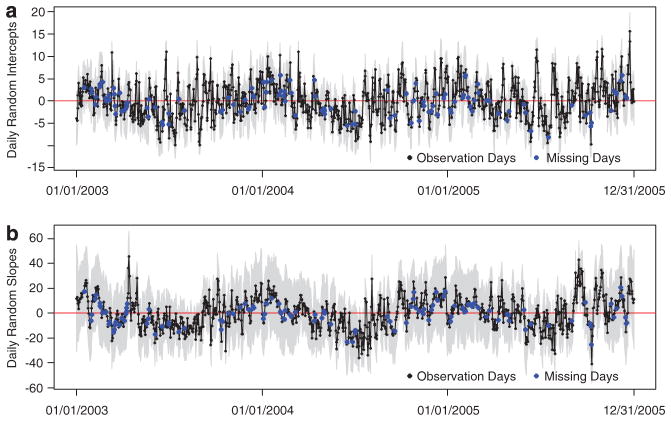
Figure 2 shows the estimated daily random effects β₀(t) and β₁(t) from equations (2) and (3) and 95% PIs are indicated by the grey areas. These parameters represent daily additive and multiplicative biases that are not explained by land use and meteorology variables. Daily random effects showed strong temporal dependence with a 1-day lag correlation of 0.75 for the intercepts and 0.84 for the slopes. Random effects for days without AOD–PM_2.5 linked measurements are indicated by the blue dots. By borrowing information across neighboring days, we obtained estimates that adhere to the temporal trends of days with PM_2.5 measurements. In a standard mixed model that assumes independent normal random effects, the estimated random effects on these days will be zeros with large uncertainties.

Figure 2.

Estimated residual temporal random intercepts β₀(t) (a) and slopes β₁(t) (b). 95% Posterior intervals (PI) are indicated by the grey areas. Days with and without AOD–monitor observation pairs are indicated by black and blue dots, respectively.

The estimated spatial random effects β₀(s) and β₁(s), as well as the SD, at each spatial location are given in the online Supplementary Materials. These parameters reflect long-term spatial residual additive and multiplicative biases. Both β₀(s) and β₁(s) exhibit moderate spatial dependence. In our study, the magnitudes of the residual spatial random effects are considerably smaller compared with the residual temporal random effects. We found greater positive residual bias in the intercepts over the Atlanta GA, Ashville NC, and Birmingham AL metropolitan areas, indicating that predictions based on only land use variables may underestimate long-term PM_2.5 levels in these regions. We also found evidence that the residual spatial variation in the AOD–PM_2.5 association was consistently higher in urban locations. Factors that can contribute to heterogeneous AOD–PM_2.5 associations warrant further investigation.

Table 1 gives the 10-fold cross-validation results comparing the prediction power of different spatial–temporal downscalers that included different combinations of AOD, meteorology, and land use variables as predictors. Overall, the full model and the model without land use variables performed the best, achieving the smallest RMSE and MAE. Predictions were also well calibrated with the 90% PI intervals, including the left-out observations 91% of the time. The overall R² value was 0.78, comparable to other studies.^3,6 Compared with the full model, the model without AOD had an 10% increase in RMSE and a larger PI length that indicates lower prediction precision. We found that daily meteorology variables are more useful than land use variables to improve prediction power. This may be attributed to our interest in predicting daily PM_2.5 concentrations. Moreover, the flexible spatial random effect specification allows monitor-specific intercepts and slopes that will capture the effect of land use when they are not included in the model. We also note that the inclusion of AOD as a predictor resulted the greatest increase in prediction performance when compared with the model without AOD. The AOD-only model also performed similarly to the full model. This may again be due to the use of flexible random effects that can explain spatial variability due to land use and temporal variability due to meteorology.

Table 1.

Results from 10-fold cross-validation experiment for predicting daily PM_2.5 concentrations using the spatial–temporal downscaler with different sets of predictors, including AOD, meteorology (Met), and land use (LU) variables.

Variables	RMSE	MAE	90% PI length	90% PI coverage	R2
Full	3.61	2.58	11.8	0.91	0.78
AOD + Met	3.61	2.58	11.8	0.91	0.78
AOD + LU	3.67	2.61	12.0	0.91	0.77
AOD only	3.67	2.61	11.9	0.91	0.77
Met + LU	4.03	2.89	13.2	0.91	0.72

Statistics for prediction performance include root mean squared error (RMSE), mean absolute error (MAE), 90% posterior interval (PI) length, 90% PI empirical coverage probability, and linear coefficient of determination (R²).

Table 2 summarizes the cross-validation results for predicting PM_2.5 concentrations on days without AOD–PM_2.5 linked pairs or at locations without PM_2.5 monitors. To evaluate the potential advantages of modeling spatial and temporal dependence, we compared our model with those with the random effects assumed to be independent normal. As expected, we observed overall poorer prediction performance compared with those given in Table 1 as the prediction involved interpolation of the random effects across space and time. Our results also highlight the advantage of capturing residual temporal correlation in the random intercepts and slopes. Compared with a standard mixed model framework, the temporal dependence reduced RMSE by 23% and the 95% PI length by 22%. We also found very minor improvement in prediction performance associated with the inclusion of spatial random effects. This may be due to the use of a large number of spatially varying land use covariates.

Table 2.

Cross-validation experiment results for predicting PM_2.5 concentrations on days without AOD monitor observation pairs or at locations without PM_2.5 monitors.

Variables	RMSE	MAE	90% PI length	90% PI coverage	R2
On days without AOD–PM2.5 observation pairs
Temporal	4.43	3.34	16.2	0.94	0.66
Independent	5.45	4.18	19.9	0.95	0.48
At locations without PM2.5 monitors
Spatial	3.75	2.69	12.2	0.91	0.79
Independent	3.81	2.72	12.3	0.91	0.79

The spatial–temporal downscaler model is compared with that assuming independent normal random effects. Statistics for prediction performance include root mean squared error (RMSE), mean absolute error (MAE), 90% posterior interval (PI) length, 90% PI empirical coverage probability, and linear coefficient of determination (R²).

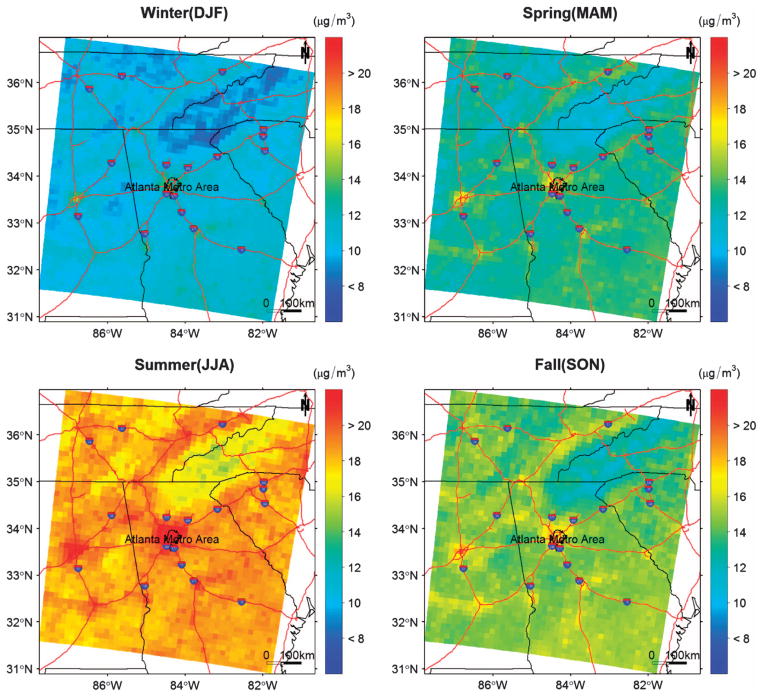
Figure 3 shows the predicted annual average PM_2.5 concentrations and their prediction SEs estimated at the center of each AOD grid cell. Annual levels were calculated by averaging predicted daily PM_2.5 concentrations when AOD observations were available. Similar spatial patterns are also evident for average PM_2.5 concentrations by seasons (Figure 4). The above analyses assume that AOD values were missing completely at random. However, because missing AOD values were mainly due to cloud cover in our study region, this assumption may be violated if days with missing AOD values were associated with higher or lower PM_2.5 levels, possibly due to differences in meteorology. To address this issue, we also estimated long-term averages by filling in days without AOD observations with PM_2.5 concentration predictions obtained from a statistical downscaler without AOD as a covariate. The resulting annual and seasonal maps show similar spatial patterns and are included in the online Supplementary Materials.

Figure 3.

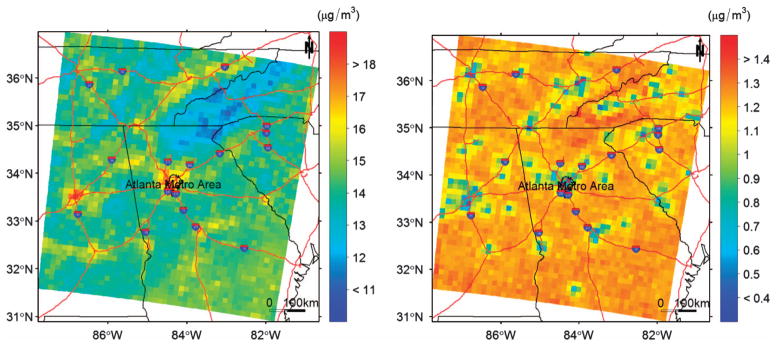
Predicted annual average PM_2.5 concentrations (left panel) at AOD grid cell centers and their prediction SEs (right panel).

Figure 4.

Predicted seasonal average PM_2.5 concentrations at AOD grid cell centers.

We found the highest level of long-term PM_2.5 concentrations in the urban centers, as well as higher levels, along major interstate highways. Lower levels of PM_2.5 appeared over the Appalachian mountain range. Seasonally, summer showed the highest concentrations and winter the lowest following the temperature dependence of secondary fine particle production. The elevated PM_2.5 levels in southern Georgia could be attributed to prescribed burns in southern Georgia and Florida in the spring, as well as transport of polluted air mass from coastal regions of the Gulf of Mexico and Florida. Limited by the size of our modeling domain, we were not able to more explicitly examine any potential transport pathways from south and southwest of the domain. As expected, lower prediction uncertainties were associated at locations with monitoring stations. Interpolating annual PM_2.5 averages concentrations at locations without monitoring stations is associated with an approximately three-fold increase in prediction SE.

DISCUSSION

We describe a Bayesian spatial–temporal hierarchical model that combines previous data fusion work for calibrating numerical model outputs and satellite-retrieved data. The main advantage of the proposed downscaler is the ability to quantify prediction uncertainty in a unified framework and to fully exploit spatial–temporal dependence in the daily AOD and PM_2.5 concentration associations. Through out-of-sample cross-validation experiments, our results highlight the utility of supplementing land use regression model with AOD data in our study region of southeastern US. Similar to the findings by Kloog et al.,⁶ we also found that effort in modeling temporal random effects provides more significant improvement in prediction power compared with modeling spatial random effects. Our results do not suggest excluding land use variables in the model, because they are important for predicting PM_2.5 concentrations at locations without monitors.

Several complex spatio-temporal calibration models have been developed for estimating daily PM_2.5 concentrations using AOD values; however, there has been limited work in examining calibration precision in terms of prediction SEs. The Bayesian inference provides simulations (realizations) from the predictive distribution that incorporate uncertainties arising from (1) model parameter estimation, (2) spatio-temporal residual errors, and (3) unstructured residual errors. More importantly, exposure simulations allow us to propagate prediction uncertainties in subsequent health effect and health impact analysis. For example, one can perform a Monte Carlo sensitivity analysis by repeatedly fitting the health model with different realizations of the predicted daily PM_2.5 concentration fields.¹³ The resulting risk estimates can then be combined under a multiple imputation framework. Alternatively, the realizations can be used as previous information of PM_2.5 exposure in a second-stage Bayesian analysis.^34,35 Finally, uncertainty quantification is accomplished via posterior simulations of point-referenced daily PM_2.5 concentrations. Therefore uncertainties associated with metrics of different spatial or temporal aggregation can be easily obtained by transforming the original exposure samples.

There are additional challenges in calibrating AOD data that our model does not address and warrant further investigation. First, AOD data contain a large number of missing values where PM_2.5 predications cannot be obtained. It is straightforward to adopt the statistical downscaler to incorporate recent approaches for the missing data problem. For example, Liu et al.⁵ consider predicting PM_2.5 concentrations with a non-AOD model using only land use and meteorology. Our results from Table 1 indicate that predictions from a non-AOD downscaler still achieve an R² of 0.7, and the model is well calibrated in terms of posterior prediction intervals. Also, Kloog et al.⁶ and Kumar et al.³⁶ describe a multiple-stage approach where the statistical downscaler can first be fitted to obtain calibrated AOD values in the first stage. The predictions and their uncertainties can then be used in a second spatial–temporal model for predicting PM_2.5 concentrations. We also did not consider interactions between the spatial and temporal random effects. This is due to our study region and the small number of same-day AOD–PM_2.5 observation pairs. Although previous studies have found the benefits of space–time interaction to be limited,^5,18 these interactions should be carefully examined for larger spatial study domain.

CONCLUSION

This study demonstrated that the publicly available satellite-retrieved AOD data can be considered as an additional covariate in land use and meteorological regression model for predicting daily PM_2.5 concentrations. Prediction performance can also be improved by incorporating spatial–temporal regression coefficients, especially for performing interpolations on days and at locations without linked AOD values and monitoring measurements. When predicted ambient concentrations are used for exposure assessment, quantitative evaluation of prediction uncertainties, for example, using prediction SEs, should be considered to ensure the accuracy, reliability, and reproducibility of health study results.