Protein Folding and Unfolding Under Force

Abstract

The recent revolution in optics and instrumentation has enabled the study of protein folding using extremely low mechanical forces as the denaturant. This exciting development has led to the observation of the protein folding process at single molecule resolution and its response to mechanical force. Here, we describe the principles and experimental details of force spectroscopy on proteins, with a focus on the optical tweezers instrument. Several recent results will be discussed to highlight the importance of this technique in addressing a variety of questions in the protein folding field.

Introduction

Mechanical processes are involved in nearly every facet of the cell cycle. Cellular functions such as chromosomal segregation, transcription, translation, protein and nucleic acid folding and unfolding, and cell locomotion all involve mechanical forces.^1,2 Recent technological advancements have enabled the mechanical manipulation of single molecules, which allow real-time observation of these biological processes at high resolution.^3,4 This article attempts to review the role of single molecule force spectroscopy in further understanding the process of protein folding and unfolding.

Proteins undergo a remarkable transformation from one-dimensional amino acid sequences into complex three-dimensional structures that carry out diverse cellular functions. Protein unfolding and refolding are fundamental biological events, yet they remain incompletely understood. Detailed characterization of the mechanisms of protein folding has relied heavily on traditional ensemble approaches in which the native (folded) state of the protein is perturbed by adding chemical denaturants such as urea, or by changing the temperature of the sample.⁵ The kinetic and thermodynamic parameters obtained from these experiments are subsequently used to map the energy landscape of protein folding.

The advent of single molecule force spectroscopy has enabled the application of mechanical force (typically in the piconewton range) to unfold single protein molecules. This exciting development has opened the door for characterizing the energy landscape of protein folding and its response to mechanical stress, a biologically important perturbant.^6-9 Single molecule techniques also have the advantage of being able to resolve rare events or intermediate states that are typically masked in traditional ensemble experiments. Thus, force spectroscopy experiments allow protein folding/unfolding to be studied from a completely different perspective compared to traditional chemical denaturation-based ensemble approaches.

In this review, we focus on the use of optical tweezers to study protein folding/unfolding at a single molecule level. We first discuss the experimental design of the optical tweezers, and the information that can be obtained from such experiments, and then describe several recent studies to illustrate the value of these approaches to understanding protein folding.

The Effect of Force on the Free Energy Landscape of Protein Folding

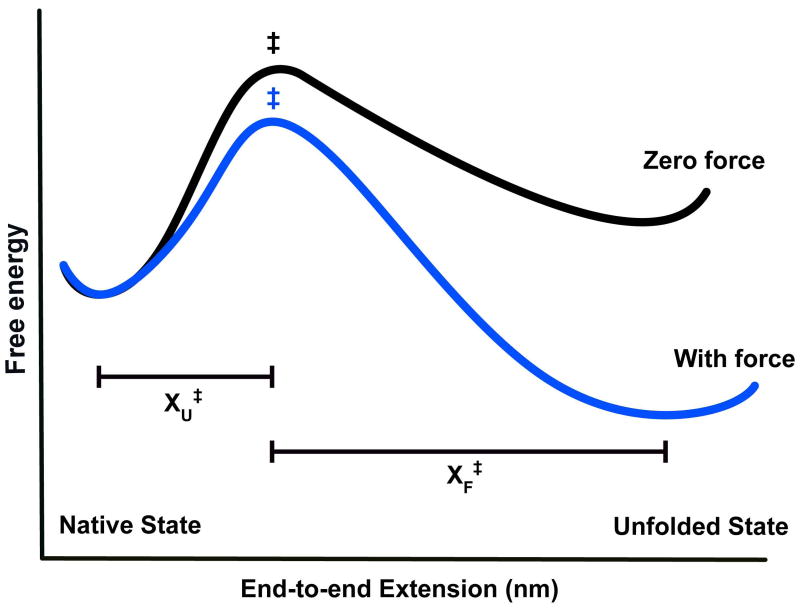
The effect of force on the free energy landscape is easiest to describe for the case of a simple two-state system where the protein exists in either the native, folded state or the unfolded state (Figure 1). The two states are separated along the reaction coordinate by a high free-energy energy barrier, the transition state (‡). Mechanical unfolding experiments have an advantage of providing a well-defined reaction coordinate, namely the end-to-end extension (ΔX) between the two pulling points of the protein molecule.^1,10

Figure 1.

The effect of force on the free energy landscape of a two-state system. In the absence of force (black curve), the native state is lower in free energy and the protein is predominantly folded. The application of force (blue curve) lowers the free energy of the transition state (‡) and the unfolded state relative to the native state. The force-dependent change in folding and unfolding rates scales with the distance to the transition state (X_F^‡ and X_U^‡, respectively).

Under zero-force conditions, the native state has a lower free energy than the unfolded state, and hence the protein is predominantly folded. The application of force ‘tilts’ the free energy surface along the mechanical reaction coordinate, thereby lowering the free energies of both the transition state and the unfolded state relative to the native state (Figure 1). As the force increases, the unfolded state becomes more energetically favorable and is preferentially populated by the protein.

The simplest model that describes how an applied force will affect the rate constant of protein folding/unfolding is a linear free energy relationship, such as that given by Bell¹¹,

$$k(\mathrm{F})=k_m{k}_{0}exp(\mathrm{F}{\mathrm{X}}^{‡}/{\mathrm{k}}_{\mathrm{B}}\mathrm{T})$$ (1)

where k(F) is the rate constant under force, k_m includes the contributions of the components of the experimental system to the observed rates, k₀ is the intrinsic rate constant in the absence of force, F is the applied force, X^‡ is the distance to the transition state, k_B is the Boltzmann constant, and T is the absolute temperature. When the force dependence of the observed rate constants is fit to the linear Bell model, the slope of the plot yields the distance to the transition state (X_U^‡ and X_F^‡, respectively for unfolding and folding). The distances reflect the placement of the free energy barrier along the mechanical reaction coordinate, the end-to-end extension. For a two-state system, the sum of the distances to the folding and unfolding transition state equals the total extension change of the molecule.¹²

Instrumentation

There are two primary experimental approaches to single-molecule force spectroscopy studies on proteins: atomic force microscopy (AFM) and optical tweezers (Figure 2).¹³ In both of these experiments, a protein molecule is tethered between a probe (e.g. an AFM cantilever tip or a micron-sized bead) and another surface. The probe is manipulated to apply force to the protein under study. It reports on both the force applied to the protein molecule and the overall end-to-end extension of the system, allowing real-time monitoring of the conformation of the molecule. While the ability to directly monitor a protein's conformational state is valuable in its own right, these studies also allow for characterization of the ways in which force itself alters the kinetics and thermodynamics of protein folding transitions.

Figure 2.

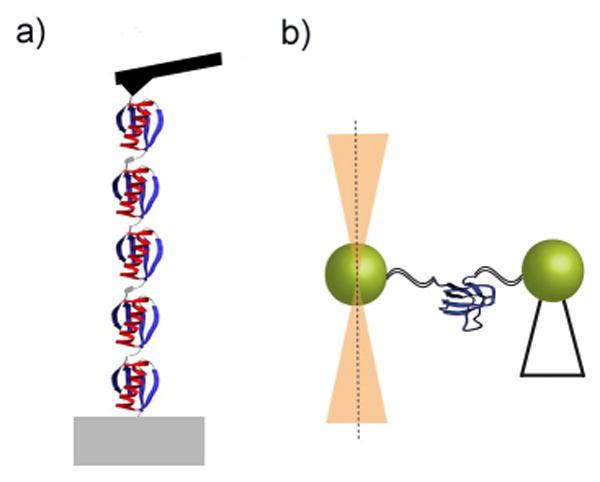
Schematic representation of (a) an atomic force microscopy setup, and (b) single-trap optical tweezers where one of the beads is held by suction on a pipette tip.

To date, most force spectroscopy studies have been performed with the use of AFM,^14-18 but optical tweezers have recently emerged as a new, complementary addition to the field. While AFM studies work by holding the protein chain between a cover slip surface and an AFM cantilever ¹⁹, optical tweezers use a laser trap to manipulate a pair of micron-sized polystyrene beads that are tethered to the protein with functionalized, double-stranded DNA segments.^20,21 Aside from the differences in the method of force application, the primary qualitative difference between data collected with AFM vs. optical tweezers is due to the spring constants of the two systems.¹³ Optical traps and AFM cantilevers have very different spring constants, on the order of 0.1 pN/nm versus 10 pN/nm, respectively. This difference alters both the accessible force ranges of the experiments and the force and position resolution of the probes. Softer springs, like those of optical traps, have greater force resolution and can access lower force regimes. The lower spring constant simplifies the study of low-force protein folding transitions, though this improvement is at the expense of losing resolution in the measured extension changes of these events.

Experimental Design

Optical Trap Instrumentation

Optical traps, or tweezers, were first developed by Arthur Ashkin when he demonstrated that a focused laser could be used to trap and manipulate micron-sized or smaller objects.²² The force is calculated based on the deflection of the laser beam when the trapped object moves from the center of the trap. For small displacements, the optical trap acts as a Hookean spring and the force is a product of the spring constant of the trap and the displacement from the center of the trap.

To create a laser trap that can measure force and extension, three components are needed: a laser, optics, and a detector. The laser produces the light used to make the trap, and the optical components focus the laser beam and allow for the manipulation and movement of the trap. Typically, the trap is created with two counterpropagating, confocal laser beams of equal intensity.²¹ The detector measures the deflection in the trapping beam, which scales linearly with the force exerted on the trapped bead.

There are two primary classes of optical tweezers designs: a dual-beam, single-trap optical tweezers with one bead held in the trap and the other on a glass pipette (Figure 2); and a dual-trap optical tweezers consisting of two single-beam traps, each holding a single bead.^13,20 Most studies described later in this review have used the single-trap configuration to mechanically manipulate single protein molecules.

Sample Preparation

In most of the protein folding studies using optical tweezers, the protein molecules are tethered between two micron-sized polystyrene beads using double-stranded DNA handles (Figure 3). One of the beads is held in an optical trap, and the other bead is held by suction on a pipette tip. The DNA handles act as spacers to isolate the protein from nonspecific interactions, and also allow for free choice of the points at which tension is applied across the protein.^23,24 Force is applied by manipulating the bead focused in the optical trap, while the bead held by suction remains stationary.

Figure 3.

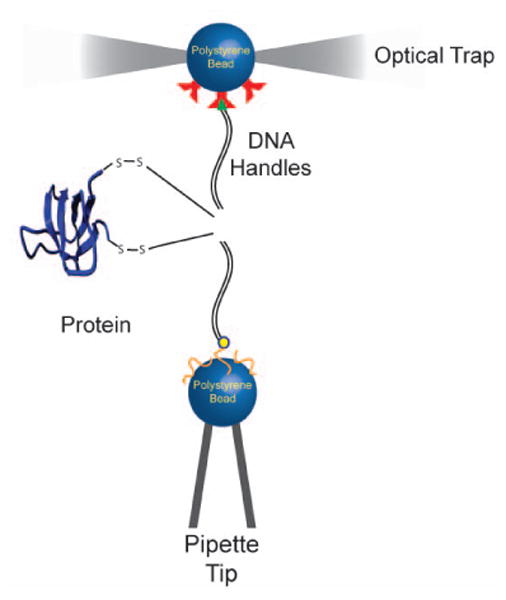
Schematic representation of the experimental setup used to apply force on single protein molecules with single-trap optical tweezers. Double stranded DNA molecules are linked to specific cysteine residues on the protein via disulfide bonds, and act as handles to apply force on the protein.

In these experiments, the beads are coated with attachment proteins such as antibodies or streptavidin/neutravidin domains. The DNA handles are synthesized via PCR with the complementary binding moieties at one of their termini, while the other terminus has a thiol group for attachment to the protein.^7,23 The protein sample has two unique solvent-exposed cysteine residues that define the pulling axis. The DNA handles are attached to the protein of interest via disulfide bonds. This technique offers precise control over the points of force application within a protein. During the experiment, the DNA-protein-DNA sample is incubated with one of the beads. In the tweezers chamber, this bead is held with the optical trap and brought close to the other complementary bead that is held on a pipette tip. Once a DNA-protein-DNA tether is formed between the two beads, force is applied on the protein molecule by manipulating the optical trap.

Types of Experiments: Force Control Modes

Force-ramp Experiments

In an optical tweezers force-ramp experiment, the two beads are moved apart and back together in alternating cycles, typically at a constant pulling speed (i.e. constant change in trap position with time). Doing so increases and decreases the force on the tethered molecule at approximately constant rates. By cycling between high and low forces, the experimentalist alternates between favoring the unfolded and folded states of the protein molecule. The resulting trajectories appear as smooth force-extension curves, with interruptions at unfolding/refolding events that show up as sawtooth-shaped “rips” (Figure 4a).

Figure 4.

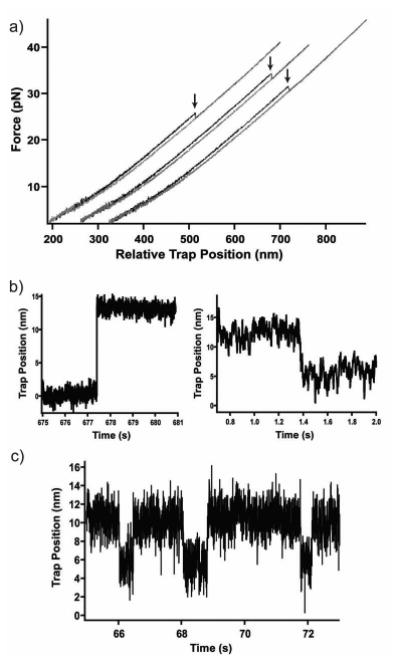
Typical traces obtained in (a) force-ramp experiments where unfolding events are observed as ‘rips’ (indicated by arrows), (b) force-jump experiments where protein unfolding (left) and refolding (right) are monitored after jumping to a set force that favors the transition, (c) constant-force experiments in which the protein ‘hops’ between two conformational states at a given force.

Repeating the force-ramp protocol multiple times yields a distribution of forces at which the unfolding and refolding events occur. This distribution is a result of the stochastic nature of single-molecule kinetics, because unfolding and folding are thermally driven events and will not necessarily occur at exactly the same time during each successive force-ramp cycle. The average unfolding force obtained from force-ramp experiments is a measure of the mechanical stability of the protein at a given pulling speed. For most experiments probing protein conformational changes, these experiments are not at equilibrium. Non-equilibrium analyses such as the Crooks fluctuation theorem (CFT) can be applied to the work distributions of the unfolding and refolding events to estimate the equilibrium free energies involved in the transitions.^25,26 Recent theoretical advances have also enabled the extraction of kinetic parameters (k₀, X^‡, and the height of the free energy barrier, ΔG^‡) from force-ramp experiments.^27,28

Constant-force Experiments

There are two principal methods to sustain a constant force on a system. The first requires an active feedback that adjusts the position of the trap to maintain a constant force on the system above the timescale of the feedback.²⁹ An alternative passive approach positions the bead in an optical trap where the potential of the trap is anharmonic and the force is constant over small displacements. ³⁰ As the force is constant, the position of the trap or the bead must be monitored in order to determine the state of the molecule.

With the force-feedback, two types of constant-force experiments are typically performed. In the first, a force-jump experiment, the force on the system is jumped to a new force where the protein is likely to fold or unfold during the observation period. The system is held at that force until the molecule unfolds or folds (Figure 4b). Typically, the lifetime of the molecule at this new force is much greater than the time constant for the force feedback and hence the system can be considered at constant force. From these data, a lifetime (and hence the rate) of the transition can be measured at the force of the jump.¹² This experiment can be repeated to obtain the average unfolding (and refolding) rates at different set forces. The force-dependence of the rates provides valuable information about the underlying potential energy surface.

Conversely, a molecule maybe meta-stable at a given force and, depending on the rates, may fold and unfold many times when held at a single force (Figure 4c). Such a rapidly interconverting system will show little hysteresis in a force-ramp experiment. As the molecule ‘hops’ between the different conformations, many transitions are observed and the lifetimes for each state as a function of force can be determined. For this experiment to be truly constant force, the lifetimes of each state must be much greater than the force-feedback time.²⁹

Constant-trap position Experiments

The last mode of force control is similar to a constant-force experiment, in that the molecule can be held in an equilibrium regime where transitions between different conformational states can be observed. In this experiment, however, the trap position is held constant, applying a constant potential to the system. When the molecule transitions to another conformational state with a different end-to-end extension, the average force changes. Lifetimes of each state are measured as a function of the average force and used to extract information about the potential energy surface of the system. A sophisticated deconvolution method recently resolved the full energy landscape of the GCN4 leucine zipper using data obtained from constant-trap position experiments.³¹ This method allows an estimation of both barrier heights and pre-exponential terms, and is sensitive to all the features in the energy landscape, not just the rate-limiting barrier.

A combination of the above-mentioned types of optical tweezers experiments provides valuable insight on a protein's free energy landscape. Next, we describe a few studies that highlight the strength of force spectroscopy in addressing a wide range of questions in the protein folding field.

The Role of Intermediates in the Folding Pathway of E. coli RNase H

Single molecule optical tweezers force spectroscopy provided the first direct observation of the entire folding process of E. coli RNase H and yielded previously unobtainable information about the role and nature of an early intermediate.⁷ Intermediates that form rapidly in the folding of many proteins, so-called ‘burst phase’ intermediates have been difficult to study in bulk due to the inherent ensemble averaging of these potentially heterogeneous processes, and because they form faster than the millisecond time scale – faster than the measurement dead time of most stopped-flow instruments. These intermediates are thought to be molten globules, which are compact and contain some secondary structure but lack significant specific tertiary interactions.^32,33 Ensemble studies on E. coli RNase H revealed a burst phase intermediate that accumulates during the folding process, and provides an excellent model to address questions about the role and nature of such intermediates.^34-36 In particular, if this burst phase intermediate is a distinct thermodynamic state with a transition barrier separating the intermediate state from the unfolded state or if the burst phase is only a redistribution of the unfolded state ensemble induced by the change to native folding conditions. In addition, questions remained about whether the intermediate is on-pathway or off-pathway and if RNase H's folding mechanism is hierarchical or can proceed through multiple distinct, parallel pathways.

When pulled from the termini, force-ramp experiments identified that the protein forms a partially folded intermediate state before refolding to the native state (Figure 5a). The extension change of this state was consistent with the model of the intermediate obtained from ensemble studies. To further investigate the refolding behavior, the molecule was first unfolded and then dropped to a lower force, allowing the protein to refold. Under constant-force feedback, the intermediate folded and unfolded many times before finally folding to the native state (Figure 5b). Importantly, the native state was observed to form directly from the intermediate, demonstrating an on-pathway obligatory state. This constant-force ‘hopping’ between the unfolded and intermediate state showed first-order behavior indicating an energetic barrier and proved that the intermediate and unfolded conformations are distinct thermodynamic states.⁷

Figure 5.

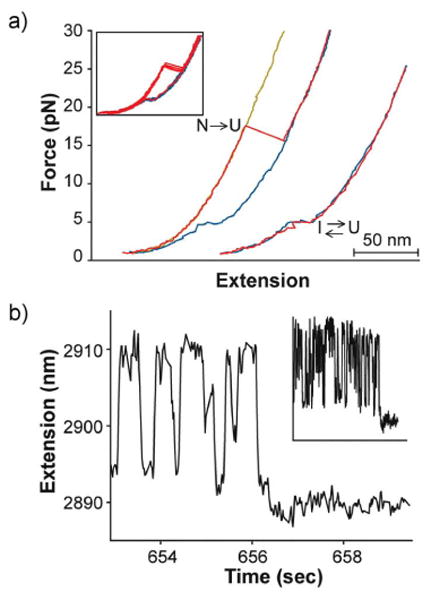
(a) Stretching (red) and relaxation (blue) force extension curves from RNase H identified the presence of a partially folded intermediate state. (b) Constant-force experiments revealed that the protein ‘hops’ between the unfolded and the intermediate states before folding to the native state, inset shows a longer time trace.

To better compare the intermediate observed under force with that obtained in ensemble experiments, the single site variant I53D of RNase H was studied. In ensemble studies, this mutation destabilizes the intermediate resulting in a two-state folding mechanism.³⁷ Characterizing this variant on the optical tweezers revealed a similar behavior with no intermediate detected during the refolding of RNase H, suggesting that the mechanical intermediate is similar to the folding intermediate observed in ensemble denaturant induced refolding studies.

The constant force feedback experiments also revealed that the folding intermediate had an unusually large distance to the transition state, in sharp contrast to the short distance to the transition state measured for natively folded proteins. This raised the question of whether this is a general property for molten globule-like intermediates, or if it is specific to the RNase H intermediate under force. The mechanical properties of a molten globule state were further characterized using sperm whale apomyoglobin as the model system.

The Mechanical Properties of a Molten Globule State

Like RNase H, the folding of sperm whale apomyoglobin has been extensively characterized in ensemble experiments.^38,39 The protein folds in a three-state manner and populates a folding intermediate similar to E. coli RNase H. Apomyoglobin populates this intermediate, molten globule state both at equilibrium (under acidic conditions), and transiently during folding to the native state at neutral pH. The single site variant H36Q populates the equilibrium molten globule under mildly acidic conditions (pH 5.0), and transiently during folding at pH 7.0;^38,39 conditions that are compatible with the optical tweezers experimental approach and thus provided a unique opportunity to study the mechanical properties of the molten globule state under both conditions.

At neutral pH, force-ramp experiments on apomyoglobin (pulled from the N- and C-termini) revealed a bimodal unfolding distribution with peaks centered at 12.5 pN and 6.1 pN.⁴⁰ The population of the low-force unfolding peak depends on the pulling speed and dwell-time at low force. The low-force peak disappeared when the protein was given more time to refold. These results suggest that, as expected, the protein folds in a three-state process; the low-force peak (∼ 6.1 pN) represents unfolding from the intermediate and the high force peak (12.5 pN) represent unfolding from the native state and the longer dwell time allows the protein to refold from the intermediate to the native state. Similar to RNase H, these data mirror the denaturant induced ensemble refolding experiments where the protein populates a molten globule intermediate.

At pH 5, where the protein adopts the equilibrium molten globule state, unfolding and refolding events (I↔U) are cooperative and reversible, with both force distributions centered at 4.5 pN (Figure 6a). Constant-trap position experiments yielded a distance to the transition state from the molten globule state, X_U^‡ = 6.1 nm (Figure 6b). Similar behavior was seen when the protein was pulled from different attachment points (residue 53 and the C-termini), and a distance X_U^‡ = 3.4 nm was obtained.⁴⁰ These distances were both much larger than those observed for unfolding the native state or for other natively folded proteins (typically around 1 nm).⁴¹ Further, these distances were similar to those suggested by the studies of the intermediate of E. coli RNase H,⁷ indicating that this large distance could be a general property of the molten globule state and independent of the direction of the applied force.

Figure 6.

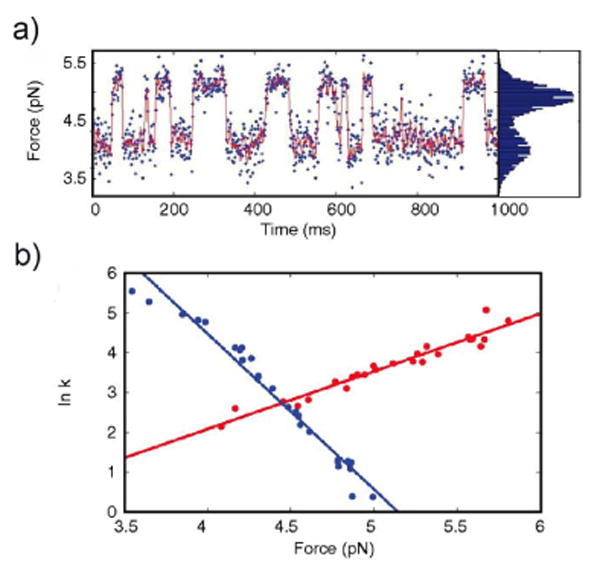
(a) Typical trace obtained from constant-trap position experiments on apomyoglobin during which the protein molecule spontaneously folds and unfolds. (b) The force-dependence of the folding (blue) and unfolding (red) rates obtained from these experiments were fit to the Bell model to estimate the distances to the transition state.

This relatively large distance to the transition state, or compliance, has two important consequences. First, it implies that the molten globule state can undergo large fluctuations (end-to-end extension changes) without committing to cross the unfolding barrier. This ability to deform is likely to play an important functional role, such as in the incorporation of heme in the case of apomyoglobin.⁴² Second, the large distance to the transition state indicates that the unfolding rates for molten globules are more sensitive to force (the change in unfolding rate per unit force is greater (k ∝ exp(FX^‡)/k_BT)), than the unfolding rates of native proteins. Thus, in the cell, the application of small amounts of force by other proteins and molecular machines will have a more dramatic effect on the probability of unfolding molten globules than natively folded proteins.

Interdomain Cooperativity in T4 Lysozyme

Many proteins have been observed to fold in an apparent cooperative manner. Understanding how different parts of the structure interact and are energetically coupled has been a long-standing question in the protein folding field and is still poorly understood. Using T4 lysozyme, different chain topologies were characterized under mechanical force.⁴³ Applying force selectively to different regions of the protein provided novel insight into the interactions between the different subdomains of the protein.

T4 lysozyme is a globular protein with two subdomains that appears to fold cooperatively at equilibrium.⁴⁴ That is, the chemically induced denaturation profile can be fit with a two state model. The subdomains are linked by the N- terminal A-helix that is structurally part of the C-terminal domain. A circular permutant of T4 lysozyme (CP13) was constructed, in which the A-helix is attached to the C-terminus, thereby creating a new N-terminus at residue 13 (Figure 7a). This topological variant selectively alters the physical connectivity of the polypeptide chain, leaving all of the native interactions intact.^45,46

Figure 7.

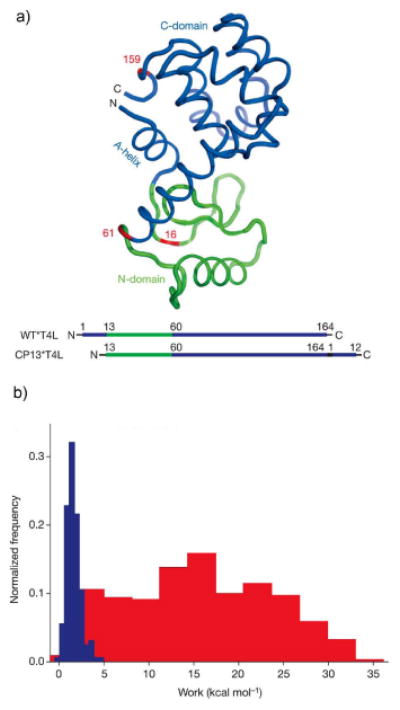
(a) Three-dimensional structure and schematic of T4 lysozyme showing the energetically coupled N- and C-domains (green and blue respectively). (b) Typical unfolding (red) and refolding (blue) work distributions used to estimate the equilibrium free energies by applying the Crooks fluctuation theorem.

Using force-ramp experiments, pulling on the wild-type protein across both domains (from positions 16 and 159), the protein appeared to unfold in a single cooperative event, whereas pulling from the same positions in CP13 resulted in unfolding via two consecutive unfolding events. The unfolding was then investigated by pulling across the N-terminal domain (positions 16 and 61) in both the wild type and circularly permuted topologies. The average force of unfolding in the wild-type protein was significantly higher than that of the circular permutant. Because the unfolding rips can only report on the extension change (unfolding) of the regions between the two pulling points, the state of the C-terminal domain, and hence cooperativity, was not clear.

The energetic coupling between the subdomains of T4 lysozyme when pulled from the N-terminal domain was further examined by applying the Crooks fluctuation theorem (CFT) on the work distributions of the unfolding and refolding events obtained from force ramp experiments (Figure 7b).^25,43 This analysis can be used to extract the equilibrium free energies from non-equilibrium mechanical unfolding transitions. Application of the CFT in the wild-type protein (residues 16 and 61) yields an unfolding free energy, ΔG = 12.3 kcal/mol. This value agrees well with ensemble equilibrium denaturation experiments that act globally to perturb the entire protein,⁴⁶ indicating a high degree of energetic coupling between the two domains. However, the CFT analysis on the force ramp experiments on CP13 yielded an unfolding free energy, ΔG = 3.6 kcal/mol, much less than that of global unfolding and in agreement with the energy required to unfold only the N-domain.

The circular permutation decouples the two domains and transforms a mechanically cooperative system into a non-cooperative one that goes through a long-lived structural intermediate where only the C-domain is folded. By using the unique ability of force as a regional perturbant, this study demonstrated that the chain topology plays a crucial role in modulating the energetic interactions between subdomains within a protein.

The Complex Folding Network of Calmodulin

AFM studies have previously reported on the near-equilibrium two-state folding/unfolding transitions of the calcium-sensing protein, calmodulin.^47,48 Recent high-resolution optical tweezers experiments revealed a more complex folding network comprised of at least six states.^8,49 Starting from the unfolded state, two on-pathway intermediates (F12, F34) compete with an-off pathway intermediate, F23. While F12 and F34 contain correctly paired subdomains, F23 is a wrongly paired intermediate that must unfold before proceeding to the native state. Folding proceeds rapidly to the native state from the F34 intermediate. However, from F12, folding can occur with equal probability to the native state, or to a trapped intermediate F123 that contains three subdomains docked in a non-native geometry.

A kinetic analysis of the constant-trap position dataset revealed that the off-pathway intermediates constrain the timescale of calmodulin folding to seconds, despite the individual domains folding on the microsecond timescale. The equilibrium free energies of the different states, extracted from constant-trap position traces,^8,31 indicated that the presence of one folded domain prevents the other domain from reaching its energetically optimal state, highlighting the energetic coupling between the two calmodulin domains. This study highlights the importance of single molecule force spectroscopy in revealing the complexity in the folding pathway of seemingly simple proteins.

The Role of Pulling Geometry in the Mechanical Unfolding of the src SH3 Domain

The geometry of force application (i.e. the axis of the applied force with respect to protein topology) plays an important role in determining the mechanical response of proteins. AFM experiments and MD simulations have shown that the average unfolding force varies with pulling geometry.^16,17,50-52 However, AFM spectroscopy uses high loading rates and protein unfolding occurs at relatively high forces that are far from equilibrium. The low loading rates and precise control over the points of force application afforded by the optical tweezers make it an excellent technique to obtain mechanistic information on different pulling geometries under conditions close to equilibrium. In particular, does the unfolding pathway vary with pulling geometry?

We investigated the response of src SH3 to mechanical force under two different pulling axes.⁵³ One axis was oriented longitudinally relative to the terminal β-strand and the other axis was oriented orthogonal to this strand (Figure 8a). The longitudinal force (parallel to the terminal β-strand, A7C/N59C) is expected to result in ‘shearing’ of the β-strands, while the orthogonal force (perpendicular to the terminal β-strand, R19C/N59C) would be expected to ‘unzip’ the strands.

Figure 8.

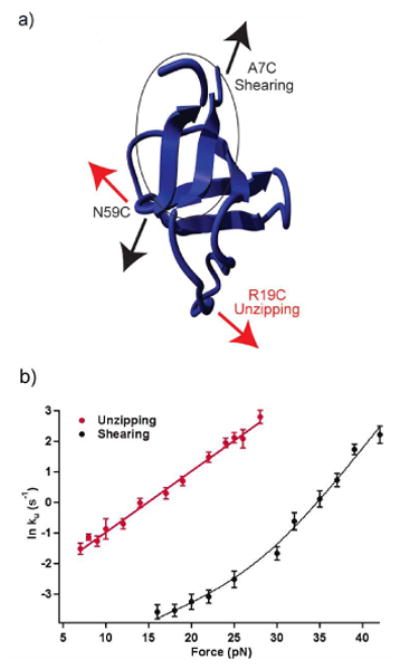
(a) The effect of pulling geometry on mechanical unfolding was studied by applying a shearing and an unzipping force on the src SH3 domain. (b) The force dependence of unfolding rates in the shearing geometry (black) is biphasic, indicating the presence of parallel unfolding pathways.

Force-ramp experiments revealed significant anisotropy in the mechanical unfolding of src SH3. The A7C/N59C shearing axis unfolds at a significantly higher average force than the R19C/N59C unzipping geometry (F_u = 35.0 pN vs. F_u= 14.0 pN). The force dependence of unfolding rates (F vs. ln k_u) was obtained by performing force-jump experiments to examine the features of the energy landscape that might cause the difference in mechanical stability between the two pulling axes.

For the unzipping direction, ln k_u increased linearly across the range of measured forces. This is consistent with a single pathway Bell model in which force continuously tilts the free energy landscape, thereby lowering the height of the barrier.¹¹ The slope of F vs. ln k_u for R19C/N59C src SH3 yielded a short distance to the transition state, X_U^‡ = 0.70 nm, which is typical of globular proteins.

The shearing geometry did not show this simple linear behavior, but rather exhibited biphasic dependence (Figure 8b). ln k_u showed a weaker dependence on force in the 15 - 25 pN range as compared to that above 25 pN.⁵³ The biphasic behavior was well captured by fitting the data to the sum of two Bell terms. These fits yielded significantly different distances to the transition state for the two force regimes, X_U^‡_low-force = 0.45 nm and X_U^‡_high-force = 1.40 nm. The biphasic force dependence likely arises from a multidimensional landscape where the protein can access two parallel trajectories, one dominating at low force and one dominating at high force. In this scenario, each pathway will have its own transition state whose location will vary along the reaction coordinate (i.e. different X_U^‡).

The S47A variant differentially affected the two unfolding regimes in the shearing geometry; it increased the unfolding rate ∼3.5-fold in the low force regime, but did not affect the high-force regime. This mutation appears to uncouple the two unfolding regimes and is additional evidence for the presence of two structurally and energetically independent transitions.

To our knowledge, this was the first direct experimental observation of a force-dependent switch between parallel unfolding pathways. Given that the distances to the transition states along the reaction coordinate appear to be different for the unzipping and shearing geometries, it is possible that the protein traverses different pathways along the two pulling axes. However, it is important to probe the detailed structural features of each pathway before making a definite conclusion. This would require evaluating the effect of many mutations, defining the mechanical transition state along the two pulling geometries by using an analysis analogous to the φ-value methodology used in traditional protein folding studies and a few AFM experiments.^6,54

Summary

The ability of force spectroscopy to detect rare intermediates and selectively perturb specific regions of the protein has been instrumental in revealing features of the energy landscape that were inaccessible in traditional ensemble experiments. Despite unprecedented accuracy, data from these experiments are still lacking a clear molecular picture of the effect of force on the disruption of the folded state. Such developments will require a merging of novel computational, theoretical and experimental approaches. The incorporation of an orthogonal probe (such as fluorescent dyes) will make force spectroscopy even more powerful by allowing the direct detection of long-range allosteric interactions and very small conformational fluctuations under force. New analytical tools for interpreting these data will need to be developed. Future innovations might also incorporate temperature and pressure control into force spectroscopy instruments, thereby enabling a comprehensive understanding of a multidimensional free energy landscape under a combination of perturbants. The future of single molecule force spectroscopy in protein folding studies holds exciting promise to a better understanding and control of protein conformational changes.