Abstract
Growth competition assays have been developed to quantify the relative fitness of HIV-1 mutants. In this article, we develop mathematical models to describe viral/cellular dynamic interactions in the assay system from which the competitive fitness indices or parameters are defined. In our previous HIV-viral fitness experiments, the concentration of uninfected target cells was assumed to be constant (Wu et al., 2006). But this may not be true in some experiments. In addition, dual infection may frequently occur in viral fitness experiments and may not be ignorable. Here, we relax these two assumptions and extend our earlier viral fitness model (Wu et al., 2006). The resulting models then become nonlinear ODE systems for which closed-form solutions are not achievable. In the new model, the viral relative fitness is a function of time since it depends on the target cell concentration. First, we studied the structure identifiability of the nonlinear ODE models. The identifiability analysis showed that all parameters in the proposed models are identifiable from the flow-cytometry-based experimental data that we collected. We then employed a global optimization approach (the differential evolution algorithm) to directly estimate the kinetic parameters as well as the relative fitness index in the nonlinear ODE models using nonlinear least square regression based on the experimental data. Practical identifiability was investigated via Monte Carlo simulations.
Keywords: Differential evolution, Global optimization, HIV/AIDS, Model identifiability, Ordinary differential equation (ODE), Statistical inverse problem, Viral fitness
1. Introduction
Replicative fitness is the ability of a virus to replicate under the selective forces present in its environment. HIV-1 replication fitness in vivo is postulated to influence which variants predominate in a quasispecies, as well as affecting treatment responses and disease progression (Quinones-Mateu et al., 2000; Nijhuis et al., 2001; Quinones-Mateu and Arts, 2001). A critical question is whether assays that measure HIV-1 replication fitness in vitro correlate with fitness in vivo, and whether such assays can be used to predict prognosis or response to therapy. If so, fitness assays might be used to determine how aggressively to initiate treatment and the optimal time to switch a failing regimen.
Viral fitness is one of the most important areas in HIV research because of its potential prognostic value for antiviral outcome. A common element to all fitness assays is the comparison of the mutant or “test” virus to a reference strain (usually a drug-sensitive, “wild-type” strain). Assays to measure HIV-1 replication fitness in vitro can differ in a number of ways, including use of growth competition versus parallel infections, use of whole virus versus recombinant virus assays, use of multiple-cycle versus single-cycle assays, and use of a reporter gene versus a viral gene or gene product to monitor virus growth (Nijhuis et al., 2001; Quinones-Mateu and Arts, 2001). Parallel assays are generally less labor-intensive than growth competition assays, although they suffer from greater experimental variability and reduced sensitivity compared to growth competition assays. Growth competition assays are generally considered to be the gold standard for measuring HIV-1 replication fitness in vitro. They are more sensitive to subtle differences in fitness than parallel infections, and are not subject to artifact due to differences in culture conditions (Collins et al., 2004; Prado et al., 2004).
It is critical to develop mathematical models and statistical methods to support viral fitness assay development and to estimate viral fitness parameters. Several studies have investigated the relative growth kinetics of two virus variants growing in competition either in vivo (Goudsmit et al., 1996, 1997) or in vitro (Holland et al., 1991; Croteau et al., 1997; Harrigan et al., 1998; Martinez-Picado et al., 1999). In these studies, a measure of fitness is typically derived by plotting the ratio of the two competing variants on a logarithmic scale against time and estimating the linear slope of this graph as the measure of fitness. Goudsmit et al. (1997) and Marée et al. (2000) introduced a new definition of relative fitness as the ratio of the production rates of two viral strains based on a viral dynamic model. Bonhoeffer et al. (2002) presented a new approach called the growth-corrected method (GM) to estimate the production rate ratio between two virus variants using time-series data (multiple data points). However, the definition of relative fitness in these papers is inconsistent with the conventional definition of relative fitness in population genetics and their methods are not efficient and accurate (Wu et al., 2006). We have designed a multiple-cycle, recombinant-virus, growth competition assay to measure relative viral fitness in cell culture using flow cytometry (Dykes et al., 2006). We also developed mathematical models and statistical methods to estimate the viral fitness parameters based on experimental data (Wu et al., 2006). From the population genetics perspective, we clarified the confusion and corrected the inconsistency in the definition of relative fitness in the HIV-1 viral fitness literature. Calculation and estimation methods based on two data points and multiple data points were proposed and were carefully studied (Wu et al., 2006). A user-friendly web-based computational tool of our methods has also been developed (http://www.urmc.rochester.edu/bstools/vfitness/virusfitness.htm).
However, in our previous work (Wu et al., 2006), we assumed that the target (uninfected) cell concentration is constant during an experiment and that dual infection of cells does not occur. In this case, a closed-form solution could be obtained from the proposed viral dynamic model. However, these key assumptions may not be true in many experiments. Recent work has shown that multiple infections of cells occurs far more frequently than previously thought both in vivo (Jung et al., 2002; Levy et al., 2004) and in vitro (Levy et al., 2004; Dang et al., 2004; Chen et al., 2005). Mathematical models of multiple infections have also been developed (Dixit and Perelson, 2004, 2005). In this paper, we extend our mathematical model of experiments in vitro to include dual infection. The assumption of constant uninfected cell concentration is also relaxed. In this case, there is no closed-form solution to the proposed model, and we use nonlinear least squares (NLS) methods combined with numerical solutions of the proposed nonlinear ordinary differential equation (ODE) models to estimate kinetic parameters and the relative fitness. Interestingly, in this case, the relative fitness is not a constant parameter; instead, it varies with the concentration of uninfected target cells. We propose this new concept and methods to estimate the varying relative fitness.
In Section 2, we briefly introduce our viral fitness experiment. We extend our earlier viral fitness model to accommodate varying concentrations of uninfected target cells in Section 3. In this case, the relative viral fitness is also a varying quantity. In Section 4, we further generalize our model to incorporate dual infections. We adopt a technique from engineering (Xia, 2003; Xia and Moog, 2003; Jeffrey et al., 2005) to study the structure identifiability of the proposed nonlinear ODE models in Section 5. In Section 6, a global optimization approach (the differential evolution algorithm) is employed to fit the nonlinear ODE models to experimental data and obtain the NLS estimates of kinetic parameters and the relative fitness. Monte Carlo simulations are performed to study practical identifiability and to evaluate the performance of parameter estimates in Section 7. We conclude the paper with a discussion of results in Section 8.
2. Growth competition assay
The design and evaluation of a growth competition assay in which viral variants are detected using flow cytometry is described in detail in Dykes et al. (2006). We designed two vectors, pAT1 and pAT2, that are identical to the lab strain pNL4-3, except that they have the mouse Thy1.1 or Thy1.2 genes cloned in place of nef, respectively. The Thy1.1 and Thy1.2 proteins differ by only one amino acid and are expressed on the surface of infected cells. A site directed mutant of RT, K103N, that is resistant to the non-nucleoside reverse transcriptase inhibitor efavirenz, and has been shown to have a mild reduction in replication fitness was cloned into pAT2 to produce pAT2K103N (Dykes et al., 2006; Koval et al., 2006). Wild-type and mutant virus stocks were produced as previously published (Dykes et al., 2006), and the two variants were used to co-infect PM1 cells, a T cell line in an equal ratio. At hours 70, 94, 115, 139, and 163, half the culture was removed and replaced with fresh media. The number of viable cells per mL of culture was determined before cells were removed by staining with trypan blue and counting in a hemocytometer. Cells removed during this process were singly and dually stained with the Thy1.1 (1:200 dilution) and Thy1.2 (1:100 dilution) antibodies (BD Biosciences). Cells were analyzed using a FACScaliber flow cytometer (Becton Dickinson), as previously published (Dykes et al., 2006). The number of viable wild-type or mutant infected cells was calculated by multiplying the total number of viable cells in the original culture by the percent of wild type or mutant as determined by flow cytometry. Under these conditions, approximately 0.03%, 0.05%, 1.08%, and 20.63% of cells were infected with both viruses at 94, 115, 139, and 163 hours, respectively.
3. Viral fitness models ignoring dual infections
Wu et al. (2006) proposed a five-compartment model to describe viral fitness experiments in vitro. We make a minor modification to the model in Wu et al. (2006) by including proliferation of infected cells. The new model is written as follows:
| (1) |
where T, Tm, Tw, M, and W are numbers of uninfected target cells, cells infected by mutant virus, cells infected by wild-type virus, mutant virus, and wild-type virus, respectively. Parameters (λ, λw, λm) represent the proliferation rates of uninfected target cells, cells infected by wild-type virus, and cells infected by mutant virus. Note that λw, and λm were assumed to be zero in Wu et al. (2006). Parameters and are the respective infection rate constants that describe the rates at which T cells become infected by M and W; Nm and Nw are the respective number of new virions produced from each of the infected cells during their life-time; parameters δ, δm and δw are the respective death rates of T, Tm and Tw; cm and cw are the respective clearance rates of mutant and wild-type virions.
The model assumes that both viral population densities are proportional to their corresponding infected cell densities. The dynamics of free virus are typically fast in comparison with the infected cells (Quinones-Mateu and Arts, 2001; Prado et al., 2004). This generally implies that a quasi-steady state is rapidly established. We, therefore, do not explicitly distinguish between free virus and infected cell load. Thus, we write the quasi-steady-state equations for virus as follows
| (2) |
where θm = Nm δm/cm and θw = Nw δw/cw, and reduce model (1) to the following form
where and . Clearly parameters, λ and δ, λw, and δw, and λm and δm, are not identifiable in the above equations. We define ρ = λ − δ, ρw = λw − δw, and ρm = λm − δm, and then we rewrite the above model as
| (3) |
Wu et al. (2006) performed simulation studies and showed that the approximation of model (1) by model (3) is quite reasonable.
In Wu et al. (2006), it was further assumed that the uninfected cell concentration T is approximately constant during the one week experiment. Then a closed-form solution of Tm and Tw to Eq. (3) can be obtained. Some kinetic parameters and viral fitness parameters can be estimated from the closed-form solution using linear regression techniques. However, the assumption of constant uninfected cell concentration T may not be realistic in many experiments. Fortunately, our flow-cytometry based growth competition assay can quantify the concentrations of uninfected cells (T), wild-type virus infected cells (Tw) and mutant virus infected cells (Tm) at distinct time points during an experiment. This allows us to estimate the kinetic parameters in Eq. (3) directly by fitting the data to the nonlinear ODE model (3) using the nonlinear least squares (NLS) method.
If we can estimate all kinetic parameters in model (3), the pure reproduction rates of the mutant and wild-type viruses can be defined as
| (4) |
respectively. Note that the uninfected cell concentration (T) in Eq. (4) varies during an experiment, but can be measured at different time points. In Eq. (4), it can be replaced by its measurements directly or by its predicted values from the regression analysis using model (3) directly.
We can define d, the log-relative fitness (LRF) of mutant virus as:
| (5) |
The relative fitness (RF) of mutant virus versus the wild-type virus at time t is defined as
| (6) |
where t = t1, t2,…, tn are measurement times and s is the selection coefficient.
After we obtain the parameter estimates (k̂m, k̂w, ρ̂m, ρ̂w, ρ̂) from fitting the experimental data, we can also get the fitted value for T(t), say, T̂(t). Then the estimated LRF and RF are
| (7) |
| (8) |
Thus, we can see that the relative fitness is not constant, instead it is a function of the concentration of uninfected cells (T), which varies during the experiment. Consequently, the relative fitness is also a function of time. The relative fitness (RF) during an experiment can be summarized by the average of the relative fitness (ARF) estimates at different time points,
| (9) |
If T(t) is a constant over time, the ARF reduces to the constant relative fitness definition introduced in Wu et al. (2006).
4. Viral fitness models with dual infections
For both the recombinant-virus assay and the whole-virus assay, we cannot completely rule out the presence of dually infected cells. Sometimes the dual infection rate is very small and we can ignore it. But sometimes it may be too large to simply ignore. Thus, we develop mathematical models and statistical methods to estimate viral fitness parameters in the situation of nonignorable dual infection. The mathematical model can be specified as
| (10) |
where T, Tm, Tw, and Tmw are numbers of uninfected cells, cells infected by mutant virus, cells infected by wild-type virus, and cells infected by both mutant and wild-type viruses (dual-infection); M, W, and R are mutant viruses, wild-type viruses, and viruses produced by dually-infected cells, respectively. Recall that each HIV-1 virion contains two RNA molecules. Thus, virions produced by dually infected cells may contain two wild-type RNAs, two mutant RNAs, or one wild-type and one mutant RNA molecule (heterozygous virus). For simplicity, we shall ignore the possibility of recombinant viruses being produced as we are studying a short-term assay. The impact of recombination in vivo has been studied by others (Fraser, 2005). Note that mutant and wild-type RNAs may not be produced at equal levels within dually infected cells, or be packaged into virions at equal efficiency. Thus, we assume Tmw produce a fraction pm of viruses with only mutant RNA, a fraction pw of viruses with only wild-type RNA and a fraction (1 − pm − pw) of viruses with heterozygous RNA. The viruses with heterozygous RNA can infect target cells and turn the target cells into Tmw directly. The “mutant” and “wild-type” viruses produced by dually infected cells are not included in the M and W equations, as these virions may contain a mixture of proteins produced by the wild-type and mutants provirus DNA in the dually infected cells. For this reason, these virions may infect cells at different rates than the true mutant and wild-type virions and are kept track separately. Parameters are infection rates of mutant virus, wild-type virus, and virus produced by dually infected cells, respectively. Parameters (λ, λm, λw, λmw) represent the proliferation rate of T, Tm, Tw, and Tmw. Parameters δ, δm, δw, and δmw are the death rates of T, Tm, Tw, and Tmw and and are dual infection rates. Let ρ = λ − δ, ρm = λm − δm, ρw = λw − δw and ρmw = λmw − δmw be the pure growths rates of T, Tm, Tw, and Tmw cells which are the differences between the corresponding proliferation rate and death rate. If the proliferation rate is zero, then the death rate of the corresponding cells can be estimated. Otherwise we cannot distinguish between the proliferation rates and the death rates. Parameters (Nm, Nw, Nmw) represent the number of virions produced from each of Tm, Tw and Tmw cells during their life time. Other notations are similar to model (1). In this model, we do not consider cells dually infected by the same virus population, and we ignore cells infected with more than two viruses. However, variations of model (10) that incorporate these effects may easily be investigated.
Note that we have not included recombination in the model, because previous studies have demonstrated that it is very unlikely to be detected under the conditions present in our assays. First, Levy et al. (2004) demonstrated that recombination rates drop dramatically with the frequency of infected cells. Secondly, recombinant virus does not result from cells dually infected with each parental strain, and HIV recombination requires that a heterozygous virus infects the cell (Hu and Temin, 1990). We have also evaluated the concordance between mutant prevalence as measured by bulk sequence analysis and the Thy marker, and found that they give very similar results under experimental conditions that are the same as we have used here (Dykes et al., 2006). This suggests that recombination is not frequent enough to disrupt the linkage between the Thy marker and RT for the dominant strains during the time course of the experiment. We do acknowledge that low-frequency recombinant events could have an impact on replication fitness over longer time frames, if the resultant recombinant mutant has substantially different fitness than either parent. This, however, is not the case in these growth competitions between a wild-type and drug resistant mutant that differ at only a single codon.
If we make the same assumption as in model (1), that the infected cell densities are proportional to their corresponding virus densities, then we can simplify model (10) to
| (11) |
where (km, kw, kR) are new parameters that are re-parameterized from . In the second equation of (11), pm Tmw are basically mutant viruses while in the third equation, pw Tmw are basically wild-type viruses. Thus, the pure reproduction rates of mutant and wild-type viruses can be defined as
| (12) |
respectively.
As in the case without dual infection, we define the log-relative fitness (LRF) of mutant viruses versus wild-type virus as:
| (13) |
The relative fitness (RF) of mutant viruses versus the wild-type viruses can be defined as
| (14) |
Thus, the relative fitness of mutant virus versus wild-type virus depends on three factors: their pure growth rate difference (ρm − ρw), infection rate difference (km − kw), and the dual infection rate difference [qw Tm(t) − qm Tw(t)].
Note that our flow-based assay can measure the concentrations of T, Tm, Tw, and Tmw, where Tmw is the concentration of cells infected by both mutant and wild-type viruses or cells infected by viruses with heterozygous RNA, but our assay cannot distinguish between these two categories of infected cells. However, if we can estimate all the kinetic parameters in Eq. (11), we can define the viral fitness of “heterozygous” viruses using the first term of the fourth equation in (11), i.e., define the pure reproduction rate of heterozygous viruses as
Thus, we can define the log-relative fitness (LRF) and the relative fitness (RF) of heterozygous viruses versus the wild-type viruses as
| (15) |
| (16) |
respectively. Similarly we can define the relative fitness of heterozygous viruses versus the mutant viruses. This definition of the relative fitness of heterozygous viruses, as well as model (10), ignores the production of heterozygous viruses by direct infection of a target cell by a mutant and a wild-type virus simultaneously. In model (10), we have assumed one virus infects first and then the singly infected cell is infected a second time with a different type of virus to become dually infected. In the definition of relative fitness of heterozygous virus, we also ignore the term (qm + qw)Tw Tm in the last equation of model (11) that corresponds to these types of sequential infections. Although this term contributes to the amount of Tmw, we consider it as the “replenishment” of Tmw from an external source instead of direct reproduction of Tmw. After we obtain the parameter estimates and the estimates of T(t), Tm(t), and Tw(t), we can get the estimates of the LRF and RF by plugging these estimates in formulas (13)-(16).
5. Identifiability analysis
Identifiability (observability) is important for biomedical system modeling. Consider a general nonlinear system,
| (17) |
where x ∈ Rn is the state variable vector, u ∈ Rm the input vector, y ∈ Rp the output vector, and θ ∈ Rq the parameter vector. The system Σθ is identifiable if the parameter θ can be uniquely determined from the input u and the corresponding output y. See Ljung and Glad (1994), Xia and Moog (2003), and Jeffrey et al. (2005) for a more detailed introduction of identifiability concepts.
The identifiability problem for linear systems has been well addressed, especially for compartmental models (Audoly et al., 1998). However, for nonlinear ODE models, a general algorithm for global identifiability analysis needs to be further investigated. Techniques based on differential algebra have been successfully applied to low dimensional problems (Ljung and Glad, 1994; Audoly et al., 2001). For a formal introduction to differential algebra, the reader is referred to Ritt (1950). These techniques are used to address differential polynomial problems to which most biomedical dynamic models belong. However, the differential algebra methods come with high computational complexity. The efficiency of differential algebra algorithms needs to be improved. Xia and Moog (2003) proposed a simple alternative method based on the implicit function theorem, which has been successfully applied to HIV dynamic models (Xia and Moog, 2003; Jeffrey et al., 2005). In this study, the procedure described in Xia and Moog (2003) and Jeffrey et al. (2005) is used to analyze the identifiability of the proposed viral fitness models.
Considering the model (11) with the assumption that parameters pm and pw are known, i.e., pm = pw = 0.25 and 1 − pm − pw = 0.5, we have
| (18) |
In our experiments, all state variables (T, Tm, Tw, Tmw) are measurable, which gives the outputs of the system as
| (19) |
By taking derivatives up to the 4th order of the first equation of Eq. (18), the four parameters (ρ, km, kw, kR) are found to be identifiable if
| (20) |
Since the 4th order derivative of y1 = T is needed to obtain the equation above, at least five measurements are necessary to evaluate . Similarly, the parameters (ρm, qm) are identifiable if
| (21) |
and the parameters (ρw, qw) are identifiable if
| (22) |
Finally, if (ρ, km, kw, kR, ρm, qm, ρw, qw) are identifiable, then ρmw is identifiable if
| (23) |
To satisfy Eq. (23), the measurements of Tmw cannot be zero.
Note that the basic assumptions of the above identifiability analyses are that the model structure is absolutely accurate and that the measurements are exact (no measurement error), which is not realistic in practice. The practical identifiability with measurement errors is studied via Monte Carlo simulations in Section 7. However, this analysis provides important information on the necessary condition for a model to be identifiable and the minimum number of measurements needed. Similar techniques can also be used to analyze the identifiability of models (3) and (11). We summarize the identifiability analysis results for the three models in Table 1.
Table 1.
Identifiability analysis of 3-D and 4-D viral fitness models
6. Model fitting and parameter estimation
Parameter estimation can be based on the maximum likelihood (ML) principle or the least squares (LS) principle. The LS method, which is the focus of this paper, is robust against the distribution assumption of measurement errors and is equivalent to the ML method if the measurement errors are normally distributed and independent with a common variance. The LS estimates can be obtained by minimizing the objective function, i.e., the sum of squared residuals of all measurements. There are two main categories of minimization methods for solving the LS problem: gradient methods and direct search methods (or global optimization methods). The gradient methods, such as the Levenberg–Marquardt method and the Gauss–Newton method, can efficiently search for local minima based on the Jacobian or Hessian matrix of the objective function. For details of gradient methods and their applications to ODE parameter estimation, the reader is referred to Nocedal and Wright (1999) and Englezos and Kalogerakis (2001).
The gradient methods perform well only if the initial guess of the solution is very close to the true solution and the objective function behaves well. However, gradient methods can be easily trapped in the local minima if the objective function has multiple local minima or is not differentiable. This defect of gradient methods can be overcome by direct search methods such as the Luus–Jaakola method (Luus and Jaakola, 1973). For instance, Linga et al. (2006) compared the Luus–Jaakola method to the Gauss–Newton method for parameter estimation of ODE models. They found that the solutions produced by the Luus–Jaakola method and the Gauss–Newton method can be very different for the same problem and the objective function value achieved by the Luus–Jaakola method is much smaller than that found by the Gauss–Newton method.
Various direct search or global optimization methods are currently available. Moles et al. (2004) compared the performance and computational cost of seven global optimization methods, including the Luus–Jaakola method and the Differential Evolution (DE) method (Storn and Price, 1997). Their results indicate that the DE method outperforms the other six methods with a medium computational cost. In addition, our preliminary results (not shown) indicate that the gradient methods, including the Gauss–Newton method, the Levenberg–Marquardt method, and the quasi-Newton method failed to obtain good parameter estimates even if the initial guess of the parameter values is just 5% away from the true parameter values. So, for this problem, a global optimization method such as the DE method should be employed. Note that global optimization methods are very computationally intensive, but that computational cost can be improved by combining stochastic global optimization methods and deterministic methods such as the scatter search method proposed by Rodriguez-Fernandez et al. (2006).
For our study, the DE method is employed to solve the LS problem and to estimate the parameters in the proposed HIV-viral fitness models. For details of the DE algorithm the reader is referred to Storn and Price (1997). The basic idea of the DE method is to use the concept of biological evolution theory to design the search strategy. Within a region specified by constraints in the parameter space, a number of parent vectors are randomly generated, then the next generation of vectors (child vectors) are generated from parent vectors according to some strategies similar to chromosome pairing. For different strategies, different numbers of groups of randomly shuffled parent vectors are involved in generating one child vector. If the fitness (the objective function) of child vectors is better than the fitness of their parents, the parents are replaced by children, and this procedure is repeated until convergence is attained. We implemented the DE algorithm in both C++ and MATLAB®, based on a MATLAB® prototype developed by Price et al. (2005). The ODE system is solved using a 4th order Runge–Kutta scheme. Our results suggest that the computational time of the C++ implementation is less than 10% of the MATLAB® implementation for the same problem.
In this study, the number of infected and uninfected T cells was rmeasured at 5 time points with three replicates at each time point (Table 2). The cell number in Table 2 refers to the total number of cells in the culture vessel. The measurement models are
| (24) |
where i = 1, 2,…, 5 and {ε1(ti), ε2(ti), ε3(ti), ε4(ti)} are assumed to be independent with mean zero and common variance σ2. If they are not independent with heterogeneous variance, the weighted (generalized) least squares method can be used. Based on the identifiability analysis (Table 1) in the previous section, all the parameters are theoretically identifiable. Thus, we fitted the dual infection model (18) to the experimental data to estimate 9 kinetic parameters and 4 ODE initial conditions simultaneously using the aforementioned differential evolution (DE) method.
Table 2.
Measured number of uninfected and infected cells at five time points with three replicates at each time point
| Replication | Time (hour) | T (cell) | Tm (cell) | Tw (cell) | Tmw (cell) | T (control group) |
|---|---|---|---|---|---|---|
| 1 | 70 | 32,554,830 | 134,173 | 26,180 | 9,818 | 28,088,137 |
| 94 | 46,645,200 | 481,950 | 103,950 | 18,900 | 46,578,042 | |
| 115 | 64,240,540 | 1,230,460 | 309,260 | 26,320 | 74,280,528 | |
| 139 | 65,563,680 | 9,863,280 | 3,000,480 | 1,364,580 | 151,063,920 | |
| 163 | 36,366,400 | 36,545,600 | 10,281,600 | 28,806,400 | 351,958,208 | |
| 2 | 70 | 35,855,330 | 158,620 | 25,235 | 10,815 | – |
| 94 | 48,652,100 | 269,500 | 73,500 | 9,800 | – | |
| 115 | 62,989,640 | 1,081,920 | 302,680 | 25,760 | – | |
| 139 | 79,088,100 | 7,907,900 | 3,103,100 | 900,900 | – | |
| 163 | 47,349,120 | 24,613,680 | 15,167,880 | 22,069,320 | – | |
| 3 | 70 | 32,597,373 | 98,175 | 22,908 | 6,545 | – |
| 94 | 52,059,000 | 315,000 | 110,250 | 15,750 | – | |
| 115 | 62,362,300 | 847,210 | 445,900 | 38,220 | – | |
| 139 | 77,218,680 | 5,576,620 | 2,117,920 | 478,240 | – | |
| 163 | 49,714,560 | 17,922,240 | 17,025,120 | 16,138,080 | – |
Since the measured number of cells is on the order of 107, we took a log transformation of the experimental data in model fitting in order to stabilize the computational algorithm. Also, note that the five parameters (km, kw, kR, qm, qw) have to be positive to make biological sense. Thus, we also used a natural log transformation for these parameters to accommodate this constraint. Confidence intervals of all the estimated parameters were obtained using the bootstrap method (Shao and Tu, 1995; Davison and Hinkley, 1997). The search regions for all parameters (ρ, ρm, ρw, ρmw, km, kw, kR, qm, qw) are given in Table 3. The fitted results for the logarithm of the numbers of infected and uninfected cells are plotted in Fig. 1 with all the experimental data superimposed on the fitted curves, which indicates good agreement between the model prediction and the experimental data.
Table 3.
Parameter estimation results for the 4D dual infection model (18)
| Parameter | Search region lower bound | Search region upper bound | Parameter estimate | Bootstrap 95% confidence interval |
|---|---|---|---|---|
| ρ (per hour) | −6.0e-02 | 6.0e-02 | 1.50e-02 | 1.29e-02, 1.71e-02 |
| ρm (per hour) | −2.0e-01 | 6.0e-02 | −2.29e-02 | −4.78e-02, 7.90e-03 |
| ρw (per hour) | −6.0e-02 | 6.0e-02 | 7.13e-03 | −2.96e-02, 4.41e-02 |
| ρmw (per hour) | −2.0e-01 | 6.0e-02 | 5.68e-04 | −3.94e-02, 1.83e-02 |
| km (per cell per hour) | 0 | 1.0e-08 | 1.51e-09 | 9.88e-10, 1.89e-09 |
| kw (per cell per hour) | 0 | 1.0e-08 | 1.11e-09 | 4.01e-10, 1.78e-09 |
| kR (per cell per hour) | 0 | 1.0e-08 | 4.36e-10 | 2.94e-23, 2.00e-09 |
| qm (per cell per hour) | 0 | 1.0e-08 | 4.15e-09 | 2.22e-09, 5.98e-09 |
| qw (per cell per hour) | 0 | 1.0e-08 | 1.10e-09 | 2.87e-11, 2.68e-09 |
Fig. 1.
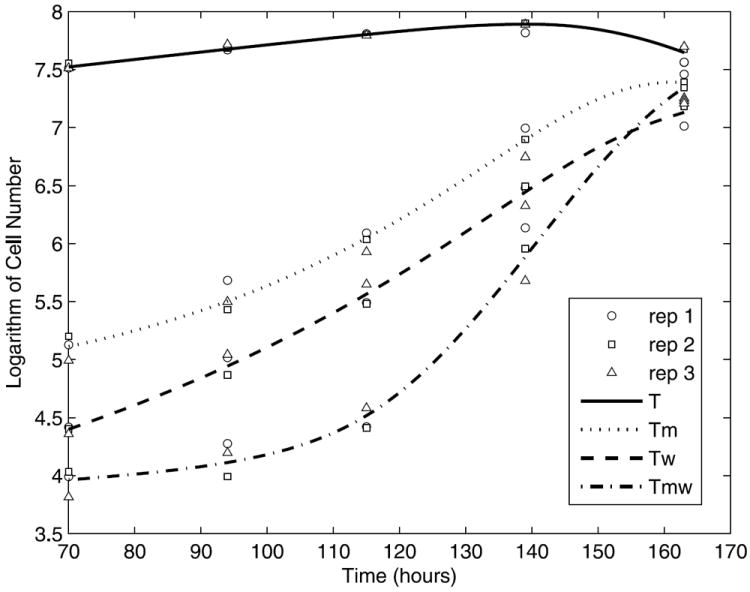
Experimental data and model fitting results (○ replicate 1, □ replicate 2, and ∆ replicate 3) and fitted curves for T (solid), Tm (dotted), Tw (dashed) and Tmw (dash-dotted).
Note that the number of uninfected T cells decreased from hour 139 to 163. To confirm this decrease is due to infection and is not a problem with the culture system, a control experiment using uninfected cells was done using the same five sampling time points (hours 70, 94, 115, 139, and 163), as listed in Table 2. The total cell number in the culture vessel was 1.51 × 108 at hour 139 and 3.52 × 108 at hour 163. Thus, the number of uninfected T cells at hour 163 in the control group is much greater (>300%) than the total number of cells (infected and uninfected) in the infection experiments at hour 163. This comparison suggests that the culture did not approach or exceed its saturation density toward the end of the experiment, and the slow down of the growth rate of uninfected cells is due to viral infection and not growth saturation or other culture effects.
The parameter estimates with their bootstrap confidence intervals for model (18) are given in Table 3. From Table 3, we can see that the infection rates of the wild-type virus and mutant virus, kw and km, are very similar, but the infection rate of heterozygous virus (kR) is about 3-fold smaller than kw and km, although the confidence intervals of kw, km and kR significantly overlap with each other. Our simulation studies in the next section show that the estimate of kR is less reliable than those of kw and km. The dual infection rate from two different routes, qw and qm, are also similar. The estimate of the pure growth rate of uninfected target cells, ρ = λ − δ, is reasonable and is positive which indicates that the proliferation rate (λ) is larger than the death rate (δ) during the experiment. However, the estimates of the pure growth rates of infected cells, ρm, ρw, and ρmw, are not reliable since their confidence intervals include zero. This may indicate that the parameters, ρm, ρw, and ρmw, are too small to be reliably estimated from the measurements with error although they are theoretically identifiable. Their practical identifiability is further investigated via Monte Carlo simulations in the next section.
Based on the fitted model, the log-relative fitness d(t) and relative fitness RF(t) as well as their corresponding 95% confidence intervals are calculated at the five time points of experimental measurements for both mutant virus versus wild-type virus and heterozygous virus versus wild-type virus, respectively, using the formulas (13)-(16). These results are given in Table 4 and plots of d(t) and RF(t) versus time t are shown in Fig. 2. From Table 4 and Fig. 2, we see that the relative fitness (RF) of mutant virus versus the wild-type virus was increasing from hour 70 to 139, but decreased at hour 163, while the relative fitness (RF) of heterozygous virus versus the wild-type virus was decreasing initially from hours 70 to 139, and then increased on hour 163. However, the variation of RF(t) of both mutant virus and heterozygous virus is relatively small (Table 4). The estimated time-varying trend may not be statistically significant. This is presumably because the concentration of uninfected target cells, T (t), is approximately constant in our experiment (Fig. 1) and other time-varying terms in RF formulas (14) and (16) are relatively small compared to the term related to T (t). The results also indicate that the heterozygous virus is less fit than the mutant virus.
Table 4.
The estimate of log-relative fitness (d) and relative fitness (RF) for mutant virus vs. wild-type virus and heterozygous virus vs. wild-type virus for model (18). 95% confidence intervals of all estimates are listed below each estimate using the bootstrap method
| Time (hour) | d(t) | RF(t) | d(t) | RF(t) |
|---|---|---|---|---|
| Mutant vs. Wild | Mutant vs. Wild | Heterozygous vs. Wild | Heterozygous vs. Wild | |
| 70 | −1.66e-02 (−3.71e-02, −5.82e-03) | 9.84e-01 (9.64e-01, 1.01e-00) | −5.05e-02 (−1.19e-01, −1.98e-02) | 9.51e-01 (8.88e-01, 9.80e-01) |
| 94 | −1.10e-02 (−2.08e-02, −9.66e-04) | 9.89e-01 (9.79e-01, 9.99e-01) | −6.89e-02 (−1.43e-01, −4.02e-02) | 9.33e-01 (8.67e-01, 9.61e-01) |
| 115 | −4.86e-03 (−1.52e-02, 4,93e-03) | 9.95e-01 (9.85e-01, 1.00e-00) | −8.93e-02 (−1.73e-01, −5.86e-02) | 9.15e-01 (8.41e-01, 9.43e-01) |
| 139 | −1.66e-03 (−1.92e-02, 1.50e-02) | 9.98e-01 (9.81e-01, 1.02e-00) | −1.01e-01 (−1.93e-01, −6.62e-02) | 9.04e-01 (8.24e-01, 9.36e-01) |
| 163 | −4.13e-02 (−9.54e-02, 2.92e-02) | 9.60e-01 (9.09e-01, 1.03e-00) | −3.84e-02 (−9.54e-02, 4.22e-03) | 9.62e-01 (9.09e-01, 1.00e-01) |
| Mean | −1.51e-02 | 9.85e-01 | −6.96e-02 | 9.33e-01 |
| SD | 1.57e-02 | 1.54e-02 | 2.60e-02 | 2.43e-02 |
Fig. 2.
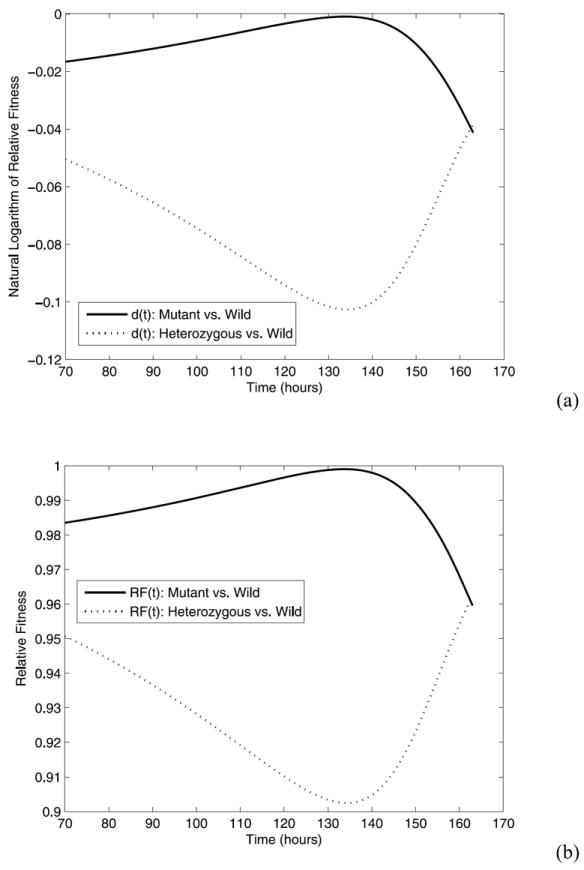
(a) Estimates of log-relative fitness d(t) for mutant virus versus wild-type virus and heterozygous virus versus wild-type virus; (b) Estimates of relative fitness RF for mutant virus versus wild-type virus and heterozygous virus versus wild-type virus.
For the purpose of comparison, we ignored the dual infection and fitted the 3D viral fitness model (3) to the same experimental data (Table 2). The parameter estimates and their corresponding bootstrap confidence intervals are given in Table 5. Comparing the results from the 3D model in Table 5 to those of the 4D model in Table 2, we find that the estimates of parameters (ρ, km, kw) are similar between the two models. But the estimates of the two parameters, ρm and ρw, may not be reliable and even the sign of the estimates of ρw from the two different models are different. These results are consistent with our practical identifiability analyses in the next section.
Table 5.
Parameter estimation results for the 3D viral fitness model (3)
| Parameter | Search region lower bound | Search region upper bound | Parameter estimate | Bootstrap 95% confidence interval |
|---|---|---|---|---|
| ρ (per hour) | −6.0e-02 | 6.0e-02 | 1.13e-02 | 9.06e-03, 1.31e-02 |
| ρm (per hour) | −2.0e-01 | 6.0e-02 | −3.25e-02 | −5.59e-02, −3.61e-03 |
| ρw (per hour) | −6.0e-02 | 6.0e-02 | −2.54e-03 | −4.35e-02, 3.32e-02 |
| km (per cell per hour) | 0 | 1.0e-08 | 1.59e-09 | 1.11e-09, 1.93e-09 |
| kw (per cell per hour) | 0 | 1.0e-08 | 1.24e-09 | 6.36e-10, 1.91e-09 |
7. Simulation studies and practical identifiability
To study the practical identifiability and sensitivity of the kinetic parameters in the ODE models when the state variables are measured with errors, we conducted intensive Monte Carlo simulations and numerical sensitivity analyses based on the 4D model (18). In the simulation studies, we used the estimated parameter values from the experimental data in Section 6 and generated the simulation data sets based on the ODE model (18). The measurement errors are assumed to be identically and independently distributed (iid) with a normal distribution N (0, σ2), where we took σ to be 0%, 5%, and 30% of the average logarithm number of all measurements, respectively, in our simulations. To study the large sample behavior of our estimates, we generated 1,000 replicates at each of 5 experimental time points for each simulation data set (compared to only 3 replicates at each time point in our current experiment). We generated 1,000 simulation data sets for each of the three different measurement error levels (σ = 0%, 5%, and 30%), respectively. We define the average relative estimation error (ARE) as , where θ̂j is the estimate of parameter θj from the j th simulation data set and N = 1,000 is the total number of simulation runs. We use the ARE to evaluate the parameter estimates. The same search regions for the real experimental data fitting in Table 3 are employed in our simulation studies.
The AREs of all 9 parameters in model (18) for three measurement error levels (0%, 5%, and 30%) are reported in Table 6. Parameters (km, kw, kR, qm, qw) are forced to be positive by taking a log-transformation in the estimation. Parameters (ρ, ρm, ρw, ρmw) can be positive or negative, depending on whether the proliferation rate is larger than the corresponding death rate. In Table 6, we also report the percentages of simulation runs that did not correctly identify the sign of the parameters (sign change). From Table 6, we can see that when there is no measurement error (σ = 0%), all the 9 parameters can be well identified (the maximum ARE is 0.4%), which confirms our theoretical identifiability analysis in Section 5. This also indicates that our parameter estimation method converges to the true parameter values when the sample size is large enough and the measurement error is small enough. However, as the measurement error increases to 5% or 30%, the ARE of parameter ρmw rapidly increases to 556% or 2062%, respectively, and the sign of parameter ρmw cannot be correctly identified in about 50% of simulation runs. The ARE of ρw also increases to 39% and 201%, while the ARE of kR increases to 28% and 106%, respectively. When the measurement error is large (σ = 30%), the sign of parameter ρw cannot be correctly identified in 43% of simulation runs. The AREs of parameters (qw, ρm) are reasonable for the case of small measurement error (σ = 5%), but increase to 49% and 59% for the large measurement error case (σ = 30%), respectively. The AREs for other four parameters (ρ, km, kw, qm) are reasonable for all cases.
Table 6.
Numerical sensitivity analysis by simulation studies. The average relative error (ARE) is calculated based on 1,000 simulation runs; 1000 simulated replicates are used for each simulation run
| Error level (%) | Sensitivity | ρ (%) | ρm (%) | ρw (%) | ρmw (%) | km (%) | kw (%) | kR (%) | qm (%) | qw (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | ARE | 0.002 | 0.017 | 0.034 | 0.400 | 0.003 | 0.004 | 0.026 | 0.003 | 0.009 |
| sign change | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 5 | ARE | 1.1 | 10.8 | 39.0 | 555.7 | 2.9 | 4.6 | 28.3 | 4.2 | 12.0 |
| sign change | 0 | 0 | 3 | 50 | 0 | 0 | 0 | 0 | 0 | |
| 30 | ARE | 6.5 | 49.1 | 201.4 | 2062.0 | 12.7 | 23.1 | 106.0 | 21.29 | 59.1 |
| sign change | 0 | 10 | 43 | 53 | 0 | 0 | 0 | 0 | 0 | |
| Sensitivity rank | 9 | 5 | 2 | 1 | 8 | 6 | 3 | 7 | 4 | |
It is also important to investigate the reliability of parameter estimation under our current experimental conditions. The estimated measurement error level from our experimental data is σ = 1.5% of average measurements. We repeated the above simulations using this actual measurement error level and studied the effect of using different numbers of time points and a different number of replicates at each time point. Besides the standard 5 time points (hours 70, 94, 115, 139, and 163) as in our current experiment, we also performed the simulations for 9 time points (hours 70, 82, 94, 106, 115, 127, 139, 151, and 163). We used the number of replicates at each time point as 3, 6, 9, and 100, respectively. Note, if the number of replicates at each time point is 3, 6, or 9, this could be done in a real experiment, but 100 replicates at each time point may not be realistic and we only used it to evaluate the performance of our estimates in a large sample with an actual measurement error level. We report the simulation results of all cases (the AREs and sign change) in Table 7.
Table 7.
Practical identifiability analyses by simulations based on 1,000 simulation runs with the measurement error level σ = 1.5%
| # of time points | # of replicates | ARE | ρ (%) | ρm (%) | ρw (%) | ρmw (%) | km (%) | kw (%) | kR (%) | qm (%) | qw (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 3 | ARE | 6.28 | 52.7 | 187 | 2130 | 13.5 | 22.0 | 108 | 21.1 | 54.9 |
| sign change | 0 | 10 | 35 | 56 | 0 | 0 | 0 | 0 | 0 | ||
| 6 | ARE | 3.91 | 34.7 | 142 | 1402 | 8.99 | 16.8 | 77.5 | 14.4 | 37.5 | |
| sign change | 0 | 2 | 23 | 48 | 0 | 0 | 0 | 0 | 0 | ||
| 9 | ARE | 3.15 | 30.0 | 133 | 1396 | 8.18 | 15.3 | 73.9 | 13.7 | 32.3 | |
| sign change | 0 | 1 | 33 | 54 | 0 | 0 | 0 | 0 | 0 | ||
| 100 | ARE | 1.01 | 8.11 | 40.1 | 459.8 | 2.32 | 4.70 | 25.2 | 3.72 | 10.3 | |
| sign change | 0 | 0 | 2 | 47 | 0 | 0 | 0 | 0 | 0 | ||
| 9 | 3 | ARE | 4.10 | 37.9 | 146 | 1786 | 10.1 | 16.8 | 88.6 | 16.1 | 36.7 |
| sign change | 0 | 3 | 26 | 47 | 0 | 0 | 0 | 0 | 0 | ||
| 6 | ARE | 3.10 | 27.9 | 118 | 1301 | 7.2 | 13.1 | 66.7 | 10.3 | 29.5 | |
| sign change | 0 | 0 | 23 | 45 | 0 | 0 | 0 | 0 | 0 | ||
| 9 | ARE | 2.72 | 21.5 | 85.6 | 1190 | 5.84 | 10.1 | 61.5 | 9.24 | 26.1 | |
| sign change | 0 | 0 | 17 | 49 | 0 | 0 | 0 | 0 | 0 | ||
| 100 | ARE | 0.76 | 6.94 | 28.74 | 410 | 1.79 | 3.43 | 22.26 | 2.98 | 7.71 | |
| sign change | 0 | 0 | 1 | 36 | 0 | 0 | 0 | 0 | 0 |
From Table 7, one can see that the ARE of parameter ρmw ranges from 410% to 2130% and the sign change ranges from 36% to 56%. This indicates that the ρmw is practically unidentifiable. Considering the practical case of 9 time points and 9 replicates for each time point, the ARE of parameter ρw is 86% and the sign change is 17%, which indicate that it may be difficult to accurately identify the parameter ρw unless the sample size is unrealistically large (say, 100 replicates for each time point). For parameter kR, the AREs are also large (ranging from 62% to 108%) for practical cases (the number of replicates is 3, 6, or 9). For parameters (ρm, qw), the AREs are reasonable (ranging from 22% to 38%) for most reasonable sample sizes. The parameters (ρ, km, kw, qm) are very well identified (the AREs ranging from 3% to 22%).
In summary, the simulation results in Table 7 suggest that if we can perform an experiment for the sample size of 9 time points and 9 replicates at each time point, we can estimate the four parameters (ρ, km, kw, qm) with a good accuracy (the AREs ranging from 3% to 10%). In addition, we can estimate parameters (ρm, qw) with a reasonable accuracy (the AREs ranging from 22% to 26%), but parameter kR can only be estimated with a large error (the ARE is 62%). The parameter ρw is difficult to identify since its ARE is as large as 87% with 17% sign change in this largest practical sample size (9 time points and 9 replicates at each time point). In this case, the ARE of parameter ρmw is 1190% with 49% sign change which indicates that the parameter ρmw is practically unidentifiable. These conclusions are consistent with those derived from the simulation results in Table 6.
To further confirm the above results and conclusions and to investigate why the estimation error is very large for parameter estimates of ρmw, ρw, and kR even when the measurement error is small, we numerically evaluated the Fisher information matrix FIM and the error covariance matrix C (Seber and Wild, 1989; Rodriguez-Fernandez et al., 2006) based on our experimental data. The FIM is
| (25) |
| (26) |
where y(ti) is the measurements of the state variables at time point ti, the θ is the parameter vector, and V = σ2 · I4 is the variance-covariance matrix of the measurements with I4 being an identity matrix of dimension 4. From our experimental data, we can obtain estimates of the standard error (SE) of all parameters. For parameters ρmw, ρw, and kR:
| (27) |
where SE denotes the standard error of the parameter estimates. For example, with a 30% measurement error, σ = 4.29. Considering that the parameters ρmw, ρw, and kR are of the order of 10−4, 10−3, and 10−10 (Table 3), respectively, the results (27) can clearly lead to a large SE for these three parameters. These results further confirm the above conclusions.
8. Discussion and conclusion
In HIV viral fitness experiments that involve growth competition assays, the concentration of uninfected target cells has been assumed to be constant. This was also a key assumption in our earlier study (Wu et al., 2006). But this may not be true in some experiments. In addition, dual infection may frequently occur in viral fitness experiments (Dang et al., 2004; Levy et al., 2004) and may not be ignorable. In order to relax these two assumptions, we have extended our earlier viral fitness model (Wu et al., 2006) to avoid these two assumptions. The resulting models then become a nonlinear ODE system for which the closed-form solutions are not achievable. In this case, the relative fitness becomes a function of time since it depends on the cell concentrations at different time points. We studied the structure identifiability of the nonlinear ODE models based on a technique developed in the fields of engineering and differential algebra (Ljung and Glad, 1994; Audoly et al., 2001; Xia and Moog, 2003; Jeffrey et al., 2005). We also employed a global optimization approach (the differential evolution algorithm) to directly estimate the kinetic parameters in the nonlinear ODE models using the least squares principle. Practical identifiability is investigated via Monte Carlo simulations. We applied the proposed models and methods to HIV viral fitness experimental data to estimate the kinetic parameters and the relative fitness.
Xia and Moog (2003) and Jeffrey et al. (2005) proposed a system identifiability analysis method based on the implicit function theorem. We employed their method to analyze the identifiability of the proposed viral fitness models. We found that for the dual infection model (18), we need at least 5 measurements for each state variable in order to identify all the kinetic parameters. This conclusion was confirmed by our numerical results. The identifiability analysis methods, such as those proposed by Xia and Moog (2003) and Jeffrey et al. (2005) and other similar methods using the framework of differential algebra (Ljung and Glad, 1994; Audoly et al., 2001), which are called structural identifiability analysis, cannot deal with practical identifiability (Rodriguez-Fernandez et al., 2006) when the outcome variables are measured with error. To study the practical identifiability, Rodriguez-Fernandez et al. (2006) proposed a method based on the correlation matrix of parameter estimates to locate the practically non-identifiable parameters. They concluded that if the correlation of two parameters is nearly one, the two parameters are not practically identifiable. In this paper, we investigated the practical identifiability of the proposed models using both Monte Carlo simulations and the covariance matrix of parameter estimates (based on the Fisher information matrix). Similar approach has been applied to an HIV dynamic model by Wu et al. (2008). We found that although all 9 parameters in model (18) are theoretically identifiable based on the identifiability analysis, three of them (ρmw, ρw, and kR) are difficult to identify practically from the experimental data; two of them (ρm, qw) can be identified but with a large error; only four of them (ρ, km, kw, qm) can be well identified from the experimental data as summarized in Table 8.
Table 8.
Practical identifiability of the 4D dual infection model (18)
| Parameter | Practical identifiability |
|---|---|
| ρmw | Not identifiable |
| ρw | Difficult to identify |
| kR | Identifiable with a larger error |
| ρm, qw | Identifiable with a medium error |
| ρ, km, kw, qm | Identifiable with good precision |
Parameter estimation of ODE models, especially for high-dimensional nonlinear ODEs with a high-dimensional parameter space, remains challenging in biomedical modeling. When a large number of unknown parameters with different orders of magnitudes need to be estimated in a high-dimensional ODE system, it is difficult to find a global solution to the problem of minimizing the objective function. Standard gradient methods are not suitable for optimizing an objective function with multiple local maxima or minima since they are easily trapped at the local solutions. Global optimization methods are needed to overcome this problem. In this paper, we employed the differential evolution method (Storn and Price, 1997) implemented in C++ and MATLAB® to estimate the unknown parameters in the proposed nonlinear ODE models. Note that the computational cost of the C++ implementation is much less than that of the MATLAB® implementation, which makes it affordable on regular PCs. However, the computational efficiency of global optimization methods may be improved in the future by considering hybrid algorithms (Rodriguez-Fernandez et al., 2006).
Monte Carlo simulation is an important tool to validate the identifiability analysis results and to perform sensitivity analyses for model parameters as well as to evaluate parameter estimation methods. It also can be used to perform simulations for different experimental scenarios so that it can provide guidance for the design of future experiments. Our intensive simulation results indicate that measurements at 9 time points with 9 replicates at each time point are necessary to reasonably estimate all the kinetic parameters in model (18) except for parameters ρmw, ρw and kR, since these three parameters are very sensitive to measurement errors. We suspect that the terms involving these three parameters may be relatively small compared to the other terms in the same equations. Thus, an interesting research topic, which is currently under our investigation, is to use model selection methods, such as the Akaike Information Criterion (AIC) or Bayesian Information Criterion (BIC), to evaluate whether these small terms should be dropped from the model. We expect to report these results in the near future.
Acknowledgments
This research was supported by the NIAID/NIH grants AI50020, AI052765, AI055290, AI065217, AI27658, and 2T32 ES007271.
References
- Audoly S, D’angio L, Saccomani MP, Cobelli C. Global identifiability of linear compartmental models. IEEE Trans Biomed Eng. 1998;45:36–47. doi: 10.1109/10.650350. [DOI] [PubMed] [Google Scholar]
- Audoly S, Bellu G, D’Angio L, Saccomani MP, Cobelli C. Global identifiability of nonlinear models of biological systems. IEEE Trans Biomed Eng. 2001;48:55–65. doi: 10.1109/10.900248. [DOI] [PubMed] [Google Scholar]
- Bonhoeffer S, Barbour AD, De Boer RJ. Procedures for reliable estimation of viral fitness from time-series data. Proc R Soc Lond B. 2002;269:1887–1893. doi: 10.1098/rspb.2002.2097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J, Dang Q, Unutmaz D, Pathak VK, Maldarelli F, Powell D, Hu WS. Mechanisms of nonrandom human immunodeficiency virus type 1 infection and double infection: Preference in virus entry is important but is not the sole factor. J Virol. 2005;79:4140–4149. doi: 10.1128/JVI.79.7.4140-4149.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins JA, Thompson MG, Paintsil E, Ricketts M, Gedzior J, Alexander L. Competitive fitness of nevirapine-resistant human immunodeficiency virus type 1 mutants. J Virol. 2004;78:603–611. doi: 10.1128/JVI.78.2.603-611.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Croteau G, Doyon L, Thibeault D, McKercher G, Pilote L, Lamarre D. Impaired fitness of human immunodeficiency virus type 1 variants with high-level resistance to protease inhibitors. J Virol. 1997;71:1089–1096. doi: 10.1128/jvi.71.2.1089-1096.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dang Q, Chen J, Unutmaz D, Coffin JM, Pathak VK, Powell D, KewalRamani VN, Maldarelli F, Hu WS. Nonrandom HIV-1 infection and double infection via direct and cell-mediated pathways. Proc Natl Acad Sci USA. 2004;101:632–637. doi: 10.1073/pnas.0307636100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davison AC, Hinkley DV. Bootstrap Methods and Their Application. Cambridge University Press; Cambridge: 1997. [Google Scholar]
- Dixit NM, Perelson AS. Multiplicity of human immunodeficiency virus infections in lymphoid tissue. J Virol. 2004;78:8942–8945. doi: 10.1128/JVI.78.16.8942-8945.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dixit NM, Perelson AS. HIV dynamics with multiple infections of target cells. Proc Natl Acad Sci USA. 2005;102:8198–8203. doi: 10.1073/pnas.0407498102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dykes C, Wang J, Jin X, Planelles V, An DS, Tallo A, Huang Y, Wu H, Demeter LM. Evaluation of a multiple-cycle, recombinant virus, growth competition assay that uses flow cytometry to measure replication efficiency of HIV-1 in cell culture. J Clin Microbiol. 2006;44:1930–1943. doi: 10.1128/JCM.02415-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Englezos P, Kalogerakis N. Applied Parameter Estimation for Chemical Engineers. Marcel-Dekker; New York: 2001. [Google Scholar]
- Fraser C. HIV recombination: What is the impact on antiretroviral therapy? J R Soc Interface. 2005;2:489–503. doi: 10.1098/rsif.2005.0064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goudsmit J, De Ronde A, Ho DD, Perelson AS. Human immunodeficiency virus fitness in vivo: Calculations based on a single zidovudine resistance mutation at codon 215 of reverse transcriptase. J Virol. 1996;70:5662–5664. doi: 10.1128/jvi.70.8.5662-5664.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goudsmit J, De Ronde A, De Rooij E, De Boer RJ. Broad spectrum of in vivo fitness of human immunodeficiency virus type 1 subpopulations differing at reverse transcriptase codons 41 and 215. J Virol. 1997;71:4479–4484. doi: 10.1128/jvi.71.6.4479-4484.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrigan PR, Bloor S, Larder BA. Relative replicative fitness of zidovudine-resistant human immunodeficiency virus type 1 isolates in vitro. J Virol. 1998;72:3773–3778. doi: 10.1128/jvi.72.5.3773-3778.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holland JJ, de la Torre JC, Clarke DK, Duarte E. Quantitation of relative fitness and great adaptability of clonal populations of RNA viruses. J Virol. 1991;65:2960–2967. doi: 10.1128/jvi.65.6.2960-2967.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu WS, Temin HM. Genetic consequences of packaging two RNA genomes in one retroviral particle: Pseudodiploidy and high rate of genetic recombination. Proc Natl Acad Sci USA. 1990;87:1556–1560. doi: 10.1073/pnas.87.4.1556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeffrey AM, Xia X, Craig I. Identifiability of HIV/AIDS models. In: Tan WY, Wu H, editors. Deterministic and Stochastic Models of AIDS Epidemics and HIV Infections with Intervention. World Scientific; Singapore: 2005. pp. 255–286. [Google Scholar]
- Jung A, Maier R, Vartanian JP, Bocharov G, Jung V, Fischer U, Meese E, Wain-Hobson S, Mayerhans A. Multiply infected spleen cells in HIV patients. Nature. 2002;418:144. doi: 10.1038/418144a. [DOI] [PubMed] [Google Scholar]
- Koval CE, Dykes C, Wang J, Demeter LM. Relative replication fitness of efavirenz-resistant mutants of HIV-1: correlation with frequency during clinical therapy and evidence of compensation for the reduced fitness of K103N + L100I by the nucleoside resistance mutation L74V. Virology. 2006;353(1):184–192. doi: 10.1016/j.virol.2006.05.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy DN, Aldrovandi GM, Kutsch O, Shaw GM. Dynamics of HIV-1 recombination in its natural target cells. Proc Natl Acad Sci USA. 2004;101:4204–4209. doi: 10.1073/pnas.0306764101. and correction (2005) 102, 1808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linga P, Al-Saifi N, Englezos P. Comparison of the Luus–Jaakola optimization and Gauss–Newton methods for parameter estimation in ordinary differential equation models. Ind Eng Chem Res. 2006;45:4716–4725. [Google Scholar]
- Ljung L, Glad ST. On global identifiability for arbitrary model parameterizations. Automatica. 1994;30:265–276. [Google Scholar]
- Luus R, Jaakola THI. Optimization by direct search and systematic reduction of size of search region. AIChE J. 1973;19(4):760–766. [Google Scholar]
- Marée AFM, Keulen W, Boucher CAB, De Boer RJ. Estimating relative fitness in viral competition experiments. J Virol. 2000;74:11067–11072. doi: 10.1128/jvi.74.23.11067-11072.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martinez-Picado J, Savara AV, Sutton L, D’Aquila RT. Replicative fitness of protease inhibitor-resistant mutants of human immunodeficiency virus type 1. J Virol. 1999;73:3744–3752. doi: 10.1128/jvi.73.5.3744-3752.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moles CG, Bangaa JR, Keller K. Solving nonconvex climate control problems: Pitfalls and algorithm performances. Appl Soft Comput. 2004;5:35–44. [Google Scholar]
- Nijhuis M, Deeks S, Boucher C. Implications of antiretroviral resistance on viral fitness. Curr Opin Infect Dis. 2001;14:23–28. doi: 10.1097/00001432-200102000-00005. [DOI] [PubMed] [Google Scholar]
- Nocedal J, Wright SJ. Numerical Optimization. Springer; New York: 1999. [Google Scholar]
- Prado JG, Franco S, Matamoros T, Ruiz L, Clotet B, Menendez-Arias L, Martinez MA, Martinez-Picado J. Relative replication fitness of multi-nucleoside analogue-resistant HIV-1 strains bearing a dipeptide insertion in the fingers subdomain of the reverse transcriptase and mutations at codons 67 and 215. Virology. 2004;326:103–112. doi: 10.1016/j.virol.2004.06.006. [DOI] [PubMed] [Google Scholar]
- Price K, Storn RM, Lampinen JA. Natural Computing Series. Springer; New York: 2005. Differential Evolution: A Practical Approach to Global Optimization. [Google Scholar]
- Quinones-Mateu ME, Ball SC, Marozsan AJ, Torre VS, Albright JL, Vanham G, van Der Groen G, Colebunders RL, Arts EJ. A dual infection/competition assay shows a correlation between ex vivo human immunodeficiency virus type 1 fitness and disease progression. J Virol. 2000;74:9222–9233. doi: 10.1128/jvi.74.19.9222-9233.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quinones-Mateu ME, Arts EJ. HIV-1 fitness: Implications for drug resistance, disease progression, and global epidemic evolution. In: Kuiken C, Foley B, Hahn BH, Marx P, McCutchan FE, Mellors J, editors. HIV Sequence Compendium 2001. Los Alamos National Laboratory; Los Alamos: 2001. [Google Scholar]
- Ritt J. Differential Algebra. American Mathematical Society, Providence; 1950. [Google Scholar]
- Rodriguez-Fernandez M, Egea JA, Banga JR. Novel metaheuristic for parameter estimation in nonlinear dynamic biological systems. BMC Bioinf. 2006;7:483. doi: 10.1186/1471-2105-7-483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seber GAF, Wild CJ. Nonlinear Regression. Wiley; New York: 1989. [Google Scholar]
- Shao J, Tu D. The Jackknife and Bootstrap. Springer; New York: 1995. [Google Scholar]
- Storn R, Price K. Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. J Glob Optim. 1997;11:341–359. [Google Scholar]
- Wu H, Huang Y, Dykes C, Liu D, Ma J, Perelson AS, Demeter L. Modeling and estimation of replication fitness of HIV-1 in vitro experiments using a growth competition assay. J Virol. 2006;80:2380–2389. doi: 10.1128/JVI.80.5.2380-2389.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu H, Zhu H, Miao H, Perelson AS. Parameter identifiability and estimation of HIV/AIDS dynamic models. Bull Math Biol. 2008;70(3):785–799. doi: 10.1007/s11538-007-9279-9. [DOI] [PubMed] [Google Scholar]
- Xia X. Estimation of HIV/AIDS parameters. Automatica. 2003;39:1983–1988. [Google Scholar]
- Xia X, Moog CH. Identifiability of nonlinear systems with applications to HIV/AIDS models. IEEE Trans Automat Control. 2003;48:330–336. [Google Scholar]


