Cognitive and Mathematical Profiles for Different Forms of Learning Difficulties

Abstract

The purpose of this study was to compare subgroups of students with various forms of learning difficulties (< 25th percentile) on cognitive and mathematics characteristics. Students with mathematics difficulty (MD, n = 105), reading difficulty (RD, n = 65), both (MDRD, n = 87), or neither (NoLD, n = 403) were evaluated on an array of cognitive measures (e.g., working memory and language) and on mathematics measures of foundational numerical competencies, computation, and problem solving. Results revealed expected level differences among groups in both domains: NoLD outperformed RD, and MD outperformed MDRD. Profile differences were noted among pairs of subgroups on cognitive measures. On mathematics measures, profile differences were noted between RD and other subgroups, but not between MD and MDRD subgroups. The most discriminating cognitive measures were processing speed and language; the most discriminating mathematics measures depended on the subgroups being compared. Results were further evaluated according to more severe (< 10th percentile) criteria for MD and RD, which generally affected level differences more than the profile patterns. Results have implications for understanding comorbid MD and RD and for conceptualizing core deficits in MD.

Mathematics and reading difficulty are common and often occur together (Badian, 1999; Barbaresi, Katusic, Colligan, Weaver, & Jacobsen, 2005). This overlap raises questions about the origins and nature of the comorbidity, such as how distinct the comorbid condition is from the sum of its constituents. Comorbidities involving reading difficulty (RD) are frequently explored, such as the overlap with attention-deficit/hyperactivity disorder (ADHD; e.g., Pennington, Willcutt, & Rhee, 2005; Willcutt, Pennington, Olson, Chhabildas, & Hulslander, 2005). These studies suggest that some cognitive deficits may be specific to RD (phonological awareness) and others specific to ADHD (behavioral inhibition), whereas still others (processing speed) may be common to both (McGrath et al., 2011; Willcutt et al., 2001). However, comorbidities of mathematics difficulty (MD), including their performance profiles compared to RD, have been considered less systematically.

The present study assessed students with MD versus RD and their combination (MDRD) on a set of mathematics skills (separate from those used to identify the study groups) and a set of cognitive dimensions, using two levels of severity for defining MD and RD. The focus of the present study is on mathematics more than reading, and occurs at the second grade. At this age/grade range, formal written arithmetic skills (e.g., addition vs. subtraction, single- vs. double-digit computation, word problems) are differentiated from and built on more elemental “number sense” skills. That term is defined in numerous ways (e.g., Berch, 2005; Gersten & Chard, 1999), but there is thought to be mapping between a nonsymbolic analog magnitude system and that of symbolic arithmetic (Ansari, 2008; Mundy & Gilmore, 2009; von Aster & Shalev, 2007). However, the causal order of events (Gilmore, McCarthy, & Spelke, 2010) and the specific system that is a deficit for children with MD (Rousselle & Noël, 2007) are not yet clear. Therefore, in the present study we emphasize skills involving a range of what we term foundational numerical competencies that assess linkages among (a) symbolic (Arabic) and analog representations of number; (b) enumeration, labeling, and quantification; and (c) set-based combinatorial procedures. Another reason to focus on mathematics is that antecedents of RD are well known (e.g., phonological awareness and rapid naming), and such language-related processes are also correlated with mathematics performance (Aunola, Leskinen, Lerkkanen, & Nurmi, 2004; Cirino, 2011; Koponen, Aro, & Ahonen, 2009; Krajewski & Schneider, 2009). Some studies differentiate phonological from other language processes in their relation to mathematics; for example, Vukovic and Lesaux (2013) found a direct contribution for phonological decoding, and that the contribution of verbal analogic skills was mediated by symbolic number skill. Beyond foundational numeric competencies and language, other abilities shown to be related to mathematics include working memory and processing speed (e.g., Fuchs et al., 2005; Fuchs et al., 2006; Swanson & Kim, 2007).

Prior Studies of MD and RD Comorbidity

Although the comorbidity of MD and RD has been studied from the perspective of genetics (e.g., Hart, Petrill, & Thompson, 2010; Hart, Petrill, Thompson, & Plomin, 2009) and in terms of natural skill development (e.g., Aunola et al., 2004; Jordan, Hanich, & Kaplan, 2003; Jordan, Kaplan, & Hanich, 2002; Krajewski & Schneider, 2009; Stock, Desoete, & Roeyers, 2009), most studies designed to elucidate the nature of comorbid MD and RD compare learning disability subgroups either on measures of cognitive function or on mathematically related competencies (e.g., Cirino, Fletcher, Ewing-Cobbs, Barnes, & Fuchs, 2007; Fletcher, 2005; Fuchs & Fuchs, 2002; Geary, Hamson, & Hoard, 2000; Jordan & Hanich, 2003; Jordan & Montani, 1997; Powell, Fuchs, Fuchs, Cirino, & Fletcher, 2009).

Cognitively, early studies (see Rourke, 1993, for a summary) focused on differentiating MD and RD subgroups in terms of nonverbal and verbal skills. Studies that focus on language skills, including articulation speed, phonological awareness, and rapid naming, have found superior performance for MD over MDRD (Geary et al., 2000; Jordan et al., 2002). In contrast, for working memory, including measures of visual matrix span, listening span, and digit span, no differences have been documented between MD and MDRD across several studies (Andersson, 2008, 2010; Chan & Ho, 2010; Geary et al., 2000). Swanson and colleagues (Swanson & Jerman, 2006; Swanson, Jerman, & Zheng, 2009) conducted two recent meta-analyses of MD and cognitive functions. The first study found prominent difficulties in verbal problem solving, rapid naming, long-term memory, and working memory (visual and verbal). The later study implemented a common criterion for MD (< 25th percentile), while controlling for reading skill and examining variability across studies. Working memory was found to be a consistent moderator of effect size differences between MD and controls; working memory was a moderator of differences between MD and RD, and long-term memory was a moderator of differences between MD and MDRD; however, phonological processes were not thoroughly examined.

Mathematically, comorbid subgroups have been compared on tasks of both mathematical cognition and mathematical performance. On tasks of quantity, some (e.g., Chan & Ho, 2010) have found that students with MD outperformed those with MDRD on tasks of magnitude comparison, sequencing, and number estimation. Others (Cirino et al., 2007; Hanich, Jordan, Kaplan, & Dick, 2001; Landerl, Fussenegger, Moll, & Willburger, 2009; Rousselle & Noël, 2007) have not found differences in nonsymbolic magnitude comparison or conceptual number knowledge, or on number tasks more generally (Landerl, Bevan, & Butterworth, 2004). Geary et al. (2000) found that in the visual (but not auditory) modality, students with MD outperformed those with MDRD on a symbolic magnitude comparison task. In terms of fact retrieval, students with MD generally outperform those with MDRD (Andersson & Lyxell, 2007; Chan & Ho, 2010; Hanich et al., 2001), but under forced retrieval or timed conditions, the difference is less apparent (Andersson, 2008, 2010; Cirino et al., 2007; Hanich et al., 2001). Procedural arithmetic results have also been variable, with some studies finding no difference between MD and MDRD (Andersson, 2008, 2010) and others reporting a difference (Chan & Ho, 2010). The majority of studies conclude that students with MD perform better than students with MDRD on mathematics story problems (Fuchs & Fuchs, 2002; Hanich et al., 2001; Jordan et al., 2003; Jordan & Hanich, 2000), although there are some recent contrasting results (Andersson, 2008, 2010).

Rationale

In light of these cognitive and mathematical studies of comorbidity, the domains of language, working memory, and foundational numerical competencies each may be relevant for differentiating learning disability subgroups, though comprehensive studies are few. Although RD is considered to be a language-based disorder, with primary deficits in phonological processing and rapid naming, there is no consensus as to the core deficit of MD or on the essential phenotypic criteria for MD. For example, MD may arise from a deficit in some quantity-specific module (e.g., in the representation of magnitude or its mapping onto a symbolic number system; Butterworth, 2005; Dehaene, Spelke, Pinel, Stanescu, & Tsivkin, 1999); if so, such a deficit should be unique to MD (not to RD). An alternative explanation for MD suggests that it stems, at least in part, from domain-general factors (i.e., that affect performance across multiple domains, such as reading and math), some of which would be involved in MD as well as RD (Geary, Hoard, Byrd-Craven, & DeSoto, 2004). Among such domain-general factors, the theoretical basis and empirical evidence for the role of working memory in MD is particularly strong (e.g., Bull & Scerif, 2001; Gathercole & Pickering, 2000; McLean & Hitch, 1999; Swanson, 2006; Swanson, Jerman, & Zheng, 2008), although working memory is defined and operates in a multitude of ways under a variety of conditions (e.g., Raghubar, Barnes, & Hecht, 2010).

The extent to which foundational numerical competencies, language, or working memory (or all) are core issues for MD may vary according to whether reading difficulties are also present (Robinson, Menchetti, & Torgesen, 2002). Thus, MDRD may result from two independent factors (e.g., foundational numerical competencies for math, versus language for reading) or from shared factors (e.g., language or working memory) or from both (e.g., quantity for mathematics, but shared processes for reading and mathematics comorbidity). Whether or not comorbid MDRD has risk factors shared between MD and RD, they may still be differentially relevant, and additional risk factors may be at play for MD or RD separately. One such additional factor is processing speed, which has been found to differentiate students with difficulties in math computation versus math problem solving (Fuchs, Fuchs, et al., 2008) and has also been identified as a shared risk factor for the overlap between RD and ADHD (e.g., Shanahan et al., 2006). Extending this overlap to RD and MD would further support its role in academic skill. A final contributor may be nonverbal reasoning, which is often included in studies involving RD or MD, to distinguish between nonverbal problem solving and visual working memory or as a predictor of mathematics (e.g., Fuchs et al., 2005; Fuchs et al., 2006) or as a component of “IQ” that minimizes verbal skills. In the Swanson et al. (2009) meta-analyses, nonverbal problem solving moderated effect size differences between MD and RD.

Because the identification of learning disability varies according to the definition used (Barbaresi et al., 2005), it is essential to be explicit in this regard. In the literature, low achievement criteria are most common, though the cut point (e.g., 10th, 25th, 35th percentile) and type of measure used (e.g., math facts, computations, problem solving) vary; some also require low performance over time (Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007). The distinction between math disability and difficulty is often made in terms of severity, by differentiating students with very low math achievement scores from those closer to, though often still below, the average range, respectively (Geary et al., 2007; Mazzocco & Kover, 2007; Murphy, Mazzocco, Hanich, & Early, 2007; Raghubar et al., 2009), with broader and more consistent difficulties more apparent in the more severe group. In the present study, we defined subgroups according to low achievement in single word decoding for reading and computations in mathematics. We also contrasted results for cut points of the 25th versus 10th percentile.

The Present Study

An ultimate goal of elucidating competencies among learning disability subgroups is to inform interventions. At the academic level, the content domain and severity of difficulty influence the focus of the intervention, and the pattern of within-domain difficulties (e.g., math fluency, math computations, math problem solving) is relevant to the selection of intervention targets. At the cognitive level, an understanding of shared versus distinct processes can inform intervention design and approach (e.g., the use of language complexity or working memory in delivering interventions). By comparing subgroups on both academic and cognitive skills, the present study affords a contrast to most available studies (which often focus on one or another), and in doing so compares different cut points. Both are needed to better understand the extent to which patterns of cognitive performance are recapitulated academically. Thus, MDRD may be associated with factors more closely associated with RD (phonological awareness), or factors more closely associated with MD (foundational numerical competencies), or it may reflect both to a comparable degree. Because foundational numerical competencies are varied, studies are needed to include a range of these measures, as subgroups of students with LD may vary in their performance, in part because such measures may rely on different basic processes. Deficits may be “additive” in one of two ways: Students with MDRD may have each of the weaknesses found in only MD or RD, or a particular weakness in MDRD may be more severe than the level of weakness found in either MD or RD. The present study has the advantages of a large sample that includes participants in each learning difficulty subgroup (MD, RD, and MDRD). We focus on second grade, which serves as a bridge between studies focusing on precursors (e.g., preschool or kindergarten) and studies that assess cognition and academics in students with established disabilities (e.g., Grade 3 and above). Whereas work has investigated deficits in understanding of math and reading precursors (Mazzocco & Thompson, 2005) and investigating deficits in math and reading at the third grade and above level (Fuchs et al., 2006), the present study deepens the knowledge base at the pivotal second grade level.

Hypotheses

Cognitively, we expected weaknesses in processing speed and nonverbal problem solving to be present (and similar) in students with MD and MDRD; we also expected that students with RD would show similar weaknesses in processing speed (Shanahan et al., 2006), but not in nonverbal reasoning. We expected a “stair-step” pattern for subgroups on language related measures, particularly phonological awareness and rapid naming (MD > RD > MDRD) given that phonological demands are present for both reading and mathematics, but are likely more intensive for reading (Robinson et al., 2002). For working memory, a similar pattern was expected, but where students with MD are more affected than RD (e.g., RD > MD > MDRD). Mathematically, we expected students with MD to exhibit consistently poor performance on measures of foundational numerical competencies, computation, and mathematical problem solving. We expected similar performance between students with MD and MDRD on measures of foundational numerical competencies and computation and did not expect difficulty for students with RD. However, for problem solving, we expected weaknesses in the RD group given the linguistic demands of such measures, more significant difficulty for students with MD, and the greatest difficulty for students with MDRD. Finally, we expected that subgroups defined on the basis of a very low cut point (< 10th percentile) would produce more prominent profile differences than when a more lenient cut point was employed (< 25th percentile).

Method

Participants

Participants were 660 second-grade students in a southeastern metropolitan area in 64 classrooms in 14 schools over two cohorts (two consecutive school years) who met criteria for inclusion in the present study based on performance on the Wide Range Achievement Test–3 (WRAT-3; Wilkinson, 1993). We used a score below the 25th percentile (and then below the 10th percentile) as the cutoff for academic difficulty; all participants met a cutoff (> 2nd percentile) on an intellectual screener (Wechsler Abbreviated Scales of Intelligence; WASI; Wechsler, 1999). We use the term difficulty instead of disability within the MD, RD, and MDRD acronyms due to the criteria of low achievement, and note that selecting students on the basis of this cutoff is not the same as identifying students clinically. Participants were part of a larger sample of students who received the screening, cognitive, and mathematical measures used in this study.

Of the 660 students, 152 (22.0%) fell below the 25th percentile cut score on WRAT-3 Reading, and 192 (29.2%) fell below the cut score on WRAT-3 Arithmetic. There were 105 students with MD, 65 with RD, 87 with MDRD, and 403 who were typically academically developing (hereafter referred to as NoLDs). There was no “buffer zone” (e.g., requiring students with MD to have reading scores well above their math scores), and therefore all students were classified into one of the four groups. When the 10th percentile cut score was utilized, 74 (11.2%) fell below the cut score on WRAT-3 Reading and 86 (13.0%) fell below the cut score on WRAT-3 Arithmetic; again, there was no buffer zone and all students were classified mutually exclusively. There were 56 students with LowMD, 44 with LowRD, 30 with LowMDRD (and therefore 530 with NoLowLD). We considered forming a buffer zone within which students would be excluded. We performed exploratory analyses in this regard. Results, summarized below, did not alter the primary conclusions.

In Table 1, we report performance on study inclusion measures (and age) at the 25th percentile. For age, MDRD students were older than each of the other three subgroups, RD and MD subgroups did not differ from one another, and NoLDs were younger than each of the other subgroups. A similar pattern existed when the low subgroups were compared. Across the four subgroups, performance was in the average range on these definitional measures, but differed by group (all p < .0001). With the 25th percentile cut point, on WRAT-3 Arithmetic, NoLD > RD > MD > MDRD. On WRAT-3 Reading, NoLDs outperformed MD, who in turn outscored both RD and MDRD subgroups, who did not differ from one another. With the 10th percentile cut point, the pattern was similar to that of WRAT-3 Reading at the 25th percentile (i.e., for reading, NoLowLD > LowMD > LowRD = LowMDRD; for math, NoLowLD > LowRD > LowMD = LowMDRD). Differences on these academic measures were expected because they were used to define the groups. Age was variably related to mathematics or cognitive processing variables across groups (particularly among those with MD) and was considered as a covariate in the profile analyses. Measures were administered individually or in groups, and included a mix of normed and experimental measures; therefore raw score performances were used for all measures for consistency. Raw scores were then z-scored to the sample as a whole for purposes of analyses.

Table 1.

Continuous Descriptive and Demographic Characteristics.

Measure	NoLD (n = 403)	RD (n = 65)	MD (n = 105)	MDRD (n = 87)	Total (N = 660)
Age (M, SD)	7.48 (0.32)a	7.73 (0.37)b	7.74 (0.48)b	8.00 (0.46)c	7.61 (0.42)
WRAT-3 Arithmetic (M, SD)	102.03 (8.53)a	98.31 (7.31)b	81.70 (6.51)c	77.88 (7.88)d	95.24 (12.74)
WRAT-3 Reading (M, SD)	108.99 (11.78)a	79.58 (10.01)c	99.25 (8.13)b	76.54 (11.74)c	100.27 (16.91)
Sex (% female)	53.9	51.8	55.9	36.1	51.7
Ethnicity
African American (%)	38.7	57.1	51.0	62.7	45.6
Caucasian (%)	37.2	21.4	26.5	28.9	32.9
Hispanic (%)	17.8	16.1	17.7	6.0	16.1
Other (%)	6.3	5.4	5.7	2.4	5.4
Lunch status (% free/reduced)	74.6	91.1	81.4	90.4	79.3
Retained in grade (%)	0.8	12.5	12.8	26.5	7.2
English second language (%)	6.0	8.9	10.8	3.6	6.7
Special education (%)	2.4	7.1	10.8	15.6	5.9

Note. Age is in years; other scores are standard scores (100/15). Within a row, among the four subgroups, columns with different superscripts are significantly different from one another (p < .05; Tukey corrected). A total of 37 students were missing demographic data; table reflects only students with data. See text for description of demographic differences. MD = mathematics difficulty; MDRD = mathematics and reading difficulty; NoLD = typically academically developing; RD = reading difficulty; WRAT-3 = Wide Range Achievement Test–3.

Other demographic variables are also presented in Table 1 (data were missing for 37 students). Among the other 623 students, the four subgroups did not differ on which of the two school years they were enrolled in the study (on cohort) or English as a second language (p > .05) status, but did differ in other regards. A greater proportion of students in the difficulty subgroups were retained or served in special education (p < .0001). Subgroups also differed in ethnicity (p < .0024), with a higher proportion of African American students in the difficulty subgroups relative to NoLDs and the opposite pattern for Caucasian students. Differences existed according to subsidized lunch status (p < .0010), with higher proportions of students in the RD subgroups receiving subsidized lunch relative to NoLDs. For most of these demograpic variables, there was no consistent or strong pattern of relations with the dependent measures. Free lunch status, special education status, and ethnicity exhibited the largest effects and were therefore considered as covariates in the major analyses, after age was also considered. However, results are reported below with age as the only covariate because their inclusion did not alter any findings.

Measures Used for Identifying Subgroups

The WRAT-3 (Wilkinson, 1993) Arithmetic assesses computational proficiency, although it begins with number competencies including counting and symbolic comparison (oral arithmetic) and then progresses to written arithmetic calculations. Average performance at Grade 2 primarily requires skill in single- and double-digit addition and subtraction. WRAT-3 Reading begins with letter identification and progresses to regular and irregular words that increase in difficulty. Reliability for each measure was ~.94 in this age range. Table 1 provides descriptive data. Table 2 shows group means, standard deviations, skew, kurtosis, and reliabilities for cognitive and mathematics variables in their original metrics, and scaled scores, where available.

Table 2.

Performance on Cognitive and Mathematics Measures (N = 660).

Measure	Raw Mean	SD	Skewness	Kurtosis	Reliability	Scale Scorea	SD
Cognitive
WJ-III Cross Out	11.51	2.67	−0.03	0.36	.91	95.63	13.14
WASI Matrix Reasoning	11.97	6.08	0.51	−0.79	.94	47.78	10.56
WASI Vocabulary	23.16	6.93	0.16	0.13	.86	45.14	10.76
CTOPP Elision	8.72	4.03	1.02	0.39	.91	9.40	2.63
CTOPP Rapid Digit Naming (s)	50.96	13.72	1.44	2.61	.84	9.41	1.90
CTOPP Rapid Letter Naming (s)	52.02	12.97	1.47	3.40	.70	9.88	1.77
WMTB-C Listening Recall	7.65	3.42	0.04	−0.04	.81	86.75	17.02
WMTB-C Digits Backward	9.88	3.55	0.05	0.37	.83	90.47	17.02
WMTB-C Counting Recall	14.40	4.41	0.48	0.31	.81	84.12	14.94
Mathematical
Number Line Average Deviation (cm)	14.87	6.34	0.51	0.12	.91
KeyMath-R Numeration	10.38	2.88	0.25	−0.16	.91	11.15	2.20
Number Sets (d-prime)	0.08	1.26	−0.69	1.05	.70–.90
Addition Strategy Really Fast Correct	8.25	3.73	−0.32	−0.87	.87
Addition Strategy Really Fast RT (ms)	4754	2250	1.19	1.61	.84
Basic Facts Addition 0–12	8.68	4.79	0.82	0.67	.88
Basic Facts Addition 0–18	6.50	3.70	0.66	0.80	.86
Basic Facts Subtraction 0–12	4.37	2.62	0.54	0.16	.91
Basic Facts Subtraction 0–18	3.09	2.44	0.95	0.86	.89
Single Digit Story Problems	7.40	3.83	0.11	−1.05	.83
Vanderbilt Story Problems	7.19	4.05	0.51	−0.50	.86
KeyMath-R Problem Solving	2.51	1.69	0.51	0.42	.72	10.82	2.10

Note. Values reflect raw data prior to standardization, and after data trimming and imputation; values also include components of composites used for analyses (two Rapid Naming variables combined for cognitive, four Basic Facts measures combined for mathematical, Vanderbilt Story Problems and Single Digit Story Problems combined for mathematical). CTOPP = Comprehensive Test of Phonological Processing; RT = response time; WASI = Wechsler Abbreviated Scales of Intelligence; WJ-III = Woodcock–Johnson–III Tests of Cognitive Abilities; WMTB-C = Working Memory Test Battery for Children.

^aScale scores reported where available. WJ-III and WMTB-C measures are expressed as standard scores (M = 100; SD = 15); CTOPP and KeyMath-R measures are expressed as scaled scores (M = 10; SD = 3); WASI measures are expressed as T-scores (M = 50; SD = 10).

Cognitive Measures Used for Investigating Differences among Subgroups

Woodcock–Johnson–III Tests of Cognitive Abilities (WJ-III; Woodcock, McGrew, & Mather, 2001) Cross Out measures processing speed by asking students to locate and circle two identical visuographic symbols in rows of six symbols; students have 3 min to complete 60 rows and earn credit by correctly circling the matching symbols in each row. As reported by the test developer, reliability is .91 for 8-year-olds.

The three central executive subtests of the Working Memory Test Battery for Children (WMTB-C; Pickering & Gathercole, 2001) were used. Each subtest has six items at span levels from 1–6 to 1–9. Passing four items at a level moves the child to the next level. Failing three items terminates the subtest. We used the trials correct score. Raw scores were used for analyses. For Listening Recall, the child determines if a sentence is true, then recalls the last word in a series of sentences. For Counting Recall, the child counts a set of 4, 5, 6, or 7 dots on a card and then recalls the number of counted dots at the end of a series. Backward Digit Recall is a standard format backward digit span. As per the test developer, test–retest reliability is .81 to .83.

We assessed phonological awareness (PA) and rapid automatized naming (RAN) with the Comprehensive Test of Phonological Processing (CTOPP; Wagner, Torgesen, & Rashotte, 1999). For PA, we used Elision, which presents a word, from which students remove a sound. The sound begins as a syllable and progresses to phonemes; they vary in position (rime, onset, middle). The result is always a real word. For RAN, we used Rapid Letter Naming and Rapid Digit Naming. For each, students are shown 36 letters or numbers and “read” them as quickly and as accurately as possible. Raw scores were used for analyses to be consistent with other measures, and the RAN measures were combined to form a composite (r = .82). Reliability estimates range from .70 to .91 in this age range.

We used two WASI (Wechsler, 1999) subtests. Vocabulary measures expressive vocabulary and verbal knowledge with 42 items. For most items, the tester says a word for the student to define. As per Wechsler (1999), split-half reliability is .86. Matrix Reasoning measures non-verbal reasoning with pattern completion, classification, analogy, and serial reasoning tasks. Students are shown a matrix with a section missing and restore the matrix by selecting from among five options. Reliability is .94. We considered these as measures of these specific cognitive skills, rather than as global measures of intellectual functioning; again, raw scores were used.

Mathematics Measures Used for Investigating Differences Among Subgroups

Foundational numerical competencies

KeyMath-R (KM-R) Numeration (Connolly, 1998) requires students to count or order sequences, use place value, and identify fractions, decimals, and percentages. Sample standardized raw scores were used. As per Connolly, reliability is .91. At Grade 2, average performance requires the ability to count, sequence numbers, appreciate magnitude, and understand place value. Number Line Estimation (Siegler & Booth, 2004) assesses approximate spatial representations of large quantities. A total of 24 number lines containing a blank line with two endpoints (0 and 100) are presented, one at a time, with a target number (e.g., 45) in a large font printed above the line. The child places the target number on the line. Accuracy is the absolute difference between the placement and the correct position. Fuchs et al. (2010) correlated procedural calculations and word problems with various ways of indexing performance; the best predictor was absolute number line error, r(280) = .46 to .59, as per Geary, Hoard, and Bailey (2012). Cronbach’s alpha on this sample was .91. The Number Sets Test (Geary, Bailey, & Hoard, 2009) assesses the speed and accuracy with which children understand and manipulate small, exact numerosities (< 10) while transcoding between those quantities and their Arabic numerals. Geary et al. (2007) found good reliability for hits (α = .88), correct rejections (α = .85), misses (α = .70), and false alarms (α = .90), which produce a d-prime score that has been shown to capture variance unique to mathematics achievement (e.g., Geary et al., 2009). We used d-prime.

Basic facts

The Math Facts Fluency Assessment (Fuchs, Hamlett, & Powell, 2003; administered in groups) includes four measures of single-digit addition and subtraction (i.e., addition with sums up to 12; addition with sums up to 18; subtraction with minuends up to 12; subtraction with minuends up to 18). For each, students have 1 min to complete as many of 25 problems as possible. For the four subtests, respectively, alpha was .88, .91, .86, and .89 (Fuchs et al., 2009). These measures intracorrelated .50 to .76, so they were formed into a composite. A portion of the Addition Strategies Assessment (Geary, Hoard, & Hamson, 1999) was used, in which students are presented 14 “really fast” single-digit addition problems horizontally on a computer screen and answer each problem as fast as possible. Response times and accuracy are recorded, each with alpha of .84 to .87.

Word problems

With KM-R Problem Solving (Connolly, 1998), students solve word problems presented orally and in written form. We used sample standardized raw scores. Split-half reliability is .72. Correlations with the Total Mathematics score of the Iowa (Hoover et al., 1993) is .60. There are three types of items: routine, “textbook-style” word problems with transparent solution strategies; nonroutine word problems without clearly perceived solution strategies; and items that require the student to demonstrate comprehension of a word problem, without solving it. Single Digit Story Problems (Jordan & Hanich, 2000; Riley & Greeno, 1988) comprises 14 word problems presented orally and in written form, involving single-digit addition or subtraction, and addresses compare, grouping, or change problem structures. Alpha in a similar sample was .83 (Fuchs et al., 2009). Vanderbilt Story Problems (Fuchs & Seethaler, 2008) has 18 word problems of compare, grouping, or change problem structures but involving multidigit addition and subtraction, including relevant information embedded in problem narratives or graphics, incorporating irrelevant information, and requiring some multistep solutions. Information is presented orally and in written form. Alpha is .86 (Fuchs et al., 2009). The latter two measures correlated .78, so a composite was formed; KM-R Problem Solving correlated less well with the other two measures, so it was considered separately.

Procedure

Students were assessed in their classrooms (for measures administered in group) or in locations within schools (for measures administered individually). Students were assessed on definitional measures and WASI in September. Other cognitive and mathematics measures were administered in October. Examiners had experience testing in schools and were trained to criterion on each measure. All individual test sessions were audiotaped, and a random sample of sessions was rescored from tapes by a second research assistant, with agreement at .98. Once testing was completed, all protocols were double entered/verified, before scores were finalized in the database. Standard scores, where available, were computed for all measures after testing was completed, tagged to the date of evaluation for that measure.

Analysis Plan

First, variable distributions, outliers, and influential observations were examined within and across the learning subgroups. A total of 51 values across the 21 original values (< 0.37% of the total) had univariate outliers that produced distributional skewness and/or kurtosis and were graphically separable from the rest of the distribution within and across groups. One approach to these extreme individual data points was to trim them to a lesser value that improved the distributions but maintained participants’ rank orderings. Similar approaches have been used elsewhere (e.g., Willcutt et al., 2005). In all, 25 students were missing data for one or more of variables (47 or 0.33% values), which were imputed with the PROC MI procedure in SAS (SAS Institute, 2002–2011); for simplicity and given the very small amount of imputed data, one of these data sets was randomly chosen for analysis. Variables were then z-scaled based on the full sample of 660 and ordered such that higher scores indicated better performance. Composites were also computed at this point, resulting in eight cognitive and eight mathematical variables used in analyses. Within math and cognitive domains, the eight variables were regressed on WRAT-3 Arithmetic scores, to examine residuals, influential observations, and multivariate outliers. Individuals with studentized residuals of plus or minus 3 or with a computed Mahalanobis distance that exceeded the critical chi-square value based on the N and k used here were then determined (n = 10 across groups, or 1.5%). Results were highly similar with and without these participants. We report the data set with trimmed outlier observations and imputed data to minimize distributional disruption and maximize the amount of data (see Table 2). Exclusion of potential multivariate outlier observations also did not affect any results substantively.

We used profile analysis via MANOVA (Stevens, 1996; Ullman, 2007; Weinfurt, 2000) as our primary analytic technique; the within-subjects factor was the array of mathematical or cognitive competencies and the between-subjects factor was learning difficulty subgroup. Three types of results are provided. Flatness refers to whether the repeated measures pooled over groups differ, that is, the overall effect of the within-subjects factor, which is minimized in this study given that each measure was z-standardized against the full sample. Elevation is the main effect of the between-groups factor across the measures. Shape is of primary interest; it is the interaction of the between- and within-subjects factors (i.e., whether the pattern of performance of the learning subgroups differs across mathematical or cognitive variables). Follow-ups to significant shape effects removed the elevation effect and involve an exploration of the pooled-within canonical structure coefficients and the canonical standardized coefficients. Canonical structure coefficients are loadings of individual variables (correlations of variables with the discriminant functions that separate the groups); standardized coefficients function as beta weights describing the unique contribution of each variable to group separation. Because there were more than two groups, residualized shape effects were evaluated with three multivariate contrasts among the learning difficulty subgroups (MD vs. RD, MD vs. MDRD, RD vs. MDRD) and an additional contrast between NoLD and RD. Among the variables contributing to the discriminant functions, groups were compared with univariate analyses, with Tukey–Kramer correction for multiple comparisons. We performed analyses first with the 25th percentile cut point and then with the 10th percentile cut point.

Results

Cognitive Profile

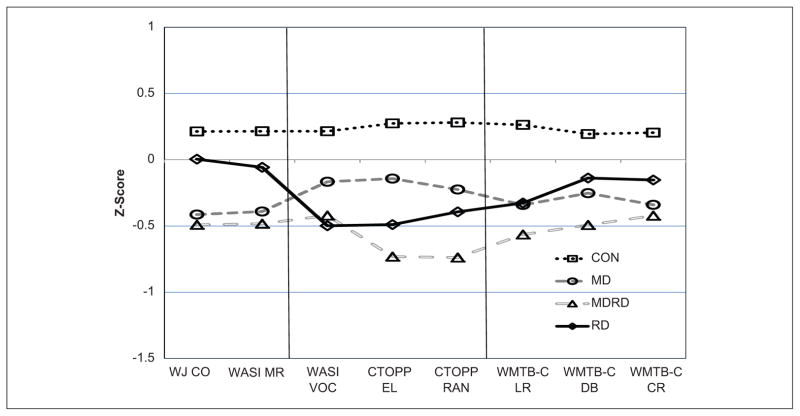
The overall multivariate group effect was significant, F(24, 1880) = 9.33, p < .001, with a large effect size (Wilks’s Λ = .721, approximately equivalent to η² = .28); the age effect was also significant, p < .001. The effect for cognitive measure, F(7, 649) = 1.59 (Wilks’s Λ = .983), p = .136, was not significant, but there was a significant interaction of group by measure, F(21, 1864.1) = 2.17 (Wilks’s Λ = .933), p < .002. This suggested that the pattern of group differences varied by cognitive measure. The four planned contrasts revealed that pairs of learning difficulty subgroups differed in their performance across cognitive measures, NoLD versus RD, F(8, 648) = 9.80 (Wilks’s Λ = .892), p = .001, MD versus RD, F(8, 648) = 3.53 (Wilks’s Λ = .958), p < .001, RD versus MDRD, F(8, 648) = 2.53 (Wilks’s Λ = .969), p = .010, and MD versus MDRD, F(8, 648) = 3.89 (Wilks’s Λ = .954), p = .001. In terms of overall severity (effect of group on a single variable representing the average of all cognitive variables), all subgroup pairs differed, except MD and RD, F(1, 655) < 1, suggesting that these groups differed in their pattern of performance but not their overall level. Figure 1 shows cognitive performance profiles, and Table 3 shows effect sizes among the three learning difficulty groups.

Figure 1.

Performance on cognitive measures (controlling for age), by learning subgroup (25th percentile).

Note. CO = Cross Out; CON = control; CR = Counting Recall; CTOPP = Comprehensive Test of Phonological Processing; DB = Digits Backward; EL = Elision; LR = Listening Recall; MD = mathematics difficulty; MDRD = mathematics and reading difficulty; MR = Matrix Reasoning; RAN = Rapid Automatized Naming; RD = reading difficulty; VOC = Vocabulary; WASI = Wechsler Abbreviated Scales of Intelligence; WJ = Woodcock–Johnson–III Tests of Cognitive Abilities; WMTB-C = Working Memory Test Battery for Children.

Table 3.

Effect Sizes Comparing Learning Difficulty Subgroups on Cognitive Measures.

Measure	NoLD vs.			RD vs.		MD vs.
	RD	MD	MDRD	MD	MDRD	MDRD
WJ-III Cross Out	0.21	0.63	0.70	0.42	0.50	0.08
WASI Matrix Reasoning	0.27	0.61	0.70	0.33	0.43	0.09
WASI Vocabulary	0.71	0.38	0.64	−0.33	−0.08	0.25
CTOPP Elision	0.76	0.42	1.00	−0.35	0.24	0.59
CTOPP Rapid Naming	0.67	0.51	1.02	−0.17	0.35	0.51
WMTB-C Listening Recall	0.59	0.60	0.83	0.02	0.24	0.22
WMTB-C Digits Backward	0.33	0.45	0.69	0.11	0.35	0.24
WMTB-C Counting Recall	0.36	0.55	0.63	0.19	0.27	0.08

Note. Effect sizes are computed as differences between least-squares means (controlling for age) of standardized variables. Positive values indicate better performance for the group listed first. CTOPP = Comprehensive Test of Phonological Processing; MD = mathematics difficulty; MDRD = mathematics and reading difficulty; NoLD = typically academically developing; RD = reading difficulty; WASI = Wechsler Abbreviated Scales of Intelligence; WJ-III = Woodcock–Johnson–III Tests of Cognitive Abilities; WMTB-C = Working Memory Test Battery for Children.

With elevation effects removed, the multivariate group effect (now representing shape) was significant, F(24, 1880) = 2.26, p < .001, with a small to moderate effect size (Wilks’s Λ = .920 approximate η² equivalent = .08). Group contrasts represent a comparison of cognitive profiles with elevation removed. The contrast of NoLD and RD was significant, F(8, 648) = 3.12 (Wilks’s Λ = .962), p < .001, and canonical contributions were explored to evaluate measures that maximally separated groups in their profiles. Canonical loadings for this subgroup difference were largest for measures of language (Elision, +0.55; Vocabulary, +0.45; Rapid Naming, +0.42); this is, students with RD showed weaknesses relative to the NoLD group in language measures. The pattern of standardized coefficients differed somewhat, with large values not only for the language measures, but also for Cross Out (−0.43), Listening Recall (+0.37), and Matrix Reasoning (−0.36). Univariate differences (Tukey corrected) were significant for Elision (p = .031). The overall pattern is consistent with Figure 1, showing that RD diverges from NoLD on language measures, but not for Cross Out or Matrix Reasoning.

The residualized contrast of MD versus RD was also significant, F(8, 648) = 3.57 (Wilks’s Λ = .957), p < .001. The largest contributions to this effect were for Cross Out (−0.47), Elision (+0.47), Vocabulary (+0.43), and Matrix Reasoning (−0.37); these measures also had the largest standardized coefficients, range |r| = .46 to .52. Univariate differences between MD and RD were significant only for Cross Out (p = .050). Again, Figure 1 shows the more general pattern that MD students scored above the RD subgroup on several language measures but below RD students on processing speed or nonverbal reasoning. For RD versus MDRD, the contrast was not significant, F(8, 648) = 1.29, p = .245, suggesting that the profile difference seen in the raw data was largely attributable to level differences.

For the MD versus MDRD comparison, the multivariate contrast was significant, F(8, 648) = 2.25 (Wilks’s Λ = .972), p < .022. The largest canonical contributions to this effect were Elision (+0.69) and Rapid Naming (+0.59); Elision and Rapid Naming also had the largest standardized coefficients (+0.77 and +0.56, respectively). Univariate comparisons revealed that students with MD outperformed those with MDRD on Elision, p = .017. Figure 1 shows this graphically, as well as the similarity on other cognitive measures.

In sum, there were consistent level differences among the subgroups, with NoLD outperforming students with RD or MD, which both outperformed students with MDRD. Differences in pattern were also observed, highlighted by students with RD who were strong in processing speed relative to the MD subgroups, and students with MD who were strong in language relative to the RD subgroups.

Mathematics Profile

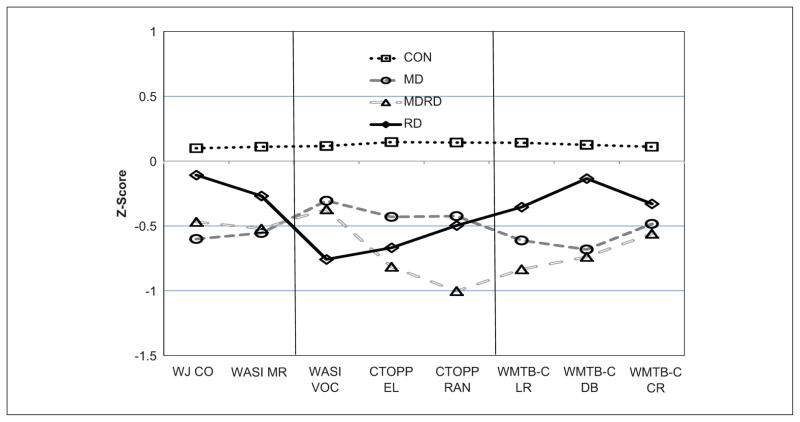
The overall multivariate group effect was significant, F(24, 1880) = 12.07, p < .001, with a large effect size (Wilks’s Λ = .659, approximate η² = .34); age was also significant, p < .001. The effect for mathematics measure was not significant, F(7, 649) = 1.92 (Wilks’s Λ = .979), p = .064, but the interaction of group by measure was, F(21, 1864.1) = 3.86 (Wilks’s Λ = .884), p < .001. This suggests that the pattern of group differences varies by measure. Planned contrasts revealed significant subgroup differences across mathematical performance for NoLD versus RD, F(8, 648) = 8.30 (Wilks’s Λ = .659), p = .001, for RD versus MD, F(8, 648) = 4.09 (Wilks’s Λ = .951), p < .001, and for RD versus MDRD, F(8, 648) = 5.90 (Wilks’s Λ = .932), p = .001. The MD versus MDRD contrast was not significant, F(8, 648) = 1.33, p = .226, indicating a similar pattern in these two subgroups. However, an overall level effect between these subgroups was noted, F(1, 655) = 8.87, p = .003, with stronger performance for MD relative to MDRD. Each of the other overall subgroup contrasts were also significant, reflecting level or elevation differences (NoLD vs. RD, p < .0001; RD vs. MD, p < .006; RD vs. MDRD, p < .001). Figure 2 shows profiles of mathematical performance, and Table 4 shows effect sizes between the three learning difficulty subgroups.

Figure 2.

Performance on mathematical measures (controlling for age), by learning difficulty subgroups (25th percentile).

Note. AS RF CORR = Addition Strategy Correct; AS RF RT = Addition Strategy Response Time; BASIC FACTS = composite of four subtests of Math Facts Fluency Assessment; CON = control; KM NUM = KeyMath-R Numeration; KM PSOLVE = KeyMath-R Problem Solving; MD = mathematics difficulty; MDRD = mathematics and reading difficulty; N LINE = Number Line Estimation; NUM SETS = Number Sets Test; RD = reading difficulty; WORD PROB = composite of Single Digit Story Problems and Vanderbilt Story Problems.

Table 4.

Effect Sizes Comparing Learning Difficulty Subgroups on Mathematical Measures.

Measure	NoLD vs.			RD vs.		MD vs.
	RD	MD	MDRD	MD	MDRD	MDRD
Number Line	0.53	0.55	0.84	0.02	0.31	0.28
KeyMath-R Numeration	0.95	0.91	1.23	−0.04	0.28	0.33
Number Sets	0.44	0.99	1.16	0.55	0.72	0.17
Addition Strategy Correct	0.50	0.64	0.79	0.14	0.29	0.15
Addition Strategy Response Time	0.16	0.49	0.67	0.34	0.52	0.18
Basic Facts	0.40	0.81	1.05	0.42	0.66	0.24
Word Problems	0.56	0.95	1.26	0.39	0.70	0.31
KeyMath-R Problem Solving	0.63	0.78	1.08	0.14	0.45	0.30

Note. Effect sizes are computed as differences between least-squares means (controlling for age) of standardized variables. Positive values indicate better performance for the group listed first. MD = mathematics difficulty; MDRD = mathematics and reading difficulty; NoLD = typically academically developing; RD = reading difficulty.

With elevation effects removed, the multivariate group effect (shape) was significant, F(24, 1880) = 3.45, p < .001, with a moderate effect size (Wilks’s Λ = .882 approximate η² equivalent = .12). The NoLD versus RD contrast was significant, F(8, 648) = 4.07 (Wilks’s Λ = .952), p < .001, and the largest canonical contributor to this effect was Numeration (+0.76), followed by response time from the Addition Strategy Task (−0.34). These measures also had the largest standardized coefficients (+1.11 and −0.54, respectively). Thus, students with RD were unexpectedly weak on Numeration and unexpectedly strong for basic fact response time. Univariate comparisons revealed that these groups differed on Numeration, p < .001.

The MD versus RD comparison was significant, F(8, 648) = 2.91 (Wilks’s Λ = .965), p < .003, with the largest canonical loadings for Number Sets (+0.44) and Numeration (−0.41). These measures also had the largest standardized coefficients (+0.68 and −0.80, respectively), followed by those of the word problems (+0.48) and the basic facts composite (+0.36). The univariate comparisons revealed that these groups did not significantly differ on any individual measure. The MD versus MDRD multivariate contrast was not significant, F(8, 648) < 1.

The RD versus MDRD comparison was significant, F(8, 648) = 2.35 (Wilks’s Λ = .971), p = .016. Since MD versus MDRD patterns did not differ except in level, the pattern for RD versus MDRD resembled that of RD versus MD. The largest canonical loadings for this effect were for Number Sets (+0.50), the basic facts composite (+0.51), and word problems (+0.52). These variables also had large standardized coefficients (+0.52. +0.51, and +0.68, respectively), as did Numeration (−0.65). RD students exhibited relative strengths in the first three areas relative to MDRD students, but a relative weakness in the latter. None of the univariate comparisons were statistically significant.

In sum, there were consistent level differences in mathematics among subgroups, with NoLD outperforming students with RD, who outperformed students with MD, followed by students with MDRD. Differences in pattern were also observed for all groups except between MD and MDRD, highlighted by an unexpected weakness for the RD group relative to NoLD on Numeration, and strengths for the RD group relative to the subgroups with MD in Number Sets, basic facts, and word problems.

Effect of Cut Point

The same procedures were repeated, this time reserving designation as learning difficulty only when performance was < 10th percentile. Results are displayed in Figures 3 (cognitive profiles) and 4 (mathematical profiles).

Figure 3.

Performance on cognitive measures (controlling for age), by learning subgroup (10th percentile).

Note. CO = Cross Out; CON = control; CR = Counting Recall; CTOPP = Comprehensive Test of Phonological Processing; DB = Digits Backward; EL = Elision; LR = Listening Recall; MD = mathematics difficulty; RAN = Rapid Automatized Naming; RD = reading difficulty; MDRD = mathematics and reading difficulty; MR = Matrix Reasoning; VOC = Vocabulary; WASI = Wechsler Abbreviated Scales of Intelligence; WJ = Woodcock–Johnson–III Tests of Cognitive Abilities; WMTB-C = Working Memory Test Battery for Children.

Cognitive

As with the 25th percentile cut point, the overall multivariate group effect was significant, F(24, 1880) = 6.48, p < .001, with a large effect size (Wilks’s Λ = .794); the age effect was also significant, p < .001. Again, the effect for cognitive measure was not significant (p = .214), but the interaction of group by measure was, F(21, 1864.1) = 1.86 (Wilks’s Λ = .942), p < .010. As before, contrasts of profiles revealed significant interactions for NoLowLD versus LowRD, F(8, 648) = 7.13 (Wilks’s Λ = .919), p = .001, for LowMD versus LowRD, F(8, 648) = 3.11 (Wilks’s Λ = .963), p < .001, and for LowRD versus LowMDRD, F(8, 648) = 2.35 (Wilks’s Λ = .971), p = .017. The primary difference from the higher cut point was that now the contrast for LowMD versus LowMDRD, F(8, 648) = 1.48 (Wilks’s Λ = .982), p = .159, was no longer significant. In terms of severity, most subgroups differed from one another, except for LowRD and LowMD (p = .271), which was similar to findings with the higher cut point. However, now students with LowMD and LowMDRD also did not differ (p = .224) from one another.

With elevation effects removed, the multivariate group effect (now representing shape) was significant, F(24, 1880) = 1.84, p < .010 (Wilks’s Λ = .935). The contrast of NoLowLD and LowRD was significant, F(8, 648) = 2.55 (Wilks’s Λ = .969), p < .001. Canonical loadings for this effect were largest for language measures (Elision, +0.56; Vocabulary, +0.64; Rapid Naming, +0.33). The pattern of standardized coefficients differed somewhat, with large values not only for the language measures, but also for Cross Out (−0.45) and Digits Backward (−0.33). Univariate differences (Tukey corrected) were significant for Elision (p = .049), for Vocabulary (p = .019). For the LowMD versus LowRD comparison, the multivariate contrast was significant, F(8, 648) = 3.10 (Wilks’s Λ = .963), p < .002. The largest canonical contributions to this effect were for Cross Out (−0.36), Elision (+0.38), Vocabulary (+0.59), and Digits Backward (−0.43); these measures also had the largest standardized coefficients, range |r| = .35 to .70. Univariate differences between LowMD and LowRD were significant only for Vocabulary (p = .016). The multivariate contrast of LowMD versus LowMDRD was not significant, F(8, 648) = 1.26, p = .259, nor was the contrast of LowRD versus LowMDRD, F(8, 648) = 1.82, p = .071.

Mathematics

As with the 25th percentile cut point, the overall multivariate group effect was significant, F(24, 1880) = 8.06, p < .001, with a large effect size (Wilks’s Λ = .752); the age effect was also significant, p < .001, and the effect for mathematical measure was not (p = .214), but the interaction of group by measure was significant, F(21, 1864.1) = 2.26 (Wilks’s Λ = .930), p < .009. The same pattern of planned contrasts also emerged, for NoLowLD versus LowRD, F(8, 648) = 17.52 (Wilks’s Λ = .822), p = .001, for LowMD versus LowRD, F(8, 648) = 2.94 (Wilks’s Λ = .965), p < .001, for LowRD versus LowMDRD, F(8, 648) = 2.72 (Wilks’s Λ = .967), p = .005, though not for LowMD versus LowMDRD, F(8, 648) < 1. The only difference in terms of overall severity was that LowMD and LowM-DRD did not differ from one another; all other subgroups differed from one another, similar to results with the 25th percentile cut point.

With elevation effects removed, the multivariate group effect (now representing shape) was significant, F(24, 1880) = 2.00, p < .002 (Wilks’s Λ = .929). In contrast to results with the 25th percentile, where contrasts were significantly different for NoLD versus RD, RD versus MD, and RD versus MDRD, now the only nominally significant multivariate contrast was for NoLowLD and LowRD, F(8, 648) = 1.95 (Wilks’s Λ = .976), p = .050. The largest canonical contributors were Numeration (+0.62), the word problems composite (+0.42), and Problem Solving (+0.57), though the largest standardized coefficients were for Numeration (+0.65), Addition Strategy correct and response times (−0.56 and −0.65), and, to a lesser degree, Problem Solving (+0.46).

Exploratory Analyses

We also ran analyses excluding students in a “buffer” zone (for the 25th percentile cut point, students with scores from the 25th to 40th percentiles were excluded; for the 10th percentile cut point, students with scores from the 10th to 25th percentiles were excluded). In the first case, 139 NoLD, 41 MD, no MDRD, and 28 RD were removed; in the second case, 127 NoLowLD, 20 LowMD, no LowMDRD, and 17 LowRD were removed. Thus, the effect was to artificially create more extreme groups, but the process did not change individual subject groupings. The primary result of these analyses was to increase the relative distances, predominantly between the NoLD and the learning difficulty subgroups, although the profile pattern was not substantively different. Where group by measure interactions were significant in the analyses reported above, they were also significant in the analyses using the buffer zone. For example, in the cognitive domain, with the 25th percentile, the initial cognitive by group interaction was p < .002, whereas with the buffer zone, the interaction was p < .022. For math at the 25th percentile, the initial math by group interaction was p < .001, whereas with the buffer zone, the interaction was p < .001 as well. For the 10th percentile cognitive, the interactions were similar in the initial (p < .010) and buffer zone (p < .014); this was also the case in the mathematics domain (p < .001 initial and with buffer zone). Patterns of subgroup profile differences across cognitive or mathematical performance were similar with and without the buffer zone. At the 25th percentile, a difference (with elevation removed) was that the RD and NoLD subgroups were no longer different across cognitive measures (p = .0675). At the 10th percentile, a difference was that MD and MDRD subgroups were now significantly different across cognitive measures (p < .024), although the largest canonical contributor to this difference (rapid naming) was similar with and without the buffer.

Discussion

The aim of this study was to evaluate the mathematical and cognitive profiles of subgroups with differing patterns of learning achievement. Differences between students with MD and RD were expected, though a key issue was whether and if so to what extent MDRD was separable from the single disorders (particularly MD) in terms of severity or the shape (profile) of performance. Although there have been some previous comparisons of these subgroups on some similar measures, the present study contributes to the literature by examining a large sample of young learners with different forms of academic difficulty on an array of mathematical competencies and cognitive resources. In doing so, this study addressed issues related to sample size, methodology, and definitional issues. Moreover, the focus on second grade expands our knowledge of competencies at this transitional age point. We discuss cognitive performance first and then consider the extent that those differences are recapitulated in the mathematical profiles.

Cognitive Performance

The cognitive measures were chosen due to their relevance to mathematics, so students with MD (and MDRD) were expected to manifest general deficits relative to those with NoLD. Students with RD were expected to outperform or perform similarly to students with MD on most measures, but to have greater weaknesses than students with MD in language. Students with MD were expected to outperform those with MDRD. Hypotheses were partially supported.

Students with MDRD performed below the level of students with either MD or RD, who did not differ from one another, but each performed below students with NoLD. In addition, all subgroups differed from one another in shape. Relative to their own overall cognitive level, the pattern for RD was characterized by weaknesses on language measures and to a lesser extent on verbal working memory. RD students were also characterized by relative strengths in processing speed and nonverbal reasoning. In contrast, the pattern for students with MD was relatively flat, which is consistent with how the cognitive measures were chosen. The pattern for MDRD was similar to that of RD, without the strengths in processing speed and nonverbal reasoning. Across groups, students with RD outperformed MD on processing speed and nonverbal reasoning, with the opposite pattern for language measures. The cognitive profile of the comorbid group was additive in two ways. First, this subgroup had the cognitive weaknesses associated with either MD or RD; second, weaknesses of the comorbid group surpassed those of MD for PA and rapid naming. These patterns are reflected in Figure 1 and in Table 3.

Differences among subgroups in language are consistent with early predictors of reading skill (e.g., Ackerman & Dykman, 1993; Schatschneider, Fletcher, Francis, Carlson, & Foorman, 2004; Wolf et al., 2002). As suggested by Robinson et al. (2002), intactness of phonological representations is relevant for both MD and RD, although to a stronger degree in the latter subgroup. Involvement of phonological representations also is consistent with some early explanations for the comorbidity of these disorders (Geary, 1993).

The processing speed results are interesting given the literature on the comorbidity of RD with ADHD, where processing speed is often considered a shared risk factor for those two disorders (e.g., McGrath et al., 2011; Shanahan et al., 2006; Willcutt et al., 2005). However, the present findings suggest that processing speed is not a global shared factor. Students with MD but not RD experienced such difficulty, regardless of the severity of cut point. Even at an absolute level, students with RD performed within the average range on this measure. Our measure of processing speed involved only speeded perceptual discrimination among pictures rather than decision speed, symbol association, or verbal output. In the mathematics literature, processing speed is frequently assessed with a measure of rapid naming, which makes it difficult to ascertain the speed component separate from the language demands of the measure. Recently, Compton, Fuchs, Fuchs, Lambert, and Hamlett (2012) found strengths in processing speed in learning disabled subgroups defined on the basis of word reading or reading comprehension. Also, Fuchs, Fuchs, et al. (2008) found that processing speed was a specific weakness for students with computational difficulties relative to those with word problems difficulties. Students with MD who exhibit fact recall difficulties by definition are slow in recall, but the extent to which this is a processing speed issue per se is currently unclear. It may be more relevant for computations than for problem solving.

Mathematical Performance

For foundational numerical competencies or computation, we expected neither NoLD nor students with RD to exhibit difficulties, but expected both groups to outperform those with MD, who would in turn outperform MDRD. For problem solving, we expected students with either MD or RD to have moderate difficulty relative to NoLD, but that students with MDRD would have more extreme difficulty. Hypotheses were only partially supported.

On mathematical measures, students with RD performed below the level of students with NoLD; students with MD performed below this level, and students with MDRD showed the weakest performance. Profile differences were noted among all subgroups, except for MD and MDRD, who differed only in severity, with the comorbid group showing weaker performance than either single-deficit group. Relative to their overall mathematics level, the pattern for RD was characterized by a strength in basic facts response time, with performance there similar to that of NoLD. Students with RD also had a relative weakness in Numeration, although performance was in the average range for all LD subgroups and in the high average range for students with NoLD. For students with MD, performance was characterized by weak Number Sets performance, particularly relative to Number Line Estimation. For MDRD, additional within-group weaknesses were noted for Numeration and for the story problems composite. Although these patterns are reflected in Figure 2 and Table 4, the effect sizes for these differences were not large, and elevation differences were more important that profile differences for these subgroups.

Although most studies reliably demonstrate weaknesses on measures of foundational numeric competencies for students with MD (Butterworth, 2005; Landerl et al., 2004), difficulties tend to be larger when symbolic representations are involved (Cirino, 2011; Holloway & Ansari, 2009; Mundy & Gilmore, 2009; Rousselle & Noël, 2007). This is consistent with the greater difficulty of students with MD on Number Sets relative to Number Line Estimation. Some studies document an advantage for MD over MDRD across measures involving numeration (Andersson, 2010; Geary et al., 2000; Jordan et al., 2003; Landerl et al., 2009), but others do not (Andersson, 2008; Geary et al., 1999; Hanich et al., 2001). Given the breadth of items of the KM-R Numeration subtest, particularly those that assess counting and reading numbers, performance may be influenced by these linguistic demands as well as quantity, such that students with RD and MD both show relative difficulty.

Basic Fact and Number Sets performance generally showed an advantage for RD over MD, even when elevation was removed, consistent with specific mathematical retrieval difficulties in MD. Problem solving inconsistently contributed to differences in pattern between MD and RD. For example, as in Figure 2 and the effect sizes of Table 4, the RD subgroup showed a difference relative to MD on the word problems composite, which is consistent with the literature (Andersson, 2008; 2010; Hanich et al., 2001; Jordan et al., 2002; Jordan & Hanich, 2000). Given that students with RD demonstrated difficulty on several measures of foundational numerical competencies relative to NoLD and similar performance relative to MD, future studies should explore the more basic cognitive demands of such measures. Doing so may elucidate not only why measures of foundational numerical competencies are related to mathematics but also how some of these same skills are weak for students with difficulty in reading.

Students with MDRD performed below the level of MD students with generally small effect sizes (range d = +0.15 to +0.33) on mathematical measures, with a similar profile of performance. These results were expected for measures of foundational numerical competencies and computations, to the extent that they are a core deficit of MD, and because computation skills represent the most common way of defining MD status (although the profile computation measures differed from definitional measures). Many of our computation measures were timed, and several studies have found similarities between students with MD and MDRD with timed performance. The advantage for students with MD is usually evidenced under untimed conditions, which allow them to rely on their better developed number combination strategies (e.g., Andersson & Lyxell, 2007; Jordan & Montani, 1997). However, this advantage may apply only to basic facts: Most studies show few differences between MD and MDRD subgroups on complex computational measures (Andersson, 2008, 2010; Chan & Ho, 2010; Cirino et al., 2007; Hanich et al., 2001; Jordan et al., 2003; Raghubar et al., 2009), with only a few exceptions (Jordan & Hanich, 2000). Thus the present study contributes to previous work in demonstrating more similarities than differences among students with MD as a function of whether they also exhibit reading difficulties, particularly in terms of their pattern of mathematical performance.

Larger differences on measures of problem solving were expected, as prior work typically shows an advantage for students with MD (Fuchs & Fuchs, 2002; Hanich et al., 2001; Jordan et al., 2003; Jordan & Hanich, 2000; Jordan & Montani, 1997; Powell et al., 2009). Students with either MD or MDRD would be expected to have difficulty with the numerical transformations required in story problems, and both may also have difficulty coping with the language demands of these tasks. However, for students with MD alone, these language difficulties may be restricted in terms of depth and breadth (e.g., restricted to retrieval processes, or weaknesses in phonological representations associated with math facts); in contrast, students with MDRD may have more severe difficulties and additional language problems. In the present study, students with MDRD versus MD did not differ on measures of mathematical problem solving, beyond the global difference among these subgroups, although these were among the largest differences across the range of mathematical measures. Andersson (2008, 2010), who also did not find a difference in story problem performance, attributed this to the reduced linguistic demands of their story problems measures. The present study also read problems aloud to emphasize their mathematical rather than reading components, in part because students were younger than in most comparative studies. Furthermore, the size of the MD versus MDRD group differences may have been affected by the definitional measure (WRAT-3), which included language-based precomputational items; at younger ages, precomputational items may play a larger role in determining MD status, relative to alternative measures or older students.

Definition Issues

Our criteria for designating subgroups were empirically based. Our original cutoff score was at the 25th percentile, although several studies utilize a lower cut point (e.g., Geary et al., 2007; Landerl et al., 2004; Mazzocco & Kover, 2007; Murphy et al., 2007). We therefore compared results across cut points, reasoning that with very low mathematical performance, core deficits may be more manifest, with fewer extraneous causes of low performances. In the present study, the general effect of the lower cut point was to amplify the difference in level among the subgroups, though primarily in terms of differences of all students with LD relative to those with NoLowLD. Present findings are in contrast to other descriptive research (e.g., Geary et al., 2007; Mazzocco & Myers, 2003; Murphy et al., 2007) suggesting students with more versus less severe MD constitute distinct subtypes of learners. We found no evidence to support this hypothesis. Cognitively, subgroup profile shapes were similar regardless of the cut point utilized, and contributors to these profiles were similar across cut points. Mathematically, whereas profile differences were noted among most of the subgroups with LD with the moderate cut point, there were minimal differences in profile among subgroups when the low cut point was utilized. In particular, the shapes of MD and RD profiles in Figures 1 versus 3 (cognitive) and 2 versus 4 (mathematical) were similar, although lower in the latter figure, consistent with definitional severity. It is possible that other definitional decisions could have altered findings, but present results suggest that differences in severity may be confounded with differences in comorbidity, which is not surprising given the strong relation between these academic skills.

Comorbidity and Educational Implications

What then might we conclude about the relations among MD, RD, and MDRD? Results showed differential cognitive and mathematical profiles patterns for MD versus RD. The LD subgroups each experienced some difficulty in all areas relative to those with NoLD (including phonology for students with MD and most mathematical areas for students with RD). Within that context, however, students with RD (and MDRD) experienced more difficulty with phonology; students with MD (and MDRD), more difficulty with processing speed, nonverbal reasoning, and most mathematical performances. On measures of foundational numerical competencies, students with RD and MD had comparable difficulties with number line estimation and the numeration measures, though only the MD subgroups experienced difficulty for the Number Sets measure. More systematic examination of measures of these foundational numerical competencies by manipulating relevant parameters (e.g., symbolic vs. nonsymbolic; subitizing vs. approximate) and identifying their concomitants would be of benefit. Working memory was certainly affected by classification as LD, though it did not specifically differentiate the groups assessed here. This is consistent with working memory as a “domain general” resource, which applies across academic areas. On the other hand, processing speed was only associated with MD, not RD. Yet because the verbal/language demands were specifically reduced on this measure relative to speeded tasks in other studies of processing speed (e.g., Shanahan et al., 2006), this may suggest that the speed difficulty associated with RD is more specific to language. In MD, it may indicate a broader problem.

Finally, the pattern of the comorbid group suggests that it arises as a function of severity, rather than from a distinct set of causes. Most difficulties associated with either MD or RD were present in the comorbid group, and in most cases the degree of difficulty was greater than that of either of the single-deficit subgroups, though underadditive in the sense of Shanahan et al. (2006). This suggests that the particular cognitive resources we examined are relevant for either or both difficulty in the development of interventions. Also, individuals with RD may be susceptible to both reading and mathematical difficulties, whether or not they also meet comorbidity criterion for MD, particularly on language-intensive problems. The reverse may also be true. A key future step would be to evaluate the role of these cognitive resources in an intervention or experimental context that contrasts single versus comorbid subgroups.

Few studies show differential impact of intervention according to comorbidity (other than in terms of level at both pre- and posttest), although such studies are often underpowered. The similar profiles we found in the present study for the MD and MDRD subgroups provide an explanation for why MD and MDRD students may respond to intervention in similar ways. At the same time, findings do provide insights into intervention design for MD, across comorbidity status. For example, deficits in processing speed and nonverbal reasoning identified across MD subgroups relative to students with RD suggest that intervention be designed to compensate for these limitations. Fuchs et al. (2013) provides one example of how studies might investigate intervention’s compensatory effects. First graders with risk for MD were randomly assigned to control or to two contrasting forms of number knowledge tutoring—with speeded practice on foundational math skills and on efficient counting strategies for deriving answers to simple calculation problems, or with nonspeeded practice designed to reinforce number knowledge content. Both intervention conditions produced superior outcomes relative to the control group, but there were important differences between the two active conditions. With speeded practice added to the number knowledge tutoring, arithmetic skill improved relative to the nonspeeded practice condition. This was true regardless of students’ pretest reasoning ability. By contrast, with nonspeeded practice, outcomes depended on children’s reasoning ability: Those with low ability suffered poor outcomes relative to high ability students in the same condition.

Limitations and Conclusions

The present results should be considered in the context of its limitations. Our criteria for designating subgroups were empirically based, and so may not directly generalize to educational settings where disability is defined via multi-disciplinary teams. Moreover, the choice of how to define subgroups was not exhaustive, and groups were formed from continuous variables. However, the clarity of the definition used here does provide an opportunity for replication; we considered multiple cut points that produced similar results, and we ran exploratory analyses that utilized a buffer zone were substantively similar to those presented. Readers should also note that the age range in the present study was restricted to the beginning of second grade. It is possible that older students are more differentiated in their patterns of cognitive and mathematics performances and that profiles may change over time, indicating the need for longitudinal designs. It is also possible that different findings may emerge when a wider range of foundational mathematics is included, specifically those that contrast nonsymbolic with symbolic numerosity or that compare performance according to plausible theoretical accounts, such as subitizing, the approximate number system, and numerosity coding (Butterworth, 2010).

Another limitation concerns the choice of criterion for MD (broad computations) or RD (single word reading). In the present study, we defined learning disabilities in terms of lower-order skill, calculations for MD and word reading for RD, which is the dominant classification strategy in the learning disabilities literature (as also reflected in comorbidity research; see Vukovic, Lesaux, & Siegel, 2010, for an exception). Fuchs, Fuchs, and Compton (in press) recently focused instead on higher-order comorbidity, defined in terms of story problem performance for MD and reading comprehension performance for RD. Results indicated that language comprehension was a distinctive dimension of comorbidity when learning disabilities was defined in terms of lower-order skill, because language comprehension was a strength for MD, relative to MD students’ other cognitive abilities. By contrast, when learning disabilities were defined in terms of higher-order skill, language comprehension was a distinctive dimension because it was a relative weakness for comorbid students. This suggests that findings of the present study might be altered if learning disabilities were defined in terms of higher-order reading and mathematics performance, with different implications for intervention design.

In sum, this study found that students with MD or MDRD were similar in terms of profile, though not severity, on mathematical but not cognitive tasks. Students with RD and those with MDRD differed in terms of both profile and elevation. The specific cut point used to define groups affected the level more than the pattern of both of cognitive and mathematical performance. Future work should continue to expand on the role of language for mathematics difficulties and for evaluating its role in foundational numerical competencies. As noted, additional research on comorbidities when higher-order performance is used for classifying learning disabilities appears warranted. Finally, further work integrating issues of comorbidity into intervention studies or other experimental contexts may have direct bearing on how to differentiate instruction for students with singular versus comorbid disorders, not only in terms of reading and mathematics but also in other areas associated with both (e.g., ADHD).

Figure 4.

Performance on mathematical measures (controlling for age), by learning difficulty subgroups (10th percentile).

Note. AS RF CORR = Addition Strategy Correct; AS RF RT = Addition Strategy Response Time; BASIC FACTS = composite of four subtests of Math Facts Fluency Assessment; CON = control; KM NUM = KeyMath-R Numeration; KM PSOLVE = KeyMath-R Problem Solving; MD = mathematics difficulty; MDRD = mathematics and reading difficulty; N LINE = Number Line Estimation; NUM SETS = Number Sets Test; RD = reading difficulty; WORD PROB = composite of Single Digit Story Problems and Vanderbilt Story Problems.