Reliability of functional magnetic resonance imaging activation during working memory in a multi-site study: Analysis from the North American Prodrome Longitudinal Study

Abstract

Multi-site neuroimaging studies offer an efficient means to study brain functioning in large samples of individuals with rare conditions; however, they present new challenges given that aggregating data across sites introduces additional variability into measures of interest. Assessing the reliability of brain activation across study sites and comparing statistical methods for pooling functional data is critical to ensuring the validity of aggregating data across sites. The current study used two samples of healthy individuals to assess the feasibility and reliability of aggregating multi-site functional magnetic resonance imaging (fMRI) data from a Sternberg-style verbal working memory task. Participants were recruited as part of the North American Prodrome Longitudinal Study (NAPLS), which comprises eight fMRI scanning sites across the United States and Canada. In the first study sample (n = 8), one participant from each home site traveled to each of the sites and was scanned while completing the task on two consecutive days. Reliability was examined using generalizability theory. Results indicated that blood oxygen level-dependent (BOLD) signal was reproducible across sites and was highly reliable, or generalizable, across scanning sites and testing days for core working memory ROIs (generalizability ICCs = 0.81 for left dorsolateral prefrontal cortex, 0.95 for left superior parietal cortex). In the second study sample (n = 154), two statistical methods for aggregating fMRI data across sites for all healthy individuals recruited as control participants in the NAPLS study were compared. Control participants were scanned on one occasion at the site from which they were recruited. Results from the image-based meta-analysis (IBMA) method and mixed effects model with site covariance method both showed robust activation in expected regions (i.e. dorsolateral prefrontal cortex, anterior cingulate cortex, supplementary motor cortex, superior parietal cortex, inferior temporal cortex, cerebellum, thalamus, basal ganglia). Quantification of the similarity of group maps from these methods confirmed a very high (96%) degree of spatial overlap in results. Thus, brain activation during working memory function was reliable across the NAPLS sites and both the IBMA and mixed effects model with site covariance methods appear to be valid approaches for aggregating data across sites. These findings indicate that multi-site functional neuroimaging can offer a reliable means to increase power and generalizability of results when investigating brain function in rare populations and support the multi-site investigation of working memory function in the NAPLS study, in particular.

1. Introduction

Multi-site functional neuroimaging studies are being increasingly utilized to study diverse conditions such as attention-deficit hyperactivity disorder (Colby et al., 2012), chronic (Abbott et al., 2011) and first-episode schizophrenia (White et al., 2011), pediatric brain cancer (Mulkern et al., 2008), and Alzheimer’s disease (Hua et al., 2013). However, multi-site investigations present unique challenges given that aggregating data across sites with different scanners and acquisition protocols introduces additional variability into measures of interest. Quantifying this variability and comparing it to variability introduced by other factors such as participant differences and imaging noise is a necessary step in establishing the reliability of multi-site imaging studies. In addition, examining and comparing statistical methods of aggregating data across sites is critical to ensuring that methods for pooling data are both valid and maximize the potential gains in power offered by multi-site studies.

Reliability refers to the consistency of some measurement of individuals over multiple assessments, assuming that individuals do not undergo true change between assessments. Several studies have utilized a traveling participant design to examine the reliability of fMRI activation indices across scanning sites. In this study design, participants travel to each site of a multi-site study and are scanned while completing the same task. Blood oxygen level-dependent (BOLD) signal for a task can therefore be compared across scanners for each participant, and the proportion of variance in activation attributable to site- versus person-related factors can be estimated. If variance in activation measures were primarily due to site-related differences rather than person- or task-related differences, imaging data would be largely scanner dependent and the generalizability of data across sites would be questionable (Gradin et al., 2010). Conversely, if activation measures showed greater variance due to person than site factors, this would indicate that person-related effects are likely to generalize across sites and would support the aggregation of data across sites. Results from prior studies employing a traveling participant design found that fMRI activation measures were highly reproducible across sites for cognitive (Yendiki et al., 2010, Brown et al., 2011, Gradin et al., 2010), motor (Gountouna et al., 2010), and emotion processing (Suckling et al., 2007) tasks, even in studies using different scanner models across sites (Yendiki et al., 2010, Brown et al., 2010). Further, the proportion of variance in activation measures attributable to person-related variability was often an order of magnitude larger than that due to site-related variability, supporting the aggregation of data across sites. However, given that the proportion of variance attributed to person- versus site-related factors is not uniform across tasks, regions of interest, and studies, a thorough examination of these factors for each task and study is necessary to ensure the validity of pooling data across sites in any multi-site study (Glover et al., 2012).

Variance component estimates can also be used to compute reliability coefficients that provide summary statistics for the consistency of measurement across multiple assessments. Generally speaking, reliability refers to consistency in the ranking of persons on a given measure over multiple assessments. Reliability coefficients can be calculated to assess relative or absolute reliability, depending on the nature of the decisions to be made from the measurements. Relative decisions are based on an individual’s measurement relative the measurements obtained from others (e.g., norm-referenced interpretations of measurements), whereas absolute decisions are based on the absolute level of an individual’s measurement independent of the measurements obtained from others (Shavelson and Webb, 1991). The distinction mainly concerns whether the main effects of a facet of observation (such as test item, measurement occasion, or in the current context, MRI scanner) are considered to contribute to measurement error and included in the error term of the reliability coefficient. In the case of relative decisions, they are not included, whereas they are included in the case of absolute decisions. Measures of relative reliability include the generalizability coefficient (G-coefficient) of generalizability theory (Shavelson & Webb, 1991), the intraclass correlation (ICC; type 3,1) statistic of Shrout and Fleiss (1979), and the Pearson correlation coefficient. Measures of absolute reliability include the absolute level ICC (type 2,1) of Shrout and Fleiss (1979) or the dependability coefficient (D-coefficient) of generalizability theory (Shavelson & Webb, 1991). In the context of multi-site fMRI studies, assessing relative agreement across scanning sites may be appropriate given that in most studies, the absolute value of activation derived from the contrast is not used for interpretation. Rather, the primary research question of many fMRI studies involves describing group differences or describing correlations between task contrasts and other variables of interest (i.e. relative questions; Barch and Mathalon, 2011). However, in cases where the absolute value of activation will be utilized for interpretation or in multi-site studies in which scanning site is not independent of other factors, assessing the absolute agreement of fMRI measurement across sites may also be valuable (Brown et al., 2011). For example, if there are significant differences in the ratio of case versus control participants across sites in a multi-site study, adjusting for site in the analysis may not be sufficient to eliminate all site effects. In such circumstances, assessment of reliability at an absolute level would inform the extent to which data are interchangeable across sites and thus the extent to which merging fMRI data across sites is valid (Friedman et al., 2008). The most appropriate reliability measure therefore depends on study design and the research question at hand.

The current study was undertaken to examine multi-site reliability of BOLD measures of activation during performance of a Sternberg-style verbal working memory task and to establish valid statistical methods for aggregating fMRI data across sites. The results are expected to inform subsequent multi-site fMRI investigations and, in particular, those conducted as part of the North American Prodrome Longitudinal Study (NAPLS), a large-scale multi-site study of individuals at clinical high risk (CHR) for psychosis. NAPLS is a consortium of 8 research centers in the US and Canada and aims to elucidate predictors and mechanisms of psychosis onset among CHR individuals. Participants undergo MRI scanning at baseline, 12- and 24- month follow-ups, as well as at conversion for those who develop fully psychotic symptoms. To examine the reliability of fMRI activation across the 8 scanning sites and to establish valid statistical methods for aggregating data across sites, data from two study samples are presented here. In the first study sample, we used a traveling participant study design and generalizability theory to characterize the proportion of variation in BOLD signal attributable to site- versus person-related factors and to assess the reliability of the person effect across testing sites and days at both a relative and an absolute level. Thus, eight healthy participants traveled to each of the eight sites in counterbalanced order and were scanned twice at each site while completing the working memory task on consecutive days. We anticipated that variance in activation indices due to person-related factors would be greater than variance due to site-related factors and that the person effect would be reliable across sites for key working memory regions. For the second study sample, fMRI data for all healthy individuals who had been recruited as control participants in the NAPLS study (for comparison to the CHR sample) were aggregated across sites using two statistical methods. In the first aggregation method, group activation maps were created for each of the eight sites separately and then combined in a hierarchical image-based meta-analysis (Salimi-Khorshidi et al., 2009). In the second aggregation method, activation maps were combined for all individuals across sites using a standard general linear model covarying for site. Similarities and differences in results of these two statistical methods for data aggregation were assessed.

2. Methods

2.1 Participants

Participants consisted of two samples of healthy individuals between the ages of 12 and 33. For the traveling participants study, each of the sites recruited one healthy participant (4 males, 4 females). Due to the travel requirements of the study, only participants over the age of 18 years were recruited. Each participant traveled to each of the eight sites and was scanned twice on consecutive days for a total of 128 scans (8 participants × 2 scans per site × 8 sites). The sites were Emory University, Harvard University, University of Calgary, University of California Los Angeles (UCLA), University of California San Diego (UCSD), University of North Carolina (UNC), Yale University, and Zucker Hillside Hospital. All participants completed all scans within a four month period (May through August of 2011). The order of visits to sites was counterbalanced across participants.

For the second study sample, 166 healthy individuals (89 males, 77 females) between the ages of 12 and 33 (mean = 20.4, SD = 4.6) were scanned at the NAPLS site at which they were recruited (as a healthy control for comparison to CHR individuals).

For both study samples, participants were excluded if they met DSM-IV criteria for a psychiatric disorder (as assessed with the Structured Clinical Interview for DSM-IV-TR; First et al., 2002), met prodromal criteria (as assessed by the Structured Interview for Prodromal Syndromes; McGlashan et al., 2001), met criteria for substance dependence in the past 6 months, had a first-degree relative with a current or past psychotic disorder, had a neurological disorder, or had a Full Scale IQ <70 (as measured by the Wechsler Abbreviated Scale of Intelligence; Wechsler et al., 1999).

Participants were recruited from the community via advertising and were compensated for their participation. All participants provided informed consent or assent for the study. Parental consent was also obtained for minors. The protocol was approved by Institutional Review Boards at each of the eight study sites.

2.2 Task Parameters

Working memory was assessed using a Sternberg-style item recognition task (Sternberg, 1966). A target set of yellow uppercase consonants was displayed for 2 seconds, followed by a fixation cross for 3 seconds. A green lowercase probe then appeared for 2 seconds followed by 2 seconds of fixation before the next trial. Participants were instructed to indicate whether the probe matched any of the letters from the previous target set by pressing designated buttons. Working memory load was manipulated by varying the load size of the target set between 3, 5, 7 and 9 consonants. There were 12 trials per load for a total of 48 trials with 50% match trials. Trials were arranged into blocks of 2 trials from the same load. Six additional fixation blocks of 18 seconds duration were interspersed throughout the task to provide a baseline. Trial randomization was optimized using OptimizeDesign software (Wager and Nichols, 2003). Each traveling participant performed the task 16 times (2 visits × 8 sites); control participants performed the task once. Four parallel versions of the test stimuli were created and used for both study samples. For the traveling participants study, test version varied in counterbalanced fashion such that no participant received the same version on successive administrations.

2.3 Behavioral Data Analysis

Response accuracy and response time were calculated for each scan for each participant. Response accuracy was calculated by dividing the number of correct trials by the total number of trials. Scans on which participants performed at less than 50% accuracy across the entire task (i.e. less than 24/48 correct trials) were excluded from further analysis. For the traveling participant study, if a participant performed at less than 50% accuracy on one day at a site, data for both days at that site were excluded from further analyses.

Mixed effects models using SPSS were used to assess potential effects of site, day at site, and visit order on total response accuracy and response time for the traveling participants study. Site, day at site, and visit order were entered as fixed effects. The mixed effect model was chosen over analysis of variance (ANOVA) to account for excluded data when a traveling participant performed with less than 50% accuracy on a given scan.

For the control study sample, we employed a one-way analysis of covariance (ANCOVA) to assess potential effects of site on total response accuracy and mean response time. Sex and age were entered as covariates.

2.4 Data Acquisition

Scanning was performed on Siemens Trio 3T scanners at UCLA, Emory, Harvard, UNC, and Yale, GE 3T HDx scanners at Zucker Hillside Hospital and UCSD, and a GE 3T Discovery scanner at Calgary. Due to scanner repairs, one traveling participant received both scans at Harvard on an alternate scanner and 8 participants from the control sample (2 at UCLA, 1 at Emory, 2 at Harvard, 1 at UCSD, and 2 at Calgary) were scanned on alternate scanners. To facilitate reliability analyses, data from these scans were excluded from further analyses. All Siemens sites used a 12-channel head coil and all GE sites used an 8-channel head coil. Anatomical reference scans were acquired first and used to configure slice alignment. At all sites scans were acquired in the sagittal plane with a 1mm × 1mm in-plane resolution and 1.2mm slice thickness. A T2-weighted image (0.9-mm in-plane resolution) was acquired using a set of high-resolution echo planar (EPI) localizers (Siemens: TR/TE 6310/67ms, 30 4-mm slices with 1-mm gap, 220-mm FOV; GE: TR/TE 6000/120ms, 30 4-mm slices with 1-mm gap, 220-mm FOV). Functional EPI sequence scans matched the AC-PC aligned T2 image (TR/TE 2500/30ms, 77 degree flip angle, 30 4-mm slices, 1mm gap, 220-mm FOV). Per Function Biomedical Informatics Research Network (FBIRN) multi-center EPI sequence standardization recommendations, both Siemens and General Electric scanners ran EPI sequences with RF slice excitation pulses that excited both water and fat, with fat suppression pulses prior to the RF excitation, and comparable reconstruction image smoothing was implemented between Siemens and GE scanners (Glover et al. 2012). The experiment was run using E-Prime Software (Psychology Software Tools), images were displayed using goggles (Resonance Technologies, Inc), and responses were collected via a button box. During the scan 182 volumes were acquired, lasting approximately 9 minutes.

In order to check the quality of data and minimize variability between sites, a quality assurance protocol was implemented across sites. Functional data were checked for motion, artifacts, and the quality of skull stripping implemented in FSL, and data diagnostics were checked for each participant. If absolute translocation greater than 3 mm occurred during 3 or less working memory trials, censor files were created to exclude these trials from analysis. Participants who showed translocation motion greater than 3mm maximum absolute displacement during more than 3 working memory trials were excluded from analyses altogether. This resulted in the exclusion of one participant from the control study sample; one additional control participant’s functional data was lost. No traveling participant scans were excluded for excessive motion.

2.5 Image Processing

Functional image analysis was performed using FSL (FMRIB’s Software Library v. 4.0; Smith et al., 2004). Motion in EPI data was corrected using a six-parameter, rigid-body 3D co-registration (FLIRT), which registered each BOLD image to the middle data point in the timeseries. Data were registered for each participant, first the EPI to the participant’s T2-weighted structural image, then the T2 to standard space brain (Jenkinson & Smith, 2001; Jenkinson et al., 2002). Data were spatially smoothed with a 5-mm (FWHM) Gaussian kernel and filtered with a non-linear high-pass filter (120s cut-off). Individual participant analyses employed FEAT (FMRI Expert Analysis Tool).

Time series statistical analysis for each participant was carried out using FILM (FMRIB’s Improved Linear Model) with local autocorrelation correction (Woolrich et al., 2001). Each trial was modeled in its entirety in a block design fashion, and correct and incorrect trials for each load were modeled separately. A univariate general linear model (GLM) was applied on a voxel-by-voxel basis such that each voxel’s timeseries was individually fitted to the resulting model, with local autocorrelation correction applied within tissue type to improve temporal smoothness estimation (Smith et al., 2004; Woolrich et al., 2001). Each voxel’s goodness-of-fit to the model was estimated; resulting parameter estimates indicated the degree to which signal change could be explained by each model. Motion parameters were entered as covariates. Analyses for the current study used the functional contrast for all trials across memory loads for which a participant gave a correct response compared to rest. Data on the BOLD response during all correct trials was chosen for complete presentation here because it was the best summary measure of working memory functioning.

2.6 Regions of Interest for Traveling Participant Reliability Analysis

Task positive regions of interest (ROI) to be investigated were selected to be consistent with prior work (Yendiki et al., 2010; Hashimoto et al., 2010; Fiebach et al., 2006, Koelsch et al., 2009) and to broadly represent areas activated by the task in group maps. Anatomically defined masks for task activated regions were created using the Wakeforest University (WFU) PickAtlas (Maldjian et al., 2003) for the following ROIs in the left and right hemispheres:

1. Anterior Cingulate Cortex

2. Dorsolateral Prefrontal Cortex

3. Supplementary Motor Cortex

4. Insula

5. Inferior Temporal Cortex

6. Superior Parietal Cortex

7. Occipital Cortex

8. Thalamus

9. Basal Ganglia

10. Cerebellum

Two additional regions that showed deactivation in group maps during working memory trials were also investigated. These task negative ROIs represented areas within the default mode network and typically show suppression during cognitive tasks (Greicius. Krasnow, Reiss, & Menon, 2003; Meindl et al., 2010). Masks were created using the WFU PickAtlas for:

1. Medial Frontal Gyrus

2. Posterior Cingulate Cortex

Anatomical ROIs were combined with functional masks to probe specific regions of the anatomical structures that were activated or suppressed during the working memory task. Thus, a group activation map for all included traveling participant scans was created from the individual t-statistic maps using the correct trials versus rest contrast for the task positive ROIs using FLAME (FMRIB’s Local Analysis of Mixed Effects) (Behrens et al., 2003; Smith et al., 2004), and using the rest versus correct trials contrast for the task negative ROIs. The GLM included regressors for site, age, and sex. To correct for multiple comparisons, the resulting Z-statistic image was thresholded using clusters determined by Z > 2.3 and a corrected cluster significance threshold of p = .05 (Forman et al., 1995; Worsley et al., 1992). A convergence analysis was used to create a mask of the voxels that overlapped between the functional group map and the anatomical mask for each ROI.

FSL’s Featquery was used to warp the functionally masked anatomical ROIs back into each participant’s space by applying the inverse of the transformation matrix used during the initial registration. A quality assurance procedure was implemented for traveling participant scans at each site to confirm registration of select functionally masked anatomical ROIs (i.e. left and right DLPFC, superior parietal cortex, thalamus, and cerebellum) to individual participant anatomical regions. Visual inspection confirmed that quality of registration of the group functionally masked anatomical ROIs to individual participant anatomical regions was very good in 88.9% of cases, acceptable in 10.9% of cases, and poor in <1% of cases. The motion-corrected, smoothed, and filtered data were probed for mean percent signal change during correct trials compared to rest.

2.7 Reliability of Activation Indices in the Traveling Participants Study

2.7.1 Determining Reliability Using G-Theory

Reliability of BOLD signal in each ROI was assessed using the generalizability theory (G-theory) framework. G-theory was developed as an extension of classical test theory to recognize and model the multiple sources of measurement error that influence a measure’s reliability, or generalizability, and to allow estimation of reliability with respect to only those sources of error relevant to the questions at hand (Barch & Mathalon, 2012). Briefly, reliability assessment using G-theory includes a generalizability study (G-study) and a decision study (D-study). The G-study extends earlier analysis of variance approaches to reliability by partitioning total variance in scores into the variance components associated with: 1) the main effect of person (i.e. the object of measurement); 2) the main effect of each characteristic feature of the measurement situation such as test site, test occasion, or test form, termed “facets” of measurement; and 3) their interactions. The objects of measurement (i.e. persons) are considered to be sampled from a population and variability among persons is referred to as “universe score variance.” A “universe of admissible observations” is thus defined by all possible combinations of all the levels of the facets. G-theory describes the dependability or reliability of generalizations made from a person’s observed score to the score he or she would obtain in the broad universe of admissible observations.

G-theory distinguishes between reliability based on the relative standing of persons versus those based on the absolute value of a score in the subsequent D-study. For relative decisions, the estimated components of variance from the G-study are used to compute a generalizability coefficient (G-coefficient) which is the ratio of the universe score variance to itself plus relative error variance. As such, the G-coefficient is an intraclass correlation and is analogous to a reliability coefficient in classical test theory. G-coefficients vary between 0 and 1 and describe the reliability of the rank ordering of individuals. The error term (σ²_rel) of the G-coefficient, ${E_{\rho }}^2$, arises from all the nonzero variance components associated with the rank ordering of individuals. Thus, variance components associated with the interaction of person with each facet or combination of facets define the error term. The G-coefficient is expressed as:

$${E_{\rho }}^2=\frac{{\sigma }_p^2}{({\sigma }_p^2+{\sigma }_{rel}^2)};$$

where ${\sigma }_p^2$ represents the variance in scores due to person.

For absolute decisions, estimated components of variance from the G-study are used to compute an index of dependability (D-coefficient). The error term (σ²_abs) of the D-coefficient (φ) arises from all the variance components associated with the score aside from the component associated with the object of measurement. The D-coefficient represents the reliability of 1 observed value within the universe of admissible observations and similarly varies from 0 to 1. It is expressed as the following:

$$\Phi =\frac{{\sigma }_p^2}{({\sigma }_p^2+{\sigma }_{abs}^2)}$$

For a more detailed discussion of G-theory see Shavelson & Webb (1991).

2.7.2 Statistical Analyses

The G-study was carried out using a two facet Person (8 levels) × Site (8 levels) × Testing Day (2 levels) crossed design. Person represented the object of measurement and was crossed with the site and day facets. Thus, variance components were estimated for the main effects of person (${\sigma }_p^2$), site (${\sigma }_s^2$), and day (${\sigma }_d^2$); the two-way interactions between person and site (${\sigma }_{ps}^2$), person and day (${\sigma }_{pd}^2$), and site and day (${\sigma }_{sd}^2$); and the residual due to the person × site × day interaction and random error (${\sigma }_{psd,e}^2$). The design can be summarized as:

$${\sigma }^2\left(X_{\mathrm{psd}}\right)={\sigma }_p^2+{\sigma }_s^2+{\sigma }_d^2+{\sigma }_{ps}^2+{\sigma }_{pd}^2+{\sigma }_{sd}^2+{\sigma }_{psd,e}^2;$$

where X_psd represents the observed activation score for a person (p) at a site (s) on a testing day (d). All facets were specified as random to maximize generalizability of results to all conditions of facets, including those not explicitly included in the current study. The VARCOMP procedure in SAS with the restricted maximum likelihood (REML) method specified was used to estimate variance components for the behavioral performance indices and for mean percent signal change in each ROI. Any observations excluded from analyses were treated as missing data by the VARCOMP procedure; variance components were estimated on remaining observations.

In addition, to assess for potential outlier sites for fMRI data, we repeated the variance component analyses for all ROIs after removing each of the sites consecutively (Friedman et al., 2008). Thus, we repeated AVOVA for each ROI eight times, excluding data from one of the eight sites and including the other 7 sites each time. Mean change in the variance component estimates across ROIs for each series of ANOVA with a given site removed were assessed by comparing the new variance component estimates to those obtained when data from all eight sites was included. A dramatic decrease in variance due to site averaged across ROIs when a specific site was removed (i.e. a change larger than 3 standard deviations from the average proportion of variance attributable to site when all sites were included) would suggest that the site was an outlier.

In the D-study, we investigated the extent to which both the relative ranking of persons and the absolute value of activation for each person was reliable, or generalizable, across scanning sites and test days. Estimated variance components from the G-study were therefore used to calculate G-coefficients and D-coefficients that describe the relative and absolute reliability, respectively, of the person effect for activation in each ROI across scanning sites and testing occasions. Reliability coefficients were interpreted using Cicchetti and Sparrow’s (1981) definition for judging the clinical significance of ICC values: <0.40 poor; 0.40-0.59 fair; 0.60-0.74 good; >0.74 excellent. G-Coefficients were calculated according to the following equation:

$${E_{\rho }}^2=\frac{{\sigma }_p^2}{({\sigma }_p^2+\frac{{\sigma }_{ps}^2}{n_s^{\prime }}+\frac{{\sigma }_{pd}^2}{n_d^{\prime }}+\frac{{\sigma }_{psd.e}^2}{n_s^{\prime }{n}_d^{\prime }})}$$

D-coefficients were calculated according to the following equation:

$$\Phi =\frac{{\sigma }_p^2}{({\sigma }_p^2+\frac{{\sigma }_s^2}{n_s^{\prime }}+\frac{{\sigma }_d^2}{n_d^{\prime }}+\frac{{\sigma }_{ps}^2}{n_s^{\prime }}+\frac{{\sigma }_{pd}^2}{n_d^{\prime }}+\frac{{\sigma }_{sd}^2}{n_s^{\prime }{n}_d^{\prime }}+\frac{{\sigma }_{psd.e}^2}{n_s^{\prime }{n}_d^{\prime }})}$$

2. 8 Aggregation of Multi-Site Data in the Healthy Control Participants Study

2.8.1 Hierarchical Model for Image-Based Meta-Analysis

The image-based meta-analysis (IMBA) approach was selected based on prior research comparing strategies for pooling fMRI data across studies (Salimi-Khorshidi et al., 2009). For each individual site, a mixed effects group-level analysis was carried out using FLAME (FMRIB’s Local Analysis of Mixed Effects) (Behrens et al., 2003; Smith et al., 2004) with each participant’s data, including parameter and variance estimates from the lower-level analysis. This inter-participant analysis for each site constituted the second level of fMRI analysis (following the first-level intra-participant modeling of each participant’s fMRI time series data). Covariates for age and sex were included in the GLM for each site. To correct for multiple comparisons, resulting Z-statistic images were thresholded using clusters determined by Z > 2.3 and a corrected cluster significance threshold of p = .05 (Forman et al., 1995; Worsley et al., 1992). Cluster p-values were determined using spatial smoothness estimation in FEAT (Jenkinson & Smith, 2001; Forman et al., 1995). The resulting statistical data, which include the combination of each participant’s effect estimates and standard errors to give a mean group effect size estimate and mixed effects variance for each of the 8 sites, were input into a third-level analysis constituting the image-based meta-analysis. Thus, the inter-site meta-analysis was conducted using the hierarchical model for image-based meta-analysis specified by Salimi-Khorshidi and colleagues (2009). The site-level effect sizes and variances were modeled to provide fixed effects inference using a fixed effects group level analysis in FLAME. The GLM included a regressor to estimate the mean effect across sites.

2.8.2 Model with Covariance for Site for Second Study

As an alternative to the IMBA approach, we examined a covariance model that could be used in contexts where a particular effect size is not estimable at one or more sites. For the mixed effects model with site as a covariate, group analysis was carried out using FLAME (FMRIB’s Local Analysis of Mixed Effects) (Behrens et al., 2003; Smith et al., 2004) with each participant’s data, including parameter and variance estimates from the lower-level analysis. The GLM for each contrast of interest included regressors for site, age, and sex. As in the IBMA method, all Z-statistic images were thresholded using clusters determined by Z > 2.3 and a corrected cluster significance threshold of p = .05.

2.9 Comparison of IBMA to Mixed Effects Covariance Analyses

Convergence of the IMBA and site covariance models was examined using the Dice Similarity Measure (DSM), a symmetric measure of the resemblance of two binary images (Bennett & Miller, 2010). The DSM coefficient ranges from 0 (indicating no overlap) to 1 (indicating perfect overlap). Z-statistic activation maps from the IMBA and covariance models were first combined to create a map of the union of overlapping voxel-wise activation for the group maps. Next, a count of the number of non-zero voxels was extracted from each of the z-statistic maps for the IMBA, covariance model, and union map, using fslmaths. The DSM coefficient was then calculated using the following equation:

$$(2\times \mid \mathrm{A}\cap \mathrm{B}\mid )∕(\mid \mathrm{A}\mid +\mid \mathrm{B}\mid )$$

where A represents the z-statistic activation map from the IBMA and B represents the z-statistic activation map from the site covariance analysis.

In addition, to explore how adjusting the cluster threshold parameters affected convergence of the IMBA and site covariance models, each model was re-run using clusters determined by Z > 1.5 and Z > 3.0 and a corrected cluster significance threshold of p = .05. Spatial overlap in the resulting z-statistic images were again compared using the DSM.

3. Results

3.1 Demographic Characteristics and Behavioral Performance in the Traveling Participant and Control Participant Samples

One traveling participant performed at less than 50% accuracy during one or both scans at 5 different sites; behavioral and fMRI data from both visits to each of these sites were excluded from further analysis. Given the exclusion of one additional traveling participant’s scans at Harvard due to scanner repairs, this resulted in a total of 116 scans included for analysis in the traveling participant sample. In the control study sample, two participants performed at less than 50% accuracy and were excluded from further analysis. The demographic characteristics and behavioral performance for included scans by working memory load are shown in Table 1 for the traveling participant and control participant samples. Mean accuracy across working memory loads was high for both traveling participants (M = 88.3, SD = 7.1) and control participants (M = 83.1, SD = 8.2), with response accuracy decreasing at higher memory loads.

Table 1.

Demographic and behavioral performance data for traveling participants, control participants, and control participants by site.

	Traveling Participants	Control Participants	Control Site 1	Control Site 2	Control Site 3	Control Site 4	Control Site 5	Control Site 6	Control Site 7	Control Site 8
Demographic Characteristics
N	8†	154*	20	23	22	25	25	9	13	17
Mean Age (SD)	26.9 (4.3)	20.5 (4.5)	18.8 (3.4)	22.0 (4.9)	20.1 (4.5)	17.4 (2.5)	20.4 (3.0)	21.1 (4.7)	23.9 (5.9)	22.4 (4.7)
Age Range	20-31	12-33	13-26	13-31	14-31	12-23	14-25	14-29	15-33	14-30
Sex	4F/4M	69F/85M	7F/13M	8F/15M	11F/11M	12F/13M	11F/14M	2F/7M	7F/6M	11F/6M
Behavioral Data
Load 3 % Correct (SD)	95.9 (7.7)	93.2 (9.2)	91.7 (9.0)	92.4 (10.6)	92.8 (10.4)	93.0 (9.8)	95.0 (7.2)	91.7 (13.2)	96.2 (5.5)	93.1 (8.5)
Load 5 % Correct (SD)	92.4 (9.2)	89.2 (10.0)	90.4 (10.6)	88.0 (9.7)	88.3 (12.0)	91.3 (9.2)	91.0 (8.7)	84.3 (8.8)	91.7 (6.8)	85.3 (12.0)
Load 7 % Correct (SD)	88.4 (9.1)	81.3 (13.6)	84.6 (13.0)	82.6 (13.3)	78.8 (13.5)	79.3 (16.5)	86.0 (11.0)	74.1 (11.4)	85.3 (11.4)	75.5 (13.7)
Load 9 % Correct (SD)	76.6 (13.4)	68.8 (13.8)	68.3 (12.8)	69.9 (15.4)	68.6 (16.9)	65.3 (9.5)	74.7 (13.5)	57.4 (9.7)	73.1 (16.0)	67.7 (10.2)
Response Time	977.0	1084.9	1053.1	1197.0	1121.8	997.5	1040.0	1250.9	1041.6	1062.6
Load 3 Correct ms (SD)	(159.9)	(232.3)	(196.9)	(342.9)	(180.2)	(210.7)	(233.8)	(163.8)	(190.5)	(151.2)
Response Time	1023.1	1145.5	1092.5	1256.9	1189.4	1016.2	1099.4	1365.0	1092.4	1182.6
Load 5 Correct ms (SD)	(227.2)	(288.2)	(309.2)	(366.4)	(227.2)	(210.2)	(313.8)	(263.7)	(189.2)	(262.0)
Response Time	1068.0	1284.0	1187.4	1372.9	1357.7	1232.7	1170.0	1573.1	1179.1	1352.3
Load 7 Correct ms (SD)	(210.6)	(395.4)	(388.4)	(507.1)	(356.8)	(435.0)	(346.1)	(387.3)	(180.3)	(341.3)
Response Time	1265.1	1534.1	1460.5	1689.7	1625.5	1435.6	1367.2	2022.6	1430.1	1503.2
Load 9 Correct ms (SD)	(330.4)	(527.1)	(397.3)	(842.0)	(609.3)	(327.9)	(411.1)	(383.8)	(394.7)	(382.2)

^†1 traveling participant data excluded at 5 sites due to scans on one or both occasions at < 50% accuracy, 1 traveling participant data excluded at 1 site due to receiving scans on alternate scanners

^*12 participants excluded from original Control sample (n = 166) : 1 due to excessive motion, 8 due to receiving scans on alternate scanners, 2 due to performance < 50% accuracy; 1 due to lost functional data

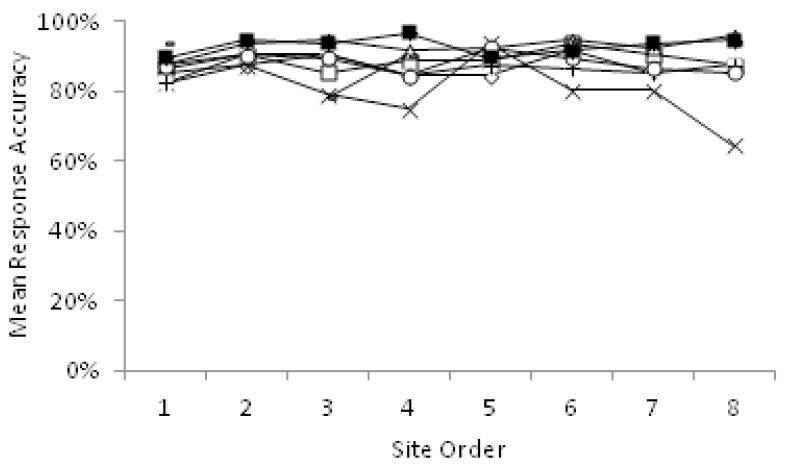
For the traveling participants study, participants (n = 8) visited each of the eight sites in counterbalanced order. Mean percent correct responses and response time for each participant in the temporal order that sites were visited, averaged across the two scans at each site, are shown in Figure 1 and Figure 2, respectively. Overall, results suggest no learning effects across scans. For percent correct responses, there was no significant effect of site, F(1,107.29) = 2.18, p = .14, day at site, F(1,107.23) = 1.51, p = .22, or visit order, F(1,107.29) = 0.07, p = .79. Similarly, for response time, there was no significant effect of site F(1,107.15) = 2.83, p = .10, day at site, F(1,107.12) = 3.36, p = .07, or visit order, F(1,107.47) = 0.20, p = .66. Thus, learning effects are not expected to confound analysis of the traveling participant fMRI data.

Figure 1.

Traveling participant total percent correct responses by site, in the order that sites were visited. Each marker corresponds to a different participant.

Figure 2.

Traveling participant mean response times (ms) by site, in the order that sites were visited. Each marker corresponds to a different participant.

In the control participant sample (n=154), ANCOVA showed a significant effect of site for overall response accuracy F(1,144) = 2.34, p = .03, and mean response time, F(1,144) = 2.92, p = .007, after controlling for the effects of age and sex. Follow-up post-hoc tests of Least Significant Differences indicated that participants at site 1 (UCLA), 2 (Emory), 4 (Zucker Hillside), 5 (UNC) and 7 (Calgary) had significantly higher response accuracy than participants at site 6 (UCSD), ps < .05, participants at site 5 had significantly higher response accuracy than participants at site 8 (Yale), participants at site 4 had significantly faster response times than participants at sites 2, 3 (Harvard), 6 and 8, and participants at sites 1,4 and 5 had significantly faster response times than participants at site 6, p < .05.

3.2 Traveling Participants fMRI Data and Variance Components Analysis

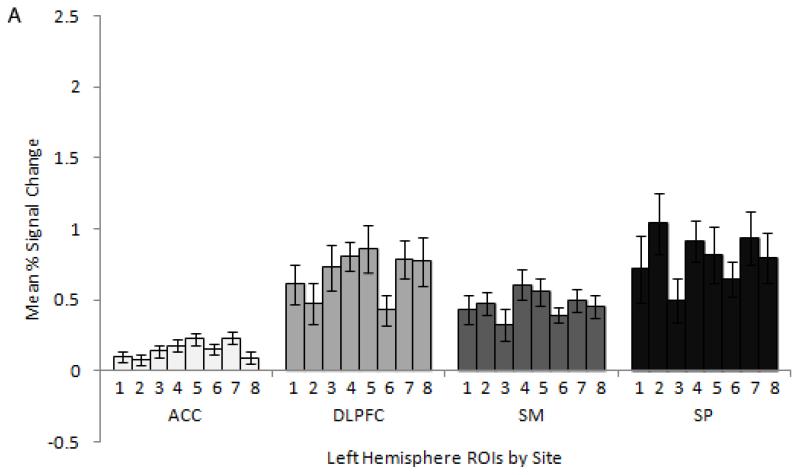
To illustrate variation in fMRI activation across sites and participants, Figure 3 shows plots of mean percent signal change across 4 example ROIs (anterior cingulate cortex, dorsolateral prefrontal cortex, supplementary motor cortex, and superior parietal cortex) averaged across the traveling participants for each of the 8 sites for the left (A) and right (B) hemispheres, and averaged across the sites for each of the 8 participants for the left (C) and right (D) hemispheres. Overall, within each ROI, activation varied more between participants when averaged across sites, than between sites when averaged across participants.

Figure 3.

Traveling participant mean percent signal change ± standard error in dorsolateral prefrontal cortex (DLPFC), anterior cingulate cortex (ACC), superior parietal cortex (SP), and supplementary motor cortex (SM) averaged across participants for each site for the left (A) and right (B) hemisphere and averaged across sites for each participant in the left (C) and right (D) hemisphere. For subplots A and B, each bar within a given ROI corresponds to a different site. For subplots C and D, each bar within a given ROI corresponds to a different traveling participant.

Variance components analysis was used to determine the proportion of variance attributable to the main effects of person, site, and day; the interactions of person × site, person × day, and site × day; and the residual due to the person × site × day interaction and random error for the behavioral performance indices, for activation in task positive ROIs, and for deactivation in task negative ROIs. Variance components results for response accuracy and response time are shown in Figure 4. Variance components for task positive ROIs in the left and right hemisphere for the correct trials versus rest contrast and for task negative ROIs for the rest versus correct trials contrast are shown in Table 2; the proportion of total variance attributed to each component is shown in Figure 5. Among individual ROIs, the proportion of variance in activation attributed to person was 10-fold larger than that attributed to site in ten out of twenty-two ROIs, and 20-fold larger than site in five ROIs, including in left DLPFC, left and right superior parietal cortex, left inferior temporal cortex, and right supplementary motor cortex. The residual variance term which includes variance due to the three-way interaction of person, site, and day was the largest variance component in twenty out of twenty-two ROIs. Mean proportion of variance attributed to each component averaged across task positive ROIs in the left hemisphere, task positive ROIs in the right hemisphere, and task negative ROIs is shown in Table 3. The proportion of variance attributed to person was larger for left hemisphere task positive ROIs and task negative ROIs compared to right hemisphere task positive ROIs. Averaged across all twenty-two ROIs, the proportion of variance attributed to person was 8-fold larger than that attributed to site, 20-fold larger than that attributed to day, and 5-fold larger than that attributed to the person × site interaction.

Figure 4.

Proportion of variance attributable to each variance component for response accuracy and response time for traveling participants.

Table 2.

Variance components for traveling participant activation in left and right hemisphere anterior cingulate cortex (ACC), dorsolateral prefrontal cortex (DLPFC), supplementary motor cortex (SM), insula (IN), inferior temporal cortex (IT), superior parietal cortex (SP), occipital cortex (OCC), thalamus (T), basal ganglia (BG), and cerebellum (C), and for deactivation in medial frontal gyrus (MFG) and posterior cingulate cortex (PCC).

	ACC	DLPFC	SM	IN	IT	SP	OCC	T	BG	C		MFG	PCC
Left Hemisphere											Task Negative Regions
Person	0.0053	0.0741	0.0363	0	0.4274	0.3268	0.0560	0.0054	0.0011	0.0020	Person	0.0241	0.0524
Site	0.0030	0	0.0033	0	0	0.0132	0.0063	0.0008	0.0002	0.0025	Site	0.0096	0.0081
Day	0.0009	0.0007	0.0006	0	0	0.0011	0.0052	0	0.0009	0	Day	0.0016	0
Person*Site	0	0.0543	0.0032	0	0.1001	0.0203	0.0070	0.0022	0	0	Person*Site	0	0.0257
Person*Day	0	0	0.0006	0.0006	0	0	0	0	0.0005	0	Person*Day	0	0.0099
Site*Day	0	0.0376	0	0.0025	0	0	0	0.0001	0	0.0001	Site*Day	0	0
Residual	0.0228	0.1629	0.0913	0.0355	0.3579	0.2167	0.1411	0.0379	0.0233	0.0472	Residual	0.0842	0.0950
Right Hemisphere
Person	0.0095	0	0.0259	0.0089	0.2179	0.0872	0.0160	0.0071	0.0030	0.0014
Site	0	0.0028	0.0005	0	0.0197	0	0.0034	0	0.0007	0.0022
Day	0.0006	0	0.0025	0	0.0133	0	0.0099	0	0.0001	0.0003
Person*Site	0	0	0	0	0	0.0350	0.0267	0	0	0
Person*Day	0.0000	0.0540	0	0	0	0.0077	0.0105	0	0	0
Site*Day	0.0023	0	0	0.0048	0	0	0	0.0033	0	0
Residual	0.0388	0.2188	0.1016	0.0440	0.4836	0.1086	0.2164	0.0424	0.0344	0.0458

Figure 5.

Proportion of variance attributable to each variance component for activation in left and right hemisphere anterior cingulate cortex (ACC), dorsolateral prefrontal cortex (DLPFC), supplementary motor cortex (SM), insula (IN), inferior temporal cortex (IT), superior parietal cortex (SP), occipital cortex (OCC), thalamus (T), basal ganglia (BG), and cerebellum (C) for the correct trials versus rest contrast, and for deactivation in medial frontal gyrus (MFG) and posterior cingulate cortex (PCC) for the rest versus correct trials contrast.

Table 3.

Percentage of variance attributed to person, site, and day; the interactions for person x site, person x day, and site x day; and residual error averaged across task-positive regions in the left and right hemispheres for the correct trials versus rest contrast, and averaged across task-negative regions for the rest versus correct trials contrast.

	Mean Proportion of Variance
	Left Hemisphere	Right Hemisphere	Task Negative Regions
Person	21.62%	14.98%	23.80%
Site	2.44%	1.15%	6.16%
Day	0.94%	0.93%	0.66%
Person*Site	4.17%	2.41%	6.73%
Person*Day	0.41%	2.66%	2.58%
Site*Day	1.82%	1.92%	0.00%
Residual	68.59%	75.96%	60.07%

Following Friedman et al., (2008) we repeated the variance component analyses for all ROIs after removing each of the sites consecutively to assess for potential outlier sites. Thus, ANOVA for each ROI was repeated eight times; each analysis excluding data from one of the eight sites and including the other seven sites. Table 4 shows the change in percentage of variance attributed to site when each site was excluded averaged across the twenty-two ROIs. All changes in the average variance attributed to site were less than 1 standard deviation from the average variance attributed to site when all sites were included; thus, no sites appeared to be outliers.

Table 4.

Change in the percentage of variance attributed to site, averaged across all ROIs, when each site is excluded from analysis.

Excluded Site	Change in Variance Attributed to Site
Site 1	−0.20%
Site 2	0.47%
Site 3	0.00%
Site 4	0.46%
Site 5	0.05%
Site 6	−0.69%
Site 7	0.49%
Site 8	−0.20%

Variance component estimates were subsequently used to calculate G-coefficients and D-coefficients for each ROI, reflecting the relative and absolute agreement of the person effect across scanning sites and days, respectively (Table 5). G-coefficients showed excellent reliability in the majority of ROIs. Thus, the reliability of the ranking of persons on activation in task positive ROIs ranged from E_ρ² = 0 for the left insula and right DLPFC to E_ρ² = 0.95 for the left superior parietal cortex. D-coefficients for task positive ROIs were lower than G-coefficients, but remained in the good to excellent range for the majority of ROIs. Reliability coefficients were highest for regions most frequently associated with verbal working memory, indicating that relative and absolute agreement of the person effect on activation was reliable, or generalizable, in the current study design across scanning sites and days for core verbal working memory regions. G-coefficients and D-coefficients similarly showed excellent reliability across the task-negative ROIs. This indicates that task-related deactivation of default mode regions was also reliable across scanning sites and days.

Table 5.

G-Coefficients and D-Coefficients for the person effect in left and right hemisphere anterior cingulate cortex (ACC), dorsolateral prefrontal cortex (DLPFC), supplementary motor cortex (SM), insula (IN), inferior temporal cortex (IT), superior parietal cortex (SP), occipital cortex (OCC), thalamus (T), basal ganglia (BG), and cerebellum (C) for the correct trials versus rest contrast, and for medial frontal gyrus (MFG) and posterior cingulate cortex (PCC) for the rest versus correct trials contrast.

	G-Coefficient		D-Coefficient
Task Positive Regions	Left	Right	Left	Right
ACC	0.79	0.80	0.70	0.77
DLPFC	0.81	0.00	0.79	0.00
SM	0.85	0.80	0.84	0.77
IN	0.00	0.76	0.00	0.74
IT	0.92	0.88	0.92	0.85
SP	0.95	0.85	0.95	0.85
OCC	0.85	0.42	0.81	0.37
T	0.67	0.73	0.66	0.71
BG	0.39	0.58	0.33	0.57
C	0.40	0.33	0.38	0.30
Task Negative Regions
MFG	0.82		0.77
PCC	0.79		0.78

3.3 Aggregation of Multi-Site Activation Data: IBMA and Mixed Effects Model with Site Covariance

Results from the hierarchical IBMA model and the mixed effects model with covariance for site both showed robust activation in expected regions for correct working memory trials compared to rest (Figure 6). Thus, in both methods, control participants showed robust activation across numerous cortical regions including bilateral superior parietal cortex, dorsolateral prefrontal cortex, lateral occipital cortex, inferior temporal cortex, insular cortex, cingulate gyrus, and supplementary motor cortex. Participants also showed activation of subcortical structures including bilateral cerebellum, caudate, putamen, and thalamus in both methods. Results from the DSM analysis which quantified the voxelwise overlap between the thresholded images for each approach showed a high degree of overlap in spatial localization of activation between the approaches. The DSM coefficient for the comparison of the hierarchical image-based meta-analysis model and the mixed effects model with covariance for site was .96 when activation maps were thresholded using clusters determined by Z > 2.3. Convergence of the z-statistic activation maps when the IBMA and mixed effects models were re-run using clusters determined by Z > 1.5 and Z > 3.0 was similarly high, yielding DSM coefficients of .96 and .95, respectively. Given that the DSM coefficient can range from 0 to 1.0, with 1.0 indicating perfect similarity between two sets, this demonstrates a high degree of similarity in results from the two methods of multi-site data aggregation and also suggests that convergence of the two methods of data aggregation was robust to changes in thresholding parameters in the current sample.

Figure 6.

Functional activation group maps for control participants for all correct trials versus rest using image-based meta-analysis method (cluster peak Z score range: 19.7 – 21.8) and mixed effects model with site covariance method (cluster peak Z score range: 13.6 – 19.1).

4. Discussion

The current study examined the reliability of brain activation during a Sternberg-style working memory task across the eight NAPLS sites and compared two statistical methods for aggregating data across sites. In the traveling participant component of the study, eight participants traveled to each NAPLS site and were scanned while completing the task on two consecutive days. Participants showed no learning effects, as indicated by no effects of order of site visit or day of scanning on response accuracy or response time. Overall, fMRI activation was observed to be highly reliable across sites. Activation levels in task-relevant ROIs were similar across sites, person-related factors accounted for eight times more variance in activation than site-related factors when averaged across ROIs, and no site appeared to be an outlier. In addition, reliability coefficients indicated excellent generalizability of the person effect across sites and testing days for core working memory ROIs and for deactivation in default mode regions. In the control participant component of the study, fMRI data for all healthy individuals who had been recruited as control participants in the NAPLS study were aggregated across sites using two statistical methods; group maps generated by each method were compared. In both the hierarchical IBMA and mixed effects model with site covariance methods, control participants showed robust activation across cortical and subcortical regions previously implicated in working memory function. Quantification of the similarity of group maps from these two statistical methods of data aggregation using the DSM coefficient confirmed a very high degree of spatial overlap in results (96%). Thus, brain activation and deactivation during the working memory task appeared reliable across the NAPLS sites, and both the IBMA and mixed effects model with site covariance methods may be valid statistical methods for aggregating data across sites.

We used generalizability theory to examine the contributions of person and multiple sources of measurement error to fMRI signal, and to assess the relative and absolute generalizability of the person effect across scanning sites and testing days. Consistent with prior studies examining variance components of the BOLD response (Costafreda, 2009; Brown et al., 2011; Yendiki et al., 2010; Gountouna et al., 2010), we found that variance in BOLD signal due to site was low across ROIs, and variance due to person was at least 10-fold larger in many ROIs, including left dorsolateral prefrontal cortex, bilateral superior parietal cortex, inferior temporal cortex, and supplementary motor cortex. Averaged across ROIs, the interaction of person by site contributed a small proportion of the total variance in BOLD signal (3.6%). Variance due to the interaction of person by site could arise from differences in the rank ordering of subjects across sites and/or from differences in the distance of the BOLD response of subjects across sites. When the interaction of person by site is large relative to the effect of person, the rank ordering of persons may vary across site with greater potential impact on between-site reliability. In the current study, variance due to person was larger than the person by site interaction for twenty one out of twenty-two ROIs and the person by site interaction term was zero in the majority of ROIs. Using the guidelines for judging the significance of ICC values defined by Cicchetti and Sparrow (1981), G-coefficients were in the excellent range for eleven out of twenty task positive ROIs and were highest in ROIs most strongly linked to working memory function. Reliability coefficients for regions showing deactivation during working memory trials (i.e. medial frontal gyrus and posterior cingulate cortex) were also in the excellent range. Of the ten ROIs for which the person by site interaction contributed any variance to BOLD signal variance, G-coefficients were in the excellent range for all but one. Overall, this indicates high reliability of the person effect across primary working memory ROIs and suggests that site-related effects and the person by site interaction had minimal effect on reliability. D-coefficients were similarly in the excellent range for nine task positive ROIs and both task negative ROIs. Parallel exploratory analyses using maximum signal change as the parameter of interest revealed a similar pattern of results for the all correct versus rest contrast (results not shown). However, it is also of note that four ROIs showed poor reliability coefficients with neither site- nor person-related factors contributing substantially to variance in activation (i.e. left insula, left basal ganglia, right DLPFC, right cerebellum). This is consistent with prior research showing that reliability is frequently lower in regions that are less robustly activated by a task (Bennett & Miller, 2010, Caceres et al., 2009, Brown et al, 2011) and may reflect the fact that when a region is minimally involved in a task, there is relatively little signal compared to noise leading to low reliability. Alternatively, this could reflect a poor fit of the design model to the acquired time series for some ROIs (Caceres et al., 2009). We also carried out parallel variance component analyses using a higher control condition contrast (see Supplementary Methods and Results for details). Thus, we explored the reliability of activation in task positive ROIs and deactivation in task negative ROIs during load 9 trials compared to load 3 trials. Averaged across ROIs, variance due to person was lower using the higher control condition contrast compared to the all correct trials versus rest contrast. However, site contributed little or no variance to BOLD signal in the majority of ROIs using the higher control contrast, and thus, the proportion of variance due to person was substantially larger in the majority of ROIs. Reliability coefficients remained in the good to excellent range for core working memory ROIs. The majority of prior studies investigating reliability in multi-site fMRI studies have investigated reliability across only a few scanning sites (Yendiki et al., 2010; Brown et al., 2011; Gountouna et al., 2010; Gradin et al., 2010), although Zou et al., (2005) also investigated reliability across a larger number of sites. Although the extent of reliability depended on the specific brain region investigated, these results confirm that larger multi-site fMRI investigations are feasible and indicate that when appropriate standardization procedures are implemented across sites, brain activation among participants can be highly reliable across sites for core verbal working memory ROIs.

Examining and comparing methods for aggregating data is an important step to ensure that statistical approaches utilized are both valid and maximize gains in power offered by multi-site investigations. Salimi-Khorshidi et al. (2008) compared image-based versus coordinate-based methods for aggregating fMRI data across sites/studies. Results demonstrated a clear advantage for the IBMA method versus coordinate-based aggregation methods for minimizing information loss while accounting for differences between sites/studies. However, in some scenarios, it may not be possible to conduct a hierarchical analysis of group maps generated for each site. For example, if one site of a multi-site study contributes control participants but few or no patient participants, a case-control contrast at that site may not be possible. Employing a mixed effects model with site covariance would allow data from such a site to be aggregated without requiring an underpowered case-control contrast. Using the control participant sample, we compared results from an IBMA versus a mixed effects model with site covariance for the Sternberg-style working memory task. Results were highly similar across the two methods of data aggregation, and quantification of the similarity of group maps using the DSM coefficient confirmed very high spatial overlap in results. Thus, in both methods, control participants showed robust activation in numerous cortical and subcortical regions including bilateral dorsolateral prefrontal cortex, inferior temporal cortex, insula, anterior cingulate cortex, supplementary motor cortex, superior parietal cortex, cerebellum, thalamus, and basal ganglia. In addition, adjusting the cluster correction threshold parameters did not significantly alter spatial convergence of the two methods. This provides further support for the strength of convergence of these methods for the current task and sample. Prior fMRI studies have found that verbal working memory tasks activate a distributed network in the brain including frontal speech regions, dorsolateral prefrontal cortex, posterior parietal cortex, anterior cingulate cortex, inferior temporal cortex, and subcortical structures including the thalamus, basal ganglia, and cerebellum (Hashimoto et al., 2010; Fiebach et al., 2006, Koelsch et al., 2009; Voytek et al., 2010). Given that the IBMA and mixed effects model produced similar results for the current task, this suggests that either model would provide a valid method for aggregating data across the NAPLS sites.

There are some limitations to the current study that should be noted. First, although variance in BOLD signal attributable to person-related factors was much higher than that attributable to site-related factors, unexplained variance was high for many ROIs. Cognitive tasks frequently show lower signal reliability relative to motor and sensory tasks (Bennett & Miller, 2010) and participant characteristics may contribute to large unexplained variances. For example, differences in arousal and attention associated with variation in brain activation change not only between scanning sessions but also during the course of one scanning session. Evolving changes in cognitive strategies are also common and can contribute to higher residual variance in cognitive tasks. Although high unexplained variance is a concern of fMRI studies generally, results from the current and prior studies suggest that results from standard cognitive tasks are often similar across scanners and can nevertheless yield important insights into differences in brain activation between control and patient groups. A second limitation is that the current study was not exhaustive in quantifying reliability or comparing approaches for aggregating data across sites. Prior studies examining these questions have examined reliability for various activation indices (e.g. ROI activation versus voxel-wise activation versus whole brain activation) and have used diverse statistical methods to quantify reliability (Bennett & Miller, 2010). Given that several multi-site investigations have already compared many of these approaches, methods for the current investigation were selected to capture activation indices that were likely to be used in subsequent investigations, to be consistent with prior studies of similar tasks to facilitate comparison (e.g. Yendiki et al., 2010) and to reflect the study questions at hand (Barch & Mathalon, 2011). Finally, the sample size of the traveling participant component of the study was relatively small and demographic variance between traveling participants may have been low relative to the general population. Given the number of sites in the NAPLS consortium, the feasibility of having a larger number of participants travel to each site was limited. Nevertheless, over sampling of similar individuals can lead to underestimates of the reliability coefficients, given the essential role of variance in determining reliability.

4.1 Conclusions

In summary, the current study demonstrated the feasibility and validity of utilizing a multi-site study to examine brain activation associated with a Sternberg-style working memory task. In the traveling participant study, variance in BOLD signal attributable to person was 8-fold larger than that due to site-related factors averaged across twenty-two ROIs, and the effect of person was generalizable across study sites and testing days for the majority of ROIs. Results from the control participant study of individuals recruited as control participants in the NAPLS study demonstrated that both the hierarchical IBMA and mixed effects model with site covariance may be valid methods for aggregating fMRI data across sites. These findings are encouraging for the continued use of multi-site fMRI investigations to study rare clinical populations, and support the multi-site investigation of brain activation during working memory function for CHR individuals in the NAPLS study in particular.

Highlights.

• We examined reliability of fMRI during a working memory task in a multi-site study

• Greater variance due to person than site factors in variance component analysis

• Consistent functional activation in task-related ROIs across sites

• Reliability coefficients showed excellent reliability for person effect in primary ROIs

• Two methods for aggregating data across sites produced similar activation maps

• Implications for design and implementation of multi-site fMRI studies