Sparse Multivariate Regression With Covariance Estimation

Abstract

We propose a procedure for constructing a sparse estimator of a multivariate regression coefficient matrix that accounts for correlation of the response variables. This method, which we call multivariate regression with covariance estimation (MRCE), involves penalized likelihood with simultaneous estimation of the regression coefficients and the covariance structure. An efficient optimization algorithm and a fast approximation are developed for computing MRCE. Using simulation studies, we show that the proposed method outperforms relevant competitors when the responses are highly correlated. We also apply the new method to a finance example on predicting asset returns. An R-package containing this dataset and code for computing MRCE and its approximation are available online.

1. Introduction

Multivariate regression is a generalization of the classical regression model of regressing a single response on p predictors to regressing q > 1 responses on p predictors. Applications of this general model arise in chemometrics, econometrics, psychometrics, and other quantitative disciplines where one predicts multiple responses with a single set of prediction variables. For example, predicting several measures of quality of paper with a set of variables relating to its production, or predicting asset returns for several companies using the vector autoregressive model (Reinsel 1997), both result in multivariate regression problems.

Let x_i = (x_i1, …, x_ip)^T denote the predictors, let y_i = (y_{i 1}, …, y_iq)^T denote the responses, and let ε_i = (ε₁, …, ε_q)^T denote the errors, all for the ith sample. The multivariate regression model is given by

$${\mathbf{y}}_i={\mathbf{B}}^T{\mathbf{x}}_i+{\mathbf{\epsilon }}_i\text{for}i=1,\dots ,n,$$

where B is a p × q regression coefficient matrix and n is the sample size. Column k of B is the regression coefficient vector from regressing the kth response on the predictors. We make the standard assumption that ε₁, …, ε_n are iid N_q(0, Σ). Thus, given a realization of the predictor variables, the covariance matrix of the response variables is Σ.

The model can be expressed in matrix notation. Let X denote the n × p predictor matrix where its ith row is ${\mathbf{x}}_i^T$, let Y denote the n × q random response matrix where its ith row is ${\mathbf{y}}_i^T$, and let E denote the n × q random error matrix where its ith row is ${\mathbf{\epsilon }}_i^T$; then the model is

$$\mathbf{Y}=\mathbf{\text{XB}}+\mathbf{E}.$$

Note that if q = 1, the model simplifies to the classical regression problem where B is a p-dimensional regression coefficient vector. For simplicity of notation we assume that columns of X and Y have been centered and thus the intercept terms are omitted.

The negative log-likelihood function of (B, Ω), where Ω = Σ⁻¹, can be expressed up to a constant as

$$g(\mathbf{B},\mathbf{\Omega })=\text{tr}\left[\frac{1}{n}{(\mathbf{Y}-\mathbf{\text{XB}})}^T(\mathbf{Y}-\mathbf{\text{XB}})\mathbf{\Omega }\right]-log|\mathbf{\Omega }|.$$ (1.1)

The maximum likelihood estimator for B is simply B̂^OLS = (X^T X)⁻¹X^T Y, which amounts to performing separate ordinary least squares estimates for each of the q response variables and does not depend on Ω.

Prediction with the multivariate regression model requires one to estimate pq parameters which becomes challenging when there are many predictors and responses. Criterion-based model selection has been extended to multivariate regression by (Bedrick and Tsai 1994) and (Fujikoshi and Satoh 1997). For a review of Bayesian approaches for model selection and prediction with the multivariate regression model see the article by Brown, Vannucci, and Fearn 2002) and references therein. A dimensionality reduction approach called reduced-rank regression (Anderson 1951; Izenman 1975; Reinsel and Velu 1998) minimizes (1.1) subject to rank(B) = r for some r ≤ min(p, q). The solution involves canonical correlation analysis, and combines information from all of the q response variables into r canonical response variates that have the highest canonical correlation with the corresponding predictor canonical variates. As in the case of principal components regression, the interpretation of the reduced-rank model is typically impossible in terms of the original predictors and responses.

Other approaches aimed at reducing the number of parameters in the coefficient matrix B involve solving

$$\widehat{\mathbf{B}}=\underset{\mathbf{B}}{argmin}\text{tr}[{(\mathbf{Y}-\mathbf{\text{XB}})}^T(\mathbf{Y}-\mathbf{\text{XB}})]\text{subject to}:C(\mathbf{B})\le t,$$ (1.2)

where C(B) is some constraint function. A method called factor estimation and selection (FES) was proposed by (Yuan et al. 2007), who applied the constraint function $C(\mathbf{B})={\sum }_{j=1}^{min(p,q)}{\sigma }_j(\mathbf{B})$, where σ_j(B) is the jth singular value of B. This constraint encourages sparsity in the singular values of B̂, and hence reduces the rank of B̂; however, unlike reduced-rank regression, FES offers a continuous regularization path. A novel approach for imposing sparsity in the entries of B̂ was taken by (Turlach, Venables, and Wright 2005), who proposed the constraint function, $C(\mathbf{B})={\sum }_{j=1}^{p}max(|b_{j1}|,\dots ,|b_{\mathit{\text{jq}}}|)$. This method was recommended for model selection (sparsity identification), and not for prediction because of the bias of the L_∞-norm penalty. Imposing sparsity in B̂ for the purposes of identifying “master predictors” was proposed by (Peng et al. 2010), who applied a combined constraint function C(B) = λC₁(B) + (1 − λ)C₂(B) for λ ∈ [0, 1], where C₁(B) = Σ_j,k |b_jk|, the lasso constraint (Tibshirani 1996) on the entries of B and $C_2(\mathbf{B})={\sum }_{j=1}^p{(b_{j1}^2+\cdots +b_{\mathit{\text{jq}}}^2)}^{0.5}$, the sum of the L₂-norms of the rows of B (Yuan and Lin 2006). The first constraint introduces sparsity in the entries of B̂ and the second constraint introduces zeros for all entries in some rows of B̂, meaning that some predictors are irrelevant for all q responses. Asymptotic properties for an estimator using this constraint with λ = 0 have also been established (Obozinski, Wainwright, and Jordan 2008). This combined constraint approach provides highly interpretable models in terms of the prediction variables. However, all of the methods above that solve (1.2) do not account for correlated errors.

To directly exploit the correlation in the response variables to improve prediction performance, a method called Curds and Whey (C&W) was proposed by (Breiman and Friedman 1997). C&W predicts the multivariate response with an optimal linear combination of the ordinary least squares predictors. The C&W linear predictor has the form Ỹ = Ŷ^OLSM, where M is a q × q shrinkage matrix estimated from the data. This method exploits correlation in the responses arising from shared random predictors as well as correlated errors.

In this article, we propose a method that combines some of the strengths of the estimators discussed above to improve prediction in the multivariate regression problem while allowing for interpretable models in terms of the predictors. We reduce the number of parameters using the lasso penalty on the entries of B while accounting for correlated errors. We accomplish this by simultaneously optimizing (1.1) with penalties on the entries of B and Ω. We call our new method multivariate regression with covariance estimation (MRCE). The method assumes predictors are not random; however, the resulting formulas for the estimates would be the same with random predictors. Our focus is on the conditional distribution of Y given X and thus, unlike in the Curds and Whey framework, the correlation of the response variables arises only from the correlation in the errors.

We also note that the use of the lasso penalty on the entries of Ω has been considered by several authors in the context of covariance estimation (Yuan and Lin 2007; d'Aspremont, Banerjee, and El Ghaoui 2008; Friedman, Hastie, and Tibshirani 2008; Rothman et al. 2008). However, here we use it in the context of a regression problem, thus making it an example of what one could call supervised covariance estimation: the covariance matrix here is estimated in order to improve prediction, rather than as a stand-alone parameter. This is a natural next step from the extensive covariance estimation literature, which has been given surprisingly little attention to date; one exception is the joint regression approach of Witten and (Tibshirani 2009). Another less directly relevant example of such supervised estimation is the supervised principal components by (Bair et al. 2006).

The remainder of the article is organized as follows: Section 2 describes the MRCE method and associated computational algorithms, Section 3 presents simulation studies comparing MRCE to competing methods, Section 4 presents an application of MRCE for predicting asset returns, and Section 5 concludes with a summary and discussion.

2. Joint Estimation of B and Ω via Penalized Normal Likelihood

2.1 The MRCE Method

We propose a sparse estimator for B that accounts for correlated errors using penalized normal likelihood. We add two penalties to the negative log-likelihood function g to construct a sparse estimator of B depending on Ω = [ω_{j′ j}],

$$(\widehat{\mathbf{B}},\widehat{\mathbf{\Omega }})=\underset{\mathbf{B},\mathbf{\Omega }}{argmin}\left\{g(\mathbf{B},\mathbf{\Omega })+{\mathrm{\lambda }}_1\sum _{j^{\prime }\ne j}|{\omega }_{j^{\prime }j}|+{\mathrm{\lambda }}_2\sum _{j=1}^p\sum _{k=1}^q|b_{\mathit{\text{jk}}}|\right\},$$ (2.1)

where λ₁ ≥ 0 and λ₂ ≥ 0 are tuning parameters.

We selected the lasso penalty on the off-diagonal entries of the inverse error covariance Ω for two reasons. First, it ensures that an optimal solution for Ω has finite objective function value when there are more responses than samples (q > n); second, the penalty has the effect of reducing the number of parameters in the inverse error covariance, which is useful when q is large (Rothman et al. 2008). Other penalties such as the ridge penalty could be used when it is unreasonable to assume that the inverse error covariance matrix is sparse. If q is large, estimating a dense Ω means that the MRCE regression method has O(q²) additional parameters in Ω to estimate compared with doing separate lasso regressions for each response variable. Thus estimating a sparse Ω has considerably lower variability, and so we focus on the lasso penalty on Ω. We show in simulations that when the inverse error covariance matrix is not sparse, the lasso penalty on Ω still considerably outperforms ignoring covariance estimation altogether (i.e., doing a separate lasso regression for each response).

The lasso penalty on B introduces sparsity in B̂, which reduces the number of parameters in the model and provides interpretation. In classical regression (q = 1), the lasso penalty can offer major improvement in prediction performance when there is a relatively small number of relevant predictors. This penalty also ensures that an optimal solution for B is a function of Ω. Without a penalty on B (i.e., λ₂ = 0), the optimal solution for B is always B̂^OLS.

To see the effect of including the error covariance when estimating an L₁-penalized B, assume that we know Ω and also assume p < n. Solving (2.1) for B with Ω fixed is a convex problem (see Section 2.2) and thus there exists a global minimizer B^opt. This implies that there exists a zero subgradient of the objective function at B^opt (see theorem 3.4.3, p. 127, in Bazaraa, Sherali, and Shetty 2006). We express this in matrix notation as

$$\mathbf{0}=2n^{-1}{\mathbf{X}}^T{\mathbf{\text{XB}}}^{\text{opt}}\mathbf{\Omega }-2n^{-1}{\mathbf{X}}^T\mathbf{Y}\mathbf{\Omega }+{\mathrm{\lambda }}_2\mathbf{\Gamma },$$

which gives

$${\mathbf{B}}^{\text{opt}}={\widehat{\mathbf{B}}}^{\text{OLS}}-{\mathrm{\lambda }}_2{(2n^{-1}{\mathbf{X}}^T\mathbf{X})}^{-1}\mathbf{\Gamma }{\mathbf{\Omega }}^{-1},$$ (2.2)

where Γ = Γ(B^opt) is a p × q matrix with entries ${\gamma }_{\mathit{\text{ij}}}=\text{sign}(b_{\mathit{\text{ij}}}^{\text{opt}})$ if $b_{\mathit{\text{ij}}}^{\text{opt}}\ne 0$ and otherwise γ_ij ∈ [−1, 1] with specific values chosen to solve (2.2). Ignoring the correlation in the error is equivalent to assuming that Ω⁻¹ = I. Thus having highly correlated errors will have greater influence on the amount of shrinkage of each entry of B^opt than having mildly correlated errors.

2.2 Computational Algorithms

The optimization problem in (2.1) is not convex; however, solving for either B or Ω with the other fixed is convex. We present an algorithm for solving (2.1) and a fast approximation to it.

Solving (2.1) for Ω with B fixed at a chosen point B₀ yields the optimization problem

$$\widehat{\mathbf{\Omega }}({\mathbf{B}}_0)=\underset{\mathbf{\Omega }}{argmin}\left\{\text{tr}({\widehat{\sum }}_R\mathbf{\Omega })-log|\mathbf{\Omega }|+{\mathrm{\lambda }}_1\sum _{j^{\prime }\ne j}|{\omega }_{j^{\prime }j}|\right\},$$ (2.3)

where ${\widehat{\sum }}_R=\frac{1}{n}{(\mathbf{Y}-{\mathbf{\text{XB}}}_0)}^T(\mathbf{Y}-{\mathbf{\text{XB}}}_0)$. This is exactly the L₁-penalized covariance estimation problem considered by (d'Aspremont, Banerjee, and El Ghaoui 2008), (Yuan and Lin 2007), (Rothman et al. 2008), (Friedman, Hastie, and Tibshirani 2008), and Lu (2009, 2010). We use the graphical lasso (glasso) algorithm of (Friedman, Hastie, and Tibshirani 2008) to solve (2.3) since it is fast and the most commonly used algorithm for solving (2.3).

Solving (2.1) for B with Ω fixed at a chosen point Ω₀ yields the optimization problem

$$\widehat{\mathbf{B}}({\mathbf{\Omega }}_0)=\underset{\mathbf{B}}{argmin}\left\{\text{tr}\left[\frac{1}{n}{(\mathbf{Y}-\mathbf{\text{XB}})}^T(\mathbf{Y}-\mathbf{\text{XB}}){\mathbf{\Omega }}_0\right]+{\mathrm{\lambda }}_2\sum _{j=1}^p\sum _{k=1}^q|b_{\mathit{\text{jk}}}|\right\},$$ (2.4)

which is convex if Ω₀ is nonnegative definite. This follows because the trace term in the objective function has the Hessian 2n⁻¹Ω₀ ⊗ X^TX, which is nonnegative definite because the Kronecker product of two symmetric nonnegative definite matrices is also nonnegative definite. A solution can be efficiently computed using cyclical-coordinate descent analogous to that used for solving the single output lasso problem (Friedman, Hastie, and Tibshirani 2007). We summarize the optimization procedure in Algorithm 1. We use the ridge penalized least squares estimate B̂^RIDGE = (X^TX + λ₂I)⁻¹X^TY to scale our test of parameter convergence since it is always well defined (including when p > n).

Algorithm 1: Given Ω and an initial value B̂⁽⁰⁾, let S = X^TX and H = X^TYΩ.

• Step 1: Set B̂^(m) ← B̂^(m−1). Visit all entries of B̂^(m) in some sequence and for entry (r, c) update ${\widehat{b}}_{\mathit{\text{rc}}}^{(m)}$ with the minimizer of the objective function along its coordinate direction given by

  $${\widehat{b}}_{\mathit{\text{rc}}}^{(m)}\leftarrow \text{sign}\left({\widehat{b}}_{\mathit{\text{rc}}}^{(m)}+\frac{h_{\mathit{\text{rc}}}-u_{\mathit{\text{rc}}}}{s_{\mathit{\text{rr}}}{\omega }_{\mathit{\text{cc}}}}\right){\left(\left|{\widehat{b}}_{\mathit{\text{rc}}}^{(m)}+\frac{h_{\mathit{\text{rc}}}-u_{\mathit{\text{rc}}}}{s_{\mathit{\text{rr}}}{\omega }_{\mathit{\text{cc}}}}\right|-\frac{n{\mathrm{\lambda }}_2}{s_{\mathit{\text{rr}}}{\omega }_{\mathit{\text{cc}}}}\right)}_{+},\text{where}{u}_{\mathit{\text{rc}}}={\sum }_{j=1}^p{\sum }_{k=1}^q{\widehat{b}}_{\mathit{\text{jk}}}^{(m)}{s}_{\mathit{\text{rj}}}{\omega }_{\mathit{\text{kc}}}.$$

• Step 2: If ${\sum }_{j,k}|{\widehat{b}}_{\mathit{\text{jk}}}^{(m)}-{\widehat{b}}_{\mathit{\text{jk}}}^{(m-1)}|<\epsilon {\sum }_{j,k}|{\widehat{b}}_{\mathit{\text{jk}}}^{\text{RIDGE}}|$ then stop, otherwise go to Step 1.

A full derivation of Algorithm 1 is found in the Appendix. Algorithm 1 is guaranteed to converge to the global minimizer if the given Ω is nonnegative definite. This follows from the fact that the trace term in the objective function is convex and differentiable and the penalty term decomposes into a sum of convex functions of individual parameters (Tseng 1988; Friedman, Hastie, and Tibshirani 2007). We set the convergence tolerance parameter ε = 10⁻⁴.

In terms of computational cost, we need to cycle through pq parameters, and for each compute u_rc, which costs at most O(pq) flops, and if the least sparse iterate has υ non-zeros, then computing u_rc costs O(υ). The worst case cost for the entire algorithm is O(p²q²).

Using (2.3) and (2.4) we can solve (2.1) using blockwise coordinate descent, that is, we iterate minimizing with respect to B and minimizing with respect to Ω.

Algorithm 2 (MRCE): For fixed values of λ₁ and λ₂, initialize B̂⁽⁰⁾ = 0 and Ω̂⁽⁰⁾ = Ω̂ (B̂⁽⁰⁾).

• Step 1: Compute B̂^(m+1) = B̂(Ω̂^(m)) by solving (2.4) using Algorithm 1.

• Step 2: Compute Ω̂^(m+1) = Ω̂(B̂^(m+1)) by solving (2.3) using the glasso algorithm.

• Step 3: If ${\sum }_{j,k}|{\widehat{b}}_{\mathit{\text{jk}}}^{(m+1)}-{\widehat{b}}_{\mathit{\text{jk}}}^{(m)}|<\epsilon {\sum }_{j,k}|{\widehat{b}}_{\mathit{\text{jk}}}^{\text{RIDGE}}|$ then stop, otherwise go to Step 1.

Algorithm 2 uses blockwise coordinate descent to compute a local solution for (2.1). Steps 1 and 2 both ensure a decrease in the objective function value. In practice we found that for certain values of the penalty tuning parameters (λ₁, λ₂), the algorithm may take many iterations to converge for high-dimensional data. For such cases, we propose a faster approximate solution to (2.1).

Algorithm 3 (Approximate MRCE): For fixed values of λ₁ and λ₂,

• Step 1: Perform q separate lasso regressions each with the same optimal tuning parameter λ̂₀ selected with a cross-validation procedure. Let ${\widehat{\mathbf{B}}}_{{\widehat{\mathrm{\lambda }}}_0}^{\text{lasso}}$ denote the solution.

• Step 2: Compute $\widehat{\mathbf{\Omega }}=\widehat{\mathbf{\Omega }}({\widehat{\mathbf{B}}}_{{\widehat{\mathrm{\lambda }}}_0}^{\text{lasso}})$ by solving (2.3) using the glasso algorithm.

• Step 3: Compute B̂ = B̂(Ω̂) by solving (2.4) using Algorithm 1.

The approximation summarized in Algorithm 3 is only iterative inside its steps. The algorithm begins by finding the optimally tuned lasso solution ${\widehat{\mathbf{B}}}_{{\widehat{\mathrm{\lambda }}}_0}^{\text{lasso}}$ (using cross-validation to select the tuning parameter λ̂₀), then computes an estimate for Ω using the glasso algorithm with ${\widehat{\mathbf{B}}}_{{\widehat{\mathrm{\lambda }}}_0}^{\text{lasso}}$ plugged in, and then solves (2.4) using this inverse covariance estimate. Note that one still must select two tuning parameters (λ₁, λ₂). The performance of the approximation is studied in Section 3.

2.3 Tuning Parameter Selection

For the MRCE methods, the tuning parameters λ₁ and λ₂ could be selected using K-fold cross-validation, where validation prediction error is accumulated over all q responses for each fold. Specifically, select the optimal tuning parameters λ̂₁ and λ̂₂ using

$$({\widehat{\mathrm{\lambda }}}_1,{\widehat{\mathrm{\lambda }}}_2)=\underset{{\mathrm{\lambda }}_1,{\mathrm{\lambda }}_2}{argmin}\sum _{k=1}^K{\Vert {\mathbf{Y}}^{(k)}-{\mathbf{X}}^{(k)}{\mathbf{B}}_{{\mathrm{\lambda }}_1,{\mathrm{\lambda }}_2}^{(-k)}\Vert }_F^2,$$

where Y^(k) is the matrix of responses with observations in the kth fold, X^(k) is the matrix of predictors of observations in the kth fold, and ${\mathbf{B}}_{{\mathrm{\lambda }}_1,{\mathrm{\lambda }}_2}^{(-k)}$ is the estimated regression coefficient matrix computed with observations outside the kth fold, with tuning parameters λ₁ and λ₂. We have found in simulations that λ₂, which controls the penalization on the regression coefficient matrix, has greater influence on prediction performance than λ₁, which controls the penalization of the inverse error covariance matrix.

3. Simulation Study

3.1 Estimators

We compare the performance of the MRCE method, computed with the exact and the approximate algorithms, to other multivariate regression estimators that produce sparse estimates of B. We report results for the following methods:

• Lasso: Perform q separate lasso regressions, each with the same tuning parameter λ.

• Separate lasso: Perform q separate lasso regressions, each with its own tuning parameter.

• MRCE: The solution to (2.1) (Algorithm 2).

• Approx. MRCE: An approximate solution to (2.1) (Algorithm 3).

The ordinary least squares estimator B̂^OLS = (X^TX)⁻¹X^TY and the Curds and Whey method of (Breiman and Friedman 1997) are computed as a benchmark for low-dimensional models (they are not directly applicable when p > n).

We select the tuning parameters by minimizing the squared prediction error, accumulated over all q responses, of independently generated validation data of the same sample size (n = 50). This is similar to performing the cross-validation approach described in Section 2.3, and is used to save computing time for the simulations. For the MRCE methods, the two tuning parameters are selected simultaneously.

3.2 Models

In each replication for each model, we generate an n × p predictor matrix X with rows drawn independently from N_p(0, Σ_X) where Σ_X = [σ_Xij] is given by σ_Xij = 0.7^|i−j|. This model for the predictors was also used by (Yuan et al. 2007) and (Peng et al. 2010). Note that all of the predictors are generated with the same unit marginal variance. The error matrix E is generated independently with rows drawn independently from N_q(0, Σ_E). We consider two models for the error covariance:

• AR(1) error covariance: ${\sigma }_{\mathit{\text{Eij}}}={\rho }_E^{|i-j|}$, with values of ρ_E ranging from 0 to 0.9.

• Fractional Gaussian Noise (FGN) error covariance:

  $${\sigma }_{\mathit{\text{Eij}}}=0.5\left({(|i-j|+1)}^{2H}-2{|i-j|}^{2H}+{(|i-j|-1)}^{2H}\right),$$

  with values of the Hurst parameter H = 0.9, 0.95.

The inverse error covariance for the AR(1) model is a tri-diagonal sparse matrix while its covariance matrix is dense, and thus this error covariance model completely satisfies the regularizing assumptions for the MRCE method, which exploits the correlated error and the sparse inverse error covariance. The FGN model is a standard example of long-range dependence and both the error covariance and its inverse are dense matrices. Varying H gives different degree of dependence, from H = 0.5 corresponding to an iid sequence to H = 1 corresponding to a perfectly correlated one. Thus the introduction of sparsity in the inverse error covariance by the MRCE method should not help; however, since the errors are highly correlated the MRCE method may still perform better than the lasso penalized regressions for each response, which ignore correlation among the errors. The sample size is fixed at n = 50 for all models.

We generate sparse coefficient matrices B in each replication using the matrix element-wise product,

$$\mathbf{B}=\mathbf{W}\ast \mathbf{K}\ast \mathbf{Q},$$

where W is generated with independent draws for each entry from N(0, 1), K has entries with independent Bernoulli draws with success probability s₁, and Q has rows that are either all one or all zero, where p independent Bernoulli draws with success probability s₂ are made to determine whether each row is the ones vector or the zeros vector. Generating B in this manner, we expect (1 − s₂)p predictors to be irrelevant for all q responses, and we expect each relevant predictor to be relevant for s₁q of the response variables.

3.3 Performance Evaluation

We measure performance using model error, following the approach of (Yuan et al. 2007), which is defined as

$$\text{ME}(\widehat{\mathbf{B}},\mathbf{B})=\text{tr}[{(\widehat{\mathbf{B}}-\mathbf{B})}^T{\sum }_{\mathbf{X}}(\widehat{\mathbf{B}}-\mathbf{B})].$$

We also measure the sparsity recognition performance using true positive rate (TPR) and true negative rate (TNR),

$$\text{TPR}(\widehat{\mathbf{B}},\mathbf{B})=\frac{\#\{(i,j):{\widehat{b}}_{\mathit{\text{ij}}}\ne 0\text{and}{b}_{\mathit{\text{ij}}}\ne 0\}}{\#\{(i,j):b_{\mathit{\text{ij}}}\ne 0\}},$$ (3.1)

$$\text{TPR}(\widehat{\mathbf{B}},\mathbf{B})=\frac{\#\{(i,j):{\widehat{b}}_{\mathit{\text{ij}}}=0\text{and}{b}_{\mathit{\text{ij}}}=0\}}{\#\{(i,j):b_{\mathit{\text{ij}}}=0\}},$$ (3.2)

Both the true positive rate and true negative rates must be considered simultaneously since OLS always has perfect TPR and B̂ = 0 always has perfect TNR.

3.4 Results

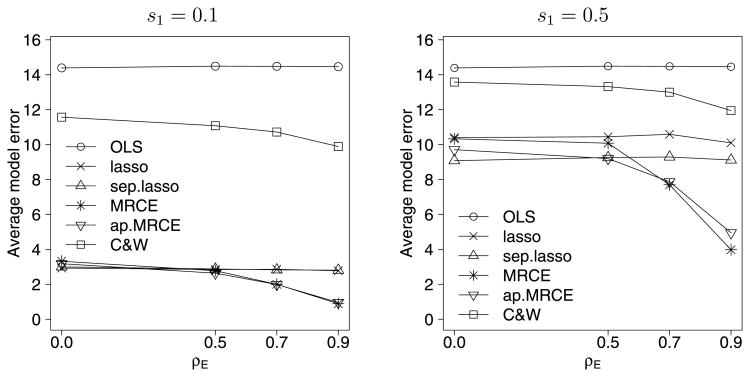
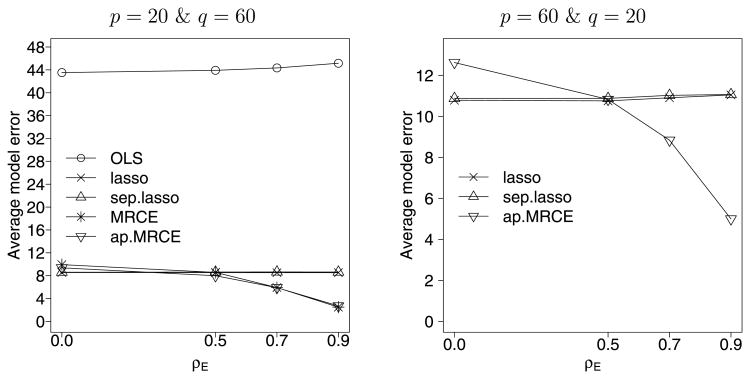
The model error performance for AR(1) error covariance model is displayed in Figure 1 for low-dimensional models, and in Figure 2 and Table 1 for high-dimensional models. Standard errors are omitted in the figures because of visibility issues, and we note that they are less than 4% of the corresponding average model error. We see that the margin by which MRCE and its approximation outperform the lasso and separate lasso in terms of model error increases as the error correlation ρ_E increases. This trend is consistent with the analysis of the subgradient equation given in (2.2), since the manner by which MRCE performs lasso shrinkage exploits highly correlated errors. Additionally, the MRCE method and its approximation outperform the lasso and separate lasso more for sparser coefficient matrices. We omitted the exact MRCE method for p = 60, q = 20, and p = q = 100 because these cases were computationally intractable. For a single realization of the model with p = 20, q = 60, and ρ_E = 0.9, using the tuning parameters selected with cross-validation, MRCE took 4.1 seconds, approximate MRCE took 1.7 seconds, lasso took 0.5 seconds, and separate lasso took 0.4 seconds to compute on a workstation with a 2 GHz processor with 4 GB of RAM. All of the sparse estimators outperform the ordinary least squares method by a considerable margin. The Curds and Whey method, although designed to exploit correlation in the responses, is outperformed here because it does not introduce sparsity in B.

Figure 1.

Average model error versus AR(1) correlation ρ_E, based on 50 replications with n = 50, p = q = 20, and s₂ = 1.

Figure 2.

Average model error versus AR(1) correlation ρ_E, based on 50 replications with n = 50 and s₁ =0.1, s₂ = 1.

Table 1.

Model error for the AR(1) error covariance models of high dimension, with p = q = 100, s₁ = 0.5, and s₂ = 0.1. Averages and standard errors in parentheses are based on 50 replications with n = 50.

ρE	lasso	sep.lasso	ap.MRCE
0.9	58.79 (2.29)	59.32 (2.35)	34.87 (1.54)
0.7	59.09 (2.22)	59.60 (2.30)	60.12 (2.02)

The model error performance for FGN error covariance model is reported in Table 2 for low-dimensional models and in Table 3 for high-dimensional models. Although there is no sparsity in the inverse error covariance for the MRCE method and its approximation to exploit, we see that both methods are still able to provide considerable improvement over the lasso and separate lasso methods by exploiting the highly correlated error. As seen with the AR(1) error covariance model, as the amount of correlation increases (i.e., larger values of H), the margin by which the MRCE method and its approximation outperform competitors increases.

Table 2.

Model error for the FGN error covariance models of low dimension. Averages and standard errors in parentheses are based on 50 replications with n = 50. Tuning parameters were selected using a 10^x resolution.

p	q	H	s1, s2	OLS	lasso	sep.lasso	MRCE	ap.MRCE	C&W
20	20	0.95	0.1, 1	14.51 (0.69)	2.72 (0.10)	2.71 (0.11)	1.03 (0.02)	1.01 (0.03)	9.86 (0.46)
20	20	0.90	0.1, 1	14.49 (0.53)	2.76 (0.09)	2.77 (0.09)	1.78 (0.05)	1.71 (0.05)	10.29 (0.36)
20	20	0.95	0.5, 1	14.51 (0.69)	9.89 (0.26)	8.94 (0.21)	3.63 (0.09)	4.42 (0.16)	11.72 (0.45)
20	20	0.90	0.5, 1	14.49 (0.53)	10.01 (0.21)	9.03 (0.18)	6.11 (0.14)	6.34 (0.13)	12.29 (0.34)

Table 3.

Model error for the FGN error covariance models of high dimension. Averages and standard errors in parentheses are based on 50 replications with n = 50. Tuning parameters were selected using a 10^x resolution.

p	q	H	s1, s2	OLS	lasso	sep.lasso	MRCE	ap.MRCE
20	60	0.95	0.1, 1	46.23 (2.04)	8.56 (0.36)	8.63 (0.37)	3.31 (0.19)	3.20 (0.18)
20	60	0.90	0.1, 1	45.41 (1.42)	8.60 (0.24)	8.69 (0.25)	5.31 (0.15)	5.03 (0.14)
60	20	0.95	0.1, 1	NA	11.15 (0.35)	11.23 (0.36)	–	4.84 (0.12)
60	20	0.90	0.1, 1	NA	11.14 (0.30)	11.21 (0.30)	–	7.44 (0.16)
100	100	0.95	0.5, 0.1	NA	58.28 (2.36)	58.86 (2.44)	–	31.85 (1.26)
100	100	0.95	0.5, 0.1	NA	58.10 (2.27)	58.63 (2.36)	–	47.37 (1.68)

We report the true positive rate and true negative rates in Table 4 for the AR(1) error covariance models and in Table 5 for the FGN error covariance models. We see that as the error correlation increases (larger values of ρ_E and H), the true positive rate for the MRCE method and its approximation increases, while the true negative rate tends to decrease. While all methods perform comparably on these sparsity measures, the substantially lower prediction errors obtained by the MRCE methods give them a clear advantage over other methods.

Table 4.

True positive rate/true negative rate for the AR(1) error covariance models, averaged over 50 replications; n = 50. Standard errors are omitted (the largest standard error is 0.04 and most are less than 0.01). Tuning parameters were selected using a 10^x resolution.

p	q	ρE	s1, s2	lasso	sep.lasso	MRCE	ap.MRCE
20	20	0.9	0.1, 1	0.83/0.72	0.82/0.74	0.95/0.59	0.94/0.62
20	20	0.7	0.1, 1	0.83/0.71	0.82/0.73	0.89/0.60	0.89/0.63
20	20	0.5	0.1, 1	0.83/0.70	0.81/0.73	0.86/0.62	0.87/0.63
20	20	0	0.1, 1	0.84/0.70	0.82/0.72	0.85/0.63	0.85/0.64
20	20	0.9	0.5, 1	0.86/0.44	0.87/0.44	0.93/0.42	0.91/0.45
20	20	0.7	0.5, 1	0.85/0.47	0.87/0.42	0.86/0.51	0.86/0.52
20	20	0.5	0.5, 1	0.83/0.52	0.87/0.44	0.83/0.54	0.85/0.48
20	20	0	0.5, 1	0.84/0.50	0.87/0.43	0.84/0.51	0.82/0.56
20	60	0.9	0.1, 1	0.83/0.70	0.80/0.74	0.94/0.58	0.93/0.61
20	60	0.7	0.1, 1	0.84/0.71	0.81/0.73	0.89/0.61	0.89/0.62
20	60	0.5	0.1, 1	0.84/0.70	0.82/0.73	0.86/0.64	0.86/0.64
20	60	0	0.1, 1	0.83/0.71	0.81/0.74	0.85/0.63	0.85/0.65
60	20	0.9	0.1, 1	0.79/0.76	0.79/0.76	–	0.89/0.66
60	20	0.7	0.1, 1	0.79/0.76	0.78/0.76	–	0.85/0.65
60	20	0.5	0.1, 1	0.79/0.76	0.79/0.76	–	0.83/0.66
60	20	0	0.1, 1	0.79/0.76	0.79/0.76	–	0.81/0.66
100	100	0.9	0.5, 0.1	0.77/0.81	0.76/0.82	–	0.87/0.72
100	100	0.7	0.5, 0.1	0.78/0.81	0.76/0.82	–	0.82/0.72

Table 5.

True positive rate/true negative rate for the FGN error covariance models averaged over 50 replications; n = 50. Standard errors are omitted (the largest standard error is 0.04 and most are less than 0.01). Tuning parameters were selected using a 10^x resolution.

p	q	H	s1, s2	lasso	sep.lasso	MRCE	ap.MRCE
20	20	0.95	0.1, 1	0.83/0.72	0.81/0.75	0.94/0.55	0.93/0.59
20	20	0.90	0.1, 1	0.84/0.71	0.83/0.73	0.90/0.59	0.89/0.61
20	20	0.95	0.5, 1	0.87/0.40	0.87/0.45	0.93/0.39	0.92/0.39
20	20	0.90	0.5, 1	0.86/0.43	0.87/0.45	0.88/0.51	0.90/0.43
20	60	0.95	0.1, 1	0.83/0.70	0.81/0.73	0.93/0.55	0.93/0.58
20	60	0.90	0.1, 1	0.83/0.70	0.81/0.73	0.90/0.58	0.90/0.60
60	20	0.95	0.1, 1	0.79/0.76	0.79/0.76	–	0.89/0.66
60	20	0.90	0.1, 1	0.79/0.76	0.78/0.76	–	0.87/0.65
100	100	0.95	0.5, 0.1	0.77/0.81	0.75/0.82	–	0.87/0.72
100	100	0.90	0.5, 0.1	0.77/0.81	0.75/0.82	–	0.83/0.71

4. Example: Predicting Asset Returns

We consider a dataset of weekly log-returns of nine stocks from 2004, analyzed by (Yuan et al. 2007). We selected this dataset because it is the most recent dataset analyzed in the multivariate regression literature. The data are modeled with a first-order vector autoregressive model,

$$\mathbf{Y}=\stackrel{\sim }{\mathbf{Y}}\mathbf{B}+\mathbf{E},$$

where the response Y ∈ ℝ ^{T−1 ×q} has rows y₂, …, y_T and the predictor Ỹ ∈ ℝ ^{T−1 × q} has rows y₁, …, y_T−1. Here y_t corresponds to the vector of log-returns for the nine companies at week t. Let B ∈ ℝ^{q × q} denote the transition matrix. Following the approach of (Yuan et al. 2007), we use log-returns from the first 26 weeks of the year (T = 26) as the training set, and the log-returns from the remaining 26 weeks of the year as the test set. Prediction performance is measured by the average mean squared prediction error over the test set for each stock, with the model fitted using the training set. Tuning parameters were selected with 10-fold CV.

Average test squared error over the 26 test points is reported in Table 6, where we see that the MRCE method and its approximation have somewhat better performance than the lasso and separate lasso methods. The lasso estimate of the transition matrix B was all zeros, yielding the null model. Nonetheless, this results in prediction performance comparable (i.e., within a standard error) to the FES method of (Yuan et al. 2007) (copied directly from table 3 on page 341), which was shown to be the best of several competitors for these data. This comparable performance of the null model suggests that the signal is very weak in this dataset. Separate lasso, MRCE, and its approximation estimated 3/81, 4/81, and 12/81 coefficients as nonzero, respectively.

Table 6.

Average testing squared error for each output (company) × 1000, based on 26 testing points. Standard errors are reported in parentheses. The results for the FES method were copied from table 3 of (Yuan et al. 2007).

	OLS	sep.lasso	lasso	MRCE	ap.MRCE	FES
Walmart	0.98 (0.27)	0.44 (0.10)	0.42 (0.12)	0.41 (0.11)	0.41 (0.11)	0.40
Exxon	0.39 (0.08)	0.31 (0.07)	0.31 (0.07)	0.31 (0.07)	0.31 (0.07)	0.29
GM	1.68 (0.42)	0.71 (0.17)	0.71 (0.17)	0.71 (0.17)	0.69 (0.17)	0.62
Ford	2.15 (0.61)	0.77 (0.25)	0.77 (0.25)	0.77 (0.25)	0.77 (0.25)	0.69
GE	0.58 (0.15)	0.45 (0.09)	0.45 (0.09)	0.45 (0.09)	0.45 (0.09)	0.41
ConocoPhillips	0.98 (0.24)	0.79 (0.22)	0.79 (0.22)	0.79 (0.22)	0.78 (0.22)	0.79
Citigroup	0.65 (0.17)	0.61 (0.13)	0.66 (0.14)	0.62 (0.13)	0.62 (0.13)	0.59
IBM	0.62 (0.14)	0.49 (0.10)	0.49 (0.10)	0.49 (0.10)	0.47 (0.09)	0.51
AIG	1.93 (0.93)	1.88 (1.02)	1.88 (1.02)	1.88 (1.02)	1.88 (1.02)	1.74
AVE	1.11 (0.14)	0.72 (0.12)	0.72 (0.12)	0.71 (0.12)	0.71 (0.12)	0.67

We report the estimate of the unit lag coefficient matrix B for the approximate MRCE method in Table 7, which is the least sparse estimate, identifying 12 nonzero entries. The estimated unit lag coefficient matrix for separate lasso, MRCE, and approximate MRCE all identified the log-return for Walmart at week t − 1 as a relevant predictor for the log-return of GE at week t, and the log-return for Ford at week t − 1 as a relevant predictor for the log-return of Walmart at week t. The FES does not provide any interpretation.

Table 7.

Estimated coefficient matrix B for approximate MRCE.

	Wal	Exx	GM	Ford	GE	CPhil	Citi	IBM	AIG
Walmart	0	0	0	0	0	0	0.123	0.078	0
Exxon	0	0	0	0	0	0	0	0	0
GM	0	0	0	0	0	0	0	0	0
Ford	–0.093	0.035	0.012	0	0	0	0	–0.040	–0.010
GE	0	0	0	0	0	0.044	0	0	0
ConocoPhillips	0	0.007	0	0	0	0	0	–0.005	0
Citigroup	0	0	0.025	0	0	0	0	0	0
IBM	0	0	0	0	0	0	0	0	0
AIG	0	0	0.031	0	0	0	0	0	0

We also report the estimate for the inverse error covariance matrix for the MRCE method in Table 8. A nonzero entry (i, j) means that we estimate that ε_i is correlated with ε_j given the other errors (or ε_i is partially correlated with ε_j). We see that AIG (an insurance company) is estimated to be partially correlated with most of the other companies, and companies with similar products are partially correlated, such as Ford and GM (automotive), GE and IBM (technology), as well as Conoco Phillips and Exxon (oil). These results make sense in the context of financial data.

Table 8.

Inverse error covariance estimate for MRCE.

	Wal	Exx	GM	Ford	GE	CPhil	Citi	IBM	AIG
Walmart	1810.0	0	–378.0	0	0	0	0	0	–10.8
Exxon	0	4409.2	0	0	0	–1424.1	0	0	–8.4
GM	–378.0	0	2741.3	–1459.2	–203.5	0	–363.7	–56.0	–104.9
Ford	0	0	–1459.2	1247.4	0	0	0	0	0
GE	0	0	–203.4	0	2599.1	0	–183.7	–1358.1	–128.5
CPhillips	0	–1424.1	0	0	0	2908.2	0	0	–264.3
Citigroup	0	0	–363.7	0	–183.7	0	4181.7	0	–718.1
IBM	0	0	–56.1	0	–1358.1	0	0	3353.5	–3.6
AIG	– 10.8	–8.4	–104.9	0	–128.5	–264.3	–718.1	–3.6	1714.2

5. Summary and Discussion

We proposed the MRCE method to produce a sparse estimate of the multivariate regression coefficient matrix B. Our method explicitly accounts for the correlation of the response variables. We also developed a fast approximate algorithm for computing MRCE which has roughly the same performance in terms of model error. These methods were shown to outperform q separate lasso penalized regressions (which ignore the correlation in the responses) in simulations when the responses are highly correlated, even when the inverse error covariance is dense.

Although we considered simultaneous L₁-penalization of B and Ω, one could use other penalties that introduce less bias instead, such as SCAD (Fan and Li 2001; Lam and Fan 2009). In addition, this work could be extended to the situation when the response vector samples have serial correlation, in which case the model would involve both the error covariance and the correlation among the samples.

Appendix: Derivation of Algorithm 1

The objective function for Ω fixed at Ω₀ is now

$$f(\mathbf{B})=g(\mathbf{B},{\mathbf{\Omega }}_0)+{\mathrm{\lambda }}_2\sum _{j=1}^p\sum _{k=1}^q|b_{\mathit{\text{jk}}}|.$$

We can solve for B with cyclical coordinate descent. Express the directional derivatives as

$$\begin{array}{l}\frac{\partial f^{+}}{\partial \mathbf{B}}=\frac{2}{n}{\mathbf{X}}^T\mathbf{\text{XB}}\mathbf{\Omega }-\frac{2}{n}{\mathbf{X}}^T\mathbf{Y}\mathbf{\Omega }+{\mathrm{\lambda }}_2\mathbf{1}(b_{\mathit{\text{ij}}}\ge 0)-{\mathrm{\lambda }}_2\mathbf{1}(b_{\mathit{\text{ij}}}<0),\\ \frac{\partial f^{-}}{\partial \mathbf{B}}=-\frac{2}{n}{\mathbf{X}}^T\mathbf{\text{XB}}\mathbf{\Omega }+\frac{2}{n}{\mathbf{X}}^T\mathbf{Y}\mathbf{\Omega }-{\mathrm{\lambda }}_2\mathbf{1}(b_{\mathit{\text{ij}}}>0)+{\mathrm{\lambda }}_2\mathbf{1}(b_{\mathit{\text{ij}}}\le 0),\end{array}$$

where the indicator 1(·) is understood to be a matrix. Let S = X^TX and H = X^TYΩ and $u_{\mathit{\text{rc}}}={\sum }_{j=1}^p{\sum }_{k=1}^q{b}_{\mathit{\text{jk}}}{s}_{\mathit{\text{rj}}}{\omega }_{\mathit{\text{kc}}}$. To update a single parameter b_rc we have the directional derivatives,

$$\begin{array}{l}\frac{\partial f^{+}}{\partial b_{\mathit{\text{rc}}}}=u_{\mathit{\text{rc}}}-h_{\mathit{\text{rc}}}+n{\mathrm{\lambda }}_{2}1(b_{\mathit{\text{ij}}}\ge 0)-n{\mathrm{\lambda }}_{2}1(b_{\mathit{\text{ij}}}<0),\\ \frac{\partial f^{-}}{\partial b_{\mathit{\text{rc}}}}=-u_{\mathit{\text{rc}}}+h_{\mathit{\text{rc}}}-n{\mathrm{\lambda }}_{2}1(b_{\mathit{\text{ij}}}>0)-n{\mathrm{\lambda }}_{2}1(b_{\mathit{\text{ij}}}\le 0).\end{array}$$

Let $b_{\mathit{\text{rc}}}^0$ be our current iterate. The unpenalized univariate minimizer ${\widehat{b}}_{\mathit{\text{rc}}}^{\ast }$ solves

$${\widehat{b}}_{\mathit{\text{rc}}}^{\ast }{s}_{\mathit{\text{rr}}}{\omega }_{\mathit{\text{cc}}}-b_{\mathit{\text{rc}}}^0{s}_{\mathit{\text{rr}}}{\omega }_{\mathit{\text{cc}}}+u_{\mathit{\text{rc}}}-h_{\mathit{\text{rc}}}=0,$$

implying ${\widehat{b}}_{\mathit{\text{rc}}}^{\ast }=b_{\mathit{\text{rc}}}^0+\frac{h_{\mathit{\text{rc}}}-u_{\mathit{\text{rc}}}}{s_{\mathit{\text{rr}}}{\omega }_{\mathit{\text{cc}}}}$. If ${\widehat{b}}_{\mathit{\text{rc}}}^{\ast }>0$, then we look leftward and by convexity the penalized minimizer is ${\widehat{b}}_{\mathit{\text{rc}}}=max(0,{\widehat{b}}_{\mathit{\text{rc}}}^{\ast }-\frac{n{\mathrm{\lambda }}_2}{s_{\mathit{\text{rr}}}{\omega }_{\mathit{\text{cc}}}})$. Similarly if ${\widehat{b}}_{\mathit{\text{rc}}}^{\ast }<0$, then we look to the right and by convexity the penalized univariate minimizer is ${\widehat{b}}_{\mathit{\text{rc}}}=min(0,{\widehat{b}}_{\mathit{\text{rc}}}^{\ast }+\frac{n{\mathrm{\lambda }}_2}{s_{\mathit{\text{rr}}}{\omega }_{\mathit{\text{cc}}}})$, thus ${\widehat{b}}_{\mathit{\text{rc}}}=\text{sign}({\widehat{b}}_{\mathit{\text{rc}}}^{\ast })(|{\widehat{b}}_{\mathit{\text{rc}}}^{\ast }|-\frac{n{\mathrm{\lambda }}_2}{s_{\mathit{\text{rr}}}{\omega }_{\mathit{\text{cc}}}})+$. Also if ${\widehat{b}}_{\mathit{\text{rc}}}^{\ast }=0$, which has probability zero, then both the loss and penalty part of the objective function are minimized and the parameter stays at 0. We can write this solution as

$${\widehat{b}}_{\mathit{\text{rc}}}=\text{sign}\left(b_{\mathit{\text{rc}}}^0+\frac{h_{\mathit{\text{rc}}}-u_{\mathit{\text{rc}}}}{s_{\mathit{\text{rr}}}{\omega }_{\mathit{\text{cc}}}}\right){\left(\left|b_{\mathit{\text{rc}}}^0+\frac{h_{\mathit{\text{rc}}}-u_{\mathit{\text{rc}}}}{s_{\mathit{\text{rr}}}{\omega }_{\mathit{\text{cc}}}}\right|-\frac{n{\mathrm{\lambda }}_2}{s_{\mathit{\text{rr}}}{\omega }_{\mathit{\text{cc}}}}\right)}_{+}.$$