Way-finding in displaced clock-shifted bees proves bees use a cognitive map

Significance

The question of the computational capacities of the brains of widely separated genera of animals is of interest to behavioral biologists, comparative psychologists, computational neuroscientists, philosophers of mind, and—we believe—much of the scientific community. Half a century ago, the claim that any nonhuman animal had a cognitive map was deeply controversial. If true, it greatly favored a computational theory of mind, as opposed to an antirepresentational behaviorist theory. Now that it is well established by behavioral and neurobiological evidence that rodents have a metric cognitive map, the question of whether insects do is a frontier question, the answer to which has broad implications in several disciplines.

Abstract

Mammals navigate by means of a metric cognitive map. Insects, most notably bees and ants, are also impressive navigators. The question whether they, too, have a metric cognitive map is important to cognitive science and neuroscience. Experimentally captured and displaced bees often depart from the release site in the compass direction they were bent on before their capture, even though this no longer heads them toward their goal. When they discover their error, however, the bees set off more or less directly toward their goal. This ability to orient toward a goal from an arbitrary point in the familiar environment is evidence that they have an integrated metric map of the experienced environment. We report a test of an alternative hypothesis, which is that all the bees have in memory is a collection of snapshots that enable them to recognize different landmarks and, associated with each such snapshot, a sun-compass–referenced home vector derived from dead reckoning done before and after previous visits to the landmark. We show that a large shift in the sun-compass rapidly induced by general anesthesia does not alter the accuracy or speed of the homeward-oriented flight made after the bees discover the error in their initial postrelease flight. This result rules out the sun-referenced home-vector hypothesis, further strengthening the now extensive evidence for a metric cognitive map in bees.

A metric cognitive map enables an animal to locate itself in space. In recent decades, accumulating behavioral and neurobiological evidence has established a broad consensus that the brains of mammals, and perhaps even all vertebrates, compute a metric cognitive map of the experienced environment on which they maintain a continuously updated representation of the animal’s position (1–7). Because a metric map is far removed from the elementary sense data from which it must be computed, and because a map is a mathematical construction carried in a symbolic memory, the conclusion that the vertebrate brain computes a metric cognitive map of the environment is a strong argument for the computational theory of mind, which is a fundamental concept of cognitive science.

The mammalian hippocampus and its putative homologs in nonmammalian vertebrates appear to play a central role in the requisite computations in vertebrates (3). Insofar as the brain’s computational capacities are thought to derive from the structure of its circuits, this theory suggests that understanding the circuitry unique to the hippocampus and its homologs might be a key to constructing a neurobiologically anchored model of these computations. Before this line of thought is pursued further, it is important to know whether the construction of a metric cognitive map is limited to vertebrates. Invertebrates, particularly the social insects, whose brains are miniscule in comparison with the vertebrate brain and lacking in a homolog of the mammalian hippocampus, are nonetheless known to possess impressive navigational abilities (8–10). It is, however, a matter of long-standing controversy whether these abilities rest on the construction and use of a metric cognitive map (11–18).

Way-finding, the ability to set a course from one familiar but otherwise arbitrarily chosen location to another location that is not perceptible from the first, is the signature of a metric cognitive map. Displacing an animal from its current location to an experimenter-chosen location within the territory the animal is presumed to be familiar with, and then observing its subsequent goal-seeking behavior, is a common test of way-finding. To set a course from the release site to the unseen goal, the navigator must read the coordinates of the release site from its map and compute the difference between those coordinates and the goal coordinates to obtain the difference vector specifying the direction and distance to move from its current location to its goal.

In most early displacement experiments with honey bees, the released bee took off on the goal vector from the capture site (17, 19), not the goal vector from the release site, suggesting that the bee lacks a true cognitive map. This conclusion came into question after the recent development of systems for tracking the flights of the released bees using harmonic radar (20, 21). When no extended landmarks and no structured skyline of the horizon were available at the release site, bees flew first on the goal vector from the capture site, as was expected from the earlier work. The bees were seemingly unaware that this initial direction was wrong and would not lead them to their intended goal. However, they were not lost; after the initial misoriented component of their flight, the bees flew toward the intended goal along novel short-cuts (18, 20). The bees seemed to become aware of the displacement only when flying the capture-site goal vector failed to bring them to the goal, at which point they were able to set the correct course to the goal from a point just as arbitrary as the experimenter-chosen release site.

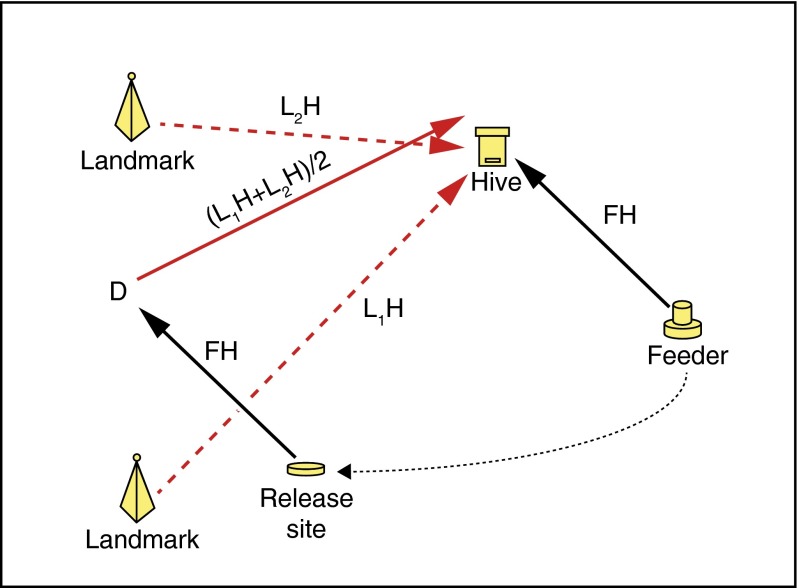
These experiments did not, however, rule out an alternative account. In this account, proposed by Collett et al. (12) and formalized by Cruse and Wehner (13), the bee never constructs an integrated cognitive map; rather, it associates with each snapshot stored in memory the home vector from that landmark. When the bee discovers that it has not arrived home, it identifies nearby landmarks, averages the associated home vectors, and flies the resulting vector (Fig. 1).

Fig. 1.

The average-vector hypothesis. Bee is captured at the feeder F bound for the hive H on vector FH and released at a release site R. It flies the vector FH from R, discovers its error at D, recognizes the landmarks L₁ and L₂, and flies the average of the associated home vectors, which is the vector (L₁H + L2H)/2.

An extension of this account is the proposal that multiple sequentially learned and retrieved views are integrated in a common memory replacing the notion of discreet views (22). All of these proposals rely on the assumption that learned views are related to each other by reference into a common reference system, the sun-compass, and lead to computations of vectors embedded in the sun-compass. The attraction of this alternative account is, first, that it relies on the well-established fact that bees and ants do store the home vectors from familiar landmarks and, second, that it avoids the assumption that the bee has an integrated readable cognitive map. However, the home vectors from landmarks are known to be compass-referenced. These vectors are equivalent to an instruction of the form: “fly northeast 100 m.” For bees and many other animals, the compass direction of vectors derived from their dead reckoning is determined by reference to the sun. In contrast, vectors computed from differences in location coordinates are terrain-referenced. Flying these vectors requires continued attention to the mapped terrain because it requires maintaining appropriate angles with respect to terrain features. The appropriate angles and the terrain features change during the course of a flight, and the angle appropriate to a given terrain feature and to the current location of the navigator, can be determined only from the map. Holding to a terrain-referenced direction is called “carrying the parallel” because, conceptually, a direction on a map is an uncountable infinite set of parallel lines in a vector space (some vectors of which reference experienced locations).

The difference in the directional referents for the two kinds of vectors makes possible a decisive test: The sun-compass is time-compensated, because the compass direction of the sun changes dramatically during the day. The time compensation depends on a time-of-day signal from the bee’s circadian clock. Therefore, a large (several hours) shift in the phase of the circadian clock introduces a large shift in the sun compass (23, 24). If the course of the flight made after discovery of the initial error (at point D in Fig. 1) depends on the sun-referenced home vectors known to be associated with familiar landmarks, a large clock-shift will introduce a large error in the postdiscovery flights (DH vector in Fig. 1), as well as in the prediscovery portions of those flights. Consequently, the clock-shifted bees should become even more lost than they already are. The proportion making it to the hive should be greatly reduced, and the times taken to make it there should be greatly increased. In contrast, if the course after point D depends on a terrain-referenced vector obtained by reading the map, clock-shifting will produce no systematic error in the postdiscovery flight. The course should be as accurate in clock-shifted bees as in unshifted control bees, in which case the clock-shifted bees should make it to the hive in the same proportions and with the same flight times as the unshifted control bees.

We ran this test under two different environmental conditions, using general anesthesia to rapidly induce clock-shifts in some groups of the bees (24). In the first experiment, sky-line cues were not available to the bees throughout their vector and homing flights because all flights were performed within an area characterized by ≤2° visual angle of the skyline but with panorama cues as seen by the flying bee (pattern of local structures on the ground were available) (Fig. 2A and Figs. S1 and S2). Visual resolution of the bees’ compound eye is in the range of 2° (25, 26). Thus, modulation of the skyline ≤2° will not be resolved. In the second experiment, there were salient skyline and panorama cues (a line of bushes) (Fig. 2B and Fig. S2) visible during both flight phases and during the initial training of the bees from the hive to the feeder. In addition, the conditions during the homing phase in the first experiment were made relatively more difficult for the clock-shifted bees by allowing the control bees to refer to an extended landmark when they arrived at the point of error discovery (an irrigation channel) (Fig. 2A), which offered a salient feature for home-directed guidance, whereas the clock-shifted experimental bees arrived at the point of error discovery in a rather low feature landscape: an open, flat grass pasture. If the experimental bees would perform their homing flights equally as well as the control bees, the spatial relations of ground structures, as learned during the orientations flights or later during foraging flights, must be sufficient for homing, indicating a terrain-based spatial reference system independent of the sun-compass.

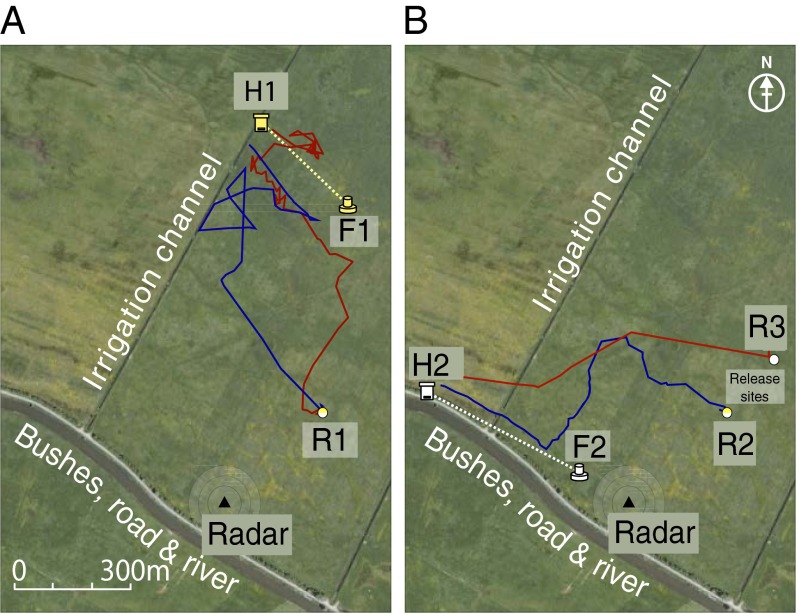
Fig. 2.

Layout of the experimental site. A large flat open field bordered by a row of bushes, a road and a river. Perpendicular to the bushes ran two irrigation channels. Representative bee flights shown. (A) In Exp. 1 bees were trained from hive H1 to the feeder F1 along the yellow dotted line. (B) In Exp. 2 bees were trained from hive H2 to feeder F2 along the white dotted line. The release site in Exp. 1 was R1. In Exp. 2 two release sites were used, R2 and R3. The radar (black triangle at the origin) was positioned ∼60 m from the row of bushes stretching along a small road and a river. H1 is located at the upper part of the western irrigation channel. H2 is located on the edge of the bushes to the south. The blue lines in the figures show representative flight paths from control bees, the red lines from clock-shifted bees.

Results

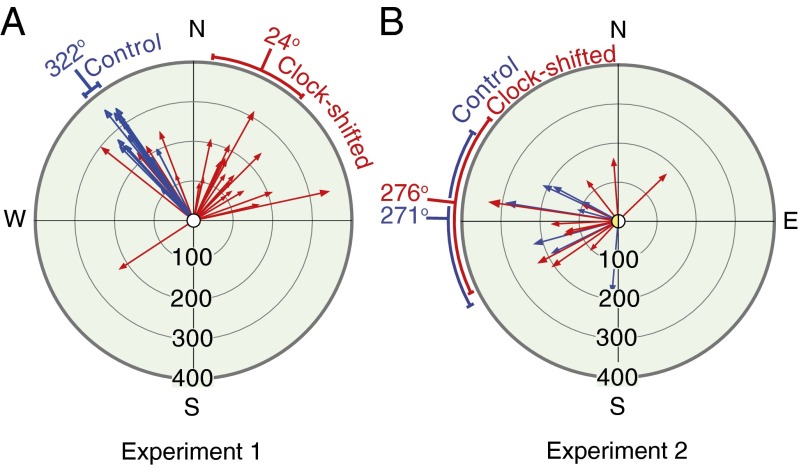
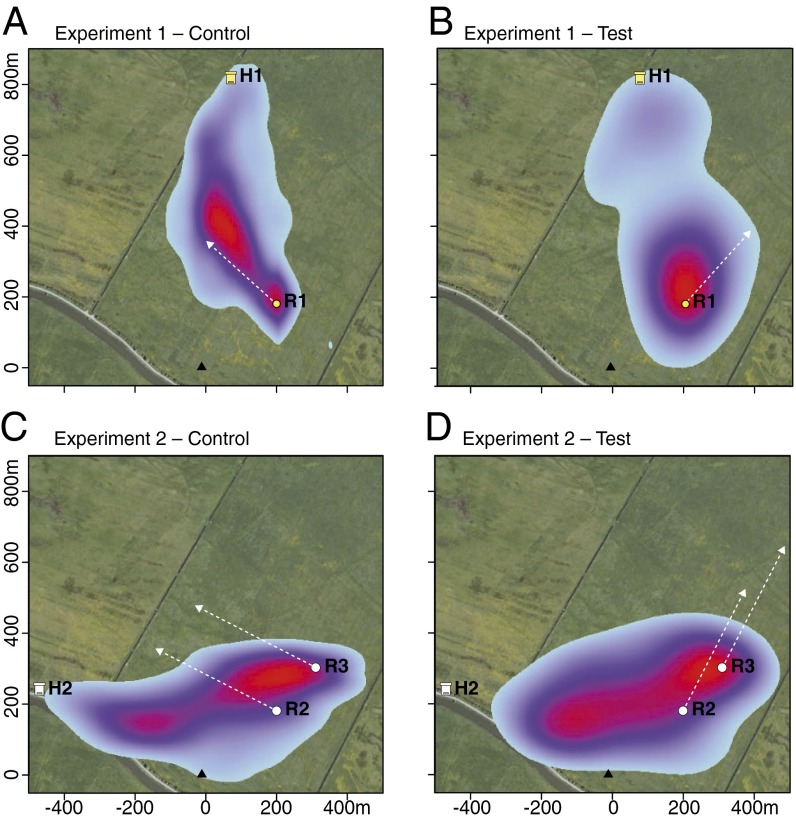
In Exp. 1, under conditions where there were no salient landmarks at the release point (R1 in Fig. 2A), bees that were not clock-shifted departed initially on the vector (denoted FH in Fig. 1), as expected (blue vectors in Fig. 3A), whereas the clock-shifted bees departed on a vector shifted by a large amount in the direction expected from the clock shift (red vectors in Fig. 3A; see also Fig. S3A). Thus, the clock-shifted and non–clock-shifted bees arrived at different error discovery locations, as illustrated by the examples in Fig. 2A, and as shown by the representations of the aggregated flight data in Fig. 4 A and B. However, the bees’ flights after they discovered their error were equally accurately directed toward the hive (Figs. 2A and 4B) and brought them to it in the same proportions and in the same flight times as the bees that were not clock-shifted. The individual flights of the clock-shifted and control bees for both experiments are shown in Figs. S4 and S5 for Exp. 1 and Figs. S6 and S7 for Exp. 2.

Fig. 3.

Initial vector flight components (vector flights) of bees in Exps. 1 and 2. Clock-shifted bees shown in red and control bees shown in blue. (A) Exp. 1: clock-shifted mean vector angle 24°, (95% CI 7°,41°); control mean vector angle 322°, (95% CI 319°, 325°). (B) Exp. 2: clock-shifted mean angle 276°, (95% CI 244°, 308°); control mean vector angle 271°, (95% CI 240°, 301°). Scale in meters.

Fig. 4.

Kernel density (kde) plots overlaid on a Google map showing the homing behavior of animals from the point of release in Exps. 1 and 2. (A) Exp. 1 control bees (n = 13); (B) Exp. 1 clock-shifted bees (n = 24); (C) Exp. 2 control bees (n = 8); (D) Exp. 2 clock-shifted bees (n = 12). The color maps indicate the probability of a bee being at a particular coordinate with blue indicating low and red indicating higher probability of occurrence. The white dashed lines indicate the expected sun-compass orientation angle under each experimental condition. Scale in meters from the radar.

If the postdiscovery flights of the clock-shifted bees had been made using sun-referenced vectors, they should have shown the systematic error seen in the prediscovery portions of the flights, and they should have become even more lost. No matter what familiar landmarks the bees encountered as they searched for the way home, the home vectors associated with those landmarks should have headed the clock-shifted bees in the wrong direction. Notice that the former feeding site F1 (Figs. S4 and S5) was not marked in any way (the feeding equipment was removed and no trained bees were flying).

In support of the conclusion that the clock-shift did not impair the postdiscovery home-bound flights, we note the following statistical results: No evidence of a difference was found between the homing flights of control and experimental animals in Exp. 1 with respect to the rate of success in getting back to the hive (P = 0.63, logistic regression). Of the 24 bees in the experimental group, 19 returned to the hive compared with 11 of 13 in the control group. Because the predictions from the map hypothesis for this test are null predictions (no effect), we computed Bayes Factors (BFs) to complement the insignificant P values obtained from the more conventional null-hypothesis significance tests. Unlike the conventional tests, a Bayesian model-selection test requires that we compare the predictions of the null to the predictions of an alternative to it. Typically, the alternative specifies a range of possible experimental effects (whereas the null specifies 0 effect). If one assumes as an alternative hypothesis in which the effect of the 6 h of 2% isoflurane anesthetic might range anywhere from no effect to a devastating effect on the proportion of experimental bees finding their way home, then the BF is 3.54 in favor of the null (Fig. S3A). A BF of 3 or greater is roughly equivalent to a P value of 0.05 or less; it signifies substantial support from the data for a conclusion. In this case, the conclusion is that the proportion of clock-shifted bees making it home is no different from the proportion of control bees making it home. Even when one assumes that the experimental effect can be at most such as to lower the true proportion making it home by no more than 20%, the BF of 1.05 still slightly favors the null hypothesis. When measuring homing components of those bees in both groups that did return home, there was no evidence of a difference in postvector flight time (P = 0.25) or postvector flight distance (P = 0.40) (Table 1). If one takes as an alternative to the null hypothesis the hypothesis that the effect of the clock-shift on homing time or flight distance might range anywhere from 0 to 1 σ, then the BF favors the null by greater than 3 (in other words, substantial support for the null relative to an alternative that posits some small effect) (Fig. S3A). Taken together, the results of Exp. 1 clearly show that clock-shifted animals were not compromised in returning home, although they initially referred to an incorrect sun-compass direction, as indicated by the strongly shifted prediscovery portions of their flights (Fig. 2A and Fig. S8A).

Table 1.

Postvector flight data of the bees in Exps. 1 and 2

Experiment	Group	No. of animals returning home/total	Mean time ± SEM (s)	Mean distance ± SEM (m)*
Experiment 1	Clock shifted	19/24	154 ± 30	1,687 ± 287
	Control	11/13	140 ± 24	1,452 ± 108
Experiment 2	Clock shifted	10/12	173 ± 64	948 ± 172
	Control	7/8	95 ± 31	772 ± 119

^*A significant difference between the total distance traveled in Exps. 1 and 2, P = 0.0007.

In Exp. 2, where there was a salient panorama cue at the release site (Fig. S2), similar proportions of animals returned home (7 of 8 in the control group and 10 of 12 in the clock-shifted group) (Table 1). Null-favoring BFs of 3.46 and 1.13 again support the conclusion that there was no difference in these proportions. As we thought might happen, erroneously oriented departures from the release site were not seen in either the control or the clock-shifted bees. The prominent panorama cue (the line of bushes) was sufficient to induce a map-based terrestrially referenced orientation from the outset or very soon thereafter. Even though the experimental animals were clock-shifted by 6 h, they did not show deviations in their initial vector-flight angles from the controls (95% confidence interval, CI: for the difference −29.32, 51.8°) (Figs. 3B and 4B and Figs. S8 B and C and S7). Both the clock-shifted and control bees flew very quickly toward and along the row of bushes toward the hive (Figs. 1B and 3 C and D). Thus, a salient landmark like the row of bushes along which the bees were trained initially appears to forestall initial reliance on the sun-compass–referenced, dead-reckoning–derived home vector. As in Exp. 1, there were no differences in postvector flight time or postvector flight distance (Table 1).

When comparing Exps. 1 and 2, there was no effect of the between-experimental variation on the overall success of the bees returning home (P = 0.73). Nor was there any evidence that the flight time was different (P = 0.78) (Fig. S8D) between experiments. However, there was a notable between-experiment difference in the overall distance traveled by the bees (P = 0.0007). The mean flight distance was shorter in Exp. 2 than in Exp. 1, even though the distance from the release site to the hive in Exp. 2 was longer than in Exp. 1. If one takes as an alternative to the null the hypothesis that the effect of the experiment on the mean distance flown was on the order of 1 σ, then the data give substantial (BF > 3) to conclusive (BF > 200) support to this conclusion, depending on whether one uses all of the data or treats the flights longer than 3,000 m as outliers (Fig. S3B). Regardless of the limit on the effect size and regardless of whether one discards the outliers or not, the BF favors the hypothesis that the mean flight distance was shorter in Exp. 2 than in Exp. 1, despite the fact that the distance between the release sites and the hive was greater in Exp. 2 than in Exp. 1 (Fig. 2). We estimate with 95% confidence that the bees in Exp. 2 only flew between 39% and 76% of the distance of those in Exp. 1 (see Fig. S3B for the cumulative distributions). Although they had a longer way to go to get home, the bees in this experiment got there more directly because they did not first make a misdirected initial vector flight. They read their map at the release site.

Discussion

The directional component of the initial flight vector at the release site has been observed in a number of previous studies in which the vanishing bearings were used to study bee navigation (27, 28).

Estimation of the directional component of this flight path via the sun-compass requires reference to an internal clock (29). It was therefore not surprising that shifting the clock led to a systematic shift in the direction of this initial flight path when salient landmarks were lacking. General anesthesia as applied here was previously shown to induce such a clock-shift (24). We therefore could ask whether the homing-flight component following the initial vector-flight component (20, 21) would also require reference to the sun-compass, and thus would lead to unsuccessful or extended homing flights. Such a result would support the hypothesis that the successful homing of displaced bees is mediated by some form of vector addition of remembered home vectors (12, 13, 20, 22). This hypothesis assumes that associations between landmarks and homing vectors are established during exploratory orientation flights and during foraging flights (30). The data presented here do not support the hypothesis that these averaged home vectors account for the bees’ ability to find their way home once they have discovered the error of their ways. The reckoning of a displacement-appropriate homing vector occurred very quickly. The clock-shifted bees were not directed away from the hive at the end of their first flight phase, and had little trouble finding the hive, even though the clock-shift directed them away from both the hive and the water channel. Because no beacons were available at the hive or the former feeding site (F1), no salient landmarks signaled the route between hive and feeder, and the skyline did not provide any information, no elementary forms of navigation could be used by the time-shifted animals. The bees’ success was also not the result of a resetting of the circadian clock, because even in strong light/dark cycles the change in timing of foraging visits after anesthesia has been shown to persist for several days (24). Rather, we argue that homing when there is no salient familiar landmark is directed by reference to earthbound landmarks rather than to a dead-reckoning–derived, sun-compass–referenced home vector, excluding the possibility of addition of two or more vectors embedded in the sun-compass reference system. This conclusion does not exclude the possibility that bees may perform such vector addition under different conditions: for example, when these vectors were specifically trained, a capacity that was shown after training to two feeding sites simultaneously (31).

Salient landmarks, like the row of bushes experienced during route training between hive and feeder (F2), override the sun-compass and guide the bees in direct flights to the hive. Interestingly, different behaviors were observed in using this landmark as a guide: it was either approached directly shortly after the release and then followed by the bees, or it was used to guide a shortcut toward the hive. In either case, a time-shift did not alter the behavior, indicating that a salient extended landmark learned during training overrides reliance on a home vector derived from sun-compass–referenced dead reckoning. Clock-shifted animals altered their sun-compass–related flights during the initial phase of their homing flights, as expected, but only if they lacked salient landmarks during their initial flight phase. An elementary account of this effect assumes a simple association of the flight route during training and the extended landmark. However, it is also possible that such a salient landmark is just one feature embedded in an integrated spatial memory storing geometric relations between multiple landmarks.

A recent analysis of GPS tracking of clock-shifted pigeons in a similar catch-and-release paradigm demonstrated pigeons can use a memory of the geometrical relation between visible terrain and not-currently visible home loft to navigate directly home (32). In the pigeon literature, this ability is called “piloting” and is contrasted to a compass strategy that relies on site-specific home vectors.

The results we report herein, together with other recent results (20, 31), imply that the bee is like mammals and birds in that its brain constructs an integrated, metric cognitive map. The map is metric because it represents directions and distances. It is integrated because it represents diverse landmarks, feeding sources, and terrain features within a single data structure, thereby permitting the computation of a course from any represented feature to any other represented feature and the terrestrially referenced carrying of the directional parallel.

There is extensive experimental and theoretical research on the neurobiology of the mammalian cognitive map (2, 33–35). The brain of the bee does not have the structures that figure prominently in the mammalian brain’s cognitive map (hippocampus, presubiculum, entorhinal cortex, anterior nucleus of the thalamus, to name some of the most prominent navigationally important structures). Therefore, in constructing neurobiologically plausible computational models of the circuit- and cellular-level mechanisms that mediate the computations involved in map construction and utilization, theorists will want to bear in mind that these computations are also realized in the brain of the bee, despite the dramatic differences in gross brain structure, in microcircuitry, and in neuronal morphology, and despite the fact that there are orders-of-magnitude fewer neurons in the entire brain of the bee than in the hippocampus of a rat.

Materials and Methods

The experiments were conducted in summer 2009 in a large open grass field close to Klein Lüben (Brandenburg, Germany, coordinates: N 52.97555, E 11.83677) (Fig. 2 and Fig. S1). The field was homogenous in character, with discernible landmarks only on the ground (patches of differently growing grass, clover flowers) (Fig. S2). A line of bushes formed the south border of the field. Two irrigation channels ran perpendicular to the bushes stretching in a NNE direction. Although the bushes were discernible over a distance of about 100 m (Figs. S1 and S2), the bees saw the irrigation channels only when they were almost directly over them. The channel on the west side was a particularly salient stimulus for the bees in Exp. 1 because their hive (H1) was immediately adjacent to this channel in the north of the field. The line of bushes was a salient stimulus for bees in the second experiment because their hive (H2) was located close to them at the west end. The release site for bees in the first experiment (R1) was selected on the basis that bees flying in a westerly and northerly direction did not see a structured skyline (Fig. S2). However, in the second experiment we hypothesized that the bees, released from R1, might well be influenced by the line of bushes. Therefore, we varied the visibility of this extended landmark by releasing bees at two sites (R1 and R2) (Figs. 2 and 4 and Fig. S7), but both release sites allowed the bees to see the row of bushes (Figs. S1 and S2).

Bees in Exp. 1 were trained to the feeder F1 and those in Exp. 2 to feeder F2. Individual bees caught departing the feeder were caught at 0900 and randomized into one of two groups: either clock-shifted (experimental bees) or control bees. We undertook the clock-shifting procedure previously described to phase-delay the clock (24). The experimental group was anesthetized with 6-h 2% isoflurane (Aerrane; Baxter) in air in a light- and gas-proof container (3.5 L; flow rate: 0.5 L/min). The control bees were kept in a similar dark container. Both groups were displaced from the feeder site and released at R1 or R2 (Fig. 2). All equipment at the training station F1 was removed during the test sessions, and no trained bees were flying between the hive and F1 at this time. There was no salient landmark between the hive and the F1. Release site R1 was selected on the ground so that both control bees and time-shifted bees flew within the area of ≤2° visual angle of the skyline (Fig. S2).

Radar Tracking.

Tracking bees with a harmonic radar was achieved as previously described (18, 21, 36). We used a system with a sending unit consisting of 9.4 GHz radar transceiver (Raytheon Marine; NSC 2525/7 XU) combined with a parabolic antenna providing ∼44 dBi. The transponder fixed to the thorax of the bee consisted of a dipole antenna with a Low Barrier Schottky Diode HSCH-5340 of centered inductivity. The second harmonic component of the signal (18.8 GHz) was the target for the radar. The receiving unit consisted of an 18.8-GHz parabolic antenna, with a low-noise preamplifier directly coupled to a mixer (18.8-GHz oscillator), and a downstream amplifier with a 90-MHz ZF-Filter. A 60-MHz ZF-Signal was used for signal recognition. The transponder had a weight of 10.5 mg and a length of 12 mm. We used a silver or gold wire with a diameter of 0.3 mm and a loop inductance of 1.3 nH. The range of the harmonic radar was 1 km. The initial part of the flight (vector flight) for these bees has already been studied (see ref. 24 for details).

Statistical Analysis.

Initially we set out to compare three primary variables: (i) the rate of success in returning home, (ii) the time taken to return home after the initial vector flight, and (iii) distance traveled after the vector flight. These variables were tested using generalized linear models that compared treatment and control levels as well as between the two experiments. The model examining the rate of successful returns home (i) used a logistic model (with log-link), whereas the time taken (ii) and postvector distance traveled (iii) were modeled using a negative binomial error structure (with log-link).

In a secondary analysis we calculated the density of the whole flight paths concentrating on the postvector flight behavior and compared this with landmarks. Kernel density maps were produced using the package “ks” (37) with the statistical software “R” (38). The color maps indicate the probability of a bee being at a particular coordinate. Kernels were produced using a plug-in estimator using a bandwidth matrix with no constraints (which allows arbitrary orientation of the kernel) (39). Each bee had an initial probability density map calculated using the position of its flight path recorded by the harmonic radar. The resultant maps from each individual bee were then integrated into a single final kernel density for each treatment level. The final kernel density visualized nonzero probability density using a color ramp, with blue indicating low and red indicating higher probability of occurrence.

Because the interesting and counterintuitive theoretical predictions in these experiments are null predictions (the prediction that there will be no experimental effect), we report Bayes Factors as well as P values. As is well known, the P value from a null hypothesis significance test cannot be used to support a null hypothesis, whereas a Bayes Factors can. A Bayes Factor gives the odds favoring one hypothesis over another. Computing a Bayes Factor requires formulating a quantitatively explicit alternative to the null hypothesis, a hypothesis that says how big the experimental effect might be. The higher the limit on the effect size is, the more the comparison will tend to favor the null hypothesis when there is in fact only a small effect. [When experimental effects are large (>2 σ), the Bayes Factor strongly favors the alternative to the null for all remotely plausible assumptions as to the upper limit on effect size.] Therefore, we compute and report the Bayes Factor for a comparison that assumes a large (but in our judgment plausible) limit on the size of the experimental effect and one that assumes that the experimental effect could be at most only small. The latter Bayes Factors will necessarily be close to 1, because the alternative to the null differs from the null by an amount that is at most small, therefore one hypothesis cannot be much more likely than the other (unless the n is very large). For the full Bayesian treatment of the data, see Figs. S3 and S8.