Extracting more information from EEG recordings for a better description of sleep

Abstract

We are introducing and validating an EEG data-based model of the sleep process with an arbitrary number of different sleep stages and a high time resolution allowing modeling of sleep microstructure. In contrast to the standard practice of sleep staging, defined by scoring rules, we describe sleep via posterior probabilities of a finite number of states, not necessarily reflecting the traditional sleep stages. To test the proposed probabilistic sleep model (PSM) for validity, we correlate statistics derived from the state posteriors with the results of psychometric tests, physiological variables and questionnaires collected before and after sleep. Considering short, in this study 3 s long, data window the PSM allows describing the sleep process on finer time scale in comparison to the traditional sleep staging based on 20 or 30 s long data segments visual inspection. By combining sleep states and using two measures derived from the posterior curves we show that the average absolute correlations between the measures and subjective and objective sleep quality measures are considerably higher when compared with the analogous measures derived from hypnograms based on sleep staging. In most cases these differences are significant. The results obtained with the PSM support its wider use in sleep process modeling research and these results also suggest that EEG signals contain more information about sleep than what sleep profiles based on discrete stages can reveal. Therefore the standardized scoring of sleep may not be sufficient to reveal important sleep changes related to subjective and objective sleep quality indexes. The proposed PSM represents a promising alternative.

1. Introduction

Sleep is by no means a monolithic state but a complex, often cyclic process of different physiological modalities, as can be observed by means of electroencephalography (EEG) and other electrophysiological measures. Sleep research and sleep medicine usually distinguish a small number of different sleep stages according to the type of sleep (rapid eye movement sleep, or REM, vs. non-REM, or NREM) and the sleep depth within NREM. The manual devised by Rechtschaffen and Kales [1] (RK) and the recently published update of sleep scoring rules [2] assign either stage wake (W), one of the NREM sleep stages S1, S2, S3, S4 (or N1, N2, and N3, respectively) or REM (R)¹ to a given 30 s interval using polysomnographic (PSG) recordings. The borders between the NREM stages are more or less arbitrarily defined. The emphasis has been put on consistent rules based on visually identifiable signal features, such that different practitioners will come to the same reasonable assignment of sleep stages to the 30 s intervals. Examples of such features are alpha or delta waves, sleep spindles, k-complexes in the EEG, rapid eye movements in the EOG (electrooculography), and low muscle tone in the submental EMG (electromyography), encompassing the three major electrophysiological sources in PSG.

Visual sleep scoring based on the above-mentioned rules, as is common practice or even gold standard in both sleep research and sleep disorder diagnosis, exhibit large variations between different experts, mainly stemming from the fact that many of the necessary features are difficult to recognize, on one hand, and from the fact that the rules linking the features to the sleep stages are too vaguely defined, on the other. There have been several successful attempts to automate the process of assigning a sleep stage in order to eradicate such variability; for example, the automatic scoring system Somnolyzer24x7 [3].

Still, strong criticism of traditional sleep staging abounds in sleep research. Himanen and Hasan [4] criticized that the division into a few sleep stages is based on the knowledge of sleep processes which was valid at the time when the rules were developed, but has not been revised since. For instance, they mentioned that at least two different wakefulness stages exist or that S2 is a heterogeneous stage which should be subdivided. Also, the time resolution of 30 s epochs is based on the old practice of paper-EEG and thus bears no useful relationship to physiological reality and is likely to miss important events on a smaller scale. Schulz [5] argues along similar lines viewing standard sleep staging as no longer fully appropriate in an age where all data is available in digital form ready for computer processing. He calls for alternatives for sleep analysis that go beyond the brittle stages, subdivide NREM sleep in a more fine-grained manner, and is not limited by what can be visually identified in the signal.

We would like to present an approach which allows for the description of sleep on a higher time resolution, allowing for continuous transitions from one sleep stage to another (probabilistic sleep model, PSM). Although we do not fully abandon the staging systematics, we primarily build our model on the underlying data structure without immediately putting too much emphasis on strict staging labels. We do, however, use staging labels as a means of providing our model with some physiological meaning resembling the RK physiological interpretation.

Our model is based on Gaussian mixture models used to describe the density of data representing sleep, implicitly containing Gaussian kernels corresponding to natural clusters in the data. While these clusters cannot be interpreted directly, we use them either to derive variables about sleep architecture or, alternatively, to calculate posterior probabilities for short data segments to belong to one of the traditional stages. These probabilities then form a continuous and high time resolution sleep profile replacing the rigid stages, potentially reflecting important information about the microstructure of sleep that is overlooked in the classical staging paradigm.

The idea of using posterior probabilities to express the belief that a given observation stems from a certain sleep stage is not new and arises automatically in certain contexts. For instance, the softmax activation function can be used in the output layer of a Feedforward Classification Network to predict the posterior probabilities given the input [6]. Considering the probabilistic output representation, Roberts et al. [7] described sleep as a mixture of three cornerstones “wake”, “REM” and “deep sleep”. The authors assumed that these sleep stages are seldom mislabeled and, furthermore, that other sleep stages such as S1 and S2 can be seen as transitions between the cornerstones. Roberts et al. [7] worked with features which are 10-dimensional parameter vectors gained from fitting an autoregressive model (AR) to short 1 s intervals of the EEG time series. Each AR model is connected to a frequency distribution, and the AR vector can be interpreted as a way of describing the frequency spectrum for the given interval. Instead of using neural network related features with posterior probabilities, Penny and Roberts [8] worked with Gaussian Observation Hidden Markov Models (GOHMM), whereby they demonstrated the applicability by means of artificially generated data. Again, AR vectors, or the according extension for multivariate time series, were employed. Flexer et al. [9] adapted this approach using a different feature vector and worked with real data. During the first step, for each of the cornerstones the density of the feature vector is approximated by a multivariate normal distribution using data intervals with staging labels only. The feature vector consists of the first reflection coefficient and a temporal complexity measure derived from the EEG time series, as well as a measure for EMG power. The temporal resolution was set to 1 s.

Rosipal et al. [10] used a hierarchical Gaussian mixture model. Once again, vectors of coefficients of fitted AR models for 3 s segments were used as feature vectors. The staging labels were used to partition the training set, and for each sleep stage, the density of feature vectors was fitted by a mixture of Gaussians (in contrast to the GOHMM model mentioned above for which a single Gaussian per sleep stage was used). The approach described by Rosipal et al. shows another subtlety: after fitting of class-conditional mixtures for each sleep stage, unlabeled data points were added to let the Gaussians better adjust to the general distribution of feature vectors.

A novel probabilistic sleep model (PSM) is presented in this paper. The PSM differs from the previous probabilistic sleep models by the important property that a rigid structure of discrete sleep stages is not considered a priori. Instead a higher number of raw sleep states – called microstates – is determined by optimizing a criterion of describing the distribution of measured physiological data as closely as possible. Microstates can be combined into subsets and their physiological interpretation and a specific task related performance can be studied. By considering data periods with staging labels, probabilities of each microstate toward one of the five standardized stages can by determined during the training process and sleep structure derived. In addition to the PSM definition and training procedure description, the aim of this study is to show that the PSM built on EEG data only can provide more information about sleep than the standardized RK staging. This is demonstrated on a task of searching for objective sleep components correlating with subjective and objective sleep quality day time measures.

In the following section we present our PSM model, as well as our strategy to validate it with respect to clinical validity. Results are presented in the subsequent section.

2. Methods

2.1. Motivation and assumptions

The main motivation behind the choice of the components of the probabilistic sleep model (PSM) were the following ideas:

• •The model, in its first instantiation is meant to be based on EEG data alone, while future extensions could encompass other electrophysiological signals, as well.
• •The main basis of the model should be a compact description of the EEG signal on a time resolution well below 30 s epochs. Here we choose 3 s as the length of nonoverlapping segments to be analyzed. We choose an autoregressive (AR) model of order 10 to describe spectral content. Coefficients from an AR model can be seen as implicit semi-nonparametric descriptors of a signal's spectrum, freeing us from using arbitrary frequency bands in a Fourier transformation. The similar way of representing sleep EEG data has been used in other studies (for example [11,12]). The selection of an AR model needs to balance the factor of underestimating and overestimating of spectral profiles of different sleep stages, therefore its rigorous selection is difficult. Moreover, this would need to be done in accordance with tuning the parameters of the PSM and the follow up correlations estimation task.
• •We describe the EEG observations by an estimated semi-nonparametric density distribution of spectral features (AR coefficients), covering the range of possible electrophysiological expressions of the underlying brain activity. We choose a Gaussian mixture model with 20 Gaussian kernels as the method for density estimation. Implicitly, such a density estimation describes the space of AR coefficients in terms of Gaussian clusters, which could be termed sleep microstates. We do not claim any physiological interpretation to such clusters given the general identifiability problem of such an approach. We do, however, consider the trajectory across such microstates as a potential description of sleep architecture containing more information than traditional sleep stages.

All model parameters (length of signal segment, AR model order, number of Gaussian kernels) were chosen empirically as being sufficient to yield a reasonably fine-grained description of sleep EEG. Since not all single microstates (clusters) are expected to possess an unambiguous physiologically interpretation, for example assigned by the RK staging rules, perfect model selection was not deemed necessary. Overfitting can definitely be excluded given the high number of signal data used for model estimation. Thus, the choice of parameters was based on empirical considerations; e.g., 3 s was deemed as a compromise between high temporal resolution and the ability to reliably estimate low frequency parts of the spectrum, while AR models of higher order or Gaussian mixture models with more kernels did not lead to significantly improved descriptions of the data density.

Validating such a data-based model of sleep poses a challenge due to the lack of direct measures of comparison. In this paper we chose to investigate the following:

• •First, we directly compare traditional sleep stages with the PSM's microstates. One of the hypotheses behind distinguishing sleep stages in sleep research is that the resulting sleep architecture (hypnogram) contains information about the quality of sleep. Among the many variables that can be calculated for that purpose are the time (percentage) spent in each sleep stage, and the frequency of stage shifts. Similar variables can be calculated when looking at microstates in the PSM. As an outside measure for sleep quality a number of objective and subjective tests performed by a subject in the morning after sleep are considered. The main hypothesis is the following: If the PSM indeed contains more information about the microstructure of sleep, then sleep architecture variables from the PSM have a higher correlation with outside quality variables than sleep architecture variables based on sleep staging.
• •Secondly, we demonstrate how the PSM can be used to derive probabilities for traditional sleep stages, as well as for the important spindle process, and thus to create a continuous sleep profile in physiologically meaningful terms.
• •Thirdly, we investigate the prototypical spectral contents of each microstate (via the AR coefficients of the cluster mean) and demonstrate how this, together with the stage probabilities can help interpret the PSM in physiological terms.

2.2. The PSM in detail

2.2.1. Modeling data density and microstates

We partition the EEG signal into disjunct 3 s segments. For each segment an autoregressive model of order 10 was fitted with the Burg method and the resulting AR(10) parameter vector was used as a feature vector x. A Gaussian mixture model is then estimated in the 10-dimensional space of AR coefficients (see Eq. (1)), based on the idea that the unobservable space of possible brain states can be partitioned into a finite number of disjunct states; in this study numbered from 1 to K. The number itself is an identifier and the meaning of each state is derived from the observed sensor data. To distinguish the states 1 to K from the classical sleep stages, we denote them as “microstates”.

$$p(x)=\sum _{k=1}^K{\pi }_{k}N(x|{\mu }_k,{\Sigma }_k)$$ (1)

2.2.2. Tying microstates to sleep stages and spindles

As mentioned above, microstates as derived through a Gaussian mixture model do not necessarily have a physiological meaning. One way to assign such meaning (out of several conceivable ways) is to calculate a relation between microstates and the traditional sleep stages in a probabilistic way. Here we use stages as defined by Rechtschaffen and Kales (henceforth, denoted as RK stages), while collapsing stages S3 and S4 into one stage SWS (slow wave sleep). Furthermore, we apply a spindle detector to the original EEG signal [3]. The spindle detector distinguishes between “possible”, “probable” and “certain” spindles, based on linear discriminant analysis on spectral features, and thus creates four classes (including “no spindle”), denoted here as 0, 1, 2 and 3, respectively. By using this additional spindle detection we assign physiological meaning to a separate spindle process, which, while being correlated with stage S2, is still independent from stages. If we again denote the AR(10) parameter vector by x, the spindle class by s and the RK label by c, then the PSM assumes the existence of an unobserved latent variable z (the microstate from the Gaussian mixture) with K possible states and the following relationship between the considered variables

$$p(z,x,c,s)=p(z)p(x|z)p_R(c|z)p_S(s|z)$$ (2)

By integrating the variable z out we have

$$p(x,c,s)=\sum _{z=1}^{K}p(z)p(x|z)p_R(c|z)p_S(s|z)$$ (3)

where the conditional probability p(x|z) is modeled by a Gaussian N(μ_z, Σ_z) for each z ∈ {1, …, K}, p_R(c|z) can be described for a given z by a vector assigning probabilities (which sum up to 1) to each of the possible sleep stages; wake, S1, S2, SWS and REM. Analogously, p_S(s|z) is a 4-dimensional vector assigning probabilities to each of the spindle classes s ∈ {0, 1, 2, 3}. If all quantities are known, then Eq. (2) assumes that after the value z has been generated with probability p(z), the AR(10)-vector x, spindle class s and RK label c are independently distributed.

Seeger [13] used the name separator model for a simpler variant of (2) with one class variable only. Miller and Uyar [14] also worked with the simpler variant, but in a general context and not for modeling of the sleep process.

2.2.3. Fitting the PSM

For fitting and validating the model data from the SIESTA database [15] were used. The database includes PSG recordings of two consecutive nights (on days 7 and 8 of a 14 days long observation time period) from 175 normal healthy subjects (81 men and 94 women, no shift workers, no depression, usual bedtime before midnight). All subjects included had a Pittsburgh Sleep Quality Index [16] of at most 5. The data were collected from 7 different sleep laboratories, age ranges from 20 to 95 years, with an average of 50.2 ± 19.5. In the study, data from the C3-M2 EEG channel were used. If artifacts occurred the channel was replaced by C4-M1. EEG segments, for which both channels show artifacts, were ignored. The artifact detection procedure of the Somnolyzer24x7 was applied for detecting eye, muscle, sweat and EEG amplitude related artifacts. A band-pass Butterworth filter of order 8 and a frequency range from 0.4 to 40 Hz was applied and EEG data were down-sampled to 100 Hz.

By combining all observations of all subjects more than N = 3,130,000 observations without artifacts were available for training and testing the PSM. On average, this represents about 9000 usable observations per night and subject. Therefore, we worked with N observed AR(10) vectors x_i, N spindle classes s_i and N RK labels c_i (i = 1, …, N). The PSM model can be derived without the RK labels. However, for the interpretation of microstates within the RK sleep structure the labels are needed. The extent to which we use RK labels, however, can be seen as a factor which determines the balance between freely fitting underlying data structure and fitting the data to most closely following the RK structure. The RK labels were obtained with the automatic sleep stager Somnolyzer24x7 [3]. Somnolyzer24x7 works with 30 s intervals and uses additional PSG data (electrooculogram, electromyogram, etc.). In this study the same RK label was used for all 3 s segments inside a 30 s interval.

The fitting procedure using the expectation-maximization (EM) algorithm is explained in Appendix A. The algorithm tries to maximize the log-likelihood by distributing the Gaussians over the space of AR(10) vectors, but in addition taking into account which spindle classes and RK labels have been observed.

After running the EM algorithm the following estimators are determined: priors $\hat{p}(z)$ and Gaussians $\hat{p}(x|z)$, with the expectation vector μ_z and the covariance matrix Σ_z, for each microstate z = 1, …, K; ${\hat{p}}_R(c|z)$ and ${\hat{p}}_S(s|z)$ the probabilities to generate a RK class c and a spindle class s, given the microstate z = 1, …, K. Assuming a sufficiently large amount of data N the fitting of the model was carried out once. Applying our model to new data means that based on the observed AR(10) vector x_i and the calculated spindle class s_i the posterior probability p(z|x_i, s_i) can be calculated

$$p(z|x_i,s_i)=\frac{\hat{p}(z)\hat{p}(x_i|z){\hat{p}}_S(s_i|z)}{{\sum }_{k=1}^K\hat{p}(k)\hat{p}(x_i|k){\hat{p}}_S(s_i|k)}$$ (4)

Next, the posterior probability p(c|x_i, s_i) can be assigned for each RK stage

$$p(c|x_i,s_i)=\sum _{z=1}^{K}p(z|x_i,s_i){\hat{p}}_R(c|z)$$ (5)

The approach presented can be seen as a form of soft clustering. Any new observation is not completely assigned to a single microstate, but is, via the posteriors, related to more than one microstate. The magnitudes of posteriors p(z|x, s) reflect how typical an observation is for each microstate compared to all other states. These posteriors describe whether an observation clearly stems from a certain state or whether it is more a border case which could have been generated by more than one state.

2.2.4. Model validation

In the main part of model validation we aim to prove that the PSM contains more information about sleep than a traditional sleep profile based on 30 s sleep stages (hypnogram). It is common practice in sleep research and medicine to calculate variables from a hypnogram that summarize a sleep night, and which supposedly measure the overall sleep quality. Among those variables are

• •The time (or percentage) spent in each sleep stage, quantifying the main components of sleep.
• •The number of sleep stage changes (shifts from one stage to the other), quantifying the fragmentation and dynamics of the sleep profile.

We chose these two variable classes since they can be easily translated into similar variables based on microstates instead of sleep stages. In order to judge the information contained in such variables, we chose to correlate them with independent outside measures of sleep quality such as subjective and objective tests performed by a subject in the evening before, or in the morning after sleep. The SIESTA dataset contains many such tests, including

• •A self-rating questionnaire about sleep and awakening quality [17].
• •Several visual analogue scales measuring mood, drowsiness and similar states.
• •Physiological measures such as blood pressure and pulse rate.
• •Paper-and-pencil psychometric test on aspects like fine motor activity or memory [18].

The corresponding variables are listed in Table 1. The main hypothesis was that variables derived from the PSM have a higher correlation with these outside measures than variables derived from sleep staging.

Table 1.

Average absolute Spearman rank correlations for the chosen subsets of microstates (statistic RTS and NOV) and for the original RK stages (statistic PRK and TRK).

Day-time variable	RTS	PRK	NOV	TRK
Pittsburgh Sleep Quality Index	0.174	0.106 (12)a	0.201	0.085 (3)a
Self-rating Question. (total) [17]	0.283	0.344 (41)b	0.274	0.178 (3)a
Self-rating Question. for Sleep Quality [17]	0.321	0.382 (42)b	0.315	0.265a (9)
Self-rating Question. for Awakening Quality [17]	0.164	0.165 (27)	0.152	0.050 (2)a
Self-rating Question. for Somatic Complaints [17]	0.302	0.191 (2)a	0.225	0.050 (1)a
Well-being Self Assessment Scale (evening) [19]	0.158	0.132 (21)	0.192	0.083 (2)a
Pulse Rate (evening)	0.204	0.136 (12)a	0.165	0.128 (16)
Pulse Rate	0.172	0.093 (8)a	0.167	0.121 (14)
Systolic Blood Pressure (evening)	0.206	0.108 (6)a	0.193	0.066 (2)a
Diastolic Blood Pressure (evening)	0.167	0.060 (2)a	0.182	0.143 (16)
Systolic Blood Pressure	0.216	0.113 (6)a	0.196	0.118 (7)a
Diastolic Blood Pressure	0.229	0.076 (2)a	0.233	0.140 (6)a
Visual Analogue Scale Test for Drive	0.233	0.149 (6)a	0.175	0.065 (0)a
Visual Analogue Scale Test for Mood	0.159	0.164 (25)	0.150	0.095 (13)
Visual Analogue Scale Test for Affectivity	0.135	0.123 (22)	0.167	0.108 (12)a
Visual Analogue Scale Test for Drowsiness	0.174	0.183 (32)	0.153	0.165 (28)
Alphabetical Cross-out Test (total score) [18]	0.157	0.104 (11)a	0.123	0.075 (14)
Alphabetical Cross-out Test (errors) [18]	0.231	0.092 (2)a	0.183	0.056 (0)a
Alphabetical Cross-out Test (variability) [18]	0.154	0.031 (2)a	0.150	0.064 (3)a
Alphabetical Cross-out Test (error-corr.) [18]	0.133	0.108 (21)	0.124	0.087 (16)
Alphabetical Cross-out Test (% errors) [18]	0.198	0.113 (11)a	0.161	0.045 (4)a
Well-being Self Assessment Scale [19]	0.154	0.153 (23)	0.175	0.128 (13)
Numerical Memory Test	0.223	0.100 (5)a	0.194	0.135 (16)
Fine Motor Activity Test (right hand) [18]	0.141	0.096 (15)	0.114	0.136 (31)
Fine Motor Activity Test (left hand) [18]	0.148	0.075 (11)a	0.121	0.162 (36)
Fine Motor Activity Test (total) [18]	0.150	0.082 (14)	0.107	0.121 (23)

^aSignificantly better RTS (NOV) over PRK (TRK).

^bSignificantly better PRK (TRK) over RTS (NOV).

2.2.4.1. Time spent in a stage or microstate: PRK and RTS

Using RK labels, the percentage of time spent in each sleep stage, with respect to the total time in bed (time from “lights out” to “lights on”), can be calculated. We denote these variables as PRK. A corresponding measure in the PSM would be “relative time spent in a microstate” (RTS). Such a variable can be calculated for a given microstate by summing the posterior probabilities of a 3 s epoch being in that microstate over the night and divide it by the total time in bed. A variable in RTS will therefore consider both the frequency how often a microstate is visited and the intensity of a visit. For instance, ten 3 s intervals with a posterior of 0.4 count as much as five intervals with 0.8.

Given the high number 20 of microstates, however, we cannot expect that a single one of them contains similar information as an entire RK stage. Therefore, we considered the combination of microstates into groups with potentially new meanings. The RTS for this combination is then the sum of the RTS values of the combined microstates. In this study the microstates were combined in a goal-oriented way such that correlations of RTS with a given outside sleep quality variable are maximized.

To get a fair performance estimate and to exclude the possibility of overfitting an experiment with 50 runs and bootstrap samples was performed. Three independent bootstrap sets with 175, 350 and 350 subjects were generated. For each selected subject recordings of both nights were used.² This was done for each run, duplicates were allowed and for a selected subject the data of both nights were used. The first sample was used to fit the PSM with 20 microstates. Furthermore, for each outside sleep quality variable from Table 1, a sequence of optimal subsets of PSM variables, each maximizing the correlation for a given subset size, was constructed. The second bootstrap sample was used to compare the performances of the sequence and to choose the subset in the sequence with the largest absolute correlation. The third bootstrap sample was used to compute the final correlation of the chosen subset and used as a performance measure. The subset sizes considered ranged from 1 to 8, with a full enumeration from 1 to 3 and a stepwise procedure from 4 to 8.

Similarly, the PRK variables were first computed on the first bootstrap sample and the RK stage with the maximum correlation was chosen. The third bootstrap sample was then used to compute the final correlation for the selected RK stage. The correlation values computed on groups of microstates were compared with the correlations considering the RK staging. A sign test with a Bonferroni correction was performed for the hypothesis of equal medians of both (α = 0.00038).

2.2.4.2. Fragmentation of sleep: NOV and TRK

Next, the second class of variables “Number of (sudden) visits” (NOV) was employed. These variables measure how often certain microstates are visited and in this way assigns their importance. A transition between any microstate and a given one was defined if the posterior probability between two consecutive 3 s segments was increased by a value higher than a threshold (in our study equal to 0.5). This approach counts sudden transitions between microstates as, for instance, can be caused by arousals or other shifts in frequency. A similar measure was defined for a combination of microstates by first adding the posteriors of all considered microstates and then testing the same condition with the sum of posteriors instead of a single posterior.

For the RK labels, a similar measure computing the number of transitions from different RK (TRK) stages to a given stage was applied. The same amount of 50 bootstrap runs were used, but a PSM with 10 microstates only was considered. This was due to the fact that calculating the NOV statistics is time-consuming and has to be repeated for each subset of microstates. This is in contrast with RTS where its value for a subset can be immediately computed as the sum of the RTS values of single microstates.

A significant age effect was observed for some of the sleep quality variables of Table 1. Therefore, if a significant correlation (α = 0.05) was observed between age and an investigated sleep quality variable, the effect was compensated by subtracting a second order polynomial fitted to the data in a least square sense. This was also done if the significant age effect was observed in the case of RTS, PRK, NOV or TRK statistics. All correlations were carried out using the Spearman correlation coefficient computed between the variables RTS, PRK, NOV and TRK, on one hand, and variables defined in Table 1, on the other.³

3. Results

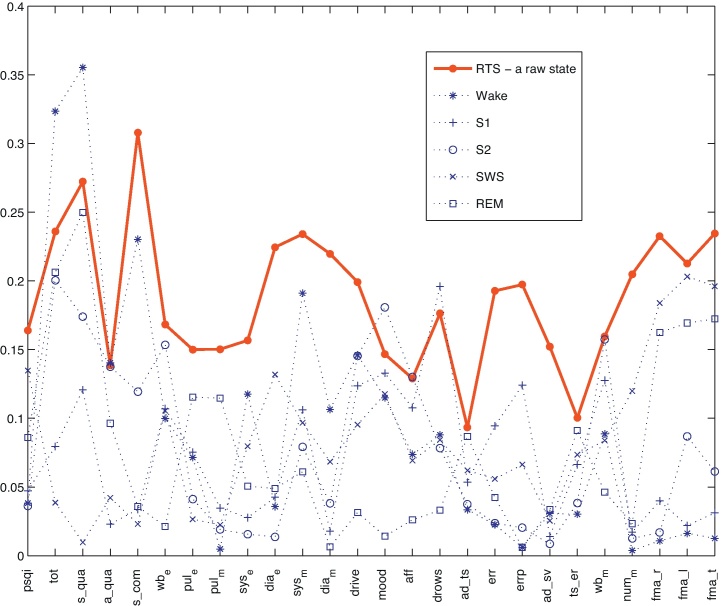
The results of correlating pairs of variables, as well as selecting the one with highest correlations, are summarized in Fig. 1, depicting absolute correlation coefficients. Here, only single microstates were considered. With the exception of four cases the correlations for the PSM variables are always significantly higher than for the RK variables. The strongest exception is the case of s_qua (Self-rating Questionnaire for Sleep Quality; [17]), where PRK computed for the wake stage shows a higher correlation (ρ = 0.36). Moderate correlations between s_qua and the RK sleep parameters were also reported in studies by Saletu et al. [20], and a similar connection between perceived sleep quality and sleep parameters was found by Keklund and Åkerstedt [21] and Kemp et al. [22].

Fig. 1.

Absolute correlations between RTS, PRK and day time sleep quality variables of Table 1. Sleep quality variables on x-axis are sorted following the order of Table 1. Dotted lines: Correlations considering PRK of five RK stages. Solid line: Correlations considering RTS of sleep microstates determined by the PSM. For each sleep quality variable a single microstate with the maximum absolute correlation was selected.

In the next step the superior performance of the PSM was thoroughly tested using the method of a goal-oriented selection of combinations of microstates described in the previous sub-section. Table 1 summarizes the results obtained. Considering 50 bootstrap runs, the second column of the table shows the average correlations between RTS for the chosen combination and sleep quality measures. Correlation values obtained by considering PRK are depicted in the third column. The number in parentheses gives the number of times the correlations for PRK defined on a RK stage was equal or higher in absolute value than the correlations for RTS defined on a microstate combination. The letter (a) in Table 1, significantly higher (α = 0.01) correlations for PSM variables (RTS, NOV), whereas (b) significantly higher correlations for RK variables (PRK, TRK). The latter is the case in only two cases, again for s_qua (subjective sleep quality) and the total subjective sleep and awakening quality score.

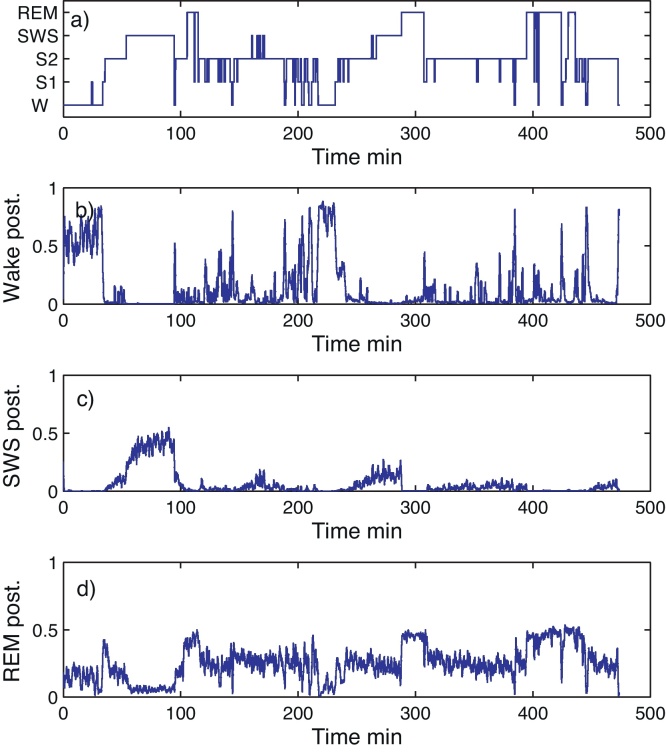
An example of a whole night hypnogram and the RK posteriors derived from (5) are depicted in Fig. 2. The figure shows increased wake posteriors corresponding to the RK wake periods. The short transitions from S2 to S1 are visible as smaller peaks. The SWS posterior tends to increase during the SWS sleep period. Decrease in the posterior peaks of the second and third SWS period in comparison to the first SWS can be observed. Finally, REM posteriors are increased during the periods of REM defined by the RK rules.

Fig. 2.

(a) Hypnogram and smoothed posteriors for (b) wake, (c) SWS and (d) REM.

The estimated priors $\hat{p}(z)$, the RK ${\hat{p}}_R(c|z)$ and spindle ${\hat{p}}_S(s|z)$ probabilities are summarized in Table 2. The states are sorted according to the value of the conditional RK probability ${\hat{p}}_R(\mathit{wake}|z)$. For instance, the microstates 2, 3, 6, 7 and 11 can be considered as largely overlapping with S2, because their fitted value ${\hat{p}}_R(\mathrm{S}2|z)$ is always larger than 0.8. Looking at the spindle probabilities $\hat{p}(s|z)$, it can be observed that in state 6 the probability of spindles presence is high (equal to 0.99), whereas in state 3 this probability is much smaller (0.25). It can be concluded that the five states together describe the S2 stage and that the spindle activity in each microstate is also reflected. As another example, the microstate 8 can be seen as part of the spindle-free REM stage. This state is partially overlapping with S1 and S2.

Table 2.

Parameters of a fitted probabilistic sleep model.

Microstate z	1	2	3	4	5	6	7	8	9	10
$\hat{p}(z)$	0.04	0.05	0.08	0.02	0.05	0.06	0.06	0.08	0.08	0.04
${\hat{p}}_R(\mathrm{wake}|z)$	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
${\hat{p}}_R(\mathrm{S}1|z)$	0.00	0.00	0.00	0.00	0.00	0.01	0.01	0.10	0.05	0.00
${\hat{p}}_R(\mathrm{S}2|z)$	0.18	0.95	0.85	0.46	0.11	0.95	0.93	0.15	0.51	0.27
${\hat{p}}_R(\mathrm{SWS}|z)$	0.82	0.04	0.14	0.53	0.89	0.04	0.04	0.00	0.00	0.73
${\hat{p}}_R(\mathrm{REM}|z)$	0.00	0.01	0.01	0.00	0.00	0.00	0.01	0.74	0.43	0.00
${\hat{p}}_S(0|z)$	0.00	0.00	0.75	0.46	0.88	0.01	0.04	1.00	0.91	0.86
${\hat{p}}_S(1|z)$	0.42	0.30	0.23	0.28	0.11	0.00	0.50	0.00	0.09	0.11
${\hat{p}}_S(2|z)$	0.39	0.58	0.02	0.15	0.01	0.08	0.38	0.00	0.00	0.02
${\hat{p}}_S(3|z)$	0.19	0.13	0.01	0.12	0.00	0.91	0.09	0.00	0.00	0.00

Microstate z	11	12	13	14	15	16	17	18	19	20
$\hat{p}(z)$	0.10	0.05	0.02	0.04	0.07	0.00	0.05	0.03	0.04	0.04
${\hat{p}}_R(\mathrm{wake}|z)$	0.01	0.03	0.03	0.09	0.09	0.48	0.60	0.70	0.85	0.96
${\hat{p}}_R(\mathrm{S}1|z)$	0.04	0.09	0.09	0.29	0.30	0.06	0.27	0.15	0.13	0.03
${\hat{p}}_R(\mathrm{S}2|z)$	0.85	0.65	0.52	0.50	0.20	0.30	0.03	0.10	0.02	0.00
${\hat{p}}_R(\mathrm{SWS}|z)$	0.02	0.00	0.01	0.03	0.00	0.15	0.00	0.00	0.00	0.00
${\hat{p}}_R(\mathrm{REM}|z)$	0.08	0.23	0.35	0.09	0.42	0.01	0.10	0.05	0.01	0.01
${\hat{p}}_S(0|z)$	0.93	0.00	0.81	0.84	0.87	0.87	0.98	0.11	0.92	0.93
${\hat{p}}_S(1|z)$	0.06	0.64	0.14	0.11	0.12	0.06	0.02	0.59	0.07	0.07
${\hat{p}}_S(2|z)$	0.01	0.31	0.04	0.03	0.00	0.05	0.00	0.26	0.01	0.00
${\hat{p}}_S(3|z)$	0.00	0.04	0.01	0.02	0.00	0.02	0.00	0.04	0.00	0.00

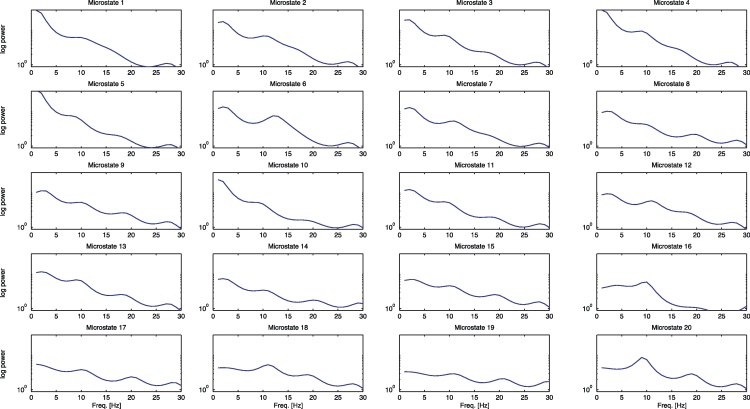
Another interpretation of the fitted microstates can be derived from the estimate of centers μ_z of each fitted Gaussian $\hat{p}(x|z)$. Using the fact that a frequency spectrum can be assigned to each AR model [23], spectra for all 20 centers of microstates 1–20 were computed (Fig. 3). The figure shows the spindle peak at 12–13 Hz for the microstate 6 or the alpha peak at 9 Hz in the microstate 20. Microstates 1, 4 and 5 show a large share of SWS reflected by a higher amount of delta frequency.

Fig. 3.

The spectra assigned to the centers of the 20 microstates.

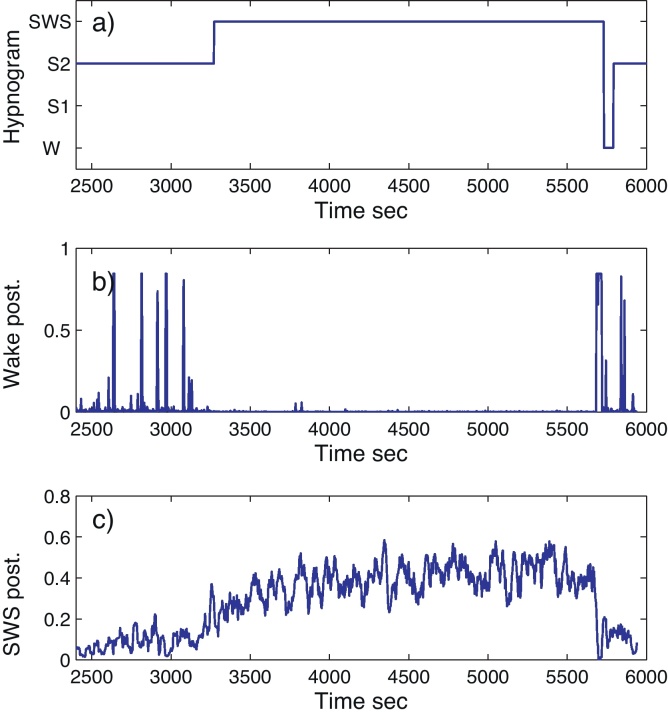
Next, we can also look at certain aspects of the PSM which overcomes well-known limits of the RK staging. Fig. 4 shows part of the hypnogram of a subject switching from S2 to SWS, then to wake and finally to S2 again. Using Eq. (5) it can be observed that the SWS posterior starts to increase at 2500 s. It continues increasing with the onset of the SWS phase from roughly 0.25 to 0.4, which can be interpreted as a deepening of SWS. Furthermore, during the first S2 phase, 5 arousals are indicated by higher posteriors values for wake. These visible peaks are not captured by the RK based sleep hypnogram (top plot).

Fig. 4.

A transition from S2 to SWS with arousals. (a) Hypnogram. (b) Posterior for wake. (c) Smoothed posterior for SWS.

4. Discussion

A probabilistic approach to modeling the microstructure sleep was presented (the PSM). The main idea consists in expressing sleep, besides using a finer temporal resolution, by posterior probabilities which stand for the plausibility that the currently observed feature vectors derived from the EEG might have been generated by certain micro-sleep-states. The microstates themselves are automatically generated during the fitting process of the model and are not pre-defined as, for instance, the RK sleep stages. The meaning of a single microstate can be derived from the attached Gaussian (as an indirect description for the frequency distribution of the EEG segment) and from the spindle and RK class probabilities assigned to the state.

Much emphasis has been put on proving that the PSM indeed contains more information than a sleep profile consisting of traditional sleep stages. While the main ideas underlying our model are not entirely new, for the first time we have statistically tested the model on a large dataset and thus derived the proof-of-concept in favor of the model. The main means behind this statistical proof was the correlation of variables derived from microstates with independent outside measures of sleep quality.

While several correlations of the PSM were significantly superior to RK, their absolute values were moderate or small (Table 1). This is the case for all similar studies we are aware of, including studies referenced in this paper. Therefore, it remains an open question if considering the sleep process without wider contextual information, for example, sleep deprivation, prior to sleep workload, or sleep environment factors, can lead to the extraction of more informative sleep parameters. It also remains an open question if the considered measures of subjective sleep quality or day-time behavior related to sleep are adequate to reliably reflect important changes of sleep patterns, or a wider collection of tests and measures should be considered and tested.

Based on the recorded polysomnography data, posterior curves can be calculated. It was demonstrated that these posteriors curves allow describing sleep in finer details; for example gradual transitions between and within the RK stages are visible. Two exemplary statistics, RTS and NOV, derived from the posterior curves were constructed. After computing posterior values of each microstate the states can be merged into combinations and their total RTS and NOV can be computed. To answer the question, which microstates should be combined, we applied an optimization process with the goal to maximize correlations between the given statistic and a given sleep quality variable.

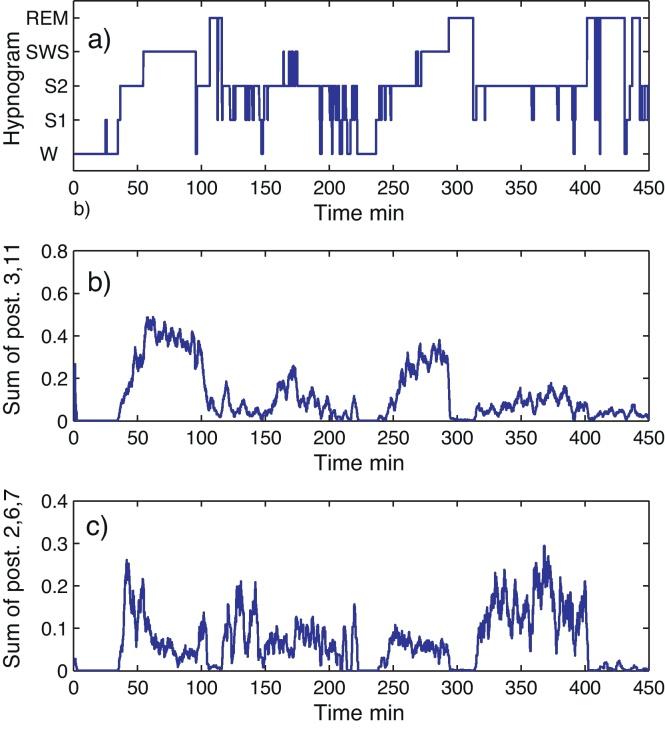
A very powerful property of the PSM is the fact that the posterior for a combination of microstates is the sum of posteriors. This feature allows defining new sleep states or sub-states by combining certain microstates. Using a larger number of 20 microstates allows partitioning the sleep space into fine details without losing the ability of re-combining the microstates according to different goals. These goals can be changed from application to application. For instance, the already described microstates 2, 3, 6, 7 and 11 from Table 2 are strongly related to S2. Two sets of these microstates can be defined (i) the spindle-rich S2R (combined states 2, 6 and 7) and (ii) S2F with few spindles (states 3 and 11). In Fig. 5 the posteriors of S2R and S2F are depicted. It can be observed that the posteriors of S2F have different heights for different S2 stages during the night. They seem to be higher if a SWS phase follows. Analogously, S2R seems to have its peaks predominantly at the beginning and end of the night.

Fig. 5.

Posteriors for two combinations of microstates. (a) Hypnogram. (b) Smoothed posterior for microstates 3, 11. (c) Smoothed posterior for microstates 2, 6, 7.

We should mention that the validation presented in this paper is only a first step toward demonstrating a potential clinical use of probabilistic continuous sleep profiles. More work needs to be done on exploring continuous sleep profiles derived by mapping microstates to the main cornerstones of sleep staging, on investigating the capability of the PSM of distinguishing pathological from normal sleep, and many more aspects. What has been achieved, though, is the important proof-of-concept that further exploring a model like PSM can be worthwhile.

In future work also emphasis will be given on the dynamical aspects of the sleep. The dynamics can be either introduced with the PSM itself or by defining statistics which make use of periodicities in the observed posterior curves. The later approach would resemble the concept of Cyclic Alternating Patterns (CAP) [24]. The potential of this line of research is also supported by the recent study of Moser et al. [25], Ferri et al. [26], Svetnik et al. [27] showing an association between the disruptions in CAP and subjective sleep quality.

Conflict of interest

The authors will disclose to the editor any pertinent financial interests associated with the manufacture of any product described in this manuscript.

Appendix A. EM algorithm

The appendix describes a variant of the EM algorithm for fitting the PSM used in the paper. First, consider a simple Gaussian mixture model [28]

$$p(x)=\sum _{k=1}^K{\pi }_{k}N(x|{\mu }_k,{\Sigma }_k)$$

with prior probabilities π_k = p(k) and Gaussian functions N(x|μ_k, Σ_k) for k = 1, …, K. Now, additionally to the vector x, consider a Rechtschaffen and Kales class c ∈ {1, 2, 3, 4, 5} and a spindle class s ∈ {0, 1, 2, 3}. Denote by H_kc the RK labels related conditional probability p_R(c|k) and similarly by G_ks the spindle class conditional probability p_S(s|k), Then, the probabilistic sleep model (PSM) defined in Eq. (3) can be written in the form

$$p(x,c,s)=\sum _{k=1}^K{\pi }_{k}N(x|{\mu }_k,{\Sigma }_k)H_{\mathit{kc}}{G}_{\mathit{ks}}$$

Define a K-dimensional binary random vector z in the following way: if the latent random variable has the value k, then z_k = 1 for this k and z_k = 0 for the remaining indexes. With this notation the following identities are defined

$$\begin{array}{ccc}\hfill & \hfill \hfill & p(z)=\prod _{k=1}^K{\pi }_k^{z_k}\hfill \\ \hfill & \hfill \hfill & p(x|z_k=1)=N(x|{\mu }_k,{\Sigma }_k)\hfill \\ \hfill & \hfill \hfill & p_R(c|z_k=1)=H_{\mathit{kc}}\hfill \\ \hfill & \hfill \hfill & p_S(s|z_k=1)=G_{\mathit{ks}}\hfill \end{array}$$

Suppose now that we would like to fit a model to observations o₁ = (x₁, c₁, s₁), …, o_N = (x_N, c_N, s_N). The E step tries to calculate the expected values of z_nk given all observations o₁, …, o_N. First the likelihood for the complete data set is needed. For now we assume that z_n are observable. By summarizing all observed vectors x_n into a matrix X, all observed RK classes into a vector C, all spindle classes into a vector S and finally all latent vectors z_n into a matrix Z, the likelihood for the complete data set can be written in the following form

$$p(X,C,S,Z|\Sigma ,\mu ,\pi ,H,G)=\prod _{n=1}^N\prod _{k=1}^K{\pi }_k^{z_{\mathit{nk}}}{\left[N(x_n|{\mu }_k,{\Sigma }_k)H_{{\mathit{kc}}_n}{G}_{{\mathit{ks}}_n}\right]}^{z_{\mathit{nk}}}$$

where the short notation Σ, μ, π, H, G for all occurring parameters was used.

The logarithm of the likelihood is then

$$lnp(X,C,S,Z|\Sigma ,\mu ,\pi ,H,G)=\sum _{n=1}^N\sum _{k=1}^K{z}_{\mathit{nk}}\left\{ln{\pi }_k+lnN(x_n|{\mu }_k,{\Sigma }_k)+ln{H}_{{\mathit{kc}}_n}+ln{G}_{{\mathit{ks}}_n}\right\}$$

which will be minimized during the M step with z_nk replaced by its expectation. For the expectation we calculate

$$p(Z|X,C,S,\Sigma ,\mu ,\pi ,H,G)=\frac{p(X,C,S,Z|\Sigma ,\mu ,\pi ,H,G)}{p(X,C,S|\Sigma ,\mu ,\pi ,H,G)}$$

Because the denominator depends on the observed data only and not on Z

$$p(Z|X,C,S,\Sigma ,\mu ,\pi ,H,G)\propto p(X,C,S,Z|\Sigma ,\mu ,\pi ,H,G)=\prod _{n=1}^N\prod _{k=1}^K{\left[{\pi }_{k}N(x_n|{\mu }_k,{\Sigma }_k)H_{{\mathit{kc}}_n}{G}_{{\mathit{ks}}_n}\right]}^{z_{\mathit{nk}}}$$

and therefore under the posterior distribution z_n are independent. To calculate the expectation of z_n under the posterior distribution, the so-called responsibility γ(z_nk) of component k for data point o_n needs to be computed

$$\gamma (z_{\mathit{nk}})=\frac{{\pi }_{k}N(x_n|{\mu }_k,{\Sigma }_k)H_{{\mathit{kc}}_n}{G}_{{\mathit{ks}}_n}}{{\sum }_{j=1}^K{\pi }_{j}N(x_n|{\mu }_j,{\Sigma }_j)H_{{\mathit{jc}}_n}{G}_{{\mathit{js}}_n}}$$

The expected value of the complete-data log likelihood function is then given by

$$E[lnp(X,C,S,Z|\Sigma ,\mu ,\pi ,H,G)]=\sum _{n=1}^N\sum _{k=1}^K\gamma (z_{\mathit{nk}})\left\{ln{\pi }_k+lnN(x_n|{\mu }_k,{\Sigma }_k)+ln{H}_{{\mathit{kc}}_n}+ln{G}_{{\mathit{ks}}_n}\right\}$$

During the M step the parameters Σ, μ, π, H and G are chosen maximizing this expectation. Each of the terms of the sum is independent from the other terms and can be maximized separately. Using the notation $N_k={\sum }_{n=1}^N\gamma (z_{\mathit{nk}})$ and adopting the formulas for Σ, μ, π from [28] we get

$$\begin{array}{ccc}\hfill & \hfill \hfill & {\mu }_k^{\mathit{new}}=\frac{1}{N_k}\sum _{n=1}^N\gamma (z_{\mathit{nk}})x_n\hfill \\ \hfill & \hfill \hfill & {\Sigma }_k^{\mathit{new}}=\frac{1}{N_k}\sum _{n=1}^N\gamma (z_{\mathit{nk}})(x_n-{\mu }_k^{\mathit{new}}){(x_n-{\mu }_k^{\mathit{new}})}^T\hfill \\ \hfill & \hfill \hfill & {\pi }_k^{\mathit{new}}=\frac{N_k}{N}\hfill \end{array}$$

For the computation of the estimator H_kc define

$$\begin{array}{ccc}\hfill & \hfill \hfill & {\gamma }_{[\mathit{kc}]}=\sum _{n:c_n=c}\gamma (z_{\mathit{nk}})\hfill \\ \hfill \end{array}$$

and consider

$$\begin{array}{ccc}\hfill & \hfill \hfill & \sum _{n=1}^N\sum _{k=1}^K\gamma (z_{\mathit{nk}})ln{H}_{k,c_n}=\sum _c\sum _{n:c_n=c}\sum _{k=1}^K\gamma (z_{\mathit{nk}})ln{H}_{k,c}=\sum _c\sum _{k=1}^{K}ln{H}_{k,c}\sum _{n:c_n=c}\gamma (z_{\mathit{nk}})=\sum _c\sum _{k=1}^{K}ln{H}_{k,c}{\gamma }_{[\mathit{kc}]}\hfill \\ \hfill \end{array}$$

Now the Lagrange function

$$\begin{array}{ccc}\hfill & \hfill \hfill & L=\sum _c\sum _{k=1}^{K}ln{H}_{k,c}{\gamma }_{[\mathit{kc}]}+{\lambda }_1\left(\sum _c{H}_{1,c}-1\right)+\cdots +{\lambda }_K\left(\sum _c{H}_{K,c}-1\right)\hfill \\ \hfill \end{array}$$

can be defined and maximized with respect to the H_kc term. We get

$$\begin{array}{ccc}\hfill & \hfill \hfill & \frac{\partial L}{\partial H_{k,c}}=\frac{{\gamma }_{[\mathit{kc}]}}{H_{k,c}}+{\lambda }_k=0,\forall k,c\hfill \end{array}$$

Therefore

$$\begin{array}{ccc}\hfill & \hfill \hfill & {\gamma }_{[\mathit{kc}]}=-{\lambda }_k{H}_{k,c},\forall k,c\hfill \\ \hfill & \hfill \hfill & N_k=\sum _c{\gamma }_{[\mathit{kc}]}=-{\lambda }_k\sum _c{H}_{k,c}=-{\lambda }_k,\forall k,c\hfill \\ \hfill \end{array}$$

The new estimators are

$$\begin{array}{ccc}\hfill & \hfill \hfill & H_{\mathit{kc}}=\frac{{\gamma }_{[\mathit{kc}]}}{N_k},c=1,\dots ,5\hfill \\ \hfill \end{array}$$

With the same approach the new values of G_ks can be computed

$$\begin{array}{c}\hfill G_{\mathit{ks}}=\frac{{\sum }_{n:s_n=s}\gamma (z_{\mathit{nk}})}{N_k},s=0,\dots ,3\\ \hfill \end{array}$$