Correlation as a Determinant of Configurational Entropy in Supramolecular and Protein Systems

Abstract

For biomolecules in solution, changes in configurational entropy are thought to contribute substantially to the free energies of processes like binding and conformational change. In principle, the configurational entropy can be strongly affected by pairwise and higher-order correlations among conformational degrees of freedom. However, the literature offers mixed perspectives regarding the contributions that changes in correlations make to changes in configurational entropy for such processes. Here we take advantage of powerful techniques for simulation and entropy analysis to carry out rigorous in silico studies of correlation in binding and conformational changes. In particular, we apply information-theoretic expansions of the configurational entropy to well-sampled molecular dynamics simulations of a model host–guest system and the protein bovine pancreatic trypsin inhibitor. The results bear on the interpretation of NMR data, as they indicate that changes in correlation are important determinants of entropy changes for biologically relevant processes and that changes in correlation may either balance or reinforce changes in first-order entropy. The results also highlight the importance of main-chain torsions as contributors to changes in protein configurational entropy. As simulation techniques grow in power, the mathematical techniques used here will offer new opportunities to answer challenging questions about complex molecular systems.

Introduction

When molecules bind in solution via noncovalent forces or proteins shift between conformational states, the associated changes in entropy can be substantial and are typically commensurate with the corresponding changes in enthalpy and free energy. As a consequence, the changes in entropy are important determinants of the equilibrium constants for such changes in state. The change in overall entropy can itself be expressed as the sum of two parts:^1,2 the change in the solvation entropy, averaged over the conformational distribution of the solute(s), and the change in the configurational entropy, which is associated with the conformational fluctuations of the solute(s). The configurational entropy depends on the overall shape and width of the joint probability density function (PDF) over the solute’s internal coordinates. Prior studies indicate that changes in not only the solvent entropy but also the configurational entropy can be substantial. For example, both NMR and computational studies point to large changes in configurational entropy when proteins bind other molecules.^1,3−10

The configurational entropy depends on the PDF of individual conformational variables, such as bond torsions, that is, on their first-order marginal PDFs; but it also depends on the correlations among these variables. In particular, one may write the full entropy as the sum of the first-order entropy and an additional term due to correlation: S_full = S₁ + S_full^corr. Intuitively, greater correlation implies lower entropy because correlation implies less freedom to explore configurational space for a given set of marginal distributions. However, it is not yet clear whether there are any physical patterns or rules as to what types of molecular processes lead to net increases versus decreases in correlation entropy or how large the contributions from correlation are likely to be. Correlation entropy is of particular interest in relation to changes in NMR order parameters, such as when proteins change conformations or bind other molecules. These changes are often interpreted, at least semiquantitatively, in terms of changes in configurational entropy.^3,5,9−16 However, such NMR data are not directly informative about changes in correlation. As a consequence, it is of interest to consider the nature of correlation contributions to the entropy changes of interest. The identification and characterization of correlated motion is also of broader interest, as correlations may be indicative of mechanistic couplings important in phenomena such as binding and allostery,¹⁷⁻¹⁹ and knowledge of the nature and range of correlations in proteins would contribute insight into the basic mechanisms of protein motions and function.

The role of correlations as determinants of changes in configurational entropy has been the topic of a number of insightful contributions. It has been proposed, based on empirical relationships among measured NMR order parameters and binding entropies, that changes in correlation entropy on binding vary linearly with changes in measures of the entropy that neglect correlation.^9,10,15 Encouraging results have been obtained for relative binding entropies, ΔΔS, among variants (e.g., mutants) of a given protein–protein system, and it will be interesting to learn how well such approaches work for the “absolute” entropy changes associated with binding or major conformational changes. Another notable contribution provides evidence, based on extensive molecular dynamics (MD) simulations, that inter-residue side-chain correlations lower the absolute configurational entropy by about 10–20%¹⁶ of the first-order rotameric entropy. However, it is still of interest to probe the potential contributions from correlations involving main-chain torsions, and, again, to examine large-scale changes like binding and conformational shifts. Another contribution has argued, based on molecular simulation data, that changes in correlations do not contribute significantly to the entropy changes associated with biomolecular functions²⁰ and thus proposed that entropic interpretations of NMR order parameters may safely neglect any contributions from changes in correlation; and a prior study of calmodulin,²¹ using quasi-harmonic analysis, reached a similar conclusion. The role of torsional correlations as determinants of binding entropy has also been addressed through application of the mutual information expansion (MIE)^22,23 to multiple long MD simulations of a protein–peptide system.²⁴ Interestingly, this analysis reported large entropic contributions from changes in pairwise torsion–torsion correlations, including correlations involving main-chain torsions and the six degrees of freedom (DOF) specifying the location of the peptide relative to the protein. These results would suggest that changes in torsional correlations, including those of the main chain, cannot be safely neglected. However, although this study provided a reasonably clear accounting of the strongest pairwise correlations in a large protein system, there were numerical problems for the many weak pairwise correlations. In addition, the simulations lacked the power to estimate third-order and higher correlation terms, which are also of interest. In summary, despite significant prior work, there are still important, unanswered questions regarding the role of torsional correlations as determinants of changes in configurational entropy.

Today, increasingly powerful techniques for both simulation and entropy analysis allow comparatively rigorous in silico studies of the configurational entropy changes associated with binding and conformational changes. The present study takes advantage of such techniques to revisit the important topic of correlation entropy for two molecular cases. The first is the experimentally studied association, in chloroform, of ethyleneurea with a designed host molecule (Figure 1),²⁵ whose small size allows correlation terms of order greater than two to be converged; the second is the 58-residue protein BPTI, where an available millisecond-duration MD simulation²⁶ allows calculation of convincingly converged pairwise correlation terms. This simulation of BPTI has been extensively studied in a variety of post-analysis works that include investigation of allostery,²⁷ isomerization rates of disulfide bonds,²⁸ NMR order parameters,²⁹ and entropy–enthalpy transduction.³⁰ The results presented here bear on the sign, magnitude, and determinants of correlation contributions to entropy changes and hence on the entropic interpretation of NMR order parameter data.

Figure 1.

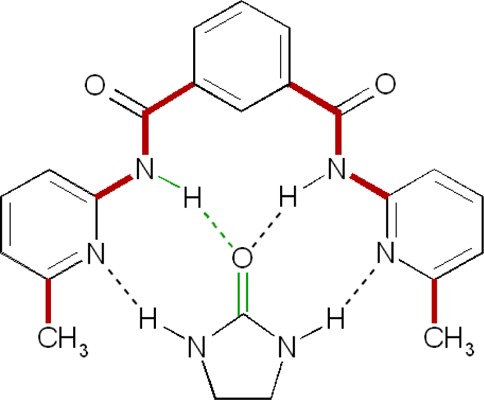
Host–guest complex. Bold red bonds indicate the host torsion angles for which the entropy was computed. Thin green lines define one distance variable (dashed green, H to O), two angle variables (N–H–O, H–O–C), and three torsional variables (central bonds N–H, H–O, O–C), which together define the relative position and orientation of the two molecules in their bound state. Dashed lines indicate hydrogen bonds.

Methods

We studied the role of correlations as determinants of entropy changes on binding and conformational change through analysis of MD simulations. The contributions of pairwise and higher-order correlations to the entropy were estimated by applying the MIE and maximum information spanning tree (MIST)^31,32 methods to the simulation trajectories. These approaches are suitable for the present purpose because they express the total entropy as a sum of terms accounting for successively higher-order correlations among the conformational variables. The following subsections detail the computational methods applied to both the host–guest and BPTI systems.

Configurational Entropy of Host–Guest Binding

Theoretical Framework

The configurational entropy S of a molecule or supramolecular complex of N_a atoms, at standard concentration, is given by^24,33

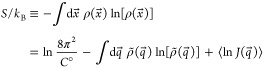1

Here k_B is Boltzmann’s constant, ρ(x⃗) is the PDF of the Cartesian coordinates x⃗ = (x₁,...,x_3Na) of the system, C° is a standard concentration (usually taken as 1 mol/L = 6.022 × 10^–4 molecules/ų), ρ̃(q⃗) = ρ[x⃗(q⃗)]J(q⃗) is the PDF of internal coordinates q⃗ = (q₁,...,q_3Na–6), J(q⃗) is the Jacobian of the transformation x⃗→q⃗, and ⟨·⟩ denotes an expectation value (mean). The first term in the second line of eq 1 arises from the overall translation and rotation of the system.

The change, ΔS, of the standard configurational entropy on the binding of host A and guest B to form the complex AB is then

2

where S̃_X, the internal entropy of molecule X = A, B, AB, is defined by

3

which is the entropy of the PDF ρ̃_X(q⃗) of the internal coordinates of system X plus the term that arises from the Jacobian J_X(q⃗) of the transformation x⃗ → q⃗ from Cartesian to internal coordinates. Of the three translational–rotational terms −k_B ln(8π²/C°) associated with systems A,B, and AB, only one survives in the change given in eq 2. Note that an isothermal change in the configurational entropy S of a system, defined as in eq 1, equals the change in the full (i.e., spatial plus momentum) thermodynamic entropy of the system.³³ (The present notation differs from that of ref (33), where a tilde is used to indicate the internal-coordinate entropy alone.)

The first term on the right-hand side of eq 3 may be estimated by the MIE or MIST^31,32 approaches based on the Boltzmann sample of internal coordinates, q⃗_i, i = 1,...,N_s afforded by a molecular simulation. The second term in eq 3 is estimated by a simple arithmetic mean,

4

where the sum runs over the points q⃗_i, i = 1,...,N_s of the same sample.

Host–Guest Simulations and Entropy Calculations

Stiff DOF do not contribute much to entropy changes, as their PDFs change little on binding. Therefore, the present entropy analysis focused on the soft variables; that is, the eight soft torsions of the host and, for the bound complex, six additional DOF specifying the relative position and orientation of the two molecules that form the complex (Figure 1). The free guest has no soft DOF and thus was treated as an “inert” participant in the binding process so that, to a good approximation, the change in internal entropy is given by

5

Here S̃_AB^′ is the entropy, eq 3, of the complex computed based on only the soft torsions of the bound host and the relative position/orientation variables. S′_A is the entropy, eq 3, of the unbound host computed using soft torsions only. Thus, the configurational entropy of a total of 14 internal coordinates had to be estimated from the simulation of the bound complex and compared with the corresponding estimate of the configurational entropies of eight internal coordinates from the simulation of the unbound host. We used the generalized AMBER force field (GAFF)³⁴ and AM1-BCC^35,36 charges to parametrize our systems. The software package AMBER 12³⁷ with PMEMD GPU support^38,39 was used to run the MD simulations at constant temperature and pressure (NPT). Production simulations ran for a duration of 5 μs for both the unbound host and the bound complex, immersed in the solvent chloroform, which was treated explicitly.^40,41 The temperature was maintained at 300 K by the Langevin thermostat with the collision frequency scaling set to 1.0 ps^–1, and the pressure was set to 1 bar using the Berendsen barostat with a relaxation time set to 2 ps. Snapshots were saved every 1 ps, resulting in five million sample points per simulation. The time series of torsion angles of interest were computed from the simulation data with the program CPPTRAJ.⁴²

Entropies were extracted from the torsional time series by several methods. First, we applied the MIE, where instead of computing the required marginal entropies by the histogram method,^23,24 we instead used the more powerful kth nearest neighbor (NN) estimation of entropy;⁴³⁻⁴⁵ this combined approach is termed the MIE-NN method.⁴⁶ We also directly applied the NN method to estimate the entropies of the full 8- and 14-dimensional PDFs of the host and complex, respectively, using extrapolations in time for multiple values of k. The extrapolation for each value of k used the phenomenological function form⁴⁴ −TS_t ≈ −TS_t→∞ + a_k/t^p, where a_k is fitted separately for each value of k but all values of k shared the exponent p and asymptote −TS_t→∞. Note, however, that different values of p and −TS_t→∞ were fitted for the free host and bound complex. We use the difference of both fit curves to estimate −TΔS_t→∞. Finally, we also applied the MIST approximation^31,32 in combination with the NN method. Like MIE, MIST is a systematic, dimension-reduction approximation based on an information-theoretic expansion of entropy. Unlike MIE, however, MIST approximations of increasing order are guaranteed to furnish decreasing upper bounds of the exact entropy.

Configurational Entropy of a Protein Conformational Change

For the protein analysis, we limit attention to the contributions of pairwise correlations, due to the computational expense of converging higher-order correlation terms. Even the pairwise contribution can be challenging to compute for a large system, because the second-order mutual information contributions, which appear in both the MIE and MIST, are greater than or equal to zero. Thus, even if two torsions are entirely uncorrelated, their mutual information will approach zero asymptotically from above with increased sampling. For a protein, the sum of many spurious positive correlation contributions from the many torsion–torsion pairs can yield a misleadingly large estimate of the overall pairwise contribution to the entropy. Here we address this problem by a combination of approaches.

First, to maximize convergence, we study a single, 1 ms trajectory of BPTI in explicit solvent,²⁶ which was generated on the Anton supercomputer.⁴⁷ This is much longer than the prior study of torsion–torsion correlations in protein–peptide binding,²⁴ which processed 2 μs of simulation trajectories generated by 200 independent 10 ns runs starting from the same conformation. The BPTI simulation, which provided over four million snapshots at 250 ps intervals, used the TIP4P-Ew water model,⁴⁸ and, for the protein, the AMBER ff99SB⁴⁹ force field with additional corrections to side-chain torsions of isoleucines was used. The original study of this simulation decomposed the trajectory into conformational clusters, or states, based on a kinetic clustering approach.²⁶ Subsequent thermodynamic analysis³⁰ indicated that Clusters 1 and 2 have free energies that are equal to within ∼0.5 kcal/mol, but their total entropies, including both the protein and the solvent molecules, differ by ∼3.2 kcal/mol. Their configurational entropies were estimated to differ by over 18 kcal/mol³⁰ based on MIST analysis. This very large difference in configurational entropy is accompanied by visibly larger conformational fluctuations for Cluster 2 versus Cluster 1. Here we expand on the prior thermodynamic analysis³⁰ by examining the role of torsional correlations as determinants of the large difference in configurational entropy between Clusters 1 and 2.

In addition to using a much longer simulation, we employ MIST instead of MIE, as the former requires postprocessing many fewer torsion–torsion pairs. This not only saves computer time but also, relative to the MIE, reduces the error from summing many small, potentially spurious pairwise contributions from large numbers of torsion–torsion pairs, as previously discussed. We also address the problem of residual pairwise contributions by repeating the calculations with a cyclic permutation technique that removes spurious entropic contributions due to inadequate sampling, as previously detailed.³⁰ Although the NN method allows well-converged entropy estimates to be obtained with less simulation data, we used the histogram method for this study because it allows the nearly 400 000 mutual information pairs to be processed considerably more quickly. The subtraction of spurious correlation from each MIST pair removes numeric bias⁵⁰ of the entropy estimate from the histogram method for a given cluster. Because the spurious correlation estimates are computed using the same number of frames as the original mutual information estimate for a given pair, any sample bias for a given cluster is removed before computing the difference in entropies between clusters that have different frame counts.

The full bond-angle-torsion coordinate system of BPTI comprises 889 torsion angles. Treating each of these torsions separately can lead to trivial high-order correlations;²³ we eliminated these by redefining the torsion angles (Φ_j) of all of the torsions that share the same rotatable bond as phase angles (ϕ_j) of a single, representative torsion angle (Φ_i):⁵¹

6

For BPTI, 500 of the torsion angles are treated as phase angles in this manner. It should be noted that in our prior analysis of this simulation³⁰ we accounted only for those phase angles that had three of the four torsion atoms in common with a master torsion angle. We now also include any torsion that shares the two atoms that form the central rotable bond. We also found very rare rotations of the NH₂ moieties within the guanidinium group of the arginine residues. The rotations are now corrected to account for their symmetry. These procedural changes caused the MIST-889c entropy estimate to slightly change from −TΔS = −18.9 to −18.1 kcal/mol (Table 2).

Table 2. Changes in Configurational Entropy when BPTI Switches from Conformational Cluster 1 to Cluster 2, Reported As −TΔS, in Kilocalories Per Mole^a.

method	–TΔS1	–TΔS2	–TΔS2corr
MIST-889	–21.1	–15.1	6.0
MIST-889c	–21.1	–18.1	3.0
MIST-157	–20.7	–15.4	5.4
MIST-157c	–20.7	–16.2	4.5

^aThe first set of results is computed by applying the MIST approach to all 889 protein torsions, without (MIST-889) and with (MIST-889c) a correction for possible incomplete sampling, based on cyclic permutations of the trajectory. The second set results from applying MIST to only the 157 torsions whose PDFs change most between the two clusters, based on their JSDM values. Again, results are presented without (MIST-157) and with (MIST-157c) the permutation correction. Column headers and units are as in Table 1.

We also determined whether restricting the set of torsions included in the entropy calculations to only those most perturbed by the conformational change affects the entropy results. We quantified the degree to which a torsion angle’s PDF changes between Clusters 1 and 2 by computing the Jensen–Shannon divergence metric (JSDM)^52,53 between the two PDFs. If P is the PDF of a torsion for Cluster 1 and Q is its PDF for Cluster 2, the JSD metric is given by

7

where S() is the Shannon entropy of the PDF in the argument. The JSDM is zero when the two PDFs are identical and attains a maximum value of 0.83 when the two PDFs are completely nonoverlapping; we considered a torsional PDF to be significantly perturbed if its JSDM between Clusters 1 and 2 was greater than 0.083. Note that, unlike the widely known Kullback–Leibler divergence,⁵⁴ the JSDM has the merit of being unaffected by the ordering of the two PDFs. Computing the JSDM between two PDFs of the same torsion angle involves only 1-D PDFs, so we obtained it from a straightforward histogram method.

Results

Configurational Entropy of Host–Guest Binding

When the host and guest are both free in solution, they both rotate freely relative to each other, and, for a standard concentration of 1 M, each effectively occupies its own volume of ∼1660 ų.^2,55,56 After they have bound to form a noncovalent complex, their relative rotation and translation is markedly constrained, and this reduction in rotational and translational freedom in itself contributes a loss in configurational entropy. Whether the net change in configurational entropy is unfavorable then depends on how the rest of the system responds to the binding event. For this small host–guest system, the overall change in configurational entropy is found to remain unfavorable, as −TΔS_full = 8.43 kcal/mol (Table 1). (Note that this entropy change, as well as the others in this section, includes the −k_B ln(8π²/C°) term in eq 2.) Most of this overall entropy change is manifested in the first-order entropy contribution, −TΔS₁ = 6.03 kcal/mol, which by definition neglects all correlation contributions. However, increased correlation clearly plays a role, given the 2.4 kcal/mol difference between the full entropy, which accounts for correlations, and the first-order entropy, which does not. Thus, we find that binding induces increased correlations, which further oppose binding. This pattern is opposite to a prior computational result, indicating that proteins with lower first-order side-chain entropies tend to have partly balancing decreases in side-chain correlations.¹⁶

Table 1. Changes in Configurational Entropy Due to Host-Guest Binding, −TΔS_m, Computed at Various Orders m = 1, 2, and 3 of the MIST and MIE Expansions and at Full Order, −TΔS_full, by Extrapolation of NN Results to Infinite Simulation Time (See Figure 2)^a.

method	–TΔS1	–TΔS2	–TΔS2corr	–TΔS3	–TΔS3corr	–TΔSfull	–TΔSfullcorr
MIE-NN	6.03	8.39	2.37	8.57	2.55
MIST-NN	6.03	7.39	1.37	7.90	1.88
k-NN						8.43	2.40

^aCorrelation contributions at each reported order are also reported: −TΔS_m^corr = −TΔS_m + TΔS₁, and −TΔS_full = −TΔS_full + TΔS₁. All values are in kilocalories per mole.

Much of the change in entropy can be attributed to changes in the relative rotational and translational DOF of the host and guest: application of the MIE-NN method to these six key variables in the bound state yields estimates for −TΔS_RT of 5.0, 5.9, and 6.1 kcal/mol, relative to the unbound state, at the first, second and third orders of the MIE, respectively. It should be noted, however, that alternative systems of internal coordinates could give different results for these quantities.²

The roles of pairwise and third-order correlations may be examined within both the MIE and MIST expansions (Table 1). Interestingly, the MIE at both second and third order agrees well with the estimate of the full-order entropy, indicating that, for this method, the pairwise correlations account for the bulk of the total correlations. However, it should be noted that there is no guarantee that higher order terms, if computable, would continue smoothly toward the full-order result. The MIST approach proceeds more gradually toward the full-order estimate and, at third order, already captures most of the correlation present in the full-order estimate.

The correlation contribution identified here is considerably larger than that previously reported for thermal perturbations of a series of dipeptides (<0.1 kcal/mol) and the much larger villin headpiece protein (<0.4 kcal/mol).²⁰ The present result corresponds to 0.17 kcal/mol change in correlation entropy per soft DOF of the complex (14 variables) or 0.30 kcal/mol per soft dihedral angle (8 dihedrals). These values may be compared with prior results for the binding of a 9-residue peptide to the 145-residue protein TSG101,²⁴ where changes in second-order correlation on binding led to an entropy penalty of ∼0.3 kcal/mol per residue of the protein–peptide system. Assuming an average of four soft dihedrals per residue, the correlation entropic penalty is ∼0.075 kcal/mol per soft dihedral, which is less than the present host–guest result. This smaller value probably reflects, at least in part, the fact that the protein has many DOF that are not closely coupled with the binding site.

The present results are well-converged. Thus, the MIE results for orders one, two, and three remained constant to within 0.1 kcal/mol over the simulation time interval 4 to 5 μs, and the MIST results at the third order were numerically even more stable than the corresponding third-order MIE results. It is worth noting that we also attempted to compute −TΔS_m at orders m ≥ 4, but convergence was not favorable, and extrapolation was not attempted, as the estimates obtained at different values of k differed from each other to a much greater extent than those in the full-dimensional k-NN estimates. It appears that these numerical problems stem in part from the much greater number of mathematical clusters of variables that must be analyzed for larger values of the order m (m > 3).

Configurational Entropy of a Conformational Change in BPTI

A prior 1 ms simulation of the 58-residue protein BPTI, using explicit water, yielded several different conformational clusters.²⁶ Subsequent thermodynamic analysis of the simulation results indicated that the total entropy of the protein–water system changes by about −TΔS = −3.0 kcal/mol on transitioning from the more crystal-structure like Cluster 1 to the more flexible Cluster 2.³⁰ Interestingly, the change in configurational entropy for this conformational shift is much larger: the second-order MIST estimates range from −15.1 to −18.1 kcal/mol (Table 2), depending on methodological details discussed later. Because the total entropy can be expressed as the configurational entropy plus an appropriately defined solvation entropy,¹ one may conclude that the strongly favorable increase in configurational entropy on going from Cluster 1 to Cluster 2 is largely canceled by an opposing decrease in solvent entropy. The estimated change in configurational entropy on going from Cluster 1 to Cluster 2 greatly exceeds that computed for the host–guest system (previously described). This is perhaps not surprising given the much larger size of the protein system; on the other hand, a change in conformational state might be expected to produce a smaller entropy change than a binding event.

It is of interest to break down the estimated change in configurational entropy between Clusters 1 and 2 into its first order and pairwise correlation contributions. At first order, the increase in torsional entropy on going from Cluster 1 to Cluster 2 is found to be about −21.1 kcal/mol (Table 2), while, as previously noted, accounting for pairwise correlations reduces this change to −15.1 to −18.1 kcal/mol. Thus, although the first-order entropy becomes much more favorable, a concurrent increase in pairwise torsional correlations effectively cancels out 3–6 kcal/mol of the first-order entropy difference. This cancelation of 15–30% of the first-order entropy by changes in correlation is in striking agreement with a prior simulation study of protein side-chain entropy, previously mentioned.¹⁶ However, it is opposite in sense to what we observe for the host–guest system, above: there, changes in correlation reinforce, rather than balance, the first-order change in configurational entropy of binding.

We tested the robustness of the present entropy estimates by two substantial variations in the method results. First, we corrected the estimate of each pairwise mutual information used in the MIST calculations for possible spurious correlation due to inadequate sampling by subtracting out pairwise entropies computed with a permuted, and hence entirely decorrelated, trajectory.³⁰ As shown in Table 2, results with (MIST-889) and without (MIST-889c) this correction for possible spurious correlations due to inadequate convergence differ by only a few kilocalories per mole We also recalculated both the first- and second-order entropies using only the 157 torsions with greatest JSDMs between Clusters 1 and 2. As shown in Figure 3, the torsions with the largest JSDM values, that is, the ones whose PDFs differ most between Clusters 1 and 2, reside in the two loops toward the top of the protein in this representation. This is not surprising because increased motion of these loops is a hallmark of Cluster 2, as illustrated in Figure 1 of a prior study of this simulation.³⁰ The use of only 157 torsions dramatically reduces the total number of mutual information pairs (12 246 versus 394 716) that need to be calculated prior to computing the MIST estimate of the configurational entropy. Even with such a large reduction in the total number of torsions, the results are all within 2 kcal/mol of those based on all 889 torsions, for both the uncorrected (MIST-157) and permutation-corrected (MIST-157c) estimates. The robustness of the overall results to these methodological variations supports their validity.

Figure 3.

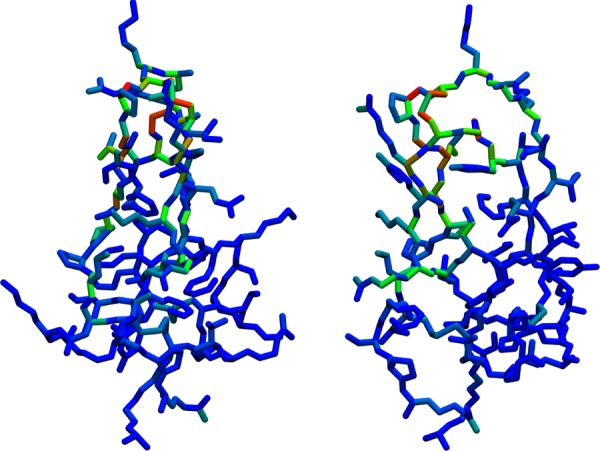
BPTI, from two viewpoints, with torsions colored based on their Jensen–Shannon divergence metric (JSDM) between Clusters 1 and 2. Dark blue represents the minimum possible divergence of 0.00, and red represents the maximum observed value of 0.75.

Figure 2.

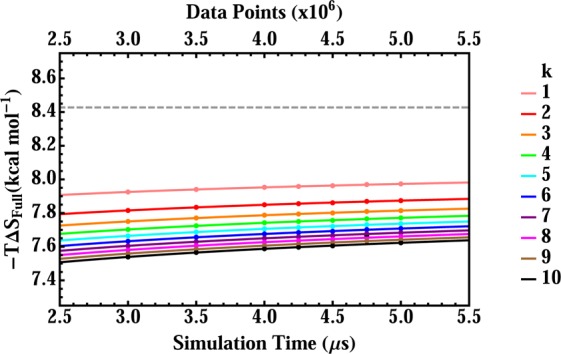
Convergence of the full-dimensional entropy change, −TΔS_full, for host–guest binding, estimated by the k nearest-neighbor method, as a function of simulation time t. Each data point is the delta entropy estimate between the host and complex for a given value of t and k, and each line is the difference in the host and complex phenomenological fit functions for a given value of k, where the fits for the host and were allowed to approach their own asymptotic values as t → ∞. The fitted values of the exponent p are 0.365 and 0.221, for the host and complex, respectively. The gray horizontal dashed line at −TΔS_full = 8.43 kcal/mol indicates delta in asymptotic values for the host and complex.

It is also of interest to determine which parts of the protein contribute most to the MIST entropy estimates. As a first level of analysis, we decomposed the change in first-order configurational entropy into main-chain and side-chain contributions and the change in correlation entropy into main-chain/main-chain, main-chain/side-chain, and side-chain/side-chain contributions. As shown in Table 3, the main-chain contribution to the first-order change is twice the side-chain contribution, and main-chain/main-chain torsion pairs similarly provide the largest contribution to the change in correlation entropy, especially after the permutation corrections are applied. These results suggest that changes in main-chain torsions play a predominant role in determining changes in configurational entropy, at least in the present system, so that a focus on side-chain contributions^16,21 may be unduly limiting.

Table 3. Decomposition of the Configurational Entropy Change, −TΔS (kcal/mol), between BPTI’s Conformational Clusters 1 and 2 into First Order (Main-Chain (M), Side-Chain (S)) and Correlation (Main-Chain Main-Chain (MM), Main-Chain Side-Chain (MS), and Side-Chain Side-Chain (SS)) Contributions.

method	M	S	MM	MS	SS
MIST-889	14.0	7.1	3.6	0.9	1.5
MIST-889c	14.0	7.1	2.4	0.6	–0.2

Figure 4 furthermore visualizes the changes in correlation throughout the protein structure. The middle panel, which displays the changes in pairwise mutual information for all torsional pairs, shows clear diagonal patterning, which indicates correlation contributions from torsions that are near each other in protein sequence and hence in space. It also shows large patches corresponding to the two loops highlighted in the left-hand panel. As shown in the graph along the top of the heat map, these loops are also subject to large changes in first-order entropy. The strong off-diagonal patches associated with loop–loop correlations mean that correlation contributions are strong for torsions that are near each other in space yet not in sequence. Torsion 154 is χ₁ of Tyr10 and has an intense stripe in the side-chain and side-chain/main-chain sections of the heat map, indicating strong correlations with many other torsions. Torsions 170 and 264, which are χ₂ and χ₃ of the disulfide bridge between the two loops (Cys14-Cys38), also have particularly intense stripes in the heat map. The right-hand panel of Figure 4 is the same as the middle one, except that it only marks those torsion pairs included in the MIST estimate of the pairwise entropy. Thus, MIST selects only highly correlated pairs within each conformational cluster, and it is interesting to see that this procedure focuses attention even more on the diagonals. Thus, torsions that are near neighbors in sequence contribute the most to the computed entropy difference.

Figure 4.

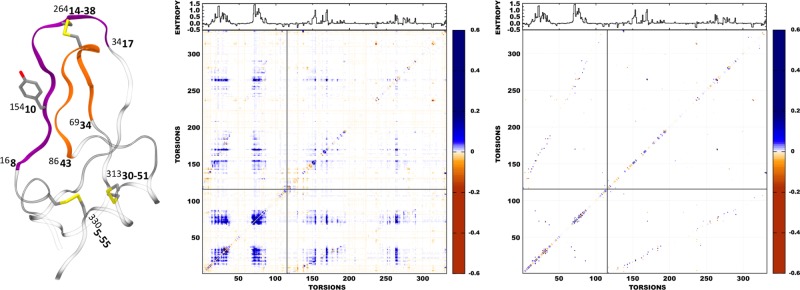
Structural analysis of the changes in pairwise correlation between Clusters 1 and 2 for torsions throughout BPTI. Left: cartoon representation of BPTI with structural features having large correlation annotated by the torsion number (superscripted) and residue number (bold). Loop 1 (purple) and loop 2 (orange) are connected by the central disulfide bridge (Cys14-Cys38) and show strong intra- and interloop correlation. Center: Mutual information heat map for all torsion pairs pertaining to the 332 nonphase side-chain and main-chain ϕ/ψ torsions. The first 116 torsions correspond to main-chain torsions starting at residue 1, and the following 216 are side-chain torsions, again starting at residue 1. Main-chain torsions of loop 1 start at torsion 16 (residue 8) and end at torsion 34 (residue 17). Main-chain torsions of loop 2 start at torsion 69, residue 34 and end at torsion 86, residue 43. The disulfide bridges are side-chain torsions 264, 313, and 330. Side-chain torsion 154 (Tyr10) shows a noticeable correlation fingerprint. (Right) The corresponding MIST solution for the same set of torsions. The mutual information and entropy values represent Cluster 2 minus Cluster 1 deltas and are reported in units of S/k_B. Furthermore, each delta in pairwise mutual information had the average delta in pairwise spurious mutual information (0.0057), as determined by the previous permutation analysis subtracted from its value to minimize numerical bias.

The estimated change in pairwise correlation entropy of about 3–6 kcal/mol corresponds to about 0.05 to 0.10 kcal/mol/residue for this protein of 58 residues. This may be compared with the value of ∼0.3 kcal/mol/residue computed for the TSG101-peptide binding system (above).²⁴ It seems reasonable that the binding reaction of the TSG101 system might lead to a larger perturbation per residue than the conformational change studied here. Inadequate sampling can cause the correlation entropy to be overestimated, and the net simulation time of 2 μs for TSG101 is much less than the 1 ms of time available for BPTI, so convergence could also play a role in the observed difference. Finally, it is worth noting that BPTI’s three disulfide bridges may dampen its total configurational flexibility relative to TSG-101, which lacks such structural constraints.

Discussion

The results presented here bear on several aspects of the contributions of torsional correlations to changes in configurational entropy. A central result is that well-converged simulations clearly show nontrivial contributions to configurational entropy changes from changes in correlations, for both binding and conformational change events. For the host–guest system, the correlation contributions amount to about 40% of the first-order entropy, and they act in the same sense as the first-order contribution; that is, they further reduce the configurational entropy of binding. For the conformational change of BPTI, the correlation contribution of 3–6 kcal/mol represents 15–30% of the first-order entropy but now acting in the opposite sense; that is, correlation acts opposite to the first-order term.

The conclusion that correlation contributes significantly to configurational entropy differences is consistent with a prior quasiharmonic study using Cartesian coordinates⁷ and with MIE^23,24 studies using bond-angle-torsion coordinates. It is also consistent with a recent study that applied MIST to side-chain rotameric states across a series of different proteins.¹⁶ However, it appears less consistent with a prior simulation study of peptides and a small protein, which indicated relatively small contributions from changes in correlation.²⁰ We conjecture that the apparent inconsistency stems largely from the different nature of the cases studied. In the prior study, changes in configurational entropy were computed for five dipeptides in solution, when T was changed from 270 to 380 K, but perhaps these small molecules were largely unstructured and uncorrelated at both temperatures. For villin headpiece, the prior study considered only a 20 K temperature change, which may have been too small to produce much change in overall motion. Moreover, the villin headpiece simulations at 300 K were terminated at 70 ns because the protein structure was beginning to change significantly after 75 ns in two of the runs. Perhaps continuing the run, so as to include the impending conformational change, would have altered the findings. Finally, for the villin study, the small magnitude of the correlation contributions observed may result in part from the study’s neglect of inter-residue correlations.²⁰ Interestingly, another prior study, of calmodulin,²¹ which also suggested that changes in correlation entropy are small, likewise studied a temperature change (295 to 346 K), rather than focusing explicitly on a conformational change or binding event. In summary, the current body of evidence seems consistent with a view that clear-cut conformational changes and binding events tend to be associated with quantitatively important entropic contributions from changes in correlation. This conclusion suggests that one cannot confidently overlook the potential importance of correlation in the entropic interpretation of NMR order parameter studies, at least for proteins undergoing well-defined binding events or conformational changes.

Recently, however, it has been suggested, based on empirical and simulation data, that the entropy contribution of correlation is roughly proportional to the first-order entropy, ΔS_full^corr ≈ −0.17ΔS₁, so that a total entropy change may be estimated as ΔS_full ≈ 0.83ΔS₁.¹⁶ Such a regularity would clearly be useful, given that computing or measuring correlations is difficult. It also can make intuitive sense, as the entropy of a set of correlated DOF may require a larger correlation correction if they become more flexible, at least up to a point, and, indeed, the present results for BPTI fit the pattern rather well. However, the host–guest binding results do not fit the pattern. Here the change in correlation entropy has the same sign as the change in the first-order entropy, such that ΔS_full ≈ −1.4ΔS₁. In respect of the sign of the relationship, this result agrees with a prior simulation study of peptide binding by the protein TSG101.²⁴ It is perhaps worth noting that although greater correlation necessarily decreases entropy, relative to the first-order entropy, the change in correlation in the course of some process may work in either direction. One may speculate, based on the available data, that binding, in particular, tends to generate decreases in both first-order and correlation entropy, but only further study could establish this point. What one may conclude at this point is that the change in correlation entropy can, in general, either reinforce or compensate the change in first-order entropy. As a consequence, entropy changes derived from changes in NMR order parameters cannot be reliably assumed to represent either upper or lower limits of the total entropy change.

The present methodology also affords a detailed look at the specific torsions and torsional correlations that determine the computed entropy changes in BPTI. We find that the estimated entropy difference between Clusters 1 and 2 of BPTI is associated largely, though not exclusively, with changes in the conformational distributions of main-chain torsions. This holds not only at first but also at second order, where changes in pairwise torsional correlations contribute. Thus, entropy estimates that neglect main-chain contributions, including main-chain correlations, risk incurring substantial errors. It is also of interest that the most significant pairwise correlations involve torsions that are close to each other in space, either because they are sequence neighbors or because they are brought together by the 3-D fold of the protein. It will be interesting to learn whether longer-ranged correlations are important for more complex and flexible proteins than BPTI, which is small and is cross-linked by three disulfide bridges.

An innovative methodological aspect of this study is that it has presented the first application of the MIE-NN and MIST-NN methods to a binding problem, albeit a simple one, and the first MD-based estimation of the change in configurational entropy on binding at full dimensionality. Such methods can have broader applicability to larger systems as well, especially when coupled to the use of information theoretic methods, like the Jensen–Shannon divergence approach used here, to select the most relevant DOF and subsequently drastically reduce the combinatorics associated with MIE and MIST calculations. Given advancing computer power, exemplified by the millisecond protein simulation of BPTI, quantitative investigation of correlations at higher than second order in a system as large as BPTI may soon become computationally feasible.

Author Contributions

^∥ A.T.F. and B.J.K. contributed equally.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States