Abstract
Understanding the anatomical and functional architecture of the brain is essential for designing neurally inspired intelligent systems. Theoretical and empirical studies suggest a role for narrowband oscillations in shaping the functional architecture of the brain through their role in coding and communication of information. Such oscillations are ubiquitous signals in the electrical activity recorded from the brain. In the cortex, oscillations detected in the gamma range (30–80 Hz) are modulated by behavioral states and sensory features in complex ways. How is this regulation achieved? Although several underlying principles for the genesis of these oscillations have been proposed, a unifying account for their regulation has remained elusive. In a network of excitatory and inhibitory neurons operating in an inhibition-stabilized regime, we show that strongly superlinear responses of inhibitory neurons facilitate bidirectional regulation of oscillation frequency and power. In such a network, the balance of drives to the excitatory and inhibitory populations determines how the power and frequency of oscillations are modulated. The model accounts for the puzzling increase in their frequency with the salience of visual stimuli, and a decrease with their size. Oscillations in our model grow stronger as the mean firing level is reduced, accounting for the size dependence of visually evoked gamma rhythms, and suggesting a role for oscillations in improving the signal-to-noise ratio (SNR) of signals in the brain. Empirically testing such predictions is still challenging, and implementing the proposed coding and communication strategies in neuromorphic systems could assist in our understanding of the biological system.
Keywords: Brain rhythms, coherence, communication, electroencephalogram (EEG), gamma, Hopf bifurcation, inhibition-stabilized network (ISN), inhibitory neuron–network–gamma (ING), limit cycle, nonlinear system, oscillations, phase code, pyramidal neuron–inhibitory neuron–network-gamma (PING), synchrony, vision
I. INTRODUCTION
Neuromorphic engineering aims to design intelligent systems that are inspired by the nervous system, and can perform valuable functions such as vision, audition, motor control, and decision making. More specifically, the field aims to understand the key aspects of the anatomical and functional architecture of the brain that support functions such as information representation, learning, memory storage, and retrieval in an adaptive and redundant hardware. In order to implement solutions based on the biological system, understanding the principles behind encoding and communication of information in the brain is as important as understanding the physical connectivity motifs that it uses.
A neuron in the central nervous system communicates mainly through fast all-or-none events called action potentials or spikes in its membrane electric potential. The earliest theories of neural coding proposed firing rates or the number of spikes generated in a neuron as the information code used to communicate with other neurons. More recent models of learning, memory formation, and retrieval in the brain also propose information coding in the relative firing times of the spikes in a neuronal population [1], [2]. Empirically observed oscillations within populations of neurons, and synchronization between oscillating populations have been suggested as signals used by the brain to encode and decode information in relative spike times.
Since oscillatory brain activity is observed during many cognitive functions, it is hypothesized to shape the functional architecture of the brain during cognitive processing. In this paper, we propose a novel mechanism for regulating such oscillations and thereby their functional role in an intelligent system such as the human brain. While excellent reviews of the extensive empirical and theoretical literature exist elsewhere (e.g., [3]-[5]), we begin by briefly summarizing the empirical evidence on oscillations during behavior and the related theoretical ideas about their functional role.
II. OSCILLATIONS IN THE BRAIN: EXPERIMENTS
Empirical evidence in humans and other mammals shows that when the subject is performing sensory processing and cognitive tasks, neural activity in the cerebral cortex is accompanied by narrowband fluctuations in firing rates, local field potentials (LFPs), and electroencephalograms (EEGs) (summarized in [6] and [7]). During slow wave sleep, oscillations in delta (2–4 Hz) range are prominent [8]. In rodents, oscillations in the 4–7-Hz or theta range accompany exploration and the formation as well as retrieval of a spatial map of its environment [9]. Oscillations in the 30–80-Hz or gamma frequency range are associated with arousal, working memory [10], and attention [11]. During cognitive tasks in humans, sustained oscillations in the gamma range [12] are induced in the prefrontal cortex [13], and their power increases in proportion to the task load [14]. During sensory processing, gamma range power in LFPs recorded in the related sensory area of the cerebral cortex is significantly enhanced following stimulus onset [Fig. 1(a)] [15], [16]. Abnormal gamma oscillations are a hallmark of cognitive disorders such as schizophrenia [17], autism [18], and language-learning impairments [19]; in the frontal cortices of infants, reduced gamma range power predicts language and cognition deficits at five years of age [20].
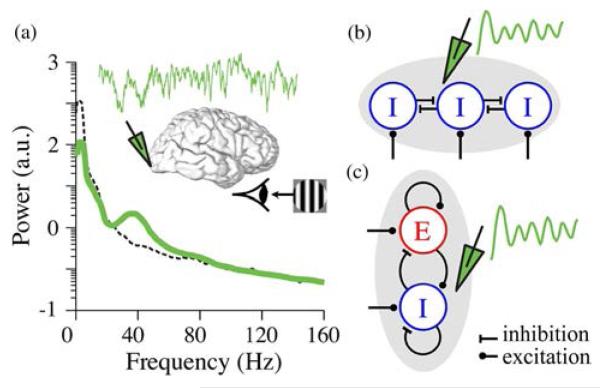
Fig. 1.
Oscillations are detected as narrowband increase in the power spectrum of electrical activity in the brain. (a) Power spectral density of LFPs recorded with a penetration electrode from the visual cortex of a macaque in response to visual stimulation (green). Dashed black curve shows the power spectrum of LFP recorded before visual stimulation. The trace and schematic in the inset shows 1 s of LFP time series (green) in response to visual stimulation. Data adapted from [21]. (b) and (c) Alternative models for local network mechanisms of oscillations [22]. (b) A schematic for inhibitory (I) neuronal network model for oscillations, also known as ING. (c) A schematic for excitatory (E)-inhibitory (I) neuronal network model for oscillations.
III. OSCILLATIONS IN THE BRAIN: THEORY
Theoretical work has proposed various functional roles for neural oscillations [3], [23]-[26], both for coding and communication, some of which also find empirical evidence.
A. Oscillations Enable Phase Coding
Oscillations have been suggested to facilitate phase coding, whereby the magnitude of total input to a neuron is converted to the position of its output spikes relative to the ongoing oscillation [24], [25], [27]. In both the hippocampus and neocortex of the brain, empirical data indicate that strongly excited neurons fire earlier in an oscillation cycle with a higher probability than those excited less strongly [28]-[31]. In the hippocampus, a phenomenon called phase precession has provided some of the best evidence for the functional role of theta oscillations in phase coding: the phase of a cell firing relative to the ongoing theta oscillations has been shown to advance systematically as the moving animal passes through the cell’s preferred location in space [28]. This mechanism enhances spatial coding and assists in the formation of assemblies of cells to represent movement trajectories.
B. Oscillations Synchronize Neural Assemblies
Oscillations in a neural ensemble synchronize the firing of participating neurons, which, in turn, could subserve important coding and communication roles such as feature binding and efficient communication.
1) Oscillatory Synchronization Facilitates Feature Binding
It has been hypothesized that neuronal spikes become synchronous if they participate in the encoding of related information [4]. This temporal binding has been suggested to underlie feature binding at higher levels of the visual processing hierarchy. Experiments in the visual cortex of multiple species show that adjacent neurons synchronize their action potentials in the gamma band such that either individual neurons or the population exhibit oscillatory behavior when optimally stimulated [15], [32]-[35].
2) Oscillatory Synchronization Enables Dynamic Routing of Information
Oscillations could also facilitate dynamic coupling between brain areas [24], [25]: Appropriate modulation of phase coupling between a pair of oscillating areas can enhance the functional connectivity between the two. This is also termed as communication through coherence. While this functional role for brain oscillations is not well established empirically, recent studies provide some evidence. Simultaneous recording of neural activity from two brain areas—frontal eye field (FEF) and visual area V4—shows that oscillatory coupling between them is strengthened at gamma frequencies, when the subject is paying attention [36]. It is thought that strong coupling with phase shifts comparable to the communication delays between areas could ensure that spikes from one area arrive at the peak phase of neuronal membrane potential in the target area to be maximally effective in their influence. More recently, it has been hypothesized that neural oscillation-based multiplexing mechanisms, similar to those used in telecommunication systems between a receiver and multiple transmitters, implement selective neural communication [26].
The proposed functions for brain oscillations are still under investigation [7], [37] as establishing their causality requires manipulating the oscillations independent of the stimulus or behavioral state. In a parallel effort, computational studies have explored models for the neural mechanisms underlying the observed oscillations (summarized recently in [7]). These models can provide insights into studying brain oscillations empirically, and guide their implementation in artificial systems. These models could also be used to theoretically explore ways in which oscillations can be regulated from within and outside the neural population in which they emerge. Equally importantly, the gained insights could shed further light on novel roles or interpretations of oscillatory brain states.
IV. MODELS OF NEURAL OSCILLATIONS
Empirical and theoretical studies have shown that oscillations in the cortex are mediated by inhibitory neurons [22], [27], [38], [39]. Inhibitory neurons act to reduce the electrical excitability of their target neurons, either by reducing the input resistance of their neuronal membrane or by making their membrane voltage more negative. Gamma-range oscillations in the cortex are thought to be mediated by inhibitory neurons that target the soma (cell body) of the electrically compartmentalized pyramidal neurons [40], [41]. These oscillations typically occur with irregular firing of single neurons, with each individual neuron skipping multiple oscillation cycles [37], [42]. Such oscillations are hence thought to emerge not through oscillatory spiking of individual neurons, but from the coordinated interaction of neurons. These interactions can cause oscillations in a neuronal network in a couple of ways that are broadly referred to as inhibitory neuron–network–gamma (ING) or pyramidal neuron–inhibitory neuron–network–gamma (PING) [22] (Fig. 1). Empirical evidence from gamma range oscillations in response to visual stimulation suggests that they are of the PING type [37], [43], [44]. Oscillations within PING architecture depend on strong excitatory–inhibitory feedback, but can emerge either due to communication delays (e.g., conduction delays along axons) [45] or due to positive feedback (recurrent excitation) [46]. Noisy versions of such models produce irregular firing of individual neurons and oscillations with noisy phase [42], [45], [47]. Other models for how narrowband activity emerges in the cortex suggest that the detected signal is the bandpass-filtered output of the local cortical network whose input resembles broadband noise [48] or that the oscillations result from quasi-cycles or population-level resonant oscillations caused by noise-induced excursion of damped oscillations in a nonlinear network [47], [49].
V. REGULATION OF GAMMA OSCILLATIONS
Many of the computational models of oscillations have a frequency range of oscillations that is constrained by biophysical “constants” such as conductance delays or the decay of inhibitory postsynaptic currents (IPSCs) [38], [45], [50]. Others offer dynamic regulation of the peak oscillation frequency with the intensity of input to the network: stronger the input, faster the oscillations. Empirical observations suggest that brain oscillations are dynamic in their frequency as well as amplitude: They can be modulated by brain states, stimulus properties, or attention.
A. Oscillations Reflect the Balance of Excitation and Inhibition in the Network
LFP oscillations in the gamma range have been proposed to reflect the strength of synchrony in neuronal populations, and find empirical support in several cortical areas [51], [52]. In the primary visual cortex (V1), the attentive states as well as several stimulus properties regulate the mean firing rates and oscillations in a highly correlated manner. The peak frequency of these oscillations increases with contrast which also increases the mean firing rates [37], but decreases with the stimulus size which decreases the mean firing rates [44]. When the contrast of visual stimulus is varied in space, the peak gamma frequency correspondingly varies between nearby cortical sites (about 400 μm apart) [37]. When the contrast is slowly varied in time, the peak frequency rapidly changes to match the contrast [37]. Spatial attention, which increases the mean firing rates in the local cortical network, increases the peak frequency of gamma [37], while reducing their power [43]. Since mean firing rates reflect the balance of excitation and inhibition experienced by the local network, the empirical data from V1 suggest that both the power and frequency of gamma range oscillations reflect this balance.
B. Regulation of Oscillations in an Inhibition-Stabilized Network
Local networks of excitatory (E) and inhibitory (I) neurons in the cortex are thought to operate in an inhibition-stabilized network (ISN) regime [53], which is characterized by strong self-excitation within the E population stabilized by feedback inhibition from the I population. This regime explains the paradoxical withdrawal of local inhibition during the phenomenon of surround suppression in V1 neurons [54]. We have recently proposed a mechanism for the regulation of oscillations in an inhibition-stabilized E–I network that captures the changes in gamma as observed in V1 [55]. In a PING network of stochastically firing neurons with strong excitatory–inhibitory feedback and recurrent excitation, our model demonstrates oscillations whose power and frequency reflect the balance of input to the local excitatory and inhibitory neurons (Fig. 2). Such networks can exhibit narrowband oscillations that are noisy versions of the underlying deterministic limit cycle phenomenon in a firing rate model [47]. Nonlinear bifurcation analysis of limit cycle phenomenon in the firing rate model suggests several regimes of their amplitude/power regulation [56], [57]. In the following sections, we use a combination of approximate analysis and confirmatory simulations of a firing rate model to propose a novel constraint on the model that allows it to operate in a regime that captures the empirical observations for both power and frequency regulation. The constraint allows it to regulate limit cycle oscillations by balancing the input to the excitatory and inhibitory neurons, suggesting that it underlies the observations in our stochastic model.
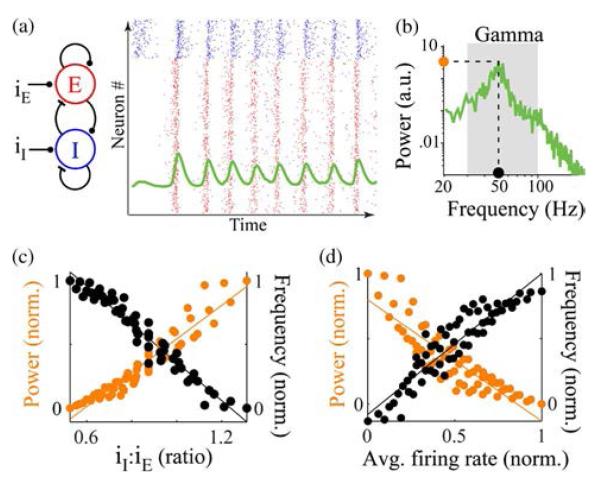
Fig. 2.
Regulation of narrowband oscillations with the balance of inputs to the excitatory (E) and inhibitory (I) neurons. (a) Schematic of the E–I network model with 800 E and 200 I neurons. Panel on the right shows spike times for a fixed level of constant input to the E and I neurons for 200 ms. Dots in each row represent spike times in one neuron, both E (red dots) and I (blue dots). The overlaid trace (green) shows fluctuations in mean spikes/second of the population calculated in 5-ms bins. (b) Power spectral density estimate of 1-s duration of spikes per second shown in (a). Dashed lines mark the peak power and peak frequency of the narrowband increase in power. (c) Normalized peak power and peak frequency plotted as a function of the ratio of inputs to the I and E populations. (d) Normalized peak power and peak frequency plotted as a function of mean spikes per second of the population. Data adapted from [52].
C. Firing Rate Model
The simplified firing rate model
| (1) |
| (2) |
describes the coevolution of excitatory (rE) firing (rI) population rates in time as a function of external input (iE and iI) to both E and I populations. (iE and iI) indicate the rate at which the populations approach their steady-state firing rates. GE and GI are response functions: they map the firing rates of the two neural populations as a function of their net inputs [46], [54]. The steady-state firing rate of each population is determined by the weighted sum of individual activities and the external input. Weights WEE, WEI, WIE, and WII are positive numbers representing strength of connections between E–E, E–I, and I–I populations, respectively. For example, WEE represents the product of the average number of recurrent excitatory contacts per cell and the average postsynaptic current arising from one presynaptic action potential. The steady-state network behavior is determined by the intersection of the drE/dt = 0 and drI/dt = 0 curves in the rErI-plane [red and blue curves in Fig. 3(a), third panel].
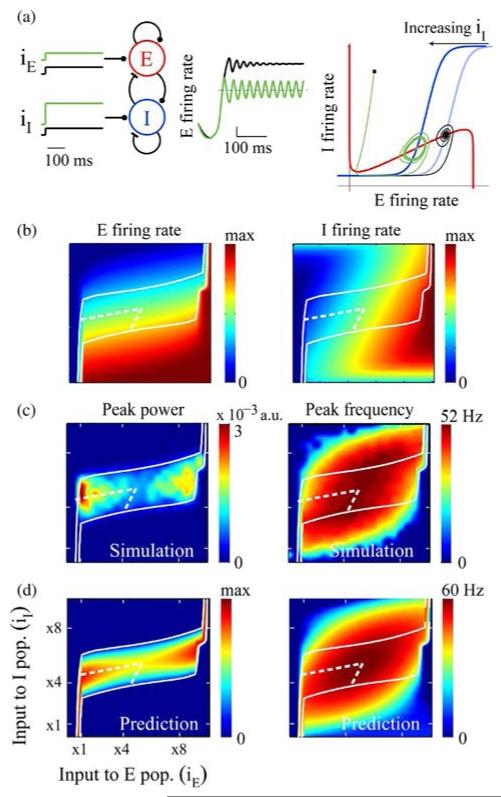
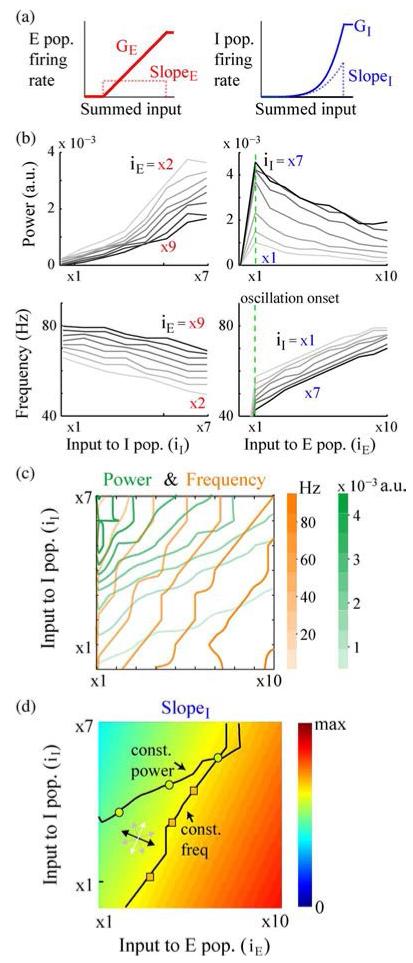
Fig. 3.
Regulation of limit cycle oscillations as a function of inputs to the E and I populations. (a) Simulation of the model described by (1) and (2) as an ISN with sigmoid E and I response functions. iE and iI are the external excitation to the two populations. Traces in the middle show time evolution of E firing rate for a fixed level of iE and two different levels of iI (low: black trace; high: green trace). Panel on the far right illustrates coevolution of E and I firing rates in a phase plot. Red and blue curves are the E and I nullclines, respectively. (b) Simulation results for E and I firing rates as a function of the two external inputs. (c) Simulation results for power and frequency of oscillations as a function of the external inputs. (d) Predicted trends for the variation of power and frequency of oscillations with external inputs (see Appendix B). The white contour in panels (b), (c), and (d) bounds the approximate analytical prediction (σ = 0 and ω2 > 0 from Appendix B) for oscillatory region (i.e., power > 0). The area bound by dashed white line marks the subregion where the analysis predicts the oscillation power to increase and frequency to decrease with increasing iI.
D. Oscillations in the Firing Rate Model of an ISN
When sufficient stimulation pushes the ISN out of a stable equilibrium, it can result in stable oscillations in the E and I firing rates [46]. Previous theoretical work has shown that in a network of spiking neurons such oscillations are present purely at a population level, and can be weak or absent at the level of a single neuron [45]-[47]. It has been previously observed that the frequency of these limit cycle oscillations is regulated by stimulus intensity in a monotonic fashion: it increases with increasing input to the excitatory population [46]. Analytical treatment also suggests model regimes in which either increasing or decreasing input to the inhibitory population increases the power in oscillations [57], [58]. However, it is not known if and how the model network can operate in a regime where the power, frequency, and mean firing rate regulation match empirical observations as seen in V1. To analyze these properties, we used the simplified rate model [46], [53], [59] described in (1) and (2).
Result 1 Increased Input to I Population Can Reduce Oscillations Frequency and Increase Their Power
Simulations of the ISN model with sigmoid response function (Appendix A) showed that there was an input regime in which increasing input to the I population not only reduced the mean E and I firing rates as expected, but also caused stable oscillations [Fig. 3(a)]. Characteristic of an ISN [53], [54], the mean local E and I population firing rates covaried when we independently modulated the input to each population [Fig. 3(b)]. The input to the E population increased the mean firing rates of both populations, while the input to the I population decreased it. There was a subspace of inputs over which the network showed sustained oscillations [Fig. 3(c)]. The oscillation power as well as frequency varied with the inputs in a nonmonotonic fashion over the entire subspace. The oscillations in the rate model exhibited a behavioral regime in the input subspace in which increasing the input to the I population not only reduced the mean firing rate, but both increased the power and decreased the frequency of network oscillations.
Result 2 An I Population With Superlinear Response Function Causes Oscillations With Lower Frequency and Higher Power
To investigate why an increased input to the I population caused slower and stronger oscillations in only part of the input subspace that caused oscillations, we revisited the characteristics of the expected bifurcation in the nonlinear network model when input to the I population was increased (Appendix B).
a) Modulation of oscillation power by the input to the I population
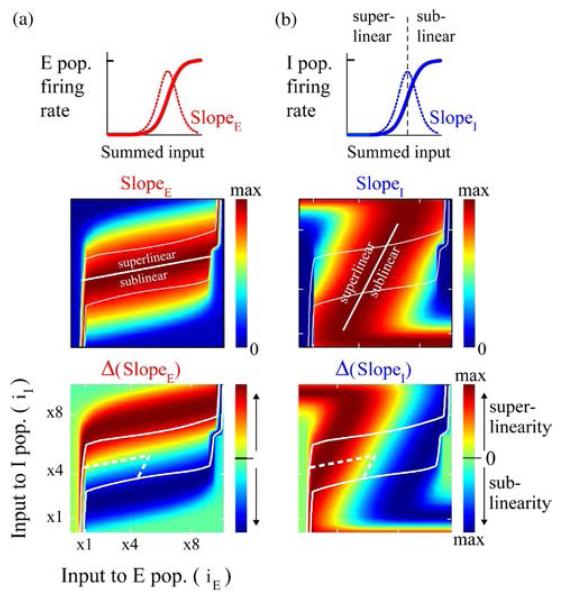
Our analysis predicted that the power in the oscillations depended on the shapes, and hence the slopes, of both the E and I response functions (Appendix B3). The predicted relationship between oscillation power and the estimated slopes of the response functions showed good correspondence with the simulation data [Fig. 3(d)]. The qualitative prediction for power varied roughly with the ratio SlopeE: SlopeI of the response functions of the two populations. We investigated the relative shapes of E and I response functions for which the ratio would increase with increased input to the inhibitory population (Appendixes B1 and B2), revealing two alternate criteria:
a highly superlinear I response function and a sublinear, linear, or weakly superlinear E response function;
a highly sublinear E response function and a superlinear, linear, or weakly sublinear I response function.
When the network oscillated in a range where the response curves satisfied one of the above criteria, increasing input to the I population would cause more powerful oscillations per our qualitative prediction. Analyzing the data from model simulations with sigmoid response functions confirmed that the subspace of the inputs where the first criterion was satisfied coincided with the region where the phenomenon was observed (Fig. 4).
Fig. 4.
Inhibitory neuronal (I) population with a strong superlinearity facilitates regulation of oscillations similar to empirical observations. (a) Schematic on the top depicts the shape of E response function and its slope at different levels of input. Estimated response function slopes (middle panel) and superlinearity (bottom panel) of E population as a function of inputs to the E and I populations. The superlinearity measure was computed as second derivative of the response function. Solid white contour in the panels bounds the approximate analytical prediction for oscillatory region (i.e., power > 0). The area bound by dashed white line marks the subregions where oscillation power increased and frequency decreased with increasing iI, as described for Fig. 3. (b) Same as in (a), but for inhibitory population.
b) Modulation of oscillation frequency by the input to the I population
Our analysis predicted that the frequency of oscillations also depended on the shapes of both the E and I response functions, but in a more complex way (Appendix B4). The predicted slope-based estimate of frequency was approximate but in close qualitative agreement with the simulations in the rate model [Fig. 3(d)]. The predicted frequency varied roughly with the product SlopeE × SlopeI of the two populations. We investigated the relative shapes of E and I response functions for which the product would decrease with increased input to I population (Appendixes B1 and B2), revealing three alternate criteria:
a superlinear response function for both E and I populations;
a highly superlinear response function for the E population and a weakly nonlinear response function for the I population;
a highly superlinear response function for the I population and a weakly nonlinear response function for the E population.
When the network oscillated in a range where response functions satisfied one of the above criteria, increasing input to the I population would cause lower frequency oscillations per our qualitative prediction. Analyzing the data from model simulations with sigmoid response functions confirmed that the subspace of the inputs where the third criterion was satisfied coincided with the region where the phenomenon was observed (Fig. 4).
Combining the independent qualitative criteria on response function slopes for the power and frequency modulation of interest, our analysis predicted that when an oscillating ISN was constrained to operate with strongly superlinear I response function and a weakly nonlinear E response function, the oscillations power would increase and frequency decrease with increased input to the I population. To illustrate this with the simplest scenario, we simulated the nonlinear rate model with piecewise and bounded power-law I response function and linear E response function (Appendix A). The simulation data confirmed the predictions from the analysis of the linearized system over a large portion of the input range in which the network showed oscillations [Fig. 5(b)].
Fig. 5.
Simulations in the rate model. (a) Response functions used for the E and I populations. (b) Power and frequency of oscillations with independent modulation of input to the I population (left panels) and the E population (right panels). The numbers next to the curves show the fixed levels of iE (left panel) and iI (right panel) at which the simulations were performed. (c) Contour plots of variation of peak power (green) and peak frequency (orange) as a function of input to the E and I populations. The figure shows most of the region where the network shows stable oscillations and both E and I populations have nonzero firing rates. (d) Estimated slope of the I response function for the range of external inputs shown in (c). The direction guide (bidirectional arrows) indicates the directions for most (black) to least (white) effective directions of input co-modulation for changing the slope of I response function. Overlaid on top are example iso-power (green circles) and iso-frequency (orange squares) modulation of network oscillations from (c).
Result 3—Increased Input to the E Population Increases the Frequency but Decreases the Power in Oscillations
Properties of ISN predicted that independently increasing the input to the excitatory population would increase both E and I firing rates (Appendix B1). Constrained by the relative E/I response function shapes developed in Result 2, the analysis (Appendixes B3 and B4) predicted that independently increasing input to the excitatory population would decrease the power of network oscillations and increase their frequency. Simulations in the nonlinear firing rate model confirmed the predictions [Fig. 5(b)].
Result 4—The Balance of Input to Both E and I Populations Determines the Frequency and Power of Oscillations
The analysis for the ISN with strongly superlinear inhibition predicted the following outcomes for the co-modulation of the two drives (Appendices B1–B4).
Higher frequency lower power oscillations accompanied by increased output firing rates: The oscillations would be faster and less powerful when the co-modulation of inputs increased the output firing rate for both populations.
Lower frequency higher power oscillations accompanied by decreased output firing rates: The oscillations would be slower and more powerful when the co-modulation of inputs suppressed the firing rates of both populations.
In addition, the analysis predicted that the changes in population firing rates (and, hence, the response slopes) were not limited to covariation. When both inputs were changed, firing rates of E and I populations could vary in different directions, and by different amounts, depending on the balance of change of the inputs to the two populations [Appendix B1, Fig. 3(c)]. Thus, the qualitative predictions for power and frequency changes not only depended on the absolute strength of the individual inputs, but also the effectiveness of their balance in changing the response slope of the two populations; a sufficient change in the slope was necessary for causing change in the power or frequency of oscillations. For differential sensitivity of power and frequency to the balance of the inputs, our analysis predicted two more scenarios:
-
3)
power-only modulation of oscillations;
-
4)
frequency-only modulation of oscillations.
Simulations in the nonlinear rate model demonstrated all four scenarios, including the frequency-only and power-only changes in network oscillations [Fig. 5(c)]. When we estimated the slope of I response function from the simulation data during frequency-only and power-only modulation, we confirmed that the co-modulation was not along the most effective direction for changing the slope of I response function. In summary, when the inputs to the E and I populations were co-modulated, the direction of change (increase/decrease) of their balance as well as the change in their absolute strengths determined their overall effect on the oscillations in the network.
VI. DISCUSSION
In the brain, electrical activity that is triggered by sensory processing, cognitive tasks, and changes in internal states shows narrowband oscillations in spike rates, LFPs, and EEGs. Extensive theoretical work and some empirical evidence suggest a functional role for such oscillations in coding and routing of information in the brain. Oscillations in the cortex are modulated both by internal states and external sensory stimuli. Although interactions between populations of excitatory and inhibitory neurons underlie these oscillations, how they are dynamically regulated is not well understood. In this study, we investigated a simplified and well-known model E–I network that parsimoniously captures the paradoxical behavior of gamma range oscillations observed in recent recordings from visual cortical neurons [37], [44], and is based on the connectivity regime of the local cortical network [53], [54]. Powerful oscillations emerge when inputs to the E and I populations result in a reduction of local activity. Oscillations grow faster when the inputs to the E and I populations result in an increase of local activity. Our analyses and simulations show that the inhibitory population constrained to operate with a strongly superlinear response curve is crucial to this demonstrated behavior. The deduced constrains find support in the empirically determined response characteristics of the excitatory (E) and inhibitory (I) neural populations involved in these oscillations.
A. Empirical Support for the Constraint on Response Nonlinearity
Our model predicts that the inhibitory neurons involved in the gamma-generating E–I network operate in the superlinear portion of their response characteristics, consistent with measurements of cortical neurons operating in the superlinear range of their rate versus membrane potential (F − Vm) [60], characteristics under stimulus-driven conditions [61]. When constrained by the experimental observations on gamma oscillations, the model also predicts that such inhibitory neurons operate in a strongly superlinear (compared to the excitatory population) portion of their response characteristics. A basis for this difference may lie in the higher firing rates and lower adaptation of fast-spiking inhibitory neurons [62], which are thought to be crucial to gamma range oscillations in the cortex [40], [41]. Additionally, recent empirical data from cerebral cortex have reported evidence for a stronger superlinearity of inhibitory neurons than excitatory neurons [63]. Even in the absence of such evidence, our qualitative analysis shows that relative strength of connections within and between populations can differentially constrain the operating range of each population during network oscillations (Appendix B4). Other nonlinear mechanisms that we have not considered here and merit further consideration, such as synaptic facilitation/depression, could also come into play in shaping the response functions of the two populations. The response functions in our model are the response of a neuronal population to a linearly increasing input; the actual transformation of the input quantity such as stimulus properties or focus of attention into synaptic currents can be nonlinear and provide yet another mechanism to differentiate the response properties of the excitatory and inhibitory populations.
B. Implications of the Analysis
Connectivity Regimes Can Achieve Functional Specialization: When gamma power in our constrained model increases with increasing input to the inhibitory population, consistent with experimental evidence [40], it is also accompanied by suppression of the local E/I firing rates. This is supported by visual cortical data showing that when a strong gamma signal is recorded at a site, it co-occurs with reduction of multiunit firing rates [44], and that the reduction applies to both excitatory and inhibitory populations [54]. The model thus predicts that cortical inhibitory neurons that have strong reciprocal connections with local excitatory neurons in an ISN-type overall connectivity participate in stimulus-induced gamma. Thus, firing rates of inhibitory neurons responsible for gamma oscillations would co-vary with the excitatory activity. On the other hand, the firing rates of inhibitory neurons not responsible for gamma generation would anti-vary with the excitatory activity in the network. Given the recent empirical characterization of the properties of different types of inhibitory neurons [64] in the cortex, this suggests that although many inhibitory neurons have essentially similar local action at a neuronal membrane, the cortical architecture ensures functional specialization of inhibitory neurons at the network level.
Oscillations May Improve Signal-to-Noise Ratio (SNR): Empirical evidence in the cortex [16], [44], [65] and our modeling shows that strong gamma co-occurs with reduced firing rates [55]. Reduced firing rates of neurons can degrade the SNR for their downstream neurons. However, the signal degradation experienced by a downstream neuron pooling from neurons with reduced firing rates could be compensated for by improved spike synchrony (as a population). Although this is theoretically possible and there is some empirical evidence [51], it is not known if this strategy is indeed exploited for reliable communication by the neural machinery.
The Regulation Mechanism Is Not Specific to Gamma Range Oscillations: In addition to the regulatory mechanism we propose here, the frequency of oscillations in the model also depends on the connection strengths in the network [(12) and (13)]. Changes in the strengths of inhibitory feedback (E-to-I and I-to-E) are predicted to shift the range of narrowband oscillations in the model accordingly. Thus, although the regulatory mechanism discussed here primarily explains empirical data on gamma range oscillations, it is applicable to oscillations in any other frequency band with a similar underlying oscillatory mechanism: an ISN–PING.
C. Relation to Other Computational Models of Oscillations
Regulation of Oscillation Frequency: The regulatory mechanism discussed here demonstrates a richer modulatory effect of external inputs than previously shown in other models of network oscillations [5]. For example, models involving I population or ING-type oscillations predict an increase in frequency [38], [50] when the input to I neurons is increased. In our model, increasing the input to the inhibitory neuronal population may increase or decrease or not change the frequency of oscillations, depending on how the input to the E population is co-modulated.
Role of I–I Coupling in an E–I Model: Although strong I–I coupling is essential for oscillations in ING models [45], [50], it has been generally understood to be inconsequential for oscillations in the PING models [45], [46], [66]. Our analysis, when constrained by experimental data, reveals a novel role for I–I coupling in the E–I models of gamma: without sufficient I–I coupling, the network can oscillate and undergo frequency modulation, but is not predicted to demonstrate the modulation of power with changing input to the neuronal populations (Appendix B1).
Alternate Mechanisms: In a network of stochastically spiking neurons, oscillations can emerge as quasi-cycles with varying amplitude and phase [47]. Bandpass filtering of broadband noise is an alternate model for such oscillations [48], and frequency and power modulation in these models has been used to propose an alternate interpretation of data in the visual cortex [67]. In the broader context of brain oscillations, any one model would most probably explain a subset of the empirical data on brain oscillations. The local architecture, types of neurons, and their biophysical properties vary widely in different brain areas, potentially necessitating other alternate mechanisms to capture the genesis as well as regulation of these oscillations.
VII. CONCLUSION
Oscillations in the electrical activity of the brain have been recorded for close to a century, and the last few decades have seen extensive theoretical exploration of how they might influence cognitive function during behavior. We have recently proposed a regulatory mechanism for such oscillations in a spiking network model that captures their observed modulation in empirical data. Here, we explored the probable underlying mechanism in a simplified model of interactions between excitatory and inhibitory neural populations. In the past, empirical challenges in independently and precisely manipulating brain oscillations have hampered progress in testing theoretical ideas. However, the recent technical advances will hopefully allow some of these ideas to be tested in alert brains. Nonetheless, the related theoretical ideas and models could inspire novel coding and communication strategies in engineered systems.
Acknowledgments
This work was supported in part by the National Eye Institutes under Grant 5T32EY020503-03, the Howard Hughes Medical Institute, and the U.S. Office of Naval Research under Grant N000014-10-1-0072.
Biographies

Monika P. Jadi received the B.E. degree in electronics and power engineering from the National Institute of Technology, Nagpur, India, in 1995, the M.S. degree in electrical engineering from the University of Missouri, Rolla, MO, USA, in 1997, and the Ph.D. degree in biomedical engineering from the University of Southern California, Los Angeles, CA, USA, in 2010.
From 1995 to 1997, she worked as a Research and Teaching Assistant at the University of Missouri. From 1997 to 2004, she worked as a Senior Staff Engineer at Motorola, contributing to the architecture and development of real-time software for paging and cellular base stations. From 2004 to 2010, she worked as a Research and Teaching Assistant with the Department of Biomedical Engineering, University of Southern California. She is currently a Postdoctoral Fellow in the laboratory of Terrence Sejnowski at the Salk Institute for Biological Sciences, La Jolla, CA, USA. Her broad research interest includes neural computation at various levels in the brain from the synapse, to single neuron to networks of neurons. She has studied the contribution of inhibitory neurons in the brain to single-neuron computation as well as oscillatory dynamics in neural networks.
Dr. Jadi has been a recipient of the Dean’s Fellowship at the University of Missouri, the Women in Science and Engineering Fellowship at the University of Southern California, and the National Eye Institute Training Fellowship at the Salk Institute. She has been a member of the Society for Neuroscience since 2004.

Terrence J. Sejnowski (Fellow, IEEE) received the B.S. degree in physics from Case Western Reserve University, Cleveland, OH, USA, in 1968 and the Ph.D. degree in physics from Princeton University, Princeton, NJ, USA, in 1978.
In 1982, he joined the faculty of the Department of Biophysics at Johns Hopkins University, Baltimore, MD, USA, and in 1989 moved to La Jolla, CA, USA. He is an Investigator with the Howard Hughes Medical Institute and a Professor at The Salk Institute for Biological Studies, La Jolla, CA, USA, where he directs the Computational Neurobiology Laboratory, and Professor of Biology at the University of California-San Diego, La Jolla, CA, USA. The long-range goal of his research is to build linking principles from brain to behavior using computational models. This goal is being pursued with a combination of theoretical and experimental approaches at several levels of investigation ranging from the biophysical level to the systems level. The issues addressed by this research include how sensory information is represented in the visual cortex.
Dr. Sejnowski is one of only 12 living scientists in all three of the National Academies: the Academy of Sciences, the Academy of Engineering, and the Institute of Medicine. He received the IEEE Neural Networks Pioneer Award in 2002 and the IEEE Frank Rosenblatt Award in 2013.
APPENDIX A
RESPONSE FUNCTIONS OF NEURONAL POPULATIONS
The response function for each subpopulation (GE and GI) represents the proportions of E/I cells firing for a given level of input activity x. The different response functions used for the simulations were sigmoidal:
piecewise power law:
piecewise linear:
| (3) |
In (3), τE/I is the threshold level of net input below which the value of the response function is 0. The slopes mE/I reflect the different rates at which E and I population response changes as a function of the input.
APPENDIX B
LIMIT CYCLE OSCILLATIONS IN A TWO-POPULATION NETWORK MODEL
By examining eigenvalues of the linearized system and using other analytical criteria, previous works have explored the parameter conditions under which such a network can exhibit nonlinear phenomena such as hysteresis and stable limit cycles [46]. They predict that when the network is in the ISN regime, it can exhibit stable oscillations over a range of inputs (iE and iI). For sigmoid response functions, such as the logistic function shown in (3), transition of the model network from stable nonoscillatory behavior to stable limit cycle oscillations has been mapped previously [56]-[58]. Here, we restate the basic results and derive approximate analytical functions showing the dependence of stable limit cycle frequency and power on response function shapes and hence the inputs.
The Jacobian or the linearization matrix of the model network [described by (1) and (2)] in the ISN regime is given by [53], [56]
| (4) |
where
The eigenvalues of the Jacobian J are the solution λ to the following equation, known as the characteristic equation:
| (5) |
Solving (4) and (5) gives the eigenvalues λ of the ISN in terms of the network parameters [53] as described in
where
| (6) |
When the ISN is operating in the positive slope region of E and I nullclines [drE/dt = 0 and drI/dt = 0 curves in Fig. 3(a)], and WEE is sufficiently large, the real part of eigenvalues [see (6)] can transition from negative to positive values in an input-dependent fashion. This happens when the response functions GE and GI are nonlinear, and, hence, their slopes (sE and sI) vary with the inputs (iE and iI). It can be shown that by meeting additional criteria [56], [68], the network can transition to stable oscillations [56], [58]. This transition can occur in more than one way depending on how the two inputs are varied. A transition, known as supercritical Andronov–Hopf bifurcation, occurs when the dynamics of the model network change from a stable equilibrium to stable oscillations via a pair of purely imaginary eigenvalues as described in
| (7) |
The strength of the network inputs at which the transition occurs (σ = 0) known point. is as a the bifurcation For network with fixed connectivity, the bifurcation is determined by the slope of the response function at a given level of input [(6) and (7)]. The change in the slope of response function with input depends on how E and I firing rates vary with the network inputs.
1) Modulation of E and I Activity by the Network Input
The steady-state activity of the E and I population in our rate model in the ISN regime can be described as a function of the input to the two populations [53]
where
| (8) |
Equation (8) indicates that, when the inputs to the two population are co-modulated, the extent of modulation of E and I population activity is determined by the balance of inputs. The criteria in (8) for modulation of the E and I activities can be restated as follows:
| (9) |
2) Modulation of the Slopes of Response Functions by the Network Input
In the ISN regime, input to the E population facilitates/increases both the E and I firing rates, and input to the I population suppresses/decreases both firing rates [see (8)]. If the response function G is nonlinear, then the slope will vary independently with the inputs to the two populations in the following way: superlinear portion of GE/I:
sublinear portion of GE/I:
| (10) |
3) Power of Oscillations
When a nonlinear system such as the firing rate E–I model goes from steady-state activity to small amplitude oscillations through supercritical Andronov–Hopf bifurcation, it can be shown that the amplitude of oscillations depends on σ in (6) and a scaling term a that depends on the system parameters [68]
or
| (11) |
Since the power of an oscillating signal is proportional to the square of its amplitude, our analysis in the firing rate model predicted that the power in the population oscillations depended approximately on σ [see (6)] and hence the slopes of the response functions
| (12) |
4) Frequency of Oscillations
The frequency of the oscillations that emerge via the set of conditions we explore here [see (7)] is accurately given by ω [see (6)] at the threshold level of input (iE or iI) or the bifurcation point [68]. For other levels of network input, the expression is corrected with an amplitude-dependent term [68]. Thus, the oscillation frequency (cycles per second) in our firing rate model was approximately given by
| (13) |
APPENDIX C
SIMULATION OF THE TWO-POPULATION MODEL
Simulation Parameters
Table 1 shows the parameter values used for generating the simulation data. Given the values of time constants, the connection weights were chosen such that the frequency of oscillations in the model was in the gamma range.
Table 1.
Canonical Model Parameters
| WEE | WIE | WEI | WII | τE(ms) | τI(ms) |
|---|---|---|---|---|---|
| 16 | 20 | 26 | I | 20 | 10 |
|
| |||||
| mE | mI | θ E | θ I | Response function (G) | |
|
| |||||
| 1 | 1 | 5 | 20 | Sigmoid | |
| .25 | 1 | Linear (E) | |||
| .005 | 12 | Power-law (I) | |||
Simulation Environment
The network was simulated using Matlab 2012a (The MathWorks, Natick, MA, USA).
Power Spectrum
Power spectral density of the average activity signal was estimated nonparametrically by calculating the discrete-time Fourier transform of the signal.
APPENDIX D
THEORETICAL ESTIMATION OF OSCILLATION POWER AND FREQUENCY
The estimate of mean firing rates was obtained by averaging over 200 ms of the simulation data. For sigmoid response function, the slope of response functions, as plotted in Fig. 4, was calculated from the mean rates using the relationship in
| (14) |
The estimate of slope along with the connection weights in the network was used to calculate the theoretical estimate of eigenvalues [see (6)] as well as the trends for frequency and power as per (19) and (13) [Fig. 1(b)]. For the choice of power law response function [see (3)], the slope of I response function, as plotted in Fig. 3(d), was estimated from the mean rates using the relation in
| (15) |
Footnotes
This paper describes mathematical models that explain how neuronal networks produce oscillations observed in the brain’s electrical activity and discusses the hypothesis that these oscillations are potentially important for coding and routing of information.
REFERENCES
- [1].Schneider G, Havenith MN, Nikolic D. Spatiotemporal structure in large neuronal networks detected from cross-correlation. Neural Comput. 2006 Oct;18:2387–2413. doi: 10.1162/neco.2006.18.10.2387. [DOI] [PubMed] [Google Scholar]
- [2].Nikolic D. Non-parametric detection of temporal order across pairwise measurements of time delays. J. Comput. Neurosci. 2007 Feb;22:5–19. doi: 10.1007/s10827-006-9441-7. [DOI] [PubMed] [Google Scholar]
- [3].Singer W. Synchronization of cortical activity and its putative role in information processing and learning. Annu. Rev. Physiol. 1993;55:349–374. doi: 10.1146/annurev.ph.55.030193.002025. [DOI] [PubMed] [Google Scholar]
- [4].Singer W, Gray CM. Visual feature integration and the temporal correlation hypothesis. Annu. Rev. Neurosci. 1995;18:555–586. doi: 10.1146/annurev.ne.18.030195.003011. [DOI] [PubMed] [Google Scholar]
- [5].Buzsaki G, Wang XJ. Mechanisms of gamma oscillations. Annu. Rev. Neurosci. 2012 Jul;35:203–225. doi: 10.1146/annurev-neuro-062111-150444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Uhlhaas PJ, Haenschel C, Nikolic D, Singer W. The role of oscillations and synchrony in cortical networks and their putative relevance for the pathophysiology of schizophrenia. Schizophr. Bull. 2008 Sep;34:927–943. doi: 10.1093/schbul/sbn062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Buzsáki G, Wang X-J. Mechanisms of gamma oscillations. Annu. Rev. Neurosci. 2012 Jan;35:203–225. doi: 10.1146/annurev-neuro-062111-150444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Pace-Schott EF, Hobson JA. The neurobiology of sleep: Genetics, cellular physiology and subcortical networks. Nature Rev. Neurosci. 2002 Aug;3:591–605. doi: 10.1038/nrn895. [DOI] [PubMed] [Google Scholar]
- [9].Buzsaki G. Theta oscillations in the hippocampus. Neuron. 2002;33:325–340. doi: 10.1016/s0896-6273(02)00586-x. [DOI] [PubMed] [Google Scholar]
- [10].Gevins A, Smith ME, McEvoy L, Yu D. High-resolution EEG mapping of cortical activation related to working memory: Effects of task difficulty, type of processing, and practice. Cerebral Cortex. 1997 Jun;7:374–385. doi: 10.1093/cercor/7.4.374. [DOI] [PubMed] [Google Scholar]
- [11].Womelsdorf T, Fries P. The role of neuronal synchronization in selective attention. Current Opinion Neurobiol. 2007 Apr;17:154–160. doi: 10.1016/j.conb.2007.02.002. [DOI] [PubMed] [Google Scholar]
- [12].Bartos M, Vida I, Jonas P. Synaptic mechanisms of synchronized gamma oscillations in inhibitory interneuron networks. Nature Rev. Neurosci. 2007 Jan;8:45–56. doi: 10.1038/nrn2044. [DOI] [PubMed] [Google Scholar]
- [13].Tallon-Baudry C, Bertrand O, Delpuech C, Permier J. Oscillatory gamma-band (30–70 Hz) activity induced by a visual search task in humans. J. Neurosci. 1997 Jan 15;17:722–734. doi: 10.1523/JNEUROSCI.17-02-00722.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Howard MW, Rizzuto DS, Caplan JB, Madsen JR, Lisman J, Aschenbrenner-Scheibe R, Schulze-Bonhage A, Kahana MJ. Gamma oscillations correlate with working memory load in humans. Cerebral Cortex. 2003 Dec;13:1369–1374. doi: 10.1093/cercor/bhg084. [DOI] [PubMed] [Google Scholar]
- [15].Eckhorn R, Obermueller A. Single neurons are differently involved in stimulus-specific oscillations in cat visual cortex. Exp. Brain Res. 1993;95:177–182. doi: 10.1007/BF00229667. [DOI] [PubMed] [Google Scholar]
- [16].Ray S, Ni AM, Maunsell JH. Strength of gamma rhythm depends on normalization. PLoS Biol. 2013 Feb;11:e1001477. doi: 10.1371/journal.pbio.1001477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Lewis DA, Hashimoto T, Volk DW. Cortical inhibitory neurons and schizophrenia. Nature Rev. Neurosci. 2005 Apr;6:312–324. doi: 10.1038/nrn1648. [DOI] [PubMed] [Google Scholar]
- [18].Orekhova EV, Stroganova TA, Nygren G, Tsetlin MM, Posikera IN, Gillberg C, Elam M. Excess of high frequency electroencephalogram oscillations in boys with autism. Biol. Psychiatry. 2007 Nov;62:1022–1029. doi: 10.1016/j.biopsych.2006.12.029. [DOI] [PubMed] [Google Scholar]
- [19].Heim S, Friedman JT, Keil A, Benasich AA. Reduced sensory oscillatory activity during rapid auditory processing as a correlate of language-learning impairment. J. Neurolinguist. 2011 Sep;24:539–555. doi: 10.1016/j.jneuroling.2010.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Gou Z, Choudhury N, Benasich AA. Resting frontal gamma power at 16, 24, and 36 months predicts individual differences in language and cognition at 4 and 5 years. Behav. Brain Res. 2011 Jul;220:263–270. doi: 10.1016/j.bbr.2011.01.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Jia X, Smith MA, Kohn A. Stimulus selectivity and spatial coherence of gamma components of the local field potential. J. Neurosci. 2011 Jun;31:9390–9403. doi: 10.1523/JNEUROSCI.0645-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Tiesinga P, Sejnowski TJ. Cortical enlightenment: Are attentional gamma oscillations driven by ING or PING? Neuron. 2009 Sep;63:727–732. doi: 10.1016/j.neuron.2009.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Buzsáki G. Rhythms of the Brain. Oxford Univ. Press; Oxford, U.K.: 2011. [Google Scholar]
- [24].Fries P, Nikolic D, Singer W. The gamma cycle. Trends Neurosci. 2007 Jul;30:309–316. doi: 10.1016/j.tins.2007.05.005. [DOI] [PubMed] [Google Scholar]
- [25].Salinas E, Sejnowski TJ. Correlated neuronal activity and the flow of neural information. Nature Rev. Neurosci. 2001 Aug;2:539–550. doi: 10.1038/35086012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Akam T, Kullmann DM. Oscillatory multiplexing of population codes for selective communication in the mammalian brain. Nature Rev. Neurosci. 2014 Feb;15:111–122. doi: 10.1038/nrn3668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Buzsáki G, Chrobak JJ. Temporal structure in spatially organized neuronal ensembles: A role for interneuronal networks. Current Opinion Neurobiol. 1995 Aug;5:504–510. doi: 10.1016/0959-4388(95)80012-3. [DOI] [PubMed] [Google Scholar]
- [28].O’Keefe J, Recce ML. Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus. 1993 Jul;3:317–330. doi: 10.1002/hipo.450030307. [DOI] [PubMed] [Google Scholar]
- [29].Wilson MA, McNaughton BL. Dynamics of the hippocampal ensemble code for space. Science. 1993 Aug;261:1055–1058. doi: 10.1126/science.8351520. [DOI] [PubMed] [Google Scholar]
- [30].Buzsaki G. Theta rhythm of navigation: Link between path integration and landmark navigation, episodic and semantic memory. Hippocampus. 2005;15:827–840. doi: 10.1002/hipo.20113. [DOI] [PubMed] [Google Scholar]
- [31].Konig P, Engel AK, Roelfsema PR, Singer W. How precise is neuronal synchronization? Neural Comput. 1995 May;7:469–485. doi: 10.1162/neco.1995.7.3.469. [DOI] [PubMed] [Google Scholar]
- [32].Gray CM, König P, Engel AK, Singer W. Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties. Nature. 1989 Mar;338:334–337. doi: 10.1038/338334a0. [DOI] [PubMed] [Google Scholar]
- [33].Gray CM, Singer W. Stimulus-specific neuronal oscillations in orientation columns of cat visual cortex. Proc. Nat. Acad. Sci. USA. 1989 Mar;86:1698–1702. doi: 10.1073/pnas.86.5.1698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Juergens E, Guettler A, Eckhorn R. Visual stimulation elicits locked and induced gamma oscillations in monkey intracortical- and EEG-potentials, but not in human EEG. Exp. Brain Res. 1999 Nov;129:247–259. doi: 10.1007/s002210050895. [DOI] [PubMed] [Google Scholar]
- [35].Neuenschwander S, Varela FJ. Visually triggered neuronal oscillations in the pigeon: An autocorrelation study of tectal activity. Eur. J. Neurosci. 1993 Jul;5:870–881. doi: 10.1111/j.1460-9568.1993.tb00939.x. [DOI] [PubMed] [Google Scholar]
- [36].Gregoriou GG, Gotts SJ, Zhou H, Desimone R. High-frequency, long-range coupling between prefrontal and visual cortex during attention. Science. 2009 May;324:1207–1210. doi: 10.1126/science.1171402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Ray S, Maunsell JHR. Differences in gamma frequencies across visual cortex restrict their possible use in computation. Neuron. 2010 Sep;67:885–896. doi: 10.1016/j.neuron.2010.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Whittington MA, Traub RD, Jefferys JG. Synchronized oscillations in interneuron networks driven by metabotropic glutamate receptor activation. Nature. 1995 Feb;373:612–615. doi: 10.1038/373612a0. [DOI] [PubMed] [Google Scholar]
- [39].Traub RD, Whittington MA, Stanford IM, Jefferys JG. A mechanism for generation of long-range synchronous fast oscillations in the cortex. Nature. 1996 Oct;383:621–624. doi: 10.1038/383621a0. [DOI] [PubMed] [Google Scholar]
- [40].Cardin JA, Carlén M, Meletis K, Knoblich U, Zhang F, Deisseroth K, Tsai L-H, Moore CI. Driving fast-spiking cells induces gamma rhythm and controls sensory responses. Nature. 2009 Jun;459:663–667. doi: 10.1038/nature08002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Sohal VS, Zhang F, Yizhar O, Deisseroth K. Parvalbumin neurons and gamma rhythms enhance cortical circuit performance. Nature. 2009 Jun;459:698–702. doi: 10.1038/nature07991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Brunel N. Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J. Comput. Neurosci. 2000 May-Jun;8:183–208. doi: 10.1023/a:1008925309027. [DOI] [PubMed] [Google Scholar]
- [43].Chalk M, Herrero JL, Gieselmann MA, Delicato LS, Gotthardt S, Thiele A. Attention reduces stimulus-driven gamma frequency oscillations and spike field coherence in V1. Neuron. 2010 Apr;66:114–125. doi: 10.1016/j.neuron.2010.03.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Gieselmann MA, Thiele A. Comparison of spatial integration and surround suppression characteristics in spiking activity and the local field potential in macaque V1. Eur. J. Neurosci. 2008 Aug;28:447–459. doi: 10.1111/j.1460-9568.2008.06358.x. [DOI] [PubMed] [Google Scholar]
- [45].Brunel N, Wang X-J. What determines the frequency of fast network oscillations with irregular neural discharges? I. Synaptic dynamics and excitation-inhibition balance. J. Neurophysiol. 2003 Jul;90:415–430. doi: 10.1152/jn.01095.2002. [DOI] [PubMed] [Google Scholar]
- [46].Wilson HR, Cowan JD. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys. J. 1972 Jan;12:1–24. doi: 10.1016/S0006-3495(72)86068-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Wallace E, Benayoun M, van Drongelen W, Cowan JD. Emergent oscillations in networks of stochastic spiking neurons. PLoS ONE. 2011 Jan;6:e14804. doi: 10.1371/journal.pone.0014804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Kang K, Shelley M, Henrie JA, Shapley R. LFP spectral peaks in V1 cortex: Network resonance and cortico-cortical feedback. J. Comput. Neurosci. 2010 Dec;29:495–507. doi: 10.1007/s10827-009-0190-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Bressloff PC. Metastable states and quasicycles in a stochastic Wilson-Cowan model of neuronal population dynamics. Phys. Rev. E, Stat. Nonlinear Soft Matter Phys. 2010 Nov;82:051903. doi: 10.1103/PhysRevE.82.051903. [DOI] [PubMed] [Google Scholar]
- [50].Wang XJ, Buzsáki G. Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model. J. Neurosci. 1996 Oct;16:6402–6413. doi: 10.1523/JNEUROSCI.16-20-06402.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Jia X, Tanabe S, Kohn A. Gamma and the coordination of spiking activity in early visual cortex. Neuron. 2013 Feb;77:762–774. doi: 10.1016/j.neuron.2012.12.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Engelhard B, Ozeri N, Israel Z, Bergman H, Vaadia E. Inducing gamma oscillations and precise spike synchrony by operant conditioning via brain-machine interface. Neuron. 2013 Jan;77:361–375. doi: 10.1016/j.neuron.2012.11.015. [DOI] [PubMed] [Google Scholar]
- [53].Tsodyks MV, Skaggs WE, Sejnowski TJ, McNaughton BL. Paradoxical effects of external modulation of inhibitory interneurons. J. Neurosci. 1997 Jun;17:4382–4388. doi: 10.1523/JNEUROSCI.17-11-04382.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Ozeki H, Finn IM, Schaffer ES, Miller KD, Ferster D. Inhibitory stabilization of the cortical network underlies visual surround suppression. Neuron. 2009 May;62:578–592. doi: 10.1016/j.neuron.2009.03.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Jadi MP, Sejnowski TJ. Cortical oscillations arise from contextual interactions that regulate sparse coding. Proc. Nat. Acad. Sci. USA. 2014 doi: 10.1073/pnas.1405300111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Ermentrout GB, Cowan JD. Temporal oscillations in neuronal nets. J. Math. Biol. 1979 Apr;7:265–280. doi: 10.1007/BF00275728. [DOI] [PubMed] [Google Scholar]
- [57].Borisyuk RM, Kirillov AB. Bifurcation analysis of a neural network model. Biol. Cybern. 1992 Jan;66:319–325. doi: 10.1007/BF00203668. [DOI] [PubMed] [Google Scholar]
- [58].Hoppensteadt FC, Izhikevich EM. Weakly Connected Neural Networks. Springer-Verlag; New York, NY, USA: 1997. [Google Scholar]
- [59].Ermentrout GB. Neural networks as spatio-temporal pattern forming systems. Rep. Progr. Phys. 1998;61:353–430. [Google Scholar]
- [60].Priebe NJ, Mechler F, Carandini M, Ferster D. The contribution of spike threshold to the dichotomy of cortical simple and complex cells. Nature Neurosci. 2004 Oct;7:1113–1122. doi: 10.1038/nn1310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Carandini M, Heeger DJ, Movshon JA. Linearity and normalization in simple cells of the macaque primary visual cortex. J. Neurosci. 1997 Nov;17:8621–8644. doi: 10.1523/JNEUROSCI.17-21-08621.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Nowak LG, Azouz R, Sanchez-Vives MV, Gray CM, McCormick DA. Electrophysiological classes of cat primary visual cortical neurons in vivo as revealed by quantitative analyses. J. Neurophysiol. 2003 Mar;89:1541–1566. doi: 10.1152/jn.00580.2002. [DOI] [PubMed] [Google Scholar]
- [63].Cardin JA, Palmer LA, Contreras D. Stimulus feature selectivity in excitatory and inhibitory neurons in primary visual cortex. J. Neurosci. 2007 Sep;27:10333–10344. doi: 10.1523/JNEUROSCI.1692-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Adesnik H, Bruns W, Taniguchi H, Huang ZJ, Scanziani M. A neural circuit for spatial summation in visual cortex. Nature. 2012 Oct;490:226–231. doi: 10.1038/nature11526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Ray S, Maunsell JHR. Different origins of gamma rhythm and high-gamma activity in macaque visual cortex. PLoS Biol. 2011 Apr;9:e1000610. doi: 10.1371/journal.pbio.1000610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Borgers C, Kopell N. Synchronization in networks of excitatory and inhibitory neurons with sparse, random connectivity. Neural Comput. 2003 Mar;15:509–538. doi: 10.1162/089976603321192059. [DOI] [PubMed] [Google Scholar]
- [67].Jia X, Xing D, Kohn A. No consistent relationship between gamma power and peak frequency in macaque primary visual cortex. J. Neurosci. 2013 Jan;33:17–25. doi: 10.1523/JNEUROSCI.1687-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Izhikevich EM. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting. 1st ed. MIT Press; Cambridge, MA, USA: 2006. [Google Scholar]