Abstract
Objective
Although recent statistical and computational developments allow for the empirical testing of psychological theories in ways not previously possible, one particularly vexing challenge remains: how to optimally model the prospective, reciprocal relations between two constructs as they developmentally unfold over time. Several analytic methods currently exist that attempt to model these types of relations, and each approach is successful to varying degrees. However, none provide the unambiguous separation of between-person and within-person components of stability and change over time, components that are often hypothesized to exist in the psychological sciences. The goal of our paper is to propose and demonstrate a novel extension of the multivariate latent curve model to allow for the disaggregation of these effects.
Method
We begin with a review of the standard latent curve models and describe how these primarily capture between-person differences in change. We then extend this model to allow for regression structures among the time-specific residuals to capture within-person differences in change.
Results
We demonstrate this model using an artificial data set generated to mimic the developmental relation between alcohol use and depressive symptomatology spanning five repeated measures.
Conclusions
We obtain a specificity of results from the proposed analytic strategy that are not available from other existing methodologies. We conclude with potential limitations of our approach and directions for future research.
Keywords: Latent curve models, growth models, structural equation modeling, disaggregation of effects
The past decade has given rise to remarkable developments in both the substantive theories that underlie the evaluation and treatment of psychopathology and in the rigorous statistical analysis of repeated measures data. Indeed, there is a broad class of research hypotheses that can be empirically evaluated in ways not possible even a few years ago. Despite the myriad of recent advances, one particularly salient challenge remains: the ability to model the complex dynamic relations that link two or more constructs together over time. Within the clinical sciences it is often of key interest to evaluate precisely how a set of behaviors jointly unfolds over time and how these relations vary dynamically both within and across individuals. This is of particular interest when evaluating prevention or intervention programs that are designed to causally induce behavioral change over time. Despite the importance of these theoretical questions, many existing analytic methods are not well suited to provide comprehensive empirical tests of the research hypotheses under study.
As we will explore in greater detail below, many statistical modeling approaches commonly used to study repeated measures data over time focus on between-person differences in stability and change. However, virtually all of our theories in the psychological sciences posit either strictly within-person processes, or joint within- and between-person processes (e.g., Curran & Bauer, 2011; Curran, Lee, Howard, Lane, & MacCallum, 2012). Omitting either of these two components from a statistical model of individual change results in a disjoint between our theoretical models and our statistical models, and this in turn undermines the validity of our empirically-based inferences (e.g., Baltes, Reese, & Nesselroade, 1977; Curran & Willoughby, 2003; Wohlwill, 1991). We believe that there currently exists such a disjoint between many theories that guide the clinical sciences and the statistical models we use to empirically evaluate these theories. The goal of our paper is to explore both the theoretical and statistical issues that relate to the disaggregation of within- and between-person processes in stability and change over time, particularly as they relate to the study of the determinants and sequelae of psychopathological behavior.
We begin with an exploration of psychological theories of individual change. We then review several existing analytic methods that are widely used for modeling two or more constructs over time, particularly as applied within the clinical sciences. Next, we propose a novel method for simultaneously estimating within- and between-person reciprocal processes using a single integrated analytic framework and highlight potential advantages of this approach in psychopathology-related research settings. Finally, we demonstrate this model using artificial data that reflects a real-world developmental process and we conclude with recommendations for practice and directions for future research.
Psychological Theories of Change
Nearly all theories within the psychological sciences posit either strictly within-person processes, or joint within- and between-person processes underlying stability and change in behavior over time (e.g., Curran & Bauer, 2011). Consider the complex relation between stress, negative affect, and substance use (e.g., Hussong, Jones, Stein, Baucom, & Boeding, 2011). Negative reinforcement models of alcohol use theorize in part that an individual consumes alcohol in order to reduce depression and anxiety that result from the presence of uncontrollable life-stressful events in the environment. However, there are two key components of this dynamic relation that must simultaneously be considered.
First, we might hypothesize that, on average, individuals who experience higher levels of negative affect tend to consume greater quantities of alcohol to reduce the unpleasant feelings of depression and anxiety. Similarly, individuals who report systematic increases in negative affect over time are more likely to also report systematic increases in substance use. These are between-person effects: overall levels and smoothed rates of change over time in depression and alcohol use are characteristics of the individual, and these individually-varying characteristics are thought to covary in potentially meaningful ways.
However, at the same time there is a more subtle component of change that is unique both to the individual and to specific points in time. Thus, in addition to the hypothesized between-person relations, it might also be predicted that if an individual experiences higher levels of depression relative to her underlying level of depression at one point in time, she is more likely to consume greater quantities of alcohol relative to her underlying level of alcohol use at a subsequent point in time. These are within-person effects: time-anchored elevations relative to an underlying person-specific level at one time point may be meaningfully related to time-anchored elevations relative to an underlying person-specific level at a later time point. These time-specific relations are distinctly different from the between-person effects hypothesized at the level of the individual.
Further, implicit in the theoretical motivation to disaggregate the levels of influence over time is the potential existence of reciprocal effects between two constructs such that earlier changes in one influences later changes in the other, and vice versa. Indeed, developmental theories commonly posit reciprocal effects between two or more constructs. For example, Patterson’s coercion model posits bidirectional relations between children’s externalizing behavior problems and parenting behavior (Patterson, Reid, & Dishion, 1992; Patterson & Yoerger, 2002); and negative reinforcement models of substance use describe reciprocal relations between earlier negative affect predicting later substance use, and earlier substance use predicting later negative affect (e.g., Hussong, Hicks, Levy, & Curran, 2001). An added complication is that theoretical models may also suggest that the magnitude of these reciprocal relations systematically vary as a function of time (Hartup, 1978; Scarr & McCartney, 1983). In other words, the within-person reciprocal relations between two constructs may become systematically stronger or weaker with the passage of time or with exposure to treatment.
In sum, many contemporary theories in the clinical sciences posit complex reciprocal relations between multiple constructs at both within-person and between-person levels of influence, and these relations may vary in magnitude or form across time or over group. However, many traditional statistical models commonly used in practice are restricted to the estimation of between-person relations (e.g., Curran et al., 2012; Curran & Bauer, 2011) and thus may at times provide less than optimal empirical tests of our theoretically-derived research hypotheses. We must have the tools available to rigorously evaluate the hypothesized across-construct reciprocal relations both at the level of the individual and at the level of individual at specific points in time in order to minimize the disjoint between our theoretical and statistical models. Developing such a model is our goal here.
Traditional Latent Curve Models of Stability and Change
Our proposed analytic approach is based on an extension of the latent curve model (LCM). The LCM draws on the strength of the structural equation model (SEM) to estimate individual variability in stability and change over time. Although there are many important historical lines of development that ultimately led to the LCM (see Bollen, 2007, for a review), this was first formally proposed by Meredith and Tisak (1984, 1990) and expanded on by many others (e.g., Browne, 1993; Browne & du Toit, 1991; McArdle, 1988, 1989; McArdle & Epstein, 1987; Muthén, 2001, 2002; Muthén & Curran, 1997).
The LCM incorporates the repeated measures of a construct as multiple indicators on one or more underlying latent curve (or growth) factors. The conceptual premise is elegant: we are interested in using the observed time-specific measures to infer the existence of an underlying and continuous but unobserved latent growth process. The latent factors capture inter-individual differences in intra-individual stability and change over time. These might be of interest in their own right, or more typically they are regressed on one or more predictors in an attempt to model the individual variability in the trajectories. There are a large number of alternative specifications that the LCM can take; see Bollen and Curran (2006) and McArdle (2009) for general discussions of the LCM and Curran and Hussong (2003) for a review of the use of LCMs within psychopathology research.
The unconditional univariate LCM
The most basic LCM is fitted to a single construct and includes no exogenous predictor variables; this is called a univariate unconditional LCM. Say we were interested in studying developmental trajectories of adolescent alcohol use. We define our repeatedly measured outcome alcohol use as yit to represent the sample realization of construct y for individual i (where i = 1, 2,…, N) at time point t (where t = 1, 2,…,T). We can link our set of repeated measures to the passage of time through the definition of some form of trajectory. A linear trajectory for yit is given as
| (1) |
where αyi and βyi represent the intercept and linear slope unique to individual i, respectively; λt is the numerical measure of time at assessment t (where t = 0,1,…, T−1)1; and εyit represents the individual- and time-specific deviation that is typically assumed indicating that the residuals are normally distributed and obtain a unique variance at each time point t.
An important characteristic of the LCM is that the individually-varying intercept and slope values are defined as random variables which can be expressed as
| (2) |
where μyα and μyβ are the mean intercept and slope, respectively, and ζyαi and ζyβi are individual deviations around these mean values. This model is presented in Figure 1 for T=5. Equation (1) is sometimes called the measurement equation, and Equation (2) the structural equation; the latter can be substituted into the former to define the reduced-form expression of the model, but we do not show this here; see Bollen and Curran (2006, Equation 3.19).
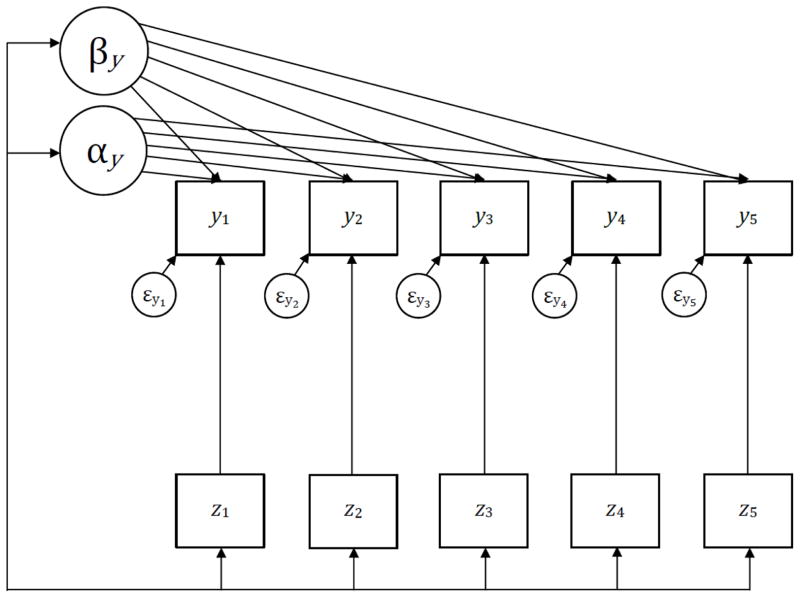
Figure 1.
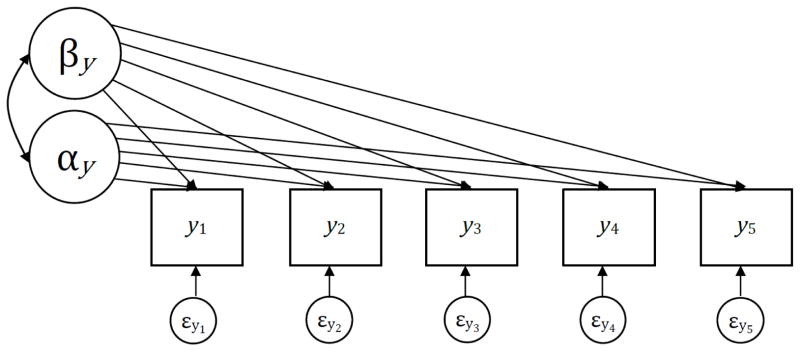
Univariate unconditional linear latent curve model for five repeated measures.
note: αy is the intercept factor with all factor loadings set to 1.0; βy is the linear slope factor with factor loadings set to 0, 1, 2, 3, 4.
We can examine two types of effects in this model: the fixed effects and the random effects. The fixed effects are the means of the intercept and slope factor and are defined as
| (3) |
and represent the overall starting point and rate of change for the entire sample. The random effects are the variances of the deviation terms; more specifically:
| (4) |
where ψyαyα represents the variance of the intercepts, ψyβyβ the variance of the slopes, and ψyβyα the covariance between intercepts and slopes. Larger values of these random effects indicate greater between-person variability in the growth parameters such that some individuals may start higher versus lower and some may increase more steeply versus less steeply.
We can also consider the covariance structure of the individual- and time-specific residuals. In virtually all applications of the LCM in practice, the covariance structure among these residuals is assumed to be a diagonal matrix with values of zero on the off-diagonal. This reflects that the residual from each assessment period is defined by some variance, but the residuals are independent across time. An example of the covariance matrix among residuals for T=3 is given as
| (5) |
where the diagonal elements represent the time-specific residual variance. This matrix can be further restricted by fixing the diagonal elements to be equal such that for all t, but this is just a simplifying condition of homoscedasticity with respect to time.
The reason that we are able to assume that the residuals are uncorrelated over time is that observed covariation among the repeated measures is modeled via the underlying latent curve factors. In other words, the covariance structure of the random effects shown in Equation (4) impose a correlational structure among the repeated measures (see, e.g., Bollen & Curran, 2006, Equation 2.41). The veracity of this assumption is in large part a function of the temporal distance between the repeated measures. The longer the elapsed time between assessment periods, the less likely the residuals will covary over time given that these relations decay towards zero.
Although not commonly a part of LCMs applied in panel data, it is possible that there is some remaining correlation among time-adjacent residuals net the underlying latent factors, particularly if the assessment periods are closely spaced in time. For example, we can expand Equation (5) to allow for time-adjacent correlations such that
| (6) |
where represents the variance and σy represents the time-adjacent covariance. This is just one type of residual covariance matrix, and many other options exist (e.g., Grimm & Widaman, 2010; Kwok, West, & Green, 2007; Rovine & Molenaar, 2000). We will return to the structure of these residual covariance matrices momentarily.
The conditional univariate LCM
The model defined above is sometimes called unconditional because there are no predictors of growth; we are only building a model of fixed and random effects for the set of repeated measures as a function of time. However, this unconditional LCM can easily be extended to include one or more predictors of growth. Because the predictors of growth are between-person characteristics (e.g., gender, ethnicity, treatment group membership), we refer to these as time-invariant covariates (TICs). For example, the intercept and and linear slope equations from the univariate LCM could be expanded to include two TICs denoted x1i and x2i such that
| (7) |
where the four γ parameters serve to shift the conditional means of the latent factors per one-unit shift in the exogenous covariates. This model is presented in Figure 2.
Figure 2.
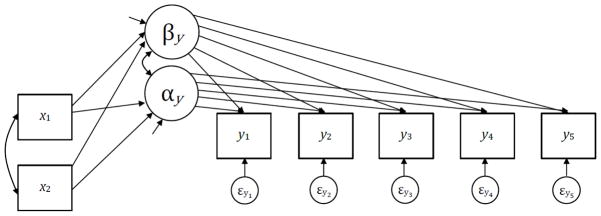
Univariate conditional linear latent curve model for five repeated measures with two exogenous predictors.
note: the single-headed arrows for each growth factor reflect that the factor variances are disturbances given the joint influence of the two exogenous predictors.
Continuing with our hypothetical example, these predictors might represent binary measures of gender and treatment group membership and our goal is to test for systematic differences in the trajectories of alcohol use as a function of these two subject characteristics. Important to our discussion here, these predictions are strictly between-person influences. That is, both the exogenous covariates and the trajectory scores are unique to the individual and are not linked to a specific point in time; this can most clearly be seen by the lack of subscript t denoting time in Equation (7). Thus, the LCM with TICs is only considering covariates that are invariant with respect to time. However, there are many situations in which we would want to include a predictor that itself varies with time; these are called time-varying covariates (TVCs).
The LCM with time-varying covariates
Just as we were able to model the random effects of the growth trajectories as a function of one or more TICs, it is possible to model the time-specific residuals as a function of one or more TVCs. To define this model we can expand Equation (1) to include a TVC denoted zit such that
| (8) |
where γyt represents the shift in the conditional mean of yit at time point t per one-unit change in zit above and beyond the influence of the underlying latent trajectories; an example of this model is presented in Figure 3. Here we show a contemporaneous relation between the TVC and the outcome, but this can easily be lagged in a variety of interesting ways (see, e.g., Curran, Muthén & Harford, 1998).
Figure 3.
Linear latent curve model for five repeated measures with unidirectional contemporaneous influences from a time-varying covariate.
Continuing with our hypothetical example, the TVC might be depressive symptomatology and we are evaluating the time-specific influence of depression on alcohol use net the impact of the underlying trajectories of alcohol use. This can be better seen with a simple rearrangement of Equation (8) such that
| (9) |
where the repeated measures are being deviated relative to the underlying latent trajectory (sometimes called de-trending) and are then regressed on the TVC. Estimation is not actually done in this two-step process, but this highlights the prediction of the outcome from the TVC above and beyond the influence of the underlying trajectory.
The regression of the outcome on the TVC provides a direct estimate of the time-specific, within-person component of the relation between yit and zit (Curran et al., 2012). Yet this comes at the (often significant) cost of omitting the between-person latent growth process that underlies the TVC. This is because we are not estimating a random trajectory process for the TVCs themselves; we are only allowing the numerical values of the TVC to vary with time but we are not formally structuring the TVCs as a function of the passage of time. However, we can reparameterize the LCM-TVC model to allow for the simultaneous estimation of latent growth curves for yit and zit; this is called the multivariate LCM.
The multivariate LCM
The multivariate (or parallel process) LCM incorporates a growth component for two or more repeated measures at the same time (e.g., McArdle, 1988, 1989); an example of this is presented in Figure 4. We do not present the equations for this model given the logical symmetry with those presented above (see Bollen & Curran, 2006, Chapter 7, for details). We continue to denote the repeated measures on the second construct as zit to represent the assessment of construct z for individual i at time point t. For example, our first set of repeated measures might assess alcohol use and our second set depressive symptomatology. The multivariate LCM would include both a measurement equation (Equation (1)) and a structural equation (Equation (2)) for the set of repeated measures on z. We simply change the subscripts to z in the prior equations to denote that these relate to a second construct of interest.
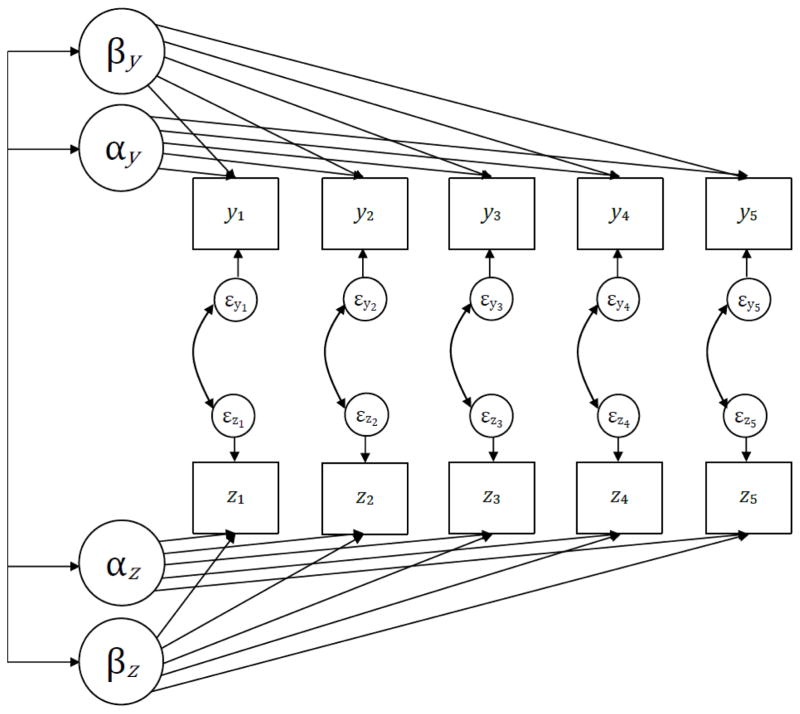
Figure 4.
Bivariate unconditional linear latent curve model for five repeated measures.
Of key interest in this multivariate model is the covariance structure among the set of latent factors. For example, the covariance structure for linear trajectories defined for both yit and zit is
| (10) |
where the diagonal elements represent the variances of the latent factors and the off-diagonal elements the covariances among latent factors.2 Time-invariant covariates can again be included just as they were before (e.g., Equation (7)), so we do not show these again here.
The covariance structure among the residuals is naturally more complicated within the multivariate LCM. Typically, residuals are not allowed to covary across-time, within construct (as shown in Equation (5)) but are allowed to covary within-time, across construct. This implies that the unexplained part of y at t=1 is linearly related to the unexplained part of z at t=1, and so on. More specifically,
| (11) |
where and represent the residual variance for yit and zit, respectively, and σzy represents the covariance between the residuals within each assessment period; these within-time covariances are represented by the curved two-headed arrows in Figure 4. Here we define these to be equal over time, but this restriction can be relaxed and tested (assuming the model remains identified; e.g., Bollen, 1989).
The multivariate LCM is a powerful analytic method for simultaneously examining the relation between two constructs over time and it has been used extensively in psychopathology-related work appearing in this very journal (e.g., Curran, Stice, & Chassin, 1997; Stice, Marti, Rohde, & Shaw, 2011; Teachman, Marker, & Smith-Janik, 2008). However, there is an important characteristic of this model of which we must be cognizant. As with the univariate LCM, the multivariate LCM is focused solely on between-person inferences when assessing stability and change over time. This can best be seen in the covariance structure among the latent factors shown in Equation (10). The diagonal elements (i.e., the variances of the factors) reflect between-person variability in the intercepts and slopes of the latent trajectories; the off-diagonal elements (i.e., the covariances among the factors) reflect the between-person linear relations among the factors. In other words, the intercepts and slopes of each construct are unique to the individual and are not a function of a specific point in time. More colloquially, each individual might be characterized by their gender, their ethnicity, their age, and their starting point and rate of change in depression and alcohol use.
Thus, the multivariate LCM provides a direct estimate of the between-person component of the relation between y and z (i.e., the relation assessed at the level of the trajectories), and the LCM-TVC provides a direct estimate of the within-person component of the unidirectional relation between y and z (i.e., the relation assessed net the trajectories), yet neither model contains simultaneous and reciprocal estimates for both. As such, the multivariate LCM and the LCM-TVC will not provide a full empirical test of a substantive theory that would posit both person-specific and time-specific developmental links between two constructs over time. We thus aspire to consider ways to simultaneously estimate both within-person (time-specific) relations and between-person (person-specific) relations for both constructs within a single model. Here we briefly describe one specific method that is most closely linked to our developments here: the auto-regressive latent trajectory model 3.
The auto-regressive latent trajectory model
The auto-regressive latent trajectory (ALT) model was first proposed by Curran and Bollen (2001) and more formally defined in Bollen and Curran (2004). The primary motivation for developing the ALT model was to combine elements of the latent curve portion of the multivariate LCM with the time-specific relations of the TVC model. The motivating focus was more on the combination of the growth process with time-specific components as opposed to disentangling within-person and between-person effects. One example of a bivariate ALT model is presented in Figure 5. Exogenous time-invariant covariates (e.g., treatment condition, gender) can be included as predictors of both the initial measures of each construct as well as the latent curve factors, although we do not show this in a path diagram here. The equations that define the ALT model are numerous and are detailed elsewhere (Bollen & Curran, 2004; Bollen & Zimmer, 2010; Curran & Bollen, 2001).
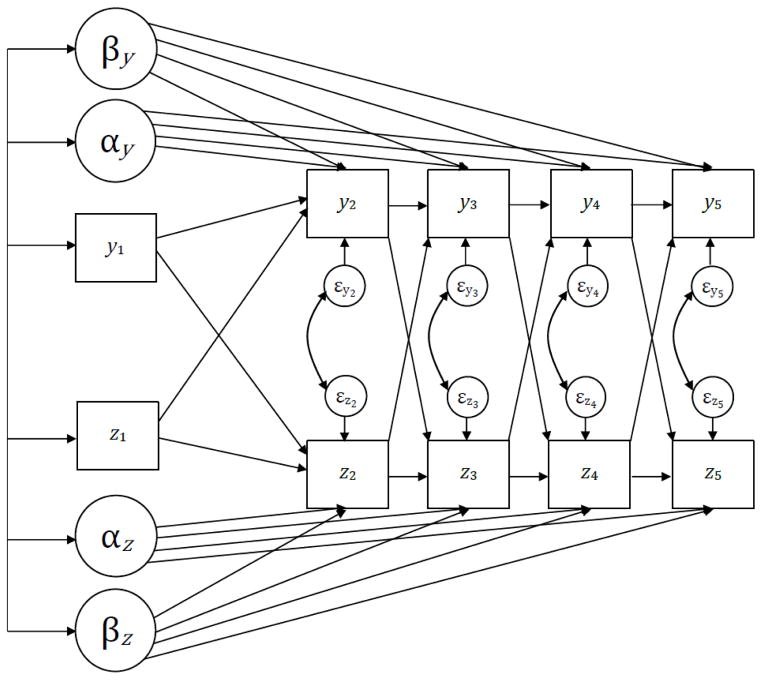
Figure 5.
Bivariate unconditional autoregressive latent trajectory model for five repeated measures.
The ALT model is a flexible analytic framework that has been applied in many types of research settings (e.g. Hussong et al., 2001; Morin, Maiaon, Marsh, Janosz & Nagengast, in press; Rodebaugh, Curran & Chambless, 2002; Zyphur, Chaturvedi & Arvey, 2008). However, as with any modeling strategy, the ALT model is not without its limitations (e.g., Delsing & Oud, 2008; Hamaker, 2005; Jongerling & Hamaker, 2011; Voelkle, 2008). Most important to our discussion here, the time-specific relations among the observed repeated measures are modeled at the level of the manifest variable itself. In other words, just as in the TVC model, the repeated measure of alcohol use is regressed directly on the repeated measure of depression and vice versa. This can be seen in the path diagram in Figure 5 in which the single-headed arrows both begin and end with an observed measure, thus reflecting the direct regression of one repeated measure on another. There are several specific consequences that result from the estimation of structural regressions among the observed repeated measures that might impact the utility of this model in practice.
Most importantly, the inclusion of the time-specific regressions among the repeated measures in both the ALT and LCM-TVC models will directly influence both the mean and covariance structure of the latent growth factors. For example, one would obtain a particular mean and covariance structure for the growth factors in an unconditional LCM, and would obtain a different mean and covariance structure for the growth factors in an LCM with TVCs; this is a natural consequence of the model parameterization and is the intended point of these models. Both the ALT and the LCM-TVC are positing that the set of repeated measures are a function of the joint contribution of the underlying latent growth factor and the time-specific influences of the TVCs. Thought another way, in the ALT model the repeated measures of one construct serve as mediators for the influence of the latent curves of that same construct on the indicators of the other construct. Because of these mediated influences, the ALT model does not provide a pure disaggregation of the between- and within-person relations over time.
If theory posits that the time-specific measures are structurally related over time (that is, if an earlier measure of one construct is believed to causally influence a later measure of another construct), then the ALT model or the LCM-TVC model is appropriate. However, if theory posits that the over-time relation between the two constructs consists of a unique between-person component and a unique within-person component, then an alternative model parameterization to the ALT and LCM-TVC is needed. It is admittedly asking much from a substantive theory to make a supposition at this level of detail, but it is an important distinction to make when choosing a specific statistical model to optimally test a specific research hypothesis. Indeed, appreciating that these types effect differ across modeling approaches might help us to better refine our theoretical models of interest.
The Latent Curve Model with Structured Residuals
Our goal for the remainder of the paper is to describe a novel parameterization of the latent curve model that provides a pure disaggregation of between-person and reciprocal, prospective within-person components of the relation between two constructs over time. Unlike the multivariate LCM, we will be able to simultaneously consider both person-specific and time-specific influences. Unlike the ALT model and the LCM with TVCs, the inclusion of the time-specific regressions will not influence the fixed-effect characteristics (e.g., the mean structure) of the underlying latent curve factors; thus the time-specific and person-specific components of change are cleanly separated from one another. To build this model we will begin with the standard multivariate LCM as a foundation for the estimation of between-person effects in the usual way. However, we will use an atypical parameterization of the SEM to impose a specific structure on the time-specific residuals of the observed repeated measures of both constructs. Because of this, we will refer to this particular parameterization as an LCM with structured residuals, or simply LCM-SR. Referring to the model in this way highlights that our proposed framework is a direct and logical expansion of the standard multivariate LCM and does not represent some wholly new analytic technique. Indeed, we will show that the standard univariate and multivariate LCMs are nested within their LCM-SR counterparts, thus allowing for a variety of likelihood ratio tests (LRTs) to evaluate relative improvement in model fit given increasing model complexity.
The univariate LCM with structured residuals
Recall that the measurement equation for the univariate LCM given in Equation (1) expressed yit as a weighted combination of the random intercept (αyi), random slope (βyi), and time-specific residual (εyit). Examining the residual more closely shows that this represents the deviation between the observed and model-implied repeated measures of yit. Simple rearrangement of Equation (1) highlights this further:
| (12) |
showing that the residual represents the deviation of the observed repeated measure from the underlying trajectory. As we described earlier, rarely are these residuals considered of substantive interest beyond defining the optimal covariance structure for a given set of data. However, when conceptualized as a time-specific estimate of the deviation between the observed repeated measure and the underlying trajectory, we can clearly see that the residual captures potentially interesting information about within-person processes of stability and change. We will capitalize on this extensively here.
More specifically, instead of allowing the residuals to covary in some unstructured way (as in Equation (6)), we can draw on the extensive literature from time series analysis and multilevel modeling to define the regression of a later residual on a prior residual. For example, for the residual defined in Equation (12), we can expand this as
| (13) |
where ρyy is the regression parameter and . In words, we are regressing the residual at time t on the residual at time t−1. This implies that the later residual is in part determined by the earlier residual above and beyond the influence of the latent curve factors.4 This model is presented in Figure 6.
Figure 6.
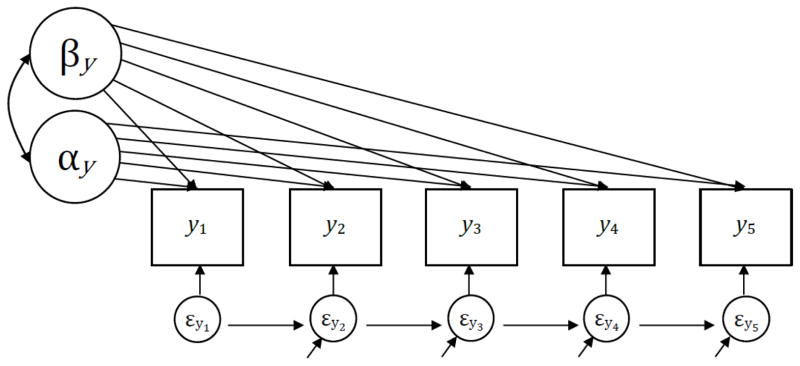
Univariate unconditional linear latent curve model with structured residuals for five repeated measures.
We refer to the model defined in Equations (12) and (13) as the univariate latent curve model with structured residuals, or the univariate LCM-SR. We stress that this particular univariate model is not a novel development and has been studied to varying degrees within the time series (Box & Jenkins, 1976; Dickey & Fuller, 1979; Lutkepohl & Saikkonen, 2000; Saikkonen & Lutkepohl, 2000), MLM (Chi & Reinsel, 1989; Diggle, 1988; Goldstein, Healey, & Rasbash, 1994; Hedeker & Gibbons, 2006), SEM (Hamaker, Dolan, & Molenaar, 2002; van Buuren, 1997), and LCM (Hamaker, 2005; Sivo, 2001; Sivo & Fan, 2008; Sivo, Fan, & Witta, 2005; Sivo & Wilson, 2000) frameworks. There are alternative terms, notation, and path diagrams used within different disciplines to describe this type of model; our intent is not to rename this model for the sake of renaming, but instead to allow us to move on to the multivariate model that has no such history in these types of frameworks.
As we described earlier, in the majority of LCM applications based on more traditional panel data (with assessments spaced by months or even years) the covariance structure among the repeated measures is frequently fully reproduced through the joint influence of the latent curve factors. As such, time-adjacent relations among residuals within a given construct are less often considered from a substantive perspective nor tend to be needed from an empirical one (with the important exception of daily diary or EMA-like designs where such influences are often required; e.g., Bolger, Davis & Rafaeli, 2003). However, there is far greater interest in these residual structures when moving from the univariate to the multivariate model in both panel and diary data designs. That is, there is often both substantive motivation and empirical support for examining how residuals are prospectively and bidirectionally related across two constructs, yet existing analytic methods are less well developed for estimating these types of relations. We allow for such cross-domain relations in the multivariate LCM-SR.
The multivariate LCM with structured residuals
Our goal is to parameterize a model that provides simultaneous estimates of person-specific, between-person processes and time-specific, within-person processes of the over-time relation between two constructs. We begin with the standard multivariate LCM we described earlier, but instead of estimating unstructured correlations among the residuals (as in Equation (11)) we will regress the residual at time t on that at time t−1 across the two constructs. More specifically, our residual structure is given as:
| (14) |
and
| (15) |
where
| (16) |
for T=3. We begin by equating the residual variances for t=2 and t=3 ( and ) but not the t=1 variances ( and ); this is because the t=1 residual variance is not conditioned on a prior measure whereas the latter measures are. In other words, the t=2 and t=3 residuals are themselves a residual given the auto- and cross-lagged regressions; in contrast, the t=1 residual is not expressed as a function of other predictors. Note also that we continue to allow for the across-construct residuals to covary within time assessment (i.e., σνzy1 and σνzy) because these are not temporally ordered as are the regressions of the later residual of one construct on the earlier residual of the other. This model is presented in Figure 7 for five repeated measures of each construct.
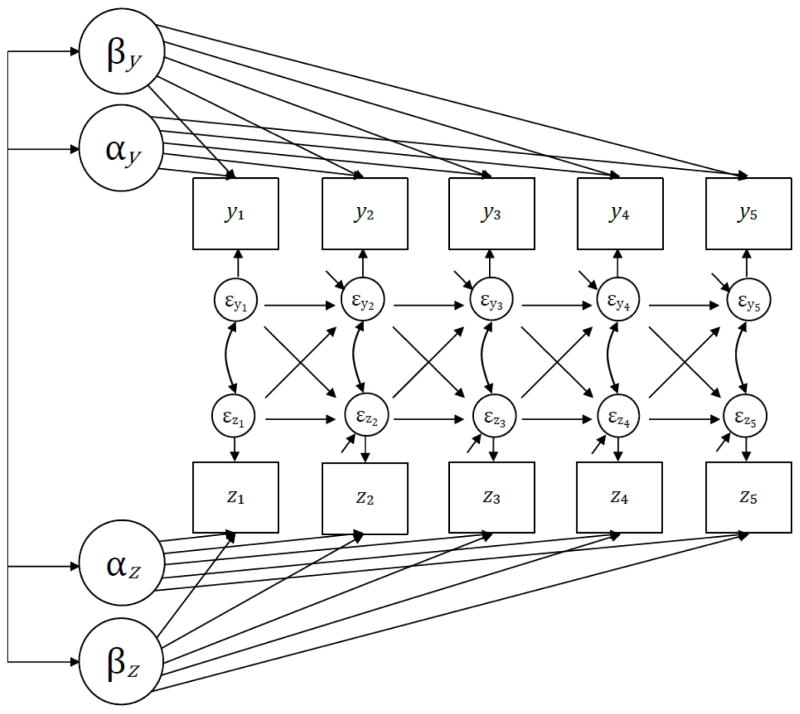
Figure 7.
Bivariate unconditional linear latent curve model with structured residuals for five repeated measures.
Although the structure of the covariance matrix from the LCM-SR in Equation (16) is similar in form to that of the standard multivariate LCM in Equation (11), the fundamental difference here is that Equation (16) represents the covariance matrix of residuals above and beyond not only the underlying latent curve factors but also the prior residuals within- and across-construct. More colloquially, the diagonal elements of this matrix are the residual variances of the residuals (excluding t=1) as a function of the four regression parameters ρyy, ρzz, ρyz, and ρzy. We can see how the multivariate LCM and LCM-SR are closely related in that if all four regression parameters are equal to zero, Equations (11) and (16) will be equal. The extent to which these matrices differ reflect the existence of the higher-order structure among the residuals, a structure that is omitted in the standard LCM.
Importantly, the inclusion of the regression structure among the residuals does not directly impact the fixed effects (i.e., means) of the latent curve factors. In other words, the mean of the latent intercept and slope are unchanged regardless of the inclusion or exclusion of the regressions among the residuals5. We view this as a distinct strength of the LCM-SR; namely, the mean structure of the repeated measures is modeled solely as a function of the latent curve factors whereas the covariance structure of the repeated measures is modeled jointly as a function of the latent curve factors and the structure imposed among the residuals. This is in direct contrast to the ALT model in which the time-specific regressions at the level of the observed variables (and not residuals) directly influences the means of the latent factors; this characteristic of the ALT has been seen as both an advantage (Bollen & Curran, 2004) and a disadvantage (Voelkle, 2008) depending upon the goals of the particular application at hand.
Finally, both the univariate and the multivariate LCM-SR can naturally be expanded to include time-invariant covariates such as gender, race, or treatment condition. As with the standard LCM, exogenous predictors can be binary, ordinal, or continuous, and interactive and non-linear effects can be estimated among two or more covariates (e.g., Curran, Bauer, & Willoughby, 2004). These exogenous predictors would be included in the structural equations for the latent curves in the usual way (e.g., as in Equation (7)), so we do not explicate this further here.
To summarize thus far, the multivariate LCM-SR is able to isolate the between-person and within-person components of the relation between two constructs over time. We believe the LCM-SR offers a unique method by which we can more rigorously evaluate bidirectional within-person relations in a way that is much more consistent with theory than is typically possible. Not only do we have unique estimates of the bidirectional and prospective influences of one construct on the other, but we can structure these relations in a variety of ways to test specific hypotheses about processes of stability and change. Next we briefly describe two of the more exciting possibilities: modeling heterogeneity in reciprocal relations over time and across group. We focus our discussion on the across-construct regressions, but all of our developments equally apply to the within-construct stabilities.
Modeling heterogeneity in reciprocal relations over time
The model we defined above assumes that the cross-domain residual regressions are equal over time.6 This is seen in that ρyz and ρzy are not indexed to denote a specific time interval. However, as we described earlier, many substantive theories within clinical psychology predict that the magnitude of the relation between two constructs changes over time. That is, two behaviors may become increasingly intertwined as children age, or a clinical intervention might be designed to “uncouple” two behaviors over time. We can explicitly test such relations in the LCM-SR in two ways.
First, we can simply remove the restriction that the cross-domain regressions are equal over time and instead allow them to take on any optimal value supported by the data. We can denote these regressions ρyzdδ and ρzydδ where dδ is simply a numerical identifier that denotes a specific adjacent pair of time points (δ = 0,1,…,T−1; e.g., d0 = 0 denotes the relation between t = 1 and t = 2, d1 = 1 denotes the relation between t=2 and t=3, and so on). Because the model in which the reciprocal relations are held equal over time is nested within this model in which they freely vary over time, we can conduct an LRT to determine if the model fit is impacted by the removal of the equality restriction over time. We will demonstrate this momentarily.
Second, we make a stronger hypothesis that the magnitude of the reciprocal relations do not simply vary in value over time, but that they are related in some systematic way with the passage of time. Thus, instead of allowing each cross-domain regression to take on any optimal unique value, we could impose a parametric constraint such that the value of the regression varies in a structured way. For example, say we hypothesized that the magnitude of the reciprocal relations between two constructs became stronger over time, and that this rate of increase was linear with respect to time.
Using the general method of constraints described by Bauer & Hussong (2009), we could allow the across-construct residual regressions to interact with time such that
| (17) |
and
| (18) |
where ρyz0 and ρzy0 are the reciprocal regressions of the across-construct residuals at the first time-adjacent measures, κyz and κzy are the increments to the regression parameters that are linearly weighted via dδ. It is easy to see that if κyz=0 then ρyzdδ=ρyz0 for all dδ, resulting in the same model as that with equal regressions over time defined in Equation (14). These linear increments are uniquely defined model parameters with associated sample estimates and standard errors, the significance of which can be tested in the usual way. Although we show a linear function here, any of a variety of interesting functions could be considered (e.g., quadratic, exponential).
Modeling heterogeneity in reciprocal relations across group
Our discussion thus far has made a fundamental assumption that the magnitude of the within-person reciprocal relations may vary as a function of time but that these are equal with respect to all between-person characteristics. In other words, although the reciprocal relations might become systematically stronger or weaker with the passage of time, these relations are assumed invariant across measures such as subject gender, race, and treatment group membership. However, this restriction can also be relaxed and we can test a variety of interesting hypotheses related to the interaction between the prospective reciprocal regressions and between-person characteristics.
Drawing further on the methods described by Bauer and Hussong (2009), we can extend the parameter constraints we used earlier to test for the interaction between the prospective time-adjacent effects and time, but allow these to also include the moderating effect of group membership. For example, say that we would like to test the moderating effects of treatment group membership on the magnitude of the within-person effects across our two constructs. We could define a binary indicator to reflect group membership where gi=0 denotes membership in the control group and gi= 1 in the treatment group. We could expand the prior equation to include both the main effect of group and the interaction between group and the specific time-adjacent measures. For example, for the regression of the residual of y on z:
| (19) |
where κyz3 tests whether the linear increment in the strength of the prospective relation is significantly different in the treatment compared to control group. These tests can be further extended in variety of interesting ways to include information about both time-invariant and time-varying influences on the magnitude of the prospective within-person effects.
Summary
The LCM-SR is a novel yet logical extension of several well-developed variations of the latent curve model. Of key importance is that the inclusion of the time-specific residual structures isolates the within- and between-person effects. These within-person effects can represent within-construct stabilities or across-construct time-adjacent effects. Both the within- and across-construct residual regressions can then be structured as a function of time or one or more person-specific individual difference measures. The LCM-SR is thus able to separate the person-specific and time-specific relations between two or more constructs and treat these as separate yet jointly contributing components of developmental change. We will now demonstrate the use of the LCM-SR using an artificially generated data set created to reflect the hypothetical within- and between-person relations between depressive symptomatology and alcohol use over time.
Artificial Data Demonstration of the LCM-SR
We demonstrate the use of the LCM-SR by fitting a series of models of increasing complexity to a single sample of artificially generated repeated measures data. The disadvantage of using artificial data is that we are not using real data related to the study of psychopathology; the advantage is that we we have full knowledge of the population-generating model and can thus unambiguously determine the extent to which we are recovering the true underlying parameters of interest. Future research is needed to more fully study the utility of the LCM-SR across a variety of research settings; our more modest intent here is to provide a demonstration of how the LCM-SR might be used in practice.
Population model
Drawing both on recent findings in the substantive literature and on our own collective experiences, we defined a population model to be consistent with a hypothetical reciprocal developmental relation between depression and alcohol use spanning adolescence. Our specific model is just one of a myriad of possible applications and we simply use this given the overlap with other substantively-focused work conducted in our research group (e.g., Hussong et al., 2001; 2008; 2011). We began by generating data for a random sample of N= 250 individuals each of whom contributed T= 5 repeated measures with no missing data. Few real-world applications offer equally spaced assessments of continuously and normally distributed measures with no missing data, but these characteristics reduce sampling variability and allow us better insight into the recovery of the population values. Importantly, we chose to present the results from just a single generated data set to highlight our proposed model building strategy; as such, there are slight differences between the population and sample values we report below, and these are due to random fluctuations associated with the use of a single data set.7
We began by defining a positive linear growth trajectory in alcohol use spanning the five repeated measures, and we included significant individual differences in both starting point and rate of change over time. We defined an intercept-only model for depression such that there was person-to-person variability in the overall level of depressive symptomatology, but depression did not systematically increase as a function of time. Finally, we allowed the latent factors for the intercept and slope of alcohol use to positively covary with one another and with the latent factor for the intercept of depression to jointly define the between-person components of the relation between alcohol use and depression over time.
We included time-adjacent auto-regressions among the time-specific residuals that were positive in value but small in magnitude; this was intended to reflect a modest within-construct autoregressive effect above and beyond the contribution of the underlying latent factors. We also defined a positive prospective within-person relation between depression and alcohol use such that higher values relative to the underlying trajectories at one time were predictive of higher values at the following time point. The strength of these prospective associations was constant for alcohol use predicting depression but linearly increased in magnitude as a function time for depression predicting alcohol use. The positive covariance between the within-time residuals of depression and alcohol use accounted for any influences that were potentially omitted from the model. These residual relations jointly define the within-person components of the relation between alcohol use and depression over time.
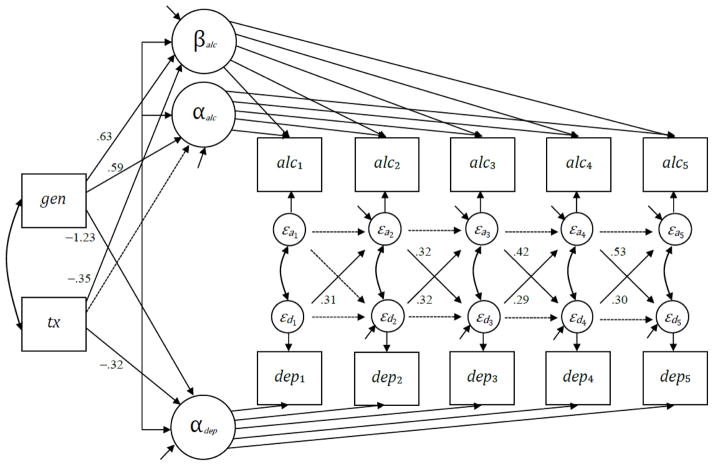
Finally, we included two exogenous time-invariant covariates that influence the three latent curve factors. Both were scaled as binary predictors to hypothetically represent subject gender (females equal to 0 and males to 1) and treatment condition (control equal to 0 and treatment equal to 1). These two predictors varied in direction and magnitude in their relation with the latent curve factors. Our final conditional multivariate LCM-SR is presented in Figure 8.
Figure 8.
Final model results for artificial data set corresponding to a bivariate conditional latent curve model with structured residuals for five repeated measures.
Note: alc=alcohol use; dep=depression; gen=gender; tx=treatment group; all numerical values are standardized and are significant at p<.05; regression coefficients for binary covariates are partially standardized; dashed lines are estimated but non-significant. Full results are in Table 1.
Data were generated and models were fitted using Version 6.11 of Mplus, although any standard SEM program could be used for these analyses. The introduction of the regression coefficients among the residuals is an atypical parameterization of the general SEM; these are sometimes called “phantom variables” and have been used in SEMs for many years (e.g., Rindskopf, 1984); all code and data are available at www.unc.edu/~curran. We will next describe the steps involved in fitting a series of LCM-SRs in increasing complexity.
Modeling building strategy
It is not possible to establish a fixed model building strategy to be used in all applications because of the unique characteristics associated with any given model and data. However, we can describe a general framework from which models can be built in increasing complexity. First, we will establish the optimally fitting model within each construct separately; this includes the identification of the optimal function of time, the testing of auto-regressions among the residuals, and the testing of equality constraints on these auto-regressions. Next, we estimate a model for both constructs simultaneously; we then conduct tests of across-construct relations both at the level of the latent factors and the time-specific residuals, and again test equality constraints on the cross-lagged regressions. Finally, we expand the multivariate model to include the set of exogenous covariates of interest. For each step we conduct LRTs to formally evaluate the change in model fit relative to the inclusion of additional parameters or the imposing of parameter constraints. Substantive conclusions are then drawn from our final conditional multivariate model.
Univariate unconditional LCM-SR for alcohol use
We began by estimating a random intercept model for alcohol use that included only a mean and variance of the intercept factor and residual variances for each of our repeated measures that we allowed to vary over time. As expected, this model fit the data poorly (χ2(7) = 283.08, p<.0001, RMSEA=.29, CFI = .47, TLI = .59). We extended this model with the addition of a linear slope factor λt= 0,1,2,3,4 consistent with Figure 1. We estimated a mean and variance for both the intercept and slope factor; a covariance between the intercept and slope factor; and we allowed the time-specific residual variances to vary over time. This model resulted in a significant improvement in model fit relative to the intercept-only model ( , p<.0001; the model as a whole reflected a good fit to the data (χ2(10) = 17.01, p=.07; RMSEA = .05, CFI=.99, TLI=.99).
There was a significant mean and variance for both the intercept (μ̂yα= 3.41, se=.17; ψ̂yαyα = 4.66, se=.66) and linear slope (μ̂yβ =.63, se=.08; ψ̂yβyβ = 1.16, se=.15), respectively. These results indicated that alcohol use was significantly increasing at a linear rate of change and that there was significant individual variability around both the starting point and rate of change over time. We then expanded this model to include an autoregressive component among the residuals. The univariate LCM and the LCM-SR are nested, thus allowing for a formal test of improvement in model fit given the inclusion of the additional parameter. The autoregressive parameter was non-significant (ρyy = .07, se = .07), and the likelihood ratio test similarly indicated that model fit was not significantly improved with the inclusion of the autoregressive residual structure ( , p=.35). We will retain this residual structure even though the LRT was non-significant because these effects were hypothesized to exist; in other applications it might be equally defensible to omit this from further models, particularly if the inclusion of these parameters leads to instability in model estimation8.
Univariate unconditional LCM-SR for depression
We again began with a random intercept model as we did for alcohol use, and this model fit the data reasonably well (χ2(13) = 23.47, p=.04, RMSEA=.06, CFI=.96, TLI=.97). We expanded this model to include a linear slope factor, but this did not lead to a significant improvement in overall model fit ( , p=.15). As such, we retained the random intercept-only model. There was both a significant mean and variance of the intercept factor (μ̂zα = .98, se=.10; ψ̂zαzα 1.83, se=.21) indicating that there was potentially meaningful individual variability in overall depressive symptomatology. We then expanded the model to include the time-adjacent auto-regressions among residuals and this again did not lead to a significant improvement in model fit ( , p=.18); as before, we will retain the residual structure as we continue our model building strategy.
Bivariate unconditional LCM-SR for alcohol use and depression
We next combined the two univariate LCMs into a single bivariate LCM consistent with Figure 4 but with the inclusion of only an intercept factor for depression. We allowed the intercept and slope factor for alcohol use to covary with one another as well as with the intercept factor for depression. We allowed the time-specific residuals to covary between alcohol use and depression, and set these covariances to be equal across time for times 2, 3, 4 and 5. We also allowed autoregressive components among the residuals of alcohol use and depression. This model did not fit the data well (χ2(42) = 170.10, p<.0001; RMSEA = .11, CFI=.86, TLI=.85). However, we know from the population generating model that the source of this misfit is due to the omission of the prospective reciprocal relations across the two constructs. Interestingly, the structured residual effects would not be a considered component from a standard LCM, and it would thus not be immediately apparent as to what was leading to the poor model fit.
Following a general model building strategy, we began by introducing the regression of the residual of alcohol use on depression while holding the regression of the residual of depression on alcohol use at zero. We then removed these regressions and introduced the regression of the residual of depression on alcohol use while holding the regressions of alcohol use on depression at zero. Finally, we introduced both sets of regressions simultaneously. This strategy allows for the unambiguous evaluation of each side of the reciprocal effects by considering them one at a time. However, alternative approaches could be used in which all regressions are considered simultaneously, or one set is introduced and then retained when including the other set. The utility of these alternatives depends on the application at hand.
We thus added the regression of the residual of alcohol use on depression to the multivariate LCM and allowed these values to be freely estimated over time. The fit of the model was significantly improved with the inclusion of these prospective regressions among the residuals relative to the multivariate LCM ( , p<.0001). We then imposed the constraint that the regressions were equal over time; this restriction did not degrade model fit ( , p=.63) and was thus retained. Because the LRT indicated these regressions were equal over time, we did not proceed to test whether the values increased as a function of time. We then fixed these regressions to zero and repeated the process for the regression of depression on alcohol use.
There was again a significant improvement in model fit with the inclusion of the regression parameters that were allowed to freely vary over time relative to the multivariate LCM ( , p<.0001). However, the imposition that these regressions were equal over time did lead to a significant decrement in model fit ( , p=.0005) and were thus not retained. Given that the magnitude of the regressions was not equal over time, these values might be systematically related to the passage of time. We thus imposed the constraint defined in Equation (17) such that the strength of the regression of depression on prior alcohol use systematically increased with time. This restriction did not lead to a decrement in model fit ( , p=.80) and was retained.
Next, we combined both sets of regressions in a single model, and this reproduced the observed data well (χ2(39) = 56.34, p=.036, RMSEA = .04, CFI=.98, TLI=.98). Interestingly, all three covariances among the latent growth factors do not significantly differ from zero (all p’s > .10). From a substantive perspective, we would thus conclude that there are no systematic between-person relations among the latent curve components of depression and alcohol use. However, these between-person effects are only one component of the more complex relation between these two constructs. To see this, we next consider the within-person components of change over time.
Consistent with the sub-models in our model-building strategy, earlier depression positively and significantly predicted subsequent alcohol use, and the magnitude of this relation was constant over time (ρ̂yz =.45, se=.06). In contrast, earlier alcohol use also positively and significantly predicted subsequent depression, but the magnitude of this relation linearly increased with time. More specifically, the prediction of depression from alcohol use was ρ̂zy =.09 (se=.07) between times 1 and 2, and this was significantly incremented by κ̂zy =.13 (se=.03) at each subsequent time-adjacent relation. The within-person component of the bivariate relation was significant and constant for depression predicting subsequent alcohol use, but the reciprocal component of this relation was significant and linearly increasing in magnitude with the passage of time for alcohol use predicting depression. Thus there are indeed strong relations between depression and alcohol use over time, but these are not at the level of the individual but at the level of prospective deviations from the underlying trajectory of each construct.
Given that we have established the optimal within-person model, our final step was to regress the three latent curve factors on our two correlated time-invariant covariates that hypothetically represented gender and treatment group membership. The fit of the conditional LCM-SR to the observed data was excellent9 (χ2(53) = 69.19, p=.07, RMSEA = .04, CFI=.99, TLI=.98). The final model is shown in Figure 8 and the full set of results are presented in Table 1. Our hypothetical measure of gender was significantly associated with both the intercept and slope of alcohol such that males started higher (γ̂yα1= 1.19, se=.31) and increased more rapidly (γ̂yβ1=.65, se=.15) compared to females. In contrast, males reported significant lower means of depression relative to females (γ̂zα1= −1.57, se=.17). Finally, our hypothetical measure of treatment group membership was not significantly related to the starting point of alcohol use (γ̂yα2=.32, se=.32), but was significantly associated with less-steep increases in alcohol use over time (γ̂yβ2= −.36, se=.15) and lower overall levels of depression (γ̂zα2 = −.41, se=.17).
Table 1.
Population and final sample values for artificially simulated data.
| Parameter | Population Value | Unstd Coeff | SE | Std Coeff | p | |
|---|---|---|---|---|---|---|
| μyα | 3.00 | 2.64* | .28 | 1.31 | <.001 | |
| μyβ | .45 | .46* | .13 | .44 | .001 | |
| μzα | 2.00 | 1.99* | .15 | 1.56 | <.001 | |
| ψyαyα | 3.60 | 3.71* | .71 | .91 | <.001 | |
| ψyβyβ | .85 | .95* | .14 | .87 | <.001 | |
| ψzαzα | .80 | .97* | .18 | .60 | <.001 | |
| ψyβyα | −.65 | −.53* | .23 | −.28 | .024 | |
| ψzαyα | .25 | .45 | .27 | .24 | .090 | |
| ψzαyβ | .15 | .05 | .10 | .06 | .603 | |
|
|
3.80 | 3.29* | .67 | 1.00 | <.001 | |
|
|
4.40 | 4.52* | .50 | .90 | <.001 | |
|
|
5.00 | 4.91* | .57 | .89 | <.001 | |
|
|
5.80 | 5.14* | .71 | .90 | <.001 | |
|
|
7.00 | 7.33* | 1.05 | .90 | <.001 | |
|
|
3.00 | 2.45* | .28 | 1.00 | <.001 | |
|
|
3.00 | 2.79* | .29 | .99 | <.001 | |
|
|
3.00 | 2.18* | .23 | .89 | <.001 | |
|
|
3.00 | 3.05* | .31 | .82 | <.001 | |
|
|
3.00 | 3.11* | .34 | .71 | <.001 | |
| σνzy | 1.05 | .50 | .31 | .18 | .108 | |
| σνzy1 | 1.05 | .81* | .16 | .17 to .25† | <.001 | |
| ρyy | .06 | .06 | .07 | .05 to .06† | .331 | |
| ρzz | .01 | .02 | .04 | .02 to .03† | .595 | |
| ρyz | .50 | .44 | .06 | .29 to .32† | <.001 | |
| ρzy | .30 | .11 | .07 | .11 | .106 | |
| κzy | .05 | .12* | .03 | N/A | <.001 | |
| γyα1 | 1.55 | 1.19* | .31 | .59 | <.001 | |
| γyβ1 | .52 | .65* | .15 | .63 | <.001 | |
| γzα1 | −1.35 | −1.57* | .17 | −1.23 | <.001 | |
| γyα2 | .05 | .32 | .32 | .16 | .311 | |
| γyβ2 | −.46 | −.36* | .15 | −.35 | .015 | |
| γzα2 | −.60 | −.41* | .17 | −.32 | .013 |
Note. Unstd Coeff = Unstandardized Coefficient. SE = Standard Error. Std Coeff = Standardized Coefficient; standardized coefficients for binary covariates are partially standardized. N/A = Parameter not available as a standardized estimate.
Standardized values for parameters constrained to equality are not computed as a single common estimate.
p<.05
There are several extensions to this model that we do not demonstrate here. For example, we considered the main effects of gender and treatment, and we could easily include the interaction between these two (e.g., Curran et al., 2004). We could also expand the predictor set to include any of a variety of additional individual difference measures as main effects or multiplicative interactions. Further, we could extend the constraints imposed on the within-person prospective effects to vary as a function not only of time but also of exogenous covariates. For example, we could directly test whether the magnitude of the relations among the within-person effects varies as a function of gender, ethnicity, or treatment group membership. We might hypothesize that the strength of the reciprocal relations between the two constructs is constant over time for the control group, but these become systematically weakened over time for the treatment group. Given the separation of the within-person and between-person components of change within a single model, a variety of intriguing tests are available in ways not previously possible.
Conclusion
This is an exciting time to be conducting research in clinical psychology. Not only have our theoretical models developed in complex and increasingly nuanced ways, but we have available an arsenal of advanced statistical techniques that can be used to rigorously empirically evaluate our research hypotheses under study. Despite the myriad of advances we have witnessed over the past decade, one challenge continues to vex substantive researchers, ourselves included: how do we best model the dynamic and reciprocal relations between two constructs over time? There are a number of well-developed modeling strategies that have tackled different aspects of this question, but the relative utility of each depends on both the theoretical model and empirical data at hand.
For example, the multivariate latent curve model examines the relation between two constructs over time, but this is primarily a between-person model that evaluates the across-construct relations at the level of the person-specific growth factors. This multivariate LCM can be redefined as an LCM with TVCs to provide an estimate of the within-person component of change, but this is at the cost of omitting the between-person component and is restricted to unidirectional influences. This model can be further redefined to correspond to an autoregressive latent trajectory model that allows both person-specific and time-specific relations, but this approach does not provide a pure disaggregation of within- and between-person components of change. All of these existing modeling approaches work well, at least under the assumption that the statistical model is well matched to the theoretical model. The extent to which the statistical and theoretical models diverge directly undermines our ability to validly test our research hypotheses. As such, if our theory posits the simultaneous existence of between-person and within-person components of stability and change, the magnitude of which may vary as a function of person-specific characteristics, then none of these existing techniques is ideally suited to the task at hand. Our motivating goal for this paper has been to describe and demonstrate a model that allows for this disaggregation of effects, and we refer to this as the latent curve model with structured residuals.
The LCM-SR is a novel yet natural extension of the multivariate LCM. It draws on the rich traditions of structuring residuals within the multilevel (e.g., Goldstein et al., 1994) and time series (e.g., Box & Jenkins, 1976) modeling frameworks, techniques that to our knowledge have not yet been incorporated into the LCM with more than a single construct. By separating the between-person effects at the level of the person-specific latent factors from the within-person effects at the level of the time-specific residuals, we are able to test a variety of hypotheses in a powerful and highly flexible way. For example, we can test whether the time-adjacent within-person effects are constant over time or may strengthen or weaken with the passage of time. We can extend these tests using the methods of Bauer and Hussong (2009) to evaluate whether the magnitude of these over-time relations themselves vary as a function of treatment group membership of individual characteristics such as gender or ethnicity. We could even test whether the reciprocal effects are moderated by a continuous covariate such as symptomatology at baseline or some measure of early executive functioning. These are just a few of the novel types of hypotheses that could be tested within the LCM-SR.
Of course our approach is not without potential limitations. Most obviously, the LCM-SR is not well suited for theoretical questions that posit relations that are not composed of separate between- and within-person components of stability and change. For example, Raudenbush and Bryk (2002, page 179) described a situation in which one might regress time-specific measures of reading achievement on how many days of instruction the child received in that same year; this model corresponds to what we have described as the LCM with TVCs. However, the entire point of their model is to statistically adjust reading scores as a function of student absenteeism in each given year and to fit the trajectory model to the adjusted readings scores, thus making the TVC model ideal. Similarly, Ferrer and McArdle (2010) described a latent change score model to examine the relation between change in one construct and subsequent change in another construct. Again, the LCM-SR is not well suited to modeling these kinds of dynamics because the within-person regressions are based on the deviations of a time-specific measure from the corresponding trajectory. These examples are not limitations of the LCM-SR in general, but rather highlight the obvious point that no single modeling framework is optimal for evaluating all possible theoretically-derived hypotheses related to individual stability and change over time.
Another potential limitation is that we must have direct access to the time-specific residuals in order to estimate the prospective reciprocal effects. However, these residuals are not uniquely identified when using discretely scaled repeated measures within nonlinear link functions in the SEM (e.g., compare Equation 1 vs. 3 in Bauer & Hussong, 2009). Thus if maximum likelihood estimation is used in an LCM with binary or ordinal repeated measures, it is not possible to structure the residuals in the way we have described here. Using a weighted least squares-based method of estimation is one option, but this itself introduces another layer of complexities (e.g., Wirth & Edwards, 2007).
Finally, careful thought is needed about both the spacing of the repeated assessments and whether sufficient numbers of observations are obtained over time to provide stable estimates of the prospective reciprocal relations. As with the standard LCM, the methods we describe here can be used with data that are unbalanced and partially missing. However, because we are modeling the relation between an earlier measure on one construct and a later measure on another construct, an adequate number of cases must provide measures at both time points on both constructs. Future attention must be paid to all of these issues to better understand the relative performance of the LCM-SR under conditions commonly encountered in psychopathology research.
In conclusion, we have described what we believe to be a novel yet logical extension of the multivariate latent curve model. We use an atypical parameterization of the standard latent curve model to allow access to the time-specific deviations of the repeated measures relative to the corresponding underlying growth trajectory; we can then use these individual- and time-specific deviations to provide unique tests of reciprocal within-person relations between two or more constructs as they unfold over time. Importantly, these within-person influences are simultaneously estimated in the presence of the between-person relations assessed at the level of the latent trajectories. The simultaneous disaggregation of levels of effect allows for a more comprehensive empirical examination of the hypothesized underlying developmental processes and allows us to move one step forward in our quest to forge stronger links between our theoretical and statistical models of human behavior.
Acknowledgments
This work was partially supported by Award Number R01DA015398 (Curran & Hussong, co-PI), F31DA035523 (Bainter, PI) and F31DA033688 (McGinley, PI). Sample data and computer code can be obtained from the first author or from www.unc.edu/~curran.
Footnotes
The selection of the time period where time is set equal to zero impacts the interpretation of the fixed and random effects of the intercept of the trajectory (Biesanz, Deeb-Sossa, Aubrecht, Bollen & Curran, 2004). The choice of zero-point plays precisely the same role in all of our proposed models as it does in the standard LCM.
It is possible to rescale some of these covariances as regressions (e.g., we could regress the slope factor for y on the intercept factor for z and vice versa), and this can provide an interesting insight into the between-person structural influence of the starting point of one construct on the rate of change of another construct (e.g., Bollen & Curran, 2006, Section 7.4.2).
Several important approaches have been proposed to examine multivariate change over time including the latent change score model (Ferrer & McArdle, 2010; McArdle & Hamagami, 2001), the trait-state-error model (Kenny & Zautra, 1995; 2001), and the trait-state-occasion model (Cole, Martin, & Steiger, 2005). Space constraints preclude a comprehensive examination of these alternative approaches, although such a review would be highly beneficial.
In some applications, the inclusion of prior lags may also be necessary (e.g., t−2); this would typically be determined by theory and empirical necessity. Given space constraints we do not explicate identification conditions to establish unique estimation of these lagged residual effects, but this would be determined in precisely the same way as for the standard LCM (Bollen & Curran, 2006, pp. 21–24).
There will likely be slight variations in value in any given application due to the persnicketiness of full information maximum likelihood estimation.
Imposing a simple equality constraint over time assumes that all measures are equally spaced. If some or all repeated assessments are unequally spaced, additional restrictions are needed to account for these differences.
To further examine this we fit the same model to 1000 separate samples of size N=250 and the mean parameter estimates pooled across the full set of replications were all within 1% of their population generating values.
The inclusion or exclusion of these non-significant auto-regressions exerted no impact on the final models to be presented below.
As well it should given that this was the population generating model used to create the artificial data.
References
- Baltes PB, Reese HW, Nesselroade JR. Life-span developmental psychology: Introduction to research methods. Oxford, England: Brooks/Cole; 1977. [Google Scholar]
- Bauer DJ, Hussong AM. Psychometric approaches for developing commensurate measures across independent studies: traditional and new models. Psychological Methods. 2009;14:101–125. doi: 10.1037/a0015583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biesanz JC, Deeb-Sossa N, Papadakis AA, Bollen KA, Curran PJ. The role of coding time in estimating and interpreting growth curve models. Psychological Methods. 2004;9:30–52. doi: 10.1037/1082-989X.9.1.30. [DOI] [PubMed] [Google Scholar]
- Bolger N, Davis A, Rafaeli E. Diary methods: Capturing life as it is lived. Annual Review of Psychology. 2003;54:579–616. doi: 10.1146/annurev.psych.54.101601.145030. [DOI] [PubMed] [Google Scholar]
- Bollen KA. Structural equations with latent variables. New York: Wiley; 1989. [Google Scholar]
- Bollen KA. On the origins of latent curve models. In: Cudeck R, MacCallum R, editors. Factor analysis at 100. Mahwah, NJ: Lawrence Erlbaum Associates; 2007. pp. 79–98. [Google Scholar]
- Bollen KA, Curran PJ. Autoregressive latent trajectory (ALT) models: A synthesis of two traditions. Sociological Methods and Research. 2004;32:336–383. [Google Scholar]
- Bollen KA, Curran PJ. Wiley Series on Probability and Mathematical Statistics. John Wiley & Sons; New Jersey: 2006. Latent Curve Models: A Structural Equation Approach. [Google Scholar]
- Bollen KA, Zimmer C. An overview of the autoregressive latent trajectory (ALT) model. In: van Montfort K, Oud JHL, Satorra A, editors. Longitudinal research with latent variables. Berlin, Germany: Springer-Verlag; 2010. pp. 153–176. [Google Scholar]
- Box GEP, Jenkins GM. Time series analysis: forecasting and control. San Francisco: Holden-Day; 1976. [Google Scholar]
- Browne MW. Structured latent curve models. In: Cuadras CM, Rao CR, editors. Multivariate analysis: Future directions. Vol. 2. Amsterdam: North-Holland; 1993. pp. 171–198. [Google Scholar]
- Browne MW, du Toit SHC. Models for learning data. In: Collins LM, Horn JL, editors. Best methods for the analysis of change. Washington, DC: American Psychological Association; 1991. pp. 47–68. [Google Scholar]
- Chi EM, Reinsel GC. Models for longitudinal data with random effects and AR(1) errors. Journal of the American Statistical Association. 1989;79:125–131. [Google Scholar]
- Cole DA, Martin NC, Steiger JH. Empirical and conceptual problems with longitudinal trait-state models: Support for a Trait-State-Occasion model. Psychological Methods. 2005;10:3–20. doi: 10.1037/1082-989X.10.1.3. [DOI] [PubMed] [Google Scholar]
- Curran PJ, Bauer DJ. The disaggregation of within-person and between-person effects in longitudinal models of change. Annual Review of Psychology. 2011;62:583–619. doi: 10.1146/annurev.psych.093008.100356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Curran PJ, Bauer DJ, Willoughby MT. Testing and probing main effects and interactions in latent curve analysis. Psychological Methods. 2004;9:220–237. doi: 10.1037/1082-989X.9.2.220. [DOI] [PubMed] [Google Scholar]
- Curran PJ, Bollen KA. The best of both worlds: Combining autoregressive and latent curve models. In: Collins LM, Sayer AG, editors. New methods for the analysis of change. Washington, DC: American Psychological Association Press; 2001. pp. 105–136. [Google Scholar]
- Curran PJ, Hussong AM. The use of latent trajectory models in psychopathology research. Journal of Abnormal Psychology. 2003;112:526–544. doi: 10.1037/0021-843X.112.4.526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Curran PJ, Lee TH, Howard AH, Lane ST, MacCallum RC. Disaggregating within-person and between-person effects in multilevel and structural equation growth models. In: Hancock G, editor. Advances in longitudinal methods in the social and behavioral sciences. Charlotte, NC: Information Age; 2012. pp. 217–253. [Google Scholar]
- Curran PJ, Muthén BO, Harford TC. The influence of changes in marital status on developmental trajectories of alcohol use in young adults. Journal of Studies on Alcohol. 1998;59:647–658. doi: 10.15288/jsa.1998.59.647. [DOI] [PubMed] [Google Scholar]
- Curran PJ, Stice E, Chassin L. The relation between adolescent and peer alcohol use: A longitudinal random coefficients model. Journal of Consulting and Clinical Psychology. 1997;65:130–140. doi: 10.1037//0022-006x.65.1.130. [DOI] [PubMed] [Google Scholar]
- Curran PJ, Willoughby MJ. Reconciling theoretical and statistical models of developmental processes. Development and Psychopathology. 2003;15:581–612. doi: 10.1017/s0954579403000300. [DOI] [PubMed] [Google Scholar]
- Delsing MJMH, Oud JHL. Analyzing reciprocal relationships by means of the continuous-time autoregressive latent trajectory model. Statistica Neerlandica. 2008;62:58–82. [Google Scholar]
- Dickey DA, Fuller WA. Distribution of the estimators for autoregressive time series with a unit root. Journal of American Statistical Association. 1979;74:427–431. [Google Scholar]
- Diggle PJ. An approach to the analysis of repeated measures. Biometrics. 1988;44:959–971. [PubMed] [Google Scholar]
- Ferrer E, McArdle JJ. Longitudinal modeling of developmental changes in psychological research. Current Directions in Psychological Science. 2010;19:149–154. [Google Scholar]
- Goldstein H, Healy MJR, Rasbash J. Multilevel time series models with applications to repeated measures data. Statistics in Medicine. 1994;13:1642–1655. doi: 10.1002/sim.4780131605. [DOI] [PubMed] [Google Scholar]
- Grimm KJ, Widaman KF. Residual structures in latent growth curve modeling. Structural Equation Modeling. 2010;17:424–442. [Google Scholar]
- Hamaker EL. Conditions for the equivalence of the autoregressive latent trajectory model and a latent growth curve model with autoregressive disturbances. Sociological Methods and Research. 2005;33:404–418. [Google Scholar]
- Hamaker EL, Dolan CV, Molenaar P. On the nature of SEM estimates of ARMA parameters. Structural Equation Modeling. 2002;9:347–368. [Google Scholar]
- Hartup W. Perspectives on child and family interaction: Past, present, and future. In: Lerner RM, Spanier GB, editors. Child influences on marital and family interaction: A life-span perspective. San Francisco: Academic Press; 1978. pp. 23–46. [Google Scholar]
- Hedeker D, Gibbons RD. Longitudinal Data Analysis. New York: Wiley; 2006. [Google Scholar]
- Hussong AM, Cai L, Curran PJ, Flora DB, Chassin L, Zucker RA. Disaggregating the distal, proximal, and time-varying effects of parent alcoholism on children’s internalizing symptoms. Journal of Abnormal Child Psychology. 2008;36:335–346. doi: 10.1007/s10802-007-9181-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hussong AM, Hicks RE, Levy SA, Curran PJ. Specifying the relations between affect and heavy alcohol use among young adults. Journal of Abnormal Psychology. 2001;110:449–461. doi: 10.1037//0021-843x.110.3.449. [DOI] [PubMed] [Google Scholar]
- Hussong AM, Jones DJ, Stein GL, Baucom DH, Boeding S. An internalizing pathway to alcohol use and disorder. Psychology of Addictive Behaviors. 2011;25:390–404. doi: 10.1037/a0024519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jongerling J, Hamaker EL. On the trajectories of the predetermined ALT model: What are we really modeling? Structural Equation Modeling. 2011;18:370–382. [Google Scholar]
- Kenny DA, Zautra AJ. The trait-state-error model for multi-wave data. Journal of Consulting and Clinical Psychology. 1995;63:52–59. doi: 10.1037//0022-006x.63.1.52. [DOI] [PubMed] [Google Scholar]
- Kenny DA, Zautra AJ. Trait-state models for longitudinal data. In: Sayer A, Collins L, editors. New Methods for the Analysis of Change. Washington D.C: American Psychological Association; 2001. pp. 241–270. [Google Scholar]
- Kwok O, West SG, Green SB. The impact of misspecifying the within-subject covariance structure in multiwave longitudinal multilevel models: A Monte Carlo study. Multivariate Behavioral Research. 2007;42:557–592. [Google Scholar]
- Lutkepohl H, Saikkonen P. Testing for the cointegrating rank of a VAR process with a time trend. Journal of Econometrics. 2000;95:177–198. [Google Scholar]
- McArdle JJ. Dynamic but structural equation modeling of repeated measures data. In: Nesselroade JR, Cattell RB, editors. Handbook of multivariate experimental psychology. New York: Plenum; 1988. pp. 561–614. [Google Scholar]
- McArdle JJ. Structural modeling experiments using multiple growth functions. In: Ackerman P, Kanfer R, Cudeck R, editors. Learning and individual differences: abilities, motivation, and methodology. Hillsdale, NJ: Erlbaum; 1989. pp. 71–117. [Google Scholar]
- McArdle JJ. Latent variable modeling of differences and changes with longitudinal data. Annual Review of Psychology. 2009;60:577–605. doi: 10.1146/annurev.psych.60.110707.163612. [DOI] [PubMed] [Google Scholar]
- McArdle JJ, Epstein D. Latent growth curves within developmental structural equation models. Child Development. 1987;58:110–133. [PubMed] [Google Scholar]
- McArdle JJ, Hamagami F. Linear dynamic analyses of incomplete longitudinal data. In: Collins L, Sayer A, editors. Methods for the analysis of change. Washington, DC: APA Press; 2001. pp. 137–176. [Google Scholar]
- Meredith W, Tisak J. “Tuckerizing” curves. Paper presented at the annual meeting of the Psychometric Society; Santa Barbara, CA. 1984. Jul, [Google Scholar]
- Meredith W, Tisak J. Latent curve analysis. Psychometrika. 1990;55:107–122. [Google Scholar]
- Morin AJS, Maiano C, Marsh HW, Janosz M, Nagengast B. The longitudinal interplay of adolescents’ self-esteem and body image: A conditional autoregressive latent trajectory analysis. Multivariate Behavioral Research. 2011;46:157–201. doi: 10.1080/00273171.2010.546731. [DOI] [PubMed] [Google Scholar]
- Muthén BO. Latent variable mixture modeling. In: Marcoulides G, Schumacker R, editors. New developments and techniques in structural equation modeling. Mahwah, NJ: Erlbaum; 2001. pp. 1–33. [Google Scholar]
- Muthén BO. Beyond SEM: General latent variable modeling. Behaviormetrika. 2002;29:81–117. [Google Scholar]
- Muthén BO, Curran PJ. General longitudinal modeling of individual differences in experimental designs: A latent variable framework for analysis and power estimation. Psychological Methods. 1997;2:371–402. [Google Scholar]
- Patterson GR, Reid JB, Dishion TJ. Antisocial boys. Eugene, OR: Castalia; 1992. [Google Scholar]
- Patterson GR, Yoerger K. A developmental model for early- and late-onset antisocial behavior. In: Reid JB, Snyder J, Patterson GR, editors. Antisocial behavior in children and adolescents: A developmental analysis and model for intervention. Washington, DC: American Psychological Association; 2002. pp. 147–172. [Google Scholar]
- Raudenbush SW, Bryk AS. Hierarchical linear models: Applications and data analysis methods. 2. Thousand Oaks, CA: Sage Publications; 2002. [Google Scholar]
- Rindskopf D. Using phantom and imaginary latent variables to parameterize constraints in linear structural models. Psychometrika. 1984;49:37–47. [Google Scholar]
- Rodebaugh TL, Curran PJ, Chambless DL. Expectancy of panic in the maintenance of daily anxiety in panic disorder with agoraphobia: A longitudinal test of competing models. Behavior Therapy. 2002;33:315–336. [Google Scholar]
- Rovine MJ, Molenaar PCM. A structural modeling approach to a multilevel random coefficients model. Multivariate Behavioral Research. 2000;35:51–88. doi: 10.1207/S15327906MBR3501_3. [DOI] [PubMed] [Google Scholar]
- Saikkonen P, Lutkepohl H. Trend adjustment prior to testing for the cointegrating rank of a vector autoregressive process. Journal of Time Series Analysis. 2000;21:435–456. [Google Scholar]
- Scarr S, McCartney K. How people make their own environments: A theory of genotype greater than environment effects. Child Development. 1983;54:424–435. doi: 10.1111/j.1467-8624.1983.tb03884.x. [DOI] [PubMed] [Google Scholar]
- Sivo S. Multiple indicator stationary time series models. Structural Equation Modeling. 2001;8:599–612. [Google Scholar]
- Sivo S, Fan X. The latent curve ARMA (p, q) panel model: Longitudinal data analysis in educational research and evaluation. Educational Research and Evaluation. 2008;14:363–376. [Google Scholar]
- Sivo S, Fan X, Witta L. The biasing effects of unmodeled ARMA time series processes on latent growth curve model estimates. Structural Equation Modeling. 2005;12:215–231. [Google Scholar]
- Sivo S, Wilson VL. Modeling causal error structures in longitudinal panel data: A Monte Carlo study. Structural Equation Modeling. 2000;7:174–205. [Google Scholar]
- Stice E, Marti N, Rohde P, Shaw H. Testing mediators hypothesized to account for the effects of a dissonance eating disorder prevention program over longer-term follow-up. Journal of Consulting and Clinical Psychology. 2011;79:398–405. doi: 10.1037/a0023321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teachman BA, Marker CD, Smith-Janik SB. Automatic associations and panic disorder: Trajectories of change over the course of treatment. Journal of Consulting and Clinical Psychology. 2008;76:988–1002. doi: 10.1037/a0013113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Buuren S. Fitting ARMA time series models by structural equation models. Psychometrika. 1997;62:215–236. [Google Scholar]
- Voelkle MC. Reconsidering the use of autoregressive latent trajectory (ALT) models. Multivariate Behavioral Research. 2008;43:564–591. doi: 10.1080/00273170802490665. [DOI] [PubMed] [Google Scholar]
- Wirth RJ, Edwards MC. Item factor analysis: Current approaches and future directions. Psychological Methods. 2007;12:58–79. doi: 10.1037/1082-989X.12.1.58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wohlwill JF. Relations between method and partial-isomorphism view. Annals of Theoretical Psychology. 1991;7:91–138. [Google Scholar]
- Zyphur MJ, Chaturvedi S, Arvey RD. Job performance over time is a function of latent trajectories and previous performance. Journal of Applied Psychology. 2008;93:217–224. doi: 10.1037/0021-9010.93.1.217. [DOI] [PubMed] [Google Scholar]