Grand Challenge Competition to Predict In Vivo Knee Loads

Abstract

Impairment of the human neuromusculoskeletal system can lead to significant mobility limitations and decreased quality of life. Computational models that accurately represent the musculoskeletal systems of individual patients could be used to explore different treatment options and ultimately to optimize clinical outcome. The most significant barrier to model-based treatment design is validation of model-based estimates of in vivo contact and muscle forces. This paper introduces an annual “Grand Challenge Competition to Predict In Vivo Knee Loads” based on a series of comprehensive publicly available in vivo data sets for evaluating musculoskeletal model predictions of contact and muscle forces in the knee. The data sets come from patients implanted with force-measuring tibial prostheses. Following a historical review of musculoskeletal modeling methods used for estimating knee muscle and contact forces, we describe the first two data sets used for the first two competitions and summarize four subsequent data sets to be used for future competitions. These data sets include tibial contact force, video motion, ground reaction, muscle EMG, muscle strength, static and dynamic imaging, and implant geometry data. Competition participants create musculoskeletal models to predict tibial contact forces without having access to the corresponding in vivo measurements, which are not released until after each year’s competition submissions. These blinded predictions provide an unbiased evaluation of the capabilities and limitations of musculoskeletal modeling methods. The paper concludes with a discussion of how these unique data sets can be used by the musculoskeletal modeling research community to improve the estimation of in vivo muscle and contact forces and ultimately to help make musculoskeletal models clinically useful.

INTRODUCTION

“Doctors have long known that people differ in susceptibility to disease and response to medicines. But, with little guidance for understanding and adjusting to individual differences, treatments developed have generally been standardized for the many, rather than the few.” – National Academy of Engineering¹

Mobility limitations arising from musculoskeletal or nervous system disorders often result in a decreased quality of life. Osteoarthritis, osteoporosis, stroke, cerebral palsy, and paraplegia are common clinical examples. Surgical and rehabilitation treatment planning for these disorders has historically been based on subjective clinical assessment of static anatomic measurements (e.g., x-rays) and dynamic functional measurements (e.g., gait analysis). In essence, the clinician creates an implicit musculoskeletal model in his or her mind and then runs the available data and potential treatments through this model to predict the patient’s post-treatment function. Due to the subjective nature of this process, two clinicians given the same clinical data can arrive at different treatment plans that would produce different outcomes.

One way to address this problem is to replace the subjective implicit models currently used in clinical practice with objective computational models that are based on principles of physics and physiology. For industrial products, computational models permit a wide range of design variations to be evaluated quickly and with minimal cost, allowing optimal designs to be identified before costly physical prototypes are constructed and tested. Applying a similar approach to the design of orthopedic treatments is more challenging due to the unique anatomic and functional characteristics of each patient. However, the potential benefits are greater, since it is either impossible or undesirable to iterate physical treatments on patients due to time and cost limitations, ethical considerations related to pain and suffering, and the potential for “burning bridges” (e.g., total knee replacement eliminates high tibial osteotomy as a treatment option). If computational models can be constructed that accurately represent the neuromusculoskeletal systems of individual patients, clinicians could use these models to explore different treatment options, reduce the level of subjectivity in the treatment planning process, and optimize clinical outcome on an individual patient basis.

While a computational approach to treatment planning is promising, significant barriers to clinical implementation exist. Validation of model predictions is the most significant barrier and the one that has received the least attention.² Model validation in this context means prediction of clinically important quantities to within the accuracy needed to address the clinical question at hand, where accuracy is quantified using absolute, relative, or root-mean-square error or R² value depending on whether an actual value or a change in value is to be predicted at one point in a motion cycle or across an entire motion cycle. For mobility-related disorders, clinically important quantities include muscle, articular contact, and ligament forces as well as tissue-level stresses and strains – internal quantities that cannot be measured directly in a clinical environment. Furthermore, the redundant nature of the human musculoskeletal system makes unique calculation of these quantities impossible using rigid body mechanics,² at least without introducing simplifying assumptions that make the accuracy of the calculated quantities questionable. In vivo measurement of articular contact (but not muscle and ligament) forces is possible through the use of instrumented implants, and these measurements have facilitated comparison between experimentally measured and model predicted hip and knee contact forces during gait.^3-7 While agreement has generally been good for the hip,^3,4 it has been poorer for the knee,^5-7 indicating the need for improved modeling methods.

This paper addresses the validation barrier for musculoskeletal models of the knee by introducing an annual “Grand Challenge Competition to Predict In Vivo Knee Loads.” The competition is based on the most comprehensive human movement and imaging data sets available for subjects implanted with force-measuring tibial prostheses. The knee is an important joint for validation efforts due to its complexity, its centrality to human locomotion, and the high frequency with which it is injured or diseased. These data sets include surface marker trajectory, ground reaction force, muscle electromyographic (EMG) activity, instrumented implant force and moment, functional strength, fluoroscopic imaging, computed tomography (CT) imaging, and magnetic resonance (MR) imaging data. Since muscle forces are the primary determinants of joint contact forces,⁸ the instrumented implant data provide the opportunity for direct validation of estimated articular contact forces and indirect validation of estimated muscle forces. One data set per year is being released for the annual competition, where competitors predict in vivo medial and lateral tibial contact forces for specified motion trials without having access to the corresponding experimental measurements. Details of the experimental data collection are presented for the first two data sets used in the first two competitions, and an overview is provided for four subsequent data sets to be used in future competitions. Our hope is that free distribution of these data sets will facilitate development of musculoskeletal modeling methods that reliably predict articular contact, muscle, and ligament forces during walking and other activities, taking the musculoskeletal modeling research community closer to the ultimate goal of clinical utility.

HISTORICAL PERSPECTIVE

Current methods for estimating muscle, articular contact, and ligament forces in the knee have evolved from methods first published in the 1970’s.^9,10 Since then, one of the primary advances in musculoskeletal modeling has been the development of new algorithms for solving the muscle redundancy problem (i.e., more unknown muscle forces than equations available from rigid multibody dynamics). These algorithms generally fall into three categories - optimization methods, EMG-driven methods, and reduction methods,² each of which uses rigid multibody dynamics to model how muscle forces produce movement of the body segments. When considering these methods, it is important to realize that joint reaction forces calculated via inverse dynamics are not articular contact forces but rather a lower bound on the contact forces that would occur if no muscle contraction was present (see Winter¹¹ for further explanation of this issue).

Optimization methods assume that the nervous system minimizes some cost function (e.g., sum of squares of muscle activations) subject to certain constraints (e.g., generate specified net joint moments) when producing human movement. Conceptually, the cost function makes the solution to the indeterminate problem unique by compensating for missing equations. Optimization methods are typically categorized as “static” or “dynamic” depending on whether inverse dynamics or forward dynamics, respectively, is used to perform the repeated simulations required to solve the optimization problem.^2,12 Static optimization solves the dynamics equations algebraically one time frame at a time to predict muscle forces consistent with an experimentally measured motion, whereas dynamic optimization numerically integrates the dynamics equations across all time frames to predict muscle forces and motion simultaneously (i.e., no experimentally measured motion necessary). Among the limitations of optimization methods are that the “correct” form of the cost function being minimized by the nervous system (if it exists) is unknown, the weight factors on the individual terms in the cost function are unknown, and the optimality assumption for the nervous system may not apply to individuals with joint pathology or neurological impairment.

EMG-driven methods attempt to circumvent these problems by using measured muscle EMG activity as additional experimental inputs.¹³ Similar to static optimization, these methods require experimental motion inputs, and similar to dynamic optimization, they can predict the net loads at the joints for quantitative evaluation. Nonetheless, EMG-driven methods possess several limitations as well. It is unclear how to incorporate deep muscles for which EMG measurements are not available, muscle force predictions require EMG and motion measurements as inputs, and methods for estimating the necessary muscle-tendon model parameter values are not yet validated.

Reduction methods seek to reformulate the muscle force estimation problem so that the number of unknown muscle forces equals the number of equations available from inverse dynamics.² The reformulation is typically achieved by either eliminating unknown muscle forces or combining muscles of similar function. Though the simplicity of this approach is appealing, it does not account for measured muscle activation patterns and muscle co-contraction.

Correct resolution of the muscle redundancy problem has important implications for accurate calculation of articular contact forces, since muscle contraction increases articular contact force. To complicate matters, calculation of tibiofemoral contact force is itself an indeterminate problem, since at least two regions of contact exist between the femur and tibia. Thus, even without the muscle redundancy problem, the contact force redundancy problem makes determination of unique contact forces in the medial and lateral compartments of the knee difficult.

While in vivo measurement of knee muscle forces is not currently possible during activities such as gait, in vivo measurement of knee contact forces provides a valuable opportunity for musculoskeletal model validation. At least ten studies have published in vivo knee contact force measurements made by instrumented implants during gait (Table 1, top half). Published studies using these devices have reported higher contact forces during overground gait compared to treadmill gait. Maximum total contact force ranged from 1.8 to 3.0 BW, typically remaining between 2.0 and 2.5 BW. Medial and lateral contact force data have been reported for only four subjects, with between 55% (treadmill gait with hands resting on handlebars) and 88% (overground gait) of the total load passing through the medial compartment.^18,20,22,24 Such data are especially valuable since they provide internal load information for evaluating musculoskeletal model fidelity and are related to clinical issues such as the development of osteoarthritis in natural knees and wear in artificial knees.

Table 1.

Summary of experimental and modeling studies reporting maximum in vivo knee contact forces during gait.

Study	No. of Subjects	Condition	Total Force	Medial Force	Lateral Force
Taylor et al. (1998)14	1	Overground	2.5	—	—
D’Lima et al. (2005)15	1	Overground	2.8	—	—
D’Lima et al. (2005)15	1	Treadmill	2.0	—	—
D’Lima et al. (2006)16	1	Overground	2.4	—	—
D’Lima et al. (2007)17	1	Overground	2.3	—	—
Zhao et al. (2007)18	1	Treadmill	2.2	1.2	1.0
D’Lima et al. (2008)19	3	Treadmill	1.8 to 2.5	—	—
Fregly et al. (2009)20	1	Overground	2.3	1.8	0.5
Heinlein et al. (2009)21	2	Overground	2.1 to 2.8	—	—
Erhart et al. (2010)22	1	Overground	2.6	1.7	0.9
Kutzner et al. (2010)23	5	Overground	2.2 to 3.0	—	—
Kutzner et al. (2011)24	3	Overground	2.1 to 2.5	1.5 to 2.0	0.5 to 0.9
Morrison et al. (1970)9	12	Model	2.1 to 4.0	—	—
Seirig et al. (1975)25	1	Model	6.7	—	—
Mikosz et al. (1988)26	1	Model	5.0	—	—
Schipplein and Andriacchi (1991)27	1	Model	3.2	—	—
Kuster et al. (1997)28	12	Model	3.4 to 3.9	—	—
Wimmer et al. (1997)29	1	Model	3.3	—	—
Komistek et al. (1998)30	1	Model	2.3	—	—
Lu et al. (1998)31	2	Model	2.2	—	—
Heller et al. (2003)32	4	Model	3.3
Taylor et al. (2004)7	4	Model	2.7 to 3.8	—	—
Shelburne et al. (2005)33	1	Model	2.9	2.4	0.5
Thambyah et al. (2005)34	10	Model	2.9 to 3.5	—	—
Shelburne et al. (2006)35	1	Model	2.7	2.2	0.5
Kim et al. (2009)5	1	Model	2.0 to 2.6	1.2 to 1.8	0.8 to 0.8
Lundberg et al. (2009)36	1	Model	3.5	2.5	1.0
Wehner et al. (2009)37	1	Model	3.3	—	—
Winby et al. (2009)38	1	Model	3.0 to 4.4	2.0 to 3.0	1.0 to 1.4
Catalfamo et al. (2010)39	1	Model	8.1	—	—
Lin et al. (2010)6	1	Model	1.8 to 3.6	1.4 to 2.7	0.4 to 0.9

Note: An expanded list of references for material presented in this article is provided as Supplementary Material.

For the most part, musculoskeletal modeling studies overestimate tibial contact forces during gait (Table 1, bottom half). These overestimates may be indicative of inaccurate muscle moment arms (e.g., due to inaccurate muscle attachment points or joint axis locations) or muscle-tendon parameter values. Predicted maximum total contact forces range from 1.8 to 8.1 BW, with most estimates being in the range of 3.0 to 3.5 BW – about 1 BW larger than typical in vivo measurements. Only one study thus far has used an EMG-driven method,³⁸ with the remaining studies using either an optimization method or a reduction method. Four studies – two reduction^30,31 and two optimization^5,6 – have predicted maximum total contact forces within the ranges reported experimentally. Both optimization studies under-predicted lateral contact force unless excessive lateral collateral ligament tension was generated or the measured lateral contact force was used as a constraint. No study has matched medial and lateral contact force measurements closely for a variety of activities using a single muscle force solution process. Consequently, model-based results or analyses that require accurate contact or muscle force estimates in the knee remain questionable.

Significant room for improvement exists in predicting in vivo knee contact and muscle forces using musculoskeletal models. Readily accessible benchmark data sets providing instrumented knee implant data and corresponding video motion, ground reaction, EMG, muscle strength, static and dynamic imaging, and implant geometric data for multiple subjects performing multiple tasks would provide the musculoskeletal modeling research community with “gold standards” for model evaluation purposes. Such a wide variety of data would facilitate the development and evaluation of new methods for predicting in vivo knee contact and muscle forces. If contact forces are consistently well predicted for different tasks performed by different subjects, then it is likely that muscle forces are also being reasonably well predicted, especially if good quantitative agreement is achieved with EMG measurements.

DATA DESCRIPTION

We are organizing a series of five “Grand Challenge Competitions to Predict In Vivo Knee Loads,” with one competition being held each year at the ASME Summer Bioengineering Conference (http://divisions.asme.org/bed/Events.cfm). The goal is for competitors to predict in vivo medial and lateral knee contact forces for specified movement trials collected from a subject implanted with an instrumented tibial prosthesis. Competitors are given access to all in vivo data (i.e., video motion, ground reaction, EMG, muscle strength, static and dynamic imaging, and implant geometry) available from the subject except the in vivo contact force measurements made by the instrumented implant for the specified movement trials. This approach ensures true model evaluation since the in vivo contact force predictions are generated in a blinded fashion where model parameters cannot be selectively tuned to achieve the desired results. The measured knee contact forces are not released until after each competing team has submitted its predictions.

The first competition was held in 2010 and the second one in 2011. Competitors thus far have been from Belgium, Canada, Denmark, France, Korea, Portugal, Singapore, and the United States, with interested future competitors from Germany, Italy, and the Netherlands. Nearly all competition submissions have over-predicted maximum total contact force for the two gait trials selected for analysis, with all submissions having a particularly difficult time predicting lateral contact force correctly. For each subsequent competition, a new comprehensive data set will be freely distributed for a different subject implanted with an instrumented tibial prosthesis.

Below we describe the data available from the first two competitions held in 2010 and 2011. These data have already been downloaded by researchers on six continents. Over 2,000 people have visited the competition website and performed over 150 unique downloads of competition data. The data were collected from two subjects implanted with a force-measuring tibial prosthesis (first subject: code JW, male, right knee, age 83 yr, mass 68 kg, height 1.66 m, neutral leg alignment; second subject: code DM, male, right knee, age 83 yr, mass 70 kg, height 1.70 m, valgus leg alignment). Both subjects received total knee replacement for primary knee osteoarthritis. Institutional review board approval was obtained, and the subjects gave informed consent for data collection and distribution. Subject JW was implanted with the first generation design consisting of four uniaxial force transducers, where the transducers measured compressive force in the four quadrants of the tibial tray.⁴⁰ Subject DM received the second generation design which measures all six components of tibial load.⁴¹ Both devices use a microtransmitter and antenna for telemetry of internal load data, and both devices permit calculation of medial and lateral contact force through the use of deformable contact models. All competition data can be accessed through the Simtk.org website (https://simtk.org/home/kneeloads). Data descriptions and “readme” files are included with the data sets, and data for subsequent competitions will be posted on the same website. Videos of the data collection from subject JW are available as Supplementary Material.

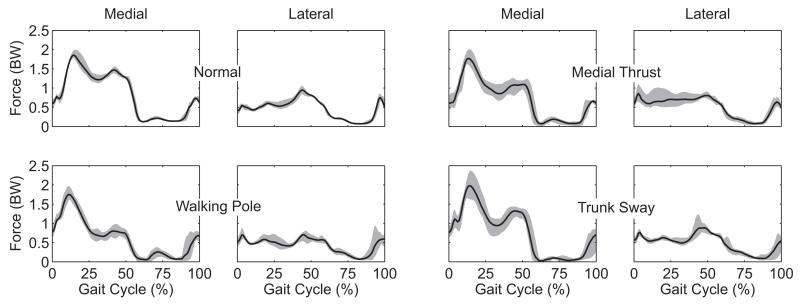
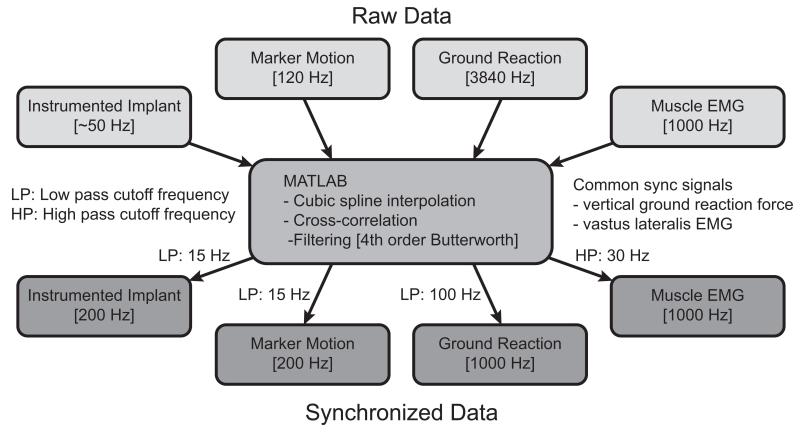
Data available for the competitions can be grouped into four categories: 1) motion data, 2) strength data, 3) imaging data, and 4) geometry data. Motion data (Table 2) include instrumented implant, marker-based video motion, ground reaction, muscle EMG, and single-plane fluoroscopy data (tibiofemoral joint only). All data were collected during a single test session with the exception of the fluoroscopy data, which were collected previously from the same subjects walking on a standard treadmill.¹⁸ Marker motion was measured using a 10-camera motion capture system (Motion Analysis Corporation, Santa Rosa, CA) and a modified Cleveland Clinic marker set that included extra markers on the feet and trunk (Fig. 1). Ground reaction forces and moments were measured using three force plates (AMTI Corporation, Watertown, MA). EMG signals were measured from 14 muscles using surface electrodes (Delsys Corporation, Boston, MA). Muscles from which EMG data were recorded include: semimembranosus, biceps femoris, vastus medialis, vastus lateralis, rectus femoris*, medial gastrocnemius, lateral gastrocnemius, and tensor fascia latae*, where an asterisk (*) denotes muscles for which a double-differential electrode was used. Motion data were collected for EMG calibration trials, static trials, isolated joint motion trials, leg motion trials, and gait motion trials. Four different gait patterns (normal, medial thrust,²⁰ walking pole,²⁰ and trunk sway⁴²) were measured to explore the extent to which gait modification can alter medial and lateral knee contact forces (Fig. 2). Raw data were synchronized using common ground reaction force and EMG signals and were spline-fitted, resampled, and filtered to produce synchronized data, which are easier to utilize than the raw data (Fig. 3). Both the raw and the synchronized data are available for download.

Table 2.

Overview of motion data available for subjects JW and DM.

		Motion Data Description
Trial Description		Instrumented Implant	Marker Motion	Ground Reaction	Muscle EMG	Knee Fluoroscopy
EMG Trials	Resting				✓
	MVC				✓
Static Trials	Toes forward	✓	✓	✓	✓
	Toes inward	✓	✓	✓	✓
	Toes outward	✓	✓	✓	✓
	Toes forward MVC	✓	✓	✓	✓
Joint Motion Trials	Right hip		✓	✓
	Left hip		✓	✓
	Right knee		✓	✓
	Left knee		✓	✓
	Right ankle		✓	✓
	Left ankle		✓	✓
Leg Motion Trials	Unloaded leg extension	✓	✓	✓	✓
	Loaded leg extension	✓	✓	✓	✓
	One-legged stand	✓	✓	✓	✓
	Two-legged squat	✓	✓	✓	✓
	Chair rise	✓	✓	✓	✓
	Calf rise	✓	✓	✓	✓
Gait Motion Trials	Normal	✓	✓	✓	✓
	Medial thrust	✓	✓	✓	✓
	Walking pole	✓	✓	✓	✓
	Trunk sway	✓	✓	✓	✓
	Treadmill					✓

Figure 1.

Description of surface marker locations used for motion capture trials.

Figure 2.

Medial and lateral contact forces measured by the instrumented tibial prosthesis of subject JW for four different gait patterns: 1) Normal gait, 2) Medial thrust gait involving knee medialization during stance phase, 3) Walking pole gait involving the use of bilateral trekking poles, and 4) Trunk sway gait involving tilting of the torso over the stance phase leg. Grey bands indicate ranges of maximum and minimum values over 5 trials of each gait pattern.

Figure 3.

Flowchart describing filtering and synchronization of raw experimental data.

Strength data (Table 3 – subject JW only) include instrumented implant, dynamometer torque-angle, and muscle EMG data for the knee under isometric, passive, and isokinetic conditions. All strength data were collected using an isokinetic dynamometer (Biodex Medical Systems, Shirley, NY), with torque data being gravity-corrected. Isometric flexion and extension data were collected using knee angles of 0, 30, and 60°, while isokinetic data were collected under maximum and submaximum concentric contraction conditions.

Table 3.

Overview of knee dynamometer data available for subject JW.

		Strength Data Description
Trial Description		Instrumented Implant	Biodex Dynamometer	Muscle EMG
Isometric	Flexion 0°	✓	✓	✓
	Flexion 30°	✓	✓	✓
	Flexion 60°	✓	✓	✓
	Extension 0°	✓	✓	✓
	Extension 30°	✓	✓	✓
	Extension 60°	✓	✓	✓
Passive	60°/s	✓	✓	✓
Isokinetic	Max concentric 60°/s	✓	✓	✓
	Submax concentric 60°/s	✓	✓	✓

Imaging data include axial CT scans and weight-bearing anteroposterior x-rays. The CT scans were performed pre- and post-operatively and spanned approximately 15 cm above and below the joint line. For subject JW, two post-operative x-ray images of the knee and pelvis regions are also available.

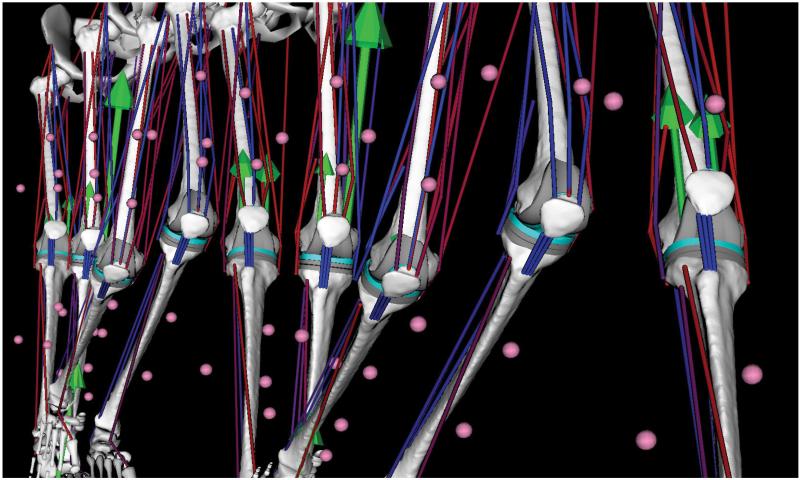
Geometry data (Table 4) include bone, implant, and combined bone-implant surface models. These models were generated from a combination of pre- and post-operative CT scan data, MR data collected from a subject of similar stature, and laser scans of implant components of the same sizes and designs. Point clouds representing the bones (femur, patella, tibia, and fibula) and metallic implant components (femoral component and tibial tray) were segmented from each subject’s post-operative CT scan data using image processing software (SliceOmatic, Montreal, Canada). Implant and bone surface models were then aligned to each subject’s point cloud data using reverse engineering software (Geomagic Studio, Research Triangle Park, NC). Implant surface models were created from the laser scan data. Bone surface models were created from either scaled MR-derived bone models (subject JW) or a combination of pre- and post-operative CT scan data (subject DM). For both subjects, these bone-implant models along with muscle lines of action derived from the scaled MR data were incorporated into subject-specific OpenSim musculoskeletal leg models⁴³ (Fig. 4). Animations of subject JW’s OpenSim leg model for one of his normal gait trials are available as Supplementary Material.

Table 4.

Overview of geometric bone and implant models available for subjects JW and DM. Bone models for were obtained from a subject of similar stature (JW) or from pre- and postoperative CT scan data (DM). Implant component models were obtained by laser scanning. Implant-bone models with implant components properly positioned and oriented on their respective bones were creating using each subject’s post-operative CT scan data. See Lin et al.⁶ for further details.

		Geometry Data Description
Anatomy Description		Stereolithography .stl File	Geomagic .wrp File
Femur	Femur bone	✓
	Femoral component surfaces	✓
	Femoral component volume	✓
	Femur with femoral component		✓
Patella	Patella bone	✓
	Patellar button volume	✓
	Patella with button		✓
Tibia-Fibula	Tibia bone	✓
	Fibula bone	✓
	Tibial insert surfaces	✓
	Tibial insert volume	✓
	Tibial tray	✓
	Tibia-fibula with tray-insert		✓
Complete Leg	All leg bones and components		✓

Figure 4.

Gait animation sequence of subject-specific OpenSim musculoskeletal leg model created for subject JW. Green arrows indicate ground reaction force acting on the foot and medial and lateral knee contact forces acting on the femur. Contact forces were calculated with a deformable knee contact model and are consistent with measurements made by the subject’s instrumented tibial prosthesis. Muscle color indicates muscle activation state based on the subject’s EMG data (red = active, blue = inactive). Pink spheres indicate motion capture surface marker locations on the shank and thigh.

Similar data have since been collected from the same two subjects along with two additional subjects (third subject: code PS, male, left knee, age 86, mass 75 kg, height 1.80 m, neutral leg alignment; fourth subject: code SC, female, left knee, age 68, mass 79 kg, height 1.63 m, neutral alignment) implanted with the second generation design. Institutional review board approval was obtained, and all subjects gave informed consent for data collection and distribution. For each subject, all data were collected during a single day of testing. Marker motion was measured using a 10-camera motion capture system (Vicon Corporation, Oxford, United Kingdom), ground reaction forces and moments were measured using three force plates (Bertec Corporation, Columbus, OH), and EMG signals were measured from 15 muscles using surface electrodes (Delsys Corporation, Boston, MA).

Compared to the first two data sets, six significant changes were made to the data collection protocol. First, additional overground gait patterns were explored (e.g., crouch gait, forefoot strike gait, bouncy gait – see Table 5). Second, normal gait data were also collected at different speeds on an instrumented split-belt treadmill (Bertec Corporation, Columbus, OH). Third, all EMG data were collected using double-differential electrodes. Fourth, fluoroscopic motion trials were more extensive, including treadmill gait, walk up/down across raised platforms, step up/down, chair rise, two-legged squat, open-chain knee flexion, and lunge. Fifth, knee laxity tests (i.e., anterior/posterior drawer, varus/valgus laxity, internal/external rotation laxity) were added, where implant motion was measured with fluoroscopy, applied force magnitude was measured with a load cell, and applied force direction and location were measured with the video motion system. Sixth, isometric knee and hip strength trials were collected from all four subjects. In addition, pre-surgery MR data are available for subject SC, the subject to be used for the third competition as well as the only female subject. Gait and fluoroscopic motion trials varied by subject based on the subject’s capabilities. Pending continued availability of funding, we hope to implant one final subject with the second generation design and to collect MR and CT data prior to implantation and CT data after implantation, facilitating the determination of patient-specific muscle lines of action. These new data sets will provide the basis for the competition in future years.

Table 5.

Summary of the different gait patterns performed by the four subjects for the most recent data collection sessions.

	Subject Code
Gait Trial Description	DM	JW	PS	SC
Normal	✓	✓	✓	✓
Medial thrust		✓		✓
Walking pole		✓		✓
Trunk sway				✓
Crouch	✓	✓	✓	✓
Forefoot strike	✓	✓		✓
Bouncy	✓	✓		✓
Smooth	✓			✓
Right turn			✓
Treadmill – Single speed	✓ *			✓ *
Treadmill – Multiple speeds	✓	✓	✓ *	✓

^*With single-plane fluoroscopy

FUTURE DIRECTIONS

Given this historical perspective and the availability of the unique in vivo data described above, where is musculoskeletal modeling headed in the future, and how will it get there? We believe that it is headed toward increased clinical applicability and increased clinical usability and that it will get there via increased subject specificity and decreased mathematical indeterminacy. Below we discuss each of these future areas of advancement, noting that advances will likely come not only from competition participants but also from the broader musculoskeletal modeling research community as it makes use of the Grand Challenge data sets.

From a global perspective, we believe that all roads lead to increased clinical applicability. For years, the musculoskeletal modeling research community has focused on tool development, with few models being used to design or inform clinical treatment. The current economic environment is making it difficult to secure research funding purely for tool development. We believe this trend is positive, as it forces the field to work harder at identifying clinical problems that can be addressed with existing modeling technology. On the clinical side, there is a trend toward “evidence-based medicine,” which involves “the integration of best research evidence with clinical expertise and patient values.”⁴⁴ Validated modeling approaches capable of predicting clinical outcome could contribute to “best research evidence.” Thus, to achieve increased clinical applicability, a convergence is needed between modelers who desire to make their model predictions clinically useful and clinicians who appreciate the predictive capabilities offered by models.

While clinical applicability is the ultimate goal, such applicability cannot be achieved without a corresponding increase in clinical usability. Existing models that have the potential to be clinically useful can be customized to individual patients and utilized to predict treatment outcomes only by highly trained researchers. In contrast, clinical utility would ideally involve patient customization and predictive algorithms that could be used directly by clinicians in a clinical setting. While existing musculoskeletal modeling programs are making significant steps in this direction, we are still far from having sophisticated musculoskeletal modeling, simulation, and optimization capabilities available as part of standard clinical practice.

To make these clinical goals a reality, musculoskeletal modeling researchers will need to achieve increased subject specificity in their modeling processes, especially for musculoskeletal geometry and muscle-tendon models. Each patient is unique. Thus, for musculoskeletal models to be used routinely in clinical practice, key model parameter values that influence the outcome of interest will need to be calibrated to movement, imaging, strength, and other data collected from the patient prior to treatment. Currently, model calibration methods vary from lab to lab, typically require significant manual adjustment by highly experienced researchers, and often sacrifice accuracy for simplicity (e.g., linear scaling of generic musculoskeletal models). Furthermore, some model parameters, especially those related to muscle-tendon models, are not observable and thus cannot be calibrated reliably using existing methods. New experimental measurement methods as well as standardized and automated calibration methods are needed for models to reach the point of broad clinical utility.

Finally, to maximize potential clinical utility, musculoskeletal modeling methods for predicting in vivo muscle and contact forces will need to achieve decreased mathematical indeterminacy without resorting to reduction methods that eliminate or group unknowns. While optimization methods provide unique solutions to the muscle redundancy problem, it is unlikely that current methods provide the correct solutions. This statement is evidenced by the need for model parameter tuning to achieve in vivo knee muscle force predictions that yield in vivo knee contact force predictions consistent with instrumented implant measurements.^5,6

At least three avenues are available for reducing and possibly even eliminating muscle force indeterminacy. The first avenue is use of deformable knee contact models,⁴⁵ as facilitated by new technologies such as surrogate contact modeling.⁴⁶ Without a deformable knee contact model, researchers typically assume that the net flexion-extension moment is the only inverse dynamic load at the knee to which contact forces and moments do not contribute, resulting in only one constraint for predicting muscle and ligament forces. When a deformable knee contact model is added, no assumptions are needed about how contact forces and moments contribute to each of the six inverse dynamic loads at the knee. Since medial and lateral contact forces are insensitive to kinematic measurement errors for three of these loads (i.e., flexion-extension moment, internal-external rotation moment, and anterior-posterior force),⁴⁷ two additional inverse dynamics loads become available as constraints if a standard motion capture system is used to measure knee kinematics.⁶

The second avenue is use of full-leg rather than knee-only musculoskeletal models. To date, the highest fidelity models used to predict knee muscle forces have been knee-only models, with models of neighboring joints often being omitted. Adding the hip and ankle joints to these models will provide additional constraints on the forces produced by biarticular muscles spanning the knee, again altering knee muscle force estimates.

The third avenue is use of patient-specific muscle synergies to constrain predicted muscle activation patterns. Lower extremity muscle EMG signals measured during human movement can be reconstructed using linear combinations of time-varying basis functions referred to as muscle synergies. For gait, only five muscle synergies are typically required to account for at least 90% of the variability in all lower extremity EMG signals.⁴⁸ From a neural control perspective, muscle synergies provide significant dimensionality reduction and limit the achievable lower extremity EMG patterns. We anticipate that future methods for predicting muscle forces will utilize muscle synergy or other analysis methods to limit predicted activation patterns.

While pursuing these advances, musculoskeletal modeling researchers will need to address at least four important challenges. The first is that muscle force validation using instrumented implant and EMG data is indirect and therefore weaker than is contact force validation. Ligaments and other soft tissues likely contribute significantly to some of the net knee loads calculated via inverse dynamics. Construction of patient-specific ligament and soft tissue models using the knee laxity data collected for future competitions would reduce the likelihood that predicted muscle forces are compensating for missing passive forces. The second challenge is that prediction of contact forces in natural knees will be more difficult than in artificial knees. Natural knee contact is difficult to model due to the presence of the menisci, an anterior cruciate ligament, and complex articular geometry where both surfaces deform. Muscle force prediction methods that work well for implanted knees are likely to work well in natural knees only to the extent that natural knee contact forces (but not necessarily contact pressures) can be modeled accurately. The third challenge is quantifying the sensitivity of model predictions to uncertainties in experimental inputs. If uncertainties in the inputs create large uncertainties in the outputs, then methods for reducing input uncertainties will need to be developed. The final challenge is addressing muscle fatigue and other history-dependent muscle behaviors. Fatigued muscles will not generate the same amount of force as rested muscles. Methods for modeling fatigue accurately may become necessary if contact and muscle force estimates are desired in situations where fatigue is likely to occur.

CONCLUSIONS

This paper has described an annual “Grand Challenge Competition to Predict In Vivo Knee Loads” based on the most comprehensive human movement and imaging data sets available to date for evaluating musculoskeletal model predictions of in vivo contact and muscle forces in the knee. The data sets include not only traditional gait lab data collected for a variety of tasks but also contact force data collected simultaneously from instrumented tibial prostheses. We have also provided a historical perspective on the use of musculoskeletal models to predict muscle and contact forces in the knee, along with our assessment of where musculoskeletal modeling is headed in the future and how will it get there. Our hope is that these data sets will contribute to making musculoskeletal modeling clinically useful for addressing a variety of orthopedic and neurological conditions.