Simulation of Finnish Population History, Guided by Empirical Genetic Data, to Assess Power of Rare-Variant Tests in Finland

Abstract

Finnish samples have been extensively utilized in studying single-gene disorders, where the founder effect has clearly aided in discovery, and more recently in genome-wide association studies of complex traits, where the founder effect has had less obvious impacts. As the field starts to explore rare variants’ contribution to polygenic traits, it is of great importance to characterize and confirm the Finnish founder effect in sequencing data and to assess its implications for rare-variant association studies. Here, we employ forward simulation, guided by empirical deep resequencing data, to model the genetic architecture of quantitative polygenic traits in both the general European and the Finnish populations simultaneously. We demonstrate that power of rare-variant association tests is higher in the Finnish population, especially when variants’ phenotypic effects are tightly coupled with fitness effects and therefore reflect a greater contribution of rarer variants. SKAT-O, variable-threshold tests, and single-variant tests are more powerful than other rare-variant methods in the Finnish population across a range of genetic models. We also compare the relative power and efficiency of exome array genotyping to those of high-coverage exome sequencing. At a fixed cost, less expensive genotyping strategies have far greater power than sequencing; in a fixed number of samples, however, genotyping arrays miss a substantial portion of genetic signals detected in sequencing, even in the Finnish founder population. As genetic studies probe sequence variation at greater depth in more diverse populations, our simulation approach provides a framework for evaluating various study designs for gene discovery.

Introduction

A founder effect can result either from a true founder event (i.e., the establishment of a new population from a limited pool of individuals) or from an extreme reduction in population size (i.e., a bottleneck in size) followed by relative genetic isolation from other populations. The population of Finland is one of the best-studied genetic isolates. The Finnish genetic architecture has been shaped by a series of founder effects and a subsequent drift in local subisolates. The initial founder effects are generally associated with two colonization waves 4,000 and 2,000 years ago to southern and western Finland. More recently, there was an internal migration movement in the 15^th–16^th centuries from a small southeastern area to the middle, western, and finally northern and eastern parts of the country.¹

The Finnish population has been extensively utilized in genetic studies. It is considered to be a relatively homogenous large founder population and hence potentially well suited for genetic mapping. The evidence of a founder effect includes enrichment of almost 40 rare recessive diseases, longer regions of linkage disequilibrium (LD), increased kinship coefficients between pairs of randomly chosen individuals, and extended runs of homozygosity.^1–10 In part because of the founder effect, identification of the genes underlying the rare diseases enriched in Finland has been remarkably successful.¹ Finnish samples have also contributed to many genome-wide association studies (GWASs) of complex traits, but because common (minor allele frequency [MAF] > 5%) variation is less influenced by human population history, a founder effect would be less likely to provide a specific advantage in this setting.

Studies of polygenic traits and disorders are now moving to a middle ground between GWAS genotyping methods (thus far focused largely on common variation, typically MAF > 5%) and sequencing-based methods that were most successfully employed for identifying extremely rare variants in single-gene disorders. This middle ground is association studies of lower-frequency (MAF < 5%) variants, analyzed either individually or in aggregate (the aggregate analysis has also been termed the rare-variant association study¹¹). As such, it is of great interest and importance to confirm the Finnish founder effect in sequencing data that include rarer variants and to assess the implications of these rare-variant association studies. As a result of the founding event and subsequent strong genetic drift, some variants that are rare in the ancestral population will have risen in frequency in a founder population, whereas others will have decreased or disappeared. These alterations in allele frequency could potentially increase power of rare-variant tests in two ways. First, some rare and potentially deleterious variants could rise to higher frequencies, out of proportion to what might be expected given their deleterious effects. Second, there is greater homogeneity of rare variation in a founder population and thus fewer background rare variants at any individual locus. As an example, a protective mutation for Alzheimer disease (MIM 104300) was discovered in part because it has a much higher frequency in the Scandinavian populations (∼0.4%) than in the general European population (<0.01%).¹²

Exome sequencing studies are emerging as a popular approach for identifying rare coding variants associated with complex traits, whereas a cheaper alternative approach is to use array-based genotyping of a defined set of coding variants. The human genetics community has aggregated an extensive list of putative functional coding variants from the exome sequences of >12,000 individuals for array-based genotyping platforms (e.g., the Illumina Infinium HumanExome BeadChip and the Affymetrix Axiom Exome Array Plate; see Exome Chip Design in the Web Resources for a description of SNP content and selection strategies). Although these arrays do not provide a complete catalog of all coding variants, the set of variants selected for array design is estimated to include >97% of the nonsynonymous variants that would be detected in any individual genome through exome sequencing. In theory, the coverage would be even higher for a founder population, which has fewer rare variants than a nonfounder population.

To increase power to detect effects of rare variants, especially those that are too infrequent to be individually tested for association, many groups have devised tests that combine evidence across multiple variants.¹³ These tests have become a standard approach for analyzing rare variants and include burden tests^14–16 and other types of tests that aggregate evidence across sets of variants.^17,18 The relative power of such tests to detect association is strongly influenced by underlying genetic architecture. Specifically, the proportion of causal variants among all variants analyzed and the distribution of effect sizes and allele frequencies of causal variants all affect test performance. Different statistical tests also have different sets of parameters, the values of which can have a large effect on the power of the tests.

Different diseases and phenotypes most likely have different architectures.¹⁹ To try to evaluate how different sample selections (founder versus nonfounder populations), analytical methods (single-variant tests versus gene-based tests), and study designs (exome sequencing versus exome array genotyping) perform with different genetic architectures, we have developed a population-genetics framework to assess the impact of the Finnish population history on genetic studies of rarer variation. Our approach has four basic stages: (1) confirming and characterizing the Finnish founder effect in sequence data, (2) developing a simultaneous simulation of sequence variation in the non-Finnish European (NFE) population and the Finnish population to closely approximate the sequence data, (3) specifying a range of models of genetic architectures to generate simulated phenotypic data, and (4) comparing operating characteristics of different gene-based tests and single-variant tests on phenotype, genotype, and sequence data from simulated founder and nonfounder populations.

With this framework in place, we address the following questions: (1) Under what types of genetic architecture(s) is it more powerful to use a founder population such as Finland? (2) Under different genetic models, what are the optimal association tests for rare variants in a founder population? (3) How does power compare between using exome sequencing data and using exome chip data, particularly in a founder population? Our results show that power to detect genetic signals—by both single-variant and gene-based tests—is higher in samples from the Finnish founder population than in equivalently sized NFE samples, especially when the phenotypic effects of variants are tightly coupled with effects on fitness. SKAT-O, VT (variable-threshold) tests, and single-variant tests have the highest mean power in a founder population across simulated data sets. At a fixed cost, genotyping strategies have far greater power than sequencing; in a fixed number of samples, however, genotyping arrays miss a substantial portion of causal variation detected in sequencing.

Material and Methods

Empirical Exome Sequencing Data

We used whole-exome sequenced samples from the Genetics of Type 2 Diabetes (GoT2D) Project. In total, 2,850 European type 2 diabetes case and control subjects from four cohorts (Diabetes Genetics Initiative [DGI], Finland-United States Investigation of NIDDM Genetics [FUSION], GoT2D-UK, and Kooperative Gesundheitsforschung in der Region Augsburg [KORA]) were whole-exome sequenced at ∼40×. Exome target capture was performed with the Agilent SureSelect Human All Exon hybrid selection kit, and sequence was obtained on a HiSeq machine. Reads were mapped to the human reference genome (hg19, UCSC Genome Browser) with the Burrows-Wheeler Aligner²⁰ and processed with the Genome Analysis Toolkit (GATK) for recalibrating base-quality scores and performing local realignment around known insertions and deletions (indels).²¹ SNPs and small indels were called with the UnifiedGenotyper module of GATK and filtered for removal of SNPs with annotations indicative of technical artifacts (such as strand bias, low variant call quality, or homopolymer runs).²¹ We kept samples from GoT2D-UK and KORA as the NFE population and samples from FUSION (Table S1, available online) as the Finnish population for our analyses. We excluded SNPs with any missing data in any individual, SNPs with Hardy-Weinberg equilibrium p < 10⁻⁵, and all nonautosomal SNPs. We carried out multidimensional scaling to identify population outliers (Figure S1). We filtered out relatives for whom the estimated genome-wide identity-by-descent (IBD) proportion to alleles shared was >0.10. We also excluded individuals with an inbreeding coefficient > 0.05 or < −0.05. We estimated IBD sharing by using PLINK’s “--genome” option²² and estimated inbreeding coefficients by using PLINK’s “--het” option. All analyses were carried out on an LD-pruned set of SNPs obtained with the PLINK option “--indep,” which recursively removes SNPs within a sliding window. The parameters for --indep are as follows: window size in SNPs = 50, n = 5 SNPs to shift the window at each step, and variance-inflation-factor threshold = 1.8. The final data set included 843 Finnish samples and 820 NFE samples.

Ethics Statement

For the GoT2D study, attendance was voluntary, and each participant provided written informed consent, including for information on genetic analyses. Local institutional review boards approved the study protocols.

Simulation of Exome Sequencing Data

Exome sequencing data were simulated with ForSim, a tool for forward evolutionary simulation.²³ The average gene coding length was set to 1,500 bp. We used a mutation rate per site of 2 × 10⁻⁸,^24–26 as well as a uniform locus-wide recombination rate of 2 Mb/cM as previously reported.²⁷ We modeled the distribution of selection coefficients for de novo missense mutations by a gamma distribution²⁸ (as in previous reports,^28,29 we assumed that ∼20% of missense sites are neutrally evolving).

For modeling the NFEs, we used a conventional four-parameter model of the history of the European population with long-term constant size followed by a bottleneck and then by an exponential expansion (Figure 1).³⁰ The four parameters used were (1) long-term ancestral effective population size, (2) bottleneck population size, (3) duration of exponential growth in generations, and (4) recent effective population size. We adapted parameters from a recent simulation that generated representative sequence data for European populations.²⁷ (See Figure 1 for final parameter values.)

Figure 1.

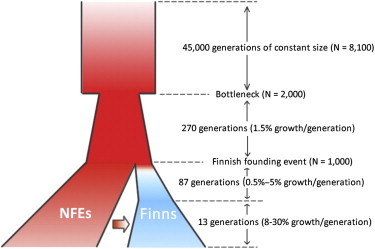
The Final Demographic Model for Simulating NFEs and Finns Simultaneously

The NFEs were modeled as long-term (45,000 generations) constant size (N = 8,100) followed by a bottleneck (N = 2,000) and then by exponential growth (1.5% growth per generation). To model the Finns, we tested three general classes of models, of which only one (class 3 in Table S2) approximated the empirical observations. In this model, after the initial founding event (100 generations ago, N = 1,000), the Finns went through a slow growth phase (0.5%–5% growth per generation) and then a more recent fast growth phase (8%–30% growth per generation); there was gene flow from the NFEs to the Finns.

We modeled the Finns as a founder population established by a small number of NFEs. The founding event was followed by a slow growth phase and a more recent fast growth phase (Figure 1). We filtered the demographic-history parameters by comparing them to empirical exome sequencing data. P(data | model) was calculated and used for model fitting (see Appendix A for further discussion). We tested two other models, neither of which agreed with the empirical observations, as well as our current model (Table S2).

Simulation of Exome Chip Data

Exome chip data were generated on the basis of simulated exome sequencing data. The process resembled that of the actual exome chip design (see Web Resources for a description of SNP content and selection strategies). Approximately 12,000 simulated exomes across 16 cohorts were pooled together. The cohorts were matched by ancestry and sample size with the real cohorts (except that non-European samples were substituted with NFE samples). Only missense variants observed three or more times in at least two data sets were selected. Approximately 90% of the selected SNPs passed the design and were used for the simulated chip. For simulating the exome chip without contribution of Finnish samples, all procedures were the same except that Finnish samples were replaced with an equal number of NFE samples.

Simulation of Phenotypic Variation

We simulated a quantitative trait (QT) with a target size of 1,000 genes and heritability of 80%. For efficiency, we modeled the heritability as completely explained by coding variants and a large target size of 1,000 genes; power scales with total heritability, with the fraction of heritability explained by coding variation, and inversely with target size. We modeled additive genetic effects and environmental effects. We did not consider nonadditive effects (dominant, recessive, epistatic, or gene-environment interactions) in our simulations. We used the joint allele frequency spectrum of both the Finns and the NFEs when calculating heritability. We scaled the effect sizes so as to cap heritability at 80%. More specifically, variance explained by a variant was calculated as 2 × MAF × (1 − MAF) × p², where p is the phenotypic effect. We summed this up over all variants and adjusted effect sizes of all variants by a uniform factor to cap heritability (additive genetic variance) at 80%.

We assume that neutral missense variants have no effect on phenotype. To assign effect sizes of causal variants (nonneutral missense variants), we implemented a range of possible mappings between a variant’s selection coefficient (s)—we modeled the distribution of selection coefficients for de novo missense mutations by a gamma distribution, so s is known for every variant in our simulated data—and its effect on phenotype (p). We modeled these mappings as p = s^τ × (1 + ε) as suggested by Eyre-Walker et al.³¹ Here, τ is the degree of coupling between p and s, and ε is a normally distributed random-noise parameter. In the case of common diseases of postreproductive onset, the role of natural selection on causal variants is not yet clear. Therefore, we tested a range of scenarios: M1 (τ = 0), M2 (τ = 0.5), M3 (τ = 1), and M4 (τ randomly chosen with equal probability among 0, 0.5, and 1 for each effect gene).

To determing the direction of effect of causal variants on a QT, we further assumed that, in each trait-affecting gene, 0%–20% of the causal variants influence the QT in the opposite direction from the remaining causal variants. This assumption is based on two different arguments: (1) the vast majority of de novo amino acid substitutions with a measurable effect reduce protein activity, and gain-of-function alterations are much less frequent and are restricted to specific residues or domains; and (2) some genes, such as APOB (MIM 107730) and PCSK9 (MIM 607786),^18,32 clearly illustrate a mixture of variants that affect QTs in both directions.

Association Tests and Power Analysis

We conducted five different gene-based tests on simulated data. We performed four burden tests—VT,¹⁴ T1 (fixed-threshold test with a 1% threshold), T5 (fixed-threshold test with a 5% threshold), and MB (Madsen and Browning)¹⁶—by running SCORE-Seq (see Web Resources for details). In these tests, the mutation information is aggregated across multiple variant sites of a gene through a weighted linear combination and then related to the phenotype of interest through appropriate regression models. The weights can be constant (T1, T5, and VT tests) or dependent on allele frequencies (MB test). The allele frequency threshold can be fixed (T1, T5, and MB tests) or variable (VT test). We also performed the unified optimal test SKAT-O by using default weights.³³ SKAT-O is a data-adaptive test that includes both burden tests and the sequence kernel association test (SKAT)¹⁷ as special cases. We carried out single-variant tests by using PLINK’s “--linear” option. We limited our analysis to variants with a MAF < 5%.

The exome-wide significance threshold for gene-based tests was set to α = 2.5 × 10⁻⁶ (after Bonferroni correction assuming 20,000 genes in the exome). Power was defined as the number of effect genes reaching genome-wide significance divided by the target size (1,000). The exome-wide significance threshold for single-variant tests was 0.05 divided by the number of variants tested (which varied with sample size, excluding singletons and doubletons). The power of the single-variant test was defined as the number of effect genes harboring genome-wide-significant variant(s) divided by 1,000.

Results

Assessing the Finnish Founder Effect

We analyzed whole-exome sequence data of NFE and Finnish samples from the GoT2D Project (see Material and Methods). If the Finnish population did indeed go through a founding event in the past, there are a number of direct predictions for the allele frequency spectra and the sharing of variants between the Finns and the NFEs. When comparing Finnish and NFE samples of the same size (n = 500), we found that the allele frequency spectra were shifted toward higher frequencies in the Finns (Figure 2). The proportion of singleton variants was much lower in the Finns than in the NFEs (28% versus 46%, respectively, for synonymous variants; 39% versus 57%, respectively, for missense variants), whereas the opposite was true for common (MAF > 5%) variants (31% versus 22%, respectively, for synonymous variants; 19% versus 12%, respectively, for missense variants). Furthermore, singleton variants in a population of Finns (n = 250) had a higher likelihood of being seen again in another population of Finns (n = 250) than did singleton variants in a population NFEs of being seen again in another population of NFEs (34% versus 23%, respectively, for synonymous singleton variants, 30% versus 20%, respectively, for missense singleton variants; Figure S2). We also observed that SNPs found in both samples tended to have higher frequencies in the Finns (paired t test p value < 0.01; Table S3). Compared to the NFEs, the Finns had a lower level of heterozygosity (on average, there were 0.6% fewer heterozygous sites per individual in the Finns, t test p value < 0.01) and reduced genetic diversity (Watterson’s estimate adjusted by sequence length was 6.14 × 10⁻⁴ for the Finns and 1.01 × 10⁻³ for the NFEs). All of these results strongly confirm the presence of a founder effect in Finland.

Figure 2.

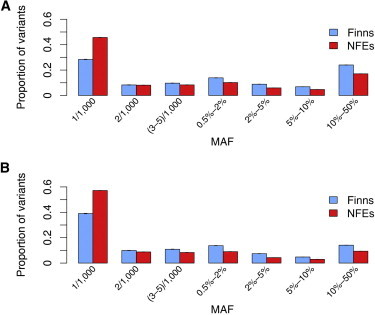
Empirically Observed Allele Frequency Spectra in 500 Finns and 500 NFEs

Means and SDs of proportions were calculated on the basis of 100 rounds of sampling. There was an excess of common variants in the Finns for both synonymous (A) and missense (B) variants.

Simulation of Coding-Sequence Variation in Hundreds of Thousands of Samples

To enable a controlled characterization of the performance of different sample selections, analytical methods, and study designs under a range of scenarios, we used the forward-simulation package ForSim²³ to generate coding-sequence data for the NFEs and the Finns simultaneously. This way, we could simulate evolution of complex traits over time in large samples and know the truth (i.e., fitness effects) about all variants. To model the NFEs, we used the conventional four-parameter model³⁰ and adapted parameters from a recent simulation that generated representative sequence data for European populations (Figure 1).²⁷ We further modeled the Finns as a founder population established by a small number of NFEs. We refined our demographic parameters for the Finnish model by comparing to exome sequencing data from the GoT2D project (see Material and Methods). In our final model, the initial founding event was followed by a slow growth phase and then a more recent fast growth phase with gene flow from the NFEs to the Finns (Figure 1). Figure 3 shows that our final demographic model reproduces the observed allele frequency spectra well. We also analyzed the missense/synonymous ratio (Figure S3) and allele sharing between the Finns and the NFEs (Figure S4); these metrics are also similar between the observed and simulated data.

Figure 3.

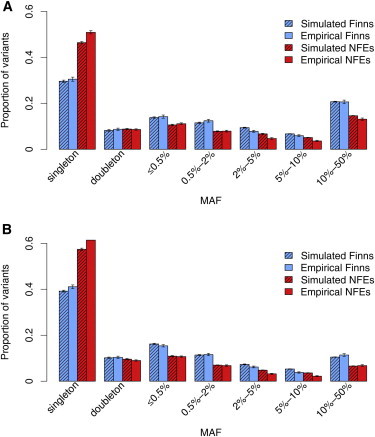
Agreement of Empirical Allele Frequency Spectra with the Modeled Spectra

Sample sizes were 843 for the Finns and 820 for the NFEs. Synonymous variants (A) and missense variants (B) are shown. Means and SDs of proportions were calculated on the basis of 100 rounds of sampling, and 1,000 genes were sampled for each round.

Specification of a Range of Disease Models

Protein-coding variation will only partially explain the phenotypic variation of any polygenic trait. However, to focus on the role of coding variation (because it is more likely to be enriched with functionally significant alleles), we simulated a heritable QT (h² = 80%) for which aggregated coding variation in each of 1,000 genes explains, on average, 0.1% of total heritability. We assumed that selectively neutral missense variants are background variants with no effects on the trait, whereas selectively nonneutral missense variants are the causal variants. We generated four different disease models by varying the degree of coupling (τ) between a causal variant’s phenotypic effect and the strength of purifying selection against that variant.³¹ Broadly, M1 (τ = 0) is characterized by rare and common alleles that have similar effects on phenotype, M2 (τ = 0.5) produces a modest correlation between variant frequency and effect size, and M3 (τ = 1) results in a sharp inverse correlation. M4 (τ randomly chosen among 0, 0.5, and 1 for each effect gene) might represent a more realistic scenario, given that different genes are likely to have different pleiotropic effects and are therefore exposed to different strengths of purifying selection. As expected, we observed that as τ increased, more phenotypic variance was explained by rare variants (Figure S5A).

Alterations in Allele Frequency in the Founder Population

With simulated data, we demonstrated alterations in allele frequency in the founder population, which could potentially increase the power of rare-variant tests. First, there was greater homogeneity of rare variation at any individual locus in a founder population. The Finns had on average 2.5× fewer rare (MAF < 5%) variants per gene than did the NFEs (mean 20.0 ± 4.5 versus 52.3 ± 7.4, respectively). This reduction in rare variants was seen for both variants we simulated as causal and those simulated as neutral, background variants (Figure S6). As seen in Figure S7, the cumulative allele frequency of causal variants and background variants per gene was similar between the Finns and the NFEs, meaning that there were fewer rare variants in the Finns, but they were each on average more common than variants in NFEs.

Second, there was increased frequency of causal variants (thus variance explained per gene) at some genes. We observed that the distribution of the variance explained per gene was wider in the Finns than in the NFEs (Figure 4). At one end of the distribution (the left tails of the graphs in Figure 4), the increased frequency of some individual causal variants led to a greater variance explained for some genes in the Finns (this was more obvious with a larger τ); at the other end of the distribution, so many causal variants were lost in Finland that other genes had lower variance explained in the Finns. As a result, some genes were detectable in smaller sample sizes in the Finns than in the NFEs, whereas it was more difficult to detect the effects of rare variation in some other genes, given that too many causal variants had been lost because of the founder effect.

Figure 4.

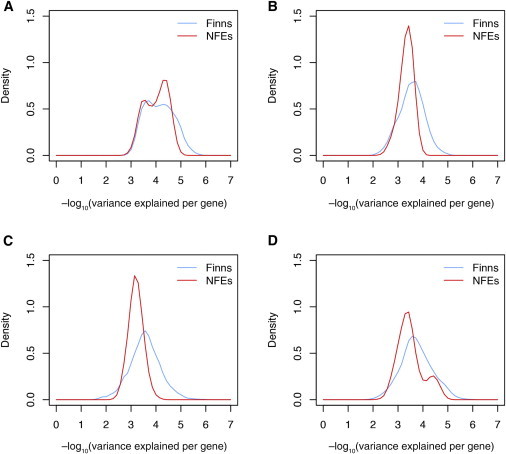
Distribution of Variance Explained per Gene

Distribution of variance explained per gene by variants with a MAF < 5% under four different disease models in either 30,000 Finns or 30,000 NFEs.

(A) M1 (τ = 0).

(B) M2 (τ = 0.5).

(C) M3 (τ = 1).

(D) M4 (τ randomly sampled from 0, 0.5, and 1 for each effect gene).

Founder Population versus Nonfounder Population in Exome Sequencing Studies

With simulated genotype and phenotype data, we compared the power of using 30,000 NFEs and the power of using 30,000 Finns in exome sequencing studies under different disease models. We implemented five gene-based tests (SKAT-O and the T1, T5, MB, and VT tests) and single-variant tests. Because we are interested in the role of lower-frequency variants, we ran all tests on variants with a MAF < 5%. In the context of exome sequencing studies, the significance threshold for calculating power was set to α = 2.5 × 10⁻⁶ (after Bonferroni correction assuming 20,000 genes in the exome).

As seen in Figure 5, as τ increased, so did the relative increase in power from using Finns in comparison to using NFEs (compare panels A, B, and C). Under M4, the biggest power gain in the Finns was seen among genes for which the τ value was 1 (Figure S8). As the value of τ increased, the phenotypic impacts of rare variants increased (Figure S5). Therefore, it is more powerful to use a founder population in models where rare variation plays a more prominent role. These results are consistent with the effect of a founder event on allele frequencies—founder effects have a greater impact on rare variants than on common variants.

Figure 5.

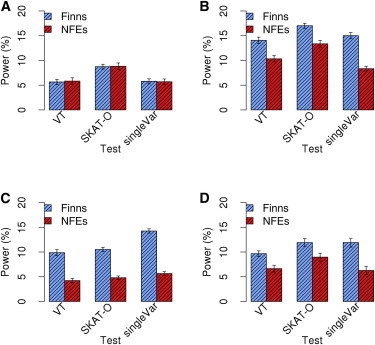
Power of Exome Sequencing Studies in 30,000 Finns versus 30,000 NFEs

We simulated a QT (h² = 80%) for which aggregated coding variation in 1,000 genes explains the total heritability. We generated models M1–M4 by varying the degree of coupling (τ) between a causal variant’s phenotypic effect and the strength of purifying selection against that variant. We compared SKAT-O, the VT test, and single-variant tests (singleVar). For each model, means and SDs of power were calculated on the basis of 20 simulated data sets.

(A) M1 (τ = 0).

(B) M2 (τ = 0.5).

(C) M3 (τ = 1).

(D) M4 (τ randomly sampled from 0, 0.5, and 1 for each effect gene).

Understanding the Excess of Power in the Founder Population

To understand why there was an excess of power in the founder population across different disease models, we considered genes detected in one population only. We observed that genes detected only in the Finns tended to have greater variance explained per gene in the Finns than in the NFEs (Figure S9), whereas the opposite was true for genes detected in the NFEs only (Figure S10). For genes detected in the Finns only, the cumulative allele frequency for background variants was similar between the Finns and the NFEs, but the cumulative allele frequency for causal variants was shifted upward in the Finns (Figure S11). For genes detected in the NFEs only, the opposite was true (Figure S12).

As shown above, the overall rise in frequency of causal variants and thus the greater variance explained for some genes could drive the power excess in the Finns. We next tested whether reduced heterogeneity could also contribute to the power difference. We selected a set of genes for which the variance explained was closely matched between the NFEs and the Finns (Figure S13). As shown in Figure S14, the accumulated allele frequencies of causal variants and background variants were similar between the two populations as well. The power gain in the Finns was retained under M3 (Figure S15), suggesting that reduced genetic heterogeneity alone could increase power when variance explained at a gene stays the same in the founder population. This effect was clearer when the τ value was 1, given that rare variants play a more prominent role.

Relative Power of Different Association Tests for Rare Variants in a Founder Population

Among the five gene-based tests we conducted, SKAT-O and the VT test performed best across a range of models in both the Finns and the NFEs (Figures 5 and S16), given that SKAT-O allows different variants to have different directions and magnitude of effects and the VT test decreases background noise by selecting an optimal frequency threshold. The single-variant test performed reasonably well under different disease models, and it was particularly powerful when τ was large, especially when used in a founder population (Figures 5 and S16). As τ increased, the effect sizes of rare causal mutations tended to increase, making it more powerful to test these variants individually. For a founder population like the Finns, as we have shown earlier, the allele frequency spectra are shifted away from the rarest variants, which gives extra power in testing rare variants individually.

Of note, LD was not taken into account in either the single-variant or the gene-based tests. For gene-based tests, LD was generally not addressed, at least for discovery of gene-wide association signals. For single-variant tests, we operated under the assumption that the causal variants are directly assessed. Incorporating LD might have further increased the power of single-variant analyses if one or more very rare variants were tagged by a single more common variant.

Exome Chip Studies versus Exome Sequencing Studies

Exome chip genotyping, despite being a much cheaper technology than exome sequencing, has not been rigorously assessed in terms of cost efficiency. Here, we used our simulation framework to try to address this question. We first confirmed that our simulations reproduced the expected differences in observed allele frequency spectra between exome chip and exome sequence data (compare Figures S17 and 3B). We then compared the cost efficiency of exome chip studies and exome sequencing studies under different disease models in the Finnish founder population. The cost of exome chip per sample was assumed to be about one-tenth of that of exome sequencing. Figure 6 shows that under M4, the power of SKAT-O was far greater in exome chip studies than in exome sequencing studies at a fixed cost (middle versus bottom line); in a fixed number of samples, however, genotyping arrays missed a substantial portion of causal variation detected in sequencing (top versus middle line). We also compared the two study designs in a nonfounder population (Figure S18) under M1–M3 (Figures S19 and S20), as well as by using different rare-variant association tests (Figure S19), and observed similar results. Despite substantial cost efficiency, the exome chip was underpowered to detect the contributions of certain genes simply because not enough causal variants in these genes were covered by the chip. This became more apparent as τ increased (Figure S20), because the allele frequency spectrum of causal variants shifted downward, and the exome chip captured fewer casual variants (Figure S21).

Figure 6.

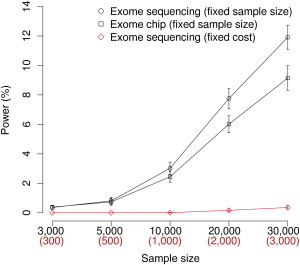
Power of Exome Chip Study versus Exome Sequencing Study in the Finns

The comparison was done under M4 with SKAT-O. Because different genes are likely to have different pleiotropic effects and are therefore exposed to different strengths of purifying selection, M4 was generated to represent a potentially more realistic scenario. The top two lines show power comparison at a fixed sample size; the bottom two lines show power comparison at a fixed cost (and thus only one-tenth of the samples were sequenced). For both exome chip and exome sequencing studies, means and SDs of power were calculated on the basis of 20 simulated data sets.

Because Finnish samples contributed to exome chip design, we went on to assess how much their inclusion would affect the power of the exome chip in Finns, i.e., how the exome chip would perform in a non-Finnish founder population. To address this question, we simulated a different exome chip with no contribution of Finnish samples (replaced with an equal number of NFE samples). As expected, the power for rare-variant association in Finns decreased when Finns were not used in the SNP-discovery process of the exome chip. The power decrease was minimal at a low sample size, reaching a difference of approximately 2% when 30,000 samples were used (Figure S22; the power dropped from ∼10% to ∼8% when Finns were not used). This suggests that the current exome chip would perform slightly less well in a non-Finnish founder population. However, the exome chip is still a far more cost-efficient strategy for such populations than exome sequencing, the power of which is negligible at a comparable cost (bottom line in Figure 6). If it is desirable to avoid the marginal loss of power in non-Finnish founder populations of interest, one could perform exome sequencing by using a representative population sample first and supplement the exome chip with the newly discovered variants to ensure that rare variation in that founder population is directly represented on the chip.

Discussion

By using forward simulations based on empirical deep resequencing data, we have shown that (1) founder populations can provide additional power, especially when the phenotypic effects of variants are tightly coupled with effects on fitness; (2) in a founder population, the single-variant test, SKAT-O, and the VT test perform best under different disease models, and the single-variant test is particularly powerful when the phenotypic effects of variants are tightly coupled with effects on fitness; and (3) exome chip genotyping is currently much more cost efficient than exome sequencing but misses a substantial portion of causal variation in a sequencing study of the same sample size. We also suggest that more than 10,000 samples will most likely be required for reaching nonnegligible statistical power to identify associations with low-frequency variation (under the assumption of a per-gene contribution of ∼0.1% of heritability). This is consistent with recent independent estimates of required sample sizes.^11,34 We are almost certainly underestimating the required sample size, given that we modeled a highly heritable trait for which all heritability is explained by coding variants in 1,000 genes, whereas the average contribution of coding variation to heritability is most likely typically lower than 0.1% per gene.

The changes in allele frequency and decreased allelic diversity in founder populations caused by the bottleneck event(s) and drift can aid in the detection of rare-variant associations. We have shown through our simulation that the power gain in the founder population is from both increased frequency of causal variants (thus variance explained per gene) at some genes and reduced genetic heterogeneity. Founder populations typically also demonstrate a higher degree of cultural and environmental homogeneity (not modeled here), which could further increase the strength of the genetic signals. However, there are also limitations with using founder populations. First, the population size might not be large enough to allow for the collection of sufficiently large numbers of cases. Second, rare variants might be recent in origin and hence specific to a single founder population; these are the variants that are potentially the least replicable, although this concern is less relevant for gene-based “burden”-type tests where variants are aggregated. Of note, the variants might be unique to founder populations, but the finding of genes is relevant to all populations. Third, a higher rate of direct and cryptic relatedness in some founder populations could confound baseline assumptions of independence among genotypes and phenotypes, and accounting for this sample structure could require more specialized approaches. Fourth, there might not be enough power to detect some genes in the founder population as a result of the loss of causal variants (Figure 4). Nevertheless, the increased power, particularly for single-variant tests, suggests that exome chip and/or exome sequencing in all available samples from founder populations would be an efficient use of resources. Different founder populations will happen to be better powered for different genes (in each population, certain genes will gain power, whereas others will lose power, but the genes that gain power will vary across populations). Thus, a potentially attractive strategy for rare-variant studies is to employ a diverse panel of well-powered founder populations.

We evaluated a variety of statistical tests that were developed under different assumptions about genetic architecture. We have shown that these tests are indeed sensitive to different disease models. SKAT-O and the VT test outperformed the other gene-based tests across a range of different genetic architectures. It is also worth noting that single-variant tests performed as well as or better than SKAT-O and the VT test, particularly in founder populations with decreased allelic diversity. This raises as one possible strategy the use of single-variant tests as a screen in founder populations and then follow-up with candidate-gene sequencing.

We have shown that exome chip genotyping studies are currently much more cost efficient than exome sequencing studies under a range of genetic models. In a fixed number of samples, however, exome chip genotyping studies miss a substantial portion of causal variation that could be detected by sequencing. Continued sharp drops in the cost of sequencing and/or targeted sequencing to follow up initial results might enable better-powered and more cost-efficient exome sequencing or whole-genome sequencing studies. Given the requirement for large sample sizes, the ability to combine studies, for example, in meta-analyses will be critical for a new wave of discoveries. Of note, as reference panels for imputation become larger and represent more populations, imputation of rare variants into samples with existing genotype data is another likely complementary approach for future studies.

Our study has a number of limitations. We have taken a forward-in-time approach for simulating population sequence data, which has substantial advantage in terms of being able to model different genetic architectures and demographic parameters, but this approach comes with the cost of requiring greater computational resources. Because of this limitation, as well as the complexity of the demographic models, we did not do a complete search through the entire parameter space for the best-fitting demographic model. Another limitation with our simulation is that the limited sample size of the empirical data provided an incomplete view of rare variants in the population, so our simulations might not be completely accurate at very low allele frequencies. Moreover, as suggested by Casals et al.,³⁵ there might be a relaxation of selection in the founder population, which we did not consider in our simulation. It is also worth noting that our empirical Finnish samples are from all across Finland (Table S1), and therefore our model for simulating the Finns ignores the demographic heterogeneity within Finland. As deeper and richer human genetic data become available, the models can be calibrated and improved. Last, but not least, our study did not explore the effects of properties such as gene size or mutation rate on power, nor did it characterize the power of rare-variant tests at noncoding loci, where causal-variant frequencies and effect sizes might be different.

In summary, our study has highlighted the usefulness of understanding the population-genetic properties of a study population to explore a range of genetic models and recognize the features and limitations of different association study designs in that population. As the field of human genetics moves forward to explore new and expanded sources of variation, such models offer a context in which researchers can interpret the data and plan future studies for gene discovery. With current approaches focused on rare variation, our work suggests that founder populations such as Finland can play an important role in genetic studies.

Consortia

The members of the GoT2D Consortium are Jason Flannick, Alisa Manning, Christopher Hartl, Vineeta Agarwala, Pierre Fontanillas, Todd Green, Eric Banks, Mark DePristo, Ryan Poplin, Khalid Shakir, Timothy Fennell, Jacquelyn Murphy, Noël Burtt, Stacey Gabriel, David Altshuler, Christian Fuchsberger, Hyun Min Kang, Xueling Sim, Clement Ma, Adam Locke, Thomas Blackwell, Anne Jackson, Tanya Teslovich, Heather Stringham, Peter Chines, Phoenix Kwan, Jeroen Huyghe, Adrian Tan, Goo Jun, Michael Stitzel, Richard N. Bergman, Lori Bonnycastle, Jaakko Tuomilehto, Francis S. Collins, Laura Scott, Karen Mohlke, Gonçalo Abecasis, Michael Boehnke, Tim Strom, Christian Gieger, Martina Müller-Nurasyid, Harald Grallert, Jennifer Kriebel, Janina Ried, Martin Hrabé de Angelis, Cornelia Huth, Christa Meisinger, Annette Peters, Wolfgang Rathmann, Konstantin Strauch, Thomas Meitinger, Jasmina Kravic, Claes Ladenvall, Tiinamaija Toumi, Bo Isomaa, Leif Groop, Kyle Gaulton, Loukas Moutsianas, Manny Rivas, Richard Pearson, Anubha Mahajan, Inga Prokopenko, Ashish Kumar, John Perry, Jeff Chen, Bryan Howie, Martijn van de Bunt, Kerrin Small, Cecilia Lindgren, Gerton Lunter, Neil Robertson, Will Rayner, Andrew Morris, David Buck, Andrew Hattersley, Tim Spector, Gil McVean, Tim Frayling, Peter Donnelly, and Mark McCarthy.

Appendix A: Fitting Finnish Demographic-History Parameters

P(data|model) for each model was calculated as below. The first two terms are the probabilities of the observed allele frequency spectra of synonymous and missense variants given the demographic model being tested. The third term is the probability of the observed synonymous/missense ratio. The last two terms calculate the probabilities of the observed allele sharing between Finns and NFEs.

$$\mathrm{P}\left(\text{data}|\text{model}\right)=\left(\begin{array}{c}s\\ s_1,\dots s_6\end{array}\right){\prod }_{i=1}^6{p}_i^{s_i}\times \left(\begin{array}{c}m\\ m_1,\dots m_6\end{array}\right){\prod }_{i=1}^6{q}_i^{m_i}\times {\prod }_{i=1}^6\left(\begin{array}{c}{s}_i+m_i\\ s_i\end{array}\right)r_i^{s_i}{\left(1-r_i\right)}^{m_i}\times {\prod }_{i=1}^6\left(\begin{array}{c}{s}_i\\ s{s}_i\end{array}\right)x_i^{s{s}_i}{\left(1-x_i\right)}^{s_i-s{s}_i}\times {\prod }_{i=1}^6\left(\begin{array}{c}{m}_i\\ s{m}_i\end{array}\right)y_i^{s{m}_i}{\left(1-y_i\right)}^{m_i-s{m}_i}$$

Abbreviations are as follows: s and m, observed total number of synonymous and missense variants, respectively; s_i and m_i, observed number of synonymous and missense variants, respectively, in the i^th frequency category; p_i, predicted proportion of synonymous variants in the i^th frequency category among all synonymous variants; q_i, predicted proportion of missense variants in the i^th frequency category among all missense variants; r_i, predicted proportion of synonymous variants in the i^th frequency category among all variants (both synonymous and missense) in the i^th frequency category; ss_i and sm_i, observed number of synonymous and missense variants, respectively, in the i^th frequency category in the Finns and shared with NFEs; x_i and y_i, predicted proportion of synonymous and missense variants, respectively, within the i^th frequency category in the Finns and shared with NFEs.

Web Resources

The URLs for data presented herein are as follows:

• Exome Chip Design, http://genome.sph.umich.edu/wiki/Exome_Chip_Design

• Online Mendelian Inheritance in Man (OMIM), http://www.omim.org/

• PLINK, http://pngu.mgh.harvard.edu/∼purcell/plink/

• SCORE-Seq: Score-Type Tests for Detecting Disease Associations with Rare Variants in Sequencing Studies, http://www.bios.unc.edu/∼lin/software/SCORE-Seq/