Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Jun 24;4:4969. doi: 10.1038/srep04969

Blue shift of spontaneous emission in hyperbolic metamaterial

Lei Gu 1, T U Tumkur 1, G Zhu 1, M A Noginov 1,a
PMCID: PMC4067613  PMID: 24957679

Abstract

Spontaneous emission is one of the most fundamental quantum phenomena in optics. Following the seminal work of Purcell and in agreement with the Fermi's Golden Rule, its rate can be controlled with the photonic density of states (PDOS). In recent years, this effect has been demonstrated in metamaterials with hyperbolic dispersion – highly anisotropic composite materials, which have a broad-band singularity of the density of photonic states. At this time, we show that hyperbolic metamaterials can control spontaneous emission spectra as well. Experimentally, DCM laser dye has been embedded into lamellar metal/dielectric metamaterial. The observed 18 nm blue shift of emission is explained by strong dispersion of the density of photonic states. On the other hand, practically no spectral shift has been observed in the excitation spectra of the same dye. This suggests that the effect of PDOS on spontaneous emission is very different from its effect on excitation and absorption.

Metamaterials are engineered composite materials consisting of subwavelength units (meta-atoms), which have rationally designed shape, composition and mutual orientation1,2. Metamaterials have unique responses to electromagnetic waves, which cannot be found in materials available in nature or fabricated using traditional synthetic routes. Metamaterials have been predicted and experimentally demonstrated to lead to many breakthrough applications such as negative index of refraction3,4,5,6, sub-diffraction imaging4,7,8,9,10, and invisibility cloaking11,12. Metamaterials with hyperbolic dispersion, in which dielectric permittivity components in orthogonal directions have different signs, have attracted a widespread attention of the research community because they can propagate waves with nearly infinitely large wave-vectors and possess a broadband singularity in the density of photonic states13. The latter property allows one to control a variety of quantum and classical phenomena, including but not limited to spontaneous emission13,14,15,16,17,18,19,20 and scattering21,22.

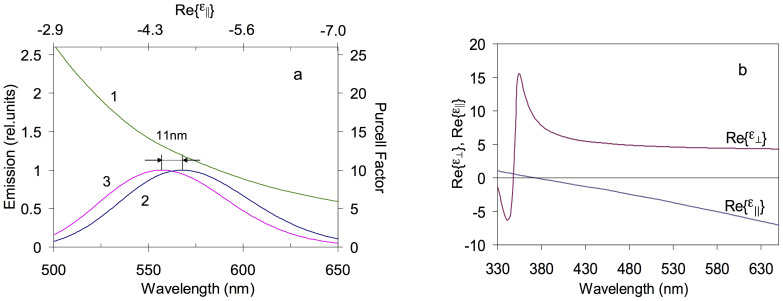
The enhancement of the spontaneous emission by environments with high local densities of electromagnetic modes (photonic states) is known as the Purcell effect23. It is quantified in terms of the Purcell factor, which is the ratio of the spontaneous decay rate in a cavity, medium, or other engineered environment and that in vacuum23. It has been shown that the Purcell enhancement factor in hyperbolic metamaterials strongly depends on effective dielectric permittivities in orthogonal directions (which, in turn, depend on constituent materials and filling factors) and, correspondingly, has strong spectral dispersion14,17, Figs. 1a and 1b. In Ref. 14, the Purcell factor was calculated for relatively large spherical dipoles embedded into a hyperbolic metamaterial, while in Ref. 17, small dipoles were positioned on top of the metamaterial's surface. Although the details of the two theoretical models differ from each other, both predict the Purcell enhancement to be maximal when the real part of effective dielectric permittivity in the direction parallel to the metamaterial's surface Re{ε∥} is slightly negative14,17, Fig. 1b. In Ref. 17, the experimental dependence of the Purcell enhancement factor on frequency has been demonstrated in emission kinetics measurements in an ensemble of quantum dots with size dispersion.

Figure 1.

Figure 1

Open in a new tab

(a) Trace 1 – spectrum of the Purcell enhancement factor calculated as the function of Re{ε∥} (upper scale) for a multilayered hyperbolic metamaterial with Re{ε⊥} = 1, Im{ε⊥} = Im{ε∥} = 0.1 [14]. Trace 2 – Emission band of the DCM dye film deposited on glass (approximated by a Gaussian function). Trace 3 – predicted shift of the emission band of the same dye embedded into a hyperbolic metamaterial (Trace 3 ∝ Trace 1 × Trace 2); both emission spectra are normalized to unity. (b) Spectra of Re{ε∥} and Re{ε⊥} in the hyperbolic metamaterial used in our experiment (calculated in the effective medium approximation for the filling factors discussed in the text and the material parameters available in the literature [18, 25]). The latter spectrum relates the values Re{ε∥} in the upper horizontal scale of Fig. 1a to the wavelengths in the lower horizontal scale. (Here ε∥ and ε⊥ denote components of dielectric permittivity parallel and perpendicular to the metamaterial surface.)

We infer that strong variation of the Purcell factor over the emission spectral band of luminescent centers should lead to a substantial reshaping of the emission spectrum and shift of the emission maximum. Our reasoning is explained in Fig. 1a, showing the spectrum of the Purcell enhancement factor (Trace 1), the emission spectrum of the dye doped polymeric film deposited on glass (Trace 2), and the blue shifted emission of the same dye embedded into a metamaterial (Trace 3 ∝ Trace 1 × Trace 2). Note that this effect is entirely different from the (very small) Lamb shift predicted in hyperbolic metamaterials in Ref. 24.

In this paper, we report on experimental observation of the blue shift in spontaneous emission of dye molecules embedded into lamellar metamaterials with hyperbolic dispersion, and demonstrate a good qualitative agreement between the experimental results and the predictions of available theoretical models14,17.

Results

Experimentally, we have fabricated lamellar Ag/polymer hyperbolic metamaterials, whose dielectric layers were impregnated with the DCM laser dye, and studied their emission spectra (at the excitation wavelength λ = 488 nm) and excitation spectra (at the emission collection wavelength λ = 650 nm). The details of the sample preparation and the spectral measurements are explained in the Methods section. Dye doped polymeric films deposited on glass were used as control samples.

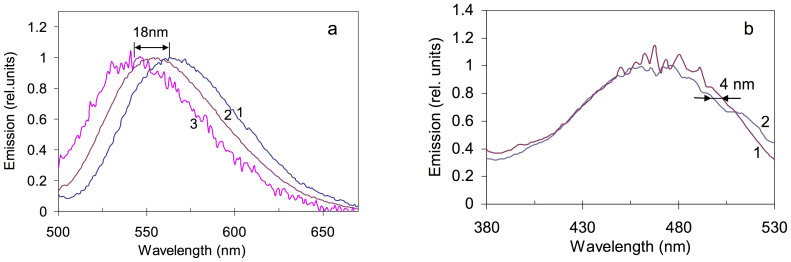
In agreement with the heuristic model discussed above, the emission spectrum of the dye embedded in the metamaterial was blue shifted in comparison with the emission spectrum of the same dye deposited onto the glass substrate. The effect was stronger in the sample, which had Ag as the top layer (18 nm shift), than in the sample, whose top layer was dye-doped PMMA (7 nm shift), Fig. 2a.

Figure 2.

Figure 2

Open in a new tab

(a) Experimental emission spectrum of DCM doped PMMA deposited on glass (1), embedded in the hyperbolic metamaterial with PMMA as the outmost layers (2), and embedded in the hyperbolic metamaterial with Ag as the outermost layer (3). (b) Experimental excitation spectra of DCM emission when the dye doped PMMA was deposited on top of glass (1) and embedded in hyperbolic metamaterial with Ag as the outermost layer (2).

At the same time, the excitation spectrum of emission experienced much smaller spectral shift than the emission spectrum did, Fig 2b. This suggests that the effect of the density of photonic states on excitation and absorption (if any) is different from the effect of the density of photonic states on spontaneous emission.

Discussion

The experimentally observed blue shift of the emission spectrum, Fig. 2a, is approximately 50% larger than the heuristic prediction, see Fig. 1a. This deviation is likely due to the fact that the model in Ref. 14 was developed for large (larger than the period of the structure a) spherical emitting dipoles, while the molecules in our experiments were much smaller than a and hardly spherical. (In addition, the spectrum of dielectric permittivities in our metamaterial is not exactly the same as in Ref. 14.) On the other hand, the theoretical model of Ref. 17 has been developed for emitters on top of a hyperbolic metamaterial, which is also not the case of our experiment. We hope that our findings will stimulate further theoretical studies and the development of the model matching our experimental conditions.

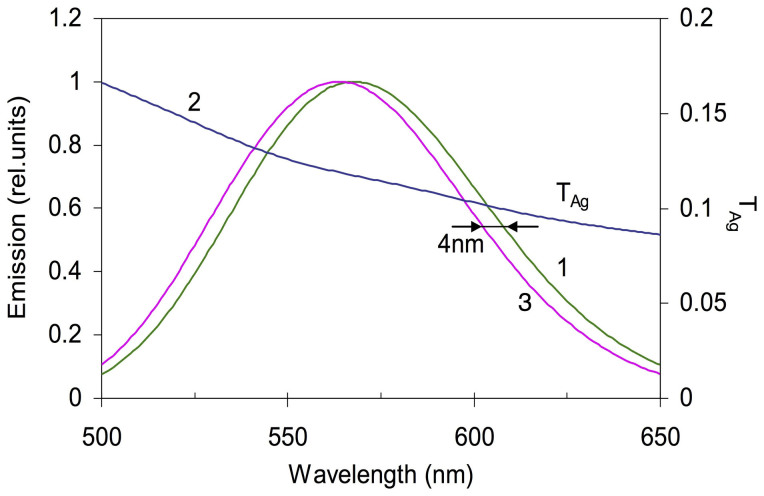
Since emitted light propagates to the surface through silver layers, whose transmission depends on the wavelength, its spectrum can, in principle, be modified. This effect is illustrated in Fig. 3, depicting the spectrum of the DCM dye emission before the silver film (Trace 1), the transmission spectrum of the 30 nm silver film (calculated using the parameters of Ref. 25, Trace 2), and the spectrum of the dye emission transmitted by the silver film (Trace 3 ∝ Trace 1 × Trace 2). As one can see in Fig. 3, the spectral shift of emission caused by transmission through the silver film is small and cannot account for the spectral shift larger than 4 nm. However, it narrows the gap between the theoretical prediction (Fig. 1a) and the experimental observation (Fig. 2a). At the same time, the effect of Ag transmission can be responsible for the small spectral shifts observed in the excitation spectrum, Fig. 2b.

Figure 3.

Figure 3

Open in a new tab

Trace 1 – Emission band of DCM doped PMMA (approximated by a Gaussian function). Trace 2 – Transmission spectrum of the 30 nm Ag film (right vertical axis). Trace 3 – spectrum of the DCM emission transmitted through Ag film (Trace 3 ∝ Trace 1 × Trace 2). Both emission spectra are normalized to unity.

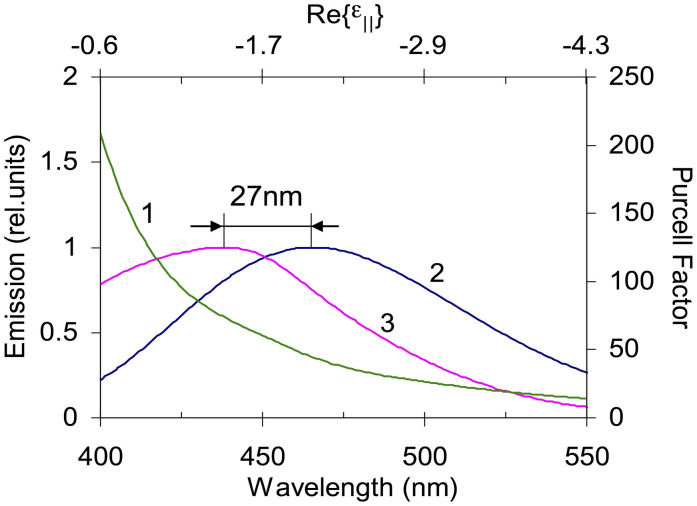
Note that if one will use the heuristic model of Fig. 1a to evaluate the change in the excitation spectrum (Fig. 4), the calculated blue shift will be enormously large, almost one order of magnitude larger than the one measured experimentally (compare Figs. 2b and 4). To no surprise, this implies that the effect of the density of photonic states on excitation and absorption is not the same as on spontaneous emission.

Figure 4.

Figure 4

Open in a new tab

Trace 1 – spectrum of the Purcell enhancement factor, same as Trace 1 in Fig. 1a. Trace 2 – excitation spectra of the DCM dye film deposited on glass (approximated by a Gaussian function). Trace 3 ∝ (Trace 1) × (Trace 2). Both excitation spectra are normalized to unity.

To summarize, we have predicted and experimentally observed sizable blue shift of spontaneous emission of DCM laser dye embedded into lamellar metamaterials with hyperbolic dispersion. The effect primarily originated from the dispersion of the Purcell enhancement factor and the density of photonic states. At the same time, practically no spectral shift has been found in the excitation spectra of the dye emission. This suggests that the effect of the density of photonic states on absorption (if any) is strongly different from the effect of the density of photonic states on spontaneous emission.

Methods

Experimental Samples

Lamellar hyperbolic metamaterials in our studies consisted of 30 nm layers of Ag and 40 nm layers of Polymethyl Methacrylate (PMMA) doped with the [2-[2-[4-(dimethylamino)phenyl]ethenyl]-6-methyl-4H-pyran-4-ylidene]-propanedinitrile (DCM) laser dye, with either Ag or dye-doped PMMA as the outermost layer. Metallic films were produced by evaporating 99.99% pure silver. The dye and PMMA were dissolved in dichloromethane. The solutions were spin coated onto the silver films to form dielectric layers. The dye concentration in dry PMMA was equal to 10 g/l (0.033 M). The material with such parameters has hyperbolic dispersion (negative dielectric permittivity Re{ε∥} in the direction parallel to the metamaterial's surface and positive dielectric permittivity Re{ε⊥} in the direction perpendicular to the metamaterial's surface) in the spectral range of interest, λ>370 nm18,21, Fig. 1b. Similar dye-doped PMMA film deposited on glass was used as a control sample.

Emission studies

The emission measurements were performed in the spectrofluorimeter setup (Fluoromax 3, Horbia) at excitation of the dye molecules with λ = 488 nm light. At the same time, the excitation spectrum of emission, which often resembles the absorption spectrum, was recorded when the detection wavelength was set close to the maximum of the emission band at ~560 nm. (Note that in many laser dyes, spontaneous emission occurs not only between pure singlet excited state S1 and ground state S0, but also between associated with them multiple vibrational states. This causes broadening of the emission band and its deviation from the Lorentzian shape. Due to fast thermalization, all components of the excited state multifold decay with the same time constant, leading to single-exponential emission kinetics26 and its independence of the emission wavelength.)

Author Contributions

L.G. and G.Z. conducted the experiments and performed the data analysis. T.U.T. fabricated the samples. M.A.N. has proposed the heuristic model and designed the experiment. L.G. and M.A.N. wrote the manuscript.

Acknowledgments

The authors acknowledge the support by the NSF PREM grant # DMR 1205457, NSF IGERT grant #DGE 0966188, and AFOSR grant # FA9550-09-1-0456.

References

  1. Engheta N. & Ziolkowski R. W. Metamaterials: Physics and Engineering Explorations. 3–30 (Wiley & Sons, New York, 2006). [Google Scholar]
  2. Noginov M. A. & Podolskiy V. A. Tutorials in Metamaterials. (Taylor & Francis, Boca Raton., 2012). [Google Scholar]
  3. Veselago V. G. The electrodynamics of substances with simultaneously negative values of ε and µ. Sov. Phys. Usp. 10, 509–514(1968). [Google Scholar]
  4. Pendry J. B. Negative Refraction Makes a Perfect Lens. Phys. Rev. Lett. 85, 3966–3969 (2000). [DOI] [PubMed] [Google Scholar]
  5. Shelby R. A., Smith D. R. & Schultz S. Experimental verification of a negative index of refraction. Science 292, 77–79 (2001). [DOI] [PubMed] [Google Scholar]
  6. Shalaev V. M. et al. Negative index of refraction in optical metamaterials. Opt. Lett. 30, 3356–3358 (2005). [DOI] [PubMed] [Google Scholar]
  7. Fang N., Lee H., Sun C. & Zhang X. Sub-Diffraction-Limited optical imaging with a silver superlens. Science 308, 534–537 (2005). [DOI] [PubMed] [Google Scholar]
  8. Blaikie R. J. & Melville D. O. S. Imaging through planar silver lenses in the optical near field. J. Opt. A-Pure Appl. Opt. 7, S176–S183 (2005). [DOI] [PubMed] [Google Scholar]
  9. Liu Z., Lee H., Xiong Y., Sun C. & Zhang X. Far-field optical hyperlens magnifying sub-diffraction-limited objects. Science 315, 1686 (2007). [DOI] [PubMed] [Google Scholar]
  10. Smolyaninov I. I., Hung Y. J. & Davis C. C. Magnifying superlens in the visible frequency range. Science 315, 1699–1701 (2007). [DOI] [PubMed] [Google Scholar]
  11. Pendry J. B., Schurig D. & Smith D. R. Controlling electromagnetic fields. Science 312, 1780–1782 (2006). [DOI] [PubMed] [Google Scholar]
  12. Cai W., Chettiar U. K., Kildishev A. V. & Shalaev V. M. Optical cloaking with metamaterials. Nat. Photonics 1, 224–227 (2007). [Google Scholar]
  13. Jacob Z., Smolyaninov I. I. & Narimanov E. E. Broadband Purcell effect: Radiative decay engineering with metamaterials. Appl. Phys. Lett. 100, 181105 (2012). [Google Scholar]
  14. Poddubny A. N., Belov P. A. & Kivshar Y. S. Spontaneous radiation of a finite-size dipole emitter in hyperbolic media. Phys. Rev. A 84, 023807 (2011). [Google Scholar]
  15. Noginov M. A. et al. Controlling spontaneous emission with metamaterials. Opt. Lett. 35, 1863–1865 (2010). [DOI] [PubMed] [Google Scholar]
  16. Jacob Z. et al. Engineering photonic density of states using metamaterials. Applied Physics B: Lasers and Optics 100, 215–218 (2010). [Google Scholar]
  17. Krishnamoorthy H. N. S., Jacob Z., Narimanov E. E., Kretzschmar I. & Menon V. M. Topological Transitions in Metamaterials. Science 336, 205–209 (2012). [DOI] [PubMed] [Google Scholar]
  18. Tumkur T. U. et al. Control of spontaneous emission in a volume of functionalized hyperbolic metamaterial. Appl. Phys. Lett. 99, 151115 (2011). [Google Scholar]
  19. Kim J. et al. Improving the radiative decay rate for dye molecules with hyperbolic metamaterials. Opt. Express 20, 8100–8116 (2012). [DOI] [PubMed] [Google Scholar]
  20. Shalaginov M. Y. et al. Broadband enhancement of spontaneous emission from nitrogen-vacancy centers in nanodiamonds by hyperbolic metamaterials. Appl. Phys. Lett. 102, 173114 (2013). [Google Scholar]
  21. Tumkur T. U. et al. Control of reflectance and transmittance in scattering and curvilinear hyperbolic metamaterials. Appl. Phys. Lett. 101, 091105 (2012). [Google Scholar]
  22. Narimanov E. E., Li H., Barnakov Y. A., Tumkur T. U. & Noginov M. A. Reduced reflection from roughened hyperbolic metamaterial. Opt. Express 21, 14956–14961 (2013). [DOI] [PubMed] [Google Scholar]
  23. Purcell E. M. Spontaneous emission probabilities at radio frequencies. Phys. Rev. 69. 674 (1946). [Google Scholar]
  24. Cortes C. L., Newman W., Molesky S. & Jacob Z. Quantum nanophotonics using hyperbolic metamaterials. J. Optics. 14, 063001 (2012). [Google Scholar]
  25. Johnson P. B. & Christy R. W. Optical Constants of the Noble Metals. Phys. Rev. B. 6, 4370–4379 (1972). [Google Scholar]
  26. Demchenko A. P. Advanced Fluorescence Reporters in Chemistry and Biology II: Molecular Constructions, Polymers and Nanoparticles. (Springer, Berlin, 2010). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES