Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Jun 24;4:5418. doi: 10.1038/srep05418

Quantitatively Mapping Cellular Viscosity with Detailed Organelle Information via a Designed PET Fluorescent Probe

Tianyu Liu 1,2,6, Xiaogang Liu 3,6, David R Spring 4,d, Xuhong Qian 5,c, Jingnan Cui 2,b, Zhaochao Xu 1,a
PMCID: PMC4067619  PMID: 24957323

Abstract

Viscosity is a fundamental physical parameter that influences diffusion in biological processes. The distribution of intracellular viscosity is highly heterogeneous, and it is challenging to obtain a full map of cellular viscosity with detailed organelle information. In this work, we report 1 as the first fluorescent viscosity probe which is able to quantitatively map cellular viscosity with detailed organelle information based on the PET mechanism. This probe exhibited a significant ratiometric fluorescence intensity enhancement as solvent viscosity increases. The emission intensity increase was attributed to combined effects of the inhibition of PET due to restricted conformational access (favorable for FRET, but not for PET), and the decreased PET efficiency caused by viscosity-dependent twisted intramolecular charge transfer (TICT). A full map of subcellular viscosity was successfully constructed via fluorescent ratiometric detection and fluorescence lifetime imaging; it was found that lysosomal regions in a cell possess the highest viscosity, followed by mitochondrial regions.

Fluorescence imaging in living cells is a powerful technique to study biological systems in vivo1. By attaching a sub-cellular targetable group, fluorescent probes are able to detect target analytes and reveal a diverse range of physical/chemical properties in specific regions of a cell2,3. However, the distribution of intracellular targets is often highly heterogeneous. It is very challenging to obtain a full map of cellular targets with detailed organelle information. Among various cell properties, viscosity is a fundamental physical parameter that influences diffusion in biological processes, such as protein–protein interactions, signal transduction and transportation of small solutes, macromolecules, and other cellular organelles in living cells4. It has been reported that local microviscosity in cells varies from 1 to 400 cP5,6; changes in intracellular viscosity are related to several diseases, such as atherosclerosis7, Alzheimer's disease8 and diabetes9. In recent years, viscosity detection is mainly done using molecular rotors, whose twisted intramolecular charge transfer (TICT) and associated emission properties depend on solvent viscosity4,10. The correlation between their fluorescence intensity and/or fluorescence lifetime and solvent viscosity makes them suitable probes for imaging viscosity in living cells via intensity-based responses5,6,11,12,13,14,15,16 or fluorescence lifetime imaging6,17,18,19. By affixing a organelle-specific group, molecular rotors can examine viscosity in membranes11,13,14,18,20, lysosomes21 and mitochondria22. Unfortunately, molecular rotors lack the ability to probe viscosities of the entire cell across different organelles, which is important for understanding intracellular reaction kinetics and developing diagnostic and treatment strategies. In order to get a full map of cellular viscosity and discriminate viscosities of different organelles with high sensitivity in vivo, new methods to design fluorescent viscosity probes are required23.

Photoinduced electron transfer (PET) is an important principle for designing fluorescent probes in a typical molecular format of ‘fluorophore-spacer-receptor’, which translates recognition events into emission intensity changes24. The intramolecular PET process, from an electron donor moiety to an electron acceptor moiety in a singlet excited state, can be modulated by changing redox potentials of the donor/acceptor pair25, varying the donor-acceptor distance26 and mutual orientation27, switching molecular conformations28,29,30, and so forth. Due to the correlation between these factors and PET rates, fluorescent probes for pH31, cations24, anions32, solvent polarity33, and conformational dynamics of macromolecules34, have been developed. In these applications, the dynamic range and sensitivity of PET probes can be adjusted accordingly, i.e., by changing substituents35. Moreover, a strong correlation between viscosity and PET has also been established, mainly ascribed to the viscosity-dependent molecular conformational changes36,37,38 or diffusion rate variations39,40 of the donor/acceptor system. However, to our knowledge, no studies on PET-based fluorescent probes for imaging viscosity in biological systems have been performed.

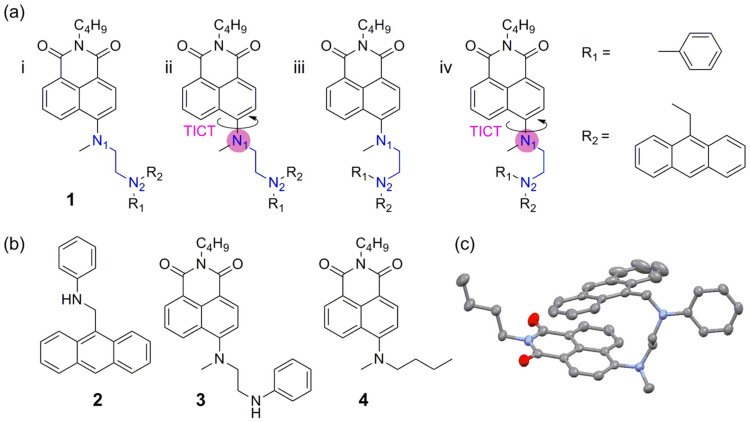
Here, we report 1 (Figure 1a) as the first fluorescent viscosity probe which is able to quantitatively map cellular viscosity with detailed organelle information based on the PET mechanism. In this compound, aniline is selected as a PET donor because of its low pKa value and high electron transfer efficiency, allowing 1 to circumvent the interference from proton and metal ions under biological conditions; anthracene is linked to the aniline nitrogen, and plays two roles: firstly, to make the PET donor more sensitive to viscosity owing to enhanced interactions with solvent molecules, and, secondly, as a donor of fluorescence resonance energy transfer (FRET) when paired with an acceptor of 1,8-naphthalimide to give a ratiometric signal41.

Figure 1.

Figure 1

Open in a new tab

Structures of compounds 1 (a) and 2–4 (b); In the TICT state of 1, N1 is positively charged as highlighted by the pink circles [a(ii) and (iv)], in contrast to delocalized charge in the ICT state [a(i) and (iii)]. (c) Crystal structure of 1; hydrogen atoms have been omitted for clarity.

Results

The FRET effect can be rationalized by considering the absorption and emission spectra of 1–3 (Figure 1). The absorption spectrum of 1 exhibits two peaks centered at 370 nm and 440 nm, contributed by anthracene and 1,8-naphthalimide moieties, respectively (Figure S1). The similarity between the UV-Vis absorption spectrum of 1 and the sum of those of 2 and 3 indicates that the ground state interactions between these two moieties are negligible (Figure S1); the spectral overlap between the emission of 2 and the absorption of 3 further suggests that anthacene/1,8-naphthalimide are a good FRET pair (Figure S2). Indeed, the crystal structure of 1 shows that the distance between anthracene and 1,8-naphthalimie is only 3.98 Å (Figures 1c and S3; Tables S1 and S2), ensuring efficient FRET. Consequently, the conformational change of 1 could be monitored via FRET from anthracene to 1,8-naphthalimide.

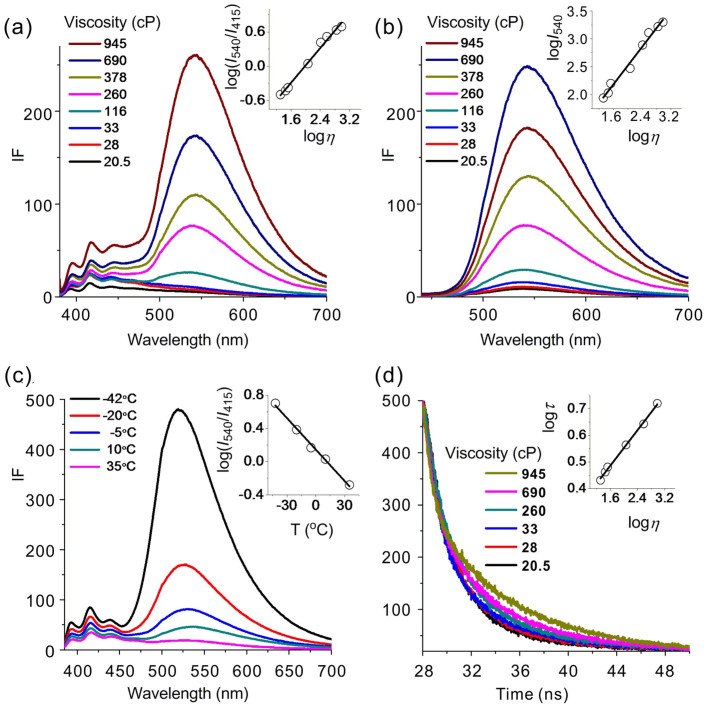
The viscosity sensing properties of 1 were examined in ethylene glycol-glycerol mixtures with viscosity varying from 20.5 cP to 945 cP. When excited at 370 nm (Figure 2a), the emission band of 1,8-naphthalimide centered at 540 nm was very weak in low viscosity solvent, but increased considerably as solvent viscosity escalated (34 fold enhancement). When only 1,8-naphthalimide was excited by 430 nm light, 38 fold enhancement of 1,8-naphthalimide emission was observed (Figure 2b). Similar to the effect of raising solvent viscosity, lowering the temperature of ethylene glycol-glycerol mixture (40/60, v/v) from 35 to −42°C also led to a considerable fluorescence enhancement (23 fold; Figure 2c). In addition, the fluorescence lifetime increased from 2.7 to 5.5 ns when solvent viscosity rose from 20.5 to 945 cP (Figure 2d). The insets in Figure 2 exhibited a good linearity between changes of fluorescence intensity and the viscosity/temperature of the solvents (also see Supporting Information). Notably, the ratio of the emission intensities of 1 at 540 and 415 nm (I540/I415; Figure 2a) and the fluorescence lifetime at 540 nm (Figure 2d) demonstrated a strong linear correlation with solvent viscosity on a logarithmic scale. Therefore, 1 could be used to detect viscosity via ratiometric fluorescent imaging or fluorescence lifetime imaging, which are independent of probe concentration and provide a built-in correction for environmental effects.

Figure 2.

Figure 2

Open in a new tab

Fluorescent spectra of 10 μM 1 (a) in ethylene glycol-glycerol mixtures with varied solvent viscosity (η), excited at 370 nm. Inset: the linearity between log(I540/I415) and logη; (b) in ethylene glycol-glycerol mixtures, excited at 430 nm. Inset: the linearity between logI540 and logη; (c) at different temperatures in ethylene glycol-glycerol mixture (40/60, v/v), excited at 370 nm. Inset: the linearity between log(I540/I415) and temperature. (d) Fluorescence lifetime of 10 μM 1 at 540 nm in ethylene glycol-glycerol mixtures with varied solvent viscosity. Inset: the linearity between logτ and logη.

The potential for interference from proton and metal ions with 1 was then evaluated. The UV–Vis absorption spectra of 1 exhibit little dependence on the pH values of solvents (Figure S4a). The fluorescence of 1 at 540 nm remained weak between pH 10.3–3.6 and then gradually increased from pH 3.6 to pH 2.3 due to the inhibited PET process via protonation of the aniline amine (Figure S4b), but by only a 5 fold enhancement. The pKa value of 1 was determined to be 3.1. This is in contrast to the strong pH dependence of NR, another popular lysosome-specific dye (Figure S4c and d). Moreover, the emission profile of 1 was unperturbed in the presence of metal ions, indicating negligible interactions with metal ions (Figure S5).

The effect of solvent polarity was also evaluated. Probe 1 exhibited typical ICT character. The fluorescence spectrum demonstrated a distinct bathochromic shift and the fluorescence quantum yield decreased substantially with increased solvent polarity (Table S3). Significantly, the quantum yield of 1 in glycerol was 0.365, which was much higher than those in other solvents. In the mixtures of water-glycerol, or ethanol-glycerol, with varied viscosity, 1 displayed almost the same ratiometric response to solvent viscosity as that in ethylene glycol-glycerol mixtures (Figures S6 and S7). These results indicated that the fluorescence increase and ratiometric responses of 1 were highly sensitive and selective to solvent viscosity.

We then examined the performance of 1 in living cells. MCF-7 cells were incubated with 3 μM 1 and they rapidly exhibited green fluorescence (Figure S8a). The fluorescence intensity gradually increased (Figure S8b–c) and reached equilibrium after ~3 min (Figure S8d). The strong fluorescence was confirmed not from the binding of 1 with proteins (Figure S9). These experiments showed that 1 could be used to image viscosity in living cells. The cytotoxicity of 1 was also examined in MCF-7 cells by a MTT assay (Figure S10). The results showed that over 90% MCF-7 cells survived after 12 h (5.0 μM 1 incubation) and the cell viability remained at ~70% after 24 h, demonstrating that 1 was of low toxicity toward cultured cell lines.

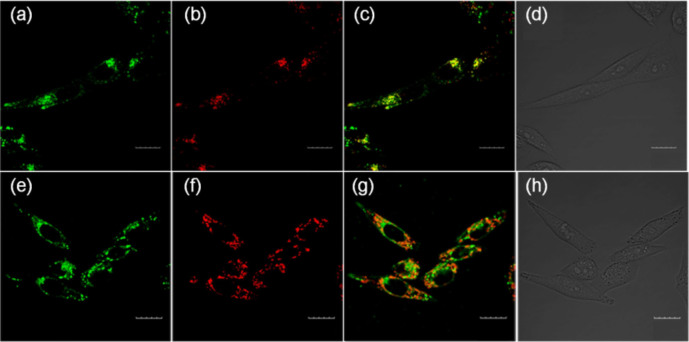
In order to identify organelles from the fluorescence imaging of 1 in cells, we then carried out fluorescence localization by co-staining cells with commercially available organelle-specific dyes (Figure 3). The highly green fluorescent regions with 1 (Figure 3a) and signals from NR (Figure 3b) overlapped perfectly (Figure 3c), indicating that these fluorescent regions were localized at lysosomes. Furthermore, the weak green fluorescent regions overlapped signals from the mitochondria tracker TMRM (Figure 3f), suggesting that these regions were mainly localized at mitochondria (Figure 3g).

Figure 3. Fluorescence co-localization imaging of MCF-7 cells stained with 3.0 μM 1 and 3.0 μM NR for 3 min at 37°C (a–d) or 3 μM MitoTracker TMRM for 3 min at 37°C (e–h).

Figure 3

Open in a new tab

(a) Image from 1. λex = 405 nm, λem = 530–570 nm; (b) image from NR. λex = 559 nm, λem = 580–610 nm; (c) merged image; (d) bright-field image; (e) image from 1. λex = 405 nm, λem = 530–570 nm; (f) image from MitoTracker TMRM. λex = 559 nm, λem = 570–610 nm; (g) merged image; (h) bright-field image. Scale bars = 20 μm.

To further ensure the accuracy of organelle localization of 1, co-staining of 1 with a variety of organelle-specific dyes in the same cell was performed (Figure 4). Another mitochondria-specific dye, MitoTracker Deep Red FM, with the emission window of 650–670 nm (Figure 4c), and NR (580–610 nm; Figure 4b) were used in addition to 1 (Figure 4a). Figure 4e showed that the fluorescence of 1 and signals from NR and Deep Red FM overlaid perfectly in the same cell.

Figure 4. Fluorescence imaging of a MCF-7 cell co-stained with 1, NR and Deep Red FM.

Figure 4

Open in a new tab

(a) Fluorescence imaging of 1 (5.0 μM) (Channel 1: λex = 405 nm, λem = 530–570 nm). (b) Fluorescence imaging of NR (5.0 μM) (Channel 2: λex = 559 nm, λem = 580–610 nm). (c) Fluorescence imaging of MitoTracker Deep Red FM (5.0 μM) (Channel 3: λex = 640 nm, λem = 650–670 nm). (d) Bright field image. (e) Merged images of (a), (b) and (c). Scale bars = 10 μm.

Co-staining experiments of 1 with NR were also conducted in other cell lines including SMMC 7721 cells (Figure S11), BV2 cells (Figure S12), cardiac muscle cells (Figure S13), Hela cells (Figure S14), PC12 cells (Figure S15) and neural stem cells (Figure S16), to test the universality of 1 and verify the organelle location profile. The results were consistent with those found in MCF-7 cells; that was, lysosome regions exhibited the strongest fluorescence. These experiments demonstrated that lysosomes had a higher viscosity than other organelles in cells; and probe 1 was potentially useful as lysosome and mitochondrial trackers.

Remarkably, 1 is able to provide quantitative information about cell viscosity, owing to its competence of performing ratiometric fluorescent imaging and fluorescence lifetime imaging. Two-photon microscopy (TPM) was employed to map the intracellular viscosity ratiometrically (Figure 5). Although the fluorescence in the blue channel (Figure 5b) was weaker than that in the green channel (Figure 5c), both channels exhibited relatively brighter fluorescence in lysosome regions. Based on the ratio values (Figure 5d) and the calibration curve (Figure 2a), the viscosities of lysosome regions, colored in purple to red, were determined ranging from 130 ± 20 to 175 ± 20 cP; the relatively lower viscosities of mitochondria, colored in blue, were found to vary from 60 ± 20 to 120 ± 20 cP.

Figure 5. TPM ratio images of MCF-7 cells stained with 5 μM 1.

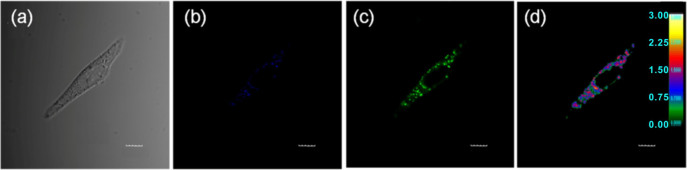
Figure 5

Open in a new tab

λex = 810 nm. (a) Bright field; (b) λem = 420–460 nm; (c) λem = 495–560 nm; (d) the ratio image. Scale bars = 10 μm.

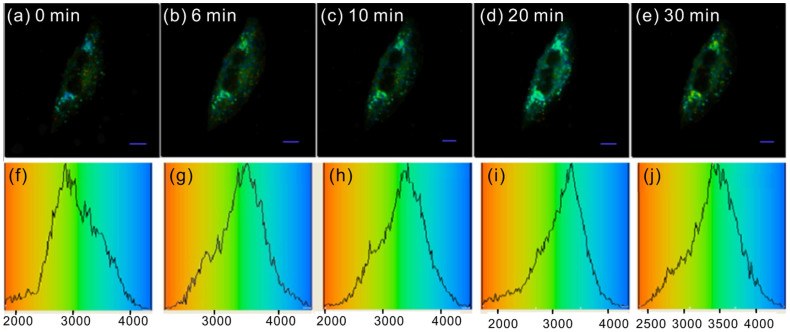
A quantitative viscosity map of a single MCF-7 cell was also obtained by fluorescence lifetime imaging with high spatial resolution (Figure 6a). The lysosome regions colored in cyan had longer lifetimes from 3.3 to 3.4 ns. According to the calibration curve (Figure 2d), the viscosity in these regions varied from 100 ± 20 to 130 ± 20 cP, which was in good agreement with results obtained by ratiometric detection. To further confirm the presence of lysosomes in these areas, dexamethasone, a lysosome stabilizer, was used to stimulate the cell (Figure 6b–e). After 30 min, the lifetime of the lysosome regions changed to 3.5–3.7 ns, indicating that the viscosity increased to 140–160 cP. In this way, the dynamic changes of cellular viscosity in the MCF-7 cell could be tracked by fluorescence lifetime imaging.

Figure 6.

Figure 6

Open in a new tab

(a–e) Fluorescence lifetime imaging (at 550 ± 25 nm) of MCF-7 cells stained with 5 μM probe 1 and stimulated by 5 μM dexamethasone for different durations; (f–j) fluorescence lifetime histograms corresponding to (a–e), respectively. Scale bars = 5 μm.

Discussion

The fluorescence enhancement of 1 with solvent viscosity is attributed to three factors, all related to the inhibition of the PET process from the aniline nitrogen to 1,8-naphthalimide. The first factor concerns the relative position between N1 and N2 in 1 (Figure 1a). With the U-shaped alignment [Figure 1a(iii–iv)] instead of the N-shaped one [Figure 1a(i–ii)], the two nitrogen atoms are much closer to each other, and their molecular orbitals have a substantially larger overlap28. Therefore, the PET rate in the U-shaped conformer is higher, leading to more effective fluorescence quenching28. In a low viscosity solvent, the aniline part together with anthracene is free to rotate, thus adopting a conformation, such as the U-shaped one, favoring PET and affording low emission intensity. In contrast, 1 is restricted to a N-shaped conformation in a highly viscous environment, reducing the PET rate and boosting the emission intensity; indeed, our DFT calculations show that the N-shaped conformer is more stable than the U-shaped analogue, and the transition to the less stable U-shaped molecular conformational is thus expected to be hindered in a high viscosity solvent (Figures S17–S19; Tables S4–S7).

The second factor regards the relative alignment of anthracene and 1,8-naphthalimide moieties. Our TD-DFT calculations suggest that the PET rate is higher when the anthracene and 1,8-naphthalimide moieties do not possess strong interactions (Figure S17a). This is reflected by a larger oscillator strength (f = 0.3733) in HOMO-2 → LUMO transition corresponding to the excitation of 1,8-naphthalimide; yet, the PET donor electrons are located in the HOMO; and the excitation transitions from HOMO to higher molecular orbitals (MO) is negligible. This energy level configuration results in a high probability of PET quenching due to the HOMO → HOMO-2 transition. When 1 possesses a folded conformation with a strong π-π stacking interaction, that is, anthracene and 1,8-naphthalimide moieties are facing each other, the HOMO-2 → LUMO transition becomes weaker (f = 0.1217) and the HOMO electrons have an increasing tendency for HOMO → LUMO transitions (f = 0.1066), leaving a lower probability of HOMO → HOMO-2 transitions and the associated PET quenching (Figure S17b). Interestingly, although this folded conformation of 1 does not favor PET, it boosts the FRET efficiency, owing to a closer distance between anthracene and 1,8-naphthalimide moieties. The above mentioned two factors are consistent with the viscosity-dependent conformational dynamics which influences the PET rate36,37,38,39,40.

The third factor controlling the PET rate in 1 is associated with the nature of the optical excitation in the 1,8-naphthalimide fluorophore, i.e., intramolecular charge transfer (ICT) or TICT. The presence of both excitation mechanisms is reflected by the double-exponential decay of the fluorescence lifetime test data (Figures S20 and S21; Table S8); the short-lived component (τ ≈ 2 ns) is attributed to ICT emission and the long-lived one (τ ≈ 7 ns) is assigned to TICT emission. In the TICT excited state, the positive charge is condensed around N1 [Figure 1a(ii) and (iv)], causing a stronger electrostatic attraction between the PET donor and acceptor. de Silva et al. have demonstrated that the PET rate can be enhanced by the molecular electric field formed between the donor and acceptor42; owing to a larger molecular electric field, the PET rate corresponding to the TICT excited state is thus expected to be higher than that of the ICT state, resulting in a very low emission intensity in a low viscosity solvent. As solvent viscosity raises, the relative weight of ICT state increases, while that of TICT state drops; consequently, PET rate decreases, leading to a stronger emission in 1.

In a high viscosity solvent, the conformation of 1 is probably best represented by the molecular structure in the crystal environment (Figure 1c). This conformation is N-shaped, and favorable for FRET, but unfavorable for PET; in addition, ICT excitation becomes more dominant. As a result, the emission of 1 was substantially enhanced (≥34-fold) as solvent viscosity increased from 20.5 to 945 cP, largely owing to the decreasing PET rate (Figure S22). In contrast, the control compound 4 (Figure 1b), in which no PET is involved, experienced only a 5-fold emission enhancement, due to the suppression of TICT formation (Figure S23); previously reported molecular rotors without the PET mechanism also exhibit considerably lower sensitivity on solvent viscosity, in comparison to 143. Interestingly, the strong fluorescence enhancement in Figure 2b (where the excitation wavelength is chosen in such a way that no FRET occurs) suggests that FRET is not a compulsory condition for the viscosity dependent emission intensification. Rather, the sterohindrance of anthracene makes it more sensitive to viscosity; and it is anticipated that changing anthracene to another bulky moiety without FRET with 1,8-naphthalimide could also make the PET system sensitive to viscosity changes (but with the risk of losing the capability of ratiometric fluorescent imaging as in 1).

In conclusion, we have designed a PET fluorescent probe 1 for quantitatively mapping viscosity in living cells via fluorescent ratiometric detection and fluorescence lifetime imaging. Lysosomal regions are revealed to have the highest viscosity, followed by mitochondrial regions in the MCF-7 cell. The viscosity-dependent fluorescence increase of 1 is mainly attributed to the inhibition of the PET process from the aniline nitrogen to 1,8-naphthalimide; the introduction of the PET mechanism in addition to the conventional TICT rotor design in 1 greatly improves its sensitivity on solvent viscosity, i.e., ~6 times larger than that of 4, in which only the TICT mechanism is involved. This new design concept affords a promising route for the development of viscosity probes with enhanced sensitivities. Lastly, it should be pointed out that 1 is only sensitive to viscosity higher than ~60 cP (Figures 2 and 3). Developing new fluorescent probes functioning in the low viscosity region (<60 cP) is the subject of our future work.

Methods

Viscosity measurements

The viscosity of the ethylene glycol/glycerol mixtures at 25°C was measured according to a previously reported method17.

Cell incubation and cytotoxicity experiment

The mammalian cells MCF-7, Hela, BV2, PC12, 7721, myocardial cell, and neural stem cell were obtained from Institute of Basic Medical Sciences (IBMS), Chinese Academy of Medical Sciences (CAMS). These cells were cultured in Dulbecco's modified Eagle's medium (DMEM, Invitrogen) under standard culture conditions (atmosphere of 5% CO2 and 95% air at 37°C), and supplemented with 10% fetal bovine serum (FBS).

The cytotoxic effects of sensor 1 were performed by reducing 3-(4,5-dimethylthiahiazol-2-y1)-2,5-diphenytetrazolium bromide (MTT) to formazan crystals using mitochondrial dehydrogenases. Briefly, MCF-7 cells were seeded in 96-well microplates at a density of 1 × 105 cells/mL in 100 μL of medium containing 10% FBS. After 24 h of cell attachment, the plates were washed with PBS (100 μL/well). The cells were then cultured in a medium with 10 μM Rlyso/R for 12 h. Six replicate cells in a culture medium without fluorescent dyes were used as the control groups. MTT (10 μL, 5 mg/mL) in PBS was subsequently added to each well. The plates were then incubated at 37°C for 4 h in a 5% CO2 humidified incubator. The medium was carefully removed, and the purple products were lysed in 200 μL DMSO. The plate was shaken for 10 min, and the absorbance was measured at 570 and 630 nm using a microplate reader (Thermo Fisher Scientific). Cell viability was calculated based on the following formula: Cell survival rate = average A570 nm of the treated group/average A570 nm of the control group × 100%.

Fluorescent imaging

The mammalian cells including MCF-7, Hela, BV2, PC12, 7721, myocardial cell, and neural stem cell were seeded in 24-well flat-bottomed plates and then incubated for 24 h at 37°C under 5% CO2 to reach 70–90% confluency. These cells were used in co-localization experimentation. Sensor 1 (5 μM) was then added to the cells and incubated for another 30 min. The cells were washed three times with phosphate-buffered saline (PBS). Fluorescence imaging was performed using an OLYMPUS FV-1000 inverted fluorescence microscope with a 60× objective lens.

Lysosome staining in live cells: Lyso-Tracker Red (LTR, 5 μM) and Neutral Red (NR, 5 μM) were used to co-stain the cells.

Mitochondria staining in live cells: MitoTracker TMRM (3 μM) and MitoTracker Deep Red FM (5.0 μM) were used to co-stain the cells.

Fluorescence lifetime imaging (FLIM)

The FLIM was measured with a B&H DCS120 microscopy. The emission was collected through a 535 ± 15 nm band pass filter. For imaging studies, MCF-7 cells were supplemented with 10% fetal bovine serum. The cells were seeded in 24-well flat-bottomed plates and then incubated for 24 h at 37°C under 5% CO2. Sensor 1 (10 μM) was then added to the cells and incubated for another 30 min. The cells were washed three times with 2 mL PBS at room temperature, and then observed under a confocal microscopy. For cell apoptosis studies, MCF-7 cells were stained with 1 (10 μM) for 30 min. 10 μM dexamethasone (1 mmol/L, DMSO) was then slowly added and fluorescence images of the resulting solution were collected after different time durations (0, 6, 10, 20 and 30 min).

Computational details

Quantum mechanical calculations were performed on representative conformations of 1 using Gaussian 0944. These conformations concern the relative positions between N1 and N2, that is, the N-shaped [Figure 1a(i–ii)] and U-shaped alignments [Figure 1a(iii–iv)], and the alignment between anthracene and 1,8-naphthalimide. The geometries of these different conformations of 1 were optimized using Becke's three-parameter and Lee-Yang-Parr hybrid functional (B3LYP)45,46,47 and a 6-31G(d) basis set48, in ethylene glycol solution, as accounted for via the polarizable continuum model (PCM)49,50. These optimizations were followed by single point and time-dependent density functional theory (TD-DFT) calculations using B3LYP/6-31 + G(d,p) in order to accurately determine the relative energetic stability of all conformers and their excitation mechanisms. More computational details are available in the Supporting Information.

Author Contributions

T.L. synthesized the compounds and performed viscosity detection and fluorescence imaging experiments. X.L. performed theoretical calculations. Z.X., J.C., X.Q. and D.R.S. designed the experiments and directed the study. All authors contributed in analyzing experimental results and writing the manuscript.

Supplementary Material

Supplementary Information

Supporting Information

srep05418-s1.pdf (2.5MB, pdf)

Acknowledgments

We are thankful for financial support from the National Natural Science Foundation of China (21276251), Ministry of Human Resources and Social Security of PRC, the 100 talents program funded by Chinese Academy of Sciences, State Key Laboratory of Fine Chemicals of China (KF1105), and the Herchel Smith Fund. D.R.S. is supported by the EPSRC, ERC, BBSRC, MRC and Wellcome Trust.

References

  1. Ueno T. & Nagano T. Fluorescent probes for sensing and imaging. Nat. Methods 8, 642–645 (2011). [DOI] [PubMed] [Google Scholar]
  2. Zhang J., Campbell R. E., Ting A. Y. & Tsien R. Y. Creating new fluorescent probes for cell biology. Nat. Rev. Mol. Cell Biol. 3, 906–918 (2002). [DOI] [PubMed] [Google Scholar]
  3. Fernández-Suárez M. & Ting A. Y. Fluorescent probes for super-resolution imaging in living cells. Nat. Rev. Mol. Cell Biol. 9, 929–943 (2008). [DOI] [PubMed] [Google Scholar]
  4. Kuimova M. K. Mapping viscosity in cells using molecular rotors. Phys. Chem. Chem. Phys. 14, 12671–12686 (2012). [DOI] [PubMed] [Google Scholar]
  5. Kuimova M. K. et al. Imaging intracellular viscosity of a single cell during photoinduced cell death. Nat. Chem. 1, 69–73 (2009). [DOI] [PubMed] [Google Scholar]
  6. Peng X. et al. Fluorescence ratiometry and fluorescence lifetime imaging: using a single molecular sensor for dual mode imaging of cellular viscosity. J. Am. Chem. Soc. 133, 6626–6635 (2011). [DOI] [PubMed] [Google Scholar]
  7. Deliconstantinos G., Villiotou V. & Stavrides J. C. Modulation of particulate nitric oxide synthase activity and peroxynitrite synthesis in cholesterol enriched endothelial cell membranes. Biochem. Pharmacol. 49, 1589–1600 (1995). [DOI] [PubMed] [Google Scholar]
  8. Zubenko G. S., Kopp U., Seto T. & Firestone L. L. Platelet membrane fluidity individuals at risk for Alzheimer's disease: a comparison of results from fluorescence spectroscopy and electron spin resonance spectroscopy. Psychopharmacology 145, 175–180 (1999). [DOI] [PubMed] [Google Scholar]
  9. Nadiv O. et al. Elevated protein tyrosine phosphatase activity and increased membrane viscosity are associated with impaired activation of the insulin receptor kinase in old rats. Biochem. J. 298 (Part 2), 443–450 (1994). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Haidekker M. A. & Theodorakis E. A. Molecular rotors-fluorescent biosensors for viscosity and flow. Org. Biomol. Chem. 5, 1669–1678 (2007). [DOI] [PubMed] [Google Scholar]
  11. Haidekker M. A. et al. New fluorescent probes for the measurement of cell membrane viscosity. Chem. Biol. 8, 123–131 (2001). [DOI] [PubMed] [Google Scholar]
  12. Haidekker M. A., Brady T. P., Lichlyter D. & Theodorakis E. A. A Ratiometric fluorescent viscosity sensor. J. Am. Chem. Soc. 128, 398–399 (2006). [DOI] [PubMed] [Google Scholar]
  13. Yasuhara K., Sasaki Y. & Kikuchi J.-I. Fluorescent sensor responsive to local viscosity and its application to the imaging of liquid-ordered domain in lipid membranes. Colloids Surf., B 67, 145–149 (2008). [DOI] [PubMed] [Google Scholar]
  14. Dakanali M. et al. Self-calibrating viscosity probes: design and subcellular localization. Bioorg. Med. Chem. 20, 4443–4450 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Yusop R. M., Unciti-Broceta A. & Bradley M. A highly sensitive fluorescent viscosity sensor. Bioorg. Med. Chem. Lett. 22, 5780–5783 (2012). [DOI] [PubMed] [Google Scholar]
  16. Liu F. et al. Ratiometric detection of viscosity using a two-photon fluorescent sensor. Chem.–Eur. J. 19, 1548–1553 (2013). [DOI] [PubMed] [Google Scholar]
  17. Kuimova M. K., Yahioglu G., Levitt J. A. & Suhling K. Molecular rotor measures viscosity of live cells via fluorescence lifetime imaging. J. Am. Chem. Soc. 130, 6672–6673 (2008). [DOI] [PubMed] [Google Scholar]
  18. Levitt J. A. et al. Membrane-bound molecular rotors measure viscosity in live cells via fluorescence lifetime imaging. J. Phys. Chem. C 113, 11634–11642 (2009). [Google Scholar]
  19. Someya Y. & Yui H. Fluorescence lifetime probe for solvent microviscosity utilizing anilinonaphthalene sulfonate. Anal. Chem. 82, 5470–5476 (2010). [DOI] [PubMed] [Google Scholar]
  20. Lopez-Duarte I., Vu T. T., Izquierdo M. A., Bull J. A. & Kuimova M. K. A molecular rotor for measuring viscosity in plasma membranes of live cells. Chem. Commun. 10.1039/c3cc47530a (2014). [DOI] [PubMed] [Google Scholar]
  21. Wang L., Xiao Y., Tian W. & Deng L. Activatable rotor for quantifying lysosomal viscosity in living cells. J. Am. Chem. Soc. 135, 2903–2906 (2013). [DOI] [PubMed] [Google Scholar]
  22. Yang Z. et al. A self-calibrating bipartite viscosity sensor for mitochondria. J. Am. Chem. Soc. 135, 9181–9185 (2013). [DOI] [PubMed] [Google Scholar]
  23. Kao Y.-T., Zhu X. & Min W. Protein-flexibility mediated coupling between photoswitching kinetics and surrounding viscosity of a photochromic fluorescent protein. Proc. Natl. Acad. Sci. U.S.A. 109, 3220–3225 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. de Silva A. P. et al. Signaling recognition events with fluorescent sensors and switches. Chem. Rev. 97, 1515–1566 (1997). [DOI] [PubMed] [Google Scholar]
  25. de Silva A. P., Moody T. S. & Wright G. D. Fluorescent PET (photoinduced electron transfer) sensors as potent analytical tools. Analyst 134, 2385–2393 (2009). [DOI] [PubMed] [Google Scholar]
  26. Kuss-Petermann M., Wolf H., Stalke D. & Wenger O. S. Influence of donor–acceptor distance variation on photoinduced electron and proton transfer in rhenium(i)–phenol dyads. J. Am. Chem. Soc. 134, 12844–12854 (2012). [DOI] [PubMed] [Google Scholar]
  27. Osuka A. et al. Geometry dependence of intramolecular photoinduced electron transfer in synthetic zinc-ferric hybrid diporphyrins. J. Am. Chem. Soc. 112, 4958–4959 (1990). [Google Scholar]
  28. Lewis F. D. & Burch E. L. Amide Conformation-dependent intramolecular photoinduced electron transfer. J. Am. Chem. Soc. 116, 1159–1160 (1994). [Google Scholar]
  29. Croney J. C., Helms M. K., Jameson D. M. & Larsen R. W. Conformational dynamics and temperature dependence of photoinduced electron transfer within self-assembled coproporphyrin:cytochrome c complexes. Biophys. J. 84, 4135–4143 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Sparano B. A. & Koide K. Fluorescent sensors for specific RNA: a general paradigm using chemistry and combinatorial biology. J. Am. Chem. Soc. 129, 4785–4794 (2007). [DOI] [PubMed] [Google Scholar]
  31. Han J. & Burgess K. Fluorescent indicators for intracellular pH. Chem. Rev. 110, 2709–2728 (2009). [DOI] [PubMed] [Google Scholar]
  32. Gunnlaugsson T. et al. Fluorescent photoinduced electron transfer (PET) sensors for anions; from design to potential application. J. Fluoresc. 15, 287–299 (2005). [DOI] [PubMed] [Google Scholar]
  33. Sunahara H., Urano Y., Kojima H. & Nagano T. Design and synthesis of a library of BODIPY-based environmental polarity sensors utilizing photoinduced electron-transfer-controlled fluorescence on/off switching. J. Am. Chem. Soc. 129, 5597–5604 (2007). [DOI] [PubMed] [Google Scholar]
  34. Doose S., Neuweiler H. & Sauer M. Fluorescence quenching by photoinduced electron transfer: a reporter for conformational dynamics of macromolecules. ChemPhysChem 10, 1389–1398 (2009). [DOI] [PubMed] [Google Scholar]
  35. Nolan E. M. et al. Zinspy sensors with enhanced dynamic range for imaging neuronal cell zinc uptake and mobilization. J. Am. Chem. Soc. 128, 15517–15528 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Finckh P., Heitele H. & Michel-Beyerle M. E. Intramolecular electron transfer in viscous solution. Chem. Phys. 138, 1–10 (1989). [Google Scholar]
  37. Thiagarajan V., Selvaraju C., Malar E. J. P. & Ramamurthy P. A novel fluorophore with dual fluorescence: local excited state and photoinduced electron-transfer-promoted charge-transfer state. ChemPhysChem 5, 1200–1209 (2004). [DOI] [PubMed] [Google Scholar]
  38. Li W., Fan W., Elmore B. O. & Feng C. Effect of solution viscosity on intraprotein electron transfer between the FMN and heme domains in inducible nitric oxide synthase. FEBS Lett. 585, 2622–2626 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Dorfman R. C. & Fayer M. D. The influence of diffusion on photoinduced electron transfer and geminate recombination. J. Chem. Phys. 96, 7410–7422 (1992). [Google Scholar]
  40. Koch M., Rosspeintner A., Angulo G. & Vauthey E. Bimolecular photoinduced electron transfer in imidazolium-based room-temperature ionic liquids is not faster than in conventional solvents. J. Am. Chem. Soc. 134, 3729–3736 (2012). [DOI] [PubMed] [Google Scholar]
  41. Shahid M., Srivastava P. & Misra A. An efficient naphthalimide based fluorescent dyad (ANPI) for F− and Hg2+ mimicking OR, XNOR and INHIBIT logic functions. New J. Chem. 35, 1690–1700 (2011). [Google Scholar]
  42. de Silva A. P. et al. New fluorescent model compounds for the study of photoinduced electron transfer: the influence of a molecular electric field in the excited state. Angew. Chem., Int. Ed. 34, 1728–1731 (1995). [Google Scholar]
  43. For example, the probe RY3 reported by Peng et al. in Ref. 6 possesses a intensity amplification by ~6 times as solvent viscosity increases from 1.2 cP (ethanol) to 950 cP (99% glycerol); the probe reported by Kuimova et al. in Ref. 17 demonstrates a intensity increase by ~12 times from 0.6 to 950 cP; the probe 2 reported by Lopez-Duarte et al. in Ref. 20 exhibits a fluorescence intensity enhancement by ~10 times from 21 to 930 cP; the probe 1 reported by Yang et al. in Ref. 22 shows a fluorescence intensity increase by ~15 times from 23.2 to 945 cP. In contrast, our probe 1 exhibits a remarkable emission intensity increase by more than 34-fold from 20.5 to 945 cP.
  44. Gaussian 09 (Gaussian Inc., Wallingford, CT, 2009).
  45. Stephens P. J., Devlin F. J., Chabalowski C. F. & Frisch M. J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional fields. J. Phys. Chem. 98, 11623–11627 (1994). [Google Scholar]
  46. Becke A. D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 98, 5648–5652 (1993). [Google Scholar]
  47. Lee C., Yang W. & Parr R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 37, 785–789 (1988). [DOI] [PubMed] [Google Scholar]
  48. Rassolov V. A., Ratner M. A., Pople J. A., Redfern P. C. & Curtiss L. A. 6-31G* basis set for third-row atoms. J. Comput. Chem. 22, 976–984 (2001). [Google Scholar]
  49. Chipman D. M. Reaction field treatment of charge penetration. J. Chem. Phys. 112, 5558–5565 (2000). [Google Scholar]
  50. Miertus S., Scrocco E. & Tomasi J. Electrostatic interaction of a solute with a continuum. A direct utilizaion of ab initio molecular potentials for the prevision of solvent effects. Chem. Phys. 55, 117–129 (1981). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supporting Information

srep05418-s1.pdf (2.5MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES