Frealix: Model-based refinement of helical filament structures from electron micrographs

Abstract

The structures of many helical protein filaments can be derived from electron micrographs of their suspensions in thin films of vitrified aqueous solutions. The most successful and generally-applicable approach treats short segments of these filaments as independent “single particles”, yielding near-atomic resolution for rigid and well-ordered filaments. The single-particle approach can also accommodate filament deformations, yielding sub-nanometer resolution for more flexible filaments. However, in the case of thin and flexible filaments, such as some amyloid-β (Aβ) fibrils, the single-particle approach may fail because helical segments can be curved or otherwise distorted and their alignment can be inaccurate due to low contrast in the micrographs. We developed new software called Frealix that allows the use of arbitrarily short filament segments during alignment to approximate even high curvatures. All segments in a filament are aligned simultaneously with constraints that ensure that they connect to each other in space to form a continuous helical structure. In this paper, we describe the algorithm and benchmark it against datasets of Aβ(1–40) fibrils and tobacco mosaic virus (TMV), both analyzed in earlier work. In the case of TMV, our algorithm achieves similar results to single-particle analysis. In the case of Aβ(1–40) fibrils, we match the previously-obtained resolution but we are also able to obtain reliable alignments and ~8-Å reconstructions from curved filaments. Our algorithm also offers a detailed characterization of filament deformations in three dimensions and enables a critical evaluation of the worm-like chain model for biological filaments.

1. Introduction

Electron micrographs of thin (tens of nanometers) films of vitrified, dilute suspensions of biological macromolecules and their assemblies can be analyzed to deduce their three-dimensional (3D) structure (Frank, 2006). Cases in which proteins form filamentous assemblies are particularly well suited to structure determination, since a single image of a helical filament can yield a full tomographic series of projections through the helical protomer. Helical filaments permitted some of the earliest examples of structure determination by electron microscopy (De Rosier and Klug, 1968) and continue to be studied in many different contexts (DeRosier, 2007).

In recent years, most investigators have been using variations on iterative algorithms originally developed for the study of so-called single particles. When adapted to helical structure determination, these methods treat short (tens of nanometers) segments of imaged filaments as independent projections of the unknown 3D structure to be determined. The length of those segments is chosen carefully. They must be long enough to allow for reliable and accurate alignment against projections calculated from the current 3D reconstruction yet, because no helical filament is perfectly rigid, short enough to approximate the canonical helical assembly depicted by the 3D reconstruction (Bluemke et al., 1988).

The single-particle approach may be less successful when applied to a class of protein filaments whose mass-per-length and persistence lengths (with regards to bending, torsion and/or stretching) are too low to be amenable to such image analysis, given a set of optical and detection conditions. Such filaments are so deformable that any given image segment would be unlikely to satisfy both length requirements. Luckily, many filaments of biological importance do not fall under this regime. Even filamentous actin (f-actin) appears to be (or can become) rigid enough when imaged in cryo-EM experiments to yield sub-nanometer resolution (Fujii et al., 2010; Galkin et al., 2012).

Fibrils formed by amyloid-β (Aβ) peptides, which are implicated in Alzheimer’s disease, present an interesting intermediate case, whence sub-nanometer reconstructions have been obtained, but with some difficulty. A strong meridional reflection at ~1/4.8 Å⁻¹ can be seen in averaged power spectra computed from existing micrographs of Aβ fibrils (Sachse et al., 2008), suggesting that a high degree of axial order is preserved in those specimens and that the images should therefore be of sufficient quality for higher-resolution reconstructions to be attainable. However, processing micrographs of unstained Aβ fibrils is challenging because they are essentially featureless in the axial direction at resolutions >4.8 Å and because the signal-to-noise ratio (SNR) in micrographs recorded onto film is insufficient to give reliable alignments (Sachse, 2007; Sachse et al., 2008). Many Aβ fibril morphologies resemble flat nanoscopic ribbons with slow twists on the order of 1 °/nm (Meinhardt et al., 2009), so that their projection images periodically exhibit thin (~4–7 nm) high-contrast crossovers with projected molecular weights of ~5–8 kDa nm⁻² and wide (~10–20 nm) low-contrast regions with projected molecular weights of ~2.3–3.4 kDa nm⁻² (Schmidt et al., 2009), which is comparable with f-actin (~2.8 kDa nm⁻², width ~6–10 nm).

Two avenues to improving the resolution of Aβ fibril structures therefore present themselves: improving the SNR of micrographs and/or improving the image analysis algorithms to make them even more robust to low SNR and filament deformations. Here, we explore the second avenue and attempt to make iterative real-space refinement of Aβ fibrils even more robust to low SNR and fibril deformations.

In previous work, knowledge about the connectivity of image segments coming from the same filaments and their geometric relationships due to helical symmetry was used as a criterion for validation of segment alignments and for the a posteriori selection of segments. For example, when analyzing micrographs of TMV, Sachse et al. (2007) discarded those segments for which either the assigned polarity contradicted that of other segments from the same filament or the shifts perpendicular to the helical axis were greater than ~10 Å. Similar a posteriori exclusion of segments is employed by the commonly-used method developed by Egelman (2000). In our approach we tested whether this type of criterion could also be used as a prior during the iterative real-space processing of filament segments to improve the overall quality of their alignments. In particular, we were interested in whether it would be possible to reliably “align” filaments with high curvature and/or low contrast.

To help answer these questions, we developed Frealix, a software tool that introduces “full filament” restraints so that helical deformations can be tracked accurately using arbitrarily short linear segments, which are not treated independently from each other.

2. Theory

2.1. Frealix

Frealix is a program for the analysis of electron micrographs of helical filaments. Its inputs are micrographs, filament coordinates, estimated helical parameters and a preexisting 3D reconstruction. Its outputs are a 3D reconstruction, refined coordinates and refined helical parameters.

Internally, each filament is represented as an assembly of (rigid-body) subunits positioned along a helix which has a space curve as its axis. The space curve and helical parameters are refined iteratively by maximizing a function which compares the experimental (noisy) image of the filament to projections of the current reconstruction as predicted by its model. The scoring function also integrates restraints derived from mechanical considerations when modeling filaments.

Below, we describe the parametrization of our model for helical filaments (Section 2.2), the function used to “score” sets of parameter values given a model and a micrograph (Section 2.3), maximization strategies we use during refinement (Section 2.4) and the 3D reconstruction protocol (Section 2.6).

2.2. Modeling helical filaments

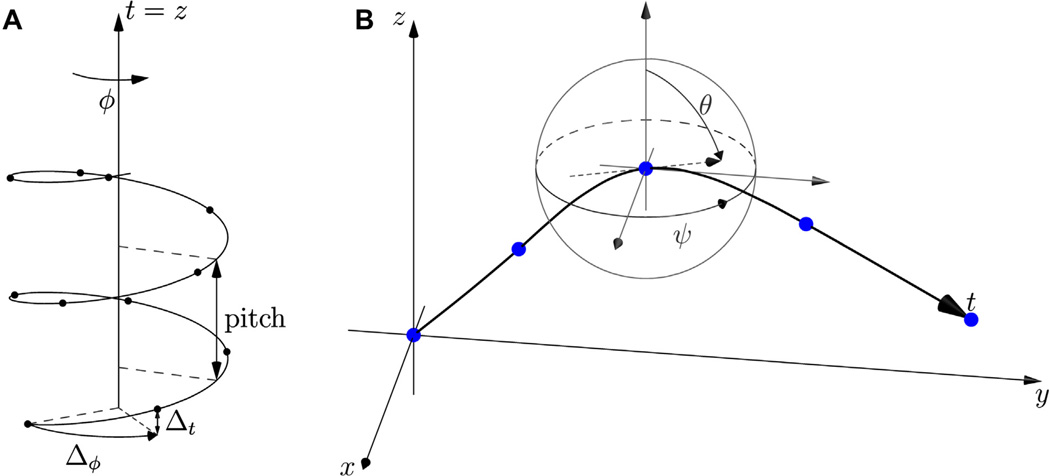
The simplest model of a straight filament without distortions can be described by two parameters: the rise (Δ_t) and twist (Δ_φ) per helical subunit (Fig. 1A). If we let the helical axis coincide with the Z axis and position the first asymmetric unit on the Z = 0.0 plane, the Z position of the ith asymmetric unit is Z = (i − 1)Δ_t and its (X,Y) coordinates are obtained from the (X,Y) coordinate of the first unit by i − 1 rotations of Δ_φ around Z. All the asymmetric units lie on a continuous helix which has a characteristic pitch, the distance along its axis over which a revolution (2π) is completed. One can define t, the distance along the helical axis: in this simple case t = Z.

Fig.1.

Helical filament parametrization. (A) Ideal straight helix. (B) A generalized helical axis is a space curve r, drawn in bold. Its x, y and z positions are functions of t, its arc length, and it interpolates a set of n waypoints (blue dots). At any given point, the derivatives of x, y and z with respect to t define the tangent vector (dashed arrow) and are related to the local (instantaneous) Euler angles ψ (in-plane) and θ (out-of-plane rotation). The helix was not drawn in this panel, for clarity.

A more generalized description of observable filaments needs to account for their elasticity with regards to bending, torsion and stretching. To achieve this in the simplest possible way, we chose to describe the axis of a filament as a space curve r defined by 3 cubic spline functions x(t), y(t) and z(t) (t, as before, is the arc length along the axis), which interpolate a set of n waypoints defined by (x_i,y_i,z_i) coordinates, where i = 1, …, n.

At waypoint i, the θ_i (out-of-plane) and ψ_i (in-plane) Euler angles are related to the curve’s tangent vector (Fig. 1B) and thus its derivatives x′(t_i), y′(t_i) and z′(t_i), and can be used as constraints when solving the splines:

$$x\prime (t_i)=\text{sin}{\theta }_i\text{cos}{\psi }_{i}y\prime (t_i)=\text{sin}{\theta }_i\text{sin}{\psi }_{i}z\prime (t_i)=\text{cos}{\theta }_i$$ (1)

where t_i is the arc length from the filament’s first waypoint to waypoint i. Interpolating cubic splines which are thus constrained by their tangents are sometimes called Hermite splines (Knott, 2000 p. 66). Conversely, Euler angles at any point along the filament axis can be computed from the local tangent vector:

$$\psi (t)={\text{tan}}^{-1}\left(\frac{y\prime (t)}{x\prime (t)}\right)\theta (t)=-{\text{tan}}^{-1}\left(\frac{y\prime (t)}{z\prime (t)\text{sin}\psi (t)}\right)\mathit{\text{or}}\theta (t)=-{\text{tan}}^{-1}\left(\frac{-x\prime (t)}{z\prime (t)\text{cos}\psi (t)}\right).$$ (2)

Arbitrary bending deformations of the helical axis can be accurately described by these three spline functions, given a sufficient number of waypoints.

We also define two additional parameters per waypoint – rotation around the helical axis (φ_i) and helical subunit number (h_i) – and use natural cubic splines to interpolate values for these parameters. This allows us to define at every point along the filament the local helical parameters Δ_φ and Δ_t, the axial twist and rise which relate a subunit to its neighbors:

$${\mathrm{\Delta }}_t(t)=\frac{1}{h\prime (t)}{\mathrm{\Delta }}_{\varphi }(t)=\frac{\varphi \prime (t)}{h\prime (t)}.$$ (3)

Each waypoint thus contributes 7 parameters to the description of a filament: x, y, z, θ and ψ describe the trajectory of the helical axis while φ and h describe the position of helical lattice points (we chose the convention that subunits be located where h(t) is integral). Every possible asymmetric, 1-start helical lattice can be modeled by these 7n parameters (where n is the number of waypoints). Multiple helical starts and symmetries can be described by adding 3 more parameters: axial symmetry, perpendicular (side dyad) symmetry and the number of starts. Although these 3 parameters can be supplied by the user, they are not optimized by Frealix.

The goal of refinement within Frealix is to find the best possible description of each imaged filament using this parametrization. In other words, optimal values for 7n parameters must be sought. We define optimal parameter values as those which maximize the scoring function described below.

2.3. Scoring function

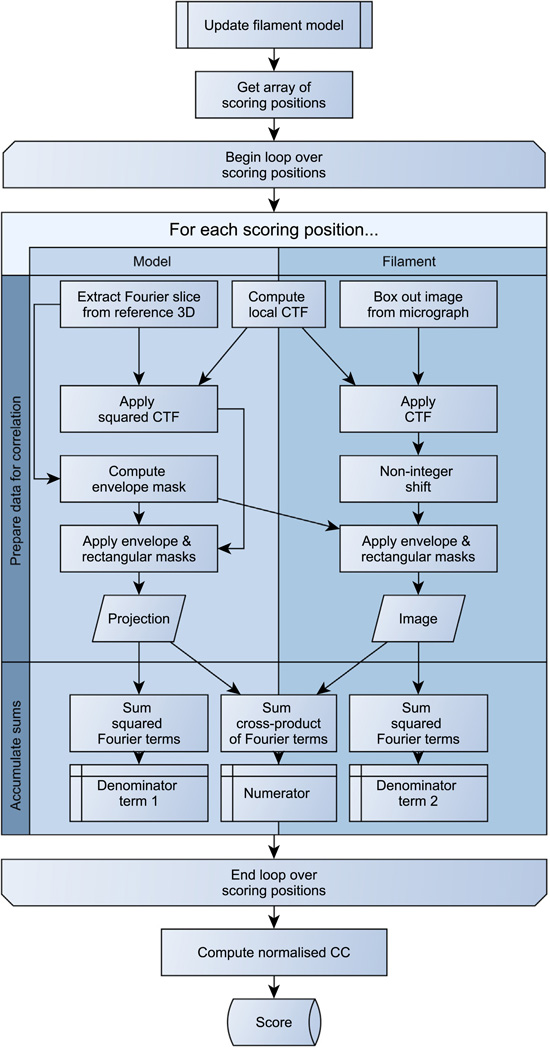
The purpose of the scoring function is to evaluate the agreement between the (3 + 7n)-parameter description (internal representation) of a filament and its experimental image, given a 3D reconstruction. To achieve this, we compute a normalized cross-correlation coefficient between projections from the reconstruction and image data along the path of the filament. Our algorithm is described below and in Fig. 2.

Fig.2.

Scoring function algorithm.

First, the model of the filament must be updated with the new parameter values to be evaluated (of which there may be up to 7n). In practice,

1. the new values for x_i, y_i, z_i, θ_i and ψ_i (i = 1,…, n) are used as constraints to solve the x(t), y(t) and z(t) splines and redefine the axial space curve;

2. the arc lengths between waypoints are recalculated using Pythagoras’ relation over very short steps, giving new values of t_i;

3. steps 1 and 2 are repeated until convergence – the axial space curve is now arc-length parametrized;

4. φ(t) and h(t) are solved as natural cubic splines, which interpolate the new φ_i and h_i values.

Once the filament model has been updated, a set of m “scoring” positions regularly spaced along the path of the filament is defined.

The helical filament will be treated using a linear approximation at each position, with m (and therefore the linear segment length) chosen such that the approximation is accurate enough even in cases of large local deformations (see Section 2.3.1). At each position:

1. the image of a small segment is extracted from the micrograph and Fourier-transformed (the segment length is such that there is no overlap with neighboring segments);

2. using the Euler angles corresponding to the model’s space curve tangent at that point (Eq. (2)), a plane through the Fourier transform of the 3D model is also extracted;

3. the pixel-wise cross-product between the image and the projection is evaluated (up to a radius corresponding to the maximum spatial frequency to be used during refinement), as well as the power of the image and the power of the projection.

The cross-correlation between the model and the experimental image of the filament is then the sum of the cross-products accumulated at each of the m points, normalized:

$$CC=\frac{{\sum }_m{\sum }_{\text{pixels}}\text{image proj}}{\sqrt{{\sum }_m{\sum }_{\text{pixels}}\text{image}}\sqrt{{\sum }_m{\sum }_{\text{pixels}}\text{proj}}}$$ (4)

Optionally a weighted, rather than linear, cross-correlation score can be computed (Stewart and Grigorieff, 2004) and/or mechanical considerations can be used to modify the scoring function (Section 2.6.3).

2.3.1. Segment length

The choice of m (the number of scoring positions), which determines the segment length, is crucial to successful refinement of helical structures. Lower m values allow for faster computation, since there are fewer projections to compute. However, since our algorithm does not use overlapping segments (each pixel in the micrograph is used only once by the scoring function), lower m values also imply longer segments, which offer less accurate approximations of local deformations such as bending of the helical axis or local variations in helical parameters.

Among other considerations, our algorithm imposes an upper bound on the segment length L (and therefore m) for a given filament by taking into account its maximal local curvature (c, in Å⁻¹, see Section 2.6.3), the spatial frequency corresponding to the target resolution for the refinement (f, in Å⁻¹; this can be specified by the user at runtime) and a maximum tolerated phase error (Φ_T, for example π/6): L ≤ $L\le \sqrt{\frac{4{\Phi }_T}{f\pi c}}$.

Future implementations of the algorithm could include similar upper bounds on L derived from torsional and stretching deformations.

2.4. Maximization strategy

Finding the best model for each filament requires that we maximize the scoring function described in Section 2.3. Because of the large number of parameters (up to 7n, where n > 3), this is a search problem in a high-dimensionality space which is likely to be multimodal because of the periodic nature of the filaments and their images. Below we describe some strategies we implemented in Frealix to approach this problem.

2.4.1. Minimizers

Frealix currently uses three types of minimizers: Powell conjugate gradient (Harwell Numerical Library, 1979), downhill simplex (Nelder and Mead, 1964) and differential evolution (Brest et al., 2006; Storn and Price, 1996). The choice of minimizer is made at runtime by the user (conjugate gradient being the default). The user has the option to start the minimizer several times at randomized positions in the neighborhood of the current best parameter values. Such multi-start strategies can lead to the discovery of better local maxima, particularly during early stages of refinement.

2.4.2. Reducing dimensionality

The refinement in 7n dimensions of a helical reconstruction can account for many possible types of filament deformations. At times it is appropriate to ignore some of these deformations and thus reduce the dimensionality of the problem, for example because such deformations are known to be insignificant at the target resolution. As an extreme example one can imagine an ideal filament, entirely rigid and with every helical subunit related to its neighbors by the canonical helical parameters. Such an idealized filament could be parametrized by 7 quantities (five to describe its straight helical axis, one for the length of the filament and one for the position along that length of one of the repeats).

Frealix allows for many combinations of refinement parameters between these two extremes (7 and 7n). Here are a few examples available in the current implementation:

• The rise per subunit can be held constant, which may be a good approximation for amyloid β fibrils (this replaces n dimensions corresponding to h_i and replaces them with a single value for the filament’s phase origin of subunits).

• One may “turn off” out-of-plane (θ) refinement, e.g. because it is not necessary when targeting 8–10 Å resolution for some specimens (e.g. Sachse et al., 2008). This removes 2n dimensions from the refinement problem (Z and θ) by constraining filaments to the plane of the micrograph, which may be approximated by using CTF estimation (Mindell and Grigorieff, 2003).

• The Z position of waypoints can be computed from the out-of-plane tilt at waypoints (θ_i angles), the filament’s average Z (defocus) and a constraint to minimize the filament’s curvature. This removes n dimensions.

• The rise and/or twist per subunit can be held constant by introducing discontinuities in the helix between waypoints, so that the internal representation of the helical assembly has sharp discontinuities halfway between waypoints, while the axis is still a continuous space curve (this is described in detail in Section 2.4.2.1). This can remove n or 2n dimensions.

There are other ways to reduce the minimization’s dimensionality:

• the number of waypoints can be reduced (see Section 2.3.1);

• rather than refining all of a filament’s free parameters simultaneously, each waypoint can be refined in turn;

• longer filaments can be “split” so that they are modeled as two independent filaments (connectivity restraints are then lost, but this can be alleviated by leaving “overhanging” ends).

2.4.2.1. Dropping continuity restraints

Frealix implements two runtime options for the user to drop continuity restraints. One option drops all restraints and treats the n waypoints as independent objects, in a manner similar to previously-described single-particle approaches.

The other option lets the user drop continuity restraints for φ and/or h. In this case, linear extrapolation from the nearest waypoint (rather than cubic spline interpolation between waypoints) is used to compute an arbitrary point’s φ(t) and h(t) parameter values. All other parameters are computed as described in Section 2.2.

2.4.3. Normal modes parametrization of the search space

Under the control of a runtime option, the minimizer can either refine directly the real-space representation of filaments (described in Section 2.2) or refine a normal mode re-parametrization thereof. The normal mode analysis describes deviations from a perfectly straight helix with constant helical parameters but it does not attempt to be mechanically realistic. Rather, it is used as an alternative way for the minimizer to address and modify the configuration of filaments. The analysis is done as follows.

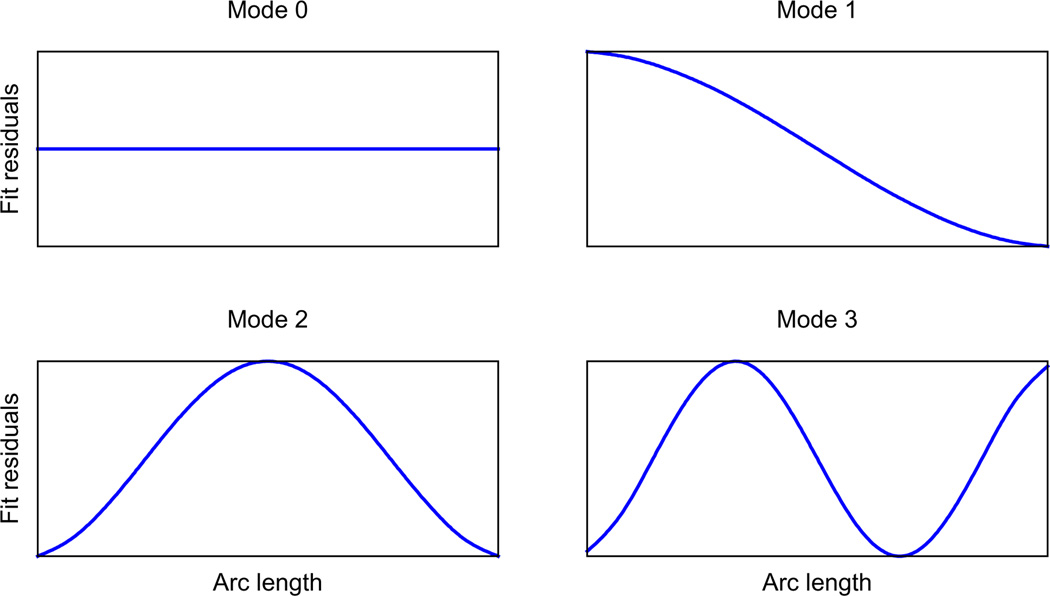
Before refinement begins, the analysis is set up by treating the n waypoints as coupled oscillators with coupling constants inversely proportional to the arc lengths between them. We then compute the one-dimensional normal mode eigenvectors and eigenvalues for the system and sort them by increasing eigenvalues (i.e. low-frequency modes first). Typical normal modes (eigenvectors) are plotted in Fig. 3 for the case where waypoints are equidistant. We then perform a linear fit of the 5 splines (x, y, z, φ, h), treat these fits as the equilibrium configuration for each dimension and use the normal modes (eigenvectors) to describe residuals from these fits. This amounts to a change of coordinate system.

Fig.3.

Normal modes of linear fit residuals in the case where waypoints are equally spaced along the filament. These modes are reminiscent of the hydrodynamic modes of an unconstrained slender rod (Howard, 2001, p. 108).

During refinement, if the user has activated that option, the minimizer refines the normal mode amplitudes corresponding to these transverse displacements rather than the actual waypoint parameter values. The normal mode amplitudes are converted to waypoint parameter values before the scoring function is called.

Normal-mode parametrization often results in a much sparser representation of the filament model. For example, decreasing the twist per unit length along the filament involves increasing the amplitude of the second mode (mode 1 in Fig. 3) for the φ spline. Without the use of normal modes, the minimizer would have to “tweak” n values to achieve the same result.

2.4.4. Refining waypoints sequentially

In some cases, only a few of the waypoints are misaligned. For those situations, Frealix has an option to refine waypoints sequentially rather than simultaneously. This reduces considerably the dimensionality of the minimization problem while retaining the full set of restraints from the full-filament model. However, it may then miss solutions that involve “moving” several neighboring waypoints together. One may iterate between sequential and simultaneous maximization of waypoints during refinement (normal-mode reparametrization can only be used during simultaneous waypoint refinement).

2.5. Refinement bootstrapping

Frealix is a refinement program. Although this may be a feature in a future release, it does not attempt an initial estimate of the helical parameters. Therefore, a good estimate of those parameters must be supplied by the user. This can be done by selecting relatively straight filaments to get estimated helical parameters using single-particle or Fourier–Bessel approaches (see for example Desfosses et al., 2013 and references therein). Once helical parameters (and a reliable 3D reconstruction) have been obtained, Frealix can be used to analyze the full dataset, including bent and twisted filaments. So far, we have implemented two ways to obtain initial values for the 7 waypoint parameters refined by Frealix:

• A Frealign (Grigorieff, 2007) parameter file and the corresponding stack of boxed images can be given as input. A normalized cross-correlation search (Roseman, 2003) is performed to find which micrograph each segment was extracted from as well as its coordinates.

• The relevant data are extracted from Boxer (Ludtke et al., 1999) coordinate files or IMOD (Kremer et al., 1996) model files (X,Y,ψ) and the output of either CTFFIND or CTFTILT (Mindell and Grigorieff, 2003; Z, θ). If the supplied X,Y coordinates are of crossovers, φ angles of i × 180° degrees are assigned to waypoints (i is the waypoint index). Otherwise, the helical parameters supplied by the user are assumed to be constant along each filament and φ and h values are assigned as a linear function of arc length (in which case the filaments are not “phased” with respect to each other).

2.6. Three-dimensional reconstruction

3D reconstruction in Frealix is done using a direct Fourier inversion similar to that of Frealign (Grigorieff, 2007). At each point along the filament where h(t) is integer, an image is extracted from the micrograph, Fourier transformed, multiplied by the local CTF, filtered with a B factor, and inserted into the 3D reconstruction. The Euler angles at which this insertion occurs can be computed from the model splines, as detailed in Section 2.2. Therefore, whereas the scoring function relies on a piecewise linear approximation of filament deformation during refinement, this assumption is dropped during reconstruction. If the helical geometry includes a point-group symmetry, the insertion is repeated in the symmetry-related orientations. Squared CTF functions are accumulated in a separate volume and once all image and CTF² data have been accumulated into their respective volumes, a Wiener-like filter is applied as described by Grigorieff (2007), yielding a single volume which is back Fourier transformed.

This real-space volume suffers from two distinct artifacts: attenuation near its edges and corruption by aliases. The attenuation is due to the convolution step during Fourier-space interpolation and is corrected exactly using the inverse of the reciprocal of the convolution kernel. The corruption by aliases, which is due to the sampling step of the interpolation operation, cannot be avoided but since the aliases are also modulated by the attenuation function, a judicious choice of convolution kernel and reconstruction volume dimensions can minimize their influence (Jackson et al., 1991). We have implemented several interpolation schemes in Frealix (nearest-neighbor, linear and windowed sinc), which can be selected at run-time by the user for use during refinement and reconstruction. The appropriate attenuation function correction is performed on the final 3D reconstruction volume, according to the user’s choice. The default is linear interpolation.

2.6.1. Helical symmetrization

Currently, to our knowledge, the most common way to impose helical symmetry on a real-space volume (for example in Frealign (Alushin et al., 2010) or SPARX-IHRSR (Behrmann et al., 2012)) is to “smear” a central slab of the volume over the full volume, with rotations matching the Z-shift of the slab. In the reconstruction algorithm used by Frealix, however, only the “central” helical asymmetric unit of the reconstructed volume is optimally reconstructed. All the other repeats will be slightly low-pass filtered, depending on their distance from the origin of the reconstruction and on filament deformations. Frealix therefore implements a helical symmetrization algorithm whereby each output voxel is mapped back into the central asymmetric unit cell and its value interpolated from the input volume at that position.

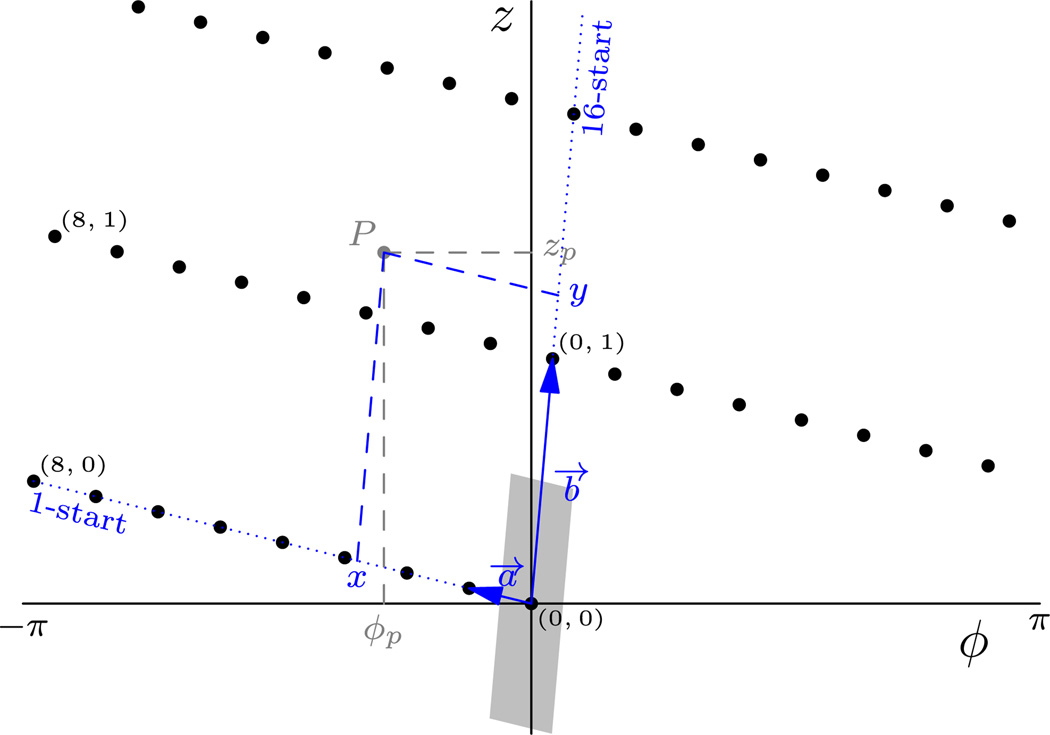
In our implementation, the primitive helical unit cell is defined by the two basis vectors a⃗ and b⃗ which, in a (φ,z) plot (Fig. 4), are the vectors that define the helical starts with the smallest absolute rise and twist per subunit, respectively. This choice is intuitive when visualizing helical reconstructions such as TMV, f-actin, etc. because it relates a given repeat to its nearest neighbors to the sides (a⃗) and above and below (b⃗). For example, in the case of a TMV reconstruction, the chosen helices are 1- and 16-start, respectively: $\mathrm{a⃗}=\left(\begin{array}{c}{\mathrm{\Delta }}_{1-\text{start}}^{\varphi }\hfill \\ {\mathrm{\Delta }}_{1-\text{start}}^t\hfill \end{array}\right)$ and $\mathrm{b⃗}=\left(\begin{array}{c}{\mathrm{\Delta }}_{16-\text{start}}^{\varphi }\hfill \\ {\mathrm{\Delta }}_{16-\text{start}}^t\hfill \end{array}\right)$.

Fig.4.

(φ,z) Plot of the real-space helical lattice of TMV. This is the real-space equivalent of (n,Z) plots (DeRosier, 2007). The two axes are scaled arbitrarily to aid visualization. Two vectors a⃗ and b⃗ are chosen to define the primitive helical unit cell. In Frealix, the helical starts with the smallest absolute rise (1-start) and twist (16-start) per subunit are selected. Any point P (gray) with cylindrical coordinates (Φ_P,z_P; light gray) can be mapped into the unit cell (gray shaded area) by first recasting its coordinates to the a⃗, b⃗ coordinates system, giving (x,y; in blue) and then shifting it by integer numbers of a⃗ and b⃗.

When looping over output voxels, the interpolating coordinates are computed by converting from Cartesian to cylindrical coordinates, then to indexed (φ,z) lattice coordinates, which can be mapped to the primitive unit cell by translation by an integer multiple of (a⃗,b⃗). The coordinates are then converted back via cylindrical coordinates to the Cartesian grid, where interpolation is carried out.

2.6.2. Fourier shell correlation

For the purposes of spectral SNR estimation, for example to apply a figure-of-merit filter, Fourier shell correlations (FSC) may be computed at every refinement round. For this, the data are split into two groups, either even- and odd-numbered filaments or the first and second halves of a filament if only one is available. 3D reconstructions are computed from each half, helical symmetry is imposed on both volumes and a mask is computed from each volume. These masks are then applied to each half-dataset reconstruction before the volumes are Fourier transformed for FSC computation.

The masks are computed from the reconstructed volumes thus: (1) the volume’s Z edges are tapered to 0.0 in real space with a cosine-edge falloff over the first and last 4 slices; (2) a Fourier-space low-pass filter is applied with a cosine falloff width of 1/40 pixels⁻¹ (equivalent to 7.5 Fourier shells for a volume of 300³ voxels) so that frequencies beyond 1/20 Å⁻¹ are zeroed; (3) the filtered volume is binarized such that the number of non-zero voxels corresponds to the expected protein volume; (4) the first and last 20% of Z slices are set to 0.0; (5) the binary mask is “softened” in real space with a cosine edge extending from the current 3D boundary with a falloff of ~16 pixels.

2.6.3. Geometrical & mechanical properties

Using the parametrization introduced in Section 2.2, it is possible to evaluate geometrical properties of each filament such as curvature and torsion. The local curvature C(t) (in units of inverse distance or radians per distance) can be evaluated from the axial space curve’s first and second derivatives r′(t) and r″ (t) (Kreyszig, 1959): $C(t)=|\mathbf{\varrho }(t)|=\frac{|\mathbf{r}\prime (t)\times \mathbf{r}″(t)|}{{|\mathbf{r}\prime (t)|}^3}$. The ϱ(t) vector lies in the plane normal to the tangent r′(t) and indicates the direction of filament bending at t, in the laboratory frame of reference. This can be affine-transformed to the frame of reference of the 3D reconstruction by using the Euler angles φ(t), θ(t) and ψ(t).

In addition to curvature, local torsional and stretching deformations can be characterized relative to the canonical (undeformed) helical twist per unit length $({\phi }_0^{\prime })$ and rise per subunit $(1/h_0^{\prime })$ (Kornyshev et al., 2007): $T(t)={\varphi }^{\prime }(t)-{\varphi }_0^{\prime }$ and $S(t)=h^{\prime }(t)-h_0^{\prime }$.

If the rigidities (persistence lengths) of a filament with respects to curvature, torsion and stretch are known, the total elastic energy associated with an observed deformed state can be evaluated by integrating the squared deformations over its arc length L (Kornyshev et al., 2007):

$$E=\frac{1}{2}{K}_{B}T{\int }_0^L{l}_{c_1}{c}_1{(t)}^2+l_{c_2}{c}_2{(t)}^2+l_{t}T{(t)}^2+l_{s}S{(t)}^{2}dt,$$

where l_c1 and l_c2 are the principal bending persistence lengths and l_t and l_s are the torsion and stretching persistence lengths. In the case of isotropic bending rigidity, a single curvature term and bending persistence length are sufficient.

Assuming that observed deformations are thermal in nature, the probability of observing a particular deformation is related to the deformation energy by Boltzmann’s constant: $P(E)\alpha \text{exp}(-\frac{E}{K_{B}T})$ (Boal, 2002). For example one might expect a normal probability distribution of curvatures, so that large curvatures are unlikely to occur: $P(E)\alpha \text{exp}(-\frac{1}{2}{l}_c\int C{(t)}^{2}dt)$ (assuming isotropic bending rigidity and thus a single bending persistence length).

If the persistence lengths are known, these Gaussian priors can be used to improve our search for the correct parameter values for a given filament, by biasing the scoring function against large filament deformations (Chen et al., 2009):

$$S=CC+{\sigma }^2(-\frac{1}{2}\int l_{c}C{(t)}^2+l_{t}T{(t)}^2+l_{s}S{(t)}^{2}dt)$$ (5)

In Frealix, the user can activate any combination of these three restraints and specify the relevant persistence lengths on input. In the current version, isotropic bending rigidity is assumed in the implementation of the curvature restraint.

3. Implementation

Frealix is implemented in Fortran 2003 with OpenMP directives for shared-memory parallelism. Image file input/output and Powell conjugate gradient minimizer routines were adapted from Frealign (Grigorieff, 2007), while the rest of the code was developed independently. It is dependent on the FFTW (Frigo and Johnson, 2005) and GSL (Galassi et al., 2003) libraries. Source code and executable binaries are available from http://grigoriefflab.janelia.org.

4. Results

To test the algorithms implemented in Frealix and help minimize the number of implementation errors, we re-processed datasets which had been analyzed previously with single-particle methodologies (Sachse et al., 2008, 2007).

4.1. Aβ(40) fibrils

We selected for analysis 450 filaments (ranging in length from ~0.3 to 1.6 µm; Fig. 5F) from 63 micrographs densitometered by Sachse et al. (2008). We included all the filaments we could select visually, regardless of their curvature or crossover-to-crossover distances, excluding only those which were bundling or aggregating with others and those for which we could not select three consecutive crossovers. The positions of crossovers were selected manually using the program Boxer (Ludtke et al., 1999), and for each filament we additionally selected two extra (non-crossover) points at either end of the filament. CTFTILT (Mindell and Grigorieff, 2003) was used to estimate the defocus of the micrographs.

Fig.5.

Aβ(40) fibril reconstructions. Central sections of 3D reconstructions of Aβ (40) fibrils computed using Frealix from the full dataset (A, 450 fibrils), the 188 most curved (B), and the 188 straightest filaments with mean crossover distance between 130 and 150 nm (D). The 188 most curved filaments were also processed using Frealign, starting from the alignment parameters determined by Frealix. The reconstruction after 15 rounds of refinement is shown in C. Scale bar: 30 Å. The reconstructions were generated assuming 2-fold axial symmetry. A negative B factor (−600 Ų) was applied, as well as a low-pass filter with cosine edge reaching 0.0 at 7.5 Å (A and D) or 8.0 Å (B and C). (E) Distribution of mean crossover-to-crossover distance (measured along the arc length of the helical axis). (F) Distribution of filament arc lengths. (G) Distribution of the total change of direction of filaments, defined as the integral of the curvature along the length of a filament. Red portion of bars (E–G) Correspond to the 16 filaments whose reconstructions are shown in Fig. 6. (H) FSC curves for Aβ(40) reconstructions. Following refinement, filaments were split into two groups and the FSC between the groups was computed. The FSC for the full set of 450 fibrils (blue) is greater than 0.5 and 0.143 until 8.5 and 7.5 Å respectively. The 188 straight filaments (yellow) gave an FSC greater than 0.5 and 0.143 until 9.0 and 7.1 Å, respectively, as compared to 8.9 and 7.2 Å (Sachse et al., 2008; grey). The 188 most curved filaments gave a very similar reconstruction & FSC curve, greater than 0.5 and 0.143 until 9.0 and 8.3 Å (red). (I) Digitized film micrograph of a somewhat “crowded” sample area. The edges of the carbon hole are visible (top & bottom right corners), as are the film label (top) and the fringes at the edge of the electron beam (corners). The image was band-pass filtered to attenuate low-frequency digitization artifacts and high-frequency noise. (J) Traces of the filaments analyzed from the same micrograph illustrate that Frealix reliably “tracks” filaments even in crowded environments. Dots indicate waypoints, which correspond approximately to crossovers.

To generate a starting model, a single fibril was reconstructed by assigning φ angles of multiples of 180° to crossover points (see Section 2.5). This reconstruction was then refined and used as a starting model for the analysis of the full dataset.

Throughout processing the rise per subunit was assumed to be constant (4.8 Å), 2-fold axial symmetry was assumed and the Z coordinates were not free parameters (they were functions of the θ_i values with each filament’s mean Z value constrained to the CTFTILT plane; see Section 2.4.2). To reduce the influence of image noise on the refinement, only data up to 1/20 Å⁻¹ were used during early rounds. This limit was gradually increased to 1/9 Å⁻¹, while ensuring throughout that only frequencies with high estimated SNR (FSC > 0.9) were used for refinement.

Successive rounds alternated simultaneous and sequential refinement of waypoints, as well as real-space and normal-mode search space parametrization. The average waypoint-to-waypoint distance was 132.7 nm (σ = 13.5 nm) and the average segment size was 4.3 nm (σ = 0.2 nm). The final reconstruction obtained from the full dataset (450 filaments) had a resolution of 7.5 Å (Fig. 5H). Its central section normal to the helical axis is shown in Fig. 5A. This reconstruction and its estimated resolution are very similar to those obtained previously (Sachse et al., 2008).

Using the same refined alignment parameters, we computed reconstructions from subsets of the data which included the same number of fibrils as were used in that study (e.g. Fig. 5B, computed from the 188 most bent fibrils). Those reconstructions had estimated resolutions of 8.0–8.3 Å, marginally lower than previously reported (Sachse et al., 2008), but suggesting that Frealix is able to align curved filaments almost as well as straight ones. This is not the case for single-particle refinement: when processed using Frealign (Alushin et al., 2010) for 15 rounds starting from the alignment parameters obtained by Frealix, the 188 most bent fibrils gave a reconstruction where most features of the peptide backbone were smeared (Fig. 5C), consistent with significant misalignments, especially in between crossovers. We also found that the Frealix algorithm was generally resistant to overlap between filaments, with no significant misalignments in “crowded” regions of micrographs (Fig. 5I and J).

After selecting fibrils with mean crossover distances between 130 and 150 nm, as was done by Sachse et al. (2008), we obtained a 7.1-Å reconstruction (Fig. 5D), matching the resolution obtained by these authors (Fig. 5H). This suggests that mean crossover distance is a correlate of Aβ peptide conformation. As in previous work, we did not reach resolutions sufficient to distinguish the β strand repeats of the cross-β structure, despite the increase in the number of fibrils analyzed. In addition to the difficulties caused by the lack of image features (power in the Fourier transform) between ~1/50 and 1/4.8 Å⁻¹ along the helical axis of amyloid fibrils and their heterogeneity (see Discussion), this may be because experimental factors during microscopy such as beam-induced specimen movement (Brilot et al., 2012) and suboptimal contrast transfer at 1/4.8 Å⁻¹ (because of variable defocus) rendered some images inadequate for registration at this spatial frequency.

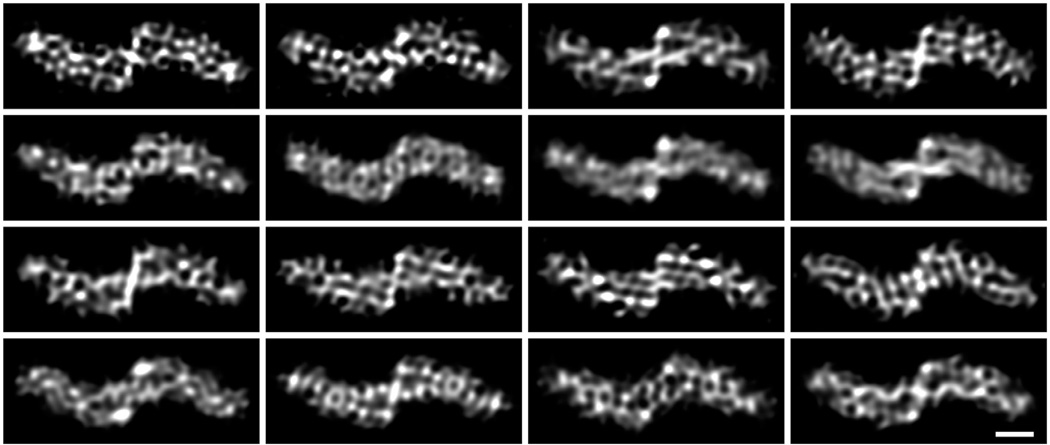
Inspection of 3D reconstructions from each individual filament would seem to support this notion. Reconstructions from filaments of similar lengths should have similar SNR (all other things being equal), yet we observed large variations in the quality of their reconstructions, indicative of significant variations in the quality of imaging and/or alignment of individual filaments, even in spatial frequencies around 1 nm⁻¹. For example, only in about 3% of reconstructions from individual Aβ(40) fibrils, all of which were longer than 0.8 µm (Fig. 5F, red bars), some internal density features were partially resolved (Fig. 6), suggesting that those fibrils had been reconstructed to higher resolution than is usual for single filament reconstructions (compare Fig. 6 to fibril 11 in Fig. 6 of Meinhardt et al., 2009). The SNR at ~1 nm⁻¹ in those reconstructions is still too low to permit reliable interpretation, but the separation between the two peptides within each protofilament (see description in Sachse et al., 2008) appears to be partially resolved in a few of the 16 filaments, particularly in the core region of the fibril, near the helical axis.

Fig.6.

3D reconstructions from individual Aβ(40) fibrils. After visual inspection, 16 of the 450 single-filament 3D reconstructions were selected because they showed features within the molecular envelope. A figure-of-merit filter was applied to each reconstruction, based on the FSC between the two halves of each filament, as well as a sharpening B factor (−100 Ų) filter. In addition, a cosine-edge low-pass filter was applied to remove remaining high-frequency data (beyond 1/8 Å⁻¹). Scale bar: 30 Å.

At 1/4.8 Å⁻¹, although in aggregate the set of fibrils has a clear diffraction line (Fig. 1C in Sachse et al., 2008), indicative of high order and sufficiently good imaging, individual fibrils vary greatly in the strength of this reflection (data not shown) and the quality of their reconstructions (Fig. 6). It is likely that disorder or conformational heterogeneity in parts of the peptide are limiting our resolution – multi-reference refinement could be applied to sort out this heterogeneity but it is not implemented in the current version of Frealix.

4.2. TMV

Starting from the approximate coordinates of 135 TMV filaments on seven micrographs, which had been picked manually by Sachse et al. (2007), and a map decimated in Fourier space to give a pixel size of 4.65 Å, we bootstrapped the analysis of TMV filaments by assuming constant helical parameters for all filaments, as described in Section 2.5.

Initial efforts to refine this structure using “full-filament” mode, where all parameters are constrained to continuous functions, yielded reconstructions of approximately 5.8 Å resolution. We hypothesized that this may have been due to the shallow helix of TMV filaments, which means that slight errors in translation (on the order of 1.4 Å) along the helical axis or in h (helical repeat number, see Section 2.2) could yield strong local maxima of the scoring function, which the minimizer was unable to escape from. In other words, very small deviations from canonical helical parameters, which are to be expected even from very rigid filaments such as TMV, may be challenging to track accurately because of the highly periodic and polymodal nature of the scoring function along those parameters.

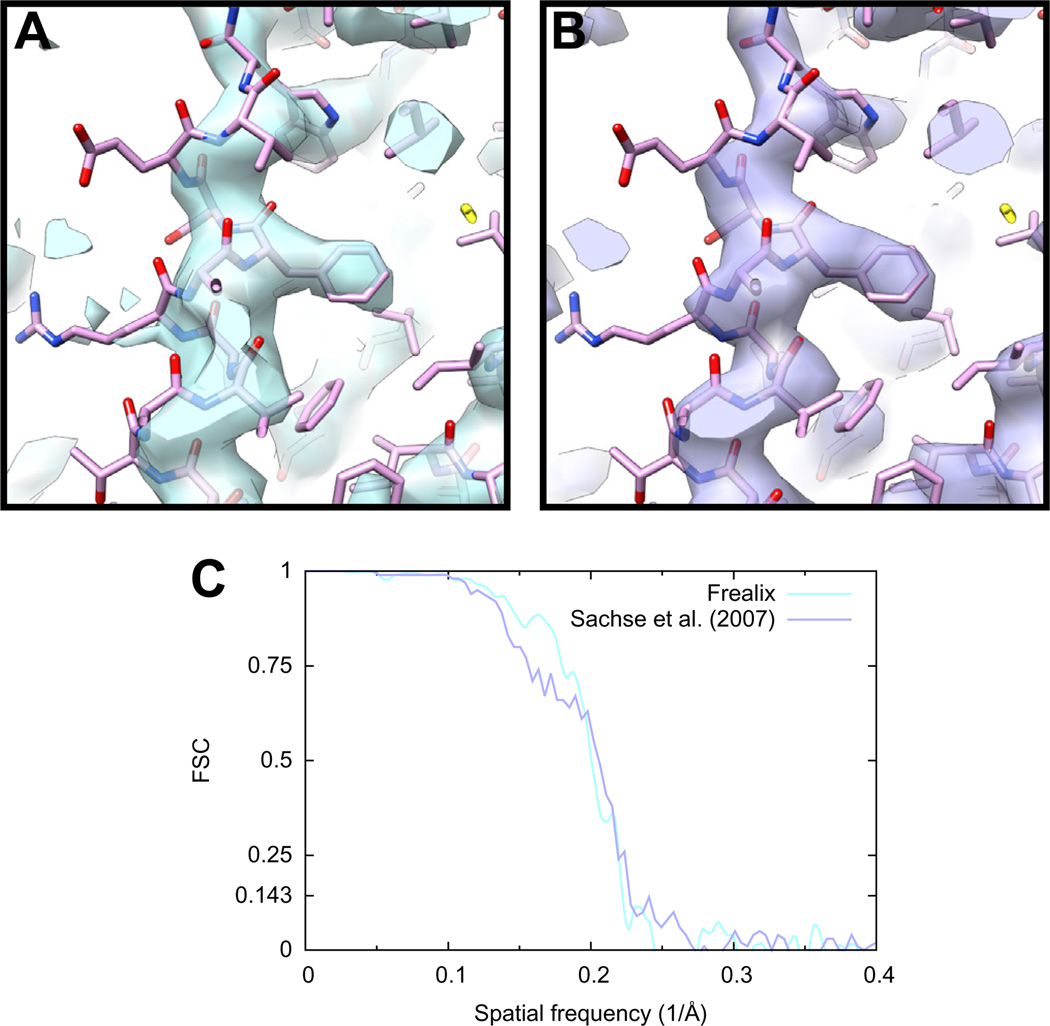
To test this, we continued refinement with an assumption of constant helical parameters and without continuity restraints on the φ and h parameters (see Section 2.4.2.1). Data up to 5.5 Å were eventually included in the refinement. We estimated the resolution of the final reconstruction to be 4.5 Å and the map was of comparable quality to that obtained by Sachse et al. (Fig. 7). The final segment size used in the scoring function was 2.4 nm on average (σ = 0.1 nm) and the waypoint-to-waypoint distance was fixed at 10 nm.

Fig.7.

TMV reconstruction using Frealix (A) compared with the reconstruction obtained by Sachse et al. from the same filaments using single-particle methods (B). The FSC curve (C) computed for the Frealix reconstruction is above 0.5 and 0.143 until 5.0 and 4.5 Å, respectively, compared to 4.7 and 4.3 Å (Sachse et al., 2007). Both reconstructions were filtered using a B factor of −280 Ų up to 1/10 Å⁻¹, amplitude matching at frequencies greater than 1/10 Å⁻¹ against a density derived from atomic coordinates fitted into the map, and a figure-of-merit filter.

4.3. Bending fluctuations

Bending fluctuations can be used to estimate the flexural rigidity of biological filaments by assuming a worm-like-chain (WLC) model is applicable (see Boal, 2002 for an overview). Since Frealix generates and refines geometrical descriptions of each filament as a “byproduct” of the structure-refinement process, we attempted to estimate the bending rigidities of TMV and Aβ(40) filaments from our data.

The smaller dimension of our micrographs was ~1.2 µm (Fig. 5I). This means that filaments whose measured arc length is >1.2 µm must be significantly curved and conversely that we could not have observed straight filaments with those arc lengths. We therefore excluded filaments with arc lengths longer than 1.0 µm from the analysis below to avoid biasing the analysis towards more bent filaments.

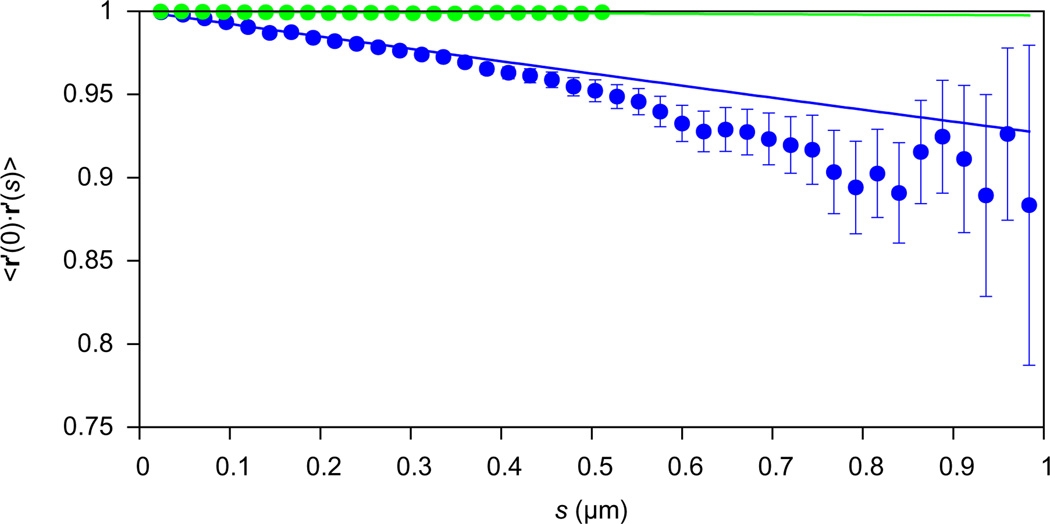
The bending persistence length l_c (Kratky and Porod, 1949) is defined in three dimensions by 〈r′ (0) . r′ (s) 〉 = e^{− s / l_c}, where the left hand side is the mean dot product between tangent vectors separated by arc length s. We calculated this quantity for 24 nm ≤ s ≤ 1 µm and the resulting fit with an exponential yielded estimates of l_c = 13.1 ± 0.7 µm and l_c = 405.2 ± 17.5 µm for Aβ(40) and TMV filaments, respectively (Fig. 8; ± denotes the asymptotic standard error of the fit). Another estimate of the persistence length can be obtained by measuring the chord length L and mid-point normal distance δu in 2D projection (Turner et al., 2006): $l_c=1/{(\frac{\delta u4\sqrt{3}}{L^{\frac{3}{2}}})}^2$. Using this method, we obtained estimates of l_c = 26 ± 2 µm and 202 ± 39 µm for Aβ(40) and TMV, respectively (± denotes standard error of the mean). These estimates are similar to previous estimates from the same micrographs (290 µm for TMV, see Sachse, 2007; 30–100 µm for Aβ(40), see Sachse et al., 2010) but TMV filaments are so rigid that on the length scales observable here, l_c estimates using either method may not be reliable. Indeed, they differ significantly from estimates reported in the literature (1.4 mm in Falvo et al., 1997; 7 mm in Schmatulla et al., 2007; 1.3 mm Zhao et al., 2008).

Fig.8.

Mean tangent dot products for Aβ(40) fibrils (blue) and TMV filaments (green). Tangent vectors were calculated at every 24 nm along all filaments shorter than 1 µm. Dot products were then computed between pairs of vectors separated by arc length s (X axis) and the mean dot product is plotted. Y error bars denote standard errors of the means. The data were fit with exp(−s/l_c) by minimizing the weighted sum of squared residuals using the Marquadt–Levenberg algorithm as implemented in Gnuplot (Williams and Kelley, 2012). The fits yielded l_c estimates of 13.1 ± 0.7 µm (Aβ) and 405.2 ± 17.9 µm (TMV; ± denotes asymptotic standard error in fit).

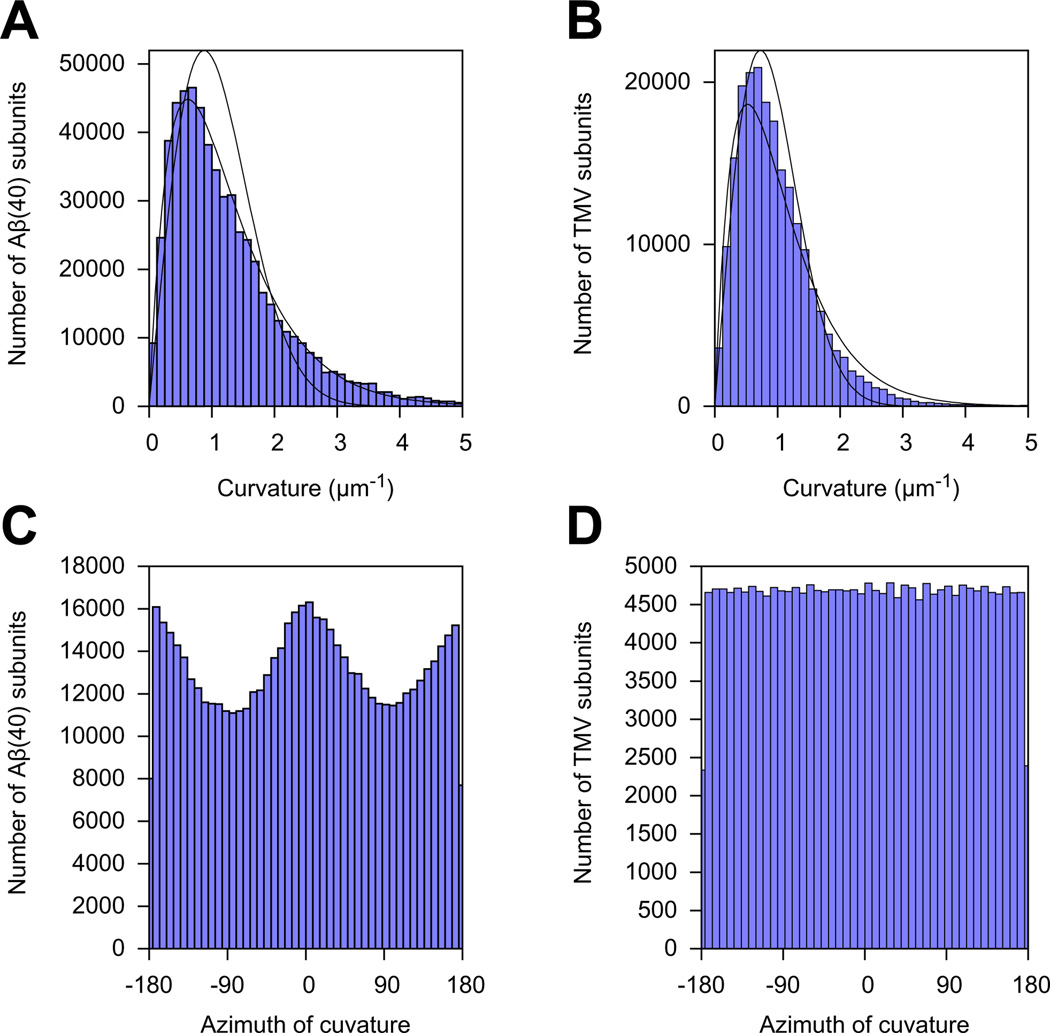
To test whether the WLC model offers a valid description of our data in the first place, we computed the distribution of curvatures of short segments of the filaments. Contrary to our expectation (see Section 2.6.3), the distributions of curvatures were not normal (Fig. 9A and B). In the case of TMV filaments, the probability P(C)dC of observing a curvature in the interval between C(t) and C(t) + dC followed approximately the theoretical prediction of Rappaport et al. (2008) for worm-like chains in three dimensions: $P(C)dC=l_c{\mathrm{\Delta }}_t{e}^{-\frac{1}{2}{l}_c{\mathrm{\Delta }}_t{C}^2}$ CdC.

Fig.9.

Statistics of local curvature measurements along TMV and Aβ(40) filaments. The local curvature was measured at the estimated position of every helical subunit along every filament. There were a total of 600,884 subunits for the Aβ40 dataset, and 211,017 subunits for the TMV dataset. (A and B) Histograms of the local curvature amplitudes. Full lines: fits of probability function proposed by Rappaport et al. (2008); dashed lines: fits of empirical function, see main text. (C and D) Histograms of the local curvature azimuths, as related to the filament structure (see Section 2.6.3 for the definition of ϱ).

In the case of Aβ(40), the curvature distribution did not seem to match that prediction. Heuristically, we found the following function described the observed distribution more accurately: $P(C)dC=4l_c{\mathrm{\Delta }}_t{e}^{-2\sqrt{l_c{\mathrm{\Delta }}_{t}C}}$ CdC. This empirical function also approximated the TMV curvature distribution quite well (Fig. 9B). This suggests that the curvatures of Aβ(40) fibrils observed in our experiments are not solely due to thermal bending of thin rods with isotropic material properties in three dimensions as commonly assumed in the WLC description. Indeed, as expected from their cross-sections, we found that TMV but not Aβ(40) had isotropic bending probabilities by recording the distribution of the azimuth of the curvature vector ϱ in the frame of the 3D reconstruction (Fig. 9C and D).

5. Discussion

All biological filaments are subject to deformations, and these can be direct impediments to analysis when the micrograph SNR is too low and sufficiently short segments cannot be aligned reliably independently from each other. Frealix uses a full-filament model to allow for the use of much shorter image segments than would be feasible otherwise, which in turn makes flexible filaments more amenable to analysis.

In the current work, we used segment lengths of ~4.3 and 2.4 nm for Aβ(40) and TMV, respectively, much shorter than in previous work (84.2 and 70 nm, respectively; Sachse et al., 2008, 2007). We demonstrate that our implementation of connectivity constraints makes it possible to use such short segments and match results from a single-particle algorithm. In the case of amyloid fibrils, we are able to align filaments accurately regardless of curvature or crossover distance (Fig. 5). We expect there will be cases involving more challenging filaments in which our use of shorter segments will be even more advantageous, and that our ability to reliably align severely deformed filaments will make it easier to generate large datasets for future analysis.

In its current incarnation, Frealix does not address all the technical challenges which stand between us and atomic-resolution reconstruction of Aβ fibrils. Even with improved imaging and, for example, beam-induced movement correction (Brilot et al., 2012), heterogeneity and disorder may need to be overcome by future versions of the software before β-strands can be resolved. Indeed, it is likely that only a core region of amyloid fibrils is ordered following the cross-β fold, with the rest of the peptide acting as noise for the purpose of alignments, and/or that there are a range of conformations the peptide can assume, each giving rise to slightly different helical parameters. This last complication may be adequately addressed by collecting larger datasets and implementing multi-reference refinement in Frealix, whereas the first issue (of partial disorder) can probably only be alleviated by improved imaging and higher micrograph SNR.

Processing TMV filaments also suggests how Frealix may be improved in future versions. When segments do not have the “freedom” to align to the reference independently of each other, one loses the ability to discard segments if their alignment parameters do not conform with those of other segments from the same filament. Sachse et al. (2007) rejected ~2 to 12% (at various iterations of the refinement) of segments because they aligned with the “wrong” polarity or with an abnormally large shift normal to the axis. One might speculate that some of these rejected segments had suffered from local deformations, beam-induced movements, ice contamination or defects in the helical assemblies. In the current implementation of our algorithm, such segments are always included in the 3D reconstruction and may thus impede convergence towards the correct global alignment parameters. This may explain why our TMV reconstruction has a slightly lower estimated spectral SNR in the 1/5 Å⁻¹ region than that of Sachse et al. (Fig. 7C). Such marginal loss in final resolution may be acceptable in cases where the flexibility of filaments calls for short segments, but future versions of Frealix could also perform similar exclusion of segments, perhaps based on localized (as opposed to filament-wide) measures of the score.

Using “full-filament” constraints comes with another penalty, at least in our initial implementation: the optimization problem is posed in a high-dimensionality space. This can make Frealix much more compute-intensive per filament than other approaches. We have begun exploring strategies to alleviate this problem (see Section 2.4), and future versions of Frealix will likely improve on the current implementation in terms of computing efficiency.

Useful lessons might be learned from other fields of study. For example, our approach of combining image correlations and prior knowledge about filament connectivity and deformation statistics (Section 2.6.3) resembles that of open active contours (Smith et al., 2010). In our case, the relative weighting of image correlation and mechanical restraint is inversely proportional to the SNR in the image (Chen et al., 2009; Sigworth, 1998). A similar functional form is also used in the field of data smoothing using spline functions. In that context, the relative weighting of fidelity to observed data versus smoothness of the fitted function is a parameter which can be optimized using generalized cross validation (Craven and Wahba, 1978). It would be interesting to see whether similar regularization approaches could be used to determine, for example, the optimal number of waypoints to model filaments accurately. Currently, the number of waypoints is chosen by the user; too few waypoints may lead to inaccuracies and too many, to overfitting.

It remains to be seen whether our particular choice of model, essentially a WLC approximation (for a review see Poelert and Zadpoor, 2012) for the helical axis, is optimal. In terms of cryo-EM image processing, we demonstrate that this is sufficiently accurate to derive sub-nanometer resolution structures. However, the distribution of curvatures (Fig. 9A) and mean tangent correlations (Fig. 8) of Aβ(40) fibrils both appear to differ from predictions from the WLC model, suggesting that it should be modified before it is used to derive accurate mechanical properties of Aβ fibrils in the semi-flexible regime. The first such modification might concern the anisotropic nature of fibrils, but other experimental factors such as the presence of air–water interfaces or local crowding (Fig. 5I and J) may also be taken into account. Frealix could provide a suitable framework for testing experimentally such future versions of the WLC model, for example by providing quantitative measurements of curvature anisotropy (Fig. 9C and D). It is possible that a WLC model that takes into account bending anisotropy would “track” Aβ fibrils more accurately between waypoints.

These considerations raise the question of whether the restraints on our scoring function are valid as currently implemented (second term in Eq. (5)). Quantitatively, we are confident they are not, since they assume Gaussian distribution of local curvatures. However, we posit that they fulfill the role of restraints adequately in a qualitative sense, since they do penalize large deviations from straightness during refinement.

Non-Gaussian distributions of local curvatures have been reported for microtubules in vivo (Bicek et al., 2009; Yang et al., 2011) and taken as evidence of non-thermal bending fluctuations. However, Rappaport et al. (2008) predict that as long as worm-like chains are free to bend in three dimensions (i.e. they are not adsorbed on a surface), the zero-curvature case should not be the most common, and that non-Gaussian curvature distributions should be expected. Our data for both TMV and Ab(40) filaments in vitro support this notion (see Section 4.3) and in the case of TMV these authors’ predicted distribution matches our observations well. As far as we are aware, we are the first to report on the in vitro distribution of 3D curvatures of filaments. We could only find one previous publication where in vitro curvature distributions were reported, a cryo-EM study of microtubules in various nucleotide-bound states (Vale et al., 1994) where curvatures were measured in 2D and followed approximately normal distributions, as expected (Rappaport et al., 2008).

Abbreviations

WLC

worm-like chain

Aβ

amyloid beta