The most informative spacing test effectively discovers biologically relevant outliers or multiple modes in expression

Abstract

Summary: Several outlier and subgroup identification statistics (OASIS) have been proposed to discover transcriptomic features with outliers or multiple modes in expression that are indicative of distinct biological processes or subgroups. Here, we borrow ideas from the OASIS methods in the bioinformatics and statistics literature to develop the ‘most informative spacing test’ (MIST) for unsupervised detection of such transcriptomic features. In an example application involving 14 cases of pediatric acute megakaryoblastic leukemia, MIST more robustly identified features that perfectly discriminate subjects according to gender or the presence of a prognostically relevant fusion-gene than did seven other OASIS methods in the analysis of RNA-seq exon expression, RNA-seq exon junction expression and micorarray exon expression data. MIST was also effective at identifying features related to gender or molecular subtype in an example application involving 157 adult cases of acute myeloid leukemia.

Availability: MIST will be freely available in the OASIS R package at http://www.stjuderesearch.org/site/depts/biostats

Contact: stanley.pounds@stjude.org

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Microarrays and next-generation sequencing technology can comprehensively profile the transcriptomes and/or genomes of multiple tissue samples in timely and affordable manner. These technologies allow researchers to identify genomic or transcriptomic features that correlate with biologically or clinically important traits. In this way, these technologies have greatly accelerated the discovery of biologically and clinically important genes.

It is also possible to discover new biological processes by identifying transcriptomic features that have outliers or multiple modes in their expression distributions. Outliers or multiple modes in the data may indicate the presence of distinct biological processes that define clinically meaningful subgroups. Thus, several methods that compute outlier and subgroup identification statistics (OASIS) have been proposed and used for this purpose.

The statistics and bioinformatics literature proposes several OASIS methods. For example, Nord et al. (2011) use a leave-one-out (LOO) procedure to detect rare copy-number variants. Given a set of data values for one variable, LOO procedures leave out one data value, compute the mean and standard deviation of the remaining data values and then compare the left-out data value to those summary statistics. Rousseeuw (1984) notes that LOO is an effective method not only for detection of single outliers, but also shows that LOO is not an effective method for detection of multiple outliers. Thus, Rousseeuw (1984) proposes least median squares (LMS) as a robust method to detect multiple outliers. LMS first identifies the narrowest interval that includes at least 50% of the data values and then uses the center and width of this interval that captures the ‘bulk’ of the data to determine whether other data values are outliers. Rousseeuw (1984) shows that LMS effectively identifies outliers even when up to 50% of the observations are outliers. Unfortunately, LMS is not widely used as an OASIS method in the genomics and bioinformatics literature. Thus, given the success of LMS in other settings, there is a strong motivation to develop LMS as an OASIS method for analysis of transcriptomic expression data.

The dip test (DT) developed by Hartigan and Hartigan (1985) is another potentially robust OASIS method that is not widely used in the bioinformatics and genomics literature. The DT evaluates the null hypothesis that a set of data values is unimodal. The dip statistic is the largest difference between the empirical distribution function (EDF) and the unimodal distribution function (UDF) that minimizes the maximum difference from the EDF. Thus, a significant dip statistic indicates compelling evidence that a particular set of data values has multiple modes. Furthermore, Hartigan and Hartigan (1985) mathematically proved that the DT has several desirable statistical properties. Therefore, there is a compelling reason to consider using the DT as an OASIS method for the analysis of transcriptomic expression data.

Tong et al. (2013) used model based clustering (Banfield and Raftery, 1993; Fraley and Raftery, 2002) to develop the systematic identification of bimodally expressed regions (SIBER) method that identifies bimodally expressed features in RNA-seq data. SIBER finds maximum likelihood estimates (MLEs) for a two-component mixture model and then computes a bi-modality index (BI) from those MLEs. The BI increases with the difference between the two MLEs for subgroup center, increases with the product of the MLEs for subgroup size and decreases with the sum of the two MLEs for variance. Tong et al. (2013) showed that SIBER identified bimodally expressed features equally or more effectively than several other methods proposed in the bioinformatics literature (Teschendorff, 2006; Tomlins, 2005).

Intuitively, the differences between consecutive ordered data values are very informative regarding the existence of outliers or multiple modes. Pyke (1965) called these differences ‘spacings’ and derived their theoretical properties under many statistical models. Pounds (2001) successfully used Pyke’s work to accurately estimate the fraction of clonable DNA. Therefore, we use Pyke’s theory to develop two novel OASIS methods for analysis of transcriptomic expression data.

2 METHODS

Suppose that we have measured the expression of 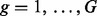features (RNA-seq read count regions or microarray probe-set) for each of 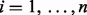subjects. Let y_ig represent the raw expression value of feature g in subject i. Let 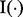be the indicator function that equals one if the enclosed statement is true and zero if the enclosed statement is false.

2.1 Positive quantile transformation

We use the positive quantile transformation (PQT) to normalize expression values. For each subject i, the PQT of each expression feature j is defined as

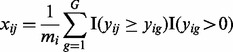(1)

where 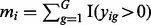is the number of features with a positive raw expression value for subject i. Note that the PQT value x_ij is the empirical quantile of the raw expression value y_ij against all positive raw expression values observed for subject i. Thus, 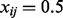implies that the raw expression value y_ij is greater than or equal to half of the strictly positive raw expression values observed for subject i. If all x > 0, then the PQT is simply a quantile transformation. By definition, 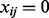for each 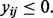Also, the maximum positive raw expression value y_ij for subject i is assigned 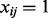for its PQT value. Thus, for each i and j, the PQT value x_ij has the simple biological interpretation as the raw expression of feature j relative to that of the features with positive raw expression in subject i.

In the next six sections, we describe OASIS methods that are applied to the normalized expression values x_ij of each feature j separately. Thus, for simplicity of notation, we omit the subscript j and index the normalized expression values only by the subject i.

2.2 LOO

LOO procedures are widely used in the genomics literature to identify outliers. For each subject i, these procedures compute the mean and standard deviation s_i of the remaining observations (with subject i left out). Then, for each subject i, an outlier t-statistic is computed as

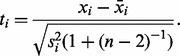(2)

This outlier t-statistic is based on the form of a 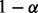prediction interval that covers 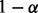of a population of normally distributed observations (Hocking, 2005). For each observation i, an outlier P-value p_i is obtained by comparing the outlier t-statistic t_i to a central t-distribution with n – 2 degrees of freedom. In this way, an outlier t-statistic t_i and P-value p_i are computed for each subject i. Thus, there are a collection of outlier t-statistics and outlier P-values.

There are two ways to summarize the outlier t-statistics and outlier P-values into one metric of the evidence that an outlier exists. First, the minimum outlier P-value (MOP)

(3)

measures the evidence that there is at least one outlier. However, MOP is driven by only one of the outlier tests (the one with the minimum P-value). The sum of squared t-statistics (SST)

(4)

is a summary which is driven by the results of all n outlier tests. Note that the LOO outlier t-statistics are not probabilistically independent because each pair of distinct outlier t-statistics is computed with n – 2 observations in common. Thus, it is not straightforward to derive the joint null distribution of the LOO outlier t-statistics, the null distribution of the LOO–MOP, or the null distribution of the LOO–SST.

Therefore, we use simulation to compute P-values that characterize the significance of the MOP and SST statistics. We compute the SST and MOP for each of a large number B of datasets of independent and identically distributed standard normal observations of sample size n. This yields a set of 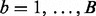MOP statistics 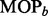and a set of 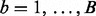SST statistics 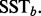The P-value that characterizes the significance of the observed MOP statistic 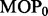is the proportion

(5)

of simulated MOP statistics that are less than or equal to the observed MOP statistic. Similarly, the P-value that characterizes the significance of the observed SST statistic 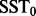is the proportion

(6)

of simulated SST statistics that are greater than or equal to the observed SST statistic.

2.3 LMS

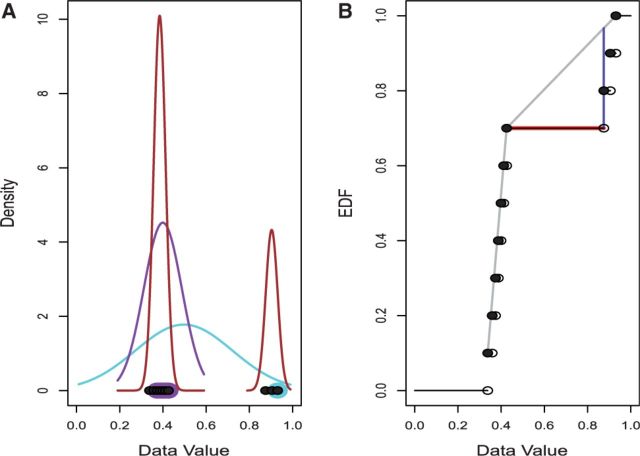
LOO is a robust method to detect a single outlier, however Rousseeuw (1984) shows that LOO is not robust at detection of multiple outliers. When multiple outliers are present, some outliers are still included in the variance estimate computed when each observation i is left out. As shown in Figure 1A, the inclusion of these outliers enlarges the variance estimate 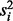and thereby decreases the LOO outlier t-statistic of Equation (2) and increases the corresponding LOO outlier P-value. Thus, the presence of multiple outliers masks their own detection by LOO.

Fig. 1.

OASIS Methods. (A) The LOO, LMS and SIBER methods. The x-coordinates of the points at the bottom show the observed data values. LOO leaves out one point (highlighted in light blue) and then fits a normal distribution to the remaining points (light blue curve). The value of the left-out observation is compared to the normal distribution obtained by leaving it out. LOO repeats this process for every observation. LMS identifies the narrowest interval that covers 50% of the observations (shown by the points highlighted in purple) and determines the normal distribution with central 50% that matches this interval (shown by the purple curve). LMS then compares all points to this normal distribution. SIBER fits two component mixtures of normal distributions (shown in brown) and then calculates distance between in a form of a BI. (B) The maximum spacing test (MAST) and DT methods. The black points show the observed data values (x-coordinate value) and their EDF (y-coordinate value). MAST determines the largest difference between consecutive ordered data values (shown by the red line) and compares its value to the distribution of the largest difference between consecutive ordered independent uniform(0,1) observations (data not shown). DT determines the cumulative distribution function of the best fitting non-parametric unimodal distribution (shown by the gray curve) and then determines the largest difference between the fitted curve and the EDF (shown by the dark blue line)

To address this issue, Rousseeuw (1984) introduces LMS as a robust method for outlier detection. Rousseeuw (1984) argues that the concept of outlier is meaningful only in the context that there exists some ‘bulk’ of densely distributed observations. Rousseeuw (1984) defines the bulk of the data as the narrowest interval that contains at least 50% of the observations and suggests that outliers are observations that are very distant from that bulk.

To identify the bulk of a set of ordered observations 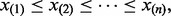first determine the ceiling of half the number of observations 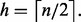Next, compute the width

(7)

of each of the 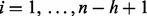intervals that contains exactly h observations. The index that minimizes Equation (7) indicates that the interval 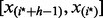defines the bulk of the data.

We then use the identified bulk 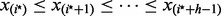to compute an outlier t-statistic and P-value for each observation. Let

(8)

be the center of the bulk of the observations and let

(9)

be a scale estimate based on the bulk, where 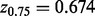and 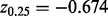are the upper and lower quantiles of the standard normal distribution. The scale estimate 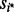is obtained by assuming that the bulk represents the inter-quartile range of a normal distribution. Finally, compute the outlier t-statistic

(10)

for each observation i. The denominator uses the term 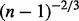because (Andrews, 1972; Shorack and Wellner, 1986) has shown that 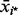converges at the rate 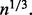An outlier P-value is obtained for each subject by comparing the outlier t-statistic 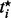to a central t-distribution with n – 2 degrees of freedom. The collection of outlier P-values can be summarized by SST and MOP statistics. However, the null distribution of the LMS–SST and LMS–MOP statistics is not easy to derive because the underlying LMS outlier t-statistics are functions of the same data and thus are not probabilistically independent. Thus, the significance of the SST and MOP statistics are determined by simulation as described in Section 2.2.

2.4 DT to detect multimodality

Hartigan and Hartigan (1985) developed the DT to detect multimodality in a distribution of data values. Multimodality in a data distribution clearly indicates the existence of distinct subgroups. The DT compares the observed EDF of the data to the UDF that minimizes the maximum difference between the EDF and the UDF (Fig. 1B). Hartigan and Hartigan (1985) call this minimax difference the dip statistic. A large value of the dip statistic indicates that the empirical distribution is substantially different from any unimodal distribution.

Hartigan and Hartigan (1985) prove that the uniform distribution is the asymptotically ‘least favorable’ unimodal distribution in the sense that the uniform distribution tends to give the larger values of dip statistic than any other unimodal distribution. Thus, Hartigan and Hartigan (1985) recommend using the uniform distribution as the null in testing the hypothesis that a distribution is unimodal. Hartigan and Hartigan (1985) do not derive the null distribution of the dip statistic but only provide look-up tables to compute P-values by interpolation. Apparently, the null distribution has yet to be derived because the ‘diptest’ package still relies on these look-up tables. Therefore, we compute the dip statistic for the observed data and compute a P-value by comparing its value to the distribution of dip statistics obtained from a large number of simulated uniform(0,1) datasets with the same sample size.

2.5 SIBER

Tong et al. (2013) propose the SIBER method. SIBER uses maximum likelihood to fit a two-component mixture model (Banfield and Raftery, 1993; Fraley and Raftery, 2002) to the data values of each expression features (Fig. 1A). For each expression feature, maximum likelihood yields the estimated centers 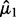and 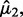scales and 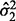and mixing weights 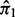and 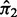for the two components. The parameter estimates are used to compute a BI defined as

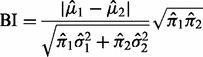(11)

for each expression feature. SIBER can fit one of three different parametric models: a negative binomial mixture, a generalized Poisson mixture and a log-normal mixture. Tong et al. (2013) do not derive a null distribution for the BI. A threshold for the BI to declare significance may be obtained by computing the BI for a large number of datasets simulated from a one-component model of the same parametric family. Also, one may simulate from the uniform distribution to compute a P-value for the BI because Hartigan and Hartigan (1985) have shown that the uniform distribution is the unimodal distribution that is most difficult to resolve from a bimodal distribution.

Thus, we obtain a P-value for the BI by comparing the observed value to a set of BI values obtained from a series of simulated uniform(0,1) datasets with the same sample size. Nevertheless, for the convenience of users who would prefer to compute P-values by simulating normal(0,1) datasets, our package also computes P-values by simulating normal(0,1) datasets.

2.6 Maximum spacing test

Pyke (1965) rigorously derived the theoretical statistical properties of ‘spacings’, the differences between consecutive order statistics. Given a set of n ordered data values 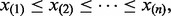the n – 1 spacings are defined as

(12)

for 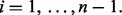Intuitively, a large spacing indicates a wide gap in the empirical distribution of the data values that may be due to multimodality or outliers (Fig. 1B).

Therefore, we use Pyke’s (1965) theory of spacings to develop the maximum spacing test (MAST) hypothesis testing procedure.

(13)

We use the uniform(0,1) distribution as a null model. Pyke (1965) shows that the spacings of a set of independent and identically distributed uniform observations are asymptotically independent and identically distributed beta(1,n) variables. The distribution of 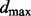is then simply derived from the distribution of the order statistics of a set of beta observations (Casella and Berger, 2001). This final distribution is used to compute a P-value for the 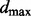statistic.

2.7 Most informative spacing test

We borrow concepts from SIBER (Tong et al., 2013) and MAST (Section 2.6) to develop the most informative spacing test (MIST). First, for each pair 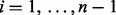of consecutive ordered data values 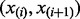, we define the ‘spacing information’

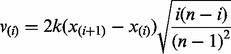(14)

as a statistic that measures both the magnitude of the spacing and its informativeness in terms of partitioning the data into distinct groups. Note that Equation (14) incorporates both the magnitude of the spacing and size of the two groups it defines with which is similar to the term 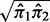in the BI of SIBER shown in Equation (11). Next, we define

(15)

as the most informative spacing statistic. The MIST procedure compares the observed value of 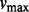to its distribution across a large collection of independent and identically distributed uniform datasets with equal sample size. The constant k is chosen such that the term 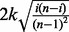attains a maximum of 1 in the case that one-half of the observations equal 0 and one-half of the observations equal 1. A P-value for MIST is computed by simulating from the uniform(0,1) distribution because the incorporation of the term 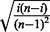in Equation (14) goes beyond the scope of Pyke’s (1965) so that it is not trivial to derive the null distribution for MIST.

2.8 Conceptual comparison of methods

Each method has a distinct set of strengths and limitations. The LOO methods of Section 2.2 tend to assign greatest significance to features with one very extreme outlier. This property allows LOO to effectively identify features with rare but extremely potent modifications in their expression. Thus, LOO will be very effective at identifying features involved in rare events that totally silence genes that are typically highly expressed or induce extreme overexpression in genes that are typically silenced. However, technical artifacts may also cause rare but extreme outliers, so caution must be exercised in attributing a biological explanation to any identified outliers. Furthermore, LOO will not identify features with multiple outliers or multiple modes due to overestimation of variability as described in Section 2.3.

LMS can effectively identify features with single outliers, multiple outliers or two modes. By using the narrowest bulk of observations to estimate center and scale for outlier identification, LMS can effectively assign significance to any feature with one or more outliers. LMS can also identify multimodal features as long as the narrowest bulk of observations is contained within one of the modes. LMS–MOP will assign the greatest significance to features with at least one very extreme outlier, and LMS–SST will assign greatest significance to features with two very narrow modes with a very wide separation. However, LMS may not effectively identify features with three or more modes because the narrowest bulk may span across two or more modes. In such a case, LMS would not assign a large significance because it would include between-group variability in its scale estimate much like LOO does in the multiple outlier case. A copy-number-variable feature with copy-number-driven expression may have three or more modes.

DT identifies features with significant evidence of multimodality. Thus, DT will identify features with two or more modes, but will not identify features with a small number of outliers. DT will also not identify features with a single mode at zero and a long right tail (such as a gene with zero expression in most cases but non-zero expression in other cases).

SIBER assigns the greatest statistical significance to features with a distribution that can be characterized by two very narrow modes (small scale estimates 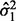and 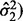of equal size 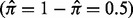that are widely separated (large 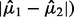as seen in Equation (11). Clearly, any feature with expression values satisfying all three of these conditions would be of great biological interest. However, Equation (11) also indicates that features with small 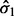and 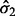will also have a very large BI and thus be considered significant. In applications with discrete expression measurements prone to inflation of zero or other small values (such as RNA-seq), SIBER may fit a mixture model with two point masses 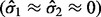to the data and obtain a very large BI even if the difference between centers 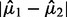is small but non-zero. This pattern of adjacent point masses is likely due to sampling variability and not of biological interest. This technical limitation of SIBER may be overcome by carefully selecting which parametric model is best to fit to the data. However, it is unlikely that any particular parametric model is appropriate for every feature. Methods that automatically incorporate model selection have been developed for differential expression analysis (Pounds and Rai, 2009; Pounds et al., 2012), but unfortunately these techniques have not been incorporated into SIBER.

MAST and MIST are based on spacings and do not use any scale estimator, as do LOO, LMS and SIBER. Instead, MAST relies exclusively on the magnitude of the spacings and MIST considers the magnitude and relative location of the spacings. These features ensure that MIST and MAST are robust against the ‘adjacent point masses’ technicality to which SIBER is sensitive. Unlike LMS, MAST and MIST do not assume that some ‘bulk’ must account for 50% of the data. Also, MAST and MIST are sensitive to detection of features that are technically unimodal but have a long right tail (a feature that is silenced in a subset but shows variable non-zero expression in other cases). However, this strength of MIST and MAST may also be a limitation in some settings. MIST and MAST will not assign a large significance to features with two biologically distinct modes with small variance that do not have a large absolute difference between their centers. The factor 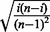in Equation (14) gives MIST greater sensitivity than MAST to detect spacings that divide subjects into two groups of roughly equal sizes; however, this factor also diminishes the sensititivy of MIST to detect spacings that define smaller subgroups relative to that of MAST.

We recommend that P-values for LOO-MOP, LOO-SST, LMS-MOP and LMS-SST be computed by simulating from a single-component normal distribution, and P-values for the DT, SIBER and MAST be computed by simulating from a uniform distribution. The theory for LOO and LMS has been derived for the normal distribution (as indicated by the use of t-statistics). The theory for spacings and the DT was derived for the uniform distribution. To use SIBER as a test of unimodality, we recommend the uniform distribution as the null because Hartigan and Hartigan (1985) have shown that the uniform distribution is the unimodal distribution that is most difficult to resolve from a bimodal distribution. For the convenience of users who may prefer to use other distributions for the null, the software computes a P-value based on simulation from the normal distribution and a P-value based on simulation from the uniform distribution for each test.

3 RESULTS

We evaluate the methods described above by their performance on the RNA-seq and exon microarray data for pediatric acute megakaryoblastic leukemia (AMKL) of Gruber et al. (2012) and on the RNA-seq data for acute myeloid leukemia (AML) in The Cancer Genome Atlas (https://tcga-data.nci.nih.gov).

3.1 Pediatric AMKL data

Gruber et al. (2012) collected RNA-seq and exon array expression data for 14 cases of pediatric AMKL. Using the clipping reveals structure (CREST) algorithm (Wang et al., 2011) that finds reads which span fusion junctions, Gruber et al. (2012) discovered that seven cases harbor a CBFA2T3–GLIS2 fusion transcript which overexpresses GLIS2. Gruber et al. (2012) also observed that CBFA2T3–GLIS2 status is strongly associated with prognosis and the expression of many other genes. Thus, the CBFA2T3–GLIS2 fusion gene defines a distinct molecular tumor subgroup (TSG) of AMKL. They also discovered several other fusion transcripts that were present in only one subject each.

RNA extraction, gene expression profiling and sequencing have been previously published (Gruber et al., 2012). Briefly, RNA was extracted from samples using TRIzol and run on Affymetrix Human Exon 1.0 ST Arrays. Affymetrix Human Exon 1.0 ST Array data for pediatric AML profiling has been deposited in the NCBI gene expression omnibus (http://www.ncbi.nlm.nih.gov/geo/) under GSE35203. Affymetrix signal data were obtained by robust multichip average as implemented in Affymetrix Power Tools. For RNA-seq, libraries were constructed as previously described (Zhang et al., 2012). Flow cells were loaded onto an Illumina GA IIx for a paired-end 101 cycle-sequencing run using SCS version 2.6 software and SBS version 4 reagents. The resulting base call files were converted to fastq format and used in the analysis pipeline. The Burrows–Wheeler alignment algorithm (Li and Durbin, 2009) was used to map reads to the reference human genome assembly GRCh37-lite. Sequencing data is deposited in the dbGaP database (http://www.ncbi.nlm.nih.gov/gap) under the accession number phs000413.v1.p1.

For each sample, we counted the number of reads that were mapped to each RefSeq annotated exon. To quantify the alternatively spliced isoforms, we focused on the reads spanning exon junctions.

We used the PQT of Section 2.1 to normalize the RNA-seq exon expression data, RNA-seq exon-junction expression data, microarray exon expression data and microarray gene-expression data. Each of the four datasets were normalized separately. We then applied each of the eight OASIS methods described above to each of the four datasets.

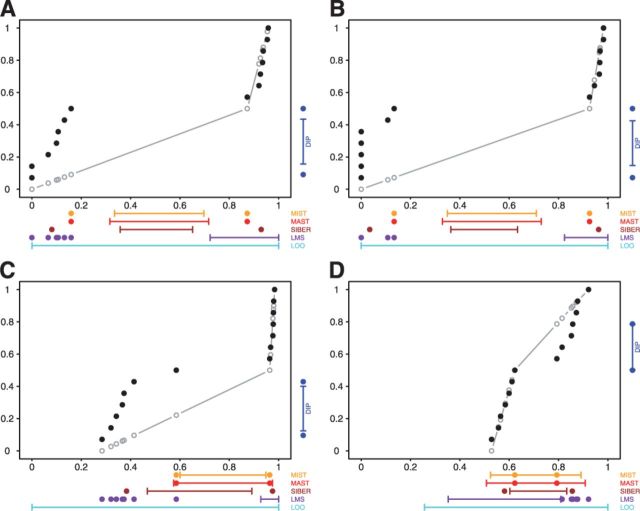
First, we checked each method’s results for analysis of each form of GLIS2 expression data (Fig. 2). LOO did not identify any outliers in GLIS2 expression as significant at the 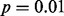level in any of the four datasets. In sharp contrast, LMS found outliers at the 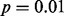level in all four datasets. Furthermore, in three of the four datasets, the outlier calls by LMS perfectly discriminated between CBFA2T3–GLIS2 fusion cases (Fig. 2A, B and C). In all four datasets, the maximum spacing perfectly separated cases with the CBFA2T3–GLIS2 fusion from the other cases. MIST and MAST identified a significant spacing that perfectly separated the fusion-positive and fusion-negative cases in the RNA-seq exon-read data (Fig. 2A and B). The maximum spacing in the microarray exon data was not significant by MAST; however, MIST did find that this spacing was significant because it separated the data into two equally sized groups (Fig. 2C). DT and SIBER obtained a significant result for all four datasets (Fig. 2). Thus, all methods except LOO successfully identified GLIS2 as significant at the 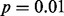level in the analysis of the RNA-seq datasets; DT, SIBER and LMS successfully identified GLIS2 as significant at the 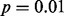level in all four datasets.

Fig. 2.

GLIS2 OASIS results for (A) RNA-seq exon read-count data, (B) RNA-seq junction read-count data, (C) exon array exon expression data and (D) exon array gene expression data. Each panel shows the results of DIP, MIST, MAST, SIBER, LMS and LOO for the indicated form of data. The DIP results are indicated by the vertical bar and two points in the right margin of the plot. The two dots indicate the vertical positions that define the dip statistic, the maximum vertical distance between the EDF (step function defined by black dots) and the best-fitting UDF (shown by the gray curve). The length of the bar corresponds to the value of the dip statistic that has 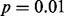so that significance at the 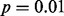level is indicated by the dots falling beyond the endpoints of the bar. The results of MIST, MAST, SIBER, LMS and LOO are shown in the bottom margin. For each of these methods, the length of the bar indicates the distance between the two points that defines significance at the 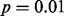level. For MIST and MAST the two points correspond to the data values that define the spacing of interest. For SIBER, the points correspond to the estimated means of the two-component mixture model. The results of LMS and LOO are shown by 99% intervals and points falling outside those intervals were identified as outliers

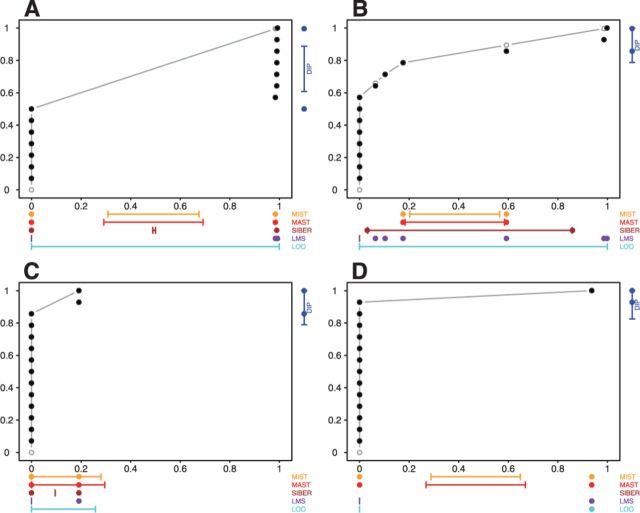
Figure 3 illustrates the data of the RNA-seq exon identified as most significant by each OASIS method. DIP, LMS-SST, MAST and MIST each identified an exon of XIST (hg19, chr23:73045950-73046451) as most significant (Fig. 3A); this exon perfectly discriminates subjects according to gender and was among the 1000 most significant features by SIBER and LMS–MOP. LMS–MOP identified an exon of HOXB9 (hg19, chr17:46698518-46700497) as most significant (Fig. 3B); LMS–SST also placed this exon among its top 1000 results. This finding is biologically relevant because CREST identified a novel NIPBL–HOXB9 fusion in the case with the greatest expression of HOXB9. SIBER identified an exon of ADAD1 (hg19, chr4:123350781-123350970) as most significant (Fig. 3C); this exon was not among the top 1000 hits by any other method. This result illustrates how SIBER is prone to fitting models with adjacent point masses to discrete expression data (Section 2.8). LOO–MOP and –SST identified an exon of OLIG3 (hg19, chr6:137814842-137815278) as the most significant finding (Fig. 3D); LMS–MOP, MAST and MIST also placed this exon among their top 1000 hits.

Fig. 3.

Most significant RNA-seq exon by each OASIS method. (A) The data for the top hit according to DIP, LMS–SST, MAST and MIST; (B) The data for the top hit according to LMS–MOP. (C) The data for the top hit according to SIBER. (D) The data for the top hit according to LOO–MOP and LOO–SST. There is no result for SIBER in (D) since it is impossible to estimate variance of one data point (one data point on the right top corner)

We also evaluated the OASIS methods in terms of their ability to identify genes that perfectly discriminated subjects according to gender, perfectly discriminated subjects according to the presence of the prognostically relevant CBFA2T3–GLIS2 fusion, or were involved in one of the other fusions. We used the Wilcoxon rank-sum test to test all features for differential expression according to CBFA2T3–GLIS2 fusion status and test all features on the X or Y chromosome for differential expression according to gender. We then used the method of Gadbury (2003) to estimate the false discovery rate (FDR; Benjamini and Hochberg, 1995) for those features that perfectly discriminate subjects according to CBFA2T3–GLIS2 fusion status. Of the four expression datasets, the RNA-seq exon expression gave the smallest FDR estimate for both the gender comparison (2.8%) and the CBFA2T3–GLIS2 comparison (1.9%). We then designated each gene with one of these exons We also assigned the ‘other-fusion related’ designation to each gene involved in one of the fusions identified in only one case.

Table 1 shows the number of features of these three designations that were included among the 1000 most significant results by each of the eight methods in the analysis of each of the four datasets. MIST identified the largest number of CBFA2T3–GLIS2 discriminating features in the analysis of the RNA-seq exon, RNA-seq junction and microarray gene expression datasets. MIST also identified the second largest number of CBFA2T3–GLIS2 discriminating microarray exon expression features. Only MIST was among the two best methods at including CBFA2T3–GLIS2 discriminating features in the analysis of all four datasets.

Table 1.

Number of designated features captured among each OASIS method’s 1000 most significant results

	Feature	Data					LMS	LMS	LOO	LOO
Cohort	Category	Type	MIST	MAST	DIP	SIBER	SST	MOP	SST	MOP
14 AMKLs	TSG	SX	386	112	108	6	269	117	27	73
14 AMKLs	TSG	SJ	326	104	165	97	310	116	112	97
14 AMKLs	TSG	AX	340	247	406	271	204	129	146	119
14 AMKLs	TSG	AG	174	125	155	136	107	87	60	61
14 AMKLs	GDR	SX	319	221	229	27	351	2	0	0
14 AMKLs	GDR	SJ	122	73	84	3	151	2	3	1
14 AMKLs	GDR	AX	46	25	59	40	11	4	1	0
14 AMKLs	GDR	AG	4	3	6	5	3	0	0	0
14 AMKLs	TOL	SX	0	8	0	0	4	1	2	2
14 AMKLs	TOL	SJ	0	1	1	3	3	1	2	0
14 AMKLs	TOL	AX	3	7	0	3	1	1	3	2
14 AMKLs	TOL	AG	4	4	0	3	3	0	2	2
157 AMLs	TSG	SX	325	318	294	269	365	350	251	316
157 AMLs	TSG	SJ	354	374	340	326	406	347	341	337
157 AMLs	GDR	SX	46	4	38	40	7	2	0	0
157 AMLs	GDR	SJ	36	0	20	11	13	1	0	3

Note: For each row, the greatest number is shown in boldface. *TSG = tumor subgroup; GDR = gender; TOL = tumor outlier; SX = sequence exons; SJ = sequence junctions; AX = array exons; AG = array genes.

MIST was also among the two best methods at including gender discriminating features among the 1000 most significant findings in the analysis of the RNA-seq exon, RNA-seq junction and microarray exon expression datasets (Table 1). None of the methods identified a large number of gender-discriminating features in the analysis of the microarray gene expression data. Thus, MIST most robustly identified gender discriminating features in this cohort.

LMS–SST, MAST and SIBER identified the largest or second largest number of features involved in one of the singleton fusions in each of the four datasets (Table 1). However, none of the methods identified a very large number of these features because so few features were involved in one of the singleton fusions.

3.2 Adult AML data

As of July 31, 2013, RNA-seq data for 157 adult cases of AML were available from the Cancer Genome Atlas (https://tcga-data.nci.nih.gov). We used a similar approach to evaluate the performance of the methods on this data. We identified 43 gender-related (GDR) features as those located on chromosomes X or Y that were differentially expressed between males and females. We also identified features that were differentially expressed according to the presence or absence of the t(8;21), t(15;17), t(9;11), and inv(16) translocations. We identified features that were underexpressed in cases with 5q deletion or underexpressed in cases with 7q deletion and located in those regions. Similarly, we identified features that were overexpressed in cases with trisomy 8. In this way, we identified 5634 TSG features as benchmarks. All these benchmark features were significant by the rank-sum test at the 1% FDR level by the method of Benjamini and Hochberg (1995).

The last four rows of Table 1 show the results. LMS–SST identified the largest number of TSG features in both the RNA-seq exon and RNA-seq junction data. MIST identified the largest number of gender related features in both the RNA-seq exon and RNA-seq junction data. LMS–MOP, MAST, SIBER and the DT each identified the second largest number of gender or TSG features in one of the four comparisons involving the TCGA cohort.

3.3 Jackknife evaluation

We also used the jackknife method (Quenouille, 1949) to evaluate the stability of our results in terms of which method captured the most features related to TSG or gender for each dataset. The jackknife repeats the entire analysis on a series of datasets obtained by leaving out one or more subjects to determine the variability of the analysis results. We repeated the analysis for all 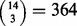possible leave-three-out jackknife datasets for the cohort of 14 cases of pediatric AMKL. We also repeated the analysis for 100 randomly chosen leave-16-out jackknife datasets for the cohort of 157 cases of adult AML. In each jackknife analysis, we identified the method (or methods in case of a tie) that placed the largest number of features of each category (TSG, gender or tumor outlier) among its top 1000 findings.

Table 2 shows the number of jackknife datasets for which each method placed the largest number features among its top 1000 results for each cohort and data type. MIST was one of the top two performers in 10 of the 16 settings; LMS–SST was one of the top two performers in nine of the 16 settings (Table 2). Thus, the jackknife evaluation shows these to be the two most robust methods among those considered here. In 14 of the 16 settings, the top performer in the analysis of the original data was also the top performer in the jackknife evaluation.

Table 2.

Number of Jackknife rounds for which each method captured the largest number of features

	Feature	Data					LMS	LMS	LOO	LOO
Cohort	Category	Type	MIST	MAST	DIP	SIBER	SST	MOP	SST	MOP
14 AMKLs	TSG	SX	330	0	0	0	34	0	0	0
14 AMKLs	TSG	SJ	247	0	0	0	118	0	0	0
14 AMKLs	TSG	AX	125	0	209	33	1	0	0	0
14 AMKLs	TSG	AG	309	0	58	0	0	0	0	0
14 AMKLs	GDR	SX	128	0	63	0	174	0	0	0
14 AMKLs	GDR	SJ	192	0	48	0	131	0	0	0
14 AMKLs	GDR	AX	106	0	253	17	0	0	0	0
14 AMKLs	GDR	AG	111	6	204	166	22	0	0	0
14 AMKLs	TOL	SX	11	142	0	1	166	1	70	0
14 AMKLs	TOL	SJ	0	113	6	232	89	61	116	49
14 AMKLs	TOL	AX	11	301	1	33	0	8	23	38
14 AMKLs	TOL	AG	235	353	0	21	78	55	38	34
157 AMLs	TSG	SX	1	1	0	0	60	32	0	6
157 AMLs	TSG	SJ	0	1	0	0	100	0	0	0
157 AMLs	GDR	SX	92	0	0	0	8	0	0	0
157 AMLs	GDR	SJ	82	0	0	0	18	0	0	0

Note: For each row, the greatest number is shown in boldface. *TSG = tumor subgroup; GDR = gender; TOL = tumor outlier; SX = sequence exons; SJ = sequence junctions; AX = array exons; AG = array genes. Sums of rows may be greater than the total number of jackknife rounds due to ties.

We also performed all 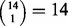possible LOO jackknifes, all 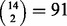possible leave-two-out jackknifes and 100 randomly chosen leave-four-out jackknifes of the cohort of 14 cases of pediatric AMKL. The results of these jackknife evaluations in terms of top performing methods were qualitatively similar to those reported for the leave-three-out jackknife in Table 2. Supplementary Table S1 gives the results for every jackknife evaluation we performed.

4 DISCUSSION

Expression features with multimodal distributions or outliers may indicate modification of biological processes that impact disease pathogenesis or prognosis. OASIS can be useful tools to discover these expression features. Here, we adapted Rousseeuw’s (1984) LMS outlier detection algorithm, the DT of Hartigan and Hartigan (1985) and Pyke’s (1965) theory of spacings into OASIS analysis methods. We also compared the performance of these methods to that of the widely used LOO procedure and the recently proposed SIBER method in two example applications.

In our first example involving a cohort of 14 cases of pediatric AMKL, six of the eight OASIS methods successfully identified GLIS2 as statistically significant at the 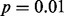level in at least one of the four datasets (Fig. 2). LMS, DIP and SIBER successfully identified GLIS2 as significant at the 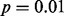level in all four datasets. Furthermore, several of the methods placed hundreds of features that perfectly discriminated subjects according to GLIS2 status or gender among their 1000 most significant findings. Included in the GLIS2 discriminatory features is a novel putative non-coding RNA molecule that was not picked up by standard gene expression analysis (data not shown). This molecule has been validated in the laboratory, and the functional consequences of the transcript are being interrogated. This indicates that these OASIS methods can successfully discover features with expression values that are indicative of important biological processes.

The results from the pediatric AMKL cohort also illustrate the strengths and limitations of the OASIS methods described in Section 2.8. MIST and MAST failed to identify GLIS2 as significant in the analysis of the microarray gene expression data (Fig. 2D) because they do not attempt to compute and use estimates of intra-group variability. By computing and using scale estimates, SIBER, LMS and DT successfully identified GLIS2 as significant at the 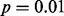level. However, for features with adjacent point masses, SIBER obtained very small-scale estimates and assigned a very high level of significance (Fig. 3C). These features typically have no mapped reads in most subjects and a very small number of mapped reads (5 or 6) in a few subjects. Intuitively, such data are not compelling evidence of potent biological differences. Our dataset included many features with adjacent point masses of low expression that were among SIBER’s 1000 most significant results. LOO assigns the greatest significance to features with one very extreme outlier (Fig. 3D). All of the 1000 most significant features by LOO showed the same pattern as Figure 3D. One extreme outlier may indicate a biologically relevant feature such as a rare fusion gene; however, an isolated event is not as interesting as a highly prevalent and potent aberration from a population perspective. Thus, in practice, the choice of OASIS method should be guided by the objective of the investigation, the properties of the dataset, and the strengths and limitations of the various OASIS methods.

We also evaluated the methods in a cohort of 157 adult cases of AML. In this cohort, MIST most effectively identified gender-related features and LMS–SST most effectively identified TSG features. The term enables MIST to most effectively identify features with large spacings that divide the cohort into subgroups of roughly equal size, such as gender-related features. However, the term is not as beneficial in identifying features that define subgroups that are less equally balanced in terms of their size. Thus, LMS–SST more effectively identified features that define the multiple subgroups (each comprising a relatively small proportion of the entire cohort) of AML. This suggests that future research should explore the use of other functions to incorporate information about subgroup size into spacings-based analysis.

Our results suggest that genomic research may benefit from more rapidly considering and adopting statistical theory and methods that were developed and established before the advent of microarray and next-generation sequencing technologies. Tong et al. (2013) show that the performance of SIBER is comparable to or superior to that of many methods proposed after the advent of modern high-throughput technologies. Interestingly, SIBER is a straightforward extension of model-based clustering which was developed by (Banfield and Raftery, 1993; Fraley and Raftery, 2002). In our example, the performance of other statistical methods was comparable or superior to that of SIBER. Thus, it appears that several of the OASIS methods proposed in recent years have only produced a mirage of innovation. This observation supports the recommendation that research in computational biology should shift some emphasis from development of methods to evaluation of existing methods (Allison et al., 2006). Existing statistical theory and methods are a valuable and a largely underappreciated resource for computational biology and genomics research.

OASIS methods may prove useful for other applications in computational biology and genomics research. Reference alignment profoundly improves the accuracy of genomic copy-number analysis of tumors (Mullighan and Downing, 2009; Mullighan et al., 2007; Pounds et al.,2009). However, reference alignment has not yet been used in the analysis of gene expression data because there is not a method to reliably identify reference genes (Petrone, 2009). Also, OASIS methods may be used to select features for class discovery analysis. Future research should explore the utility of OASIS methods for these purposes.